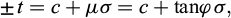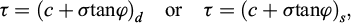| Numéro |
Rev. Fr. Geotech.
Numéro 175, 2023
|
|
|---|---|---|
| Numéro d'article | 9 | |
| Nombre de pages | 9 | |
| DOI | https://doi.org/10.1051/geotech/2023006 | |
| Publié en ligne | 23 octobre 2023 | |
Article de recherche / Research Article
Charles Augustin de Coulomb, the artisan of modern geotechnical engineering
Charles Augustin de Coulomb, l’artisan de la géotechnique d’aujourd’hui
Norwegian Geotechnical Institute (NGI), Oslo, Norway
* Corresponding author: suzanne.lacasse@ngi.no
The paper puts in perspective the influence of Charles-Augustin de Coulomb on the research and practice of modern geotechnical engineering. In his “Essai” (1773), Coulomb presented clear propositions on friction and cohesion on a sliding plane, giving birth to today’s soil mechanics. Coulomb’s theory started with the suggestion that the strength on a slip plane must involve a combination of friction and cohesion. Coulomb used calculus to obtain active earth pressure and show how friction and cohesion together affect lateral earth pressure. Coulomb was a gifted experimental scientist and wrote, when discussing friction, cohesion and interlocking that “only experiment can help us to decide the reality of the different causes” [for resistance]. With his fundamental equation [±t = c + µσ = c + tanϕ σ], Coulomb brought his theory to design. Design guidelines and standards are written in terms of cohesion and friction, and Coulomb’s fundamental slip plane model still dominates today’s soil mechanics. Coulomb’s insight led to further developments by Terzaghi, Hvorslev, Skempton, and the ensuing work at Imperial College and Cambridge University in the UK, at Harvard and at MIT (Lambe, Whitman, and Ladd) in the USA. Coulomb’s work, originally for masonry, has enabled the geotechnical profession to map soil behaviour, and continues to inspire new generations of researchers to look into improved and novel models and interpretations of the shear strength of soil and rock.
Résumé
L’article met en perspective l’influence de Charles-Augustin de Coulomb sur la recherche et la pratique de la géotechnique moderne. Dans son Essai (1773), Coulomb présente des propositions claires sur le frottement et la cohésion sur un plan de glissement, donnant naissance à la mécanique des sols actuelle. La théorie de Coulomb a commencé avec la suggestion que la force sur un plan de glissement doit impliquer une combinaison de frottement et de cohésion. Coulomb a utilisé ses calculs pour obtenir la pression active de la terre et montrer comment le frottement et la cohésion affectent ensemble la pression latérale des terres. Coulomb était également un expérimentateur doué et écrivait, lorsqu’il parlait de friction, de cohésion et d’enchevêtrement, que « seule l’expérience peut nous aider à décider de la réalité des différentes causes » [de la résistance]. Avec son équation fondamentale [±t = c + µσ = c + tanϕ σ], Coulomb a appliqué sa théorie au dimensionnement. Les recommandations et les normes de conception sont écrites en termes de cohésion et de frottement et le modèle de plan de glissement fondamental de Coulomb domine toujours la mécanique des sols d’aujourd’hui. La perspicacité de Coulomb a conduit à d’amples développements par Terzaghi, Hvorslev, et Skempton, et aux travaux qui ont suivi à l’Imperial College et l’Université de Cambridge au Royaume-Uni et à Harvard et au MIT (Lambe, Whitman et Ladd) aux États-Unis. Les travaux de Coulomb, à l’origine pour la maçonnerie, permettent à la profession géotechnique de cartographier le comportement des sols et continuent d’inspirer de nouvelles générations de chercheurs à se pencher sur des interprétations améliorées et nouvelles de la résistance au cisaillement à la fois des sols et des roches.
Key words: cohesion / friction / shear strength / design / testing
Mots clés : cohésion / frottement / résistance au cisaillement / dimensionnement / essais
© CFMS-CFGI-CFMR-CFG, 2023
1 Preamble
Who in 1773 would have believed that Charles Augustin de Coulomb (1736–1806), a physicist who discovered the laws that govern magnetic attraction and repulsion in 1780 and invented the torsion balance, would also be still shaping the geotechnical engineering of the 2020s? Coulomb presented his “Essai on ‘some statical problems’” to the French Academy in 1773. It is a happy coincidence, on this 250th anniversary of the Coulomb’s Essai, that it is also the 100th anniversary of the principle of effective stress proposed by Karl Terzaghi’s in his 1923 “Erdbaumechanik” (Soil Mechanics).
In a remarkable 2022 paper on Coulomb’s Legacy in geotechnical engineering, Salençon described the life that made Coulomb who he was, and discussed the friction and cohesion components in Coulomb’s memoir, the rationale of Coulomb’s stability analyses, and Coulomb’s approach to earth pressures using wedges and triangular surfaces. Salençon concluded with an apotheosis on the legacy of Coulomb’s Essai in soil mechanics and geotechnics: the formulation of an approach to the design of structures (or yield stress design), and the determination of active and passive thrusts, applicable to the stability analysis of slopes, excavations, dams, etc.
In the present issue of RFG, the reader will have already perused 6 articles on Coulomb’s contributions: Coulomb standing at the origin of yield stress design stability analyses in geotechnics considering equilibrium and the resistance of materials (Salençon, 2023); the design of embedded walls relying on Coulomb’s active and passive limit equilibrium analyses (Schmitt, 2023); Coulomb’s work on earth pressure on a retaining wall paving the road for numerous successive developments, including the changes in earth pressure induced by seismic forces (Callisto, 2023); Coulomb’s principles influencing the advent of computational limit analysis for stability and deformation analysis (Krabbenhoft, 2023); Coulomb’s yield design theory applying to the stability analysis of reinforced soil structures, with as a bonus two possible ways of modelling reinforced soil (de Buhan, 2023); and Coulomb’s principles adapted to the limit equilibrium analysis of soil-nailed wall facings (de Sauvage, 2023).
The present paper attempts to put a last perspective on the central role Coulomb’s works are still playing in present day research and practice of geotechnical engineering. The clear propositions by Coulomb of friction and cohesion on a sliding plane, active earth pressure and friction and cohesion together affecting lateral earth pressure, with his fundamental equation:
are universal and Coulomb’s theory quickly found applications in design (where t is shear stress, c is cohesion, σ is normal stress, and ϕ is the friction angle of the grain skeleton).
2 The applicability of the Coulomb material 250 years after the Essai
The simplest expression for the shear strength in terms of the normal effective stress is represented by a straight line of the Coulomb form (Fig. 1), τ = c’ + tanϕ’σ’, where the prime (‘) expresses in terms of effective stresses.
The definition of cohesion in physics is the act or process of sticking together tightly, or the molecular attraction by which the particles of a body are united throughout the mass. Janbu (1973, 1985) used the terminology of attraction (a) instead of cohesion, defined as a = c/tanϕ’, to describe the mutual action by which bodies, particles, etc., tend to cohere (as opposed to repulse).
Fifty years before Cauchy, Coulomb saw the friction and cohesion as the strength components of a material. Equilibrium will fail if the shear force on a slip plane exceeds the sum of these two strength components. Coulomb noted that when friction and cohesion become zero, his equation gives the fluid pressure. Coulomb wrote about water pressures in section X of the Essai and was aware that it played a role. For soils, Coulomb probably did not have adequate apparatus for the measurement of the cohesion since Collin only published the first measurements of undrained shear strength in 1846. However the question of friction and cohesion of soils fascinated Coulomb for the rest of his life (Kerisel, 1973).
In an ideal Coulomb material, failure takes place along two sets of parallel shear planes inclined at an angle ±αf = ± (45° + ½ϕ’) (Janbu, 1973). The planes form rhombic elements (Fig. 2), with two modes of failure actually occurring in a test specimen: a shear stress-induced failure leading to conjugate shear planes with their long axis in the s1-direction; and tensile-strain-induced cracks in the σ1-direction even when the whole stress field is compressive, e.g. in an undrained or constant volume condition.
A shear failure is likely to dominate in plastic (ductile) materials, while the strain-induced cracks may dominate in brittle materials. Both types of failure may be visible simultaneously. In dilatant materials, failure takes longer to develop. A cut slope in a dilatant material may start to crack at the crest (giving early warning) and the soil mass may gradually slump over a limited distance before reaching a new, maybe temporary, equilibrium. Contractant materials can fail abruptly, without warning and often at small strains, for example in sensitive clays.
Under constant volume, for either plane strain or axisymmetric conditions, the strains cause a shortening of the major axis and a simultaneous elongation of the minor axis. So, vertical cracks along the major axis can occur even when all stresses are compressive. The existence of cracks does not therefore contradict the behaviour of a perfect Coulomb material. In a way, it also refutes the suggestion of a “Mohr–Coulomb” error by Schofield (1998, 2005).
The Coulomb cohesion–friction model is a useful model to assist design. With its simple representation (Fig. 3), all three states of concern for a design are available: at rest under K0-conditions, the limit state (at failure), and the actual design conditions with a prescribed or selected factor of safety.
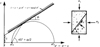 |
Fig. 1 Linear strength of an ideal Coulomb material (u is pore pressure, σ1 major principal stress, σ3 minor principal stress). Définition de la résistance linéaire d’un matériau idéal de Coulomb (u est la pression interstitielle, σ1 la contrainte principale majeure, σ3 la contrainte principale mineure). |
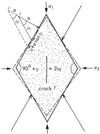 |
Fig. 2 Theoretical failure element in an ideal Coulomb material (Janbu, 1973). Rupture (théorique) d’un élément pour un matériau de Coulomb idéal (Janbu, 1973). |
 |
Fig. 3 Limiting conditions in practice: at rest (in situ), design and limit state. Conditions limites en pratique : au repos (in situ), dimensionnement et rupture. |
3 Terzaghi and the Coulomb equation for the shear strength of soils
Terzaghi (1959) tested the suitability of the Coulomb equation to represent the shear strength of cohesive soils1. While looking at the values of c and tan ϕ, Terzaghi noted that:
“If the shear strength T of a cohesive soil is determined for a given initial water content and under equal test conditions but for different values of the vertical stress per unit area of the horizontal shear plane, the result of the tests in most cases can be expressed with sufficient accuracy by the Coulomb equation.”
The term “test conditions” included the construction of the shear apparatus, the duration of the applied vertical stress, the quality of the soil sample and the time to failure in the shear test. The dominating influence of the test conditions on the values c and tan ϕ in the Coulomb equation was illustrated by the results of tests on remoulded clay from a Vienna deposit2. The specimens with an initial void ratio of 0.77 were tested under different conditions in the direct shear box (admittedly a poor test by today’s standards, and the undrained/constant volume conditions could not be maintained, as demonstrated later by Taylor (1948) of MIT).
Terzaghi’s test conditions were: (1) rapid increase of the stress at different levels and rapid increase of the shearing force (to simulate undrained conditions at the time, so the void ratio remains the same); (2) complete consolidation under different stresses followed by a rapid increase in the shearing force to failure (called then a “quick test”); and (3) complete consolidation under different stresses followed by an extremely slow increase of the shearing force to failure (“slow test”), assuming that the excess pore water pressures at failure were approximately zero. Terzaghi affirms that “the results of the three series of tests could be described with sufficient accuracy” (Terzaghi’s language) by the equations in Table 1.
Investigations of the same Vienna clay by Hvorslev (1937) showed that the friction angle, independent of the void ratio, was 17°30’.
Terzaghi concluded that his test results showed a dependence on the test conditions of the values of c and ϕ in the Coulomb’s equation. Thereby, using Coulomb’s law, Terzaghi introduced slightly the concept of stress-induced and inherent anisotropy for clays already in the 1930s.
Terzaghi observed that the most important difference in the tests was the extent to which the void ratio was allowed to adapt itself to the changes in stress imposed on the sample. As long as this “adaptation” was not fully completed, part of the force on the specimen was carried by the pore water (or increased pressure in the pore water).
The pore water pressure does not appear in the Coulomb’s equation, as the normal stress is in terms of the total applied vertical load divided by the area of the horizontal shear plane. Consequently, the existence of the piezometric pressure is only betrayed by the effect of the test conditions on the values c and ϕ. Terzaghi therefore emphasized that Coulomb’s equation gives the relationship between τ and σ for soil specimens but that one needs to consider initial void ratio, testing apparatus, drainage conditions, test procedures, etc.
Coulomb provided the general relationship for shear resistance. The practitioner and theoretical modeller still have to determine which test conditions are the relevant ones. This is still true today. One of the most common errors committed in design occurs when a designer selects shear strength values obtained from non-relevant tests, procedures, stress history or stress path.
Terzaghi even suggested adding an index to make it very clear that the validity of the Coulomb’s equation depends on the conditions analysed. Terzaghi suggested:
where the index “d” would indicate drained (“slow” conditions), and the index “s” would indicate that the shear force is increased so rapidly that the void ratio of the soil remains unchanged. Terzaghi even suggested that a partial fulfilment of these two lower and upper boundaries could be indicated by the index “ds”. Maybe the profession should have adopted such nomenclature to ensure that the Coulomb’s validity conditions would be remembered.
From then on, Terzaghi and researchers at MIT (Lambe, Whitman, Ladd and Einstein) and Harvard (Casagrande), Imperial College (Skempton and colleagues) and NGI (Bjerrum) pursued their theoretical and experimental works, confirming the validity of Coulomb’s equation under different stress and strain conditions. Each of them stressed the necessity of replicating the in situ conditions in the laboratory. Even in the UK, where Coulomb’s work has been critically discussed (Schofield, 1998, 2005), critical state soil mechanics agrees with this Coulomb’s law.
Terzaghi’s verifying Coulomb’s equation on Vienna Clay (void ratio = 0.77, all specimens).
Vérification de la loi de Coulomb par Terzaghi sur l’argile de Vienne (indice des vides = 0,77).
4 Is there a fundamental error in the Mohr–Coulomb equilibrium (Schofield, 1998, 2005)?
4.1 Schofield’s hypothesis of an error
Schofield (1998, 2005) suggested that Coulomb had made a fundamental error when defining equation (1). The error rests, in Schofield’s interpretation, on the observation that equation (1) omits a component of strength, called “interlocking” (first mentioned by Taylor in 1948). Schofield also mentioned that the Coulomb theory, with a straight envelope (linear equation), takes no account of “strain boundary conditions”, that Coulomb wrongly interpreted strength data, and that Coulomb, when considering failure on an inclined plane, assumed that the slip direction was the same as the direction of the plane.
Schofield used as argumentation that Taylor’s tests showed that the peak strength of sand was equal to a combination of an angle of friction plus a term for “interlocking”. Figure 4 reproduces Taylor’s original figure illustrating the Coulomb and Taylor interpretation (directly reproduced from Taylor’s 1948 book). Very little difference in the two interpretations can be seen.
Schofield added: “… mistaking interlocking for cohesion, [Terzaghi and Hvorslev] attributed peak strengths of their stiff reconstituted clay soil to surface chemistry among soil grains.” That statement is, however, not a Coulomb error.
 |
Fig. 4 Original figure of Coulomb’s strength envelope and Taylor’s strength envelope (Taylor, 1948). Taylor’s caption: “Plot illustrating the rational interpretation of Coulomb’s empirical law.” Comparaison de l’interprétation de Coulomb et Taylor (1948) (copie de la figure originale par Taylor (1948)). |
4.2 Taylor’s interpretation
Taylor (1948) in no way described Coulomb’s theory as an error. On the contrary, Taylor called the Coulomb’s parameters as empirical coefficients, but wrote that he accepted Coulomb’s procedure. Taylor then mentioned the complex factors affecting the shear strength of a soil, and that different conditions should be accounted for by the engineers using the Coulomb equation. Taylor went on in his Chapter 15:
“Curves of the type shown in [Fig. 4], are representative, in their simplest form, of the strength of a given soil when it has been subjected to a given magnitude of precompression. At different depths in a given soil deposit, there usually are different amounts of precompression; thus, a different envelope may hold for each different depth. Sometimes, however, the variation with depth is not large within a given deposit, and the envelope that is valid for an average depth may sometimes be accepted as representative of the entire strata.”
Taylor’s above paragraph validates Coulomb’s strength theory.
Christian and Baecher (2015) and Burland (2008) reiterated that Taylor’s concept of interlocking is not inconsistent with Coulomb’s theory, but complementary, bringing in new results from Taylor’s research. For Coulomb, shear strength was the sum of friction and cohesion, whereas for Taylor, after reflection and new testing of sands, shear strength was the sum of friction and interlocking.
4.3 Conclusion on the so-called Coulomb error
That the vocabulary has changed or expanded over 250 years is expected and normal. That one refines the components and physical understanding of soil and rock resistance is also expected and normal. That one finds, though testing, observations and/or reasoning, additional factors and sub-classes of conditions that affect soil and rock resistance is also expected and normal. However, to suggest that the Mohr–Coulomb’s equation wrongly interpreted strength data or developed a faulty relationship is questionable. To declare a 250-year old theory to be in error because part of a component of the resistance is not fully explained with today’s terms and understanding, given the experimental facilities available in the 18th century compared to today’s, is shortsighted and simply bids for unfair comparisons.
Coulomb’s principle was the precursor for developing the tools to meet the geotechnical profession’s responsibility of ensuring the safety of people and preserving material property and the environment.
Through an understanding and knowledge of the strength components of a material, the geotechnical engineer can become intimate with the foundation soil and continue to rely on experience, peer review, and simple order of magnitude hand-calculation checks. Coulomb, without doubt, laid the groundwork for the understanding of soil and rock resistance.
5 Coulomb, the Artisan of modern geotechnical engineering
The geotechnical profession has greatly evolved as it moves forward into the 21st century, 100 years after the statement of the effective stress principle by Terzaghi (1923). This statement was reported in English in Terzaghi (1925) and recollected by Skempton (1960). The principles of effective stress, 150 years after Coulomb’s equation, changed soil mechanics.
Due to the revolution in computers and information technology in all aspects of geotechnical engineering, the profession is today endeavouring, among others, to develop new machine learning applications, massaging multi-data through the internet and considering digital twinning to generate massive “laboratory” datasets. There are much attraction and promising features in the new techniques.
But, the data will still have to observe Coulomb’s law. The profession stands at a paradigm shift from dedicated verifiable data toward vast numbers of “measurements” in anonymous distributed systems. These new developments will flourish and be helpful, but fundamentals must not be forgotten. A basic understanding of the behaviour of soils, observing the Coulomb’s original equilibrium principles, remains an absolute requirement for the teaching and practice of geotechnical engineering. Fundamentals should not take a back seat to numerical developments and artificial intelligence interpretations.
Coulomb’s principles have found applications over the entire whelm of today’s geotechnical practice. A few examples are briefly summarized below.
5.1 In praise of testing
Coulomb was an experimental scientist and wrote, when discussing friction, cohesion and interlocking that “only experiment can help us to decide the reality of the different causes” [of shear resistance].
Following Coulomb’s philosophy, Karl Terzaghi set up a laboratory to measure soil and interface properties everywhere he worked (first Royal Ottoman College of Engineering in Istanbul [now the Istanbul Technical University], then MIT, and so Harvard in the USA). Many of the remarkable advancements in geotechnical engineering are due to Terzaghi’s, Casagrande’s and Hvorslev’s experimental works in the MIT and Harvard years.
If only clay deposits could talk, like the Atchafalaya clay and New Orleans flood-protection levee sites or the sensitive clays supporting embankments and buildings in Norway, they would tell how important it is to thoroughly understand the geology and the stress history of a soft deposit, and to use a proven methodology like for example, MIT’s Chuck Ladd’s SHANSEP approach (Stress History and Normalized Soil Engineering Properties, Ladd et al., 1977) to understand a deposit, and then apply Coulomb’s equation. Geotechnical engineers need to have a sense of how soil behaves by “touching and feeling a sample,” and understanding which in situ and laboratory tests are specifically needed to determine representative soil properties and to establish the most representative stress history and corresponding shear strength profile. These “in situ” conditions are then used to apply Coulomb’s equation.
5.2 Design of offshore installations
Design of offshore foundations for the development of energy (oil and gas, wind, tidal and the ocean infrastructure serving the offshore industry), generally in harsh environments (including the Arctic), requires knowledge on the behaviour of the soil subjected to static, cyclic and dynamic loads. The yield stress design of Coulomb is also part of the solution for these newer foundations, although many new factors and conditions have been found to affect the Coulomb shear strength parameters. Likewise, the behaviour of sands, silts and clays under cyclic loading (which was not a topic in 1773) is still represented today in stress paths, using Coulomb’s law. The soil behaviour in the working stress ranges (serviceability limit state) is key to the solution for offshore design. The expected behaviour under cyclic loading is determined by tests under changing external static (permanent) and cyclic stresses. The soil resistance depends on the mean normal stress level and the degree of shear mobilization (Fig. 3), or Coulomb’s principles.
5.3 Reliability-based design and effect of uncertainties on computed safety
In reading the conclusion on the design of retaining walls in Coulomb’s Essai (reproduced in Fig. 5), one can already sense that Coulomb was aware that many factors are important and may affect the soil resistance, and that they should be considered to ensure that the design is safe enough (or reliable enough), if one wants, perhaps, to optimize the design.
In the first sentence in the text reproduced in Figure 5, Coulomb’s “These remarks” refer to the effect of pore water pressure, moisture content, potential blocking of drains, and presence of ice and fissures in the retaining wall. In the enclosed excerpt, Coulomb lists additional aspects that are not accounted for, such as quality of material and freeze-thaw effects. Coulomb then makes a value judgment on what would be an acceptable design for a retaining wall, given the aspects that one could not, at the time, account for. Ignorance of such factors (or uncertainties) will lead to an overestimate or underestimate of the in situ shear strength, leading to the necessity of reducing the uncertainties in the evaluation of the shear strength along sliding planes in situ (which was also pointed out by Terzaghi in 1959).
The observations by Coulomb in Figure 5 can be interpreted as an indication of the uncertainties involved in a calculation, and their potential effect on the calculated safety margin of a retaining wall. Coulomb can therefore also be perceived as the precursor of the awareness of the importance of including uncertainties in a safety evaluation, and thereby reliability-based design.
 |
Fig. 5 Excerpt from the Essai concluding on retaining wall design (translation Heyman, 1972). Extrait de l’Essai sur le dimensionnement des murs de soutènement (traduction Heyman, 1972). |
5.4 Guidelines, standards and codes
Design guidelines and standards are written in terms of cohesion and friction and Coulomb’s fundamental slip plane model still dominates today’s recommendations for verifying the safety of foundation works. The parameters needed to check the serviceability limit state (SLS) prescribed in guidelines, standards and codes are based on Coulomb’s equation. Likewise, the verification of the ultimate limit state (ULS) is based on the Coulomb principles. The yield design approach is still the essence of a majority of design codes.
6 Envoi
The value of Coulomb’s works lies not only in the groundbreaking discovery he made in the 18th century, but mainly in the developments to which the discovery led over the next 250 years. Coulomb probably did not foresee the significance of his work for an entire branch of civil engineering and for resource and infrastructure development on a worldwide scale. He would not have been able to fathom that, following his principles and with a correct interpretation of his equation, the civil and geotechnical engineering profession would have installed 400 m high offshore platforms and large wind turbines founded on suction anchors to power entire countries; built extremely daring, elegant bridges and long uderwater tunnels to ensure rapid transportation of people and goods; exploited thousands of high hydropower dams; and simply ensured that a family living on a slope could sleep at peace at night.
Coulomb’s objective with his Essai was to share his knowledge (Fig. 6) and hope that it would come in use in the future to someone likewise interested. Charles Augustin de Coulomb certainly reached his objectives.
This paper shows that the basic ingredients of Coulomb’s equation are still, together with the effective stress principle inspired to Karl Terzaghi by Coulomb’s work, the mainstay of geotechnical practice. Originally for masonry (or a very stiff type of soil), Coulomb’s equation enables the geotechnical profession to map soil behaviour and determine shear resistance. Coulomb’s work continues to inspire new generations of researchers to look into improved and novel interpretations of the shear strength of soil and rock.
Coulomb’s contribution to the design of structures in his presentation to the French Academy of sciences in 1773 deserves the attention and recognition from engineers and scholars it has received. There have been new developments since, but the origin of the understanding was with Coulomb’s equation. That the profession discovers limitations, additional influential factors (e.g., anisotropy, soil sensitivity, cyclic loading) or extensions does not invalidate the theory, rather it validates it and brings forward the potential of the yield design approach initiated by Coulomb in his 1773 Essai.
In closing, Gustave Eiffel named 72 engineers and scientists in the “Brotherhood of the Eiffel Tower” to outline the importance and necessity of teamwork, cooperation and collaboration in engineering. The 300-m high Eiffel Tower built in 1889 to celebrate the ideals of the French Revolution, “Liberté, Égalité et Fraternité”, is a triumph of human ingenuity and engineering collaboration. Gustave Eiffel did not think of the tower as his own. When Eiffel dedicated the Tower, he recognized the many contributors to French science and technology during the period 1789–1889 by inscribing 72 names on four sides of the tower, just below the first level galleries (Nuttle, 2020). A young Breton poet, Olivier de Gourcuff, described the proud tower as in Figure 7.
Who were the scientists chosen by Gustave Eiffel to be member of the “Brotherhood of the Eiffel Tower”? Many of them made ingenious discoveries. Two were agronomists, six astronomers, nine chemists, four industrialists, one geographer, fifteen civil engineers, seventeen mathematicians, two physicians, two mechanical engineers, two mineralogists, one biologist, and eleven physicists (Nuttle, 2020). Charles Augustin de Coulomb’s name is inscribed on the Eiffel Tower, together with the likes of Ampère, Becquerel, Bréguet, Carnot, Cauchy, Coriolis, Foucault, Fourier, Lamé, Laplace, Lavoisier, Navier, Poisson, and Tresca.
Charles Augustin de Coulomb was a physicist by training but he was also an engineer: being an engineer requires specialized knowledge, an insatiable interest in how things work, and a knack for solving problems. Charles Augustin de Coulomb mastered all aspects, and this gave birth to the basics for the science of soil mechanics and geotechnical engineering.
 |
Fig. 6 Coulomb’s objective when presenting his scientific findings to the Academy. Intention de Coulomb en présentant son travail scientifique à l’Académie. |
 |
Fig. 7 The Eiffel Tower by Olivier de Gourcuff (1853–1938). La tour Eiffel par Olivier de Gourcuff (1853–1938). |
References
- Buhan P de. 2023. Application of the yield design theory to the stability analysis of reinforced soil structures. Rev Fr Geotech (this issue). [Google Scholar]
- Burland JB. 2008. Interlocking, and peak and design strengths. Discussion to A.N. Schofield (2006). Geotechnique 58(6): 527–532. [CrossRef] [Google Scholar]
- Callisto L. 2023. From “De la pression des terres, et des revêtements” to the seismic analysis of retaining structure. Rev Fr Geotech (this issue). [Google Scholar]
- Christian JT, Baecher GB. 2015. D.W. Taylor and the foundations of modern soil mechanics. J Geotech Geoenviron Eng 141(2): 02514001. [Google Scholar]
- Collin A. 1846. Recherches expérimentales sur les glissements des terrains argileux, accompagnées de considérations sur quelques principes de la mécanique terrestre. Paris : Carrillan Coeury. [Google Scholar]
- Coulomb C-A. 1773. Essai sur une application des règles de maximis et minimis à quelques problèmes de statique, relatifs à l’architecture. Mémoires de Mathématique et de Physique présentés à l’Académie Royale des Sciences et lus dans ses Assemblées, vol. 7, 1776, pp. 343–382. Repr. Théorie des machines simples, Bachelier, Paris, 1809, 1821. [Google Scholar]
- Heyman J. 1972. Coulomb’s memoir on statics. Cambridge University Press (reprinted by Imperial College Press 1998). [Google Scholar]
- Hvorslev MJ. 1937. Über die Festigkeitseigenschaften gestörter bindiger Böden. Kopenhagen 1937, G.E.C. Gad, Vimmelskaftet 32 (in German). [Google Scholar]
- Janbu N. 1973. Shear strength and stability of soils: The applicability of the Coulombian material 200 years after the Essai. In: Norsk geoteknisk forening. Oslo: Norwegian Geotechnical Institute, 47 p. [Google Scholar]
- Janbu N. 1985. Soil models in offshore engineering. Geotechnique 35(3): 241–281. [CrossRef] [Google Scholar]
- Kerisel J. 1973. Bicentenary of the 1773 paper of Charles Augustin Coulomb. In: Proc. 8th International Conference of Soil Mechanics and Foundation Engineering, Moscow, pp. 1–26. [Google Scholar]
- Krabbenhoft. 2023. Computational limit analysis and extension. Rev Fr Geotech (this issue). [Google Scholar]
- Ladd CC, Foott R, Ishihara K, Schlosser F, Poulos HG. 1977. Stress-deformation and strength characteristics. In: State-of-the-Art Report, Proc. of I9th, X International Conference of Soil Mechanics and Foundation Engineering, Tokyo. [Google Scholar]
- Nuttle W. 2020. The brotherhood of the tower – 72 engineers and scientists named by Gustave Eiffel. In: Eiffel’s Paris – An Engineer’s Guide. https://medium.com/eiffels-paris-an-engineers-guide. [Google Scholar]
- Salençon J. 2022. The Coulomb’s essai legacy in soil mechanics. Rev Fr Geotech 170(1): 1–9. [Google Scholar]
- Salençon J. 2023. Coulomb’s contribution to soil mechanics. Rev Fr Geotech (this issue). [Google Scholar]
- Sauvage J de. 2023. An adaptation of limit equilibrium methods for the design of soil-nailed wall facings. Rev Fr Geotech (this issue). [Google Scholar]
- Schmitt MP. 2023. French practice for design of embedded walls – History and background. Rev Fr Geotech (this issue). [Google Scholar]
- Schofield AN. 1998. The “Mohr–Coulomb” error. In: Proceedings Colloquium “Mécanique et géotechnique”, 19 May, 1998, Paris. [Google Scholar]
- Schofield AN. 2005. Disturbed soil properties and geotehnical design. Thomas Telford, 142 p. [CrossRef] [Google Scholar]
- Schofield AN. 2006. Interlocking, and peak and design strengths. Geotechnique 56(5): 357–358. [CrossRef] [Google Scholar]
- Schofield AN. 2008. Interlocking, and peak and design strengths. Closure to discussion to A.N. Schofield (2006). Geotechnique 58(6): 527–532. [CrossRef] [Google Scholar]
- Skempton AW. 1960. Terzaghi’s discovery of effective stress. In: From theory to practice in soil mechanics. New York: Wiley, pp. 42–53. [Google Scholar]
- Taylor DW. 1948. Fundamentals of soil mechanics. New York: Wiley; London: Chapman and Hall, 711 p. [Google Scholar]
- Terzaghi K. 1923. Die Bezichungen zwishen Elastizität und Innendruck. Akademie der Wissenschaften in Wien. Sitzungsberichte, Mathematisch-naturwissenschaftliche Klasse. Part II, a. 132(3/4) 195–124 (in German). [Google Scholar]
- Terzaghi K. 1925. Principles of soil mechanics: VII – Friction in sand and in clay. Eng New Record 95(26): 1026–1029. [Google Scholar]
- Terzaghi K. 1959. The Coulomb equation for the shear strength of cohesive soils. Translated from die Bautechnik Jahrgang 16 Heft 26 17, June 1938, NGI Report F.151, 3 August 1959, 20 p. [Google Scholar]
Cite this article as: Suzanne Lacasse. Charles Augustin de Coulomb, the artisan of modern geotechnical engineering. Rev. Fr. Geotech. 2023, 175, 9.
All Tables
Terzaghi’s verifying Coulomb’s equation on Vienna Clay (void ratio = 0.77, all specimens).
Vérification de la loi de Coulomb par Terzaghi sur l’argile de Vienne (indice des vides = 0,77).
All Figures
 |
Fig. 1 Linear strength of an ideal Coulomb material (u is pore pressure, σ1 major principal stress, σ3 minor principal stress). Définition de la résistance linéaire d’un matériau idéal de Coulomb (u est la pression interstitielle, σ1 la contrainte principale majeure, σ3 la contrainte principale mineure). |
| In the text | |
 |
Fig. 2 Theoretical failure element in an ideal Coulomb material (Janbu, 1973). Rupture (théorique) d’un élément pour un matériau de Coulomb idéal (Janbu, 1973). |
| In the text | |
 |
Fig. 3 Limiting conditions in practice: at rest (in situ), design and limit state. Conditions limites en pratique : au repos (in situ), dimensionnement et rupture. |
| In the text | |
 |
Fig. 4 Original figure of Coulomb’s strength envelope and Taylor’s strength envelope (Taylor, 1948). Taylor’s caption: “Plot illustrating the rational interpretation of Coulomb’s empirical law.” Comparaison de l’interprétation de Coulomb et Taylor (1948) (copie de la figure originale par Taylor (1948)). |
| In the text | |
 |
Fig. 5 Excerpt from the Essai concluding on retaining wall design (translation Heyman, 1972). Extrait de l’Essai sur le dimensionnement des murs de soutènement (traduction Heyman, 1972). |
| In the text | |
 |
Fig. 6 Coulomb’s objective when presenting his scientific findings to the Academy. Intention de Coulomb en présentant son travail scientifique à l’Académie. |
| In the text | |
 |
Fig. 7 The Eiffel Tower by Olivier de Gourcuff (1853–1938). La tour Eiffel par Olivier de Gourcuff (1853–1938). |
| In the text | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.