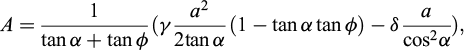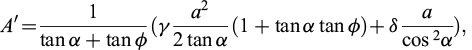EDP Sciences logo
Authentification abonné
Rechercher
Menu
Accueil Accueil (fr) Tous les numéros Numéro 175 (2023) Rev. Fr. Geotech., 175 (2023) 2 Full HTML
Accès gratuit
Numéro
Rev. Fr. Geotech.
Numéro 175, 2023
Numéro d'article 2
Nombre de pages 8
DOI https://doi.org/10.1051/geotech/2023011
Publié en ligne 23 octobre 2023

© CFMS-CFGI-CFMR-CFG, 2023

This contribution to the colloquium organised on the occasion of the 250th anniversary of the presentation of Coulomb’s Essay to the French Academy of Sciences, comes as a follow up to the paper The Coulomb’s Essai Legacy in Soil Mechanics that appeared last year in the Revue Française de Géotechnique (Salençon, 2022). Despite the point of view adopted here being slightly different, similarities between both texts should be no surprise.

****

1 About the Essai

Coulomb’s Memoir entitled Essai sur une application des règles de Maximis et de Minimis à quelques Problèmes de Statique relatifs à l’Architecture can be considered a landmark contribution to the history of Soil Mechanics and Geotechnics, it being acknowledged that it also deals with the stability of vaults and arches through the same rationale based upon the necessary condition that the equilibrium of the considered structure under the loads exerted on it should be compatible with the resistance of its constituent materials. It was presented to the French Academy of Sciences in 1773, shortly after Coulomb returned from Martinique, a French West Indies Island, where he had been in charge of organizing and overseeing the earthworks and excavations, the design of the vaults and retaining walls and the quarrying of stone necessary to the implantation of Fort Bourbon. It is clearly an outcome of the experimental and theoretical practical studies Coulomb had been carrying on there, during 8 years: “This Memoir, written some years ago, was only intended for my own personal use in the many works I am in charge of. If I now dare to present it to the Academy, it is because it always kindly welcomes the weakest attempt, when it has utility as its object.”

The temporality of Coulomb’s Memoir is worth being recalled as it obviously appears after Galileo’s Discorsi, to which we will refer later on (Galileo, 1638a, b), and after Hooke’s Law had been revealed (Hooke, 1676, 1678), which means that the concept of Elasticity was well established at the time, but it is important to keep in mind that the Principle of virtual velocities was still to be plainly stated by Lagrange (1788, 1797, 1888) some 15 years later, the concepts of stress vector and stress tensor would wait 50 years before being introduced by Cauchy (1823) and, finally, 100 years would elapse before Tresca (1864, 1867a, b, 1869, 1870) would lay the bases of the theory of Plasticity.

2 Galileo’s cantilever beam analysis

Galileo’s analysis of the equilibrium of a cantilever beam appears in the 2nd Day of the Discorsi. It can be considered as a first appearance of a Yield design rationale and comes out as an unescapable reference on the topic.

As a starting point Galileo introduces and defines the concept of resistance, “absolute resistance” being that offered to a direct pull, i.e., a tension test (Fig. 1).

Then he observes that the resistance of the considered specimen, when subjected to a transverse force, is far lesser than this absolute resistance (Fig. 2a). Looking for an explanation of the discrepancy, he resorts to a thought experiment, where he imagines a lever, whose equilibrium yields the relationship between the absolute resistance and the transverse force exerted: Figure 2b shows an attempt by the author at schematising Galileo’s approach. Hence, the cornerstone of Galileo’s rationale consists in matching equilibrium with resistance: the considered structure, modelled as a lever, subjected to the transverse force at point C and to the absolute resistance of its constituent material in section AB must be in equilibrium.

We will just retain the principle of this analysis by Galileo, forgetting about the many criticisms it has received that can be explained by the fact that the resistance of the constituent material in compression, since it has not been defined nor mentioned, is implicitly assumed to be infinite.

To conclude on this topic, it may be worth mentioning that, without any reference to Galileo’s or Mariotte’s (1684) analyses, Coulomb also considered that problem in the Essai (cf. Salençon, 2022)

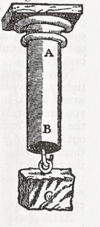thumbnail Fig. 1

Galileo’s definition of “absolute resistance” (Galileo, 1638a).

Définition de la résistance absolue (Galilée, 1638a).
thumbnail Fig. 2

(a) Bearing capacity of a cantilever beam (Galileo, 1638a); (b)Author’s attempt at illustrating Galileo’s approach.

(a) Le problème de la poutre console (Galilée, 1638a) ; (b) Tentative d’illustration du raisonnement de Galilée.

3 Friction and cohesion in Coulomb’s Essai

Coulomb’s approach to the resistance of material starts with the fundamental acknowledgement that “Friction and cohesion are not active forces such as gravity that always fully exerts its effect, but only coercive forces; those two forces are assessed through their limits of resistance” (Fig. 3).

Regarding friction, Coulomb refers to Amontons (1699), stating that “The resistance due to friction is proportional to the pressure exerted”1. Regarding cohesion, he adopts the definition given by van Musschenbroek “Cohœrentia vocatur ea corporum conditio, qua quomodocunque, & â quacunque causa conjunctæ, divulsioni resistunt…” and states that “Cohesion is measured by the resistance that solid bodies oppose to the direct disunity of their parts. …Total cohesion is proportional… to the fracture surface.” This phenomenological definition, similar to Galileo’s statement in the Discorsi about “a certain cement that held the parts glued together” could not be more precise in the absence of the concepts of stress-vector and stress-tensor. This explains Coulomb’s error when he assumes “that adhesion forces are equally resistant, whether they are directed parallel or perpendicular to the fracture plane”2. As a matter of fact, Coulomb’s stability analyses in the Memoir do refer to cohesion as the resistance parallel to the fracture plane, i.e., identical to the present definition of the concept.

Then, the resistance to be overcome is the result of the addition of the effects of cohesion and friction, considered as two independent physical phenomena.

Incidentally, it may be worth mentioning that, a few years later, Coulomb was awarded a Double-Prize from the French Academy of sciences for his Memoir on friction (Coulomb, 1781), the result of a comprehensive experimental work (Fig. 4).

thumbnail Fig. 3

About friction and cohesion in Coulomb’s Memoir.

Frottement et cohésion dans l’Essai de Coulomb.
thumbnail Fig. 4

Experimental devices for the measurement of friction (Coulomb, 1781).

Montages expérimentaux pour la mesure du frottement (Coulomb, 1781).

4 Coulomb’s approach to active and passive thrusts

The overall stability analysis of retaining walls subjected to earth pressure is the third topic to be treated by Coulomb in the Essai, after he has already laid down his rationale fundamentals in his determination of the resistance of masonry pillars. We will concentrate on the first step of his analysis that consists in determining the pressure exerted on the wall by the earth bulk it retains.

In the same way as in his two preceding analyses, Coulomb resorts to a thought experiment (Fig. 5), where he delimitates a “solid rectangular triangle” CBa in the soil mass, which is subjected to gravity forces, sustained by a horizontal force A and retained by the effects of cohesion and friction along Ba.

He then writes the equilibrium equation for the forces exerted along Ba, assuming that the resistance due to friction and cohesion is totally mobilized. At this point, he introduces a crucial distinction between two cases, depending on the role played by the horizontal force.

  • Either, this force prevents the solid triangle from its tendency to “flowing” downwards, in which case the resisting forces shall be directed upwards along Ba. In that case, now known as active thrust, the equilibrium equation along Ba results in4;

A=1tanα+tanɸ(γa22tanα(1−tanαtanɸ)−δacos2α),(4.1)

which stands as a minimum value for a force to be exerted at point F in order to restrain Cba from flowing down.

  • Or, the horizontal force tends to impulse triangle Cba upwards and, consequently, the resisting forces shall be directed downwards along aB. This corresponds to what is presently called passive thrust. The equilibrium equation along Ba yields:

A′=1tanα+tanɸ(γa22tanα(1+tanαtanɸ)+δacos2α),(4.2)

which provides a minimum value for a force to be exerted at point F in order to impulse Cba upwards.

Hence, Coulomb rightly states that:

“It has just been proven that, when cohesion and friction both contribute to maintaining the triangle at rest, the limits to the value of a force that can be exerted at point F, perpendicular to CB, without causing the triangle to move, will lie between A and A’.”

After what, since the thought experiment can be performed for any value of angle α, it is necessary to look for the strongest constraints on the horizontal force and, as announced in the Essay’s very title, to refer to the “Rule of Maximis and Minimis”:

“The limits of the horizontal force that can be exerted in F without setting the fluid in motion, will lie between the limits A and A’, where A will be a maximum and A’ a minimum”.

It is worth noting that, as a logical consequence of this statement, Coulomb explains that triangular surfaces have been chosen for simplicity’s sake, but non-triangular wedges ought to be considered too, for which he proposes a kind of method of slices (Fig. 6).

thumbnail Fig. 5

Earth pressure on a retaining wall (Coulomb, 1773)3.

Poussée des terres sur un mur de soutènement (Coulomb, 1773)3.
thumbnail Fig. 6

Coulomb’s approach to non-triangular wedges (Coulomb, 1773).

Esquisse d’une analyse par des coins non-triangulaires (Coulomb, 1773).

5 Beyond Coulomb’s analysis

Compared with Galileo’s rationale, the innovation brought out by Coulomb is, besides acknowledging that compatibility between equilibrium and resistance only stands as a necessary condition, the maximization/minimization process he performs with respect to the parameter that defines the thought experiment he imagines.

Hence, the governing principles that come out from Coulomb’s stability analyses can be listed as follows:

  • Make a clear distinction between the imposed loads exerted on the structure under concern, and the resistances of the constituent materials that can be mobilized under the restrictions imposed by the limits of resistance.

  • Acknowledge, as a necessary condition for stability that equilibrium of the structure must be mathematically compatible with the constraints imposed by the constituent materials resistances.

  • Expressing this necessary condition, most often in a weaker form, derive constraints to be imposed to the exerted loads as necessary conditions for the stability of the considered structure.

  • Consequently use optimization processes to tighten these constraints.

It shall be underscored that no energy concept is ever involved.

Various authors followed the same purely statical reasoning path as Coulomb for purely cohesive or frictional materials, testing and checking surfaces with various shapes; just citing historical landmarks: Fellenius’ slip-circle (1926, 1927) and Rendulic’s (1935) log-spiral methods, Taylor’s ϕ-circle (1937), various slice-methods, with the necessity, except for some specific cases, of complementary hypotheses to make the problem statically determinate, e.g., when constituent materials with Coulomb’s criterion are concerned.

Other applications of the above-listed governing principles introduce an energy balance viewpoint, which proceeds from the remark that checking a global equilibrium equation is equivalent to writing that the work by the “driving” forces exerted on the structure can be balanced by the work by resisting forces in the dual rigid body motion, under the constraints imposed by the material limits of resistance. Implementation of such “kinematical” approaches meets with the same difficulties as mentioned here-above in expressing the work by resisting forces and calls for complementary hypotheses similar to those already evoked.

Within the framework of continuum mechanics, Macquorn Rankine’s (1856) and Lévy’s (1867) analyses propose partial statical solutions, where a volume of soil is considered as being in limit equilibrium. The method was at the origin of numerous analyses that could take into account friction conditions at the contact between the retaining wall and the bulk of soil; without claiming to be exhaustive, as recalled in (Hansen, 1953): (Kötter, 1888, 1892, 1903; Müller-Breslau, 1906; Résal, 1910; Caquot and Kerisel, 1948), etc. (Fig. 7).

Sokolovski’s seminal books (1960, 1965), whose titles explicitly refer to Statics, are typical representatives of the many approaches, where limit equilibrium is assumed in a presumed rupture zone, that result in an estimate for the corresponding exerted load.

This short review evidences the multiplicity of stability analysis methods that can be derived as a follow-up to Coulomb’s work and, consequently, the difficulty in qualifying them from a safety viewpoint and assessing their validity, at least from a theoretical viewpoint.

thumbnail Fig. 7

Excerpt of the table of contents of the Comptes rendus de l’Académie des sciences, vol. 174, 19225.

Extraits de la table des matières des Comptes rendus de l’Académie des sciences, vol. 174, 19225.

6 theory of yield design

A “Theory of yield design” was proposed (Salençon, 1983, 2013) that proceeds directly and solely from the governing principles listed in Section 5. It introduces the concept of domain of potential stability, denoted by K, (Fig. 8a, in the case of a multi-parameter loading process), which is defined through the necessary “Compatibility Equilibrium/Resistance” condition that results in a “statical interior approach”.

Coulomb’s results now come out as “statical exterior approaches” (Fig. 8b). Indeed, revisiting Coulomb’s rationale in Section 4, we can state that:

  • As a function of parameter α, equation (4.1) yields a value A(α) such that global equilibrium of the corresponding “solid triangle” will be incompatible with the material resistance due to friction and cohesion, in the optimal case where they are supposed to be fully mobilized along Ba, if the horizontal force applied at point F is inferior to A(α). In which case, consequently, the necessary “Compatibility Equilibrium/Resistance” condition cannot be satisfied. A(α) cannot, therefore, lie inside K and comes out as a statical lower bound for active thrust.

  • In the same way, equation (4.2) yields a value A’(α) such that global equilibrium of the corresponding “solid triangle” will be incompatible with the material resistance due to friction and cohesion, in the optimal case where they are fully mobilized along aB, if the horizontal force applied at point F is superior to A’(α). Hence, A’(α) cannot lie inside K and comes out as a statical upper bound for passive thrust.

Through the use of the principle of virtual work, the definition of K also results in a “kinematical approach”, with an energy balance aspect, that fully complies with the fundamental laws of mechanics (Fig. 9). It relies on the core concept of maximum resisting work in a potential collapse mechanism, which can be mathematically derived from the strength criterion of the constituent materials without any ambiguity.

Summing it up in a few words, the theory of yield design explores the concept of limit equilibrium from both a statical and a kinematical viewpoint, through fully consistent mechanical approaches.

Regarding the kinematical approach, which relies on the statement that the work by external forces shall not be superior to the maximum resisting work in any potential collapse mechanism, it results in relevant upper bounds inasmuch as the maximum resisting work remains finite. It turns out that this condition is satisfied only when the considered potential collapse mechanism is “orthogonal” to the resistance criterion. These are the “relevant” virtual velocity fields, in which the work by resisting forces is assigned a finite upper-bound by the resistance criterion of the constituent materials. It must be underlined that this concept is purely mathematical, only derived from the resistance criterion of the constituent materials: the normality rule that defines relevant virtual velocity fields has nothing to do with the concept of constitutive equations for the constituent materials.

In the case of a constituent material with friction and cohesion, relevant virtual velocity fields turn out to be somewhat counterintuitive in view of experimental observations. This explains the difficulties encountered with these materials when implementing classical methods and the necessity of complementary hypotheses, with the exception of Rendulic’s log-spiral method (that includes Coulomb’s triangular wedge method as a particular case).

thumbnail Fig. 8

Yield design theory: statical interior and exterior approaches.

Théorie du calcul à la rupture : approches statiques par l’intérieur et par l’extérieur.
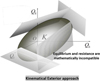thumbnail Fig. 9

Yield design theory: kinematical exterior approach.

Théorie du calcul à la rupture : approche par l’extérieur cinématique.

7 yield design or (plastic) limit analysis?

As already pointed out in Section 1 when evoking its scientific temporality, Coulomb’s Memoir appeared one hundred years before the elaboration of the mathematical theory of Plasticity that was initiated by Tresca’s Memoirs to the French Academy of sciences. Then, famous authors worked out the two fundamental concepts of the mathematical theory of plasticity, namely the plastic yield criterion as a measure of stress intensity (Beltrami, 1885; Huber, 1904; Mises, 1913) and the plastic flow rule as a constitutive equation. These two concepts were linked to each other through the theory of a plastic potential by von Mises in 1928 and equivalently, 20 years later, through the principle of maximum plastic work (Hill, 1948, 1950), from which it results that the plastic flow rule, as part of a constitutive equation, is derived by a normality rule from the yield criterion and said to be “associated”.

Within the elastoplastic framework, an existence theorem for the solution to quasi-static evolution problem can be established. For a non-hardening material, the domain of existence of this solution turns out to be identical to the domain of potential stability defined in Section 6, a result that endows the latter with the status of a domain of safety from a theoretical viewpoint. The well-known “limit theorems” of the theory of limit loads, mathematically identical to the interior and exterior approaches of the theory of yield design, provide lower- and upper-bound estimates for this domain.

The mathematical formulations of the theory of yield design and the plastic theory of limit loads are therefore similar (cf. Salençon, 2020), which often results in confounding them. As regards practical applications, this confusion is of no consequence, as long as it does not induce the conviction that the information gained from the theory of yield design is only relevant when the normality rule holds as a constitutive equation.

Let it be emphasized that, from a theoretical viewpoint, the relevance of upper bound stability assessments obtained through the yield design theory only depends on the relevance of the adopted resistance criteria for the constituent materials and the subjacent assumption of no or, more precisely, negligeable geometry changes for the considered structure. This defines the relevance framework for all mechanically consistent limit equilibrium stability analyses, either statical or kinematical, provided they fully comply with the governing principles listed in Section 5.

8 As a conclusion

Based upon the governing principles gained from Coulomb’s insight, the yield design rationale offers an approach to the stability analysis of structures that can be implemented even whenever the loading history of the structure under concern and the constitutive equations of its constituent materials are not fully defined, keeping in mind that, whatever its sophistication, any model or method shall not be interpreted beyond its limits of relevance.

As a theoretical basis of Ultimate Limit State Design (ULSD), it helps in making the crucial distinction between active and resisting forces, following Coulomb’s very definition, and assigning them appropriate safety factors.

References

  • Amontons G. 1699. Moyen de substituer commodement l’action du feu, à la force des hommes et des chevaux pour mouvoir les Machines. Mémoires de l’Académie Royale des sciences, année 1699, pp. 112–126. Available from https://gallica.bnf.fr/ark:/12148/bpt6k35013/f265.image.langEN. [Google Scholar]
  • Beltrami E. 1885. Sulle condizioni di resistenza die corpi elastici. Rendiconti Istituto. Lombardo di Scienze e Lettere 18(2): 704–714. [Google Scholar]
  • Caquot A, Kerisel J. 1948. Tables de poussée, de butée et de force portante des fondations. Paris : Gauthier-Villars. [Google Scholar]
  • Cauchy AL. 1823. Recherches sur l’équilibre et le mouvement intérieur des corps solides ou fluides, élastiques ou non élastiques. Bulletin de la Société Philomatique 1823: 9–13; Œuvres complètes d’Augustin Cauchy publiées sous la direction scientifique de l’Académie des sciences, Gauthier-Villars, Paris, 1882, 2, 2, pp. 300–304. [Google Scholar]
  • Coulomb C-A. 1773. Essai sur une application des règles de Maximis et Minimis à quelques Problèmes de Statique relatifs à l’Architecture. Mémoires de Mathématique et de Physique présentés à l’Académie Royale des Sciences et lus dans ses Assemblées 7: 343–382. Reprinted in Théorie des machines simples, Bachelier, Paris, 1809 & 1821. [Google Scholar]
  • Coulomb C-A. 1781. Théorie des machines simples en égard au frottement de leurs parties, et à la roideur de leurs cordages. Recueil des savants étrangers de l’Académie royale des sciences 10: 161–332. https://ia600209.us.archive.org/18/items/mmoiresdemath10acad/mmoiresdemath10acad.pdf. [Google Scholar]
  • Fellenius W. 1926. Jordstatiska beräkningar med friktion of kehesion och under antagande av cirkulärcylindriska glidytor. Kungliga Väg-och Vatten-byggnadskåren 1851-1926, Festskrift, Stockholm, pp. 79–127. [Google Scholar]
  • Fellenius W. 1927. Erdstatische Berechnungen mit Reibung und Kohäsion, Adhäsion, und unter Annahme kreiszylindrischer Gleitflächen. Berlin: W. Ernst und Sohn, 1939. [Google Scholar]
  • Galileo Galilei. 1638a. Discorsi e dimostrazioni matematiche intorno à due nuove scienze. Leyden: Elsevier. [Google Scholar]
  • Galileo Galilei. 1638b. Dialogues concerning two new sciences. Crew, H. & Salvio, A. translators, Dover, New York, 1954. [Google Scholar]
  • Hansen J.B. 1953. Earth pressure calculation. Copenhagen: The Danish Technical Press. [Google Scholar]
  • Hill R. 1948. A variational principle of maximum plastic work in classical plasticity. Q J Mech Appl Math 1: 18–28. [CrossRef] [Google Scholar]
  • Hill R. 1950. The mathematical theory of plasticity. Oxford (G.B.): Clarendon Press. [Google Scholar]
  • Hooke R. 1676. A description of helioscopes and some other instruments made by Robert Hooke, printed by T.R. for John Martyn, Printer to the Royal Society, at the Bell in St. Paul’s Church-Yard, London, 31. [Google Scholar]
  • Hooke R. 1678.Lectures De Potentia restitutiva or of Spring, explaining the power of springing bodies, John Martyn, Printer to the Royal Society, at the Bell in St. Paul’s Church-Yard, London. [Google Scholar]
  • Huber MT. 1904. The specific shear strain work as criterion of material strength. In Polish Czasopismo Techniczne, Lwów, 22, Pisma, 2, PWN, Warsaw, 1956; Engl. Transl. in Archives of Mechechanics, 56, 173–190, 2004. [Google Scholar]
  • Kötter F. 1888. Über das Problem der Erdderuck bestimmung. Verhandlungen der Deutschen Physikalishen Gesellshaft, Berlin 7. [Google Scholar]
  • Kötter F. 1892. Die Entwicklungen der Lehre vom Erddruck. Jahresbericht der Deutschen Mathematiker-Vereinigung 2. [Google Scholar]
  • Kötter F. 1903. Die Bestimmung des Druckes an gekrümmten Gleitflächen. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, Berlin. [Google Scholar]
  • Lagrange J-L. 1788. Méchanique analitique. À Paris, chez la Veuve Desaint, rue du Foin S. Jacques. [CrossRef] [Google Scholar]
  • Lagrange J-L. 1797. Sur le principe des vitesses virtuelles. Journal de l’École polytechnique. Ve cahier, Tome II, prairial an VI, pp. 115-118, Imprimerie de la République, Paris. [Google Scholar]
  • Lagrange J-L. 1888. Œuvres complètes, vol. 11. Paris : Gauthier-Villars. [Google Scholar]
  • Lévy M. 1867. Essai sur une théorie rationnelle de l’équilibre des terres fraîchement remuées et ses applications sur le calcul de la stabilité des murs de soutènement. Comptes rendus des séances de l’Académie des sciences, Paris 68: 1456–1458. [Google Scholar]
  • Macquorn Rankine WJ. 1856. On the stability of loose Earth. Philos Trans Royal Soc 147: 9–27. [Google Scholar]
  • Mariotte E. 1684. Traité du mouvement des eaux et des autres corps fluides… Œuvres de M. Mariotte, de l’Académie Royale des Sciences, new ed. (The Hague, 1740), 461. [Google Scholar]
  • Massarsch KR, Fellenius BH. 2012. Early Swedish contributions to geotechnical engineering. In: ASCE GeoInstitute Geo-Congress, Oakland, March 25–29, 2012, Full-scale Testing in Foundation Design, State of the Art and Practice in Geotechnical Engineering, ASCE, Reston V.A., Hussein M.H., Massarsch K.R., Likins G.E., Holtz R.D. (Eds.), Geotechnical Special Publication 227, pp. 239–256. [Google Scholar]
  • Mises R von. 1913. Mechanik der plastischen Formänderung von Kristallen. Zeischrift für angewandte Mathematik und Mechanik 8: 161–185. [Google Scholar]
  • Mises R von. 1928. Mechanik der Festen Körper im plastisch deformablen Zustand. Göttingen Nachrichten Mathematik und Physik 1: 582–592. [Google Scholar]
  • Müller-Breslau H. 1906. Erddruck auf Stützmauern. Stuttgart: Kröner. [Google Scholar]
  • Musschenbroek P. van 1748. Institutiones Physicae conscriptae in usus academicos. Lugduni Batavorum apud Samuelem Luchtmans et filium, Leyden. [Google Scholar]
  • Rendulic L., 1935. Ein Beitrag zur Bestimmung der Gleitsicherheit. Der Bauingenieur 16(19-20): 230–233. [Google Scholar]
  • Résal J. 1910. La poussée des terres. Paris : Béranger. [Google Scholar]
  • Salençon J. 1983. Calcul à la rupture et analyse limite. Paris : Presses de l’École nationale des Ponts et Chaussées. [Google Scholar]
  • Salençon J. 2013. Yield design. New York: ISTE Ltd, London and John Wiley & Sons. [CrossRef] [Google Scholar]
  • Salençon J. 2020. Elastoplastic modeling. New York: ISTE Ltd, London and John Wiley & Sons. [CrossRef] [Google Scholar]
  • Salençon J. 2021. About Tresca’s Memoirs on the fluidity of solids (1864–1870). C R Mecanique 349(1): 1–7. [Google Scholar]
  • Salençon J. 2022. The Coulomb’s Essai legacy in soil mechanics. Rev Fr Geotech 170(1): 1–9. [Google Scholar]
  • Sokolovski VV. 1960. Statics of soil media. London: Butterworths scient. Publ. [Google Scholar]
  • Sokolovski VV. 1965. Statics of granular media. Oxford: Pergamon Press. [Google Scholar]
  • Taylor DW. 1937. Stability of earth slopes. J Boston Soc Civil Eng 24(3): 337–386. [Google Scholar]
  • Tresca H. 1864. Mémoire sur l’écoulement des corps solides soumis à de fortes pressions. Comptes rendus des séances de l’Académie des sciences, Paris 59: 754–758. [Google Scholar]
  • Tresca H. 1867a Sur l’écoulement des corps solides soumis à de fortes pressions. Comptes rendus des séances de l’Académie des sciences, Paris 64: 809–812. [Google Scholar]
  • Tresca H. 1867b Sur les applications de l’écoulement des corps solides au laminage et au formage. Comptes rendus des séances de l’Académie des sciences, Paris 64: 1132–1136. [Google Scholar]
  • Tresca H. 1869. Mémoire sur le poinçonnage et la théorie mécanique de la déformation des métaux. Comptes rendus des séances de l’Académie des sciences, Paris 68: 1197–1201. [Google Scholar]
  • Tresca H. 1870. Mémoire complémentaire sur le poinçonnage des métaux et des matières plastiques. Comptes rendus des séances de l’Académie des sciences, Paris 70: 27–31. [Google Scholar]
1

The friction coefficient now commonly denoted by tan ϕ appears originally in Coulomb’s Memoir as 1/n.

2

This is the origin of Coulomb’s incorrect statement that the resistance to compression of masonry pillars made from purely cohesive materials is double their resistance to traction.

3

Parameter α does not appear in the original Figure 8 of the Memoir and was added here by the author.

4

With γ denoting the specific weight of the soil, CB = a, and δ standing for the cohesion.

5

This excerpt, by the number of analytical contributions devoted to earth pressure calculation and limit equilibrium, shows that the issue came out as the subject of a kind of mathematical challenge at that time in France!

Cite this article as: Jean Salençon. Galileo, Coulomb, the origins of Yield Design Analyses. Rev. Fr. Geotech. 2023, 175, 2.

All Figures

thumbnail Fig. 1

Galileo’s definition of “absolute resistance” (Galileo, 1638a).

Définition de la résistance absolue (Galilée, 1638a).
In the text
thumbnail Fig. 2

(a) Bearing capacity of a cantilever beam (Galileo, 1638a); (b)Author’s attempt at illustrating Galileo’s approach.

(a) Le problème de la poutre console (Galilée, 1638a) ; (b) Tentative d’illustration du raisonnement de Galilée.
In the text
thumbnail Fig. 3

About friction and cohesion in Coulomb’s Memoir.

Frottement et cohésion dans l’Essai de Coulomb.
In the text
thumbnail Fig. 4

Experimental devices for the measurement of friction (Coulomb, 1781).

Montages expérimentaux pour la mesure du frottement (Coulomb, 1781).
In the text
thumbnail Fig. 5

Earth pressure on a retaining wall (Coulomb, 1773)3.

Poussée des terres sur un mur de soutènement (Coulomb, 1773)3.
In the text
thumbnail Fig. 6

Coulomb’s approach to non-triangular wedges (Coulomb, 1773).

Esquisse d’une analyse par des coins non-triangulaires (Coulomb, 1773).
In the text
thumbnail Fig. 7

Excerpt of the table of contents of the Comptes rendus de l’Académie des sciences, vol. 174, 19225.

Extraits de la table des matières des Comptes rendus de l’Académie des sciences, vol. 174, 19225.
In the text
thumbnail Fig. 8

Yield design theory: statical interior and exterior approaches.

Théorie du calcul à la rupture : approches statiques par l’intérieur et par l’extérieur.
In the text
thumbnail Fig. 9

Yield design theory: kinematical exterior approach.

Théorie du calcul à la rupture : approche par l’extérieur cinématique.
In the text

Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.

Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.

Le chargement des statistiques peut être long.