| Numéro |
Rev. Fr. Geotech.
Numéro 156, 2018
|
|
|---|---|---|
| Numéro d'article | 4 | |
| Nombre de pages | 9 | |
| DOI | https://doi.org/10.1051/geotech/2019005 | |
| Publié en ligne | 29 mai 2019 | |
Article de recherche / Research Article
Étude de l’influence de la plasticité du sol sur la transmission des mouvements du sol affectant l’interaction sol-structure
Studying the influence of soil plasticity on the transmission of ground movements affecting the soil-structure interaction
1
Université de Lorraine, CNRS, CREGU, GeoRessources laboratory, École des Mines de Nancy, Campus Artem, CS14234,
54042
Nancy Cedex, France
2
Faculté de Génie, Université Libanaise,
Roumieh,
MontLiban, Liban
★ Auteur de correspondance : elio.el-kahi@univ-lorraine.fr
De nombreux bâtiments peuvent être endommagés par des mouvements de terrain associés à des excavations souterraines, des tunnels, des mines ou des excavations en milieu urbain. L’évaluation du mouvement du terrain transmis au bâti est alors l’une des préoccupations majeures et la plasticité du sol peut avoir une influence significative sur le comportement de la structure dû à l’interaction sol-structure (ISS). Le but de cette étude est d’étudier le comportement d’une structure existante assise sur un sol soumis à un mouvement de terrain en tenant compte de la plasticité du sol. Une approche analytique, associée à une résolution numérique, est appliquée pour examiner l’effet du comportement non linéaire du sol, basée sur un modèle élasto-plastique modifié de Winkler. Les résultats révèlent l’influence de la prise en compte d’un comportement élasto-plastique sur l’évaluation de la transmission des mouvements du terrain. Ils montrent la différence de la réponse de la structure, selon que le sol est élastique ou élasto-plastique, ce qui affecte directement la prévision des dommages structurels. De plus, une nouvelle corrélation est proposée pour évaluer la réponse structurelle en tenant compte des paramètres d’ISS pour un sol élasto-plastique.
Abstract
Many buildings may suffer damage due to ground movements associated to underground excavations such as tunneling, mines or urban excavations. Assessment of the transmitted ground movement is then one of the major concerns and soil plasticity may have a significant influence on structural behavior due to the soil-structure interaction (SSI). The purpose of this study is to investigate the behavior of an existing structure sitting on a soil subjected to a ground movement with considering soil plasticity. An analytical approach, with a numerical solution, is applied to examine the effect of the non-linear behavior of soil based on a modified Winkler elastic model. Results reveal the influence of considering an elastoplastic behavior on the evaluation of the transmission of ground movements, and display the discrepancy in the response of the structure whether the soil is elastic or elastoplastic; this directly affects the prediction of structural damage. In addition, a new correlation is proposed to evaluate the structural response considering SSI parameters for an elastoplastic soil.
Mots clés : modèle analytique / taux de déflexion / interaction sol-structure / plasticité du sol / modèle de Winkler
Key words: analytical model / deflection ratio / soil-structure interaction / soil plasticity / Winkler model
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2019
1 Introduction
Les mouvements de terrain désignent une large gamme de déplacements du sol, d’origine naturelle ou anthropique, tels que le phénomène de retrait-gonflement des sols argileux, l’influence d’excavations du sous-sol à proximité d’ouvrages (tunnels, parking, etc.) et les mouvements associés à la stabilité de vides souterrains tels que les affaissements miniers et les fontis. Ces mouvements de terrain peuvent se produire en l’absence de toute structure à proximité. On se place ici dans un cadre quasi statique et on appelle mouvements du terrain en champ libre ces déplacements sans prise en compte de l’influence des constructions éventuelles en surface. En cas de présence d’une structure, tout ou partie de ce mouvement peut être transmis au bâtiment (ElKahi et al., 2018) qui subit alors un tassement différentiel pouvant causer des dommages structurels (Ricceri et Soranzo, 1985). Il n’est pas approprié de considérer que les mouvements en champ libre sont systématiquement entièrement transmis au bâtiment (Boscardin et Cording, 1989 ; Potts et Addenbrooke, 1997 ; Mair, 2013) en raison d’une interaction entre le sol et la structure (ISS). On appelle Δ0 la déflexion maximale qu’aurait subi un bâtiment si les mouvements en champ libre étaient intégralement transmis. En supposant que le mouvement du sol en champ libre est à peu près circulaire sous le bâtiment, on peut le caractériser par son rayon de courbure R. Une relation géométrique peut alors être déterminée pour calculer Δ0 en fonction de R et de la longueur du bâtiment L (Éq. (1) et Fig. 1, Deck, 2002). L’estimation de R ou de Δ0 n’est pas l’objet de cet article. Pour des mouvements d’origine minière, Deck (2002) a regroupé des formules empiriques permettant de décrire les affaissements en surface. Pour le creusement de tunnels, la formule de Peck (1969) reste encore aujourd’hui très utilisée. Dans les deux cas, l’ordre de grandeur des mouvements en champ libre est très variable, avec des rayons de courbure variant de quelques centaines de mètre à quelques kilomètres. Pour un bâtiment de 20 m de longueur, ces courbures sont alors associées à des déflexions du bâti de l’ordre millimétrique à centimétrique.
 (1)
(1)
Avec Δ0 la déflexion maximale d’un bâtiment, L la longueur du bâtiment et R le rayon de courbure du mouvement en champ libre du terrain.
On appelle alors Δ la déflexion réelle du bâtiment, causée par le mouvement en champ libre, compte tenu de la prise en compte des phénomènes d’ISS et Δ/Δ0 désigne alors le taux de transmission des mouvements en champ libre (Fig. 2). Dans le cas d’un mouvement en champ libre symétrique par rapport au centre du bâti, la déflexion Δ correspond au tassement différentiel du bâti. Dans le cas d’un mouvement en champ libre dissymétrique, la déflexion Δ est un paramètre plus intéressant que le tassement différentiel car elle permet ne pas tenir compte du mouvement rotationnel de corps rigide du bâti. Le rapport Δ/L, appelé taux de déflexion, est fréquemment utilisé pour étudier le comportement de structures soumises à un tassement différentiel (Serhal et al., 2016).
L’objectif de cette étude porte sur l’évaluation du taux de transmission Δ/Δ0 des mouvements en champ libre. Ce dernier a fait l’objet d’évaluations basées sur des approches numériques (Potts et Addenbrooke, 1997 ; Haji et al., 2018), analytiques (Basmaji et al., 2017 ; ElKahi et al., 2018), expérimentales (Farrell et Mair, 2011 ; Hassoun et al., 2018) et observationnelles (Aissaoui, 1999 ; Goh et Mair, 2011). Mis à part les méthodes observationnelles qui s’appuient sur des observations réelles d’ouvrages existants, toutes ces méthodes sont aujourd’hui appliquées à des ouvrages simplifiés, de type poutre, dans un soucis d’évaluation de la tendance globale des phénomènes et non d’étude spécifique d’un cas particulier. Toutes ces approches convergent pour suggérer que le taux de transmission peut être estimé en fonction d’un paramètre de rigidité relative ρ* entre le bâti et le terrain. Bien qu’il existe plusieurs expressions de ce paramètre (Boscardin et Cording, 1989 ; Potts et Addenbrooke, 1997 ; Franzius et al., 2004), on s’appuiera ici sur l’équation (2) qui présente l’avantage d’être adimensionnelle et d’être bien adaptée à la représentation synthétique de Δ/Δ0 (Deck et Singh, 2010).
 (2)
(2)
Avec EI la rigidité équivalente du bâti (E le module de Young équivalent du bâti et I son inertie équivalente), Es le module de Young du terrain et L la longueur du bâti.
Les méthodes numériques offrent une grande flexibilité pour la prise en compte d’un comportement complexe du sol (Potts et Addenbrooke, 1997) et/ou d’une géométrie complexe du bâti. Utilisées pour apprécier la tendance globale des phénomènes, elles peuvent soulever des difficultés pour aboutir à des résultats synthétiques et généraux couvrant l’étendue de la gamme de variation réaliste des paramètres. Les méthodes analytiques peuvent être une alternative intéressante, surtout lorsque les modèles de comportement utilisés pour le bâti se limitent à une poutre de rigidité EI et de longueur L, comme c’est actuellement le cas pour les approches numériques (Deck et Singh, 2010 ; Basmaji et al., 2017). Ainsi, par leur facilité d’application et sous-réserve de justifier la validité des résultats, les approches analytiques apparaissent comme un outil complémentaire de l’approche numérique, en permettant des calculs rapides pour une large plage de variation des paramètres du modèle.
Ainsi, l’approche analytique développée par Deck et Singh (2010), sur laquelle s’appuie l’étude présentée dans cet article, en est l’illustration. Il s’agit d’une approche 2D en statique où Deck et Singh (2010) ont combiné le modèle de Winkler à celui d’une poutre d’Euler-Bernoulli élastique de longueur L, de largeur B, d’inertie I et de module de Young E pour étudier le taux de transmission des mouvements en champ libre (Fig. 3). Le modèle consiste à chercher la position d’équilibre statique du bâti sous l’effet de son poids propre lorsqu’il repose sur un terrain initialement incurvé selon un profil parabolique symétrique représentant les mouvements du terrain en champ libre. Cette approche repose sur plusieurs hypothèses fortes dont la forme des mouvements du terrain en champ libre et le choix mécanique du terrain. Concernant la forme des mouvements, un travail préliminaire a permis de comparer différents profils associés à la même valeur de Δ0 (trapézoïdal, sinusoïdal, triangulaire, semi-triangulaire, etc.). Les résultats montrent une influence limitée à 15 % sur la valeur finale du taux de transmission obtenu (ElKahi et al., 2018).
Concernant le modèle mécanique du terrain, Basmaji et al. (2017) ont développé une approche comparable en utilisant le modèle de sol à deux paramètres de Pasternak. Ce modèle prend en compte une interaction entre les ressorts ce qui permet de ne pas négliger l’influence des terrains à l’extérieur du bâti. La comparaison des résultats montre que pour le cas de Pasternak, le taux de transmission est plus important que dans le cas de Winkler. Une comparaison avec des valeurs de taux de transmission issues d’essais expérimentaux (Farrell et Mair, 2011) ou des modélisations numériques (Mair, 2013) montre que les deux solutions basées sur les modèles de Winkler ou Pasternak encadrent ces valeurs, bien que les deux modèles de sol soient élastiques.
L’objectif de cette étude est d’introduire la prise en compte de la plasticité dans l’approche analytique pour étudier son influence sur le taux de transmission au bâti des mouvements en champ libre. D’un point de vue macroscopique, l’apparition de plasticité dans le sol devrait avoir un effet comparable à une réduction de la rigidité du terrain. On s’attend donc à observer une réduction du taux de transmission de la déflection lorsque la plasticité est prise en compte. Dans cette étude, la plasticité est introduite dans l’approche analytique basée sur le modèle de Winkler.
Les résultats proposés prennent la forme d’abaques permettant d’estimer l’ordre de grandeur du taux de transmission des mouvements du terrain en fonction des propriétés géométriques et mécaniques du bâti et du terrain.
 |
Fig. 1 Présentation du déplacement en champ libre Δ0 (ElKahi et al., 2018). Presentation of the free-field deflection Δ0 (ElKahi et al., 2018). |
 |
Fig. 2 Comportement des structures soumises au mouvement du terrain. (a) structure de haute rigidité sur sol souple ; (b) structure de rigidité intermédiaire sur sol intermédiaire ; (c) structure flexible sur sol dur (ElKahi et al., 2018). Behavior of structures subjected to ground movement. (a) high-stiffness structure on soft ground; (b) intermediate stiffness structure on intermediate ground; (c) flexible structure on stiff ground (ElKahi et al., 2018). |
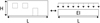 |
Fig. 3 Bâtiment similaire à une poutre élastique d’Euler-Bernoulli. Building modelled similar to an elastic Euler-Bernoulli beam. |
2 Modèle analytique
L’approche analytique consiste à rechercher l’équilibre statique d’un système composé d’une poutre reposant sur un terrain de déflexion initiale Δ0. Elle s’appuie sur un comportement élasto-plastique parfait du terrain, modélisé par des éléments de Winkler (Fig. 4) dont le module de réaction est Kw (Éq. (3)) et la pression maximale est limitée par la valeur pult (Éq. (4)). Dans la phase élastique, le modèle de Winkler suppose que la réaction du sol en chaque point sous une fondation est proportionnelle au tassement du terrain à cet endroit (Deck, 2002). Le paramètre pult caractérise la capacité portante du sol et correspond à la contrainte maximale que les ressorts peuvent supporter. Si les forces appliquées dépassent la capacité portante du sol, un ressort continue à se déformer, mais ne peut supporter aucune contrainte supplémentaire. Les surcharges sont ainsi transférées aux ressorts voisins qui sont encore dans leur plage élastique.
 (3)
(3)
 (4)
(4)
Les conventions de contrainte normale sont celles de la mécanique des sols (compression positive) et le tassement w(x) est compté également positivement.
Le bâti est modélisé par une poutre d’Euler-Bernoulli élastique chargée par une charge uniformément répartie q en partie supérieure représentant le poids propre de l’ouvrage et par la réaction du sol p(x) en partie inférieure (Fig. 5). La déformée de la poutre y(x) dépend du moment fléchissant M(x) et elle est déterminée à l’aide de l’équation (5) :
 (5)
(5)
Les relations entre M(x), l’effort tranchant V(x), la réaction du terrain p(x) et la charge du bâtiment q peuvent être définies comme suit :
 (6)
(6)
 (7)
(7)
En combinant (5), (6) et (7), l’équation différentielle du déplacement du bâtiment peut s’écrire comme suit :
 (8)
(8)
La déflexion initiale du terrain est considérée symétrique et de forme polynomiale (Éq. (9)). La fonction polynomiale v(x) représente alors un déplacement du terrain en champ libre concave pour −L/2 ≤ x ≤ L/2. La recherche de l’équilibre statique du système conduit à introduire le mouvement de corps rigide d du bâti (Fig. 6) et à ajouter une condition de non-interpénétration entre le bâti et le terrain (Éq. (10)).
 (9)
(9)
 (10)
(10)
Le déplacement d’un point du bâti est ici la somme d’un mouvement de corps rigide d, qui correspond au tassement identique des deux extrémités du bâti, et de la déformée y(x). Le mouvement de corps rigide du bâti est donc ici un mouvement de translation pure, sans rotation. Compte tenu de la symétrie, la déflexion maximale du bâti est au milieu et la solution cherchée est Δ = y (0).
Il convient de noter que selon les valeurs numériques considérées, l’équilibre du système peut conduire à une zone de traction sous le bâti n’ayant aucun sens physique et qui devra être interprété comme l’occurrence d’un décollement entre le terrain et l’ouvrage. Ce cas particulier ne sera pas traité ici. Il conviendra donc de vérifier que les solutions obtenues sont toutes caractérisées par des valeurs de p(x) > 0 sur toute la longueur du bâti. Si le modèle est ici appliqué au cas d’un mouvement de terrain symétrique par rapport au bâti (Éq. (9)), il peut aisément être étendu à des mouvements quelconques. La réponse finale du bâti ne sera alors pas symétrique et l’équation (10) nécessite d’être modifiée en introduisant des valeurs de tassements des extrémités d1 et d2 différentes, signifiant que le mouvement de corps rigide inclut également une rotation du bâti.
La solution du problème implique la résolution des équations (3), (4), (8), (9) et (10). Compte tenu de la symétrie, trois conditions aux limites sont requises pour obtenir une solution (Deck et Singh, 2010). Les extrémités du bâti sont des bords libres dont le tassement est égal au mouvement de corps rigide d. La flèche du bâtiment y, le moment de flexion y” et l’effort tranchant y”’ sont alors nuls aux extrémités de la poutre (x = −L/2 et L/2).
Compte tenu du comportement non linéaire du sol, la solution de ces équations est obtenue de manière itérative à l’aide du logiciel Mathematica. Si le formalisme mathématique du modèle est analytique, sa résolution est numérique. Une première solution élastique est obtenue à partir des équations (3), (8), (9) et (10) et des conditions aux limites. Après avoir obtenu la solution, il y a deux cas possibles :
-
les contraintes appliquées au sol sont positives et inférieures à pult (le sol est toujours dans la plage élastique) ; dans ce cas, la déformation maximale du bâtiment peut être calculée directement à partir de l’expression de y(x) et la solution obtenue est identique à celle de Deck et Singh (2010) ;
-
certaines des contraintes appliquées au sol sont plus grandes que pult ; dans ce cas, une procédure de résolution numérique utilisant la méthode des différences finies est mise en œuvre et une approche itérative est appliquée pour trouver la solution et déterminer la déformée maximale du bâtiment en tenant compte de la plasticité.
Un élément de contrôle de la procédure de calcul consiste à vérifier l’équilibre statique final du système. L’intégrale de p(x) avant et après la prise en compte de la plasticité doit toujours être égale à la charge externe appliquée au bâtiment (Fig. 7). Il faut bien noter que le cas présenté dans cette étude ne peut pas être comparé au cas d’une fondation sur un sol horizontal, car dans notre cas le sol est initialement déformé selon les mouvements en champ libre. La figure 8 illustre la solution obtenue pour un cas caractérisé par une longueur L = 20 m, une rigidité EI = 5333 MN.m2, une charge q = 100 KN/m, une capacité portante du sol pult = 120 KN/m, un module de réaction de Winkler Kw = 3850 KN/m3 et un rayon de courbure du mouvement du sol en champ libre R = 1500 m. Ce cas correspond à une situation, où la plasticité du terrain intervient et la solution d’équilibre obtenue conduit à une déflexion finale de la poutre inférieure à celle prévue en considérant un comportement élastique du terrain. À l’issue du premier calcul élastique, la déflexion maximale du bâtiment est égale à 0,6 cm correspondant à un taux de transmission Δ/Δ0 égal à 0,18. Cependant, aux limites du bâtiment, il existe une zone où p(x) > pult, la plasticité du sol doit alors être prise en compte. En conséquence, en appliquant le processus itératif de résolution, on obtient une réduction de la flèche maximale de la poutre Δ à 0,35 cm, auquel est associé un taux de transmission Δ/Δ0 de 0,10, soit une réduction de 45 % par rapport à la solution élastique.
En se basant sur le modèle numérique développé par Basmaji et al. (2017), le code aux éléments finis Plaxis 2D a été́ utilisé pour faire un modèle de l’interaction sol-structure et pour produire un déplacement en champ libre de la surface. Le modèle numérique proposé est réalisé en 2D (hypothèse de déformation plane). Il se compose de deux couches de sol de largueur L = 800 m. La première couche est une couche élasto-plastique d’épaisseur h1 = 100 m, et la seconde couche est une couche élastique d’épaisseur h2 = 25 m. Les conditions aux limites sont présentées sur la figure 9 : déplacements horizontaux nuls aux limites latérales, déplacements verticaux et horizontaux nuls aux limites du modèle inférieur L1 et L2, et un déplacement libre sur la partie centrale de la limite inférieure pour imposer l’affaissement à la surface. La seconde couche a pour unique objectif d’induire des conditions limites raisonnables sur la base inférieure de la première couche. Elle permet d’éviter l’occurrence de déformations plastiques trop importantes dans la partie inférieure du modèle qui pourraient compromettre la convergence des calculs et la précision des résultats à proximité des bâtiments. La couche élasto-plastique a une cohésion et un angle de frottement qui varient en fonction de la valeur pult selon la formule de Terzaghi.
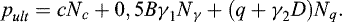 (11)
(11)
Avec 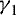 le poids volumique du sol sous la base de la fondation,
le poids volumique du sol sous la base de la fondation,  le poids volumique du sol latéralement à la fondation, q la surcharge verticale latérale à la fondation, c la cohésion du sol sous la base de la fondation, B la largeur de la fondation, D la profondeur d’encastrement de la fondation (profondeur à laquelle se trouve la base de la fondation) et Nc, Nq, Nγ les facteurs de portance qui ne dépendent que de l’angle de frottement interne Ф du sol sous la base de la fondation.
le poids volumique du sol latéralement à la fondation, q la surcharge verticale latérale à la fondation, c la cohésion du sol sous la base de la fondation, B la largeur de la fondation, D la profondeur d’encastrement de la fondation (profondeur à laquelle se trouve la base de la fondation) et Nc, Nq, Nγ les facteurs de portance qui ne dépendent que de l’angle de frottement interne Ф du sol sous la base de la fondation.
Pour le bâtiment, on considère une poutre de longueur 20 m et de 3,5 m de hauteur avec une charge uniforme appliquée sur cette poutre tel que la somme du poids propre et la charge appliquée sur la poutre soit égale à 100 KN/m. Deux calculs sont réalisés. Le premier est réalisé sans bâtiment afin de calculer Δ0, le mouvement des terrains en champ libre. Le second est réalisé avec le bâti afin de calculer Δ la déflexion maximale du bâtiment en cas de mouvement du sol. Le taux de transmission Δ/Δ0 est alors déduit. Les résultats du modèle numérique donnent une flèche maximale de la poutre de 0,323 cm pour un Δ0 de 3,421 cm ce qui est associé un taux de transmission Δ/Δ0 de 0,095. À noter que la flèche maximale est calculée en tenant compte juste de la flèche sans le déplacement causé par le mouvement de corps rigide. Ainsi, la comparaison du cas étudié par les deux modèles montre une cohérence entre les résultats analytiques et numériques.
 |
Fig. 4 Modèle de Winkler. Winkler model. |
 |
Fig. 5 Présentation de la charge du bâtiment q, réaction du sol p(x) et la déformation du bâtiment y(x) (ElKahi et al., 2018). Presentation of the building load q, ground reaction p(x) and building deflection y(x) (ElKahi et al., 2018). |
 |
Fig. 6 Déplacement du sol et de la structure en équilibre statique (ElKahi et al., 2018). Displacements of the ground and the building under static equilibrium (ElKahi et al., 2018). |
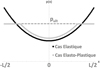 |
Fig. 7 Présentation de la réaction du sol pour un cas élastique et un cas élasto-plastique. Presentation of the soil reaction for an elastic case and an elastoplastic case. |
 |
Fig. 8 Déplacement vertical à l’interface sol-structure selon le comportement élastique et élasto-plastique du sol. Vertical displacements at the soil-structure interface according to the elastic and elastoplastic behavior of the ground. |
 |
Fig. 9 Conception et conditions aux limites utilisées pour le modèle numérique. Design and boundary conditions used for the numerical model. |
3 Résultats et discussion
Afin d’étudier l’effet de la plasticité du sol sur le rapport de transmission de déflexion Δ/Δ0, un plan d’expérience est établi, en étudiant 18 900 combinaisons possibles de pult, EI, Kw, L, R et q, comme indiqué dans le tableau 1. Le modèle étant réalisé en déformation plane, la rigidité de la poutre à prendre en compte est EI/B où EI est la rigidité du bâti et B sa largeur. Pour un bâti de largeur 2 × 4 m = 8 m constitué de 2 façades et un mur de refend de 30 cm d’épaisseur, deux approches sont possibles. La première consiste à modéliser la totalité du bâti en estimant la rigidité EI globale et en considérant B = 8 m. La seconde consiste à ne modéliser qu’un mur (façade ou refend) en estimant la rigidité EI d’un mur seul et en considérant B = 30 cm.
La longueur du bâtiment a été prise entre 10 et 30 m pour modéliser des bâtiments de petite et moyenne taille (Deck et Singh, 2010). La charge de la poutre représente le poids propre du bâtiment et la surcharge. Par conséquent, 100 kN/m correspond approximativement au poids d’un mur de 3 m de hauteur, d’épaisseur de 0,5 m avec une surcharge ; 200 kN/m est environ le poids d’un mur de 10 m de haut et 400 kN/m est environ le poids d’un bâtiment entier avec trois murs de 5 m de haut et une surcharge.
La rigidité de la poutre EI est comprise entre 20 et 500 GN.m2. La plus petite valeur représente la rigidité d’un mur en maçonnerie de 0,5 m d’épaisseur avec une hauteur de 5 m et d’un module de Young équivalent à 3000 MPa pour la maçonnerie. La valeur la plus élevée est approximativement la rigidité d’un mur de béton de 0,2 m d’épaisseur, de 12 m de hauteur avec un module de Young équivalent à 20 000 MPa.
Le module d’Young du sol varie entre 40 MPa (sol souple) et 500 MPa (sol rigide) et le rayon de courbure du terrain en champ libre est défini entre 250 et 5000 m pour être représentatif d’un large éventail de scénarios.
En considérant que les structures sont couramment construites avec des fondations filantes de longueur L et largueur B telles que L >> B, et que la fondation est réalisée à la surface du sol, la capacité portante peut être obtenue par la relation de Terzaghi qui dépend essentiellement de l’angle de frottement interne et de la cohésion du sol sous la base de la fondation. Pour montrer le rôle essentiel que peut jouer la limitation de la capacité́ portante de sol sur la déflexion du bâtiment, la capacité́ portante du sol est considérée variable entre q et 4 q. Néanmoins, compte tenu des coefficients partiels de sécurité utilisés pour le dimensionnement des fondations à l’ELU (1,35 ou 1,5 sur les charges), on peut considérer que les cas considérés (pult = Xq) correspondent approximativement à des situations standards.
Pour représenter les résultats, le coefficient de rigidité relative de l’équation (2) est remplacé par l’équation (12), où le module de Young du terrain est remplacé par le coefficient de réaction Kw et la rigidité du bâti est divisée par la largeur caractéristique B du bâti. La rigidité relative est ici également sans dimension. L’équivalence entre les équations (2) et (12) nécessite d’exprimer le module de réaction Kw en fonction du module de Young du terrain. Cette question a fait l’objet de nombreuses recherches dont on pourra trouver des synthèses dans Imanzadeh (2013) par exemple. Basmaji et al. (2017) ont également développé des abaques apportant une réponse à cette question lorsque le modèle Winkler est utilisé pour étudier la déflexion d’une structure.
 (12)
(12)
Les résultats obtenus pour l’ensemble des configurations étudiées sont représentés sur la figure 10. Ils montrent que le taux de déflexion élastique en fonction de la rigidité relative forme une courbe continue qu’il est possible d’approximer à partir d’un méta-modèle basé sur l’utilisation de la fonction tangente hyperbolique (Éq. (13)).

 (13)
(13)
Ils montrent également que la prise en compte du comportement élasto-plastique du sol réduit la flèche maximale calculée pour le bâtiment. Dans un soucis de synthèse des résultats, il est possible d’introduire un coefficient de réduction a pour exprimer le taux de transmission de la déflexion élasto-plastique en fonction du taux de transmission de la déflexion élastique (Éq. (14)) :
 (14)
(14)
Avec 0 < a < 1 un facteur dépendant des paramètres du problème (L, EI, KwB, R, [qui intervient dans la formule de Δ0], q et pult). Le paramètre R caractérise le mouvement du terrain en champ libre. Il est préféré au paramètre Δ0 dans la mesure où Δ0 dépend à la fois de R et de la longueur du bâti. Si pult n’est pas atteint, alors a = 1 et le sol a toujours un comportement élastique. Le tableau 2 résume l’effet d’un accroissement de chaque facteur sur la valeur du coefficient a. Pour obtenir l’expression analytique de a, plusieurs analyses de données ont été effectuées. Les tentatives d’exprimer le paramètre a par une combinaison linéaire des paramètres d’entrée du modèle n’ont pas abouti à des résultats satisfaisants. Pour cette raison, la technique des réseaux de neurones a été utilisée (Shahin et al., 2001). Le réseau est construit avec une proportion de 10 % retenue pour la validation. Le réseau final obtenu est composé d’une couche et 3 neurones H1, H2 et H3 évalués en minimisant la variance des résidus (Éq. (15)).
 (15)
(15)
 (16)
(16)
La figure 11 représente les valeurs réelles en fonction des valeurs prévues du coefficient a. Elle permet ainsi de visualiser les résidus. Le coefficient de détermination obtenu est ici de R2 = 0,9026 et la racine de l’erreur quadratique moyenne est de 0,12. La figure 11 montre que la formulation de a a globalement tendance à surestimer les grandes valeurs de a et à sous estimer les petites valeurs de a.
Le réseau a été reconstruit avec d’autres proportions de validation (20 et 30 %). Les résultats obtenus sont sensiblement identiques, avec une racine de l’erreur quadratique moyenne variant de 0,16 à 0,20 et des coefficients associés à chaque facteur qui sont globalement semblables en termes de signe et d’intensité. En première approximation, l’application de l’équation (15) permet donc d’avoir une estimation de l’influence de la prise en compte de la plasticité sur le comportement du bâti. Cette équation doit être utilisée en tenant compte des unités des différents paramètres et des limites d’application considérées (cas sans décollement, situation symétrique, etc.)
 |
Fig. 10 Taux de transmission de la déflection Δ/Δ0 contre la rigidité relative ρ* pour un comportement élastique/élasto-plastique du sol. Deflection transmission ratio Δ/Δ0 versus the relative stiffness ρ* for elastic/elastoplastic behavior of soil. |
 |
Fig. 11 Graphique des valeurs observées en fonction des valeurs prévues. Graph of observed values versus expected values. |
4 Conclusions
Cette étude développe une approche analytique basée sur le modèle élastique de Winkler pour évaluer l’influence de la plasticité du sol sur la transmission des mouvements du terrain affectant l’interaction sol-structure. Ceci est fait en limitant la valeur maximale de la réaction du terrain à la capacité portante du sol.
Pour étudier l’effet de la plasticité du sol sur la déflexion d’une structure, une application sur un bâtiment, modélisé sous forme d’une poutre simple, a été développée avec l’existence d’une zone plastique sous celui-ci. En appliquant la méthodologie de limitation de la réaction du sol, les résultats montrent que la déflexion du bâtiment diminue lorsque l’on considère le comportement d’un sol élasto-plastique. Pour une courbure concave du terrain, les contraintes dans le sol sont limitées à la capacité portante ultime dans les zones plastiques aux limites du bâtiment et tendent à augmenter au milieu par rapport au cas élastique.
L’influence de la plasticité du sol sur le taux de transmission de la déflexion Δ/Δ0 par rapport à la rigidité relative ρ* a également été étudiée en évaluant numériquement une large gamme de 18 900 valeurs des paramètres d’ISS et de capacités portantes du sol pult. Les résultats montrent une différence significative dans le taux de transmission de la déflexion entre le comportement du sol élastique et élasto-plastique. Les résultats du comportement élastique créent une enveloppe supérieure qui englobe les résultats élasto-plastiques.
En conséquence, une équation est proposée pour estimer le taux de déflexion transmis au bâti en fonction des différents paramètres géométriques et mécaniques du problème : capacité portante du sol, rigidité du sol, longueur de la structure, rigidité de la structure, poids propre de la structure et le rayon de la courbure.
Remerciements
Les travaux présentés dans cet article ont été financés par une bourse de recherche du Conseil National pour la Recherche Scientifique au Liban (CNRS-L) et de l’Université libanaise.
Références
- Aissaoui K. 1999. Amélioration de la prévision des affaissements dans les mines à l’aide des approches empiriques, numériques et analytiques. PhD Thesis, INPL. [Google Scholar]
- Basmaji B, Deck O, Heib M. 2017. Analytical model to predict building deflections induced by ground movements. Eur J Environ Civ Eng 10: 1–23. [Google Scholar]
- Boscardin M, Cording E. 1989. Building response to excavation‐induced settlement. J Geotech Eng 115: 1–21. [Google Scholar]
- Deck O. 2002. Étude des conséquences des affaissements miniers sur le bâti. PhD Thesis, École des Mines Nancy. [Google Scholar]
- Deck O, Singh A. 2010. Analytical model for the prediction of building deflections induced by ground movements. Int J Numer Anal Methods Geomech 36: 62–84. [CrossRef] [Google Scholar]
- ElKahi E, Khouri M, Deck O, Rahme P, Mehdizadeh R. 2018. Studying the influence of uncertainties on the transmission of ground movements affecting the soil-structure interaction. 10e journées Fiabilité des Matériaux et des Structures, Bordeaux. [Google Scholar]
- Farrell RP, Mair RJ. 2011. Centrifuge modelling of the response of buildings to tunnelling. Proceedings of the Seventh International Symposium on Geotechnical Aspects of Underground Construction in Soft Clay, Rome, Vol. 2, pp. 549–554. [Google Scholar]
- Franzius JN, Potts DM, Addenbrooke TI, Burland JB. 2004. The influence of building weight on tunnelling-induced ground and building deformation. Soils Found 159: 3–17. [Google Scholar]
- Goh K, Mair R. 2011. Building damage assessment for deep excavations in Singapore and the influence of building stiffness. Geotech Eng 42: 1–12. [Google Scholar]
- Haji K, Marshall A, Franza A. 2018. Mixed empirical-numerical method for investigating tunneling effects on structures. Undergr Space Technol 73: 92–104. [CrossRef] [Google Scholar]
- Hassoun M, Villard P, Alheib M, Emeriault F. 2018. Soil reinforcement with geosynthetic for localized subsidence problems: Experimental and analytical analysis. Int J Geomech 18(10): 04018133. DOI: 10.1061/(asce)gm.1943-5622.0001265. [CrossRef] [Google Scholar]
- Imanzadeh S. 2013. Effects of uncertainties and spatial variation of soil and structure properties on geotechnical design. Cases of continuous spread footings and buried pipes. PhD. Thesis, Université Bordeaux. [Google Scholar]
- Mair R. 2013. Tunneling and deep excavations: Ground movements and their effects. Proceedings of 15th European Conference on Soil Mechanics and Geotechnical Engineering Geotechnics of Hard Soils – weak rocks, Vol. 4, pp. 39–70. [Google Scholar]
- Peck RB. 1969. Deep excavations and tunnels in soft ground. Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, State of the Art Volume, pp. 225–290. [Google Scholar]
- Potts D, Addenbrooke T. 1997. A structure’s influence on tunneling-induced ground movements. Proc Inst Civ Eng – Geotech Eng 125: 109–125. [Google Scholar]
- Ricceri G, Soranzo M. 1985. An analysis on allowable settlements of structures. Riv Ital Geotech 4: 177–188. [Google Scholar]
- Serhal J, Deck O, Al Heib M, Hage Chehade F, Abdel Massih D. 2016. Damage of masonry structures relative to their properties: Development of ground movement fragility curves. Eng Struct 113: 206–219. [CrossRef] [Google Scholar]
- Shahin M, Jaksa M, Maier H. 2001. Artificial neural network applications in geotechnical engineering. Aust Geomech 36: 49–62. [Google Scholar]
Citation de l’article : Elio El Kahi, Olivier Deck, Michel Khouri, Rasool Mehdizadeh, Pierre Rahme. Étude de l’influence de la plasticité du sol sur la transmission des mouvements du sol affectant l’interaction sol-structure. Rev. Fr. Geotech. 2018, 156, 4.
Liste des tableaux
Liste des figures
 |
Fig. 1 Présentation du déplacement en champ libre Δ0 (ElKahi et al., 2018). Presentation of the free-field deflection Δ0 (ElKahi et al., 2018). |
| Dans le texte | |
 |
Fig. 2 Comportement des structures soumises au mouvement du terrain. (a) structure de haute rigidité sur sol souple ; (b) structure de rigidité intermédiaire sur sol intermédiaire ; (c) structure flexible sur sol dur (ElKahi et al., 2018). Behavior of structures subjected to ground movement. (a) high-stiffness structure on soft ground; (b) intermediate stiffness structure on intermediate ground; (c) flexible structure on stiff ground (ElKahi et al., 2018). |
| Dans le texte | |
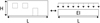 |
Fig. 3 Bâtiment similaire à une poutre élastique d’Euler-Bernoulli. Building modelled similar to an elastic Euler-Bernoulli beam. |
| Dans le texte | |
 |
Fig. 4 Modèle de Winkler. Winkler model. |
| Dans le texte | |
 |
Fig. 5 Présentation de la charge du bâtiment q, réaction du sol p(x) et la déformation du bâtiment y(x) (ElKahi et al., 2018). Presentation of the building load q, ground reaction p(x) and building deflection y(x) (ElKahi et al., 2018). |
| Dans le texte | |
 |
Fig. 6 Déplacement du sol et de la structure en équilibre statique (ElKahi et al., 2018). Displacements of the ground and the building under static equilibrium (ElKahi et al., 2018). |
| Dans le texte | |
 |
Fig. 7 Présentation de la réaction du sol pour un cas élastique et un cas élasto-plastique. Presentation of the soil reaction for an elastic case and an elastoplastic case. |
| Dans le texte | |
 |
Fig. 8 Déplacement vertical à l’interface sol-structure selon le comportement élastique et élasto-plastique du sol. Vertical displacements at the soil-structure interface according to the elastic and elastoplastic behavior of the ground. |
| Dans le texte | |
 |
Fig. 9 Conception et conditions aux limites utilisées pour le modèle numérique. Design and boundary conditions used for the numerical model. |
| Dans le texte | |
 |
Fig. 10 Taux de transmission de la déflection Δ/Δ0 contre la rigidité relative ρ* pour un comportement élastique/élasto-plastique du sol. Deflection transmission ratio Δ/Δ0 versus the relative stiffness ρ* for elastic/elastoplastic behavior of soil. |
| Dans le texte | |
 |
Fig. 11 Graphique des valeurs observées en fonction des valeurs prévues. Graph of observed values versus expected values. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




