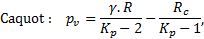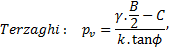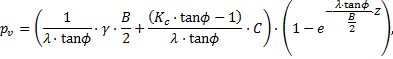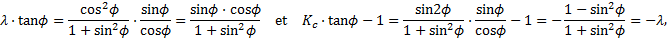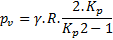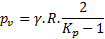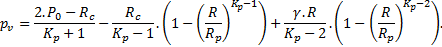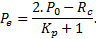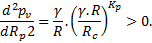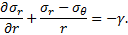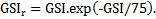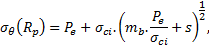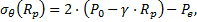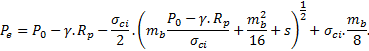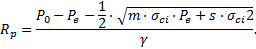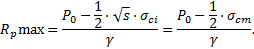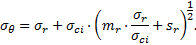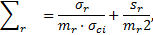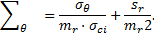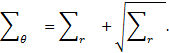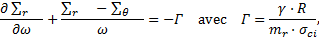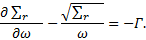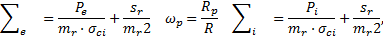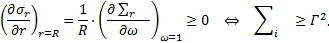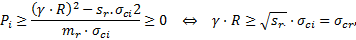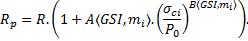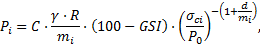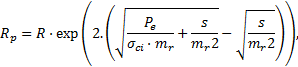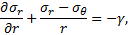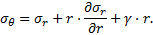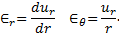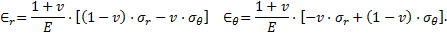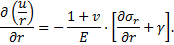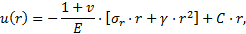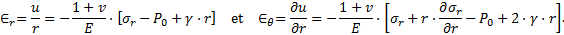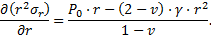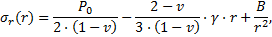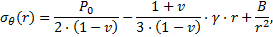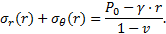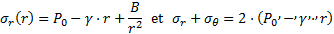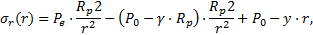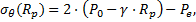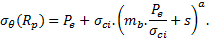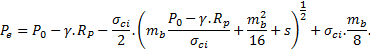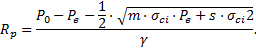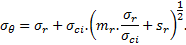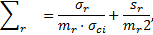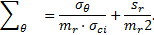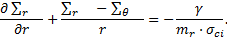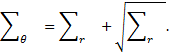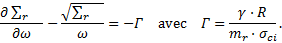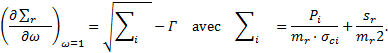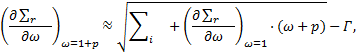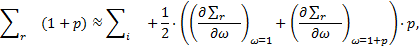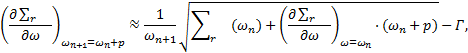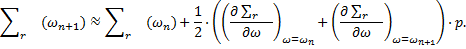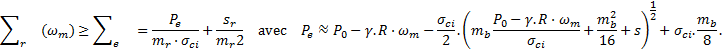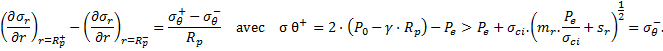© CFMS-CFGI-CFMR-CFG, 2024

1 Introduction

Les démarches récentes de conception des soutènements en tunnel profond (Ö.G.G., 2010 : Russo, 2008) font appel à la notion de « comportement du terrain à l’excavation », en développant une typologie des modes d’instabilités, sur des bases essentiellement descriptives et empiriques. En suivant Russo (2008, 2014), on peut distinguer quatre types de comportement :

• blocs instables ;

• terrain cassant (« buckling », « spalling », « rock bursting ») ;

• terrain boulant (« caving ») ;

• terrain poussant (« squeezing »).

Le premier type ne relève pas a priori du champ de notre analyse. En effet, il s’agit d’un phénomène intrinsèquement lié à la nature discontinue du milieu rocheux, décrit par des familles de discontinuités. La stabilité de bloc est souvent estimée par la méthode d’équilibre limite « du bloc-clé » sous son poids propre, sans tenir compte des forces d’interactions entre blocs autour de l’excavation. Cependant, elle peut faire l’objet d’approches plus réalistes (Ghazal et al., 2011) en rapport avec l’objet de notre analyse.

Le deuxième type correspond à des phénomènes de rupture de la matrice rocheuse, par flambage, écaillage ou éclatement, sous fortes contraintes. On peut considérer qu’il s’agit de phénomènes localisés aux parois de l’excavation, dans un massif rocheux de bonne qualité, mais qui, dans certaines conditions peuvent tendre vers les deux types suivants.

Les types de comportement « boulant » et « poussant » sont pleinement dans le champ de notre analyse. Il s’agit de comportement de « milieu continu équivalent », ayant de fortes analogies avec le comportement des sols. Le comportement « boulant » traduit l’écoulement gravitaire dans la section excavée, d’un volume de roche désagrégée. Le comportement « poussant » traduit la convergence rapide et évolutive d’un volume de roche à l’intérieur de la section excavée. Dans le milieu continu équivalent, ces deux comportements résultent du dépassement d’un seuil de plasticité ou de rupture, sous l’effet des contraintes autour de l’excavation. Dans le milieu discontinu réel, il s’agit de la mobilisation cinématique de fractures multiples, préexistantes ou néoformées, dans une zone de l’excavation que nous désignerons par l’acronyme ZMF (Zone de Mobilisation des Fractures).

Face à ce type de comportement, une des principales questions pratiques qui se pose au « chargé de soutènement » est de savoir si, quand et comment, un phénomène évolutif de convergence peut se transformer en rupture par écoulement gravitaire. Cette question est également pertinente pour le creusement au tunnelier à voussoirs, qui tend à se généraliser aux conditions de tunnel profond. En effet, le type de tunnelier utilisé (ouvert à bouclier simple ou double) permet au terrain de converger librement dans des limites géométriques prédéfinies, entre la roue d’abattage et le bouclier d’une part, et entre le bouclier et les voussoirs d’autre part, avant d’être bloqué par le mortier de scellement des voussoirs. Il y a donc lieu d’évaluer la charge de terrain susceptible de se développer dans des conditions de terrain poussant ou boulant. Notre analyse est une contribution à la réponse.

1 Pression minimale de soutènement

En théorie, l’existence possible d’une pression minimale nécessaire à la stabilité d’une cavité cylindrique résulte de la prise en compte de la gravité dans l’équilibre du domaine plastique autour de la cavité.

Caquot (1934) et Terzaghi (1943) ont proposé des formulations permettant d’estimer la pression verticale de terrain s’exerçant sur le soutènement d’un tunnel en section courante en fonction de ses dimensions transversales, de sa profondeur et des caractéristiques du terrain de couverture, suivant le modèle de Mohr-Coulomb.

Ces formulations classiques ont fait l’objet, par ailleurs de développements plus récents, notamment dans le but d’analyser la stabilité du front de taille (Anagnostou et Kovári, 1994 : Carranza-Torres et al., 2013) par des approches tri-dimensionnelles.

Ces formulations tendent vers les valeurs limites suivantes, lorsque que la profondeur Z augmente (Z >> R) :

$$\begin{array}{ll}\mathrm{Caquot}:\hfill & p_v=\frac{\gamma .R}{K_p-2}-\frac{R_c}{K_p-1}\hfill \end{array},$$(1)

$$\begin{array}{ll}Terzaghi:\hfill & p_v=\frac{\gamma .\frac{B}{2}-C}{k.\tan \varphi }\hfill \end{array},$$(2)

avec les notations explicitées au Tableau 1 :

B(m), largeur fonction de la largeur et de la hauteur de la section excavée ;

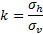$k=\frac{{\sigma }_h}{{\sigma }_v}$ rapport entre la contrainte horizontale et la contrainte verticale.

La formulation de Terzaghi (1943) est basée sur l’hypothèse du « silo », c’est-à-dire l’équilibre en frottement d’une tranche de terrain sous l’effet de son poids et du frottement s’exerçant sur ses bords verticaux, égal à k.σ_v.tan(ϕ) + c.

Cependant, comme rappelé d’ailleurs par Terzaghi lui-même, l’existence d’un rapport simple et constant entre la contrainte horizontale et la contrainte verticale sur une ligne verticale de cisaillement n’est pas une hypothèse rigoureuse. Ainsi, le rapport k varierait entre 1 à la clé du tunnel et 1,5 à la hauteur égale à 2.B, et l’effet de voûte s’annulerait au-delà de 5.B pour retrouver l’état de contrainte géostatique.

En pratique, la valeur de k est choisie sur des bases empiriques.

Champagne de Labriolle (2018) propose alors une expression vérifiant l’hypothèse de plans de glissement verticaux sur les bords du « silo » :

$$p_v=\left(\frac{1}{\lambda \cdot \tan \varphi }\cdot \gamma \cdot \frac{B}{2}+\frac{\left(K_c\cdot \tan \varphi -1\right)}{\lambda \cdot \tan \varphi }\cdot C\right)\cdot \left(1-e^{-\frac{\lambda \cdot \tan \varphi }{\frac{B}{2}}\cdot Z}\right),$$

avec :

$$\begin{array}{lll}\lambda \cdot \tan \varphi =\frac{{\cos }^2\varphi }{1+{\sin }^2\varphi }\cdot \frac{\sin \varphi }{\cos \varphi }=\frac{\sin \varphi \cdot \cos \varphi }{1+{\sin }^2\varphi }\hfill & \text{et}\hfill & K_c\cdot \tan \varphi -1=\frac{\sin 2\varphi }{1+{\sin }^2\varphi }\cdot \frac{\sin \varphi }{\cos \varphi }-1=-\frac{1-{\sin }^2\varphi }{1+{\sin }^2\varphi }=-\lambda \hfill \end{array},$$

que l’on peut réécrire ainsi, pour Z >> B :

$p_v=\left(\frac{1}{\tan \varphi }+2.\tan \varphi \right).\gamma .\frac{B}{2}-\frac{C}{\tan \varphi }=\left(\frac{2.\sqrt{K_p}}{K_p-1}+\frac{K_p-1}{\sqrt{K_p}}\right).\gamma .\frac{B}{2}-\frac{R_c}{K_p-1}$.

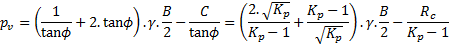avec :

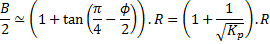$\frac{B}{2}\simeq \left(1+\tan \left(\frac{\pi }{4}-\frac{\varphi }{2}\right)\right).R=\left(1+\frac{1}{\sqrt{K_p}}\right).R$ pour un tunnel circulaire.

L’analyse de « l’effet de voûte » dans les terrains frottants a conduit d’autres auteurs à des formulations différentes :

$p_v=\gamma .R.\frac{2.K_p}{K_{p}2-1}$ (Atkinson et Potts, 1977),

$p_v=\gamma .R.\frac{2}{K_p-1}$ (Ono et Yamada, 1993).

Ces formulations appellent deux remarques :

• Il s’agit d’approches, basées sur l’hypothèse d’un équilibre limite du terrain entre le tunnel et la surface ;

• La pression verticale limite à grande profondeur s’annule pour des valeurs relativement faibles de la cohésion équivalente, de l’ordre de C = γ.R ;

• A contrario, en l’absence de cohésion, la pression verticale est non nulle.

Il alors intéressant de comparer les différentes formulations pour une cohésion nulle (Fig. 1).

On remarque le caractère très conservatif de la formulation de Terzaghi. A contrario, utilisée en analyse à rebours (« back-analysis »), elle peut conduire à une surestimation des caractéristiques (ϕ, C).

La formulation de Caquot (1934) a été modifiée pour le cas des tunnels profonds avec un domaine plastique (ZMF) limité autour de l’excavation, par Caquot et Kérisel (1956) et généralisée par Detournay (1984) :

$$p_v=\frac{2.P_0-R_c}{K_p+1}-\frac{R_c}{K_p-1}.\left(1-{\left(\frac{R}{R_p}\right)}^{K_p-1}\right)+\frac{\gamma .R}{K_p-2}.\left(1-{\left(\frac{R}{R_p}\right)}^{K_p-2}\right).$$(3)

Cette formulation fait l’hypothèse d’un champ de gravité radial autour de l’excavation, ce qui est acceptable au voisinage angulaire de la clé.

Le premier terme représente la condition de continuité P_e de la contrainte radiale à la limite de la zone plastique (ZMF) :

$$P_e=\frac{2.P_0-R_c}{K_p+1}.$$(4)

Dans la formulation originelle de Caquot et Kérisel, ce premier terme était nul.

La dérivation de la formule (3) p_v en fonction de R_p donne : 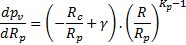$\frac{d{p}_v}{d{R}_p}=\left(-\frac{R_c}{R_p}+\gamma \right).{\left(\frac{R}{R_p}\right)}^{K_p-1}$ qui s’annule pour $R_p=\frac{R_c}{\gamma }$.

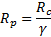La dérivée seconde étant :

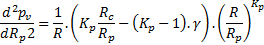$\frac{d^2{p}_v}{d{R}_{p}2}=\frac{1}{R}.\left(K_p\frac{R_c}{R_p}-\left(K_p-1\right).\gamma \right).{\left(\frac{R}{R_p}\right)}^{K_p}$ qui devient, pour $R_p=\frac{R_c}{\gamma }$ :

$$\frac{d^2{p}_v}{d{R}_{p}2}=\frac{\gamma }{R}.{\left(\frac{\gamma .R}{R_c}\right)}^{K_p}>0.$$

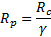La pression 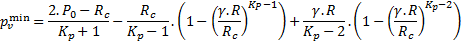$p_v^{\min }=\frac{2.P_0-R_c}{K_p+1}-\frac{R_c}{K_p-1}.\left(1-{\left(\frac{\gamma .R}{R_c}\right)}^{K_P-1}\right)+\frac{\gamma .R}{K_p-2}.\left(1-{\left(\frac{\gamma .R}{R_c}\right)}^{K_p-2}\right)$ est alors la valeur minimale et p_v^min est égale à la pression P_e d’apparition de la ZMF lorsque R_c = γ.R.

Fig. 1 Comparaison des formules de pression de soutènement. Comparison between minimal support pressure formulas.

2 Prise en compte de la gravité dans la méthode Convergence-Confinement

À la suite de Pacher (1964), des travaux plus récents ( Roussef, 1998 : Mohammadi et al., 2013 : Oreste et al., 2019) ont introduit l’effet de la gravité dans les formulations de la courbe de convergence du terrain (« Ground Response Curve »).

Il faut rappeler que la méthode « Convergence-Confinement » théorisée par Panet (1973), et sa dérivée, la méthode du « taux de déconfinement » utilisée dans les modèles numériques, est un concept permettant de prendre en compte, dans un modèle bi-dimensionnel, le phasage tri-dimensionnelle de creusement et de soutènement d’un tunnel circulaire, dans l’hypothèse des conditions axisymétriques autour de l’axe d’un tunnel profond dans un milieu non pesant.

Notamment, la proximité du front de taille est prise en compte par une pression fictive, P_i à l’intérieur de l’excavation, variant entre deux états d’équilibre réels, la contrainte initiale supposée isotrope P_i = P₀ et la pression radiale sur le soutènement loin du front P_i = P_s.

Cependant, en introduisant dans l’équation d’équilibre indéfini, un terme gravitaire supposé radial au voisinage angulaire de la clé, mais qui, en fait, rompt la symétrie axiale, il apparaît que la pression fictive ne peut être indépendante des composantes gravitaire et angulaire.

Cela étant posé, on peut considérer que les développements qui vont suivre sont valables à une certaine distance du front de taille et au voisinage de la clé (θ = π/2), σ_r, σ_θ étant alors des contraintes principales et l’équation d’équilibre se simplifiant en :

$$\frac{\partial {\sigma }_r}{\partial r}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=-\gamma .$$(5)

Pour prendre en compte l’effet de la gravité, Roussev (1998) et par la suite Mohammadi et al. (2013) font l’hypothèse qu’il possible de superposer deux solutions de contraintes dans la ZMF.

La première solution vérifie l’équation d’équilibre pour un terrain non pesant (ϒ = 0 dans (5)) et le critère de plasticité, à savoir un critère de type Mohr-Coulomb pour le premier et Hoek et Brown pour le second, en considérant toutefois une contrainte initiale réduite P₀– γ.R_p à la limite de la ZMF (r = R_p).

La deuxième solution vérifie l’équation d’équilibre (5) dans la ZMF, en considérant une contrainte radiale nulle à la limite de la ZMF, suivant l’hypothèse de Caquot et Kérisel. Compte tenu de la non-linéarité du critère de Hoek et Brown, ces développements conduisent à des solutions implicites, obtenues par des méthodes itératives. Les auteurs introduisent par ailleurs, des caractéristiques résiduelles dans la ZMF, ce point faisant l’objet du paragraphe suivant.

Cependant, la comparaison de l’approche de Roussev avec la formulation de Detournay montre que la superposition des deux solutions de contraintes introduit une erreur car la résistance de la ZMF est alors doublement mobilisée, d’une part par la composante géostatique dans le milieu non pesant et d’autre part par la composante gravitaire.

Plus récemment, Oreste et al. (2019) intègre directement par une méthode de différence finie unidimensionnelle dans la direction radiale, l’équation d’équilibre (5) et le critère de plasticité de type Hoek et Brown avec des caractéristiques résiduelles.

3 Estimation des paramètres de résistance résiduelle

On peut déduire de l’équation d’équilibre (5) que, si la contrainte déviatorique (σ_θ−σ_r) tend vers une faible valeur, la composante gravitaire devient prépondérante. En paroi du tunnel et en l’absence de soutènement, cette contrainte est égale à la résistance à la compression résiduelle notée σ_cr. Il apparaît donc que l’estimation de cette grandeur est fondamentale dans l’évaluation de l’équilibre de la section du tunnel.

Cai et al. (2007) proposent d’estimer les caractéristiques de résistance résiduelle à partir de l’indice GSI_r, c’est-à-dire l’indice GSI de la ZMF. À partir de propositions logiques autour du principe de détermination du GSI, de simulation numérique de l’endommagement et d’expérimentation in situ par des essais de cisaillement sur bloc, les auteurs proposent une méthodologie pour déterminer GSI_r suivant la description du massif rocheux endommagé en fonction des deux paramètres « Block Volume » et « Joint Conditions factor ». À partir des données bibliographiques et des expérimentations, ils proposent une estimation préliminaire à partir de la formule :

$$\text{GS}{\text{I}}_{\text{r}}=\text{GSI}\text{.exp}\left(\text{-GSI/75}\right).$$(6)

Logiquement, les auteurs estiment les paramètres de résistance résiduelle de la ZMF suivant le critère de Hoek et Brown à partir des formules proposes par Hoek pour les paramètres de « pic » (voir Tab. 1), en remplaçant GSI par GSI_r et en choisissant « le facteur de dommage » D à la valeur zéro, l’endommagement étant pris en compte dans la valeur de GSI_r.

Antérieurement, Russo et al. (1998) ont proposés, à partir des relations entre les paramètres de « pic » (m_b, s) et les paramètres résiduels (m_r, s_r) données par Hoek et Brown (Hoek et Brown, 1988,1993) et Faiella et Ribacchi (Ribacchi, 1993) d’autres relations entre GSI et GSI_r, ainsi que Oreste (2014).

Le graphe présenté (Fig. 2) montre les différentes relations proposées entre GSI_r et GSI, les relations de Hoek et Brown et Faiella et Ribacchi étant inversées par Russo et al. (1998) à partir de m_r et s_r pour obtenir une valeur équivalente de GSI_r.

On peut constater que les relations proposées par Russo et al. (1998) à partir de Hoek et Brown, Faiella et Ribacchi, et par Oreste donnent des valeurs du GSI_r relativement proches du GSI alors que Cai et al. (2007) et Russo et al. (1998), donnent des valeurs nettement plus faibles, notamment pour les valeurs initiales élevées de GSI. Cet aspect fait l’objet d’une argumentation sérieuse de la part de Cai et al., à partir de la fragmentation de blocs et de la dégradation des caractéristiques de joint au sein de la ZMF.

Intuitivement, il conviendrait d’enrichir cette formulation par l’influence de deux facteurs, qui seraient l’indice d’endommagement de la roche D_i défini comme le rapport de la contrainte orthoradiale maximale à la résistance à la compression de la roche intacte (Martin et al., 1999), d’une part, et le niveau de déformation dans la ZMF d’autre part. Sur ce dernier point, Cai et al. (2007) reconnaissent que la valeur de GSI_r peut évoluer, engendrant un mécanisme de radoucissement (« Strain Softening ») et qu’il convient de tenir compte de l’objectif de dimensionnement à atteindre en terme de déformation.

Enfin, il faut considérer avec prudence la validité de l’hypothèse du Milieu Continu Équivalent pour des valeurs du GSI supérieure à 60.

Fig. 2 Relations entre GSI et GSIr proposées dans la littérature. Relations between GSI and GSIr in literature.

4 Résolution des contraintes dans la Zone de Mobilisation des Fractures

Un comportement du massif « élasto-fragile » est retenu pour simplification, avec un critère en résistance de « pic » à l’extérieur de la ZMF et un critère résiduel à l’intérieur, déterminé par la valeur GSI_r.

Le critère de Hoek et Brown (H&B) en résistance de « pic » est atteint à la limite r = R_p de la ZMF :

$${\sigma }_{\theta }\left(R_p\right)=P_e+{\sigma }_{ci}.{\left(m_b.\frac{P_e}{{\sigma }_{ci}}+s\right)}^{\frac{1}{2}},$$(7)

avec les notations explicitées au Tableau 1 :

P_e, la contrainte radiale à la limite de la ZMF.

En prenant comme hypothèses simplificatrices (voir en annexe) que P₀ la contrainte in situ à l’axe du tunnel est isotrope, égale à γ.Z et que ν le coefficient de Poisson est égal à 0,5, la condition de continuité à la limite r = R_p de la ZMF s’écrit :

$${\sigma }_{\theta }\left(R_p\right)=2\cdot \left(P_0-\gamma \cdot R_p\right)-P_e,$$(8)

dans le domaine élastique.

De (7) et (8), on en déduit :

$$P_e=P_0-\gamma .R_p-\frac{{\sigma }_{ci}}{2}.{\left(m_b\frac{P_0-\gamma .R_p}{{\sigma }_{ci}}+\frac{m_b^2}{16}+s\right)}^{\frac{1}{2}}+{\sigma }_{ci}.\frac{m_b}{8}.$$(9)

On obtient R_p en fonction de P_e en résolvant (9) :

$$R_p=\frac{P_0-P_e-\frac{1}{2}\cdot \sqrt{m\cdot {\sigma }_{ci}\cdot P_e+s\cdot {\sigma }_{ci}2}}{\gamma }.$$(10)

Il existe une valeur R_p^max pour laquelle la contrainte P_e à la limite de la ZMF est nulle (hypothèse de Caquot et Kérisel) :

$$R_p\max =\frac{P_0-\frac{1}{2}\cdot \sqrt{s}\cdot {\sigma }_{ci}}{\gamma }=\frac{P_0-\frac{1}{2}\cdot {\sigma }_{cm}}{\gamma }.$$(11)

La pression gravitaire égale à ϒ. (R_p^max−R) est un majorant de la pression intérieure nécessaire à l’équilibre. Elle tend vers la contrainte in situ P₀ lorsque que σ_cm tend vers zéro (GSI→0) et que la ZMF atteint la surface.

Le critère H&B en résistance résiduelle dans la ZMF, s’écrit :

$${\sigma }_{\theta }={\sigma }_r+{\sigma }_{ci}\cdot {\left(m_r\cdot \frac{{\sigma }_r}{{\sigma }_{ci}}+s_r\right)}^{\frac{1}{2}}.$$(12)

Pour la suite, on adoptera la transformation suivante, proposée par Londe (1988) :

$${\sum }_r=\frac{{\sigma }_r}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2},$$(13a) $${\sum }_{\theta }=\frac{{\sigma }_{\theta }}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2}.$$(13b)

Le critère H&B en résistance résiduelle dans la ZMF, prend alors la forme canonique suivante :

$${\sum }_{\theta }={\sum }_r+\sqrt{{\sum }_r}.$$(12b)

En posant :

r = R.ω et dr = R.dω, l’équation d’équilibre (5) s’écrit alors :

$$\begin{array}{lll}\frac{\partial {\sum }_r}{\partial \omega }+\frac{{\sum }_r-{\sum }_{\theta }}{\omega }=-\Gamma \hfill & \text{avec}\hfill & \Gamma =\frac{\gamma \cdot R}{m_r\cdot {\sigma }_{ci}}\hfill \end{array},$$

Σ_r vérifie alors l’équation différentielle suivante :

$$\frac{\partial {\sum }_r}{\partial \omega }-\frac{\sqrt{{\sum }_r}}{\omega }=-\Gamma .$$(14)

L’équation (14) n’admet pas de solution explicite. Le principe d’une résolution numérique par la méthode de Runge-Kuta d’ordre 2 est présenté en annexe.

Les grandeurs adimensionnelles suivantes sont approchées numériquement :

$$\begin{array}{lll}{\sum }_e=\frac{P_e}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2}\hfill & {\omega }_p=\frac{R_p}{R}\hfill & {\sum }_i=\frac{P_i}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2}\hfill \end{array},$$

avec P_e, la contrainte radiale à la limite de la ZMF, R_p le rayon à la limite de la ZMF et P_i ≥ 0 la pression intérieure minimale à la paroi du tunnel.

Si la contrainte radiale diminue dans la ZMF, le déviateur diminue aussi suivant le critère :

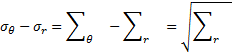${\sigma }_{\theta }-{\sigma }_r={\sum }_{\theta }-{\sum }_r=\sqrt{{\sum }_r}$ et conduit à la rupture en traction sous l’effet de la force volumique gravitaire.

Une condition de non-rupture en traction dans la ZMF est donc nécessaire mais non suffisante et serait :

$$\begin{array}{lll}{\left(\frac{\partial {\sigma }_r}{\partial r}\right)}_{r=R}=\frac{1}{R}\cdot {\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega =1}\ge 0\hfill & \iff \hfill & {\sum }_i\ge {\Gamma }^2\hfill \end{array}.$$

Cette condition implique l’existence d’une pression intérieure minimale non nulle si :

$$\begin{array}{lll}{P}_i\ge \frac{{\left(\gamma \cdot R\right)}^2-s_r.{\sigma }_{ci}2}{m_r\cdot {\sigma }_{ci}}\ge 0\hfill & \iff \hfill & \gamma \cdot R\ge \sqrt{s_{r\cdot }}\cdot {\sigma }_{ci}={\sigma }_{cr}\hfill \end{array},$$(15)

avec σ_cr, la résistance en compression résiduelle dans la ZMF.

Cependant, on peut remarquer que pour un tunnel dans un massif rocheux, même de qualité très médiocre (s_r ≈ 4.10⁻⁴, σ_ci ≈ 10 MPa), la rupture en traction n'est que rarement possible.

5 Étude paramétrique en conditions de tunnel profond

5.1 Comparaison entre milieu pesant et milieu non pesant

Une étude paramétrique a été menée pour les plages de paramètres définies ci-dessous :

• σ_ci = [5−140 MPa] ;

• m_i = [5−30] ;

• GSI = [15−90] ;

• P₀ = [8−57 MPa] ↔ Z = [300−2100 m].

Les conditions non prises en compte dans cette étude sont les profondeurs de tunnel inférieures à 300 m.

Nous rappelons également que les cas étudiés pour des valeurs de GSI supérieures à 60 doivent être considérés avec prudence, les hypothèses du Milieu Continu Équivalent étant rarement vérifiées dans ces conditions.

L’étude a été menée pour un rayon de tunnel standard de 5 m. Un cas de grande section est examiné en section 7.

La figure 3 illustre les résultats obtenus. Ils mettent en évidence la faible incidence de la prise en compte de la gravité en conditions de tunnel profond. Cependant, pour les valeurs élevées de R_p (R_p>10.R), il apparaît que l’influence du poids de la ZMF devient significative.

Ces cas extrêmes correspondent à des cas théoriquement stables mais peu représentatifs : en effet, on peut estimer que la convergence radiale qui en résulterait est de l’ordre du rayon de la section ! : u_r≈u_e. manque. (R_p/R)²≈R lorsque u_e, la convergence radiale à l’apparition de la ZMF, est de l’ordre de 1% de R. L’instabilité de la section se traduirait alors par la fermeture totale de celle-ci. Par ailleurs, on peut remarquer que ces valeurs restent très en deçà de R_p^max définie en (11).

Fig. 3 Graphes Rp/R et Pe / P0 – comparaison milieu pesant et non pesant. Graph Rp/R-Pe / P0–comparison between with or without weight media.

5.2 Pression intérieure minimale

Comme le montre la figure 4, on constate qu’une pression intérieure minimale n’est généralement pas théoriquement nécessaire pour la stabilité, pour l’ensemble des cas étudiés, sauf pour des roches de très faible compétence (P₀ / σ_ci>3).

Ce résultat contredit l’hypothèse de Pacher (1964), ayant servi de base à la Nouvelle Méthode Autrichienne, théorisée par Rabcewicz (1969).

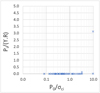Fig. 4 Pression minimale en fonction de la compétence de la roche. Minimal pressure, depending on rock competency.

5.3 Corrélations

Le premier objectif de l’étude paramétrique est d’examiner la dépendance de [R_p], [P_i] résultant de la formulation proposée aux caractéristiques géomécaniques de base, à savoir la résistance σ_ci et le paramètre de « fragilité » m_i de la roche, la contrainte initiale P₀ et l’indice GSI du massif rocheux.

Cette étude n’a pas pour objectif de substituer une corrélation simplifiée à la démarche rigoureuse présentée précédemment mais de mettre en évidence l’influence des paramètres géomécaniques. On peut cependant espérer qu’une formule approximative simple sera utile afin d’exploiter rapidement des observations sur site.

Ainsi, des corrélations correctes sont obtenues avec le rayon R_p de la ZMF pour Pi = 0, de la forme :

$$R_p=R.\left(1+A⟨GSI,m_i⟩.{\left(\frac{{\sigma }_{ci}}{P_0}\right)}^{B⟨GSI,m_i⟩}\right).$$(16)

On constate que la puissance B décroît à l’inverse de m_i tandis que le multiplicateur A décroît à l’inverse de m_i et de GSI, avec en première approximation (Fig. 5) :

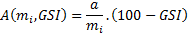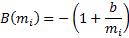$A\left(m_i,GSI\right)=\frac{a}{m_i}.\left(100-GSI\right)$ et $B\left(m_i\right)=-\left(1+\frac{b}{m_i}\right)$ avec a = [1,0−2,0] et b = [3,0−1,5].

Fig. 5 Graphes Rp/R-σci / P0 et corrélation. Graph Rp/R-σci / P0 and correlation.

6 Étude paramétrique de la pression intérieure minimale

Il a été montré en section 5, qu’une pression minimale positive nécessaire à l’équilibre apparaît dans des conditions particulières de « tunnel en roche tendre » pour lesquelles le rayon de ZMF atteint une valeur extrême. Une étude paramétrique a été menée pour les plages de paramètres correspondants à ces conditions :

• σ_ci = [2−20 MPa] ;

• m_i = [5−15] ;

• GSI = [15−75] ;

• P₀ = [1,25−15 MPa] ↔ Z = [50−600 m].

6.1 Pression intérieure minimale

On constate que la pression minimale P_i est une fonction décroissante de 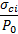$\frac{{\sigma }_{ci}}{P_0}$. Cette pression est nulle si 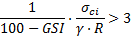$\frac{1}{100-GSI}\cdot \frac{{\sigma }_{ci}}{\gamma \cdot R}>3$ et non nulle si 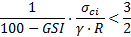$\frac{1}{100-GSI}\cdot \frac{{\sigma }_{ci}}{\gamma \cdot R}<\frac{3}{2}$ (17) (Fig. 6).

La pression intérieure minimale est également une fonction décroissante de m_i, et en moindre mesure, de l’indice GSI . Comme il existe, sauf pour les très faibles résistances de la roche, une bonne corrélation entre la pression minimale P_i et la pression gravitaire maximale de la ZMF qui serait de la forme P_i = 1/K x ϒ. (R_p−R), on peut rechercher une corrélation générale de la forme, valable si 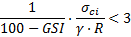$\frac{1}{100-GSI}\cdot \frac{{\sigma }_{ci}}{\gamma \cdot R}<3$ :

$$P_i=C\cdot \frac{\gamma \cdot R}{m_i}\cdot \left(100-GSI\right)\cdot {\left(\frac{{\sigma }_{ci}}{P_0}\right)}^{-\left(1+\frac{d}{m_i}\right)},$$(18)

avec C = [0,1−0,4] et d = [3,0−1,5] (Fig. 7).

On peut également remarquer que la pression intérieure minimale est couramment très inférieure à la pression gravitaire γ. (R_p−R) (« poids du mort-terrain »). Cependant, cette pression peut être atteinte dans des roches très tendres ductiles ou altérées et intensément fracturées (roches argileuses, roches « de faille »…), ayant un comportement plastique à la profondeur du tunnel. Il apparaît également que ces conditions dépendent des dimensions de la section, en fonction du rapport σ_ci/(ϒ.R) qui en fixe le seuil d’apparition (16).

Fig. 6 Pression minimale en fonction de la compétence de la roche et corrélation. Minimal internal pressure, depending on rock competency and correlation.

Fig. 7 Pression intérieure minimale en fonction du rayon de la ZMF. Minimal internal pressure vs. EFZ radius.

7 Études de cas

7.1 Cas 1 d’après Oreste et al.

Le premier cas étudié est celui présenté par Oreste et al. (2019), déjà évoqué en section 2.

Le Tableau 2 rappelle les données du cas étudié (Fig. 8).

La comparaison des valeurs R_p du rayon de la ZMF en fonction de la pression intérieure appliquée P_i, obtenues à partir de la résolution numérique de (14) avec celles obtenus par Oreste et al. est présentée sur la figure 11.

On constate des différences importantes entre les valeurs maximales obtenues pour P_i = 0 :

La rayon R_p calculée en différences finies pour le critère H&B dans le cas d’un milieu non pesant (γ = 0) par Oreste et al. est supérieur de 15 % à celui estimé par :

$$R_p=R\cdot \exp \left(2.\left(\sqrt{\frac{P_e}{{\sigma }_{ci}\cdot m_r}+\frac{s}{m_{r}2}}-\sqrt{\frac{s}{m_{r}2}}\right)\right),$$(19)

d’après Carranza-Torres et al. (1999) ;

Le rayon R_p approchée numériquement par (14) pour un milieu pesant est supérieur de 17 % à celui calculé par (19) pour un milieu non pesant, alors que les valeurs calculées en différences finies par Oreste et al. présentent un écart de 50 %, ce qui est surprenant car, comme le montre la figure 9, l’influence de de la composante gravitaire semble relativement faible.

En effet, l’augmentation relative du rayon de la ZMF dans le milieu pesant est corrélée à une diminution des contraintes radiales et orthoradiales.

Or, dans un milieu non pesant et en l’absence de pression interne (P_i = 0), on montre que l’effort orthoradial N, résultante sur un plan radial, de la contrainte σ_θ au sein de la ZMF est égal à : 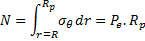$N={\int }_{r=R}^{R_p}{\sigma }_{\theta }dr=P_e.R_p$ avec P_e, la contrainte radiale sur la limite R_p de la ZMF (Fig. 10).

Dans un milieu pesant, le poids W de la ZMF modifie l’équilibre. Dans le cas présenté, on constate que l’effort N dans le milieu pesant est approximativement égal à la somme de N dans le milieu non pesant et du poids W de la tranche (W = ¼.π. (R_p²−R²). Cependant, W ne représente que 13 % de l’effort N.

Fig. 8 Rayon Rp de la ZMF en fonction de la pression intérieure Pi, comparaison avec Oreste et al. (2019). EFZ radius, depending on internal pressure Pi, comparison with Oreste et al. (2019).

Fig. 9 Variation des contraintes radiale et orthoradiale dans la ZMF. Variation of radial/tangential stress in EFZ.

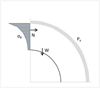Fig. 10 Équilibre d’une tranche de la ZMF. Equilibrium of an EFZ part.

7.2 Cas 2 : comparaison avec des méthodes empiriques pour les cavités minières

Le deuxième cas étudié est une comparaison avec deux méthodes empiriques d’évaluation de la stabilité des cavités d’extraction, utilisées pour l’exploitation minière dans les massifs rocheux compétents. L’intérêt de ce cas réside dans l’usage limité des soutènements (boulons, tirants) dans les cavités d’extraction, justifié par leur existence temporaire, malgré leurs grandes dimensions. Ainsi, sur 139 « stopes » étudiés par G. W. Capes (2009), leur hauteur moyenne atteint 48 m pour 15 m de largeur.

Deux méthodes empiriques couramment utilisées sont illustrées par les graphes en figure 11.

La méthode du « graphe de portée critique » (« critical span graph ») est notamment utilisée pour les exploitations minières en développement subhorizontale, par « chambres et piliers » par exemple ; la méthode du « graphe de stabilité » est utilisée pour les exploitations en développement subverticale de type « sub-level open stoping » (« dépilage par chambre vide ») par exemple. En première analyse, les dimensions pluri-décamètriques des cavités rendent l’hypothèse du Milieu Continu Équivalent pertinente, même dans un massif rocheux moyennement fracturé (50 < RQD < 75).

Le Tableau 3 présente les données du cas étudié, pour une cavité de 15 m de rayon équivalent située à 1000 m de profondeur :

La portée critique est obtenue directement à partir du RMR, en retenant la valeur RMR’ = GSI + 5, en l’absence d’eau et sans correction de pendage.

Le nombre de stabilité N est déterminé à partir de l’indice Q’ de Barton modifié pour J_w et SRF égaux à 1, et des paramètres d’ajustement A, B, C (Potvin Y.,1988) avec (Tab. 4) :

Les graphes présentés en figure 11 montrent clairement qu’une cavité non soutenue de cette dimension dans un massif rocheux de qualité moyenne est potentiellement instable.

En revanche, la résolution numérique de (14) conduit à une cavité stable pour une pression intérieure nulle et un rayon R_p de 17 m !

Plusieurs facteurs peuvent expliquer cette conclusion divergente :

– La prise en compte par les critères empiriques de toute instabilité conduisant à des volumes importants en « hors-profils » stériles, préjudiciables au rendement de l’exploitation ;

– La non prise en compte par l’approche théorique de la géométrie réelle des cavités minières, très éloignée de la forme circulaire, et qui conduit à des concentrations de contraintes et des instabilités locales.

On peut déduire de cette comparaison qu’il faut distinguer l’instabilité générale théorique des phénomènes régressifs d’instabilités locales conduisant à une forme stable.

Fig. 11 À gauche « graphe de portée critique » de Lang (d’après E. García-Gonzalo et al., 2016) ; à droite « graphe de stabilité » de Mathews (d’après G. W. Capes, 2009). At left: critical span graph from Lang (after E. García-Gonzalo et al., 2016); at right: stability graph from Mathews (after G. W. Capes, 2009).

7.3 Cas 3 : tunnel à faible profondeur

Le troisième cas étudié, tiré d’un cas réel, est celui d’un tunnel urbain à faible profondeur (Z < 10.R) dans un terrain de type schistes (shale) intensément tectonisé.

Le Tableau 5 présente les données du cas étudié :

Pour le jeu de caractéristiques n°1, pour une pression intérieure P_i nulle ; le rayon R_p atteint 12,6 m et l’équilibre ne peut être atteint pour une pression intérieure pression minimale P_i^min = 6 kPa. Même si la pression d’équilibre apparaît faible au regard des capacités usuelles des soutènements, un risque d’instabilité existe en cas de défaillance d’un élément de soutènement. Il faut également rappeler que cette analyse ne prend pas en compte de critère de déformation, critique dans ce cas.

7.4 Cas 4 : tunnel à grande profondeur en terrain poussant

Le quatrième cas étudié, est celui d’une galerie de reconnaissance du Tunnel de Base de la liaison ferroviaire Lyon-Turin dans les formations du Houiller, intensément tectonisées. Le Houiller briançonnais est constitué en proportion variable, de grès, de schistes graphiteux et de houille. La galerie de reconnaissance a été creusée à la profondeur maximale de 600 m. À cette profondeur, des mesures ont mis en évidence des contraintes in situ quasi-isotropes.

Cet ouvrage de 13 m de diamètre excavé en section quasi-circulaire en méthode traditionnelle, a rencontré d’importantes difficultés de réalisation (fortes convergences, éboulements…) et a fait l’objet de nombreuses auscultations, de travaux de recherche et de calage sur les mesures à l’aide de modèles numériques.

En particulier, un évènement bien documenté est un éboulement de 700 m³ ayant affecté 15 m de galerie à l’arrière du front de taille. Des mesures extensomètriques en forage ont mis en évidence l’extension d’une Zone d’Endommagement jusqu’à plus de 20 m de la paroi, soit R_p/R>4. Les relevés géologiques au front avant l’éboulement ont permis d’identifier la présence d’une zone de faille à remplissage de matériaux complètement tectonisés à matrice argileuse.

Hors zone de faille, les paramètres de résistance obtenus par calage sur les mesures de convergence sont les suivants : φ = 25° et C ≈900−1000 kPa, sans distinction de paramètres résiduelles. L’indice GSI résultant des observations aux fronts de taille était de l’ordre de 25.

Le Tableau 6 présente les données utilisées pour l’analyse de stabilité hors zone de faille :

Pour ce jeu de caractéristiques, pour une pression intérieure P_i nulle ; le rayon R_p atteint 27 m mais la section reste théoriquement stable sans soutènement et la pression nécessaire pour compenser l’effet du poids de la ZMF est de 35 kPa, ce qui est admissible par un soutènement de type « souple » (boulons, béton projeté et cales compressibles, cintres coulissants…) tel qu’il a été mis en œuvre dans l’ouvrage en 1^ère phase.

Le Tableau 7 présente un jeu de caractéristiques dégradés applicable à une zone de faille :

Pour ce jeu de caractéristiques, l’équilibre ne peut être atteint pour une pression intérieure nulle. Une pression minimale P_i^min = 308 kPa est nécessaire pour un rayon plastique R_p, qui atteint théoriquement 205 m ! C’est la pression nécessaire pour compenser l’effet du poids de la ZMF, ce qui pourrait conduire à la ruine d’un soutènement de type rigide (cintres lourds, coque de béton projeté) pour une telle section. En revanche, il est intéressant de constater que la galerie pilote en section réduite (R = 2,5 m) qui a été réalisée pour traverser la zone de faille serait théoriquement stable sans soutènement (P_i^min = 0) et que, dans ce cas, la pression nécessaire pour compenser l’effet du poids de la ZMF se réduit à 70 kPa.

Conclusion

Dans l’hypothèse d’un Milieu Continu Équivalent pour le massif rocheux et en introduisant la composante gravitaire dans l’équation d’équilibre générale, la généralisation au cas des tunnels profonds de la formulation de Caquot pour un critère de résistance résiduel permet de poser les conditions d’existence d’une pression intérieure minimale, nécessaire à la stabilité de la section. La comparaison avec la formulation classique de la « charge de Terzaghi » montre que celle-ci ne semble pas applicable au cas des tunnels profonds. Terzaghi (1946) lui-même recommandait une approche empirique, basée sur une classification. Il est d’ailleurs intéressant de constater que pour les classes du massif rocheux les plus défavorables, la charge estimée par Terzaghi représente la pression gravitaire d’une hauteur de terrain comprise en 4.R et 20.R, comparable à l’extension théorique de la Zone de Mobilisation des Fractures.

L’emploi d’un critère de résistance linéaire de type Mohr-Coulomb introduit cependant une approximation de la résistance réelle à la paroi du tunnel, dans un sens probablement non conservatif. Le développement analytique de la formulation avec le critère non linéaire de Hoek et Brown présente donc un intérêt majeur. L’influence du rapport des contraintes « σ_horizontale/σ_verticale » différent de l’unité n’a cependant pas été examiné et pourrait jouer un rôle dans l’apparition de l’instabilité. La présence d’écoulement ou de pression interstitielle n’a pas non plus, été prise en compte, alors qu’il s’agit d’un facteur souvent déterminant dans le déclenchement de la rupture.

Nonobstant ces hypothèses restrictives, l’existence d’une pression minimale s’avère être un indicateur pertinent d’évaluation du comportement à l’excavation de type « terrain boulant », se traduisant par une instabilité générale de la section non soutenue. Une large étude paramétrique a permis d’identifier la dépendance de cet indicateur aux paramètres de base du critère de Hoek et Brown, la résistance de la roche intacte σ_ci et le paramètre de fragilité m_i, ainsi qu’à l’indice GSI de description du massif rocheux, à partir des relations empiriques proposes par Hoek et Brown (1997).

Les conditions géologiques correspondant à l’apparition de ce type de comportement en tunnel profond sont celles d’un massif de roche tendre (σ_ci < 20 MPa), assez ductile (m_i < 15) ou très fortement altérée et fracturée (GSI < 15). Ces conditions théoriques semblent correspondre à quelques cas connus de l’auteur mais pourraient être confirmés par une étude systématique des cas réels suffisamment renseignés.

Ces conditions géologiques ne diffèrent pas nettement de celles rencontrées dans un « terrain poussant », susceptibles de fortes convergences.

Le terme anglais « squeezing » traduit par « comportement poussant » ne comporte pas de notion de vitesse ou d’évolution, contrairement au terme « creeping » traduit couramment par « fluage ». La conclusion tirée de l’analyse de la « condition d’instabilité » est que ce sont des matériaux présentant un faible « frottement interne » qui sont susceptibles de s’effondrer sous l’effet de leur poids, car l’effet de voûte généré autour de la section est insuffisant. Mais ces matériaux présentent également une forte tendance aux fortes convergences à grande profondeur, généralement avec une composante différée importante, de type fluage.

Il s’agirait alors de voir ces types de comportement à l’excavation comme deux degrés d’une même échelle.

Dans le graphe de Russo (2008, 2014), ces deux comportements – « squeezing » vs. « caving » – se distinguent :

– par une plus faible compétence σ_cm / (2.P₀) pour le premier, qui résulte d’un massif de roche tendre fortement altérée et fracturée sous forte couverture ;

– par un plus faible indice RMR pour le second, qui résulte de la prise en compte, en complément du GSI, de la résistance de la roche, de l’orientation défavorables des discontinuités et de la présence d’eau.

Comme le définit Russo (2014), le comportement de « caving » modéré inclus des instabilités locales de type « cloche » liées simplement à la densité de la fracturation, à la présence d’eau, à l’orientation défavorable des discontinuités et à la géométrie de l’excavation. En revanche, le comportement de « caving » sévère (« immediate collapse of the tunnel contour ») pourrait correspondre au cas théorique d’une pression minimale positive, examiné en section 6.1.

Cependant, l’existence théorique d’une pression minimale positive dépend en premier lieu du rapport σ_cm / (ϒ.R) et donc des dimensions de l’excavation, contrairement à la compétence du massif σ_cm / (2.P₀) et de son inverse, le Nombre de Stabilité N_s. Le comportement « boulant » serait alors la conséquence d’un comportement « poussant » dans une excavation de trop grande dimension, justifiant ainsi la pratique de l’excavation « en section divisée » dans les terrains difficiles, en plus de la stabilité nécessaire du front de taille.

Au-delà des aspects théoriques, la connaissance du comportement géomécanique résiduel de la Zone de Mobilisation des Fractures autour du tunnel est la clé d’une meilleure compréhension du phénomène. L’approche proposée par la définition de l’indice GSI_r de la ZMF, sur la base des travaux de Cai et al. (2007) est un premier pas qui devra être poursuivi à partir d’observations et de modélisations plus systématiques.

En effet, la conviction de l’auteur est de ne pas perdre de vue les bases descriptives et naturalistes de la Mécanique des Roches. Les moyens modernes d’auscultation, comme l’endoscopie en forage ou les méthodes géophysiques de type micro-sismique, couplés aux mesures de déformations doivent être généralisés pour progresser dans cette compréhension. En parallèle et sur cette base expérimentale, les modélisations numériques à l’échelle du Volume Élémentaire Représentatif permettront de valider les approches empiriques et de progresser dans la formulation du comportement résiduel. Sans cette étape essentielle, le recours à des modélisations 3D sophistiquées resterait un artifice pour cacher notre ignorance.

Annexe

Résolution des contraintes dans le domaine élastique

À une certaine distance du front de taille et au voisinage de la clé (θ ≈ π/2), on fera l’hypothèse que σ_r, σ_θ sont les contraintes principales (Fig. 12).

Dans le repère orthoradial (voir Fig. 1), l’équation d’équilibre s’écrit :

$$\frac{\partial {\sigma }_r}{\partial r}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=-\gamma ,$$(I) $${\sigma }_{\theta }={\sigma }_r+r\cdot \frac{\partial {\sigma }_r}{\partial r}+\gamma \cdot r.$$(Ib)

L’hypothèse de déplacement radiale conduit à :

$$\begin{array}{ll}{\in }_r=\frac{d{u}_r}{dr}\hfill & {\in }_{\theta }=\frac{u_r}{r}\hfill \end{array}.$$(II)

Les relations de l’élasticité en déformation plane s’écrivent :

$$\begin{array}{ll}{\in }_r=\frac{1+v}{E}\cdot \left[\left(1-v\right)\cdot {\sigma }_r-v\cdot {\sigma }_{\theta }\right]\hfill & {\in }_{\theta }=\frac{1+v}{E}\cdot \left[-v\cdot {\sigma }_r+\left(1-v\right)\cdot {\sigma }_{\theta }\right]\hfill \end{array}.$$(III)

En combinant (Ib), (II) et (III), on obtient :

$$\frac{\partial \left(\frac{u}{r}\right)}{\partial r}=-\frac{1+v}{E}\cdot \left[\frac{\partial {\sigma }_r}{\partial r}+\gamma \right].$$

La solution générale est de la forme :

$$u\left(r\right)=-\frac{1+v}{E}\cdot \left[{\sigma }_r\cdot r+\gamma \cdot r^2\right]+C\cdot r,$$

C étant une constante.

En posant :

σ_r (r = 0) = P₀ = γ ⋅ Z la contrainte initiale gravitaire à l’axe du tunnel et σ_r (r = Z) = 0.

u(Z) → 0 pour 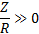$\frac{Z}{R}\gg 0$ alors il vient 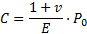$C=\frac{1+v}{E}\cdot P_0$ et :

$$\begin{array}{lll}{\in }_r=\frac{u}{r}=-\frac{1+v}{E}\cdot \left[{\sigma }_r-P_0+\gamma \cdot r\right]\hfill & \text{et}\hfill & {\in }_{\theta }=\frac{\partial u}{\partial r}=-\frac{1+v}{E}\cdot \left[{\sigma }_r+r\cdot \frac{\partial {\sigma }_r}{\partial r}-P_0+2\cdot \gamma \cdot r\right]\hfill \end{array}.$$(IIIb)

En combinant (Ib), (III) et (IIIb), on obtient :

$$\frac{\partial \left(r^2{\sigma }_r\right)}{\partial r}=\frac{P_0\cdot r-\left(2-v\right)\cdot \gamma \cdot r^2}{1-v}.$$(IV)

La solution générale est de la forme :

$${\sigma }_r(r)=\frac{P_0}{2\cdot \left(1-v\right)}-\frac{2-v}{3\cdot \left(1-v\right)}\cdot \gamma \cdot r+\frac{B}{r^2},$$

avec B, constante dépendante des conditions limites

$${\sigma }_{\theta }(r)=\frac{P_0}{2\cdot \left(1-v\right)}-\frac{1+v}{3\cdot \left(1-v\right)}\cdot \gamma \cdot r+\frac{B}{r^2},$$

alors :

$${\sigma }_r(r)+{\sigma }_{\theta }(r)=\frac{P_0-\gamma \cdot r}{1-v}.$$

On fera alors l’hypothèse simplificatrice ν ≈ 0.5 qui conduit à :

$${\sigma }_r\left(r\right)=P_0-\gamma \cdot r+\frac{B}{r^2}\text{ et \hspace{0.17em}}{\sigma }_r+{\sigma }_{\theta }=2\cdot (P_0-\gamma \cdot r)$$

À la limite de la ZMF : σ_r (R_p) = P_e d’où l’on tire : B = (P_e − P₀ + γ ⋅ R_p) ⋅ R_p2.

Et$${\sigma }_r(r)=P_e\cdot \frac{R_{p}2}{r^2}-\left(P_0-\gamma \cdot R_p\right)\cdot \frac{R_{p}2}{r^2}+P_0-y\cdot r,$$(V) $${\sigma }_{\theta }(R_p)=2\cdot \left(P_0-\gamma \cdot R_p\right)-P_e,$$(VI)

et (équation 8, sect. 4).

Résolution des contraintes dans la Zone de Mobilisation des Fractures (R ≤ r ≤ R_p)

Le critère de Hoek et Brown (H&B) en résistance de « pic » à la limite r = R_p de la ZMF s’écrit :

$${\sigma }_{\theta }(R_p)=P_e+{\sigma }_{ci}.{\left(m_b.\frac{P_e}{{\sigma }_{ci}}+s\right)}^a.$$(VII)

Pour la suite, on supposera a = 0,5.

De la condition (VI) à la limite r = R_p de la ZMF et de (VII), on déduit :

$$P_e=P_0-\gamma .R_P-\frac{{\sigma }_{ci}}{2}.{\left(m_b\frac{P_0-\gamma .R_p}{{\sigma }_{ci}}+\frac{m_b^2}{16}+s\right)}^{\frac{1}{2}}+{\sigma }_{ci}.\frac{m_b}{8}.$$(VIII)

On obtient R_p en fonction de P_e en résolvant (VIII) :

$$R_p=\frac{P_0-P_e-\frac{1}{2}\cdot \sqrt{m\cdot {\sigma }_{ci}\cdot P_e+s\cdot {\sigma }_{ci}2}}{\gamma }.$$(IX)

Le critère H&B en résistance résiduelle dans la ZMF, s’écrit :

$${\sigma }_{\theta }={\sigma }_r+{\sigma }_{ci}.{\left(m_r.\frac{{\sigma }_r}{{\sigma }_{ci}}+s_r\right)}^{\frac{1}{2}}.$$(X)

Pour la suite, on adoptera la transformation suivante :

$${\sum }_r=\frac{{\sigma }_r}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2},$$(XIa) $${\sum }_{\theta }=\frac{{\sigma }_{\theta }}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2}.$$(XIb)

L’équation d’équilibre (I) s’écrit alors :

$$\frac{\partial {\sum }_r}{\partial r}+\frac{{\sum }_r-{\sum }_{\theta }}{r}=-\frac{\gamma }{m_r\cdot {\sigma }_{ci}}.$$

Le critère H&B en résistance résiduelle dans la ZMF, prend alors la forme canonique suivante :

$${\sum }_{\theta }={\sum }_r+\sqrt{{\sum }_r}.$$

En posant :

r = R.ω et dr = R.dω, Σ_r vérifie alors l’équation différentielle suivante :

$$\begin{array}{lll}\frac{\partial {\sum }_r}{\partial \omega }-\frac{\sqrt{{\sum }_r}}{\omega }=-\Gamma \hfill & \text{avec}\hfill & \Gamma =\frac{\gamma \cdot R}{m_r\cdot {\sigma }_{ci}}.\hfill \end{array}$$(XII)

L’équation (XII) n’admet pas de solution explicite.

Résolution numérique par la méthode de Runge-Kuta d’ordre 2

À la paroi du tunnel, pour r = R et σ_r(R) = P_i, on peut écrire :

$$\begin{array}{lll}{\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega =1}=\sqrt{{\sum }_i}-\Gamma \hfill & \text{avec}\hfill & {\sum }_i=\frac{P_i}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2}.\hfill \end{array}$$

Pour un pas de discrétisation p suffisamment petit, on peut écrire :

$${\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega =1+p}\approx \sqrt{{\sum }_i+{\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega =1}\cdot (\omega +p)}-\Gamma ,$$ $${\sum }_r(1+p)\approx {\sum }_i+\frac{1}{2}\cdot \left({\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega =1}+{\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega =1+p}\right)\cdot p,$$

…

$${\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{{\omega }_{n+1}={\omega }_n+p}\approx \frac{1}{{\omega }_{n+1}}\sqrt{{\sum }_r({\omega }_n)+{\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega ={\omega }_n}\cdot ({\omega }_n+p)}-\Gamma ,$$ $${\sum }_r({\omega }_{n+1})\approx {\sum }_r({\omega }_n)+\frac{1}{2}\cdot \left({\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega ={\omega }_n}+{\left(\frac{\partial {\sum }_r}{\partial \omega }\right)}_{\omega ={\omega }_{n+1}}\right)\cdot p.$$

La résolution atteint la limite de la ZMF pour ω_m ≈ ω_p tel que :

$$\begin{array}{lll}{\sum }_r({\omega }_m)\ge {\sum }_e=\frac{P_e}{m_r\cdot {\sigma }_{ci}}+\frac{s_r}{m_{r}2}\hfill & \text{avec}\hfill & P_e\approx P_0-\gamma .R\cdot {\omega }_m-\frac{{\sigma }_{ci}}{2}.{\left(m_b\frac{P_0-\gamma .R\cdot {\omega }_m}{{\sigma }_{ci}}+\frac{m_b^2}{16}+s\right)}^{\frac{1}{2}}+{\sigma }_{ci}.\frac{m_b}{8}.\hfill \end{array}$$

Cependant, la dérivée à la limite de la ZMF ne vérifie pas la continuité avec la zone élastique :

$$\begin{array}{lll}{\left(\frac{\partial {\sigma }_r}{\partial r}\right)}_{r=R_p^{+}}-{\left(\frac{\partial {\sigma }_r}{\partial r}\right)}_{r=R_p^{-}}=\frac{{\sigma }_{\theta }^{+}-{\sigma }_{\theta }^{-}}{R_p}\hfill & \text{avec}\hfill & {\mathrm{\sigma \; \theta }}_{}^{+}=2\cdot \left(P_0-\gamma \cdot R_p\right)-P_e>P_e+{\sigma }_{ci}.{\left(m_r.\frac{P_e}{{\sigma }_{ci}}+s_r\right)}^{\frac{1}{2}}={\sigma }_{\theta }^{-}.\hfill \end{array}$$

Références

Liste des tableaux

Liste des figures

	Fig. 1 Comparaison des formules de pression de soutènement. Comparison between minimal support pressure formulas.
Dans le texte

	Fig. 2 Relations entre GSI et GSIr proposées dans la littérature. Relations between GSI and GSIr in literature.
Dans le texte

	Fig. 3 Graphes Rp/R et Pe / P0 – comparaison milieu pesant et non pesant. Graph Rp/R-Pe / P0–comparison between with or without weight media.
Dans le texte

	Fig. 4 Pression minimale en fonction de la compétence de la roche. Minimal pressure, depending on rock competency.
Dans le texte

	Fig. 5 Graphes Rp/R-σci / P0 et corrélation. Graph Rp/R-σci / P0 and correlation.
Dans le texte

	Fig. 6 Pression minimale en fonction de la compétence de la roche et corrélation. Minimal internal pressure, depending on rock competency and correlation.
Dans le texte

	Fig. 7 Pression intérieure minimale en fonction du rayon de la ZMF. Minimal internal pressure vs. EFZ radius.
Dans le texte

	Fig. 8 Rayon Rp de la ZMF en fonction de la pression intérieure Pi, comparaison avec Oreste et al. (2019). EFZ radius, depending on internal pressure Pi, comparison with Oreste et al. (2019).
Dans le texte

	Fig. 9 Variation des contraintes radiale et orthoradiale dans la ZMF. Variation of radial/tangential stress in EFZ.
Dans le texte

	Fig. 10 Équilibre d’une tranche de la ZMF. Equilibrium of an EFZ part.
Dans le texte

	Fig. 11 À gauche « graphe de portée critique » de Lang (d’après E. García-Gonzalo et al., 2016) ; à droite « graphe de stabilité » de Mathews (d’après G. W. Capes, 2009). At left: critical span graph from Lang (after E. García-Gonzalo et al., 2016); at right: stability graph from Mathews (after G. W. Capes, 2009).
Dans le texte