| Numéro |
Rev. Fr. Geotech.
Numéro 152, 2017
|
|
|---|---|---|
| Numéro d'article | 3 | |
| Nombre de pages | 10 | |
| DOI | https://doi.org/10.1051/geotech/2017008 | |
| Publié en ligne | 7 septembre 2017 | |
Article de recherche / Research Article
Un critère hyperbolique simple de résistance des roches
A simple hyperbolic criterion for rocks strength
1
Université Paris-Est, Laboratoire Navier (UMR 8205), CNRS, École des Ponts ParisTech, IFSTTAR,
77455
Marne-la-Vallée, France
2
École Nationale Supérieure de Génie Civil,
Hanoï, Vietnam
★ Auteur de correspondance : amade.pouya@enpc.fr
Nous présentons un critère de résistance des roches en enrichissant le critère de Drucker-Prager par un paramètre supplémentaire. Ce critère a une forme de surface de résistance hyperbolique dans l'espace des contraintes principales. Nous montrons qu'il résout certains défauts de critères classiques ou largement utilisés pour les roches qui sont les critères de Mohr-Coulomb, Drucker-Prager et Hoek et Brown. Il permet de modéliser un angle de frottement décroissant avec la contrainte moyenne, un rapport de résistance de traction sur compression qui peut mieux s'ajuster aux données expérimentales. Comparé au critère de Hoek et Brown qui a été proposé pour améliorer les mêmes défauts des critères de Mohr-Coulomb et Drucker-Prager, ce critère a l'avantage de s'exprimer en fonction des invariants des contraintes et faciliter donc la mise en place de modèles numériques. Par ailleurs, du fait de sa forme hyperbolique, il permet de définir un comportement asymptotique pour les fortes contraintes de confinement contrairement au critère parabolique de Hoek et Brown. Une comparaison de ce critère avec une série de données expérimentales de résistance des roches a montré qu'il permet de représenter ces données de manière satisfaisante et comparable à d'autres critères.
Abstract
A simple rock strength criterion is established by enriching the Drucker-Prager criterion by an additional parameter. This strength surface of this criterion has a hyperbolic shape in the octaedric-mean stress plane. We show that it solves some problems of classical Mohr-Coulomb, Drucker-Prager and Hoek and Brown criteria which are widely used for rock strength. It allows modeling friction angle decrease with the mean stress and leads to a better estimation of the tensile on compressive strength ratio compared to the Mohr-Coulomb and Drucker-Prager criteria. Compared to the Hoek and Brown criterion which was proposed to improve the same aspects of previous criteria, the new criterion proposed here has the advantage of being expressed in stress invariants instead of principal stresses and this facilitates its implementation in numerical models. Furthermore, due to its hyperbolic form, it has an asymptotic behavior for high confining stresses in contrast to parabolic criterion Hoek and Brown. A comparison of this criterion to a series of experimental data rocks strength showed that it allows to reproduce these data with a sufficient accuracy comparable to other criteria.
Mots clés : critère de résistance / Mohr-Coulomb / Drucker-Prager / Hoek et Brown / forme hyperbolique
Key words: strength criterion / Mohr-Coulomb / Drucker-Prager / Hoek and Brown / hyperbolic shape
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2017
1 Introduction
Un critère de résistance des roches doit pouvoir reproduire les données expérimentales de résistance de ces matériaux de manière satisfaisante et avec un nombre minimum de paramètres. Il doit aussi présenter des facilités de mise en place dans des codes numériques puisque la plupart des études de calcul et de dimensionnement des ouvrages géotechniques se font de nos jours en s'appuyant sur la modélisation numérique. Les trois critères de Mohr-Coulomb (MC), Drucker-Prager (DP) et Hoek et Brown (HB) sont très largement utilisés pour la modélisation de la résistance des roches et, plus généralement, les géomatériaux. Ces trois critères ne dépendent chacun que de deux paramètres. Avec deux paramètres de cohésion et d'angle de frottement interne, le critère MC qui est le plus largement utilisé, permet de modéliser la résistance des sols et des roches et des ouvrages géotechniques avec une précision souvent suffisante pour des applications d'ingénieur. Cependant, il n'est proposé comme modèle numérique que dans quelques grands codes du génie civil et beaucoup d'autres codes, en particulier dans le domaine pétrolier, utilisent le critère DP qui est d'une plus grande facilité de mise en œuvre numérique. Ces deux critères supposent un angle de frottement constant tandis que l'expérience montre que cet angle décroit avec la contrainte moyenne. Ces critères surestiment aussi la résistance en traction roches. Le critère HB a été proposé essentiellement pour pallier ces défauts mais souffre d'autres points faibles et d'une mise en œuvre numérique difficile.
Un grand nombre de travaux a été mené pour modifier ou enrichir ces critères de différentes manières afin soit d'améliorer leur qualité de représentation des données expérimentales, soit de faciliter leur utilisation pour des calculs théoriques et numériques. Le travail présenté dans ce papier s'inscrit dans cette même démarche. Après un rappel des forces et des faiblesses de ces trois grands critères, nous passons en revue les critères proposés dans les années récentes pour les améliorer. Nous montrons ensuite qu'un enrichissement du critère DP avec un paramètre supplémentaire et une expression judicieusement choisie permet d'apporter de grandes améliorations à la fois sur la qualité de représentation des différents aspects du comportement des roches et sur la facilité de mise en œuvre numérique.
Nous allons ci-dessous décrire, d'abord, les points forts et de faiblesse des trois critères classiques de résistance rappelés ci-dessus, et, ensuite, quelques critères/variantes ayant été proposés dans les années récentes pour remédier aux problèmes des critères précédents, avant de présenter et discuter un nouveau critère de résistance obtenu par une extension de celui de Drucker-Prager.
2 Critères de résistance
Les critères de ruptures des roches sont identifiés en général à partir des données de compression simple ou de compression sous pression de confinement et parfois de vrais essais de compression triaxiaux. Les valeurs à la rupture des trois contraintes principales, majeure médiane et mineure, sont notées respectivement σ1, σ2, σ3. Le critère de rupture est exprimé soit en fonction de ces contraintes, soit en fonctions des invariants des contraintes I1, J2 définis ci-dessous :
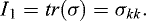 (1)
(1)
 (2)
(2)
Certains critères incluent aussi l'invariant J3 lié au déterminant du tenseur des contraintes ou à l'angle de Lode dont la définition sera donnée plus loin. Nous restons ici dans le cadre des critères ne portant que sur les deux premiers invariants ou sur les contraintes principales.
2.1 Critère de Mohr-Coulomb
Le critère de Mohr-Coulomb est le critère le plus largement utilisé pour décrire la résistance des sols et des roches. Ce critère s'exprime en fonction des contraintes principales et ne fait intervenir que les deux contraintes majeure et mineur σ1 et σ3 :
 (3)
(3)
Les contraintes de compressions sont ici comptées négativement. Ce critère présente trois points faibles sur le plan physique : il suppose un angle de frottement constant, surestime la résistance en traction et ne tient pas compte de l'effet de la contrainte principale intermédiaire.
En effet, ce critère suppose une relation linéaire entre les contraintes et donc une valeur constante de l'angle de frottement φ, tandis que les essais de compression sous pression de confinement montrent une tendance de φ à décroître avec la contrainte moyenne. Une méthode pratique parfois utilisée pour pallier ce défaut dans les analyses d'ouvrages souterrains est alors de considérer différentes valeurs de l'angle de frottement dans différentes zones à différentes valeurs de la contrainte moyenne. Les valeurs de la contrainte moyenne sont estimées à partir d'une analyse élastique préliminaire de l'ouvrage. Cela complique bien sûr la modélisation.
En ce qui concerne la résistance en traction, on peut noter que les paramètres des critères de résistance des roches sont en général identifiés à partir des données d'essais de compression. Il est alors naturel que ces critères reproduisent bien la résistance en compression du matériau et moins bien sa résistance en traction. Les paramètres de cohésion C et d'angle de frottement φ du critère MC conduisent en général à une surestimation de la résistance en traction. En effet, les résistances en traction et compression pour ce critère sont données par :
 (4)
(4)
Le rapport RT/Rc varie alors entre 1/3 et 1/5 pour des valeurs typiques d'angle de frottement entre 30 et 40°, tandis qu'on mesure en général des valeurs pas plus grandes que 1/10 pour ce rapport. Ce défaut est parfois résolu en introduisant une troncature dans le critère MC qui le limite dans le domaine des tractions à une valeur plus faible que RT (Fig. 1).
Le critère MC a un autre point faible du fait qu'il s'exprime en fonction des contraintes principales majeure et mineure seules et ne tient donc pas compte de l'effet de la contrainte médiane. Ce point est amélioré dans les travaux Mogi (1971) qui introduisent l'effet de la contrainte moyenne dans un critère qui garde la même structure que le critère MC.
Enfin, le fait que le critère MC s'exprime en fonction des contraintes principales pose des difficultés sur le plan de la modélisation numérique. En effet, dans une modélisation basée sur le formalisme de l'élastoplasticité, la contrainte doit être projetée sur la surface du critère et le calcul de la vitesse de déformation nécessite, du moins pour les modèles à potentiel associé, de connaître la normale à cette surface :
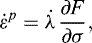 (5)
(5)
où 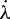 est le multiplicateur plastique et ∂F/∂σ donne la direction de la normale à la surface du critère. Or, quand le critère s'exprime en fonction des contraintes principales extrêmes, la surface de résistance F(σ) = 0, n'est pas lisse et présente des arêtes et des points anguleux où la normale ∂F/∂σ n'est pas définie. Le critère de Mohr-Coulomb définit, en effet, une surface de résistance dans l'espace des contraintes principales qui a la forme d'un cône de section hexagonale (Fig. 2). Elle comporte des arêtes et un sommet sur lesquels la normale extérieure n'est pas définie. Ceci pose de grandes difficultés pour la modélisation numérique. On doit alors prévoir les régimes de faces et les régimes d'arêtes pour modéliser l'évolution de la contrainte et de la déformation plastique. La troncature par une surface limitant les tractions (Fig. 1) élimine le sommet mais crée d'autres arêtes et points de singularités et ne résout pas la difficulté. C'est pour résoudre les difficultés liées à ces points singuliers de la surface de résistance que des critères plus complexes faisant appel au troisième invariant des contraintes ou à l'angle de Lode ont été proposés (Abba et Sloan, 1995 ; Sloan et Booker, 1986). C'est aussi ces difficultés qui expliquent que beaucoup de codes numériques, notamment dans le domaine pétrolier, utilisent de préférence le critère DP.
est le multiplicateur plastique et ∂F/∂σ donne la direction de la normale à la surface du critère. Or, quand le critère s'exprime en fonction des contraintes principales extrêmes, la surface de résistance F(σ) = 0, n'est pas lisse et présente des arêtes et des points anguleux où la normale ∂F/∂σ n'est pas définie. Le critère de Mohr-Coulomb définit, en effet, une surface de résistance dans l'espace des contraintes principales qui a la forme d'un cône de section hexagonale (Fig. 2). Elle comporte des arêtes et un sommet sur lesquels la normale extérieure n'est pas définie. Ceci pose de grandes difficultés pour la modélisation numérique. On doit alors prévoir les régimes de faces et les régimes d'arêtes pour modéliser l'évolution de la contrainte et de la déformation plastique. La troncature par une surface limitant les tractions (Fig. 1) élimine le sommet mais crée d'autres arêtes et points de singularités et ne résout pas la difficulté. C'est pour résoudre les difficultés liées à ces points singuliers de la surface de résistance que des critères plus complexes faisant appel au troisième invariant des contraintes ou à l'angle de Lode ont été proposés (Abba et Sloan, 1995 ; Sloan et Booker, 1986). C'est aussi ces difficultés qui expliquent que beaucoup de codes numériques, notamment dans le domaine pétrolier, utilisent de préférence le critère DP.
 |
Fig. 1 Le critère de Mohr-Coulomb tronqué par une valeur de résistance en traction dans le plan de Mohr. Mohr-Coulomb criterion truncated by a given value for the tensile strength. |
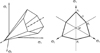 |
Fig. 2 La surface du critère de Mohr-Coulomb dans l'espace des contraintes principales. Mohr-Coulomb criterion surface in the space of principal stresses. |
2.2 Critère de Hoek et Brown
Le critère HB (Hoek et Brown, 1988) a été introduit essentiellement pour améliorer le critère MC en ce qui concerne la variation de l'angle de frottement avec la contrainte moyenne. Il permet aussi une meilleure estimation de la résistance en traction. Comme le critère MC, le critère HB n'implique que les contraintes principales majeure et mineure, mais postule une relation non linéaire entre ces contraintes. Dans sa version la plus courante, cette relation est de forme parabolique et s'écrit :
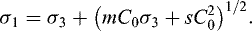 (6)
(6)
C0 représente la résistance en compression simple de la roche intacte, s un facteur réducteur exprimant l'effet de l'endommagement, et m un paramètre exprimant l'effet de la contrainte moyenne. Nous ne considérons pas l'effet de l'endommagement et prenons donc s = 1, si bien qu'on finit par deux paramètres pour ce critère comme pour le MC. La forme parabolique de ce critère permet effectivement de représenter un angle de frottement tangent décroissant avec la contrainte moyenne. Ce critère prévoit une résistance en traction (en posant σ1 = 0, σ3 = -RT) :
 (7)
(7)
En notant que Rc = C0 et en supposant m >> 2 et faisant un développement limité (1 + 4/m2)1/2 ≈ 1 + 2/m2, on trouve que :
 (8)
(8)
On peut ainsi atteindre des valeurs aussi petites qu'on souhaite pour le rapport RT/RC, et il est courant de trouver pour m des valeurs typiquement autour de dix.
Mais le critère HB possède les mêmes défauts que le MC pour la modélisation numérique du fait qu'il s'exprime en fonction des contraintes principales. Son implantation dans des codes numériques pose des difficultés encore plus grandes que le MC car sa surface de résistance est à la fois courbe et possède des singularités du type arêtes et sommets. Il n'y a pas à notre connaissance de code aux éléments finis largement diffusé dans lequel ce critère ait pu être implanté. Les travaux de recherche sur l'implantation de ce critère dans des codes numériques montrent sa complexité (Sørensen et al., 2015).
Notons aussi que, même si pour les grandes valeurs de la contrainte moyenne l'angle de frottement tangent du critère HB tend vers zéro, on ne peut pas définir un modèle tangent à ce critère. En effet, la pente de la courbe parabolique de ce critère tend vers zéro mais la parabole ne possède pas d'asymptote. Or, l'existence d'un critère asymptotique, qui établirait une relation linéaire entre les contraintes principales, serait de grand intérêt pour simplifier le modèle de résistance sous grandes contraintes moyennes.
2.3 Critère de Drucker Prager
Le critère DP s'exprime en fonction des invariants de contraintes et s'exprime sous la forme suivante :
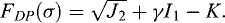 (9)
(9)
I1 et J2 sont les invariants de contrainte définis ci-dessus. Le paramètre γ est lié au frottement interne et Κ à la cohésion du matériau. La surface de résistance dans l'espace des contraintes principales est un cône de section circulaire.
On note que ce critère fait intervenir la contrainte principale intermédiaire via l'invariant J2. C'est une amélioration par rapport au MC, même si on peut estimer que la façon dont l'effet de la contrainte intermédiaire est exprimée ici n'est pas la plus adéquate [si on se réfère aux travaux de Mogi (1967)]. Ce critère présente surtout un grand avantage de simplicité sur le plan de modélisation numérique car il s'exprime en fonction des invariants de contraintes. En effet, son expression conduit à une surface de résistance sous la forme d'un cône de section circulaire. Cette surface est régulière partout sauf en un point de sommet du cône. La dérivée par rapport à σ est définie par une formule simple :
 (10)
(10)
Cette expression est définie partout sauf au sommet du cône où J2 = 0. Cela conduit à une grande simplicité de modélisation et explique que le critère DP soit très largement utilisé et plus souvent disponible dans les codes numériques que le critère MC. Différentes formules ont d'ailleurs été établies pour définir le critère de DP le plus proche d'un critère MC. On peut définir en particulier le critère DP dont la section dans le plan octaédrique serait le cercle inscrit dans l'hexagone du MC ou passant par ses sommets internes ou externe (Fig. 3). Ces relations sont les suivantes :
Cercles passant par :
 (11a)
(11a)
 (11b)
(11b)
 (11c)
(11c)
Le point faible du critère DP reste, comme celui de MC, d'abord un angle de frottement constant et ensuite une estimation trop forte de la résistance en traction du moins si les paramètres sont identifiés à partir de données de compression. En effet, l'angle de frottement est lié, par les équations (11) au paramètre γ qui est constant. Les résistances en compression et traction simple sont données par :
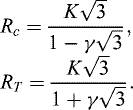 (12)
(12)
Le rapport RT/RC qu'on obtient d'après ces relations et l'équation (11b) est :
 (13)
(13)
Ainsi, les valeurs estimées de RT/RC seront alors toujours plus grandes que 1/3.
Notre objectif dans la suite sera d'apporter une modification à ce critère pour améliorer ces défauts qu'il partage avec le critère MC, tout en gardant un critère exprimé en contraintes principales pour garder les avantages de DP pour la modélisation numérique.
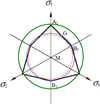 |
Fig. 3 Le critère de Mohr-Coulomb et les trois critères de Drucker-Prager correspondant aux cercles passant par les sommets internes et externes et au cercle tangent aux faces de l'hexagone. The Mohr-Coulomb criterion and its approximations by three Drucker-Prager criteria corresponding to the circles in octahedral plane passing through the internal or the external vertices or tangent to the faces of the hexagon. |
2.4 Autres critères
En notant les défauts des critères de MC et de DP, beaucoup d'auteurs ont tenté des variantes de ces critères en les enrichissant par des paramètres supplémentaires. Nous allons citer ci-dessous les principaux modèles proposés et commenter brièvement leurs avantages et inconvénients.
En partant du critère de MC, Mogi (1967) a proposé une variante qui tient compte de l'influence de la contrainte principale intermédiaire sous la forme :
 (14)
(14)
Ce critère s'exprime comme le MC en fonction des contraintes principales et pose les mêmes difficultés de modélisation numérique. Dans une version ultérieure, le premier membre de l'équation (14) a été remplacé par la contrainte octaédrique qui se déduit du second invariant J2. Mais le second membre dans cette version s'exprime toujours en termes de contraintes principales.
You (2009) et Rafiai (2011) ont proposé une autre variante du critère MC impliquant les trois contraintes principales dans des expressions exponentielles. Ewy (1999) a proposé une forme modifiée du critère de Lade et Duncan (1975) qui exprime le critère par des polynômes de troisième degré en contraintes principales. Le concept d'état critique de Barton (1976) a aussi été utilisé pour proposer un critère de MC modifié qui s'exprime sous la forme (Singh et al., 2011) :
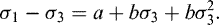 (15)
(15)
Ce critère possède un paramètre de plus et permet donc naturellement de reproduire une certaine décroissance de l'angle de frottement avec la contrainte moyenne. Mais son domaine de validité reste limité du fait de la présence du terme quadratique en σ3. En effet, la pente d(σ1 – σ1)/dσ3 dont on déduit l'angle de frottement tangent tend vers l'infini pour des valeurs croissantes de σ3, ce qui limite l'intervalle de validité du critère.
Tous ces critères s'exprimant en fonction des contraintes principales posent les mêmes difficultés de modélisation numériques évoquées ci-dessus.
D'autres travaux sont partis du critère DP et ont essayé d'améliorer ses défaut tout en s'appuyant sur les invariants des contraintes.
Wiebols et Cook (1968) ont enrichi le critère de DP en ajoutant un terme supplémentaire de second degré en I1 :
 (16)
(16)
Ce critère possède un paramètre de plus que DP et permet donc de mieux ajuster les données expérimentales et reproduit aussi une certaine décroissance de l'angle de frottement avec la contrainte moyenne. Mais son domaine de validité reste limité du fait de la présence du terme quadratique en I1 pour les mêmes raisons que pour celui de Singh et al. (2011).
Un autre critère a été proposé par Pantelis et Exadaktylos (2013) qui porte sur les invariants des contraintes en introduisant une forme hyperbolique. Il s'écrit :
 (17)où A, B et C sont fonctions de la contrainte moyenne et de l'angle de Lode. Ce critère est la meilleure extension proposée au critère MC en termes d'invariants. Il conduit à une surface de résistance lisse et différentiable et qui possède, de plus, des formes tangentes asymptotiques pour la contrainte moyenne tendant vers l'infini. Mais il reste compliqué du fait de l'intervention de l'angle de Lode et on peut difficilement imaginer qu'il soit largement utilisé comme l'ont été les critères MC, HB et DP. Il n'est d'ailleurs pas possible d'extraire une forme plus simple en y supprimant la dépendance de l'angle de Lode. Nous allons montrer ci-dessous qu'une autre voie d'extension simple partant du critère de DP est possible qui permet de résoudre beaucoup des inconvénients des critères ci-dessus.
(17)où A, B et C sont fonctions de la contrainte moyenne et de l'angle de Lode. Ce critère est la meilleure extension proposée au critère MC en termes d'invariants. Il conduit à une surface de résistance lisse et différentiable et qui possède, de plus, des formes tangentes asymptotiques pour la contrainte moyenne tendant vers l'infini. Mais il reste compliqué du fait de l'intervention de l'angle de Lode et on peut difficilement imaginer qu'il soit largement utilisé comme l'ont été les critères MC, HB et DP. Il n'est d'ailleurs pas possible d'extraire une forme plus simple en y supprimant la dépendance de l'angle de Lode. Nous allons montrer ci-dessous qu'une autre voie d'extension simple partant du critère de DP est possible qui permet de résoudre beaucoup des inconvénients des critères ci-dessus.
3 Nouveau critère proposé
Le critère DP constitue un enrichissement du critère de Von Misès qui s'écrit :
 (18)
Le critère Drucker-Prager introduit un paramètre supplémentaire γ pour tenir compte de l'effet de la contrainte moyenne sous la forme (9). Dans le même esprit, nous proposons d'introduire un paramètre supplémentaire qui permet de dissocier la résistance en traction de la résistance en compression et exprimer aussi une dépendance de l'angle de frottement à la contrainte moyenne. Nous avons vu ci-dessus que différentes expressions ont été proposées pour introduire ce paramètre supplémentaire et nous avons discuté de leurs avantages et inconvénients. Nous proposons de considérer une nouvelle expression qui permet d'introduire ce paramètre supplémentaire de manière plus judicieuse et présentant, comme nous allons le voir, plusieurs avantages :
(18)
Le critère Drucker-Prager introduit un paramètre supplémentaire γ pour tenir compte de l'effet de la contrainte moyenne sous la forme (9). Dans le même esprit, nous proposons d'introduire un paramètre supplémentaire qui permet de dissocier la résistance en traction de la résistance en compression et exprimer aussi une dépendance de l'angle de frottement à la contrainte moyenne. Nous avons vu ci-dessus que différentes expressions ont été proposées pour introduire ce paramètre supplémentaire et nous avons discuté de leurs avantages et inconvénients. Nous proposons de considérer une nouvelle expression qui permet d'introduire ce paramètre supplémentaire de manière plus judicieuse et présentant, comme nous allons le voir, plusieurs avantages :
 (19)En admettant cette forme, on obtient comme surface de critère de résistance une forme parabolique dans l'espace de contraintes principales qui est parfaitement lisse et différentiable en tout point. Dans la pratique, il s'avère plus simple d'écrire ce critère en changeant de paramètres sous la forme :
(19)En admettant cette forme, on obtient comme surface de critère de résistance une forme parabolique dans l'espace de contraintes principales qui est parfaitement lisse et différentiable en tout point. Dans la pratique, il s'avère plus simple d'écrire ce critère en changeant de paramètres sous la forme :
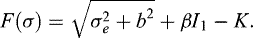 (20)Dans cette expression,
(20)Dans cette expression, 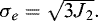 est la contrainte équivalente de Von Misès et les deux paramètres b et β vérifient les conditions :
est la contrainte équivalente de Von Misès et les deux paramètres b et β vérifient les conditions :
 (21)
(21)
Nous verrons la justification de ces inégalités plus loin. Ce critère ne possède qu'un paramètre de plus que celui de DP et s'exprime en fonction des deux premiers invariants des contraintes. Il définit une surface de résistance lisse partout, ce qui est un grand avantage pour la modélisation numérique. Nous allons montrer dans la suite que ce critère possède aussi de bonnes propriétés qualitatives sur les plans théoriques et phénoménologiques (représentativité des données expérimentales).
4 Propriétés théoriques et qualitatives du nouveau critère
4.1 Angle de frottement
La forme du critère dans le plan de la contrainte déviatorique σe en fonction de σm = I1/3 est une hyperbole d'axe de symétrie parallèle à σm (Fig. 4). La pente dσe/dσm est décroissante en passant d'une valeur initiale infinie (tangente verticale) à une valeur asymptotique de 3β. Ceci conduit donc à une décroissance de l'angle de frottement tangent avec la contrainte moyenne.
Si on considère, par exemple, le cas d'un essai de compression sous pression de confinement avec σ1 ≥ σ2 = σ3. Dans ce cas, σ1 – σ3 représente le déviateur et σ3 la pression de confinement. Le critère (20) conduit alors à la relation suivante entre σ1 et σ3 :
 (22)
Nous avons tracé le diagramme de ce critère sur la Figure 5. On remarque la diminution de l'angle de frottement avec la pression de confinement. L'angle de frottement minimum est donné par la pente de l'asymptote au critère précisée dans la section suivante.
(22)
Nous avons tracé le diagramme de ce critère sur la Figure 5. On remarque la diminution de l'angle de frottement avec la pression de confinement. L'angle de frottement minimum est donné par la pente de l'asymptote au critère précisée dans la section suivante.
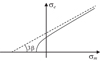 |
Fig. 4 Le critère hyperbolique dans le plan (σe, σm). Hyperbolic criterion in the (σe, σm) plane. |
 |
Fig. 5 Le critère hyperbolique dans le plan du déviateur (σ1 − σ3) – pression de confinement (σ3) pour un essai de compression sous confinement. Hyperbolic criterion in the (σ1 − σ3) – (s3) (deviator-confining pressure) plane for a compression test under confining pressure. |
4.2 Comportement asymptotique
Pour des états de contraintes à fortes valeurs moyennes, il est utile de pouvoir présenter un comportement asymptotique du critère de résistance. Comme nous l'avons dit ci-dessus, le critère de HB ne possède pas de modèle asymptotique tangent car une forme parabolique ne possède pas d'asymptote. En revanche, pour les grandes valeurs de la contrainte moyenne, le critère (20) possède un critère DP tangent qui s'écrit :
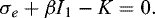 (23)
Si on considère le cas d'un essai sous pression de confinement, cette équation asymptotique s'écrit :
(23)
Si on considère le cas d'un essai sous pression de confinement, cette équation asymptotique s'écrit :
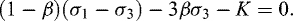 (24)La pente du critère, comparée à celle du MC, définit un angle de frottement :
(24)La pente du critère, comparée à celle du MC, définit un angle de frottement :
 (25)Cet angle représente l'angle de frottement minimum du matériau obtenu sous fortes contraintes moyennes.
(25)Cet angle représente l'angle de frottement minimum du matériau obtenu sous fortes contraintes moyennes.
4.3 Rapport de la résistance en traction sur la résistance en compression
Rappelons que les contraintes de compression sont comptées négativement. Dans un essai de compression simple ayant atteint la limite de résistance Rc on a σe = Rc et I1 = -Rc, tandis que dans le cas d'un essai de traction simple avec une résistance RT on a σe = RT et I1 = RT. En reportant ces valeurs dans l'équation (20), et en posant :
 (26)
(26)
Soit :
 (28)
Le rapport RT/Rc peut alors varier de 0 à 1 quand β varie de 1 à 0. Si, inversement, on connaît ce rapport RT/Rc, en posant :
(28)
Le rapport RT/Rc peut alors varier de 0 à 1 quand β varie de 1 à 0. Si, inversement, on connaît ce rapport RT/Rc, en posant :
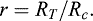 (29)
(29)
l'équation (28) permet de calculer
 (30)
Cela simplifie beaucoup l'identification des paramètres : il suffit de connaître les paramètres d'un modèle de MC ou d'un modèle de DP équivalent ainsi que le rapport souhaité pour RT/Rc pour pouvoir écrire le critère sous la forme (20).
(30)
Cela simplifie beaucoup l'identification des paramètres : il suffit de connaître les paramètres d'un modèle de MC ou d'un modèle de DP équivalent ainsi que le rapport souhaité pour RT/Rc pour pouvoir écrire le critère sous la forme (20).
5 Comparaison avec les données expérimentales
Afin d'évaluer la pertinence du critère hyperbolique, les données expérimentales existantes dans la littérature obtenues avec les essais poly-axiaux sont étudiées. Notons que dans les essais poly-axiaux les trois contraintes principales peuvent être appliquées indépendamment. Dans ce travail, cinq types de roches sont considérés :
-
dolomite de Dunham (Mogi, 1971) ;
-
calcaire de Solenhofen (Mogi, 1971) ;
-
grès de Shirahama (Takahashi et Koide, 1989) ;
-
shale de Yuubari (Takahashi et Koide, 1989) ;
-
amphibolite KTB (Chang et Haimson, 2000).
Ces données expérimentales ont été aussi utilisées par Colmenares et Zoback (2002), Benz et al. (2008), Rafiai (2011) pour évaluer les critères de rupture pour les roches.
À côté du critère hyperbolique, deux critères les plus couramment utilisés, Drucker-Prager (DP) et Mohr-Coulomb (MC), sont aussi considérés dans ce travail. La Figure 6 présente la méthode de détermination des paramètres du critère de DP à partir des données expérimentales de la dolomite de Dunham. À partir des données expérimentales, les valeurs de  sont tracées en fonction de I1. La courbe de tendance linéaire obtenue à partir de ces données permet de déterminer les deux paramètres : γ = 0,516 et K = 159 MPa. La détermination des paramètres du critère de MC pour le même matériau est présentée sur la Figure 7. La courbe de tendance linéaire est obtenue à partir des données de σ1 et σ3 et permet de déterminer les deux paramètres du critère : Rc = 440 MPa, et kp = dσ1/dσ3 = 3,45, soit φ = 33,4°. Pour le cas du critère hyperbolique (Eq. (20)), les valeurs de J2 sont d'abord tracées en fonction de I1 (ici la compression est comptée positive). Ensuite, une courbe de tendance polynomiale d'ordre 2 est tracée. On obtient alors les trois paramètres pour cet ajustement J2 = a1I12 + a2I1 + a3 dont on déduit les paramètres du critère par les équations a1 = β 2/3, a2 = −2Kβ/3, a3 = (K2 − b2)/3. L'exemple pour le cas de la dolomite de Dunham est présenté sur la Figure 8 (avec compression I1 comptée positive) et on a obtenu a1 = 0,0346 ; a2 = −325 MPa ; a3 = 41 MPa2. Les mêmes méthodes ont été utilisées pour les autres roches.
sont tracées en fonction de I1. La courbe de tendance linéaire obtenue à partir de ces données permet de déterminer les deux paramètres : γ = 0,516 et K = 159 MPa. La détermination des paramètres du critère de MC pour le même matériau est présentée sur la Figure 7. La courbe de tendance linéaire est obtenue à partir des données de σ1 et σ3 et permet de déterminer les deux paramètres du critère : Rc = 440 MPa, et kp = dσ1/dσ3 = 3,45, soit φ = 33,4°. Pour le cas du critère hyperbolique (Eq. (20)), les valeurs de J2 sont d'abord tracées en fonction de I1 (ici la compression est comptée positive). Ensuite, une courbe de tendance polynomiale d'ordre 2 est tracée. On obtient alors les trois paramètres pour cet ajustement J2 = a1I12 + a2I1 + a3 dont on déduit les paramètres du critère par les équations a1 = β 2/3, a2 = −2Kβ/3, a3 = (K2 − b2)/3. L'exemple pour le cas de la dolomite de Dunham est présenté sur la Figure 8 (avec compression I1 comptée positive) et on a obtenu a1 = 0,0346 ; a2 = −325 MPa ; a3 = 41 MPa2. Les mêmes méthodes ont été utilisées pour les autres roches.
La comparaison entre le critère de DP et les données expérimentales est présentée sur la Figure 9. Dans cette figure, pour chaque roche, on trace la relation entre σ1 et σ2 pour chaque valeur de σ3. D'une manière générale, le critère de DP permet de reproduire correctement la forme de l'évolution, augmentation de σ1 quand σ2 augmente, pour le cas de la dolomite et du calcaire. Par contre, pour les autres roches, σ1 est moins dépendant de σ2, ce critère est moins pertinent pour prédire la rupture du matériau.
À l'inverse, pour le cas du critère de MC, Figure 10, le critère permet de prédire correctement le comportement du grès, du shale et de l'amphibolite car σ1 est moins dépendant de σ2 pour ces matériaux. La pertinence du critère de MC est moins évidente pour la dolomite et le calcaire.
La comparaison entre le critère (20) et les données expérimentales est présentée sur la Figure 11. On constate que le critère arrive à reproduire relativement bien l'évolution de σ1 en fonction de σ2 pour les cas des cinq roches. Par contre, la prédiction n'est pas satisfaite quantitativement dans certains cas, pour le calcaire, par exemple.
Afin d'évaluer quantitativement la pertinence des trois critères pour prédire la résistance de ces matériaux, la valeur de σ1 obtenue par les critères est tracée en fonction de la valeur expérimentale (voir la Fig. 12 comme exemple pour le cas du critère de Drucker-Prager et la dolomite de Dunham). À partir de la courbe de tendance linéaire, on obtient le coefficient de corrélation (R2) sur le graphique. La pertinence du critère est meilleure quand ce coefficient est plus proche de l'unité. L'ensemble des résultats est présenté dans le Tableau 1. Comme constaté auparavant sur les Figures 10 et 11, le critère de DP est plus pertinent que celui de MC pour le cas de la dolomite et du calcaire et moins pertinent pour le cas du grès, du shale et de l'amphibolite. En ce qui concerne le critère (20), il est même plus pertinent que le critère de DP pour le cas de la dolomite et du calcaire. Par contre, il est moins pertinent que les deux autres critères pour le grès et l'amphibolite. Pour le shale, son coefficient de détermination est proche de celui du critère DP.
 |
Fig. 6 Détermination des paramètres du critère de Drucker-Prager pour la dolomite de Dunham. Determination of Drucker-Prager parameters for the Dunham dolomite. |
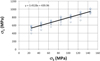 |
Fig. 7 Détermination des paramètres du critère de Mohr-Coulomb pour la dolomite de Dunham. Determination of the Mohr-Coulomb parameters for the Dunham dolomite. |
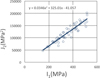 |
Fig. 8 Détermination des paramètres du critère hyperbolique pour la dolomite de Dunham. Determination of the hyperbolic criterion parameters for the Dunham dolomite. |
 |
Fig. 9 Comparaison entre le critère de Drucker-Prager et les données expérimentales sur (a) la dolomite de Dunham, (b) le calcaire de Solenhofen, (c) le grès de Shiraham, (d) le shale de Yuubari, et (e) l'amphibolite KTB. Comparison between the Drucker-Prager criterion and experimental data for (a) Dunham dolomite, (b) Solenhofen lime stone, (c) Shiraham sandstone, (d) Yuubari shale and (e) KTB amphibolite. |
 |
Fig. 10 Comparaison entre le critère de Mohr-Coulomb et les données expérimentales sur (a) la dolomite de Dunham, (b) le calcaire de Solenhofen, (c) le grès de Shiraham, (d) le shale de Yuubari, et (e) l'amphibolite KTB. Comparison between the Mohr-Coulomb criterion and experimental data for (a) Dunham dolomite, (b) Solenhofen lime stone, (c) Shiraham sandstone, (d) Yuubari shale and (e) KTB amphibolite. |
 |
Fig. 11 Comparaison entre le nouveau critère (20) et les données expérimentales sur (a) la dolomite de Dunham, (b) le calcaire de Solenhofen, (c) le grès de Shiraham, (d) le shale de Yuubari, et (e) l'amphibolite KTB. Comparison between the new criterion and experimental data for (a) Dunham dolomite, (b) Solenhofen lime stone, (c) Shiraham sandstone, (d) Yuubari shale and (e) KTB amphibolite. |
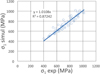 |
Fig. 12 L'évaluation du critère de Drucker-Prager pour prédire le comportement de la dolomite de Dunham. Evaluation of the quality of the Drucker-Prager predictions for the Dunham dolomite data. |
Évaluation des critères de rupture à travers le coefficient de corrélation R2.
Evaluation of the quality of the different failure criteria through the correlation coefficient R2.
6 Conclusion
Un certain nombre de critères de résistance ont été proposés dans les années récentes pour améliorer ceux de Mohr-Coulomb et de Drucker-Prager dont les points faibles principaux sont un angle de frottement constant et une estimation élevée de la résistance en traction. Mais ces nouveaux critères souffrent d'autres défauts qui sont, suivant les cas :
-
difficultés de modélisation numérique quand ils sont exprimés en fonction des contraintes principales comme le critère Hoek et Brown ;
-
domaines de validité réduits quand ils font intervenir des termes quadratiques en contraintes ;
-
expressions trop compliquées quand ils font intervenir le troisième invariant des contraintes.
Le critère que nous avons ici proposé par l'équation (20), a l'avantage d'une forme simple s'exprimant en fonction des invariants des contraintes tout en possédant les propriétés attendues. Il s'obtient à partir d'un enrichissement judicieux du critère de Drucker-Prager avec un paramètre additionnel. L'intérêt de ce critère est qu'avec un seul paramètre supplémentaire nous pouvons améliorer les critères précédents sur plusieurs aspects : diminution de l'angle de frottement avec la contrainte moyenne, meilleure estimation de la résistance en traction et facilités d'implémentation dans des codes numériques. Nous avons, en outre, montré que ce critère peut bien représenter les données expérimentales sur la résistance des roches avec une précision comparable à d'autres critères couramment utilisés.
Références
- Abba AJ, Sloan SW. 1995. A smooth hyperbolic approximation of the Mohr-Coulomb yield criterion. Comput Struct 54: 427–441. [CrossRef] [Google Scholar]
- Barton N. 1976. The shear strength of rock and rock joints. Int J Rock Mech Min Sci Geomech Abstr 13: 255–279. [CrossRef] [Google Scholar]
- Benz T, Schwab R, Kauther R, Vermeer P. 2008. A Hoek-Brown criterion with intrinsic material strength factorization. Int J Rock Mech Min Sci 45: 210–222. [CrossRef] [Google Scholar]
- Chang C, Haimson B. 2000. True triaxial strength and deformability of the German Continental deep drilling program (KTB) deep hole amphibolite. J Geophys Res 105: 18999–19013. [CrossRef] [Google Scholar]
- Colmenares LB, Zoback MD. 2002. A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks. Int J Rock Mech Min Sci 39: 695–729. [CrossRef] [Google Scholar]
- Ewy R. 1999. Wellbore-stability predictions by use of a modified Lade criterion. SPE Drill Complet 14(2): 85–91. [CrossRef] [Google Scholar]
- Hoek E, Brown ET. 1988. The Hoek-Brown failure criterion – a 1988 update. In: Curran JC, ed. Proc. 15th Canadian Rock Mech. Symp. Toronto: Dept. Civil Engineering, University of Toronto. pp. 31–38. [Google Scholar]
- Lade P, Duncan J. 1975. Elasto-plastic stress-strain theory for cohesionless soil. J Geotech Eng Div ASCE 101: 1037–1053. [Google Scholar]
- Mogi K. 1967. Effect of the intermediate principal stress on rock failure. J Geophys Res 72: 5117–5131. [CrossRef] [Google Scholar]
- Mogi K. 1971. Fracture and flow of rocks under high triaxial compression. J Geophys Res 76: 1255–1269. [CrossRef] [Google Scholar]
- Pantelis L, Exadaktylos G. 2013. A smooth hyperpolic failure criterion for cohesive-frictional materials. Int J Rock Mech Min Sci 58: 85–91. [Google Scholar]
- Rafiai H. 2011. New empirical polyaxial criterion for rock strength. Int J Rock Mech Min Sci 48: 922–931. [CrossRef] [Google Scholar]
- Singh M, Raj A, Singh B. 2011. Modified Mohr-Coulomb criterion for non-linear triaxial and polyaxial strength of intact rocks. Int J Rock Mech Min Sci 48: 546–555. [CrossRef] [Google Scholar]
- Sloan SW, Booker JR. 1986. Removal of singularities of Tresca and Mohr-Coulomb yield functions. Communications. In: Applied Numerical Methods 2: 173–179. [Google Scholar]
- Sørensen ES, Clausen J, Damkilde L. 2015. Finite element implementation of the Hoek-Brown material model with general strain softening behavior. Int J Rock Mech Min Sci 78: 163–174. [Google Scholar]
- Takahashi M, Koide H. 1989. Effect of the intermediate principal stress on strength and deformation behavior of sedimentary rocks at the depth shallower than 2000 m. In: Maury V, Fourmaintraux D, eds. Rock at great depth, vol. 1. Rotterdam: Balkema. pp. 19–26. [Google Scholar]
- Wiebols G, Cook NGW. 1968. An energy criterion for the strength of rock in polyaxial compression. Int J Rock Mech Min Sci 5: 529–549. [CrossRef] [Google Scholar]
- You MQ. 2009. True-triaxial strength criteria for rock. Int J Rock Mech Min Sci 46: 115–127. [CrossRef] [Google Scholar]
Citation de l'article : Amade Pouya, Manh Truong Nguyen, Anh Minh Tang. Un critère hyperbolique simple de résistance des roches. Rev. Fr. Geotech. 2017, 152, 3.
Liste des tableaux
Évaluation des critères de rupture à travers le coefficient de corrélation R2.
Evaluation of the quality of the different failure criteria through the correlation coefficient R2.
Liste des figures
 |
Fig. 1 Le critère de Mohr-Coulomb tronqué par une valeur de résistance en traction dans le plan de Mohr. Mohr-Coulomb criterion truncated by a given value for the tensile strength. |
| Dans le texte | |
 |
Fig. 2 La surface du critère de Mohr-Coulomb dans l'espace des contraintes principales. Mohr-Coulomb criterion surface in the space of principal stresses. |
| Dans le texte | |
 |
Fig. 3 Le critère de Mohr-Coulomb et les trois critères de Drucker-Prager correspondant aux cercles passant par les sommets internes et externes et au cercle tangent aux faces de l'hexagone. The Mohr-Coulomb criterion and its approximations by three Drucker-Prager criteria corresponding to the circles in octahedral plane passing through the internal or the external vertices or tangent to the faces of the hexagon. |
| Dans le texte | |
 |
Fig. 4 Le critère hyperbolique dans le plan (σe, σm). Hyperbolic criterion in the (σe, σm) plane. |
| Dans le texte | |
 |
Fig. 5 Le critère hyperbolique dans le plan du déviateur (σ1 − σ3) – pression de confinement (σ3) pour un essai de compression sous confinement. Hyperbolic criterion in the (σ1 − σ3) – (s3) (deviator-confining pressure) plane for a compression test under confining pressure. |
| Dans le texte | |
 |
Fig. 6 Détermination des paramètres du critère de Drucker-Prager pour la dolomite de Dunham. Determination of Drucker-Prager parameters for the Dunham dolomite. |
| Dans le texte | |
 |
Fig. 7 Détermination des paramètres du critère de Mohr-Coulomb pour la dolomite de Dunham. Determination of the Mohr-Coulomb parameters for the Dunham dolomite. |
| Dans le texte | |
 |
Fig. 8 Détermination des paramètres du critère hyperbolique pour la dolomite de Dunham. Determination of the hyperbolic criterion parameters for the Dunham dolomite. |
| Dans le texte | |
 |
Fig. 9 Comparaison entre le critère de Drucker-Prager et les données expérimentales sur (a) la dolomite de Dunham, (b) le calcaire de Solenhofen, (c) le grès de Shiraham, (d) le shale de Yuubari, et (e) l'amphibolite KTB. Comparison between the Drucker-Prager criterion and experimental data for (a) Dunham dolomite, (b) Solenhofen lime stone, (c) Shiraham sandstone, (d) Yuubari shale and (e) KTB amphibolite. |
| Dans le texte | |
 |
Fig. 10 Comparaison entre le critère de Mohr-Coulomb et les données expérimentales sur (a) la dolomite de Dunham, (b) le calcaire de Solenhofen, (c) le grès de Shiraham, (d) le shale de Yuubari, et (e) l'amphibolite KTB. Comparison between the Mohr-Coulomb criterion and experimental data for (a) Dunham dolomite, (b) Solenhofen lime stone, (c) Shiraham sandstone, (d) Yuubari shale and (e) KTB amphibolite. |
| Dans le texte | |
 |
Fig. 11 Comparaison entre le nouveau critère (20) et les données expérimentales sur (a) la dolomite de Dunham, (b) le calcaire de Solenhofen, (c) le grès de Shiraham, (d) le shale de Yuubari, et (e) l'amphibolite KTB. Comparison between the new criterion and experimental data for (a) Dunham dolomite, (b) Solenhofen lime stone, (c) Shiraham sandstone, (d) Yuubari shale and (e) KTB amphibolite. |
| Dans le texte | |
 |
Fig. 12 L'évaluation du critère de Drucker-Prager pour prédire le comportement de la dolomite de Dunham. Evaluation of the quality of the Drucker-Prager predictions for the Dunham dolomite data. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.





