| Numéro |
Rev. Fr. Geotech.
Numéro 152, 2017
|
|
|---|---|---|
| Numéro d'article | 2 | |
| Nombre de pages | 15 | |
| DOI | https://doi.org/10.1051/geotech/2017013 | |
| Publié en ligne | 24 août 2017 | |
Article de recherche / Research Article
Conséquences du mode d'effondrement sur les mécanismes de transfert de charge et sur le dimensionnement des géosynthétiques sur cavités potentielles
Consequence of the sinkhole mode on the load transfer mechanisms and on the design of geotextile-reinforced embankments overlying voids
1
3SR, université de Grenoble Alpes,
38041
Saint-Martin d'Hères, France
2
SMSID, INSA de Lyon,
69621
Villeurbanne, France
3
EGIS Géotechnique,
38180
Seyssins, France
4
Le Cnam,
75141
Paris, France
★ Auteur de correspondance : laurent.briancon@insa-lyon.fr
Le bon dimensionnement des renforts géosynthétiques sur cavité nécessite une connaissance approfondie des mécanismes de report de charge de la zone de sol effondrée vers les zones stables. Actuellement, la charge agissant sur la nappe géosynthétique est le plus souvent estimée en utilisant le mécanisme d'effondrement proposé par Terzaghi et en supposant une répartition uniforme des contraintes sur la nappe. Pour analyser plus en détail ces mécanismes de report de charge, des expérimentations en vraie grandeur et des simulations numériques mettant en œuvre une modélisation éléments discrets ont été réalisées. En testant numériquement différents modes d'ouverture de la cavité (ouverture progressive du diamètre de la cavité et tassement progressif du sol situé sous la nappe au droit de la cavité), il a été démontré que le mécanisme d'ouverture de la cavité avait une influence importante sur le mode de distribution de la charge sur la nappe (répartition des charges tronconiques pour une ouverture progressive du diamètre de la cavité et parabolique inversée lors d'un tassement progressif du sol situé sous la nappe) et sur les mécanismes de foisonnement du sol. L'analyse des mécanismes de transfert de charge a montré que pour le matériau granulaire testé le coefficient K à considérer dans la formulation de Terzaghi utilisée pour évaluer l'intensité du report de charge est de 1,3. Globalement la confrontation entre les résultats numériques et expérimentaux montre que l'ensemble des mécanismes complexes qui sont mobilisés lors de l'effondrement du sol sur la nappe sont assez bien pris en compte dans la modélisation numérique (foisonnement du sol, mise en tension de la nappe dans les zones d'ancrages, transfert de charge, etc.). Enfin, une amélioration des méthodes de dimensionnement actuelles est proposée dans un contexte normatif incluant les calculs aux états limites et avec prise en compte des coefficients de sécurité.
Abstract
The good geosynthetic sizing of the reinforcements on cavity requires a thorough knowledge of the mechanisms of load transfer of the zone of ground collapsed towards the stable zones. At present, the load acting on the geosynthetic sheet is estimated most of the time by using the mechanism of collapse proposed by Terzaghi and by supposing a uniform distribution of the stress on the sheet. To analyze more in detail these mechanisms of load transfer, full-scale experiments and DEM numerical simulations were performed. By testing two numerical processes, it was demonstrated that the cavity opening modes have a great influence on the shape of the load distribution transmitted to the geosynthetic sheet above the cavity and on the expansion mechanisms of the soil. An approximate conical load distribution seems well adapted when considering a progressive cavity diameter opening process, whereas an inverted load distribution seems more suitable for a gradual settlement process. In both cases and for the 20/40 mm used rolled gravel in the experimentation, the intensity of the load transfer mechanism can be approached by the Terzaghi's formulation using an appropriate value for the ratio between the horizontal and vertical stresses estimated at 1.3. The confrontation between the numerical and experimental results shows that all the complex mechanisms which are mobilized during the collapse of the ground on the geosynthetic is well enough taken into account in the numerical modelling (soil expansion, tension and displacement of the geosynthetic in the anchorage zones, distribution of load, etc.). An improvement of the design method is finally proposed from the results of this study with the consideration of a normative context including SLS and ULS calculations and with consideration of the safety factors.
Mots clés : renforcement géosynthétique / effondrement localisé / expérimentation en vraie grandeur / modélisation numérique / dimensionnement analytique
Key words: geosynthetic reinforcement / localized sinkhole / full-scale experiment / numerical modelling / analytical design
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2017
1 Introduction
L'aménagement progressif du territoire conduit à l'exploitation de nouvelles zones, actuellement délaissées, car présentant des risques pour la sécurité des usagers. C'est notamment le cas des zones d'effondrements potentiels qui sont liées à la présence de cavités souterraines. Les techniques de reconnaissance de ces cavités ne permettent en général pas de les détecter de manière exhaustive et les travaux de comblement sont souvent très onéreux sans pouvoir systématiquement apporter la garantie d'une solution pérenne. L'incidence du risque d'effondrement localisé de surface, qui subsiste pour les infrastructures de transport est d'autant plus préjudiciable lorsqu'elle se situe en déblai ou, lorsqu'en remblai, l'épaisseur de celui-ci est réduite. Depuis quelques années, le développement de la technique de renforcement par géosynthétique positionné à la base des plates-formes a permis d'apporter des solutions techniques économiques pour limiter temporairement les conséquences d'un effondrement localisé tout en répondant à la maîtrise des déflections de surface nécessaire à la poursuite du trafic.
En France, les premières études menées sur cette thématique dans le cadre du projet RAFAEL (renforcement des assises ferroviaires et autoroutières contre les effondrements localises) ont débouché sur une méthode de dimensionnement simplifiée qui a été reformulée (Briançon et Villard, 2006, 2008 ; Villard et Briançon, 2008) en prenant en compte les mécanismes d'interaction jusqu'alors négligés entre la nappe géosynthétique et le sol environnant.
Un projet Fond Unique Interministériel (FUI) a été conduit sur ce sujet (2010–1014) par la société Texinov et une thèse expérimentale et numérique (Huckert, 2014) dont les travaux seront en partie résumés ici a été menée dans ce cadre. À la suite de ces travaux, des modélisations numériques complémentaires prenant en compte notamment le mode d'ouverture de la cavité (Huckert et al., 2016) ont permis de préciser certains mécanismes tels que la géométrie de la répartition de la charge agissant sur le géosynthétique ou le phénomène de foisonnement du cylindre de sol situé au droit de la cavité. Ces nouveaux éléments et ceux apportés par les résultats de la thèse d'Audrey Huckert (2014) ont permis de faire évoluer les méthodes de calcul existantes (Villard et Briançon, 2008) et débouchent sur une procédure de dimensionnement plus réaliste.
2 Expérimentations en vraie grandeur
2.1 Description générale
Les expérimentations consistent à simuler l'ouverture progressive d'une cavité circulaire sous un remblai granulaire de 1 m d'épaisseur renforcé par géosynthétique. Le comportement mécanique et cinématique de la plate-forme renforcée est analysé en cours d'ouverture de la cavité et lors d'essais de chargement.
L'ouverture progressive de la cavité est simulée par un dispositif enterré préalablement dans le sol de fondation : l'ouverture d'une trappe permet de vidanger un volume rempli de billes d'argile et laissant apparaître une cavité circulaire de 0,75 m de diamètre sous la nappe géosynthétique, le dégonflage des chambres à air concentriques permet ensuite d'augmenter progressivement la taille de la cavité à des diamètres de 1,25 m puis 2,2 m (Fig. 1).
Trois plots expérimentaux (numérotés 1 à 3) ont été réalisés, permettant de tester deux géosynthétiques (Fig. 2). Le géosynthétique GSY 1 est un géotextile conventionnel en polyéthylène constitué d'un support non tissé renforcé dans le sens production par des câbles en polyester haute ténacité. Les raideurs en traction du géosynthétique GSY 1 sont respectivement de 3000 et de 250 kN/m dans les sens production et transversal. Le géosynthétique GSY 2 est un géosynthétique plus souple non conventionnel en polyéthylène constitué d'une grille tricotée (8 mm x 20 mm) renforcé par des câbles en polyester haute ténacité qui lui confèrent une raideur en traction dans le sens production à 3 % d'environ 700 kN/m. Les paramètres mécaniques du sol de la plate-forme et des interfaces ont été soigneusement déterminés par des essais de caractérisation en laboratoire (essais de cisaillement et de frottement à la boîte 0,3 m x 0,3 m). Les propriétés principales des sols (poids volumique γd, teneur en eau w, angle de frottement interne φ', cohésion c', et diamètres minimal et maximal des granulats dmin et dmax) et de l'interface ainsi que les caractéristiques mécaniques des nappes géosynthétiques sont présentés dans les Tableaux 1 et 2.
L'instrumentation mise en place permet de mesurer pour chaque étape d'ouverture de la cavité et chaque phase de chargement :
-
les tassements de surface, par le biais d'un suivi topographique et de mesures manuelles ;
-
les déplacements au sein de la plate-forme granulaire, par l'utilisation d'un géoradar associé à des déflecteurs métalliques positionnés dans la plate-forme granulaire au droit de la cavité (Fig. 1) ;
-
les déformations du géosynthétique, obtenues par fibres optiques équipées de réseaux de Bragg (FBG) espacés de 0,5 m au droit de la cavité et de l'ancrage du renforcement (Fig. 2) ;
-
la flèche du géosynthétique, par un capteur de déplacement laser positionné sous la nappe géosynthétique (Fig. 3) et dont la position horizontale peut être ajustée depuis le regard de visite ;
-
les transferts de charge, par des capteurs de pression totale (CPT) de 0,4 x 0,4 m positionnés en bord de cavité (Fig. 1 et 2).
Le Tableau 3 récapitule les caractéristiques techniques des capteurs et moyens de mesure utilisés.
 |
Fig. 1 Dispositif d'ouverture des cavités. Cavity device. |
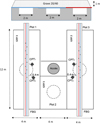 |
Fig. 2 Plots expérimentaux. Experimental sections. |
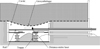 |
Fig. 3 Mesure de la flèche du géosynthétique au distance-mètre laser. Geosynthetic deflection measure using a laser distance sensor. |
Caractéristiques des dispositifs instrumentaux utilisés.
Monitoring devices characteristics.
2.2 Résultats expérimentaux
2.2.1 Phase 1 – Ouverture de la cavité (plots 1, 2 et 3)
La Figure 4 présente les résultats des mesures de tassement obtenues par topographie ou mesure manuelle. Les tassements augmentent pendant l'ouverture de la cavité et atteignent des valeurs de 0,14 m sur les plots 1 et 2, et 0,28 m sur le plot 3 une fois la cavité de 2,2 m de diamètre ouverte. Après 20 jours, un accroissement de tassement de 0,05 m est mesuré sur les trois plots. Cela s'explique notamment par le rééquilibrage progressif des transferts de charge au sein du remblai, les pluies orageuses et un possible déplacement du géosynthétique dans les zones d'ancrage.
La campagne géoradar vient compléter ces résultats en précisant la cinématique du remblai renforcé au droit de la cavité (Fig. 5). En effet, les réflecteurs métalliques positionnés sur la nappe géosynthétique et ceux localisés à 0,3 m et 0,6 m au-dessus, montrent clairement la géométrie cylindrique de l'effondrement sur les trois plots. En supposant que les déflections de surface et du géosynthétique sont des paraboles de révolution, il est possible d'estimer un facteur de foisonnement du remblai lors de l'ouverture de la cavité de 1,037 ± 0,05 compte tenu des incertitudes de mesure et de la non-symétrie des courbes.
La Figure 6 présente les déformations du géosynthétique. Ces dernières augmentent avec l'ouverture de la cavité et sont maximales au droit et à la périphérie de la cavité. Pour une cavité de diamètre donné, les déformations diminuent dans les zones d'ancrage en raison du frottement mobilisé.
Enfin, les contraintes verticales sous le remblai augmentent linéairement avec l'ouverture de la cavité. Les valeurs mesurées sous les capteurs CPT1 et CPT3 sont les plus élevées car plus proches du bord de la cavité ou le report de charge est le plus intense.
 |
Fig. 4 Tassements de surface sur les plots 2 et 3. Surface settlements in sections 2 and 3. |
 |
Fig. 5 Comportement cinématique du remblai renforcé sur le plot 3. Cinematic behavior of the reinforced embankment in section 3. |
 |
Fig. 6 Déformations du géosynthétique (plot 1). Geosynthetic strain (section 1). |
2.2.2 Phase 2 – Essais de circulation
Après ouverture de la cavité et comblement de la déflection de surface, un essai de circulation (surcharge d'une tonne centrée sur la cavité) est réalisé sur les plots 1 et 3. La Figure 7 montre les déplacements de la nappe géosynthétique, atteignant un incrément de 6 mm (au centre de la cavité) sur le plot 1, et 3,5 mm (à 0,3 m du centre de la cavité) sur le plot 3. La déflexion du géosynthétique GSY 2 de par sa faible rigidité avant l'essai de traficabilité sur le plot 3 étant plus importante, l'accroissement de déformation nécessaire à la reprise des efforts est plus faible.
 |
Fig. 7 Incréments de déplacement du géosynthétique pour la phase de circulation. Vertical displacement of the geosynthetic due to the circulation trials. |
2.3 Synthèse des essais
L'étude expérimentale montre un bon comportement des renforcements géosynthétiques mis en place, qui ont parfaitement joué leur rôle. Intégré à un remblai granulaire, le géosynthétique participe au mécanisme d'effondrement et permet de maîtriser les tassements de surface même pour une cavité de grand diamètre. L'ensemble des résultats expérimentaux obtenus constitue une base de données qu'il convient d'analyser plus en profondeur. Des résultats originaux ont, cependant, été obtenus sur l'évolution des mécanismes de transfert de charge lors des cycles de chargement et lors des ouvertures progressives de la cavité, sur le mode de répartition de la charge appliquée sur la nappe au droit de la cavité, sur la valeur du coefficient de foisonnement ou encore sur la géométrie du volume de sol effondré au droit de la cavité.
3 Modélisation numérique
3.1 Description du modèle numérique
Afin de prendre en considération les grandes déformations et l'évolution des mécanismes de transfert de charge dans le matelas granulaire, un code de calcul 3D (Villard et al., 2009) a été utilisé. Ce code permet de rendre compte du comportement des matériaux granulaires par le biais d'une modélisation discrète, basée sur le principe de la dynamique moléculaire (Cundall et Strack, 1979), et du comportement en traction et en membrane du géosynthétique par l'intermédiaire d'une modélisation continue (Villard et Giraud, 1998). Plusieurs géométries du modèle numérique, adaptées chacune au diamètre des cavités testées, ont été utilisées. Par raison de symétrie, la cavité a été positionnée dans l'un des coins du modèle (Fig. 8).
Le modèle de base utilisé pour comparaison avec les résultats expérimentaux se compose :
-
d'un ensemble de particules discrètes qui interagissent entre elles au niveau de leur point de contact et qui permettent de restituer le comportement macroscopique d'un matériau granulaire. Chaque particule, dont l'élancement est proche de celui des formes réelles de grain, est constituée de deux sphères indissociables de même diamètre juxtaposées l'une à l'autre. Pour le modèle numérique de base (4 m x 4 m), 32 000 particules de différentes tailles ont été utilisées, les plus grosses particules ayant, tout comme pour le matériau réel, une taille deux fois plus importante que la taille des plus petites particules ;
-
d'une nappe géosynthétique continue constituée d'éléments triangle à trois nœuds de faible épaisseur (Villard et Giraud, 1998). Des raideurs en traction différentes dans la direction de renforcement et la direction perpendiculaire ont été considérées pour rendre compte du comportement anisotrope du géosynthétique mis en œuvre lors des expérimentations. Pour le modèle de base, un total de 12 800 triangles a été utilisé ;
-
d'un ensemble de sphères régulièrement agencées et positionnées à la base du modèle pour simuler l'action d'un sol support élastique. Les positions de ces sphères sont pilotées en déplacement pour simuler l'ouverture de la cavité. Deux mécanismes d'ouverture ont été étudiés : une ouverture progressive de la cavité par augmentation de son diamètre (jusqu'à l'obtention d'un diamètre D, procédure A) et un abaissement progressif de l'ensemble des sphères du sol support situées sous le remblai au droit de la cavité de diamètre fixe D (procédure B). Pour le modèle de base, 12 800 sphères ont été utilisées pour modéliser le sol support ;
-
de parois non frictionnelles positionnées sur le pourtour du modèle et des conditions en déplacement (sur X et Y) des nœuds situés à la périphérie de la nappe géosynthétique pour assurer la condition de symétrie du problème.
Le comportement macroscopique de l'assemblée granulaire est lié, entre autre, à la compacité initiale et à la distribution granulométrique de l'échantillon numérique ainsi qu'à la forme des grains (Szarf et al., 2011). Compte tenu qu'il n'existe pas de relation directe entre le comportement macroscopique (angle de frottement interne, angle de dilatance et module d'Young) et les paramètres microscopiques de contact (rigidité normale Kn, rigidité tangentielle Ks et coefficient de frottement μ), il est nécessaire de calibrer les paramètres numériques du matériau granulaire en simulant numériquement un essai triaxial (Salot et al., 2009). Les paramètres du modèle numérique (Villard et al., 2016) présentés dans le Tableau 4 permettent de rendre compte d'un sol granulaire peu dense ayant un angle de frottement au pic de 36,5°, un angle de frottement au palier de 31° et un module d'Young de 19 MPa. Le comportement du géosynthétique est pris en considération via ses raideurs en traction dans la direction de renforcement (Jx = 3000 kN/m) et dans la direction perpendiculaire (Jy = 250 kN/m). Le comportement d'interface entre les éléments du remblai granulaire et le géosynthétique est restitué par une loi de contact de type Coulomb définie par un angle de frottement d'interface et des raideurs normales et tangentielles kn et ks (Tab. 4). Une fois le modèle numérique établi, le remblai granulaire est soumis à la gravité puis au test d'effondrement par déplacement des sphères du sol support situées sous le remblai au droit de la cavité suivant les procédures A ou B. L'intérêt du modèle numérique est qu'il permet de suivre l'évolution des forces d'interaction entre les particules lors de l'ouverture de la cavité, qu'il intègre les grands déplacements dans le remblai granulaire, qu'il tient compte naturellement des réarrangements dans le sol lorsque celui-ci se désorganise (foisonnement ou recompaction), et qu'il permet de modéliser les mécanismes d'interaction complexes à l'interface sol/géosynthétique comme le roulement ou le glissement des particules de sol sur la nappe. Les résultats attendus sont les déplacements de chaque particule du matelas granulaire, les déformations et tensions dans la nappe géosynthétique ainsi que les forces d'interaction au sein du remblai granulaire et aux interfaces sol/géosynthétique.
 |
Fig. 8 Géométrie du modèle numérique de base. Geometry of the numerical samples. |
Paramètres numériques définissant le matériau granulaire et le comportement d'interface sol/géosynthétique.
Numerical parameter for the granular material and the behavior of soil/geosynthetic interface.
3.2 Comparaison entre les résultats expérimentaux et numériques
Les résultats du modèle numérique sont confrontés dans cette partie aux résultats expérimentaux jugés les plus représentatifs obtenus sur le plot 1 avec le géotextile GSY 1. Les paramètres et la géométrie du modèle sont conformes à ceux de l'expérimentation et le processus de calcul est en tout point semblable au protocole expérimental à savoir une ouverture progressive du diamètre de la cavité jusqu'à un diamètre nominal de 2,2 m. Sur les Figures 9 et 10 sont comparés respectivement les tassements de surface, les déplacements verticaux et les déformations de la nappe géosynthétique pour un diamètre d'ouverture de la cavité de 2,2 m. Comme on peut le constater sur la Figure 9, les tassements de surface et les déplacements verticaux du géosynthétique sont assez bien restitués par le modèle numérique. On peut aussi noter que la géométrie de la zone de sol impliqué dans l'effondrement est localisée principalement au-dessus de la cavité et ce que ce soit numériquement ou expérimentalement. Par comparaison entre les volumes de sol initial (cylindre de sol au-dessus de la cavité) et effondré (délimité par la déflexion de surface et la déformation du géosynthétique) on estime le coefficient d'expansion du sol numérique à 1,048 ce qui reste très comparable à la valeur de 1,037 obtenue expérimentalement avec l'hypothèse d'une déflexion de surface et une déformée du géosynthétique paraboliques. Ce résultat est très satisfaisant si l'on considère que la forme des particules et la densité initiale du matériau de remblai n'ont été que très approximativement prises en compte dans la modélisation numérique. Si l'on compare (Fig. 10) les valeurs numériques des déformations de la nappe géosynthétique aux valeurs ponctuelles enregistrées par les réseaux de Bragg, on constate également, au regard du niveau de précision pouvant être atteint in situ, une assez bonne adéquation entre les résultats. Par ailleurs, il est possible de déterminer numériquement la contrainte verticale au voisinage de la cavité en considérant l'ensemble des efforts verticaux du sol sur la nappe géosynthétique sur le pourtour de la cavité (surface annulaire définie par des rayons internes et externes de 1,1 m et 1,5 m) et de comparer cette valeur aux mesures fournies par les capteurs de pression totale. À la fin du processus d'ouverture de la cavité, à D = 2,2 m l'accroissement de contrainte obtenu avec le modèle numérique sur les bords de la cavité est de 34 % contre une valeur expérimentale de 49 %. Là encore, compte tenu des incertitudes potentielles liées aux mesures (proximité avec les bords de la cavité et pivotement éventuel des capteurs), les résultats obtenus sont satisfaisants.
 |
Fig. 9 Comparaison entre les résultats numériques et expérimentaux des tassements de surface et déflexions du géosynthétique. Surface settlement and geosynthetic deflection – Comparison between numerical and experimental results. |
 |
Fig. 10 Comparaison entre les résultats numériques et expérimentaux des déformations dans la nappe géosynthétique. Comparison between experimental and numerical geosynthetic strain. |
3.3 Apport du modèle numérique à la compréhension des mécanismes de transferts de charge dans le remblai granulaire
L'outil numérique permet d'investiguer certains phénomènes, dont les mécanismes de transfert de charge, qui sont difficiles à quantifier ou à appréhender par des mesures in situ. Physiquement, les transferts de charge sont liés à une modification progressive des orientations et intensités des forces d'interaction entre les grains du remblai granulaire suite à une modification des conditions aux limites. Ils sont donc fortement tributaires de l'historique de chargement et donc du mode d'ouverture de la cavité. D'un point de vue pragmatique, l'efficacité du transfert de charge peut être définie comme le ratio entre la charge transmise sur le pourtour de la cavité et le poids (Ws) du cylindre de sol situé au-dessus de la cavité. Connaissant les efforts d'interaction entre les particules de la plate-forme granulaires et la portion de nappe située au-dessus de la cavité (Fg) il est possible de quantifier l'efficacité (E) du transfert de charge en utilisant la relation E = (Ws−Fg)/Ws. De même, connaissant les efforts d'interaction en tout point de la nappe il est possible, en considérant des secteurs annulaires centrés sur la cavité, de déterminer avec précision la géométrie de la distribution des contraintes verticales sur la nappe. L'influence du mode d'ouverture de la cavité sur l'efficacité des transferts de charge est mise en évidence sur la Figure 11.
Pour chaque diamètre de cavité testé (procédure B) deux points sont représentés. Le premier caractérise l'efficacité maximale du transfert de charge obtenue au cours du processus d'effondrement pour des déformations faibles de la plate-forme granulaire et le second caractérise l'efficacité résiduelle obtenue après ouverture de la cavité. L'écart entre ces deux points augmente avec la taille de la cavité et le taux de déformation du matelas granulaire (Fig. 11). On notera également que les tailles des modèles numériques et le nombre d'éléments ont été adaptés aux diamètres des cavités : mailles de 0,5 m x 0,5 m x 1 m pour des diamètres de cavité de 0,1 à 0,2 m (modèle C), mailles de 1 m x 1 m x 1 m pour des diamètres de cavité de 0,2 à 0,5 m (modèle B), et mailles de 4 m x 4 m x 1 m pour des diamètres de cavité de 0,5 à 2,5 m (modèle A dit modèle de base). Sur la Figure 11, on constate que les valeurs de l'efficacité des transferts de charge sont assez voisines d'un mode d'ouverture à l'autre et ce quel que soit le diamètre de cavité considéré (les valeurs des efficacités des transferts de charge obtenues avec la procédure A étant comprises entre les deux valeurs obtenues avec la procédure B). En revanche, les valeurs des tassements de surfaces et des déplacements de la nappe, présentés pour une valeur particulière du ratio D/H sur la Figure 12 et dans le Tableau 5, sont très différentes d'un mode d'ouverture à l'autre, ce qui laisse présumer que la géométrie des distributions de charges sur la nappe varie en fonction du mode d'ouverture de la cavité.
Par ailleurs, les valeurs des coefficients de foisonnement du matériau granulaire situé au-dessus de la cavité (Tab. 5) sont légèrement différentes d'un mode d'ouverture à l'autre. Logiquement, le coefficient de foisonnement obtenu avec la procédure A est plus important puisque la zone cisaillée et décompactée lors de l'effondrement est plus importante du fait de l'augmentation progressive du diamètre de la cavité.
Enfin, sur la Figure 13, on présente les distributions de contraintes sur la nappe géosynthétique en fonction du mode d'ouverture de la cavité et ce pour trois valeurs du ratio D/H. On constate sur cette figure ; et ce quelle que soit la valeur du ratio D/H considérée, une très nette différence sur la géométrie des distributions de charge sur la nappe à savoir : une répartition tronconique pour la procédure A (avec des concentrations de charge au centre de la cavité) et une distribution de charge plutôt constante voire inversée pour la procédure B (avec une concentration d'effort plus importante sur le pourtour intérieur de la cavité). Ceci est lié au fait que les transferts de charge vers les bords de la cavité sont systématiquement remis en cause par l'augmentation progressive du diamètre de la cavité (procédure A) alors qu'ils sont peu perturbés tout au long de la procédure B. À la fin du processus d'effondrement, les efforts de cisaillement à la périphérie du cylindre de sol effondré sont assez similaires d'un mode d'ouverture de la cavité à l'autre ce qui explique que les efficacités du transfert de charge soient dans les deux cas très proches. En termes de tassement de surface, le mode d'ouverture de la cavité le plus discriminant est le mode d'ouverture par augmentation progressive de son diamètre.
 |
Fig. 11 Efficacité du transfert de charge en fonction du ratio D/H pour les deux modes d'ouverture de la cavité. Efficiency versus D/H for the two cavity opening processes. |
 |
Fig. 12 Comparaison des tassements de surface et déplacements verticaux du géosynthétique en fonction du mode d'ouverture de la cavité (D/H = 2,2 m). Vertical geosynthetic displacements and surface settlements (m) for both process and for H/D = 2.2. |
Comparaison des résultats avec les deux modes d'ouverture.
Comparison between both processes.
 |
Fig. 13 Comparaison des géométries des distributions de contraintes verticales sur la nappe en fonction du mode d'ouverture de la cavité pour trois diamètres de cavité. Increase in the vertical stresses acting on the upper face of the geosynthetic for the three ratios D/H. |
4 Méthode de dimensionnement
Les études antérieures à ces travaux (Briançon et Villard, 2008 ; Villard et Briançon, 2008) ont conduit au développement d'une méthode de dimensionnement prenant en considération le comportement en membrane du géosynthétique, un modèle d'effondrement cylindrique du sol de remblai au-dessus de la cavité et une distribution de contrainte sur le géotextile verticale et uniforme. Le modèle d'effondrement cylindrique est basé sur l'hypothèse d'un confinement latéral générant par cisaillement un report de charge vers le pourtour de la cavité (Blivet et al., 2000). Cette méthode prend aussi en compte dans les zones adjacentes à la cavité les déplacements de la nappe géosynthétique nécessaires à la mobilisation des efforts à l'interface sol/géosynthétique et à la mise en tension de la nappe. Une loi d'interaction de type élasto-plastique avec un critère de rupture de type Mohr-Coulomb est utilisée. Nous proposons d'intégrer à cette méthode les derniers développements faisant suite aux expérimentations en vraie grandeur et aux modélisations numériques présentées en Sections 2 et 3 (Huckert et al., 2016 ; Villard et al., 2016) et en particulier des répartitions de contraintes non uniformes sur la nappe au droit de la cavité en fonction du mode d'ouverture de la cavité. À noter que la méthode de dimensionnement proposée s'applique à tout type de renforcement. En effet, il a été démontré pour des cavités circulaires (Gourc et Villard, 2000) qu'un geotextile bidirectionnel de raideurs (Jx et Jy) avait un comportement en flexion similaire à celui d'un géotextile monodirectionnel de raideur J = (Jx + Jy).
4.1 Principe du dimensionnement
Les équations de base nécessaires au dimensionnement sont synthétisées ci-dessous. Pour plus de détails sur leur formulation, le lecteur pourra se reporter aux articles suivants : Briançon et Villard, 2006 ; Briançon et Villard, 2008 ; Villard et Briançon, 2008 ; Huckert et al., 2016.
Quelle que soit la géométrie de la distribution de charge sur la nappe, la prise en compte du comportement en membrane de la nappe et de la mobilisation du frottement dans les zones d'ancrage adjacentes à la cavité (Fig. 14) conduit à l'équation (1) qui suppose que l'augmentation de longueur de la nappe au-dessus de la cavité (ΔL) résulte de sa déformation au-dessus de la cavité et des déplacements de la nappe dans la zone d'ancrage. Suite à la définition de la géométrie de la distribution de charge sur la nappe q(x), il est possible, par un processus itératif et par intégration numérique, de résoudre assez simplement l'équation (2) ou TH, composante horizontale de la tension dans la section de nappe située au-dessus de la cavité, est l'inconnue à déterminer. On note U0 le déplacement minimal nécessaire à l'obtention du frottement maximal à l'interface sol/géosynthétique et β l'angle que fait la nappe avec l'horizontale au point A.
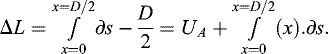 (1)
Avec :
(1)
Avec :
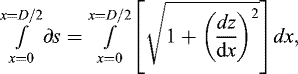 (2)
(2)
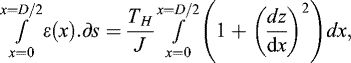 (3)
(3)
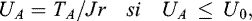 (4)
(4)
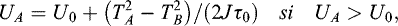 (5)
(5)
 (6)
(6)
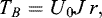 (7)
(7)
 (8)
(8)
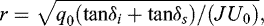 (9)
(9)
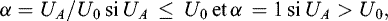 (10)
(10)
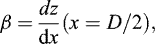 (11)
(11)
L'équilibre d'un tronçon de nappe situé au-dessus de la cavité conduit aux équations (12) et (13) qui permettent d'établir respectivement pour une distribution de charge donnée, la relation entre la charge appliquée et les déplacements verticaux de la nappe, et les tensions en tout point de la nappe.
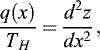 (12)
(12)
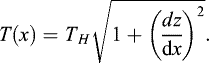 (13)
(13)
Pour une distribution de charge uniforme q, l'équation (12) conduit à :
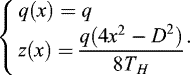 (14)
(14)
Pour une distribution de charge en cône (Fig. 15) correspondant à une ouverture concentrique de la cavité, on aura :
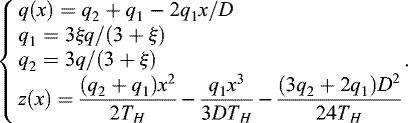 (15)
(15)
Alors que pour une distribution de charge en cône inversé (Fig. 15) correspondant à un affaissement progressif de la cavité, on aura :
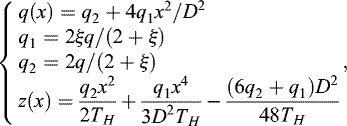 (16)
(16)
q1 et q2 sont liés par l'intermédiaire du coefficient ξ = q1/q2 à la valeur de la contrainte moyenne q agissant sur la nappe au droit de la cavité (Fig. 15).
La valeur de la contrainte moyenne q agissant sur la nappe peut être obtenue en considérant le mécanisme d'effondrement cylindrique proposé par Terzaghi (1943) :
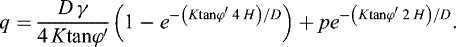 (17)
(17)
Dans la formulation initiale, le coefficient K définissant le ratio entre les contraintes horizontales et verticales à la périphérie du cylindre de sol effondré. Terzaghi (1943) proposa une valeur de K = 1 dans l'étude de l'effondrement d'un cylindre de sol au droit d'une trappe mobile. De nombreux auteurs ont proposé d'autres valeurs pour ce coefficient K, notamment K = Ka dans le projet RAFAEL (Blivet et al., 2000) mais aucune définition n'a pour l'instant fait l'unanimité.
En considérant que l'effondrement du volume de sol au droit de la cavité est de forme cylindrique, que le foisonnement du sol est homogène sur tout le volume, et en faisant une hypothèse forte sur l'allure de la déformée de surface il est possible, connaissant l'équation de la déformée de la nappe z(x), d'estimer la valeur du tassement de surface à partir de la flèche maximale de la nappe au droit de la cavité. Par exemple, l'hypothèse d'une déflection de surface parabolique et d'une répartition de charge verticale uniforme conduit à l'équation (18). On notera que l'hypothèse d'une charge non uniforme (Eqs. (15) et (16)) et d'une déformée de surface non parabolique implique une reformulation de l'équation (18). Ces équations nécessitent de fixer une valeur moyenne du coefficient de foisonnement Ce. Aucune étude n'a à ce jour permis de définir avec précision une règle générale permettant de fixer cette valeur.
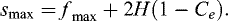 (18)
(18)
À partir d'un critère de tassement imposé en surface, connaissant le mode d'ouverture de la cavité et pour des conditions géométriques et des caractéristiques des sols constituant la plate-forme définies, il est possible de déterminer le module J du géosynthétique pour une déformation donnée. Malgré quelques hypothèses encore non validées par l'expérimentation, notamment sur le coefficient K à considérer dans l'équation (17) ou la valeur du foisonnement du sol, cette méthode de dimensionnement analytique permet de prendre en compte de façon réaliste les mécanismes développés dans la plate-forme granulaire et à l'interface sol / géosynthétique.
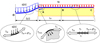 |
Fig. 14 Mécanismes pris en considération pour le dimensionnement. Physical mechanisms taking into account for the design. |
 |
Fig. 15 Influence de la forme de la distribution de contrainte sur les déplacements verticaux de la nappe géosynthétique. Comparison between analytical and numerical geosynthetic deflection. |
4.2 Application de la méthode de dimensionnement au cas expérimental
La méthode de dimensionnement a été appliquée au plot 3 du site expérimental en considérant les paramètres présentés dans le Tableau 6. Trois types de répartition de charge sur la nappe ont été pris en considération à titre de comparaison (tronconique, paraboloïde inversé et uniforme). Le coefficient K considéré dans le mécanisme d'effondrement cylindrique proposé par Terzaghi (Eq. 17) a été fixé à 1,3 pour correspondre à ce qui a été mis en évidence numériquement. On note La la longueur à partir de l'axe de la cavité pour laquelle l'ancrage est supposé fixe.
Paramètres pris en compte pour le calcul analytique.
Parameters taking into account for the analytical method.
4.3 Confrontation par rapport aux résultats numériques et expérimentaux
Les résultats analytiques, ceux du modèle numérique et les valeurs expérimentales obtenues sur le plot 3 sont comparés (Fig. 15) pour les déplacements de la nappe géosynthétique au droit de la cavité et (Fig. 16) pour les déformations de la nappe géosynthétique, et ce pour un diamètre de la cavité de 2,2 m et différents modes d'ouverture de la cavité.
Comme on peut le constater (Fig. 15), les résultats numériques et analytiques correspondant à une ouverture progressive de la cavité sont en parfaite adéquation avec les résultats expérimentaux.
On observe aussi que le modèle analytique prenant en compte une répartition tronconique de la charge correspond bien au mode d'ouverture de la procédure A modélisé numériquement. Enfin, le cas de la répartition uniforme qui est habituellement considéré dans les méthodes de dimensionnement existantes est représentatif d'aucun des deux modes d'ouverture.
La concordance des résultats numériques et analytiques se vérifie aussi avec les mesures de déformation de la nappe dans les zones d'ancrage (Fig. 16). Il apparaît clairement que la procédure numérique B correspondant à un affaissement progressif du sol sous le remblai est en bon accord avec le cas de chargement de type parabolique inversé. De même, le mécanisme d'ouverture progressif du diamètre de la cavité simulé expérimentalement est bien restitué numériquement dans les zones d'ancrage par la procédure A et analytiquement par le cas du chargement tronconique.
En revanche, l'hypothèse émise analytiquement d'une augmentation rapide de la tension ou de la déformation sur les bords de la cavité suite au changement d'orientation de la nappe semble plus ou moins réaliste. On constate, en effet, que ce soit numériquement ou expérimentalement, une augmentation progressive de la tension et de la déformation au droit de la cavité liée probablement à une certaine souplesse et à un écrasement des appuis.
Quoi qu'il en soit, la comparaison des modélisations et méthodes analytiques sur un cas type met en évidence une significative amélioration dans la prise en compte des mécanismes réels permettant de rendre plus fidèlement compte de la répartition des contraintes sur le géosynthétique au droit de la cavité.
Cependant, certains mécanismes nécessitent d'être encore étudiés, c'est notamment le cas du foisonnement du sol au droit de la cavité ou l'intensité du transfert de charge vers les bords de la cavité.
 |
Fig. 16 Influence de la forme de la distribution de contrainte sur la déformation de la nappe dans les zones d'ancrage. Influence of the load distribution shape on the geosynthetic strain in anchorage areas. |
4.4 Intégration des coefficients de sécurité
La mise en application de la méthode de dimensionnement proposée à des cas concrets nécessite la définition d'une stratégie de dimensionnement à court ou long termes et la prise en compte de facteurs de sécurité partiels conformément aux normes en vigueur. Comme pour les autres ouvrages renforcés, les situations de calcul à considérer doivent être sélectionnées et classées conformément aux principes définis dans la norme NF EN 1990 en distinguant les situations de projet durables, les situations de projet transitoires, les situations de projet accidentelles et les situations de projet sismiques. Les effets des actions doivent être déterminés en combinant les actions :
-
pour les états limites ultimes, les combinaisons d'actions pour les situations durables et transitoires, celles pour les situations accidentelles et celles pour les situations sismiques ;
-
pour les états limites de service, les combinaisons caractéristiques, les combinaisons fréquentes, et les combinaisons quasi-permanentes.
En conformité avec les normes existantes sur les ouvrages renforcés, on retiendra l'approche 2 (NF EN 1997-1/NA) pour la justification des renforcements par géosynthétique de structure au-dessus de cavités. Pour la vérification des états limites de service, les facteurs partiels sont pris égaux à 1 conformément à l'annexe nationale (NF EN 1997-1/NA).
Les ouvrages de renforcement par géosynthétique sur cavités peuvent atteindre la ruine par rupture des éléments liés au renforcement :
-
rupture du géosynthétique ;
-
rupture des ancrages.
Les risques de ruine par déformation excessive de la structure peuvent aussi être analysés lors des calculs aux états limites ultimes, si celle-ci vont bien au-delà de l'exploitation normale de l'ouvrage.
Les différents états limites ultimes à considérer sont :
-
les états limites d'instabilité par défaillance du renforcement, soit par insuffisance de résistance à la traction, soit par insuffisance de la résistance de l'interaction entre le renforcement et le sol ;
-
les états limites d'instabilité par déformation excessive de la structure.
En outre, on doit vérifier qu'aucun de ces états limites ne peut être atteint ni au cours de la construction ni pendant sa durée d'utilisation prévue.
Par ailleurs, la particularité des ouvrages de renforcement par géosynthétiques sur cavités par rapport aux autres ouvrages de renforcement consiste dans le besoin de vérifier le tassement de surface pour garantir la poursuite du bon fonctionnement de l'ouvrage même après l'ouverture la cavité. Il s'en suit la nécessité d'analyser l'état limite de service correspondant au cours de la construction et pendant sa durée d'utilisation prévue.
4.4.1 États limites ultimes pour la rupture en traction du géosynthétique
Les vérifications aux états limites ultimes visent à éviter la ruine de l'ouvrage après l'ouverture de la cavité. Compte tenu des mécanismes décrits précédemment, on peut définir les vérifications minimales qu'il y a lieu d'effectuer aux états limites ultimes :
-
résistance en traction du géosynthétique ;
-
tassement en surface évalué pour vérifier le risque d'instabilité de la structure en surface ;
-
capacité d'ancrage dans les zones adjacentes à la cavité.
La vérification à l'état limite ultime vis-à-vis de la rupture en traction du géosynthétique fait l'objet d'une démarche particulière qui doit prendre en compte le comportement à long terme du produit. La vérification de la stabilité du sol au-dessus du géosynthétique permet de calculer la résistance de traction du géosynthétique (TELU). La vérification aux états limites ultimes s'écrit (Eq. 19) :
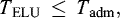 (19)
(19)
avec Tadm la résistance admissible du géosynthétique qui peut être évaluée à partir de la résistance ultime à court terme (TULT) mesurée suivant la norme NF EN ISO 10319 (Eq. 20) :
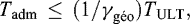 (20)
(20)
avec γgéo le coefficient qui intègre le facteur partiel de la résistance en traction (γM;t) et les coefficients réducteurs qui permettent de prendre en compte le comportement dans le temps du géosynthétique (Eq. 21) :
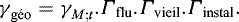 (21)
(21)
4.4.2 États limites de service pour l'évaluation des tassements en surface
Les vérifications aux états limites de service visent à s'assurer que les tassements en surface resteront admissibles après l'ouverture de la cavité. Les vérifications consistent à effectuer les mêmes calculs qu'aux états limites ultimes, mais en appliquant aux actions et matériaux des coefficients partiels égaux à 1, et en se fixant un « coefficient global » de sécurité qui est censé assurer que les tassements et les déplacements de l'ouvrage sont acceptables.
La vérification aux états limites de service doit faire l'objet d'une démarche particulière dans le cas des ouvrages sur cavité, dans la mesure où il convient d'intégrer l'influence du comportement dans le temps des géosynthétiques non seulement sur le calcul de stabilité, mais aussi sur le calcul des déformations.
Dans la pratique, il conviendrait d'intégrer dans cette vérification les lois de comportement (fonction du temps) du sol, du géosynthétique et de l'interaction. Cependant, pour les dimensionnements courants on utilise le plus souvent des approches analytiques simples qui ne permettent pas d'intégrer les interactions de ces différents comportements entre eux (endommagement, fluage, vieillissement du géosynthétique, lois de contrainte-déformation du sol). Elles se limitent souvent à superposer les différents effets de ces comportements par le biais de coefficients réducteurs. Si l'on procède ainsi lors des vérifications aux états limites de service, il convient de prendre en compte les coefficients réducteurs sur le fluage, le vieillissement et l'endommagement du géosynthétique pour calculer la déformation du géosynthétique à l'état limite de service (εadm), à la différence de la vérification aux états limites ultimes, pour laquelle ils sont pris en compte à la rupture du produit.
Ainsi, pour l'endommagement à la mise en œuvre, il a été montré que pour les géosynthétiques ne subissant que des endommagements internes, sous réserve de rester loin d'une déformation de rupture, la loi effort/déformation du géosynthétique n'est pas affectée par la mise en œuvre (Γinstal, εadm = 1), alors que pour ceux subissant des endommagements externes, ou en absence d'information, il convient de considérer un coefficient réducteur (Γinstal, εadm) identique à celui utilisé dans l'équation (21).
Dans le principe, il est possible de raisonner de manière analogue pour le vieillissement. Cependant, en absence de données suffisantes, on admet qu'un coefficient réducteur (Γvieil, εadm) identique à celui utilisé dans l'équation (21) peut être considéré.
À la différence des deux paramètres précédents, le fluage doit être pris en compte à partir de l'ouverture de la cavité et jusqu'à son comblement. Ceci amène à distinguer la durée de fluage (tflu) de la durée de service (ts). La prise en compte du fluage se fera par un coefficient réducteur (Γflu, εαdm) obtenu à partir de la perte d'effort calculée entre les courbes isochrones (t = 10 h et t = tflu) à la déformation admissible (εadm). Ce coefficient réducteur est en général très inférieur à celui utilisé dans l'équation (21).
La vérification à l'état limite de service vis-à-vis de la rupture en traction du géosynthétique s'écrit à la déformation admissible (εadm) (Eq. 22) :
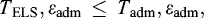 (22)
(22)
avec Tadm, εadm la résistance admissible du géosynthétique (à la déformation admissible [εadm]) qui peut être évaluée à partir de la courbe effort déformation à court terme mesurée suivant la norme NF EN ISO 10319 (TULT, εULT) (Eq. 23) :
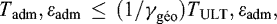 (23)
(23)
avec γgéo le coefficient qui intègre le facteur partiel de la résistance en traction (γM;t) et les coefficients réducteurs à la déformation admissible (εadm) qui permettent de prendre en compte le comportement dans le temps du géosynthétique (Eq. 24) :
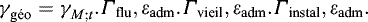 (24)
(24)
4.4.3 Vérification vis-à-vis des ancrages
La vérification aux états limites ultime et de service se fait de manière analogue à celles des autres ouvrages de renforcement. On vérifie que la résistance d'ancrage (Ra) affectée du coefficient partiel correspondant au type d'état limite est supérieure ou égale à la plus grande des valeurs de traction aux états limites ultime et de service (Eq. 25) :
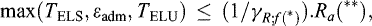 (25)
(25)
(*) la valeur de (γR;f) est choisie en fonction de l'état limite considéré ; (**) il est proposé d'appliquer le coefficient partiel sur la résistance globale d'ancrage (EBGEO, 2011)
La sécurité des ancrages doit être assurée de part et d'autre de la cavité. Cela nécessite en particulier de la vérifier pour les recouvrements longitudinal et latéral (par rapport au sens de production du géosynthétique). Cela suppose de prendre en compte le coefficient de frottement géosynthétique/géosynthétique pour l'une des faces, l'autre face étant au contact du sol du terrain naturel ou du remblai étant affecté du coefficient d'interaction correspondant. Par défaut EBGEO (2011) propose :
-
pour le couvrement longitudi;1;nal, une valeur de frottement géosynthétique/géosynthétique, tan δgeo,geo = 0,2 ;
-
pour le recouvrement latéral, une largeur de recouvrement de (2.ε.D) avec un recouvrement minimal de 0,5 m.
5 Conclusion et perspectives
Les résultats numériques et expérimentaux ont montré que lors de la formation d'une cavité sous un remblai granulaire renforcé par géosynthétique, la répartition des charges sur la nappe n'est pas uniforme et qu'elle est largement influencée par le mode d'ouverture de la cavité. En particulier, une distribution de charge tronconique pour laquelle la charge est plus importante au centre de la cavité a été obtenue lorsque le diamètre de la cavité augmente progressivement. Ceci est lié au fait que les mécanismes de transfert de charge qui se mettent en place au début de la formation de la cavité sont sans cesse remis en cause lors de l'augmentation progressive de son diamètre. A contrario, lorsque le sol sous le remblai s'effondre progressivement, les mécanismes de report de charge vers les bords de la cavité générés au tout début de la formation de la cavité perdurent lors de l'effondrement de sorte que la répartition de charge sur la nappe est plus importante au voisinage des bords de la cavité. Malgré ces mécanismes, le report de charge global de la zone effondrée vers les zones stables semble peu influencé par le mode d'ouverture de la cavité. Il a ainsi été montré que la formule de Terzaghi pouvait être utilisée pour estimer ce report de charge en prenant pour le coefficient K (rapport entre les contraintes horizontales et verticales au voisinage du cylindre de sol effondré) une valeur de 1,3 pour le matériau granulaire testé. Enfin, il a aussi été montré que le mécanisme de foisonnement du sol n'était pas homogène dans le volume de sol effondré et qu'il était fortement influencé par le mode d'ouverture de la cavité. Une valeur moyenne du coefficient de foisonnement prenant en compte l'augmentation de volume du sol dans les zones cisaillées ou décompactées lors de l'effondrement doit être considérée. Ces nouveaux développements ont été intégrés aux méthodes de dimensionnement existantes. En testant différentes répartition de charge sur la nappe il a été constaté que celle qui conduisait aux déformations de la nappe et aux déflections de surface les plus importantes était induite par une ouverture progressive du diamètre de la cavité.
Enfin, au travers des travaux réalisés, il est apparu que le modèle numérique était tout à fait apte à rendre compte des mécanismes d'interaction entre la nappe et le sol ainsi que des mécanismes de transfert de charge au sein du remblai. Les développements futurs sont orientés vers l'utilisation de cette technique de renforcement pour les couches de sols traités cohésives dont le mode de rupture et les interactions avec la nappe sont encore mal connus car très peu étudiés.
Glossaire
dmin et dmax : Taille minimale et maximale des grains de sol (m)
fmax : Déflexion maximale du GSY (m)
kn : Raideur normale de contact entre une particule de sol et la nappe géosynthétique (MN/m3)
ks : Raideur tangentielle de contact entre une particule de sol et la nappe géosynthétique (MN/m3)
q : Charge répartie moyenne appliquée sur la nappe au droit de la cavité (kPa)
q(x) : Distribution de la charge sur le GSY (kPa)
q0 : Charge répartie agissant au niveau des zones d'ancrage (kPa)
q1 : Valeur maximum de la partie non uniforme de la distribution de charge sur le GSY (kPa)
q2 : Valeur de la part uniforme de la distribution de la charge sur le GSY (kPa)
smax : Tassement en surface (m)
Ce : Coefficient de foisonnement
Fg : Somme des forces d'interaction entre les particules de la plate-forme granulaires et la portion de nappe située au-dessus de la cavité (kN)
J : Raideur par unité de largeur du GSY (kN/m)
K : Rapport entre la contrainte horizontale et la contrainte verticale dans le sol
Kn : Rigidité normale de contact entre deux particules du sol (MN/m2)
Ks : Rigidité tangentielle de contact entre deux particules du sol (MN/m2)
La : Longueur à partir de l'axe de la cavité pour laquelle l'ancrage est supposé fixe (m)
T : Tension dans le GSY (kN/m)
Tadm : Résistance admissible de traction du GSY (kN/m)
TA : Tension horizontale dans le géosynthétique au point A (kN/m)
TB : Tension horizontale dans le géosynthétique au point B (kN/m)
TELS : Résistance de traction du GSY à l'ELS (kN/m)
TELU : Résistance de traction du GSY à l'ELU (kN/m)
TH : Composante horizontale de la tension dans la section de nappe située au-dessus de la cavité (kN/m)
TM : Tension dans la nappe géosynthétique au point M (kN/m)
Tmax : Tension maximale du géosynthétique (kN/m)
U0 : Déplacement relatif minimal nécessaire à la mobilisation totale du frottement à l'interface sol/GSY (m)
UA : Déplacement horizontal de la nappe géosynthétique au point A (m)
Ws : Poids du cylindre de sol situé au-dessus de la cavité (kN)
CPT : Capteur de pression totale
α : Fraction entre le déplacement au point A et U0
β : Angle que fait la nappe avec l'horizontale au point A (rd)
γ : Poids volumique humide du sol (kN/m3)
γd : Poids volumique sec du sol (kN/m3)
γgeo : Facteur intégrant le facteur partiel de la résistance en traction et les coefficients de réduction
γM;t : Facteur partiel de la résistance en traction
δi : Angle de frottement entre le géosynthétique et le sol situé en dessous (°)
δgeo geo : Angle de frottement dans les zones de recouvrement géosynthétique (°)
δs : Angle de frottement entre le géosynthétique et le sol situé au-dessus (°)
ε : Déformation du géosynthétique (%)
μ : Coefficient de frottement microscopique
φ' : Angle de frottement interne du sol (°)
σ : Contrainte appliquée sur la nappe (kPa)
σ0 : Contrainte appliquée sur la nappe due au poids du remblai (kPa)
τ0 : Contrainte de cisaillement maximale à l'interface (kPa)
τi : Contrainte de cisaillement à l'interface sol inférieur / GSY (kPa)
τs : Contrainte de cisaillement à l'interface sol supérieur / GSY (kPa)
ΔL : Augmentation de longueur de la nappe au-dessus de la cavité (m)
Γflu : Coefficient de réduction lié à la diminution de la résistance en traction lors du fluage des renforcements géosynthétiques
Γflu, εadm : Coefficient de réduction lié à la diminution de la résistance en traction lors du fluage pour la déformation admissible (εadm) sur la période (tflu)
Γinstal : Coefficient de réduction correspondant à la diminution de la résistance en traction due à l'endommagement des renforcements géosynthétiques lors de leur installation et lors du compactage des remblais
Γinstal, εadm : Coefficient de réduction lié à la diminution de la résistance en traction à l'endommagement des renforcements pour la déformation admissible (εadm)
Γvieil : Coefficient de réduction lié à la diminution de la résistance en traction due au vieillissement des produits géosynthétiques dépendant des conditions d'environnement
Γvieil, εadm : Coefficient de réduction lié à la diminution de la résistance en traction au vieillissement pour la déformation admissible (εadm)
Références
- Blivet JC, Khay M, Villard P, Gourc JP. 2000. Design method for geosynthetic as reinforcement for embankment subjected to localized sinkholes. In: Geo-Eng2000, International Conference on Geotechnical and Geological Engineering, Melbourne, Australia, 1–6. [Google Scholar]
- Briançon L, Villard P. 2006. Dimensionnement des renforcements géosynthétiques de plates-formes sur cavités. Rev Fr Geotech 117 (4): 51–62. [CrossRef] [Google Scholar]
- Briançon L, Villard P. 2008. Design of geosynthetic reinforcements of platforms subjected to localised sinkholes. Geotext Geomembr 26 (5): 416–428. [CrossRef] [Google Scholar]
- Cundall PA, Strack ODL. 1979. A discrete numerical modelling method for granular assemblies. Geotech 29 (1): 47–65. [CrossRef] [Google Scholar]
- EBGEO. 2011. Recommandations for design and analysis of earth structures using geosynthetic reinforcements (EBGEO). German Geotechnical Society, 265 p. [Google Scholar]
- Gourc JP, Villard P. 2000. Reinforcement by membrane effect: application to embankments on soil liable to subsidence. In: Geosynthetics ASIA 2000, 2nd Asian Geosynthetics Conference, Kuala Lumpur, Malaysia, (1): 55–72. [Google Scholar]
- Huckert A. 2014. Approches expérimentale et numérique du dimensionnement de renforcements géosynthétiques sur cavités et inclusions rigides. Thèse de l'université de Grenoble, France, 224 p. [Google Scholar]
- Huckert A, Briançon L, Villard P, Garcin P. 2016. Load transfer mechanisms in geotextile-reinforced embankments overlying voids: experimental and analytical approaches. Geotext Geomembr 44 (3): 442–456. [CrossRef] [Google Scholar]
- NF EN 1990 Eurocode 0 – Bases de calcul des structures (indice de classement : P 06-100-1) avec son annexe nationale (NF P 06-100-2) et son amendement NF EN 1990/A1 (indice de classement : P 06-100-1/A1) avec son annexe nationale NF EN 1990/A1/NA (indice de classement : P 06-100-1/A1/NA). [Google Scholar]
- NF EN 1997-1 Eurocode 7 – Calcul géotechnique – Partie 1 : règles générales (indice de classement : P 94-251-1) avec son annexe nationale NF EN 1997-1/NA (indice de classement : P 94-251-1/NA). [Google Scholar]
- NF EN ISO 10319. 2008. Géosynthétiques – Essai de traction des bandes larges. [Google Scholar]
- Salot C, Gotteland Ph, Villard P. 2009. Influence of relative density on granular materials behavior: DEM simulations of triaxial tests. Granul Matter 11 (4): 221–236. [CrossRef] [Google Scholar]
- Szarf K, Combe G, Villard P. 2011. Polygons vs. clumps of discs: a numerical study of the influence of grains shape on the mechanical behaviour of granular materials. Powder Technol 208 (2): 279–288. [CrossRef] [Google Scholar]
- Terzaghi K. 1943. Theoretical soil mechanics. New York, NY: John Wiley & Sons. [CrossRef] [Google Scholar]
- Villard P, Briançon L. 2008. Design of geosynthetic reinforcements for platforms subjected to localized sinkholes. Can Geotech J45: 196–209. [CrossRef] [Google Scholar]
- Villard P, Giraud H. 1998. Three-dimensional modelling of the behaviour of geotextile sheets as membrane. Text Res J 68 (11): 797–806. [CrossRef] [Google Scholar]
- Villard P, Chevalier B, Le Hello B, Combe G. 2009. Coupling between finite and discrete element methods for the modelling of earth structures reinforced by geosynthetics. Comput Geotech 36: 709–717. [Google Scholar]
- Villard P, Huckert A, Briançon L. 2016. Load transfer mechanisms in geotextile-reinforced embankments overlying voids: numerical approach and design. Geotext Geomembr 44 (3): 381–395. [CrossRef] [Google Scholar]
Citation de l'article : Pascal Villard, Laurent Briançon, Audrey Huckert, Philippe Delmas. Conséquences du mode d'effondrement sur les mécanismes de transfert de charge et sur le dimensionnement des géosynthétiques sur cavités potentielles. Rev. Fr. Geotech. 2017, 152, 2.
Liste des tableaux
Caractéristiques des dispositifs instrumentaux utilisés.
Monitoring devices characteristics.
Paramètres numériques définissant le matériau granulaire et le comportement d'interface sol/géosynthétique.
Numerical parameter for the granular material and the behavior of soil/geosynthetic interface.
Comparaison des résultats avec les deux modes d'ouverture.
Comparison between both processes.
Paramètres pris en compte pour le calcul analytique.
Parameters taking into account for the analytical method.
Liste des figures
 |
Fig. 1 Dispositif d'ouverture des cavités. Cavity device. |
| Dans le texte | |
 |
Fig. 2 Plots expérimentaux. Experimental sections. |
| Dans le texte | |
 |
Fig. 3 Mesure de la flèche du géosynthétique au distance-mètre laser. Geosynthetic deflection measure using a laser distance sensor. |
| Dans le texte | |
 |
Fig. 4 Tassements de surface sur les plots 2 et 3. Surface settlements in sections 2 and 3. |
| Dans le texte | |
 |
Fig. 5 Comportement cinématique du remblai renforcé sur le plot 3. Cinematic behavior of the reinforced embankment in section 3. |
| Dans le texte | |
 |
Fig. 6 Déformations du géosynthétique (plot 1). Geosynthetic strain (section 1). |
| Dans le texte | |
 |
Fig. 7 Incréments de déplacement du géosynthétique pour la phase de circulation. Vertical displacement of the geosynthetic due to the circulation trials. |
| Dans le texte | |
 |
Fig. 8 Géométrie du modèle numérique de base. Geometry of the numerical samples. |
| Dans le texte | |
 |
Fig. 9 Comparaison entre les résultats numériques et expérimentaux des tassements de surface et déflexions du géosynthétique. Surface settlement and geosynthetic deflection – Comparison between numerical and experimental results. |
| Dans le texte | |
 |
Fig. 10 Comparaison entre les résultats numériques et expérimentaux des déformations dans la nappe géosynthétique. Comparison between experimental and numerical geosynthetic strain. |
| Dans le texte | |
 |
Fig. 11 Efficacité du transfert de charge en fonction du ratio D/H pour les deux modes d'ouverture de la cavité. Efficiency versus D/H for the two cavity opening processes. |
| Dans le texte | |
 |
Fig. 12 Comparaison des tassements de surface et déplacements verticaux du géosynthétique en fonction du mode d'ouverture de la cavité (D/H = 2,2 m). Vertical geosynthetic displacements and surface settlements (m) for both process and for H/D = 2.2. |
| Dans le texte | |
 |
Fig. 13 Comparaison des géométries des distributions de contraintes verticales sur la nappe en fonction du mode d'ouverture de la cavité pour trois diamètres de cavité. Increase in the vertical stresses acting on the upper face of the geosynthetic for the three ratios D/H. |
| Dans le texte | |
 |
Fig. 14 Mécanismes pris en considération pour le dimensionnement. Physical mechanisms taking into account for the design. |
| Dans le texte | |
 |
Fig. 15 Influence de la forme de la distribution de contrainte sur les déplacements verticaux de la nappe géosynthétique. Comparison between analytical and numerical geosynthetic deflection. |
| Dans le texte | |
 |
Fig. 16 Influence de la forme de la distribution de contrainte sur la déformation de la nappe dans les zones d'ancrage. Influence of the load distribution shape on the geosynthetic strain in anchorage areas. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




