| Numéro |
Rev. Fr. Geotech.
Numéro 154, 2018
|
|
|---|---|---|
| Numéro d'article | 1 | |
| Nombre de pages | 8 | |
| DOI | https://doi.org/10.1051/geotech/2018001 | |
| Publié en ligne | 9 avril 2018 | |
Article de recherche / Research Article
Méthode de décomposition modale : description quantitative de la granulométrie et autres paramètres
Modal decomposition method: quantitative description of particle size distribution and other parameters
Département CGM, École Polytechnique,
CP. 6079, Succ. CV
Montréal
(Qc),
H3C 3A7, Canada
★ Auteur de correspondance : robert.chapuis@polymtl.ca
La méthode de décomposition modale (MDM) a été développée pour extraire d’une courbe granulométrique ses composantes lognormales, et leurs proportions dans l’échantillon analysé. Pour les études des eaux souterraines, on récupère des échantillons de sol de classe 4 ou 5, remaniés à très remaniés. Malgré le remaniement, la MDM récupère l’information sur la stratification. Elle permet alors de bien prédire la conductivité hydraulique, en tenant compte de cette stratification, une information clé pour bien comprendre la migration de l’eau souterraine. De plus, la MDM peut analyser la distribution des valeurs d’autres paramètres géotechniques.
Abstract
The modal decomposition method (MDM) was developed to extract from a grain size distribution curve its lognormal components and their proportions in the analysed sample. For groundwater studies, the recovered soil samples belong to classes 4 and 5, thus are remoulded or highly remoulded. Even if they are remoulded, the MDM can recover the information about stratification. This enables a good prediction of the hydraulic conductivity, taking into account this stratification, a key information for a correct understanding of groundwater migration. In addition, the MDM can analyse the distribution of the values of other geotechnical parameters.
Mots clés : décomposition modale / granulométrie / perméabilité / stratification
Key words: modal decomposition / grain size distribution / permeability / stratification
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2018
1 Introduction
Pour toute étude géotechnique ou hydrogéologique, des analyses granulométriques sont réalisées par tamisage et sédimentation. Les résultats des analyses sont utilisés pour classer le sol, vérifier ses propriétés par rapport aux exigences d’un cahier des charges. On obtient aussi des informations qui sont utilisées pour prédire certaines propriétés, par exemple, la conductivité hydraulique saturée Ksat (m/s) du matériau, ou encore, si le sol n’a pas de plasticité, sa surface spécifique, SS (Chapuis et Légaré, 1992).
Cependant, une courbe granulométrique contient beaucoup plus d’informations utiles pour comprendre l’origine du matériau, prédire ses propriétés mécaniques et hydrauliques, saturées et non saturées (Chapuis, 2016). Néanmoins, il faut d’abord extraire cette information puis la compléter par le facteur de forme des grains (RF, roundness factor), et la valeur in situ de la porosité, n, qu’il faut comparer aux valeurs extrêmes que peut prendre la porosité de ce matériau à l’état le plus lâche, nmax, et à l’état le plus dense, nmin (Chapuis, 2012a).
L’article montre comment décomposer une courbe granulométrique en 1, 2 ou 3 composantes lognormales, avec leurs proportions. Il donne ensuite des exemples d’études réalisables avec l’aide de la décomposition modale pour analyser des distributions d’autres paramètres.
2 Problème de qualité des échantillons
Le problème initial est apparu avec les forages réalisés par des puisatiers pour des études hydrogéologiques. Les sols aquifères sont échantillonnés par des tubes à paroi épaisse, comme les cuillères fendues, ce qui donne des échantillons remaniés, de classe 4. Les classes 1 à 5 ont été définies en géotechnique (Tab. 1), pas en hydrogéologie. Pendant leurs forages, les puisatiers peuvent aussi prélever des échantillons de classe 5 avec une « pompe à sable ».
Les échantillons de sol aquifère, de classe 4 ou 5, sont souvent des mélanges de fines strates, qui deviennent invisibles dans l’échantillon remanié. La stratification subhorizontale est la règle et pas l’exception dans les aquifères formés d’alluvions. Les essais de laboratoire sur de tels échantillons composés et remaniés ne reflètent pas les propriétés in situ, qui sont influencées par la stratification dont le rôle est important. Pour les projets avec une composante hydrogéologique, une stratigraphie détaillée est nécessaire car les couches grossières sont des autoroutes pour l’eau et les contaminants.
On voit au tableau 1 que les granulométries des échantillons de classe 4 ou 5 sont déterminées avec une représentativité plus ou moins bonne. Si le projet vise à évaluer la capacité d’une formation alluvionnaire à fournir du sable et gravier qui sera utilisé comme remblai, la granulométrie sur des échantillons de classe 5 est adéquate. Cependant, pour un projet d’hydrogéologie, la granulométrie sera inadéquate parce que les échantillonnages de classes 4 et 5 ont fait disparaître l’information sur la stratification du sol échantillonné.
Jusqu’à récemment, il n’existait pas de méthode pour extraire l’information sur les strates dans un échantillon de classe 4 ou 5. Cette lacune a été comblée récemment (Chapuis et al., 2014) par une méthode de décomposition modale (MDM) qui extrait d’une courbe granulométrique ses composantes (une par strate), avec leurs proportions. Cette technique de MDM s’est révélée très utile pour diverses applications, qui ont fait l’objet d’un ouvrage récent (Chapuis, 2016).
Les 5 classes d’échantillons, les outils échantillonneurs et les propriétés pouvant être évaluées.
3 Méthode de décomposition modale
La méthode de décomposition modale (MDM) a été développée suite à plusieurs observations scientifiques, d’une part, et surtout à cause du besoin d’analyser de façon cohérente des centaines de courbes obtenues pour de grands projets, d’autre part. La MDM est utilisable pour les courbes granulométriques et aussi pour les courbes de distribution des valeurs d’autres paramètres.
En géotechnique, la granulométrie est obtenue par tamisage (échantillons de 300 g à plus de 1000 kg) et sédimentation (spécimens de 50 à 100 g). Elle est tracée comme le pourcentage p de la masse solide qui est inférieur à la taille d (mm) versus log (d). On obtient ainsi une courbe p(d) qui représente une fonction cumulative ou GSDC, définie comme l’intégrale de la distribution de la densité de probabilité des tailles (histogramme), courbe rarement tracée et utilisée. Par définition, d10 est la taille telle que 10 % de la masse solide de l’échantillon est formé de particules de tailles inférieures à d10.
En géologie, la granulométrie est tracée comme p versus Φ(d) = −log2 (d) où d est en millimètres (Udden, 1914 ; Wentworth, 1922 ; Krumbein, 1938). Lorsque le graphe apparaît comme une série de segments, chacun d’eux peut être vu comme le résultat de plusieurs facteurs tels que : les différentes zones sources, le mode de transport, les types d’érosion et de dépôt des grains. Cette interprétation visuelle des graphes log-phi est incertaine (Christiansen et al., 1984 ; Sengupta et al., 1991). Les techniques graphiques dépendent de l’opérateur et sont jugées inexactes (Middleton, 1976 ; Ashley, 1978).
Les géologues utilisent des lois normales, lognormales, hyperboliques, fractales, etc. (Mercier, 2013). On utilise en théorie les moments statistiques pour définir les valeurs de 5 paramètres : moyenne, médiane, variance, coefficient de dissymétrie (skewness) et coefficient d’aplatissement (kurtosis). En pratique, les 5 valeurs sont estimées par des formules approximatives qui sont correctes uniquement si la granulométrie respecte le modèle, et qui impliquent les tailles d5, d16, d25, d50, d75, d84 et d95, soit 7 points de la courbe pour 5 paramètres. Le résultat est qualitatif. On le complète par des adjectifs ou des indices qui décrivent comment la granulométrie s’écarte du modèle. D’un point de vue mathématique, ces méthodes dépendent de l’opérateur et de ses hypothèses, et semblent peu performantes dans le cas des courbes asymétriques ou polymodales.
On peut aussi supposer que la granulométrie mesurée est la somme de plusieurs distributions lognormales (Chapuis et al., 2014). Examinons le mélange de trois strates dans un échantillon de classe 4 ou 5. Le pourcentage de la masse solide qui est plus petite que la taille d est p[ln (d/1 mm)] = p [ln(D)] pour ce mélange, ln étant le logarithme Népérien, p1[ln D], p2[ln D] et p3[ln D] pour chacun des trois sols. Donc, si mj (j = 1, 2 ou 3) est le pourcentage des solides qui appartenait initialement à la strate no j, on obtient :
 (1)
(1)
Par définition la somme des mj vaut 1 (100 %). L’équation (1) est utilisée pour résoudre le problème direct qui est celui de produire, avec 3 sols, un mélange qui aura des caractéristiques souhaitées. C’est le problème résolu pour établir des formulations pour du béton de ciment ou du béton bitumineux. Le problème inverse, c’est-à-dire trouver quels sols composent un mélange, et dans quelles proportions, est un problème plus complexe à résoudre. C’est une solution de ce problème qui a été présentée par Chapuis et al. (2014), et qui est résumée ci-après.
Dans l’équation (1), pour un sol naturel ou un matériau concassé, on va supposer que chaque fonction pj [ln d] est lognormale. Cette hypothèse est pratique pour couvrir toute la gamme très large des tailles de particules, en particulier pour les GSDCs ayant une forme de S. Parce que la GSDC définit le produit final d’une série de processus, tels que : la fragmentation par diverses méthodes, le transport et l’érosion par l’eau douce, l’eau salée et le vent, l’altération, etc. un argument mathématique suggère qu’une fonction lognormale, unimodale ou multimodale, devrait décrire le résultat final (Doeglas, 1946 ; Folk et Ward, 1957 ; Visher, 1969 ; Clark, 1976).
Une variable aléatoire x suit une loi de distribution lognormale si y = ln (x) suit une loi de distribution normale (gaussienne) d’espérance µ et d’écart-type σ (ou de variance σ2). La distribution de ln(D) suit alors une densité de probabilité normale pour x > 0 :
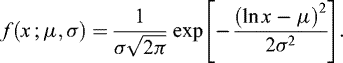 (2)
(2)
La fonction de répartition, ou GSDC, du pourcentage passant versus d, donc p [ln D], est :
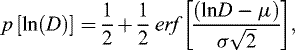 (3)
où erf est la fonction erreur. Pour la granulométrie totale, on obtient alors :
(3)
où erf est la fonction erreur. Pour la granulométrie totale, on obtient alors :
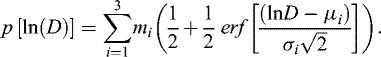 (4)
(4)
La GSDC est alors décrite par une équation ayant de 1 à 3 modes, donc un ensemble de 2, 5 ou 8 paramètres, soit de 0 à 2 pour les pourcentages mj, car Σmj = 1, et de 2 à 6 pour les µj et σj. On pourrait aussi utiliser une décomposition à 4 modes, soit 11 paramètres, mais selon l’expérience de l’auteur, il semble adéquat de limiter la décomposition modale à 3 modes.
En pratique, la décomposition modale procède avec la méthode des moindres carrés ordinaires (Chapuis et al., 2014). Plusieurs exemples de décomposition modale ont été présentés dans Chapuis et al. (2014) pour de l’argile et des couches individuelles de sable : celles-ci donnent des distributions unimodales (2 paramètres). Par comparaison, des échantillons de classe 4 (cuillère fendue), ou de classe 5 (en vrac), dans lesquels des couches sont mélangées par échantillonnage ou excavation, manipulation, et transport, donnent 2 ou 3 modes.
On présente ici un exemple d’échantillon de classe 5 (35 kg) prélevé dans une excavation. La courbe granulométrique (GSDC) obtenue compte 14 points (Fig. 1). Son ondulation indique la présence de plusieurs strates. La figure 2 montre la densité de probabilité, f, définie à partir des points expérimentaux (data = données du laboratoire), par la formule suivante :
 (5)
(5)
Les valeurs di sont celles des tailles successives (tamisage et sédimentation). L’indice i varie de 1 (plus grande taille) à N, la plus petite taille. L’équation (5) fonctionne de i = 2 à (N–1), en interpolation, et pas en extrapolation aux deux extrémités de la GSDC. Les points tirés de l’équation (5) donnent le nombre de pics ou modes (strates) dans l’échantillon. Les données expérimentales (Eq. (5)) indiquent 2 pics nets et un 3e pic intermédiaire moins marqué. La MDM procède ensuite selon les 5 étapes suivantes :
-
on trace la courbe granulométrique expérimentale (Fig. 1) et la densité de probabilité expérimentale (Eq. (5), Fig. 2). Cette dernière donne le nombre de pics ;
-
les positions des pics aident à trouver des valeurs préliminaires pour les espérances µi et les écart-types σi (Eq. (4)). En diminuant µ1 on déplace le pic no 1 sur la gauche alors qu’en augmentant µ1 on déplace le pic no 1 vers la droite, etc. ;
-
l’étalement des valeurs expérimentales autour de chaque pic (Fig. 2) aide à trouver une valeur préliminaire pour chaque σi. En augmentant la valeur de σ1, on augmente l’étalement autour du pic no 1, etc ;
-
les valeurs préliminaires des µi et σi sont utilisées comme points de départ pour trouver le meilleur ajustement entre les données expérimentales et l’équation théorique (Eq. (4)), avec la méthode ordinaire des moindres carrés dont la LSE est définie par l’équation (6) ;
-
on trace les résultats de la LSE dans le graphe de la courbe granulométrique expérimentale (Fig. 1) et dans celui de la densité de probabilité expérimentale (Fig. 2).
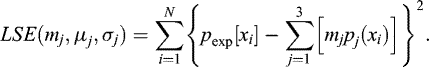 (6)
(6)
Le minimum de la LSE peut être trouvé par divers codes numériques, incluant le « solveur » du logiciel Excel, ce qui fournit les valeurs des inconnues mj, µj et σj.
Pour l’exemple des figures 1 et 2, la MDM trouve 3 modes, avec les valeurs suivantes pour les paramètres : m1 = 0,423, µ1 = −1,143, σ1 = 0,548 ; m2 = 0,021, µ2 = 0,175, σ2 = 0,135 ; et m3 = 0,555, µ3 = 2,045, σ3 = 0,768. On obtient ainsi une description mathématique de la GSDC.
On note sur les figures 1 et 2 que les données expérimentales sont bien ajustées par le modèle théorique sauf pour la partie des gros éléments (28 mm et plus), dont le pourcentage est imprécis dans un tel échantillon, même s’il fait 35 kg.
La MDM représente la courbe granulométrique par une équation mathématique. Cette capacité est utile quand on doit évaluer les caractéristiques physiques d’une formation aquifère ou aquitard à l’aide d’une série de courbes granulométriques. Des exemples de plusieurs formations aquifères stratifiées sont présentés brièvement par Chapuis (2013). Dans ce cas, les quantifications incluent l’anisotropie de la conductivité hydraulique, K, et donnent une image claire des propriétés à différentes échelles, éliminant le recours aux artificiels effets d’échelle.
L’équation mathématique obtenue pour la courbe granulométrique conduit aussi à l’obtention d’une formule mathématique pour la surface spécifique, SS, d’un sol non plastique (Chapuis et al., 2014), qui a été vérifiée avec l’équation plus ancienne de SS (Chapuis et Légaré, 1992).
 |
Fig. 1 Granulométrie d’un échantillon de classe 5 prélevé dans une excavation. |
 |
Fig. 2 Densité de probabilité, échantillon de classe 5 prélevé dans une excavation. |
4 Évaluation des capacités de la MDM
Pour vérifier la capacité de la MDM, on a fabriqué des mélanges de trois sols à un seul mode (gravier, sable silt), avec des proportions mj connues. Les valeurs des µj variaient entre −8 et 3 et les valeurs des σj entre 0,24 et 2,82. On a vérifié si la MDM pouvait récupérer les 3 modes des mélanges, les valeurs des μj et σj et les trois pourcentages mj, donc les 8 paramètres. Les résultats (Chapuis et al., 2014) ont confirmé cette capacité, sauf lorsque l’un des constituants représente moins de 2 % de la masse solide totale. Cette imprécision semble liée au nombre limité de points de la GSDC, qui peut aller de 6 (tamisage seulement, granulométrie serrée) à 25 environ (tamisage et sédimentation). Quand un des constituants représente moins de 2 % de la masse totale des solides, il est préférable de l’ignorer et donc de passer de 3 à 2 modes dans la MDM (Chapuis et al., 2014).
Pour améliorer la définition de la granulométrie, en particulier dans les cas des sables stratifiés, on peut utiliser plus de tamis que ceux demandés par les normes d’analyse par tamisage. On verra cette possibilité dans la section 5 pour un échantillon de sable stratifié.
Par comparaison, la granulométrie laser, qui utilise des spécimens de petite taille (1 à 3 g), est connue pour donner des pourcentages incorrects dans le cas de mélanges bimodaux (Campbell, 2003). Par ailleurs, Leys et al. (2005), avec un appareil « Coulter multisizer », ont trouvé que leur programme numérique de décomposition éprouvait des difficultés quand l’un des deux constituants représentait moins de 10 % de la masse solide totale.
5 Exemple d’un échantillon de sable stratifié
Comme exemple, examinons le cas d’un échantillon remanié de sable prélevé dans un aquifère stratifié. Si l’on tamise avec seulement la série des tamis prescrits pour les contrôles de qualité sur les chantiers, la granulométrie manquera de précision. Cependant, comme le laboratoire dispose de nombreux tamis métriques et US, on utilise ici la série de tamis US du tableau 2.
Suivant la procédure en 5 étapes, on trace la densité de probabilité expérimentale (Eq. (5), Fig. 3) : elle donne trois pics bien marqués. Les positions des pics aident à trouver des valeurs préliminaires pour les espérances µi et les écart-types σi (Eq. (4)). Celles-ci sont utilisées comme points de départ pour trouver le meilleur ajustement avec la LSE. On reporte ensuite les résultats de la LSE sur la courbe granulométrique expérimentale (Fig. 4) ainsi que sur le graphe de la densité de probabilité (Fig. 3).
Résultats de l’analyse granulométrique d’un sable stratifié.
 |
Fig. 3 Densité de probabilité d’un sable stratifié, beaucoup de tamis. |
 |
Fig. 4 Granulométrie d’un sable stratifié, beaucoup de tamis. |
6 Exemple d’un aquifère stratifié
Le site se trouve sur le territoire de la ville de Sorel, à environ 100 km au nord-est de Montréal, sur la rive droite (Sud) du fleuve Saint-Laurent. Le terrain de 150 m × 150 m est relativement plat. Il fait partie de la plaine de débordement de la rivière Richelieu, qui draine le lac Champlain et rejoint le Saint-Laurent près de Sorel. La stratigraphie comprend une couche de 5,0 à 5,5 m de sable silteux, stratifié, qui repose sur une épaisse couche d’argile Champlain.
Le site et son aquifère de sable stratifié ont été utilisés comme site expérimental pour des classes d’étudiants et pour quelques projets de recherche. Les essais réalisés in situ incluent des relevés piézométriques, des essais de perméabilité, essais de pompage, essais de traceur non réactif en écoulement convergent, échantillonnages de l’eau dans les piézomètres, et utilisation de diverses techniques géophysiques.
Pour l’investigation géotechnique, et l’installation d’une trentaine de piézomètres hydrauliques, un tubage lisse de calibre NW a été enfoncé par battage dans le sol. L’intérieur a été lavé à l’eau propre en utilisant exclusivement des jets latéraux et des jets orientés vers le haut. L’eau de lavage était injectée à faible pression et débit élevé, afin de remanier le moins possible les sols situés sous le sabot de battage. Des échantillons ont été prélevés avec une cuillère fendue standard. Les indices de pénétration, entre 4 et 10, indiquaient une faible compacité. Selon les analyses granulométriques les échantillons contenaient de 20 % à 75 % de silt argileux, et a priori la perméabilité prédite à partir de la granulométrie était faible.
On montre ici une application de la MDM pour l’ensemble du site. Elle comprend d’abord la prédiction des valeurs de la conductivité hydraulique, K, à petite échelle, à partir des granulométries (Chapuis, 2004, 2012a, b). Elle inclut l’analyse des valeurs de K à moyenne échelle, obtenues par les essais de perméabilité in situ dans les piézomètres. Elle finit avec la prédiction de la conductivité hydraulique à grande échelle, celle tirée d’un essai de pompage assez long pour atteindre et maintenir un régime permanent.
Chaque échantillon de cuillère fendue était de couleur uniforme. Le remaniement inhérent à ce mode d’échantillonnage ne permettait pas de voir s’il y avait une stratification. Dans certains cas, l’échantillon avait été divisé en plusieurs parties, parce que le laboratoire avait décelé une certaine variation dans la consistance de l’échantillon et dans la quantité de sable présente.
La MDM a été utilisée pour étudier les échantillons plusieurs années après leur prélèvement et analyses par tamisage et sédimentation. La MDM a révélé que les échantillons étaient bimodaux, mais que quelques-uns contenaient un peu de sable grossier et de petit gravier, ce qui en faisait des échantillons à 3 modes (Chapuis et al., 2014).
Pour les échantillons du forage 14-45, les analyses granulométriques brutes sont montrées dans la figure 5. Les résultats de la décomposition modale apparaissent dans la figure 6. On trouve que la composante fine a quelques variations selon la profondeur dans ce forage (Fig. 7), mais que le sable est plus régulier et toujours très uniforme (écart-type inférieur à 0,5).
Des résultats semblables ont été trouvés pour les 125 échantillons de sol analysés pour ce site et l’ensemble des forages. Pour estimer la conductivité hydraulique horizontale, parallèle aux strates, on a utilisé les équations classiques des sols stratifiés. La valeur résultante est contrôlée entièrement par la valeur K du sable fin, qui a été prédite par la méthode de Chapuis (2004). La distribution des valeurs de K ainsi prédites à petite échelle est tracée dans la figure 8. La distribution des valeurs de K obtenues par des essais de perméabilité à niveau variable dans les piézomètres (Dallaire, 2004) est aussi montrée dans la figure 8.
Par expérience, les valeurs K obtenues par essais de pompage sont habituellement situées entre le 60e et le 80e percentiles de la distribution des valeurs K obtenues par des essais de perméabilité in situ correctement réalisés et correctement interprétés (Chapuis, 2013). Ces percentiles sont tracés sur la figure 8, avec les valeurs moyennes de K selon les essais de pompage.
La distribution des valeurs K obtenues par les essais de perméabilité dans les piézomètres (échelle moyenne) se situe nettement en dessous des valeurs K tirées d’essai de pompage (Fig. 8). On pourrait en conclure que cet aquifère présente un effet d’échelle. Cependant, la distribution des valeurs de K à petite échelle correspond bien aux valeurs de K à grande échelle (pompage, Fig. 8). On peut donc conclure que cet aquifère ne présente pas d’effet d’échelle.
Comment expliquer la différence entre les prédictions à petite échelle et les mesures à échelle moyenne ? Cette différence est liée à la stratification fine de la formation. Dallaire (2004) a essayé de « développer » les piézomètres hydrauliques pour éliminer les fines particules adjacentes au sol filtre et à la crépine, mais le développement s’est avéré inefficace. Il en est résulté que les valeurs de K à échelle moyenne ont sous estimé les valeurs K de pompage (Fig. 8) par un facteur de 2,5, à cause du beurrage des parois forées par les couches de sols fins, pendant le forage et pendant l’installation des piézomètres.
Comme le sable est stratifié horizontalement, les valeurs de K à petite échelle dans le sens horizontal, agissent in situ en parallèle. La composition donne alors à grande échelle :
 (7)
(7)
L’équation (7) montre que les valeurs de K qui sont supérieures à l’espérance µln K ont plus de poids dans le débit total (à grande échelle) que les valeurs de K qui sont inférieures à l’espérance.
Pour le site de Sorel, la distribution des valeurs K prédites à petite échelle peut être décrite par un seul mode approximativement avec µ1 = −5,395 et σ1 = 0,570. L’équation (7) prédit alors une valeur K (grande échelle) de 5,34 × 10−3 cm/s, en accord avec la valeur moyenne mesurée par les essais de pompage, qui est de 5,7 × 10−3 cm/s.
Pour ce site, la MDM a permis de mieux décrire la couche supérieure des sédiments récents d’origine fluviatile. Celle-ci comprend des strates centimétriques de sable fin et de silt argileux. Le sable fin a été déposé lors des grandes crues, par de l’eau à faible vitesse (dans la plaine de débordement), et le silt argileux a été déposé dans des étangs temporaires entre deux crues majeures. Des excavations réalisées sur le site ont permis d’évaluer à 1 cm l’épaisseur moyenne des strates. La couche supérieure est ainsi formée d’environ 500 à 550 strates. Considérant que la déposition des sédiments a débuté il y a environ onze mille ans suite à la dernière déglaciation, on en déduit que les crues majeures ont été espacées en moyenne d’environ 11000/[(500 à 550)/2] années, soit environ 40 années.
Par ailleurs, la MDM a permis de confirmer que les strates de sable fin étaient continues et que toute excavation sur le site pourrait être asséchée par un système de pointes filtrantes, comme l’ont démontré des essais de pompage réalisés dans un piézomètre de 5 cm de diamètre.
 |
Fig. 5 Granulométries des échantillons récupérés dans le forage 14-45. |
 |
Fig. 6 Décomposition modale des échantillons récupérés dans le forage 14-45. |
 |
Fig. 7 Espérances et écart-types des deux modes identifiés dans le forage 14-45. |
 |
Fig. 8 Distributions des valeurs K, à petite échelle et moyenne échelle, et comparaisons avec la valeur de K à grande échelle (pompage). |
7 Discussion
Il est difficile de discuter dans un article tous les aspects de la méthode de décomposition modale pour les granulométries, d’une part, et pour la distribution de tout autre paramètre, d’autre part. Le lecteur intéressé pourra trouver plus d’information dans un ouvrage (Chapuis, 2016) sur l’analyse des granulométries et d’autres groupes de données. Des méthodes détaillées sont fournies avec des exemples, des images de fichiers informatiques avec des instructions, pour la conductivité hydraulique saturée, Ksat, la porosité in situ, la courbe de rétention capillaire, et la conductivité hydraulique non saturée, Kunsat.
Le livre insiste sur les processus de contrôle de la qualité, qui devraient être utilisés dans tous les projets d’ingénierie, en particulier pour les valeurs de conductivité hydraulique saturée, Ksat, de porosité n, de teneur en eau volumique θ(uw), et de conductivité hydraulique non saturée, Kunsat. Après quelques rappels et mises au point, cet ouvrage présente les essais requis pour établir la gamme des porosités que peut prendre un sol, puis traite de l’analyse granulométrique et de la décomposition modale des courbes granulométriques, avec l’extraction du nombre de strates présentes dans l’échantillon, leurs pourcentages respectifs, et leurs granulométries respectives. Des exemples sont fournis pour utiliser la MDM avec un chiffrier. Certains points sont par la suite développés : comment estimer la surface spécifique d’un sol non plastique et celle d’un sol plastique, comment estimer la qualité des échantillons, et comment évaluer la valeur in situ de la porosité, ce qui nécessite de connaître la granulométrie, la forme des particules, et un indice de résistance mécanique du sol (pressiomètre, pénétromètre…). L’ouvrage présente alors les méthodes qui sont fiables pour prédire la valeur de Ksat, avec leurs gammes d’utilisation.
Des exemples sont ensuite présentés pour illustrer la prédiction de Ksat dans le cas des aquifères, et pour un tapis d’argile compactée. On explique aussi comment prédire la courbe de rétention d’eau d’un sol. Plusieurs méthodes sont présentées, incluant les plus récentes pour les sols à granulométries grossières (Chapuis et al., 2015). L’ouvrage présente des exemples de prédictions de la courbe de rétention d’eau, explique comment prédire la conductivité hydraulique non saturée de différents sols, comment prédire la porosité effective, ne, et la dispersivité longitudinale, αL, dans des alluvions stratifiées, deux paramètres essentiels pour les essais de traceurs et la migration des contaminants. L’ouvrage explique enfin comment évaluer le risque d’érosion interne dans un sol, et comment utiliser la MDM pour quantifier la migration des solides.
8 Conclusion
La MDM se révèle utile pour analyser les grands ensembles de courbes granulométriques, pour en extraire des caractéristiques, des tendances, et examiner diverses hypothèses, telles que la stratification interne de la formation, l’influence de la méthode de forage et de la méthode d’échantillonnage sur la qualité de l’échantillon, etc. Utiliser la décomposition modale nous fait examiner les courbes plus en détail, afin de mieux les comprendre. Cependant, la méthode d’ajustement de courbe, par les moindres carrés, ne devrait pas être utilisée comme une boîte noire. L’utilisateur doit interpréter les résultats de la décomposition modale de manière à répondre aux questions sous étude. Il doit aussi utiliser des informations complémentaires pour obtenir une interprétation sensée, cohérente, des conditions in situ.
La MDM est aussi très utile pour analyser tout grand ensemble de données expérimentales, obtenues au laboratoire ou sur le terrain. Par exemple, à partir de la MDM d’une granulométrie, on peut prédire la conductivité hydraulique saturée, Ksat, du sol échantillonné, en tenant compte de sa stratification, détectée et quantifiée par la MDM de la GSDC (Chapuis, 2016). La petite échelle est celle des échantillons prélevés par les sondages. L’échelle moyenne est celle des essais de perméabilité in situ, en cours de forage ou dans des piézomètres. La grande échelle est celle des essais de pompage. On peut ensuite utiliser la MDM pour analyser les distributions des nombreuses valeurs de Ksat à petite échelle et à moyenne échelle, et en tirer des prédictions réalistes pour la valeur de Ksat à grande échelle, qui sera obtenue par essais de pompage (aquifère) ou par un essai de débit de fuite à grande échelle dans le cas d’un bassin rendu étanche par un tapis d’argile compactée.
Références
- Ashley GM. 1978. Interpretation of polymodal sediments. J Geol 86: 411–421. [CrossRef] [Google Scholar]
- Campbell JR. 2003. Limitations in the laser sizing of soils. In: Advances in regolith. Canberra, ACT (Australia): CRC LEME, pp. 38–42. [Google Scholar]
- Chapuis RP. 2004. Predicting the saturated hydraulic conductivity of sand and gravel using effective diameter and void ratio. Can Geotech J 41(5): 787–795. [CrossRef] [Google Scholar]
- Chapuis RP. 2012a. Estimating the in situ porosity of sandy soils sampled in boreholes. Eng Geol 141–142: 57–64. [CrossRef] [Google Scholar]
- Chapuis RP. 2012b. Predicting the saturated hydraulic conductivity of soils: a review. Bull Eng Geol Environ 71(3): 401–434. [CrossRef] [Google Scholar]
- Chapuis RP. 2013. Permeability scale effects in sandy aquifers: a few case studies. Proc. 18th ICSMFE, Paris, Sept. 2013, Presses de l’École des Ponts, pp. 505–510. [Google Scholar]
- Chapuis RP. 2016. Extracting information from grain size distribution curves. Canada : Geotics Éditions Montreal. Distribution par BiTech Publishers. Available from www.bitech.ca. [Google Scholar]
- Chapuis RP, Légaré PP. 1992. A simple method for determining the surface area of fine aggregates and fillers in bituminous mixtures. In: Effects of aggregates and mineral fillers on asphalt mixture performance. ASTM STP 1147: 177–186. [Google Scholar]
- Chapuis RP, Dallaire V, Saucier A. 2014. Getting information from modal decomposition of grain size distribution curves. Geotech Test J 37(2): 282–295. [CrossRef] [Google Scholar]
- Chapuis RP, Weber S, Duhaime F. 2015. Permeability test results with packed spheres and non-plastic soils. Geotech Test J 38(6): 950–964. [Google Scholar]
- Christiansen C, Blaesild P, Dalsgaard K. 1984. Re-interpreting ’segmented’ grain-size distributions. Geol Mag 121: 47–51. [CrossRef] [Google Scholar]
- Clark MW. 1976. Some methods for statistical analysis of multimodal distributions and their application to grain-size data. J Int Assoc Math Geol 8: 267–282. [CrossRef] [Google Scholar]
- Dallaire V. 2004. Study of scale effects in an alluvial aquifer (in French). MSc Thesis, École Polytechnique, Montréal, Canada. [Google Scholar]
- Doeglas DJ. 1946. Interpretation of the results of mechanical analyses. J Sediment Pet 16: 19–40. [Google Scholar]
- Folk RL, Ward WC. 1957. Brazos River Bar: A study in the significance of grain size parameters. J Sediment Pet 27: 3–26. [Google Scholar]
- Krumbein WC. 1938. Size frequency distribution of sediments and the normal phi curve. J Sediment Pet 8: 84–90. [Google Scholar]
- Leys J, McTainsh G, Koen T, Mooney B, Strong C. 2005. Testing a statistical curve-fitting procedure for quantifying sediment populations within multi-modal particle-size distributions. Earth Surf Process Landf 30: 579–590. [CrossRef] [Google Scholar]
- Mercier JL. 2013. Indices granulométriques et lois de distributions. Géomorphol Relief Process Environ 19(4): 379–392. [CrossRef] [Google Scholar]
- Middleton GV. 1976. Hydraulic interpretation of sand size distributions. J Geol 84: 405–426. [CrossRef] [Google Scholar]
- Sengupta S, Ghosh JK, Mazumder BS. 1991. Experimental–theoretical approach to interpretation of grain size frequency distributions. In: Principles, methods and application of particle size analysis. Cambridge (UK): Cambridge University Press, pp. 264–279. [Google Scholar]
- Udden JA. 1914. Mechanical composition of clastic sediments. Bull Geol Soc Am 25: 655–744. [CrossRef] [Google Scholar]
- Visher GS. 1969. Grain size distributions and depositional processes. J Sediment Pet 39: 1074–1106. [Google Scholar]
- Wentworth CK. 1922. A scale of grade and class terms for clastic sediments. J Geol 30: 377–392. [CrossRef] [Google Scholar]
Citation de l’article : Robert P. Chapuis. Méthode de décomposition modale : description quantitative de la granulométrie et autres paramètres. Rev. Fr. Geotech. 2018, 154, 1.
Liste des tableaux
Les 5 classes d’échantillons, les outils échantillonneurs et les propriétés pouvant être évaluées.
Liste des figures
 |
Fig. 1 Granulométrie d’un échantillon de classe 5 prélevé dans une excavation. |
| Dans le texte | |
 |
Fig. 2 Densité de probabilité, échantillon de classe 5 prélevé dans une excavation. |
| Dans le texte | |
 |
Fig. 3 Densité de probabilité d’un sable stratifié, beaucoup de tamis. |
| Dans le texte | |
 |
Fig. 4 Granulométrie d’un sable stratifié, beaucoup de tamis. |
| Dans le texte | |
 |
Fig. 5 Granulométries des échantillons récupérés dans le forage 14-45. |
| Dans le texte | |
 |
Fig. 6 Décomposition modale des échantillons récupérés dans le forage 14-45. |
| Dans le texte | |
 |
Fig. 7 Espérances et écart-types des deux modes identifiés dans le forage 14-45. |
| Dans le texte | |
 |
Fig. 8 Distributions des valeurs K, à petite échelle et moyenne échelle, et comparaisons avec la valeur de K à grande échelle (pompage). |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




