| Numéro |
Rev. Fr. Geotech.
Numéro 155, 2018
|
|
|---|---|---|
| Numéro d'article | 4 | |
| Nombre de pages | 8 | |
| DOI | https://doi.org/10.1051/geotech/2018008 | |
| Publié en ligne | 12 décembre 2018 | |
Article de recherche / Research Article
Aléa vibratoire dans les sols : indicateurs pertinents et classification simplifiée
Vibration hazard in soils: relevant indicators and simplified classification
1
L2EC, Laboratoire Vibrations, 4 Rue des Frères Montgolfier,
95420
Magny-en-Vexin, France
2
Université Paris-Est, GERS, SV, IFSTTAR
14-20 bd Newton,
77447
Marne-La-Vallée, France
3
IMSIA (UMR 9219), Ensta-ParisTech 828, Boulevard des Maréchaux,
91762
Palaiseau Cedex, France
★ Auteur de correspondance : jamaleddine.ak@gmail.com
Reçu :
22
Mai
2018
Accepté :
5
Novembre
2018
La caractérisation de l’aléa sismique constitue un enjeu majeur dans le domaine du génie civil. En ingénierie des vibrations, il n’existe pas de domaine d’étude similaire bien que cette question soit décisive pour la prédiction de l’impact et de la gêne occasionnée (population, environnement, ouvrages, industrie de pointe). Cette caractérisation passe nécessairement par la connaissance des diverses sources de vibrations : exploitation des infrastructures (ferrées et routières), travaux de construction ou de rénovation (vibrofonçage, battages). Elle dépend fortement du mode de propagation des ondes mécaniques entre la source et le récepteur selon les sols (sites) et leur stratification. La nocivité des vibrations (i.e. capacité à occasionner des dégâts) dépendra donc du type de source, de la propagation, mais également de la réponse dynamique du récepteur exprimée en fonction de ses propriétés modales. Dans cet article, des simulations numériques sont combinées à des enregistrements de vibrations, liées à l’exploitation d’infrastructures ou engendrées par des chantiers. Dans l’hypothèse de sols à comportement viscoélastique et pour une configuration stratigraphique donnée, les niveaux de vibrations envisageables à la surface libre s’estiment en fonction de la distance à la source. Les enregistrements considérés permettent d’identifier des indicateurs pertinents et de proposer une classification simplifiée des sources et des sites. On combine ainsi les caractéristiques spectrales des sources (représentées par leur Transformée de Fourier) et la propagation entre la source et le récepteur au moyen d’une fonction de transfert (rapport spectral entre vibration à une distance donnée et celle au niveau de la source). La correspondance entre les propriétés spectrales des sources et celles d’un site donné est quantifiée par le facteur d’immunité (IMF) indépendamment du récepteur à considérer. Cette quantification représente l’ « aléa vibratoire » qui indique le niveau vibratoire attendu en entrée au niveau du récepteur. Ceci est similaire à la définition de l’aléa sismique utilisée dans l’Eurocode 8 pour les études de dimensionnement et renforcement sismique. En utilisant les paramètres comme le gradient de vitesse et le contenu spectral des enregistrements, les effets induits ont été analysés pour de multiples sources. Des indicateurs pertinents (vitesse moyenne à faible profondeur et gradient de vitesse) sont introduits afin de proposer une classification simplifiée de l’aléa vibratoire pour les différentes sources considérées. En cas d’absence de mesure pour une source et un site donnés, cette classification empirique pourra être utilisée afin d’estimer le niveau vibratoire attendu en entrée d’un récepteur.
Abstract
The characterization of the seismic hazard represents a major issue in the field of civil engineering. In vibration engineering, a similar field of study is not present although this question is decisive for the prediction of the generated impact (on population, environment, structures, and high-tech industry instruments). This characterization necessarily involves the knowledge of the various sources of vibrations: operation of infrastructure (railways and road traffic), construction or renovation work (vibro-driving, pile-driving). The characterization strongly depends on the propagation mode of mechanical waves between the source and the receiver taking into consideration soils (sites) and their stratification. The nocivity of vibrations (i.e. ability to cause damage/degree of harmfulness) will therefore depend not only on the type of source and on the propagation of waves in soils, but also on the dynamic response of receivers expressed by their modal properties. In this paper, numerical simulations results are combined with vibration recordings, generated by the operation of infrastructure or by construction sites. Assuming a viscoelastic response for soils and for a given stratigraphic configuration, potential vibration on the free surface are computed and considered as a function of the distance from the source. The studied records enabled the identification of relevant proxies and the proposition of a simplified classification for sources and sites. The spectral characteristics of vibration sources (represented by their Fourier Transform) in one hand; and those of the propagation between the source and the receiver on the other hand are thus combined by means of a transfer function (spectral ratio between vibration at a given distance and that at the source). The matching between the spectral properties of the sources and those of a given site is quantified by the immunity factor (IMF) independently from the receivers properties. This quantification represents the “vibration hazard” which indicates the vibration level expected as the input at the receiver level. This definition is similar to that of seismic hazard used in Eurocode 8 for seismic design and reinforcement studies. Using parameters such as the velocity gradient and the spectral content of the recordings, the induced effects in soil were analyzed for multiple sources. Relevant indicators (harmonic average shear-wave velocity at shallow depth and velocity gradient-proxy) are introduced in order to propose a simplified classification of the vibration hazard for the different sources considered. In the absence of measurement for a given source and site, this empirical classification can be used to estimate the expected vibration level at the input level of a receiver.
Mots clés : vibrations / aléa vibratoire / gradient de vitesse / classification des sites
Key words: vibration / vibration hazard / velocity-gradient / site classification
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2018
1 Notion d’aléa vibratoire
Les vibrations d’origine anthropique dans les sols posent des problèmes accrus du fait de l’augmentation de l’exploitation des infrastructures qui les génèrent. À l’avenir, ces questions deviendront de plus en plus sensibles pour les ouvrages de génie civil en milieu urbain (nuisances, vieillissement des ouvrages, industries sensibles, etc.). Les sources de vibrations peuvent générer différents types d’excitations suivant leur contenu spectral, qui varie fortement d’une source à l’autre et dépend de plusieurs paramètres caractérisant la source elle-même. Cet article approfondit le sujet des sources vibratoires et leur lien avec les sols. Cela a été l’objet de plusieurs articles publiés par la RFG, en particulier dans le numéro 14 bis (Communications présentées aux deuxièmes journées nationales géotechniques) où des sources de tirs à l’explosif, compactage, fonçage, trafic routier, etc. ont été traitées. En raison de l’absence d’un cadre réglementaire précis similaire aux Eurocodes (e.g. Eurocode 8 pour le génie parasismique), un traitement empirique du sujet est généralement mis en œuvre (Simon et al., 2010). La prédiction de mouvement vibratoire et la gestion des vibrations peuvent prendre une importance particulière dans les travaux d’ingénierie et de construction. Un cas représentant cette importance est le vibro-compactage de haut niveau pour le renforcement et la densification des sols en tenant compte des seuils qui peuvent influencer les ouvrages d’art existants (Brûlé et Javelaud, 2010). Un résumé de caractéristiques mécaniques des différentes sources vibratoires principalement du battage des pieux et du compactage est fourni dans la littérature. Le battage de pieux génère des vibrations de vitesse particulaire de quelques mm/s tandis que le compactage dynamique génère des vibrations de vitesse particulaire qui varie entre 10 et 30 m/s. Le vibro-compactage génère des vibrations qui varient dans une plage de fréquence entre 10 et 80 Hz et des déplacements de quelques millimètres (Semblat et Pecker, 2009).
L’estimation préalable des sollicitations vibratoires représente l’aléa vibratoire, ou « niveau de vibration attendu », à considérer à la base des ouvrages/structures récepteurs. La définition de l’aléa vibratoire considère à la fois les caractéristiques des sites (la stratification, contrastes des rigidités, vitesses des ondes, géologie, etc.) et la typologie des sources. C’est une étape très importante vers la formalisation de l’ingénierie vibratoire en génie civil et l’amélioration des normes liées aux effets des vibrations. L’objectif de cet article est de proposer des indicateurs pertinents et une classification simplifiée de l’aléa vibratoire, pour un site donné (un modèle de stratification de sol donné) et pour une typologie de source (continue ou à impact successifs). Un critère de qualification important concernant la classification des sources vibratoires est la nature impulsionnelle ou continue de la source. En France, les seuils tolérables de vibrations dépendent fortement du critère de continuité (Circulaire du 23 juillet, 1986). Dans le même contexte, dans la littérature, les sources de vibrations discontinues sont associées à des seuils exprimés en vitesse particulaire maximale (PGV). Ceux-ci sont généralement plus élevés que ceux associés aux sources de vibrations continues (TRANSVIB-Symposium international, 2006 ; Vibrofonçage, vibratory pile-driving, 2006). L’objectif de cet article est de présenter une méthodologie permettant d’estimer a priori l’aléa vibratoire, ou « niveau de vibration attendu » pour tout type de source.
Cette notion d’aléa est utile pour de futures études d’impact vibratoire sur les structures et ouvrages : en représentant l’effet de la source et de la propagation dans les sols, cette notion devra être combinée avec la réponse dynamique de l’ouvrage et/ou structure pour aboutir à une véritable prédiction d’impact. Les récepteurs peuvent être caractérisés par une réponse en fréquence qui peut aller de quelques Hz (ouvrages hydrauliques, bâtiments de grande hauteur, voies ferrées), à une centaine de Hz (appareils sensibles de haute technologie, parties sensibles du corps humain), en passant par les dizaines de Hz comme pour le cas de bâtiments de hauteur limitée, construction agricoles, etc. (Gordon, 1999 ; Duarte et Filho, 2003 ; Gupta et al., 2008 ; Feldmann et al., 2009 ; Genta, 2012).
L’article est structuré de la manière suivante : la section 2 discute de la pertinence d’indicateurs en vitesse de propagation et gradient de vitesse à faible profondeur, la section 3 propose des grandeurs caractérisant l’aléa vibratoire, la section 4 présente la classification simplifiée issue de ces analyses.
2 Pertinence d’indicateurs en vitesse de propagation et gradient de vitesse
Dans le domaine du génie parasismique, la classification des sites sur lesquels un ouvrage ou une structure peut être fondé, est un sujet largement étudié. La classification de sites considère d’une manière simplifiée et forfaitaire, la réponse sismique d’un profil de sols (variations de l’amplitude des ondes sismiques et modulation de leur contenu fréquentiel par rapport au rocher à la traversée des couches géologiques superficielles) afin d’éviter des études détaillées et coûteuses (Dobry et al., 2000 ; Rodriguez-Marek et al., 2001 ; Zhao et al., 2006 ; Semblat et Pecker, 2009 ; Pitilakis et al., 2013). En ingénierie vibratoire, les approches similaires sont encore rares et faiblement développées. La classification des sites vis-à-vis de leur réponse sismique est principalement réalisée en utilisant le paramètre VS,30 c’est-à-dire la moyenne harmonique des célérités des ondes de cisaillement dans les 30 premiers mètres du sol depuis la surface (Borcherdt, 1994 ; Eurocode, 2008). Les doutes sur la capacité du paramètre VS,30 à prédire seul, et dans toutes les configurations, le mouvement sismique du sol ont conduit à suggérer d’autres paramètres pertinents pour l’analyse. L’utilisation de la fréquence fondamentale du sol f0 en complément de VS,30 a ainsi été proposée (Luzi et al., 2011 ; Cadet et al., 2012 ; Brûlé et Javelaud, 2014). Une autre suggestion consiste à utiliser le gradient de vitesse d’onde de cisaillement, noté B30 qui décrit la variation moyenne de célérité dans le sol dans les 30 premiers mètres (Régnier et al., 2014).
Dans le domaine vibratoire, les longueurs d’ondes mises en jeu sont plus courtes qu’en génie parasismique, du fait d’un contenu fréquentiel assez différent (typiquement 0–120 Hz dans le domaine vibratoire comparativement à 0–10 Hz dans le domaine sismique). Pour les problèmes de vibration nous proposons d’adapter les indicateurs utilisés dans le domaine du génie parasismique. Dans le domaine de vibration, les longueurs d’ondes peuvent être inférieures à un mètre et ne pas dépasser quelques mètres. A contrario, les longueurs d’onde dans le domaine sismique varient entre quelques dizaines de mètres et quelques centaines de mètres. Pour le domaine de vibrations, les indicateurs sont donc définis en utilisant la célérité moyenne des ondes de cisaillement dans les 3 premiers mètres, soit VS,3 définie par l’équation (1), et le gradient de célérité dans les 10 premiers mètres, soit B10, comme discuté dans (Jamal-Eddine et al., 2017). Ces paramètres sont définis sur la base des profondeurs maximales atteintes par les ondes de surface en présence de sources localisées en surface.
 (1)
(1)
Les sites considérés dans cet article présentent un paramètre VS,3 variant de 100 à 400 m/s et des gradients B10 compris entre 0 à 1. Le paramètre de gradient, B10 , décrit la variation d’impédance avec la profondeur pour les 10 premiers mètres, comme le montre l’équation (2) et la figure 1. Dans la figure 1, la ligne rouge est l’expression graphique de la formule 2 obtenues par interpolation linéaire des valeurs log (VS,z) en fonction de log(z) sur les dix premiers mètres.
 (2)
où z est la profondeur de la section de sol considérée, AZ est l’ordonnée à l’origine de la régression et VS(z) la vitesse de l’onde de cisaillement à la profondeur z.
(2)
où z est la profondeur de la section de sol considérée, AZ est l’ordonnée à l’origine de la régression et VS(z) la vitesse de l’onde de cisaillement à la profondeur z.
Une plus grande valeur du gradient de vitesse B10 indique une variation plus rapide de l’impédance du sol avec la profondeur. Une valeur plus faible du gradient de vitesse B10 indique une colonne de sol plus homogène dans les 10 premiers mètres de profondeur. La figure 2 montre, pour une valeur constante de VS,3 = 400 m/s, plusieurs valeurs de gradient B10 associées à différents profils multicouches. Un total de 170 sites (stratigraphies à couches de sol horizontales et parallèles) a été considéré ; leurs caractéristiques ont été choisies de façon à varier le plus possible les facteurs représentatifs des profils : gradient B10, VS,3, nombre de couches au-dessus du demi-espace rocheux et profondeur du demi-espace rocheux à la base de toutes les stratigraphies considérées (voir Tab. 1).
 |
Fig. 1 Présentation simplifiée de la définition d’un gradient de célérité (B10 dans ce cas). A simplified representation for the definition of the velocity-gradient (B10 in this case). |
 |
Fig. 2 Exemples de variation du gradient B10 pour différents profils et une valeur VS,3 constante de 400 m/s. Examples of the variation of the gradient B10 for different soil profiles and a constant value VS,3 of 400 m/s. |
Plages de variations des caractéristiques des sites modélisés.
Range of variation for the properties of the modelled soil profiles.
3 Caractérisation de l’aléa vibratoire dans le domaine spectral
3.1 Appariement source-site
Les réponses spectrales des différents sites, représentant les déplacements associés avec chaque fréquence suite à la transformation de Fourier, ont été regroupées par valeur de gradient. Les valeurs du déplacement spectral normalisé ont ensuite été moyennées pour chaque valeur de gradient. L’analyse spectrale a montré que la sensibilité des sites aux différentes fréquences dépend du gradient B10. Ceci est dû au fait que les gradients B10 sont fortement influencés par la profondeur des couches et par le contraste entre les matériaux des différentes couches. Les sites de plus forts gradients ont des fréquences fondamentales plus élevées (Jamal-Eddine et al., 2017).
L’appariement des propriétés spectrales des sources avec celles d’un site donné devrait faciliter l’évaluation de l’aléa vibratoire du site. Les propriétés spectrales des sites sont représentées par la réponse spectrale moyenne provenant de modélisations par éléments finis sur les vingt premiers mètres à proximité de la source, représentant le champ proche pour considérer l’amortissement géométrique (Jamal-Eddine et al., 2017). Les modélisations par éléments finis ont été réalisées en utilisant le code CESAR-LCPC (Humbert et al., 2005) avec un comportement viscoélastique des matériaux de façon à modéliser un amortissement matériel de type Rayleigh. Les excitations mécaniques ont été imposées en déplacement dans les modèles par éléments finis et les sources sont caractérisées par leur vitesse particulaire dans la base de données du CEREMA (Projet VIBREN, 2018). La figure 3 montre une coupe schématique du problème de propagation étudié.
Dans cette étude, chaque enregistrement en vitesse particulaire lié à une source, provenant de la base de données du CEREMA, est généralement bien caractérisé par ses amplitudes spectrales. Les propriétés spectrales représentent la distribution brute de l’énergie en fréquence (transformée de Fourrier) tandis que les propriétés spectrales relatives représentent la même distribution mais rapportée à l’énergie totale du signal. Les données correspondent aux trois directions de l’espace (verticale, horizontale et transversale) et proviennent principalement de quatre types de sources : battage de pieux (21 enregistrements), vibrofonçage (30 enregistrements), trafic de poids lourds (15 enregistrements) et trafic ferroviaire (15 enregistrements). La majorité des mesures utilisées dans l’analyse ont été réalisées entre 3,5 et 4,5 m de la source avec l’exception des enregistrements de trafic de poids lourd et un seul enregistrement de train à respectivement 9,4 ou 10,4 et 12,5 m de la source. L’enregistrement le plus proche de la source est considéré comme représentatif du contenu spectral de la source elle-même. À ce propos, nous remarquons que la prise de mesures à une distance non négligeable de la source conduit à une diminution importante des amplitudes vibratoires, plus particulièrement sur les hautes fréquences. Toutefois, le choix d’utiliser le signal le plus proche de la source comme étant représentatif de celle-ci a été imposé par le manque d’observations à la source et de la difficulté de traiter par la modélisation numérique aux EF les problèmes dynamiques non-linéaires en proximité de la source (comme la liquéfaction engendrée par vibrofonçage). En outre, on s’intéresse surtout aux vibrations induites à de plus grandes distances. Les résultats obtenus représentent donc une première approximation des niveaux vibratoires, surtout lors d’une prévision à plus courte distance de la source (< 10 m). Néanmoins, les procédures introduites pourront ensuite être appliquées avec d’autres modèles rhéologiques pour les sols (la mobilité cyclique, liquéfaction fluide) pour une estimation plus fine à des distances et pour des sources particulières. Les résultats seront moyennés sur la distance mais traités séparément pour chaque type de source.
Afin d’étudier l’appariement source-site, il est nécessaire de définir l’amplitude spectrale relative pour les sources, d’une part, et pour la réponse du site, d’autre part. En premier lieu, le contenu spectral obtenu via la transformée de Fourier doit être représenté non pas en valeurs brutes, mais en amplitude spectrale relative par rapport à l’énergie totale du signal. Pour les différents sites, la même analyse est réalisée ; la réponse spectrale relative traduit alors la réponse du site et/ou l’énergie spectrale contenue dans le signal. Dans l’équation (3), R(f) représente la réponse du site à une distance donnée sous la forme du rapport spectral entre la transformée de Fourier de la vibration à cette distance et celle au niveau de la source (le champ proche dans ce cas) ou celle du signal imposé comme source. La réponse spectrale relative est ainsi calculée en utilisant l’équation (3) :
 (3)
où E(f) est soit l’amplitude spectrale relative pour les spectres des sources, soit la réponse relative du site à une fréquence donnée obtenue via l’analyse par éléments finis. La figure 4 montre un exemple d’amplitude spectrale relative pour chacune des quatre sources considérées. La fréquence varie de 0 à 120 Hz. R(f) est la réponse (ou contenu) spectral(e) du site ou de la source. L’appariement entre le contenu spectral d’une source et la réponse d’un site est ensuite réalisé en quantifiant l’écart-type défini par l’équation (4). Les fréquences de la plage d’intérêt [0–120 Hz] sont représentées par n valeurs dans l’équation (4).
(3)
où E(f) est soit l’amplitude spectrale relative pour les spectres des sources, soit la réponse relative du site à une fréquence donnée obtenue via l’analyse par éléments finis. La figure 4 montre un exemple d’amplitude spectrale relative pour chacune des quatre sources considérées. La fréquence varie de 0 à 120 Hz. R(f) est la réponse (ou contenu) spectral(e) du site ou de la source. L’appariement entre le contenu spectral d’une source et la réponse d’un site est ensuite réalisé en quantifiant l’écart-type défini par l’équation (4). Les fréquences de la plage d’intérêt [0–120 Hz] sont représentées par n valeurs dans l’équation (4).
 (4)
(4)
Plus σ est faible, plus la source et le site ont des valeurs E(fi) similaires. L’appariement du site et de la source représente le risque de résonance d’un site (ou effet de site) pour une source donnée comme le montre figure 5a pour un enregistrement de battage de pieu et un sol de [Vs,3 = 100 m/s; B10 = 0,2] . Lorsque l’amplitude spectrale relative E(f) du site varie de façon très similaire à celle de la source, σ est faible (σ = 0,32). A contrario, pour du battage avec un sol de type [Vs,3 = 200 m/s; B10 = 0,8] (Fig. 5b), les E(f) présentent des variations très dissemblables ce qui conduit à un σ fort (σ = 3) dans ce cas d’étude particulier.
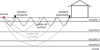 |
Fig. 3 Problème de propagation des vibrations de la source jusqu’au récepteur dans un milieu multicouche hétérogène. Vibration propagation problem from the source to the receiver in a hetrogeneous multilayered soil. |
 |
Fig. 4 Exemples d’amplitude spectrale relative pour quatre sources différentes : (a) vibrofonçage ; (b) battage ; (c) circulation de poids lourds ; (d) circulation ferroviaire. Examples of relative spectral amplitude for four different sources: (a) vibrodriving, (b) pile driving, (c) truck circulation, (d) railway circulation. |
 |
Fig. 5 (a) Correspondance spectrale entre un enregistrement de battage de pieu et un sol de type [VS,3 = 100 m/s ; B10 = 0,2] ; (b) correspondance spectrale entre un enregistrement de battage et un sol de type [VS,3 = 200 m/s ; B10 = 0,8]. (a) Spectral matching between a pile driving recording and a soil of [VS,3 = 100 m/s; B10 = 0.2]; (b) Spectral matching between a pile driving recording and a soil of [VS,3 = 200 m/s; B10= 0.8]. |
3.2 Facteur d’impact par bande de fréquence
Pour chaque bande de fréquence, un facteur de Composante Spectrale Cumulée, ou « CSC », peut être attribué afin d’isoler les fréquences les plus influentes dans le problème de propagation. Un tel facteur CSC peut être par exemple le cumul des amplitudes relatives comprises dans une certaine bande de fréquences. Par conséquent, si un site se compose principalement de sols faibles et qu’il a une fréquence de résonance comprise entre 0 et 20 Hz dénoté f1 et f2, le facteur d’impact pour cette bande sera élevé. Si cette bande comprend par exemple 40 % de l’amplitude, la composante spectrale cumulée CSCsite sera égale à 0,4 et ainsi de suite comme le montre l’équation (5).
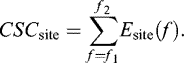 (5)
(5)
Dans l’équation (5), le contenu fréquentiel a été divisé en cinq bandes de 20 Hz de largeur, en partant de 0 Hz.
Pour certaines fréquences, il peut exister un accord très grand entre le site et la source, mais parfois dans des bandes de fréquence qui n’ont pas forcément un impact fort. Pour un sol faible, un très bon appariement source-site pourrait être obtenu à hautes fréquences, ce qui pourrait réduire la valeur de σ et donc indiquer un aléa vibratoire élevé. Cependant, ces fréquences ont une influence négligeable sur le problème puisque leur atténuation en fonction de la distance est bien plus importante que pour les basses fréquences. À partir de ce constat, un facteur d’immunité IMF peut être défini comme indiqué dans l’équation (6). De cette manière, les imprécisions liées à l’utilisation directe de l’indicateur σ peuvent être évitées. Le facteur d’immunité IMF décrit l’immunité d’un site contre l’excitation vibratoire d’une source. Une grande valeur d’IMF indique un aléa plus petit et vice-versa. Un exemple clair justifiant la nécessité de la pondération des valeurs de σ est présenté dans la figure 5a. Le bon appariement sur les hautes fréquences (dans la gamme 100–120 Hz) peut réduire la valeur de σ et refléter ainsi une valeur forte d’aléa alors que l’impact réel de cette gamme de fréquence est négligeable comme le montre la figure 5a.
 (6)
où nb est le nombre de bandes de fréquence qui est ici égal à 6 et σ(ib) représente les valeurs du σ pour la bande de fréquence « ib ».
(6)
où nb est le nombre de bandes de fréquence qui est ici égal à 6 et σ(ib) représente les valeurs du σ pour la bande de fréquence « ib ».
3.3 Quantification pour quelques types de sources à partir de la base de données du CEREMA
Le facteur d’immunité IMF est calculé pour différentes sources (Fig. 6a–d) et différents types de site (VS,3 = 100, 200, 400 m/s et B10∈ [0 ;1]). Pour VS,3 = 400 m/s, les valeurs de B10 ne dépassent pas la valeur de 0,6 ; cela est dû au fait qu’obtenir un gradient plus élevé nécessite des matériaux très durs sous la couche superficielle qui dépassent les valeurs ordinaires associées aux propriétés mécaniques des sols et des roches. Dans la figure 6, les couleurs plus foncées associées avec les plus petites valeurs d’immunité indiquent un aléa plus fort. Pour le vibrofonçage, les réponses des différents sites tendent à être plus ou moins stables et similaires, avec des sites généralement plus sensibles à l’aléa lorsqu’ils sont plus rigides (e.g. VS,3 = 400 m/s) comme le montre la figure 6a. Ceci peut être attribué au fait que l’excitation provenant du vibrofonçage tend à se concentrer sur une bande de fréquence étroite car la sollicitation est relativement monofréquentielle (bande de fréquence connue a priori).
Pour le battage de pieux, la distribution d’aléa vibratoire est illustrée dans la figure 6b. L’aléa le plus élevé est généralement associé aux sols les plus faibles. L’influence du gradient semble tout à fait remarquable : il marque un changement net de l’aléa vibratoire entre des sols plus faibles avec des gradients plus forts et des sols plus rigides avec des gradients plus petits, ces derniers présentant un plus faible aléa. Une répartition d’aléa similaire est causée par la circulation des poids lourds, comme le montre la figure 6c. Les sols plus faibles sont plus sensibles aux basses fréquences et, pour un même type de sol, plus le gradient est élevé plus le sol est sensible aux hautes fréquences comme mentionné précédemment (Jamal-Eddine et al., 2017). Pour le battage de pieux et le trafic poids lourds, une plus grande part de l’énergie a tendance à être concentrée à basse fréquence. Ceci explique pourquoi les sols plus faibles, c’est-à-dire avec des valeurs plus petites de VS,3 et de B10, sont plus sensibles aux sources de battage de pieux et de circulation de poids lourds.
Enfin, la figure 6d montre la répartition d’aléa vibratoire pour la circulation ferroviaire. On pourrait en déduire que l’aléa vibratoire le plus élevé est dans la frange médiane des sites, c’est-à-dire dans les sols ayant un VS,3 d’environ 200 m/s et un gradient B10 autour de 0,5. Les trains sont des sources de vibrations très complexes et les effets des sources ferroviaires dépendent généralement de multiples facteurs tels que la taille, la vitesse, la masse du train, la qualité de la voie et ses propriétés. Dans cette étude, les enregistrements retenus concernent des trains à différentes vitesses mais toujours inférieures aux célérités des ondes de surface dans le sol (i.e. régime « sub-Rayleigh »). Le régime « super-Rayleigh » atteint pour des trains à très grande vitesse dans des sols faibles est généralement l’aléa vibratoire ferroviaire le plus important pour ce type de sols (Kaynia et al., 2000 ; Madshus et Kaynia, 2000).
 |
Fig. 6 Facteur d’immunité IMF par site (VS,3 = 100, 200, 400 m/s et B10 ∈ [0 ;1]) pour les sources (a) de vibrofonçage ; (b) de battage ; (c) de circulation de poids lourds ; (d) de circulation ferroviaire. Immunity factor by site (VS,3 = 100, 200, 400 m/set B10∈[0;1]) for the sources (a) of vibrodriving, (b) of pile driving, (c) truck circulation, (d) train circulation. |
4 Classification simplifiée de l’aléa vibratoire pour un site donné
Comme illustré précédemment, les vibrations du sol dépendent donc fortement de la source d’excitation. Différents sites répondent très différemment suivant le type de source. Le battage de pieux et la circulation des poids lourds ont tendance à causer plus de vibrations dans les sols plus faibles. Le vibrofonçage tend à provoquer des vibrations similaires dans différents sites avec un aléa légèrement plus élevé dans les sols plus rigides. Les vibrations causées par le trafic ferroviaire dépendent de facteurs multiples, mais ont tendance à accroître l’aléa vibratoire dans les sols de rigidité moyenne. À partir de ces résultats, une classification simplifiée préliminaire de l’aléa vibratoire dans les sols est proposée dans le tableau 2 pour différents types de source. Cette classification simplifiée décompose l’aléa vibratoire en cinq catégories : très élevé, élevé, moyen, faible et très faible, décrivant des valeurs de facteur d’immunité IMF entre 0,05 et 0,3 en cinq bandes de 0,05 respectivement. Pour faciliter la lecture de la classification, une couleur est associée à chaque niveau d’aléa vibratoire. Pour le vibrofonçage, les niveaux d’aléa ont tendance à être généralement faibles (couleurs vertes dans le tableau). Les sols faibles sont généralement plus sensibles à l’aléa vibratoire pour le battage des pieux et le trafic de poids lourds, représentés par les couleurs rouge et orange, et l’aléa s’affaiblit avec les sols les plus rigides. Pour la circulation ferroviaire, l’aléa a tendance à être généralement élevé (couleur orange) et plus particulièrement dans les sites à rigidité moyenne (couleur rouge).
Classification simplifiée préliminaire de l’aléa vibratoire relatif dans différents types de sols (caractérisés par VS,3 et B10) et quatre types de sources (vibrofonçage, battage, circulation de poids lourds, circulation ferroviaire).
Preliminary simplified classification of the relative vibration hazard in different types of soils (characterized by VS,3 et B10) and four types of sources (vibrodriving, pile driving, truck circulation, train circulation.
5 Conclusion
Cet article propose le nouveau concept d’aléa vibratoire et développe une méthodologie des indicateurs pertinents et une classification simplifiée. La classification des sources et des sites proposée repose sur la comparaison des caractéristiques spectrales des sources, d’une part, et des sites, d’autre part. Elle s’appuie sur des paramètres familiers aux ingénieurs tels que les vitesses d’ondes de cisaillement et les gradients de vitesse à de faibles profondeurs (VS,3 et B10 dans ce cas). La classification présentée contribuera à mieux prévoir et comprendre les nuisances et désordres dus aux vibrations sur les infrastructures. Cependant, des études plus approfondies et plus détaillées sont encore nécessaires pour caractériser finement l’aléa vibratoire : nombre d’enregistrements plus importants, effets paramétriques de certaines sources (e.g. qualité des voies pour les trains, vitesse de circulation pour les trains et les poids lourds). Une autre perspective viserait à inclure le facteur d’immunité dans les textes réglementaires afin de prévoir l’amplification des vibrations en fonction des caractéristiques des sites et des sources. L’aléa liquéfaction à proximité des sources de vibrofonçage n’a pas était traité dans cet article mais pourrait faire l’objet de travaux ultérieurs.
Références
- Arnould P, Canou J, Gonin H, et al. 2006. Vibrofonçage : Guide technique. Paris, France : Presse de l’école nationale des Ponts et chaussés, 382 p. ISBN-102-85978-423-3. [Google Scholar]
- Borcherdt R. 1994. Estimates of site-dependent response spectra for design (methodology and justification). Earthq Spectr 10(4): 617–653. [Google Scholar]
- Brûlé S, Javelaud E. 2010. Méthode H/V appliquée aux travaux de compactage dynamique haute énergie dans le cadre de l’Eurocode 8. Actes des Journées Nationales de Géotechnique et de Géologie de l’Ingénieur, Grenoble, France, pp. 585–582. [Google Scholar]
- Brûlé S, & Javelaud E. 2013. Méthode H/V en géotechnique. Application à un modèle bicouche. Rev Fr Géotech 142: 3–15. https://doi.org/10.1051/geotech/2013142003. [Google Scholar]
- Cadet H, Bard P-Y, Duval A-M, Bertrand E. 2012. Site effect assessment using KiK-net data: Part 2 – Site amplification prediction equation based on f0 and VSZ. Bull Earthq Eng 10(2): 451–489. [Google Scholar]
- Circulaire du 23 juillet. 1986. Circulaire du 23 juillet relative aux vibrations mécaniques émises dans l’environnement par les installations classées pour la protection de l’environnement. J off Répub fr: 12742. [Google Scholar]
- Communications présentées aux deuxièmes journées nationales géotechniques organisées par les comités français de mécanique des sols, mécanique des roches, géologie de l’ingénieur (11–12 mars 1981, Nantes). 1981. Rev Fr Géotech 14 bis Supplément. [Google Scholar]
- Dobry R, Borcherdt RD, Crouse CB, et al. 2000. New site coefficients and site classification system used in recent building seismic code provisions. Earthq Spectr 16(1): 41–67. [CrossRef] [Google Scholar]
- Duarte MLM, Filho MR. 2003. Perception threshold of people exposed to sinusoidal vibration. Proceedings of the Tenth International Congress on Sound and Vibration, pp. 3791–3798. [Google Scholar]
- Eurocode 2008. Calcul des structures pour leur résistance aux séismes – Partie 1 : règles générales, actions sismiques et règles pour les bâtiments, EN 1998-1, Commission Européenne de Normalisation (CEN), Brussels. [Google Scholar]
- Feldmann M, Heinemeyer C, Butz C, et al. 2009. Design of floor structures for human induced vibrations. JRC-ECCS joint report. [Google Scholar]
- Genta G. 2012. Vibration of structures and machines: practical aspects. Berlin (Germany): Springer Science & Business Media. [Google Scholar]
- Gordon CG. 1999. Generic vibration criteria for vibration-sensitive equipment. In: Optomechanical Engineering and Vibration Control. Int Soc Optics Photonics 3786: 22–34. [Google Scholar]
- Gupta S, Liu WF, Degrande G, Lombaert G, Liu, WN. 2008. Prediction of vibrations induced by underground railway traffic in Beijing. J Sound Vib 310(3): 608––630. [Google Scholar]
- Humbert P, Dubouchet A, Fezans G, Remaud D. 2005. CESAR-LCPC, un progiciel de calcul dédié au génie civil. Bull lab Ponts Chaussées 256(257): 7–35. [Google Scholar]
- Jamal-Eddine AK, Lenti L, Semblat JF. 2017. Vibrations in soils: a spectral prediction method. Proced Eng 199, 2675–2680. [Google Scholar]
- Kaynia AM, Madshus C, Zackrisson P. 2000 Ground vibration from high-speed trains: prediction and countermeasure. J Geotech Geoenviron Eng 126(6): 531–537. [Google Scholar]
- Luzi L, Puglia R, Pacor F, Gallipoli MR, Bindi D, Mucciarelli M. 2011. Proposal for a soil classification based on parameters alternative or complementary to VS30. Bull Earthq Eng 9: 1977–1898. [Google Scholar]
- Madshus C, Kaynia AM. 2000. High-speed railway lines on soft ground: dynamic behaviour at critical train speed. J Sound Vib 231(3): 689–701. [Google Scholar]
- Pitilakis K, Riga E, Anastasiadis A. 2013. New code site classification, amplification factors and normalized response spectra based on a worldwide ground-motion database. Bull Earthq Eng 11(4): 925–966. [Google Scholar]
- Projet VIBREN : recueil et analyse des signaux vibratoires. 2018. Disponible sur https://github.com/CEREMA/dtermed.vibren. [Google Scholar]
- Régnier J, Bonilla LF, Bertrand E, Semblat JF. 2014. Influence of the VS profiles beyond 30 m depth on linear site effects: Assessment from the KiKnet data. Bull Seismol Soc Am 104(5): 2337–2348. [CrossRef] [Google Scholar]
- Rodriguez-Marek A, Bray JD, Abrahamson NA. 2001. An empirical geotechnical seismic site response procedure. Earthq Spectr 17(1): 65–87. [Google Scholar]
- Semblat J, Pecker A. 2009. Waves and vibrations in soils: earthquakes, traffic, shocks, construction works. Pavia (Italy): IUSS Press. [Google Scholar]
- Simon B, Plumelle C, Briançon L, Liausu P. 2010. Amélioration et renforcement des sols – AMSOL – Tome 1. Expertise techniques-Le Moniteur, 496. [Google Scholar]
- TRANSVIB-Symposium international sur le vibrofonçage et la vibrocompaction. 2006. Éditeur ENPC, ISBN 2-7208-2466-6, p. 399. [Google Scholar]
- Zhao JX, Zhang J, Asano A, et al. 2006. Attenuation relations of strong ground motion in Japan using site classification based on predominant period. Bull Seismol Soc Am 96(3): 898–913. [Google Scholar]
Citation de l’article : Abdul-Karim Jamal-Eddine, Luca Lenti, Jean-François Semblat. Aléa vibratoire dans les sols : indicateurs pertinents et classification simplifiée. Rev. Fr. Geotech. 2018, 155, 4.
Liste des tableaux
Plages de variations des caractéristiques des sites modélisés.
Range of variation for the properties of the modelled soil profiles.
Classification simplifiée préliminaire de l’aléa vibratoire relatif dans différents types de sols (caractérisés par VS,3 et B10) et quatre types de sources (vibrofonçage, battage, circulation de poids lourds, circulation ferroviaire).
Preliminary simplified classification of the relative vibration hazard in different types of soils (characterized by VS,3 et B10) and four types of sources (vibrodriving, pile driving, truck circulation, train circulation.
Liste des figures
 |
Fig. 1 Présentation simplifiée de la définition d’un gradient de célérité (B10 dans ce cas). A simplified representation for the definition of the velocity-gradient (B10 in this case). |
| Dans le texte | |
 |
Fig. 2 Exemples de variation du gradient B10 pour différents profils et une valeur VS,3 constante de 400 m/s. Examples of the variation of the gradient B10 for different soil profiles and a constant value VS,3 of 400 m/s. |
| Dans le texte | |
 |
Fig. 3 Problème de propagation des vibrations de la source jusqu’au récepteur dans un milieu multicouche hétérogène. Vibration propagation problem from the source to the receiver in a hetrogeneous multilayered soil. |
| Dans le texte | |
 |
Fig. 4 Exemples d’amplitude spectrale relative pour quatre sources différentes : (a) vibrofonçage ; (b) battage ; (c) circulation de poids lourds ; (d) circulation ferroviaire. Examples of relative spectral amplitude for four different sources: (a) vibrodriving, (b) pile driving, (c) truck circulation, (d) railway circulation. |
| Dans le texte | |
 |
Fig. 5 (a) Correspondance spectrale entre un enregistrement de battage de pieu et un sol de type [VS,3 = 100 m/s ; B10 = 0,2] ; (b) correspondance spectrale entre un enregistrement de battage et un sol de type [VS,3 = 200 m/s ; B10 = 0,8]. (a) Spectral matching between a pile driving recording and a soil of [VS,3 = 100 m/s; B10 = 0.2]; (b) Spectral matching between a pile driving recording and a soil of [VS,3 = 200 m/s; B10= 0.8]. |
| Dans le texte | |
 |
Fig. 6 Facteur d’immunité IMF par site (VS,3 = 100, 200, 400 m/s et B10 ∈ [0 ;1]) pour les sources (a) de vibrofonçage ; (b) de battage ; (c) de circulation de poids lourds ; (d) de circulation ferroviaire. Immunity factor by site (VS,3 = 100, 200, 400 m/set B10∈[0;1]) for the sources (a) of vibrodriving, (b) of pile driving, (c) truck circulation, (d) train circulation. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




