EDP Sciences logo
Authentification abonné
Rechercher
Menu
Accueil Tous les numéros Numéro 163 (2020) Rev. Fr. Geotech., 163 (2020) 7 Full HTML
Accès gratuit
Numéro
Rev. Fr. Geotech.
Numéro 163, 2020
Chutes de bloc, Risques Rocheux et Ouvrages de Protection (C2ROP)
Numéro d'article 7
Nombre de pages 9
DOI https://doi.org/10.1051/geotech/2020016
Publié en ligne 2 octobre 2020

© CFMS-CFGI-CFMR-CFG, 2020

1 Introduction

L’aléa de chute de blocs est caractérisé par le détachement brutal d’une masse rocheuse, depuis une paroi (sub)verticale, qui se propage rapidement vers l’aval sous l’effet de la gravité par phases de vol libre, glissement, roulement et/ou rebonds successifs (Varnes, 1978). Ces événements, fréquents en zones de montagne (Badoux et al., 2016 ; Haque et al., 2016), représentent un aléa majeur pour les infrastructures collectives et les habitations, et ont souvent de graves conséquences (Fig. 1). En France, par exemple, le détachement d’un volume rocheux de 30 m3 en 2014 a provoqué le déraillement du train touristique des Pignes (département des Alpes-de-Haute-Provence), faisant deux victimes et neuf blessés (Assali, 2015). Sur la même période, un événement rocheux de 50 m3 a détruit une maison dans la municipalité d’Isola (département des Alpes-Maritimes), conduisant au décès de deux enfants. De même, l’endommagement des voies et la perturbation du trafic ferroviaire suite à un événement rocheux survenu en 2015 entre Moûtiers et Bourg-Saint-Maurice (département de la Savoie) ont induit 1,34 M€ de réparations, et 5,4 M€ de dommages indirects.

Ces différents événements illustrent bien notre vulnérabilité face aux événements rocheux, et soulignent que les collectivités locales et les pouvoirs publics sont encore fréquemment démunis en matière de méthode de diagnostic et d’analyse du risque de chute de blocs. Dans ce contexte, l’évaluation des risques par une approche de type quantitative, appelée QRA (de l’anglais quantitative risk assessment), est devenue incontournable pour l’aménagement des territoires et le choix des mesures de mitigation. À la différence des approches qualitatives, où le risque est exprimé à partir de critères objectifs et résumé par les termes fort, moyen et faible (Ferrari et al., 2016), les approches quantitatives offrent des valeurs de risque objectives et reproductibles (Corominas et al., 2014). Chaque terme de l’équation du risque, dont les composantes principales sont l’aléa, la vulnérabilité et l’exposition, sont fidèlement quantifiés, offrant des informations sur les dommages potentiels (en euros par an, par exemple ; Agliardi et al., 2009).

En pratique, pourtant, les approches de type QRA pour la gestion des risques rocheux restent encore peu employées (Hungr et al., 1999 ; Corominas et al., 2005 ; Agliardi et al., 2009 ; Hantz, 2011 ; Moos et al., 2017 ; Farvacque et al., 2019a, 2019b ; Corominas et al., 2019). Cette rareté est principalement liée à la difficulté à évaluer précisément chacune des composantes du risque. De plus, les quelques études qui proposent une approche de type QRA dans le domaine rocheux font généralement l’hypothèse de la stationnarité du processus (Eckert et al., 2018), de sorte que l’étalement urbain ou l’évolution de l’occupation des sols (Lopez-Saez et al., 2016 ; García-Hernández et al., 2017 ; Beniston et al., 2018), qui modifient le fonctionnement du processus, ne soient pas intégrés. D’ailleurs, le risque rocheux est toujours évalué uniquement pour les bâtiments et les infrastructures déjà existantes (Corominas et al., 2005 ; Agliardi et al., 2009 ; Moos et al., 2017). Des approches mathématiques cohérentes pour évaluer le risque comme une fonction continue de l’espace dans des zones propices à l’établissement de nouveaux enjeux (comme de nouvelles constructions) font donc défaut. Ce manque d’approches adaptées aux zones encore non urbanisées exclut toute anticipation du risque de chutes de blocs dans un contexte d’urbanisme évoluant rapidement et substantiellement (Farvacque et al., 2019a), ou de zonage du risque sur la base de seuils d’acceptabilité (Arnalds et al., 2004 ; Hantz, 2011 ; Eckert et al., 2018). Enfin, le risque rocheux − comme la plupart des autres risques naturels – est toujours exprimé par le dommage moyen (Eckert et al., 2008 ; Agliardi et al., 2009 ; Eckert et al., 2009 ; Favier et al., 2014, 2016). Cependant, cette moyenne arithmétique est souvent inadaptée aux contraintes budgétaires, politiques, sociales ou environnementales auxquelles doivent faire face les différents gestionnaires (Bernier, 2003 ; Jonkman et al., 2003 ; Zheng et Albert, 2019).

Dans ce contexte, l’objectif de cette contribution est :

  • de renforcer les bases formelles du calcul du risque dans le domaine des chutes de blocs ;

  • d’évaluer les effets des changements environnementaux sur le risque rocheux ;

  • de proposer une méthode où le risque de chute de blocs est quantifié sur des bâtiments théoriques répartis de manière homogène le long de la pente par des mesures du risque alternatives à la moyenne arithmétique.

À cet effet, nous proposons une procédure holistique de QRA où le risque rocheux est quantifié en combinant un modèle de simulation trajectographique avec des courbes de vulnérabilité et un large spectre de volume rocheux et de zones de départ de chutes de blocs. La faisabilité et l’intérêt de cette procédure sont illustrés sur le cas d’étude réel de la commune de Crolles, dans les Alpes françaises. Par ailleurs, nous mesurons l’effet des changements environnementaux sur le risque de chute de blocs en appliquant la QRA dans différents contextes d’utilisation et d’occupation des sols. Enfin, nous proposons une approche innovante où deux mesures de risque, basées sur des quantiles de la distribution des dommages, sont introduites. Ces dernières permettent une meilleure prise en compte des événements extrêmes et permettent d’envisager la gestion du risque à divers horizons temporels.

Les travaux présentés dans cet article résument l’essentiel des travaux développés dans une thèse de doctorat (Farvacque, 2020), où l’ensemble des méthodologies, résultats et conclusions sont détaillés. Des applications et extensions dans d’autres contextes et étendues aux enjeux linéaires y sont proposées, notamment dans la cordillère des Andes.

thumbnail Fig. 1

Exemples d’événements chutes de blocs survenus en France : (A) route départementale de Savoie, février 2014 ; (B) commune de Lumbin (département de l’Isère), janvier 2002 ; (C) axe ferroviaire du département de la Corrèze, août 2011. © J.-P. Clatot − AFP (A) ; S. Gominet − IRMa (B) ; Assali, 2015 (C).

Illustrative examples of rockfall events: (A) departmental road in Savoie, Feb. 2014; (B) Lumbin municipality (Isère department), Jan. 2002; (C) railway track in the Corrèze department, Aug. 2011. © J.-P. Clatot − AFP (A); S. Gominet − IRMa (B); Assali, 2015 (C).

2 Méthodologie de l’évaluation quantitative du risque

2.1 Le risque comme espérance des dommages

Le risque est classiquement défini comme une combinaison du phénomène dommageable et de ses conséquences (Renn, 2008a, 2008b ; Eckert et al., 2012 ; Aven, 2016) exprimé en dommage moyen attendu par an. À partir de la distribution cumulée des dommages ℒ (d), intégrée sur la distribution des volumes des événements rocheux, le risque peut alors être exprimé comme (Cruden et Varnes, 1996 ; UNISDR, 2019) : (1) où Rz représente les conséquences attendues suite à l’activité de chute de blocs sur un enjeu z, associé à une exposition spatiotemporelle q(z) et une valeur Ƶ. Ces enjeux sont généralement physiques (personnes, infrastructures routières/ferroviaires, bâtiments, etc. ; Agliardi et al., 2009 ; Hantz, 2010 ; Michoud et al., 2012), mais d’autres aspects moins tangibles peuvent être introduits. L’occurrence temporelle des chutes de blocs (en événements/an, quel que soit le volume) est introduite à travers le facteur λ. Néanmoins, la soudaineté et la complexité du phénomène, le manque de retour d’expérience, et la difficulté de certains formalismes induisent à quantifier le risque rocheux de la façon suivante : (2)où f(v) correspond à la fréquence annuelle de départ d’un bloc rocheux de volume v, pz(E | v) à la probabilité de propagation jusqu’à l’enjeu z avec une énergie E pour un volume v, et Dz(E) au dommage subi sur l’élément z suite à un impact rocheux d’énergie E. Il apparaît donc que la variabilité de l’aléa est réduite à celle du couple volume–énergie cinétique et, qu’en outre, le dommage n’est supposé dépendre que de l’énergie cinétique. Enfin, en pratique, le risque rocheux est calculé numériquement via des sommes discrètes sur un ensemble de simulations trajectographiques pour plusieurs classes de volumes vCl : (3)où f(vCl) correspond à la fréquence annuelle de départ des blocs rocheux pour la classe de volume vCl, pz(vCl) à la probabilité d’atteinte de l’enjeu z par un bloc rocheux dont le volume appartient à vCl, et à la moyenne de la distribution des dommages produits par les blocs impactant l’enjeu z dans la classe de volume vCl.

2.2 Mesures de risque alternatives basées sur les quantiles

La moyenne (espérance mathématique) des dommages n’est qu’une valeur de risque ne pouvant rendre compte de l’ensemble des contraintes auxquelles doivent faire face les gestionnaires du risque (Bernier, 2003 ; Jonkman et al., 2003 ; Zheng et Albert, 2019). D’autres mesures du risque, comme la value-at-risk (VaR) et l’expected shortfall (ES), calculées sur la distribution complète des dommages (Éq. (1)), ont été introduites. Ces dernières, très populaires dans le domaine financier (Guerra et Centeno, 2012 ; Emmer et al., 2015), ont été choisies pour leur efficacité à évaluer les dommages liés aux événements de faibles probabilités (ou événements rares/extrêmes).

La value-at-risk et l’expected shortfall sont des mesures de risque dites « quantile-based » qui sont définies pour un seuil de confiance α ∊ (0,1) (McNeil et al., 2015). Ces deux mesures permettent d’évaluer les dommages minimum et moyen attendus dans les (1-α) % pires scénarios de la distribution des dommages. La VaR est un quantile de la distribution des dommages, calculé de la façon suivante : (4) où ℒ (d) est la distribution des dommages et Pr {D ≥ d} la probabilité que le dommage D soit supérieur ou égal à une valeur de dommage d.

De la même manière, l’expected shortfall est une mesure de risque étroitement liée à la value-at-risk, mais elle est davantage sensible à la queue de distribution. Cette mesure est définie comme la moyenne des dommages au-delà de la VaR par : (5)

Étant donné que le quantile α doit être défini par le gestionnaire en fonction de son attitude face au risque, avec α = 0 étant neutre face au risque et α = 1 conservateur (Zheng et Albert, 2019), il est difficile de proposer des valeurs arbitraires pour α. Dans cette contribution, les mesures value-at-risk et expected shortfall ont été évaluées pour différentes périodes t (en année), correspondant à des horizons de gestion du risque définis par un certain niveau de confiance α comme (Farvacque, 2020) : (6) où λ représente l’occurrence temporelle des chutes de blocs (en événements/an, quel que soit le volume).

En s’appuyant sur l’équation (1), le risque rocheux pour les mesures value-at-risk et expected shortfall est calculé comme : (7) où VaRα et ESα correspondent au dommage mesuré sur la distribution complète des dommages par la value-at-risk et l’expected shortfall au quantile α, respectivement.

3 Site d’étude

Le cadre méthodologique présenté dans la section précédente a été appliqué au cas d’étude réel de la commune de Crolles, située dans le département de l’Isère, au nord-est de l’agglomération grenobloise, sur les contreforts du Massif de la Chartreuse. Cette commune péri-urbaine, surplombée par une falaise calcaire haute de 300 m, est soumise à un aléa rocheux générateur de risque. Les archives historiques (catalogue d’événements, photographies), les cicatrices d’impacts observées sur les arbres, les cratères sur le sol, ainsi que les blocs récents de plusieurs mètres cubes observés sur le versant confirment la régularité de l’activité rocheuse, et traduisent également l’intensité élevée et le caractère destructeur du phénomène. Par ailleurs, le versant de Crolles a connu de profondes modifications de l’occupation et de l’usage des sols depuis 1850, à l’origine d’une évolution rapide de l’aléa de chute de blocs. Le paysage viticole dominant au début du XXe siècle a progressivement disparu. La déprise agro-sylvo-pastorale et l’urbanisation ont conduit à une expansion du front urbain, et à une densification et expansion de la forêt dans la partie aval (Fig. 2).

thumbnail Fig. 2

Évolution de l’occupation du sol du versant sud-est du Massif de la Chartreuse entre 1911 (A) et 2017 (B).

Southeastern slopes of the Chartreuse Mountains in 1911 (A) and 2017 (B).

4 Évaluation des différentes composantes du risque de chute de blocs

4.1 Aléa rocheux

La définition de l’aléa rocheux implique trois notions :

  • la susceptibilité ;

  • la fréquence ;

  • la propagation.

La susceptibilité consiste à identifier les zones depuis lesquelles des événements rocheux sont susceptibles de se déclencher. La fréquence correspond au nombre de blocs qui se décrochent annuellement de la falaise pour différentes classes de volumes. Enfin, l’objectif de la propagation est d’évaluer les trajectoires potentielles de ces événements rocheux.

4.1.1 Susceptibilité

Les zones de départ de chutes de blocs ont été identifiées à partir d’une approche géomorphométrique dite slope angle frequency distribution (SAFD ; Loye et al., 2009). Cette dernière, basée sur l’utilisation d’un modèle numérique de terrain (MNT), permet de décomposer la distribution des pentes sur le site en plusieurs distributions gaussiennes considérées comme des unités morphologiques caractéristiques (par exemple, pentes abruptes, pieds de pente, plaines, etc.). Le terrain est ensuite considéré comme source potentielle de chutes de blocs si son inclinaison dépasse une valeur limite. Dans le cas pratique de l’étude de Crolles, cette approche a été réalisée pour les 300 m de parois sub-verticales qui surplombent le village à partir de l’application Excel nommée Histofit (Loye et al., 2009). Le seuil de pente définissant les zones potentielles de chutes de blocs a ainsi été évalué à 49°.

4.1.2 Fréquence de départ des événements rocheux

La relation volume–fréquence des événements rocheux a été établie en suivant la procédure proposée par De Biagi et al. (2017), qui examine séparément:

  • l’occurrence temporelle d’événements récents de chutes de blocs ;

  • la distribution en volume associée.

À Crolles, la temporalité des chutes de blocs a été évaluée sur la base d’un catalogue d’événements isolés répertoriés le long d’un transect de 900 m du versant. L’enquête de terrain indique que ces événements ont potentiellement été libérés d’une surface de falaise d’environ 11,5 hm2, et qu’ils auraient eu lieu au cours des 100 dernières années comme en témoigne le grand nombre de cicatrices d’impact visibles sur les arbres ou l’absence de lichens sur les blocs. Ainsi, en considérant uniquement les blocs d’un volume supérieur à u = 1 m3 (volume minimum susceptible d’endommager significativement le bâti), la fréquence des événements rocheux λ est évaluée à 0,015 événement/an/hm2. Par ailleurs, la distribution des volumes rocheux spécifique au site de Crolles a été déterminée en utilisant la statistique des valeurs extrêmes (EVT), à travers la méthode Peak Over Threshold (loi de Pareto généralisée GPD ; Coles, 2001), appliquée au catalogue d’événements répertoriés sur le versant. Les estimateurs du maximum de vraisemblances lorsque u = 1 m3 sont . La fréquence cumulée des événements rocheux est ainsi exprimée comme : 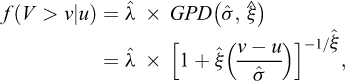(8) où V correspond au volume (en m3) et à l’occurrence temporelle des chutes de blocs de volume supérieur à u. u, , sont les paramètres de position, d’échelle, et de forme de la distribution GPD, respectivement.

4.1.3 Propagation et énergies des blocs

Les trajectoires des événements rocheux ont été simulées au moyen du logiciel Rockyfor3D (Dorren, 2012), qui modélise la trajectoire d’un bloc en 3D à partir de séquences de chute libre dans l’air, de rebonds sur la surface de la pente, et d’impacts contre des arbres. Rockyfor3D prend en compte l’hétérogénéité de l’occupation et de l’usage des sols, à travers des facteurs de rugosité et d’élasticité du sol, et de densité du couvert forestier. Les résultats fournis sont utilisés pour évaluer la distribution des énergies d’impact sur les enjeux considérés, et déterminer des probabilités d’atteinte. Une description détaillée du modèle Rockyfor3D est proposée dans Dorren (2012).

À Crolles, les trajectoires des événements rocheux ont été modélisées en grand nombre (10 000 simulations par zone de départ) pour des volumes compris entre 1 et 20 m3 (tirage aléatoire mais homogène). Les volumes supérieurs à 20 m3 n’ont pas été inclus dans l’analyse afin de rester dans l’intervalle de validité du modèle Rockyfor3D et de préserver l’efficacité du stockage et du traitement des données. La topographie du site est décrite par un modèle numérique de terrain de 5 m de résolution (RGE, IGN), affranchi des merlons de protection. L’utilisation et l’occupation des sols (LULC) est évaluée à partir d’une carte du versant en 2017 et d’observations de terrain.

4.2 Vulnérabilité des enjeux

Les énergies des blocs fournies par le logiciel Rockyfor3D ont été converties en valeurs de dommage à partir de courbes de vulnérabilité. Ces dernières permettent de transformer l’énergie d’un bloc en un dommage D compris entre 0 (pas de dommage) et 1 (destruction totale). Le dommage sur le bâti est évalué au moyen de la courbe de vulnérabilité d’Agliardi et al. (2009), issue de la rétro-analyse d’un événement rocheux en 2004 à Fiumelatte (Italie). Cette relation est donnée par l’expression suivante : (9) où E correspond à l’énergie du bloc (en Joules).

Le choix pour cette relation est motivé par :

  • des longueurs de pente (> 500 m) et des classes de volume comparables entre Crolles et Fiumelatte :

  • le manque d’événements dommageables à Crolles qui permettraient une rétro-analyse spécifique :

  • la rareté des fonctions de vulnérabilité dans la littérature.

L’approche développée par Mavrouli et Corominas (2010) ne serait, par exemple, pas applicable à notre étude car :

  • elle considère le point précis d’impact du bloc sur la structure, nécessitant ainsi des informations détaillées sur le bâti (information non disponible à l’échelle de notre site d’étude) ;

  • elle est développée pour des volumes trop petits (jusqu’à : 4 m3) en comparaison des événements rocheux susceptibles de se produire à Crolles.

4.3 Exposition et valeur des enjeux

Dans le cas des bâtiments, comme nous ne tenons pas compte de l’élément touché (colonne angulaire, mur non porteur, colonnes centrales, etc. ; Mavrouli et Corominas, 2010), et que les bâtiments sont des éléments statiques, le facteur d’exposition est égal à 1. Enfin, en définissant la valeur de chaque bâtiment par sa surface au sol (emprise de l’enjeu sur le MNT), le risque rocheux est exprimé comme la surface moyenne du bâti détruite chaque année (en m2/an).

5 Synthèse des résultats

5.1 Analyse quantitative du risque de chutes de blocs

Considérant des volumes rocheux de 1 à 20 m3 issus des 300 m de parois sub-verticales qui surplombent le village de Crolles, le risque rocheux, exprimé en surface moyenne détruite chaque année, a été évalué pour chaque bâtiment référencé dans le plan cadastral de la municipalité (Farvacque et al., 2019a, 2019b). Sur le plan spatial, la cartographie du risque rocheux démontre que les enjeux menacés sont principalement situés sur le front urbain (Fig. 3). Le risque par bâtiment excède rarement 0,01 m2 détruits par an, mais un quartier où le risque peut dépasser cette valeur fait exception. Par ailleurs, le risque rocheux pour le bâti de Crolles a été calculé pour 19 classes de volume. La distribution du risque en fonction de ces classes de volume met en évidence la proportion importante du risque total liée aux classes comprises entre 7 et 12 m3 (Fig. 4). La décroissance du risque pour des volumes supérieurs résulte de la diminution des fréquences d’occurrence pour des événements de fortes magnitudes. À l’inverse, pour des classes de volume inférieures, le risque diminue du fait de la protection induite par le couvert forestier (Farvacque et al., 2019a, 2019b).

thumbnail Fig. 3

Cartographie du risque chutes de blocs pour le bâti de Crolles.

Rockfall risk for buildings currently existing in the Crolles urban area.
thumbnail Fig. 4

L’histogramme représente la distribution du risque de chutes de blocs pour chaque classe de volume. Courbe en pointillé rouge : distribution du risque quand le dommage est fixé à 1 (destruction totale du bâtiment à chaque impact).

Distribution of the rockfall risk (% of the total value) for each volume class. The red dotted curve represents the risk when the physical vulnerability is set at 1 (total destruction of the building in case of impact).

5.2 Influence des changements paysagers sur le risque rocheux

Pour approfondir notre approche, notre méthodologie de calcul, déjà appliquée dans le contexte actuel de la commune de Crolles, a été étendue à trois types d’occupation et d’usage des sols observés par le passé sur le versant de la commune. Ces derniers, proposés par Lopez-Saez et al. (2016), reprennent la cartographie de l’occupation des sols de 1850 (paysage binaire forêt–vigne), 1956 (mosaïque de forêt, vigne, culture, prairie et friche) et 1975 (mosaïque de forêt, culture, prairie et friche). Nos différents résultats, exprimés pour chaque bâtiment référencé dans le plan cadastral de Crolles, ont permis de démontrer que la politique de reboisement du versant depuis les années 1850 (+32 %) a conduit à une réduction du risque rocheux d’environ 50 % (Farvacque et al., 2019a, 2019b). Néanmoins, cette diminution n’a pas été proportionnelle à la progression du couvert forestier. En effet, la réorganisation parcellaire du paysage en aval du versant entre 1956 et 1975 a fortement contrebalancé l’action protectrice de la forêt contre les chutes de blocs. Par exemple, l’abandon des vignes au profit de la prairie entre 1850 et 1956 a multiplié le risque rocheux par un facteur 5. Par ailleurs, l’étude au cas par cas des bâtiments a permis de démontrer que les secteurs les plus à risque varient en fonction de la structure paysagère (Fig. 5). Aujourd’hui, le risque rocheux est concentré sur quelques bâtiments situés à l’aval d’une parcelle de prairie de faible rugosité, elle-même localisée à la débouché d’un talweg, ce qui induit une augmentation des probabilités d’impact (Fig. 3).

thumbnail Fig. 5

Cartographie du risque de chutes de blocs sur le plan urbain de Crolles pour différents scénarios d’occupation et d’usage des sols.

Distribution of the rockfall risk at Crolles for different landscape patterns.

5.3 Quantification du risque rocheux par des mesures alternatives du risque

Les autres mesures du risque alternatives à la moyenne des dommages, qui sont la value-at-risk (VaR) et l’expected shortfall (ES), ont été évaluées sur des bâtiments théoriques (surfaces individuelles de 100 m2) répartis de manière homogène le long de la pente. Pour des raisons pratiques, cette démarche est illustrée pour un secteur réduit de la commune de Crolles, nommé Le Brocey, où l’occupation des sols est actuellement associée à des parcelles agricoles. Le risque a donc été évalué sur l’ensemble de la zone urbanisable dans le futur pour des horizons de gestion du risque rocheux compris entre 100 et 10 000 ans. Les cartes obtenues à partir de la VAR (Fig. 6A–C) montrent une absence de risque pour t < 100 ans (certitude à 98 % ; Fig. 6A). Au-delà de cet horizon t, le nombre de bâtiments à risque augmente, préférentiellement le long des couloirs rocheux, mais reste très restreint et le taux de destruction annuel n’excède jamais 0,5 m2 pour t = 1000 ans (certitude à 99,8 % ; Fig. 6C). Les cartes obtenues à partir de l’ES démontrent au contraire qu’un faible risque existe sur l’ensemble du secteur considéré (Fig. 6B–D). En amont des couloirs, par exemple, 2 % des événements rocheux attendus sur 100 ans endommageront, en moyenne, plus de 0,1 m2/an (Fig. 6B). Nos résultats démontrent aussi que tant que le risque VaR est égal à 0 m2/an, le risque ES est strictement égal au risque moyen.

thumbnail Fig. 6

Cartographie du risque rocheux (en m2 détruits par an) dans un quartier de la municipalité de Crolles (Le Brocey) à partir de la value-at-risk (A, C) et de l’expected shortfall (B, D) pour des horizons t de 100 ans (A, B) et 1000 ans (C, D).

Map of the value-at-risk (A, C) and expected-shortfall (B, D) at Le Brocey and for temporal horizons t of 100 years (A, B) and 1000 years (C, D). Values are expressed in m2 destroyed per year.

6 Conclusion

Cette contribution propose un renforcement des fondamentaux du calcul quantitatif du risque rocheux à travers une combinaison de modèles analytiques, statistiques, ou numériques. Contrairement aux études précédentes où le risque rocheux est généralement évalué sur des scénarios prédéfinis (quelques événements), nous prenons systématiquement en compte un large éventail de volumes de chutes de blocs et de zones de départ. À cet égard, le spectre complet de l’aléa rocheux est intégré dans le calcul du risque.

Notre cadre méthodologique a été testé sur le site d’étude de la commune de Crolles, dans les Alpes françaises. Les résultats obtenus démontrent la faisabilité de la QRA dans le contexte des chutes de blocs, mais mettent également en évidence la valeur ajoutée de ces procédures dans la gestion des risques. En effet, la QRA permet, par exemple, d’identifier et de hiérarchiser les zones à risque. Ainsi, les différents résultats permettent une meilleure compréhension du risque, de proposer des approches coût–bénéfice, et sont un atout majeur pour l’aménagement du territoire et l’optimisation du positionnement et du dimensionnement des ouvrages de protection.

Par ailleurs, l’implémentation de non-stationnarités liées à l’occupation des sols dans le calcul du risque rocheux a permis de mieux comprendre les interactions entre la structure du paysage et le risque de chutes de blocs. Cette approche dynamique démontre l’intérêt de la prise en compte systématique de l’évolution future du paysage dans l’évaluation quantitative des risques naturels rocheux.

Enfin, l’introduction des nouvelles mesures de risque (VaR et ES), encore inédites dans le domaine des chutes de blocs, présente l’avantage de mieux prendre en compte les événements extrêmes et d’envisager la gestion du risque à divers horizons temporels. Plus précisément, nos résultats se traduisent comme le risque rocheux minimum (VaR) et moyen (ES) induits par les pires scénarios rocheux (1-α % des événements) attendus sur t années. La value-at-risk et l’expected shortfall permettent ainsi la quantification du risque sur un horizon temporel t, contrairement à la moyenne qui n’inclut pas le temps nécessaire pour atteindre les dommages attendus (Embrechts et al., 1997). Ces mesures du risque constituent donc des alternatives intéressantes pour les choix d’aménagement du territoire ainsi que la prise en compte des différentes contraintes court terme/long terme auxquelles doivent faire face les gestionnaires du risque. Cela devrait aider à trouver le juste équilibre entre la nécessité de sécurité et le besoin de développement durable dans divers contextes.

Remerciements

Ces recherches ont été financées par une subvention doctorale de la région Rhône-Alpes (ARC Environnement 3), le projet national C2ROP (Chutes de blocs, Risques Rocheux, Ouvrages de Protection), le Labex OSUG@2020, et le projet Irstea ZORRINO (Zonage réglementaire du risque en montagne par optimisation des pertes). Ces travaux sont également soutenus par l’Agence nationale de la recherche et ont été menés dans le cadre du programme CDP Risk@Univ. Grenoble Alpes (ANR-15-IDEX-02).

Références

  • Agliardi F, Crosta GB, Frattini P. 2009. Integrating rockfall risk assessment and countermeasure design by 3D modelling techniques. Nat Hazards Earth Syst Sci 9(4): 1059–1073. [CrossRef] [Google Scholar]
  • Arnalds P, Jónasson K, Sigurõsson S. 2004. Avalanche hazard zoning in Iceland based on individual risk. Ann Glaciol 38: 285–290. [CrossRef] [Google Scholar]
  • Assali P. 2015. Modélisation géostructurale 3D de parois rocheuses par lasergrammétrie et photogrammétrie terrestres en milieu ferroviaire. Bull Eng Geol Environ 74(4): 1255–1265. [CrossRef] [Google Scholar]
  • Aven T. The reconceptualization of risk. In: Routledge handbook of risk studies. Routledge, 2016, pp. 76–90. [Google Scholar]
  • Badoux A, Andres N, Techel F, Hegg C. 2016. Natural hazard fatalities in switzerland from 1946 to 2015. Nat Hazards Earth Syst Sci 16(12): 2747–2768. [CrossRef] [Google Scholar]
  • Beniston M, Farinotti D, Stoffel M, et al. 2018. The european mountain cryosphere: a review of its current state, trends, and future challenges. Cryosphere 12(2): 759–794. [CrossRef] [Google Scholar]
  • Bernier J. 2003. Décisions et comportement des décideurs face au risque hydrologique. Hydrol Sci J 48(3): 301–316. [CrossRef] [Google Scholar]
  • Coles S. 2001. An introduction to statistical modeling of extreme values. In: Springer series in statistics. London: Springer. [CrossRef] [Google Scholar]
  • Corominas J, Copons R, Moya J, Vilaplana JM, Altimir J, Amigó J. 2005. Quantitative assessment of the residual risk in a rockfall protected area. Landslides 2(4): 343–357. [CrossRef] [Google Scholar]
  • Corominas J, Matas G, Ruiz-Carulla R. 2019. Quantitative analysis of risk from fragmental rockfalls. Landslides 16(1): 5–21. [CrossRef] [Google Scholar]
  • Corominas J, van Westen C, Frattini P, et al. 2014. Recommendations for the quantitative analysis of landslide risk. Bull Eng Geol Environ 73: 209–263. [Google Scholar]
  • Cruden D, Varnes DJ. 1996. Landslide types and processes. Special Report − National Research Council, Transportation Research Board 247: 36–75. [Google Scholar]
  • De Biagi V, Napoli ML, Barbero M, Peila D. 2017. Estimation of the return period of rockfall blocks according to their size. Nat Hazards Earth Syst Sci 17(1): 103–113. [CrossRef] [Google Scholar]
  • Dorren L. 2012. Rockyfor3d (v5.1) revealed − Transparent description of the complete 3d rockfall model. EcorisQ paper: 32. [Google Scholar]
  • Eckert N, Keylock C, Bertrand D, et al. 2012. Quantitative risk and optimal design approaches in the snow avalanche field: review and extensions. Cold Reg Sci Technol 79–80: 1–19. [CrossRef] [Google Scholar]
  • Eckert N, Naaim M, Giacona F, et al. 2018. Repenser les fondements du zonage règlementaire des risques en montagne « récurrents ». La Houille Blanche (2): 38–67. [CrossRef] [EDP Sciences] [Google Scholar]
  • Eckert N, Parent E, Faug T, Naaim M. 2008. Optimal design under uncertainty of a passive defense structure against snow avalanches: from a general Bayesian framework to a simple analytical model. Nat Hazards Earth Syst Sci 8(5): 1067–1081. [CrossRef] [Google Scholar]
  • Eckert N, Parent E, Faug T, Naaim M. 2009. Bayesian optimal design of an avalanche dam using a multivariate numerical avalanche model. Stoch Environ Res Risk Assess 23(8): 1123–1141. [CrossRef] [Google Scholar]
  • Embrechts P, Klüppelberg C, Mikosch T. 1997. Modelling extremal events. Berlin, Heidelberg: Springer. [CrossRef] [Google Scholar]
  • Emmer S, Kratz M, Tasche D. 2015. What is the best risk measure in practice? A comparison of standard measures. J Risk 18(2): 31–60. [CrossRef] [Google Scholar]
  • Farvacque M. 2020. Évaluation quantitative du risque rocheux : de la formalisation à l’application sur les linéaires et les zones urbanisées. Ph.D. thesis. Université Grenoble Alpes (ComUE). [Google Scholar]
  • Farvacque M, Lopez-Saez J, Corona C, Toe D, Bourrier F, Eckert N. 2019a. How is rockfall risk impacted by land-use and land-cover changes? insights from the french alps. Glob Planet Change 174: 138–152. [CrossRef] [Google Scholar]
  • Farvacque M, Lopez-Saez J, Corona C, Toe D, Bourrier F, Eckert N. 2019b. Quantitative risk assessment in a rockfall-prone area: the case study of the Crolles municipality (Massif de la Chartreuse, French Alps). Geomorphol Relief Process Environ 25(1): 7–19. [CrossRef] [Google Scholar]
  • Favier P, Eckert N, Bertrand D, Naaim M. 2014. Sensitivity of avalanche risk to vulnerability relations. Cold Reg Sci Technol 108: 163–177. [CrossRef] [Google Scholar]
  • Favier P, Eckert N, Faug T, Bertrand D, Naaim M. 2016. Avalanche risk evaluation and protective dam optimal design using extreme value statistics. J Glaciol 62(234): 725–749. [CrossRef] [Google Scholar]
  • Ferrari F, Giacomini A, Thoeni K. 2016. Qualitative rockfall hazard assessment: a comprehensive review of current practices. Rock Mech Rock Eng 49(7): 2865–2922. [CrossRef] [Google Scholar]
  • García-Hernández C, Ruiz-Fernández J, Sánchez-Posada C, Pereira S, Oliva M, Vieira G. 2017. Reforestation and land use change as drivers for a decrease of avalanche damage in mid-latitude mountains (NW Spain). Glob Planet Change 153: 35–50. [CrossRef] [Google Scholar]
  • Guerra M, Centeno M. 2012. Are quantile risk measures suitable for risk-transfer decisions? Insur Math Econ 50(3): 446–461. [CrossRef] [Google Scholar]
  • Hantz D. 2010. Évaluation quantitative de l’aléa d’éboulement en pied de falaise. In: Journées nationales de géotechnique et de géologie de l’ingénieur, Grenoble. [Google Scholar]
  • Hantz D. 2011. Quantitative assessment of diffuse rock fall hazard along a cliff foot. Nat Hazards Earth Syst Sci 11(5): 1303–1309. [CrossRef] [Google Scholar]
  • Haque U, Blum P, da Silva PF, et al. 2016. Fatal landslides in europe. Landslides 13(6): 1545–1554. [CrossRef] [Google Scholar]
  • Hungr O, Evans S, Hazzard J. 1999. Magnitude and frequency of rock falls and rock slides along the main transportation corridors of southwestern british columbia. Can Geotech J 36(2): 224–238. [CrossRef] [Google Scholar]
  • Jonkman S, van Gelder P, Vrijling J. 2003. An overview of quantitative risk measures for loss of life and economic damage. J Hazard Mater 99(1): 1–30. [CrossRef] [Google Scholar]
  • Lopez-Saez J, Corona C, Eckert N, Stoffel M, Bourrier F, Berger F. 2016. Impacts of land-use and land-cover changes on rockfall propagation: insights from the Grenoble conurbation. Sci Total Environ 547: 345–355. [CrossRef] [Google Scholar]
  • Loye A, Jaboyedoff M, Pedrazzini A. 2009. Identification of potential rockfall source areas at a regional scale using a DEM-based geomorphometric analysis. Nat Hazards Earth Syst Sci 9(5): 1643–1653. [CrossRef] [Google Scholar]
  • Mavrouli O, Corominas J. 2010. Rockfall vulnerability assessment for reinforced concrete buildings. Nat Hazards Earth Syst Sci 10(10): 2055–2066. [CrossRef] [Google Scholar]
  • McNeil AJ, Frey R, Embrechts P. Quantitative risk management: concepts, techniques and tools. In: Princeton series in finance. Princeton, NJ: Princeton University Press, 2015, revised edition. OCLC: ocn894625411. [Google Scholar]
  • Michoud C, Derron MH, Horton P, et al. 2012. Rockfall hazard and risk assessments along roads at a regional scale: example in Swiss Alps. Nat Hazards Earth Syst Sci 12(3): 615–629. [CrossRef] [Google Scholar]
  • Moos C, Fehlmann M, Trappmann D, Stoffel M, Dorren L. 2017. Integrating the mitigating effect of forests into quantitative rockfall risk analysis − Two case studies in Switzerland. Int J Disaster Risk Reduct 32: 55–74. [Google Scholar]
  • Renn O. 2008a. Concepts of risk: an interdisciplinary review − part 2: integrative approaches. GAIA Ecol Perspect Sci Soc 17(2): 196–204. [Google Scholar]
  • Renn O. 2008b. Concepts of risk: an interdisciplinary review part 1: disciplinary risk concepts. GAIA Ecol Perspect Sci Soc 17(1): 50–66. [Google Scholar]
  • United Nations International Strategy for Disaster Reduction. 2019. Global assessment report on disaster risk reduction 2019. Global Assessment Report on Disaster Risk Reduction (GAR). Geneva: UN. [CrossRef] [Google Scholar]
  • Varnes D. 1978. Slope movement types and processes. In: Schuster RL, Krizek RJ, eds. Special Report 176. − Landslides: analysis and control, Transp. Res. Board. Washington, DC: National Research Council, pp. 11–33. [Google Scholar]
  • Zheng K, Albert LA. 2019. A robust approach for mitigating risks in cyber supply chains: a robust approach for mitigating risks in cyber supply chains. Risk Anal 39(9). [Google Scholar]

Citation de l’article : Manon Farvacque, Nicolas Eckert, Franck Bourrier, Christophe Corona, Jérôme Lopez-Saez, David Toe. Évaluation quantitative du risque rocheux : de la formalisation à l’application sur les zones urbanisées ou urbanisables. Rev. Fr. Geotech. 2020, 163, 7.

Liste des figures

thumbnail Fig. 1

Exemples d’événements chutes de blocs survenus en France : (A) route départementale de Savoie, février 2014 ; (B) commune de Lumbin (département de l’Isère), janvier 2002 ; (C) axe ferroviaire du département de la Corrèze, août 2011. © J.-P. Clatot − AFP (A) ; S. Gominet − IRMa (B) ; Assali, 2015 (C).

Illustrative examples of rockfall events: (A) departmental road in Savoie, Feb. 2014; (B) Lumbin municipality (Isère department), Jan. 2002; (C) railway track in the Corrèze department, Aug. 2011. © J.-P. Clatot − AFP (A); S. Gominet − IRMa (B); Assali, 2015 (C).
Dans le texte
thumbnail Fig. 2

Évolution de l’occupation du sol du versant sud-est du Massif de la Chartreuse entre 1911 (A) et 2017 (B).

Southeastern slopes of the Chartreuse Mountains in 1911 (A) and 2017 (B).
Dans le texte
thumbnail Fig. 3

Cartographie du risque chutes de blocs pour le bâti de Crolles.

Rockfall risk for buildings currently existing in the Crolles urban area.
Dans le texte
thumbnail Fig. 4

L’histogramme représente la distribution du risque de chutes de blocs pour chaque classe de volume. Courbe en pointillé rouge : distribution du risque quand le dommage est fixé à 1 (destruction totale du bâtiment à chaque impact).

Distribution of the rockfall risk (% of the total value) for each volume class. The red dotted curve represents the risk when the physical vulnerability is set at 1 (total destruction of the building in case of impact).
Dans le texte
thumbnail Fig. 5

Cartographie du risque de chutes de blocs sur le plan urbain de Crolles pour différents scénarios d’occupation et d’usage des sols.

Distribution of the rockfall risk at Crolles for different landscape patterns.
Dans le texte
thumbnail Fig. 6

Cartographie du risque rocheux (en m2 détruits par an) dans un quartier de la municipalité de Crolles (Le Brocey) à partir de la value-at-risk (A, C) et de l’expected shortfall (B, D) pour des horizons t de 100 ans (A, B) et 1000 ans (C, D).

Map of the value-at-risk (A, C) and expected-shortfall (B, D) at Le Brocey and for temporal horizons t of 100 years (A, B) and 1000 years (C, D). Values are expressed in m2 destroyed per year.
Dans le texte

Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.

Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.

Le chargement des statistiques peut être long.