| Numéro |
Rev. Fr. Geotech.
Numéro 170, 2022
|
|
|---|---|---|
| Numéro d'article | 1 | |
| Nombre de pages | 9 | |
| DOI | https://doi.org/10.1051/geotech/2021032 | |
| Publié en ligne | 4 février 2022 | |
Letter / Lettre
The Coulomb’s Essai Legacy in Soil Mechanics
L’héritage de l’Essai de Coulomb en Mécanique des sols
Hong Kong Institute for Advanced Study, City University of Hong Kong,
83 Tat Chee Avenue,
Kowloon Tong, Hong Kong
* Corresponding author: jean.salencon@academie-sciences.fr
In 1973, in Moscow, Professor Jean Kerisel delivered a special opening lecture to the 8th International Conference of Soil Mechanics and Foundation Engineering (Kerisel, 1973). It was devoted to celebrating Charles-Augustin Coulomb’s work on the occasion of the 200th anniversary of the publication of the famous Essai sur une application des règles de Maximis et de Minimis à quelques Problèmes de Statique relatifs à l’Architecture (Coulomb, 1773)1. This Memoir stands as a most popular landmark text in civil and construction engineering and an inescapable reference in theoretical soil mechanics and geotechnical engineering textbooks. It has been the subject of a great many valuable analyses by distinguished scholars dealing either with soil mechanics (e.g., Schofield, 1998) or the stability of vaults, or both topics (e.g., Heyman, 1972). The present contribution, which takes advantage of the approaching 250th anniversary of the Essai, only intends to sketch out, recall and comment some seminal concepts introduced and formalised by Coulomb that are still retained in theoretical soil mechanics.
Résumé
En 1973, lors du 8e Congrès international de mécanique des sols et des travaux de fondation à Moscou, le Professeur Jean Kerisel a donné une conférence d’ouverture spéciale (Kerisel, 1973), qui était consacrée à célébrer l’œuvre de Charles-Augustin Coulomb à l’occasion du 200e anniversaire de la publication du célèbre Essai sur une application des règles de Maximis et de Minimis à quelques Problèmes de Statique relatifs à l’Architecture (Coulomb, 1773). Ce mémoire est une référence incontournable dans les manuels théoriques de mécanique des sols et de géotechnique. Il a fait l’objet d’un grand nombre d’analyses précieuses par d’éminents chercheurs traitant soit de la mécanique des sols (p. ex. Schofield, 1998), soit de la stabilité des voûtes, ou de ces deux sujets (p. ex. Heyman, 1972). La présente contribution, à l’approche du 250e anniversaire de l’Essai, a pour objet de rappeler et commenter quelques concepts fondateurs introduits et formalisés par Coulomb tels qu’ils sont encore utilisés aujourd’hui en mécanique théorique des sols.
Key words: Coulomb’s Memoir / Coulomb’s wedge / active and passive thrust / stability analyses / yield design
Mots clés : Mémoire de Coulomb / coin de Coulomb / poussée et butée / analyses de stabilité / calcul à la rupture
Note on an application of the rules of maximum and minimum to some statical problems, relevant to architecture. Cf. (Heyman, 1972).
© CFMS-CFGI-CFMR-CFG, 2022
1 Introduction
1.1 A short biography relevant to the Essai2
Charles-Augustin Coulomb (Fig. 1) was born in Angoulême (France) in 1736 and first educated in the Collège des Quatre-Nations in Paris, where, albeit being supposed to prepare for medical studies, he decided to study mathematics. Family discords resulted in his decision to settle in Montpellier (France), where, after presenting a geometrical Essay “Sur les courbes moyennes proportionnelles”, he was accepted to the Société Royale des sciences de Montpellier and participated in the studies there developed from 1757 till 1759. Back in Paris in 1759, he prepared the entrance examination to the École Royale du génie de Mézières3, where he was admitted in 1760, despite not being a noble stricto sensu, and graduated as First lieutenant in 1761. After a short period in Britany, Coulomb was sent to the island of Martinique (French West Indies), where he spent 8 years devoted to the building of Fort-Bourbon on the slopes of Morne Garnier. It was only in 1772, when Fort-Bourbon had almost been completed, that Coulomb was finally given permission to return to France. During his long stay in the island, Coulomb had been in charge of organizing and overseeing the earthworks and excavations necessary to the implantation of the fort, design of the vaults and retaining walls, and the quarrying of stone.
1.2 The temporality of Coulomb’s Memoir
When read at the French Academy of sciences in 1773, Coulomb’s Essai sur une application des règles de Maximis et de Minimis à quelques Problèmes de Statique relatifs à l’Architecture was probably introduced by Bossut, who had been his professor in mathematics at the École Royale du génie de Mézières and was, at the time, a member of the Academy. It is the first of Coulomb’s twenty-two scientific contributions published by the Academy. In its original form, it counts with 42 pages including figures. In the Introduction to this memoir, Coulomb clearly describes the contents and purpose of the work he dares present to the Academy: “This Memoir, written some years ago, was only intended for my own personal use in the many works I am in charge of. If I now dare to present it to the Academy, it is because it always kindly welcomes the weakest attempt, when it has utility as its object”.
Incidentally, it may be worth quoting the terms in which the Essai was briefly evoked by Delambre in Coulomb’s obituary read on January 5, 1807 at the Academy5: “His observations and the theory that had guided him made the subject of a Memoir he read at the Academy of Sciences, which earned him the title of corresponding member”, more precisely, Coulomb was elected as the corresponding member of Bossut (July 6, 1774).
In order to resist any temptation to parachronism in our comments, it is worth noting that Coulomb’s Essai was published 50 years before Cauchy’s introduction of the mathematical concepts of stress vector and stress tensor (Cauchy, 1823) and one century ahead of the series of Memoirs, where Tresca laid down the bases of the theory of plasticity (Tresca, 1864a, b, 1867a, b, 1869a, b, 1870, 1872). Galileo’s Discorsi had been published in 1638 (Galileo, 1638a, b) and Hooke’s Law, announced in the form of an anagram in 1676 (Hooke, 1676), had been revealed in 1678 (Hooke, 1678). Completing these chronological references, we may add that the concepts of Energy and Virtual velocities had been introduced and defined by Johann Bernoulli in a letter to Varignon6 in 1717, together with a restricted version of the Principle of virtual velocities limited to small rigid body motions. The full expression of this principle was only to be stated in 1788 by Lagrange, with a precise definition of the concept of resisting forces in 17977. In the Memoir, Coulomb refers to Bossut, Musschenbroek (1748), Amontons8, Euler and Bernoulli (Jakob).
2 Friction and cohesion in Coulomb’s Memoir
The cornerstone of Coulomb’s Memoir is laid down in Preliminary proposition IV, which is devoted to Friction and reads as follows (Fig. 2): “Friction and cohesion are not active forces such as gravity that always fully exerts its effect, but only coercive forces; those two forces are assessed through their limits of resistance”.
Regarding friction, Coulomb refers to Amontons and adopts the rule that “The resistance due to friction is proportional to the pressure exerted” and, in Preliminary proposition V, he defines the concept of cohesion9 in the same way as Musschenbroek (1748, p. 285)10: “Cohesion is measured by the resistance that solid bodies oppose to the direct disunity of their parts”. Unfortunately, this phenomenological definition is not precise enough and generates some confusion in the Memoir itself, such as: “Adhesion forces are equally resistant, whether they are directed parallel or perpendicular to the fracture plane”11.
 |
Fig. 2 Defining friction and cohesion in Coulomb’s Memoir. Définition du frottement et de la cohésion dans le Mémoire de Coulomb. |
3 The rationale of Coulomb’s stability analyses
The paragon of Coulomb’s rationale for the analysis of the stability of structures comes out clearly from Preliminary proposition VIII that is devoted to determining the resistance of masonry pillars (Fig. 3). It proceeds from a thought experiment where, the pillar being supposed to be cut along a section CM, Coulomb assumes momentarily that the cohesion throughout ABMC and CDM is infinite and hence considers as obvious “that the mass of the column will tend to slide along CM; from what it follows that if these two parts were united by a force of adhesion equal to the natural cohesion of the pillar, breaking this column along CM, would require the component of the weight of P along this direction to be equal to or greater than the adhesion along CM”.
With δ denoting this “natural cohesion”, it results in the condition:
 (3.1)
(3.1)
Afterwards, remarking that angle x, which defines the inclination of CM, is arbitrary, and since the column must be able to sustain the imposed load P whatever the choice of CM, Coulomb states that it is necessary to look for the minimum of (3.1) with respect to x, that is:
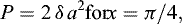 (3.2)
and concludes that “the greater weight the column may be able to sustain without breaking out is equal to 2δa2… and the angle of minimum resistance or collapse will be 45 degrees”.
(3.2)
and concludes that “the greater weight the column may be able to sustain without breaking out is equal to 2δa2… and the angle of minimum resistance or collapse will be 45 degrees”.
Incidentally, we may note that this result, when announced in the Introduction of the Memoir, suffers from an unfortunate misprint: “to determine the greatest weight the pillar can bear, it is necessary to look among all sections that whose cohesion is in equilibrium with a weight that is a minimum: since any pressure greater than that determined by this condition, would be insufficient12 to break the pillar.”
In Preliminary proposition IX (the 1st one), Coulomb wishes to take friction into account in the analysis of the same problem. He states that, in that case, the resistance to be overcome along CM is the result of the addition of the effects of cohesion and friction, (thus, considered as two independent phenomena). He refers to Amontons’ Law for friction and implements what is now currently considered as Coulomb’s Law or criterion in soil mechanics, with 1/n standing for tan φ that is used presently. Then, according to the same principles as before, he determines the value of angle x that corresponds to the minimum value for P, i.e.,
 (3.3)
which yields the maximum load that the column can sustain without breaking out.
(3.3)
which yields the maximum load that the column can sustain without breaking out.
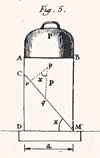 |
Fig. 3 Resistance of a masonry pillar. Résistance d’un pilier en maçonnerie. |
4 Comments on this analysis
One cannot miss noting the similarity of Coulomb’s reasoning with Galileo’s analysis of the bearing capacity of a cantilever beam (Fig. 4) in the Discorsi, where Galileo assumes that “… It is clear that, if the cylinder breaks, fracture will occur at the point B where the edge of the mortise acts as a fulcrum for the lever BC, to which the force is applied; the thickness of the solid BA is the other arm of the lever along which is located the resistance…” (Galileo, 1638b) and then writes down the equilibrium equation for the moments about point B between the applied load on the one side and the “…resistance to fracture … offered to a longitudinal pull” on the other side, to determine “… the absolute resistance of the prism BD”.
In fact, it turns out that, in Preliminary proposition VII of the Memoir, without referring to Galileo’s analysis, Coulomb also studies the resistance to fracture of a cantilever beam (Fig. 5), distinguishing two cases depending on the mechanical properties of the constituent material:
-
first, assuming the beam to be made from an “elastic wooden material”, for which he determines what we would now call the elastic limit in a monotonous loading process starting from the natural initial state;
-
then, for a beam made from a “rigid” material, for which he determines the maximum load it can sustain, exactly in the same way as Galileo, but it is noteworthy that he remarks that the solution is not satisfactory as it would require the material to be able to sustain an infinite pressure at point h. For this reason, he indicates that point h should be moved up to a point h’ to be determined.
The common feature to Galileo’s and Coulomb’s analyses lies in the fact that they both imagine a rupture mode for the structure they are considering, and write down the corresponding global equilibrium equation between the applied load and the maximum value allowed to the material resistance. It must be underscored that, obviously, no energy concept is ever referred to.
The innovation brought out by Coulomb in his analysis of the resistance of a masonry pillar is the minimization process with respect to parameter x in order to obtain the minimum value given by (3.1) for the applied load. Thus, Coulomb acknowledges the fact that the condition written in (3.1) just stands as a necessary condition, with the result that he shall look for the strongest constraint it imposes on the applied load. But he does not question the fact that the result of that strongest constraint has not actually been proven to be the maximum load sustainable by the pillar, and should only come out as an upper-bound estimate.
 |
Fig. 4 Bearing capacity of a cantilever beam (Galileo, 1638a, p. 114). Résistance d’une poutre console. |
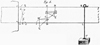 |
Fig. 5 Coulomb’s analysis of a cantilever beam. Le problème de la poutre console dans le Mémoire de Coulomb. |
5 Coulomb’s approach to earth pressure
5.1 Active and passive thrusts
In Preliminary propositions IX (the 2nd one) to XV, Coulomb analyses the stability of retaining walls subjected to earth pressure. It is clear that this problem has been one of the most important he had to deal with when constructing Fort-Bourbon in Martinique. The first step of his analysis consists in determining the pressure exerted on the wall by the earth mass it retains. As our goal here is to highlight Coulomb’s contribution to soil mechanics, we will concentrate on this first step, which may be considered Coulomb’s most seminal contribution to the topic, leaving aside the wall stability analysis issue as a whole.
In a thought experiment referring to Figure 6, Coulomb delimitates a “solid rectangular triangle CBa in the soil mass, subjected to gravity forces”, sustained by a horizontal force A and retained by cohesion and friction along Ba. He then follows a reasoning similar to the one presented in Section 4 and writes the equilibrium equation for the forces exerted along Ba, assuming that the resistance due to friction and cohesion is totally mobilized. At this point, he introduces a distinction between two cases, depending on the role played by force A. Using the words “glisser” and “couler”, i.e., slide and flow, to describe the motion of the surface:
-
either force A prevents the solid triangle from its tendency to “flowing” downwards, in which case the resisting forces along Ba shall be directed upwards;
-
or, force A tends to impulse this triangle upwards and, consequently, the resisting forces along Ba shall be directed downwards.
In other words, Coulomb brings out the physical concepts of active and passive thrust.
In his geometrical description of triangle CBa, Coulomb refers to CB = a and Ca = x; he also sticks to the notation 1/n for the friction coefficient, which results in rather complicated expressions (impaired by misprints in the Memoir). Denoting angle CBa by α and the specific weight of the soil by γ and making 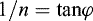 , his results for the values of force A can now be expressed respectively as:
, his results for the values of force A can now be expressed respectively as:
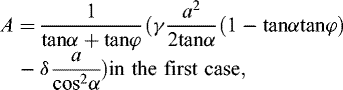 (5.1)
and
(5.1)
and
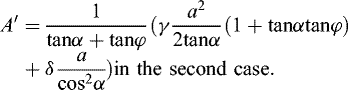 (5.2)
(5.2)
This being established, he states that13 “it has thus been proven that, when cohesion and friction both contribute to maintaining the triangle at rest, the limits to the value of a force that can be exerted at point F, perpendicular to CB, without causing the triangle to move, will lie between A and A’”.
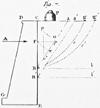 |
Fig. 6 Earth pressure on a retaining wall. Pression des terres sur un mur de soutènement. |
5.2 Coulomb’s wedge
Then, in preliminary proposition X, Coulomb remarks that the argument in the proof he has just given applies not only to such triangles as CBa, but must also be considered for any surface CBeg delimited by a curve Beg (Fig. 6). It follows that, in order that force A be sufficient to sustain the soil mass acting on CB, it is necessary to determine, among all surfaces CBeg, the one that yields the maximum value for A, which corresponds to the concept of active thrust. In the same way, passive thrust will correspond to curves such as CBe’g’ and looking for the minimum value for A’.
In fact, for the construction of Fort-Bourbon, Coulomb was essentially interested in the determination of the active thrust. Referring to experimental observations, he restricts the maximization process on A to considering triangular surfaces, which results in the maximizing value for angle α in (5.1) being equal to
 (5.3)
which, as noted by Coulomb, only depends on friction angle ϕ. From this result, Coulomb concludes that the value of force A, obtained by substituting (5.3) in (5.1), is sufficient to sustain the infinite mass CBlg.
(5.3)
which, as noted by Coulomb, only depends on friction angle ϕ. From this result, Coulomb concludes that the value of force A, obtained by substituting (5.3) in (5.1), is sufficient to sustain the infinite mass CBlg.
This is the origin of the popular Coulomb’s triangular wedge method.
5.3 Beyond triangular surfaces
Further on, in Preliminary proposition XV entitled “About surfaces of maximum pressure in fluids with cohesion”, Coulomb revisits the determination of the maximum value for force A, still considering solid surfaces but no longer assuming that they are delimited by a straight line14: “Up to now, we have assumed that the surface that produces the maximum pressure was triangular; the simplicity of the results derived from this assumption, their easy practical applicability and the desire to be useful and accessible to the Artists15, are the reasons that decided for that choice; but if we would want to determine the curve that produces the maximum pressure in an exact way, here is, I think, the way it could be done”.
Without getting into details, it may be interesting to expose the principle of the method he proposes to solve this optimization problem. Referring to (Fig. 7), the solution is based upon what Coulomb considers as an “obvious” property of the line CBg that is supposed to delimit the surface that results in the maximum pressure on CB, which reads as follows: “Let PMg be a portion of surface CBg, it is obvious that this portion shall be, among all surfaces that can be constructed from PM, the one that produces the maximum pressure on that line”. Then, introducing another such portion P’M’g, with the same property, he considers the equilibrium of portion PMP’M’. The argument consists in considering triangle MM’q as elementary, and treating it with equation (5.1), as subjected to the vertical and horizontal loads that result from the limit equilibrium of PMg and P’M’g. Although only a partial implementation of this heuristic method is given in the memoir, it can be considered a kind of “slice-method.
 |
Fig. 7 Coulomb’s proposed method for determining the maximum pressure on CB. Méthode propose par Coulomb pour déterminer la pression maximale sur CB. |
6 About Coulomb’s approach to earth pressure calculation
Similar to the analysis of the resistance of a masonry pillar, Coulomb’s approach to earth pressure calculation is based only on statical arguments. Motion is only mentioned as a description of collapse, without any genuine kinematical consideration. For example, sliding of solid rectangular triangle CBa appears just as a phenomenological description in the thought experiment presented in (Fig. 6). Nonetheless, Coulomb rightly observes that, depending on the supposed mechanical effect of the applied force A, resisting forces along Ba must be taken into account as directed upwards or downwards, which leads him, through a careful application of the rule of Maximis and minimis, to the optimal values of the geometrical parameter in either case (Fig. 6) and, consequently, to the limits imposed to force A: with upward resisting forces, maximization yields a “limit” for active thrust, while, with downward resisting forces, minimization provides a “limit” for passive thrust.
The analysis outline presented in (Fig. 7) shows that Coulomb is aware that, since he only considers triangular surfaces, his maximization process is not complete: the value he obtains for the active thrust is just an underestimation of the maximum value he is looking for. Similarly, we may say that, for passive thrust, the minimization process only results in an overestimation. But, as it can be explained by the temporality we mentioned in Section 1.2, he does not imagine and would not be able to handle any other type of static approach.
7 The Coulomb’s Memoir legacy
Roughly speaking, we can distinguish two main aspects in the legacy of Coulomb’s Essai as regards soil mechanics and geotechnics.
The first one is theoretical and concerned with the formulation of an approach to the design of structures in general, and earth-structures in particular, which states that the statical stability of the concerned structure implies, as a necessary condition, that equilibrium of the concerned structure on the one side and resistance of its constituent materials on the other side must be compatible with each other.
The second one, both theoretical and practical, is related to the determination of active and passive thrusts, stability analysis of slopes, dams, etc.
7.1 Yield design of structures
7.1.1 Governing principles
The examples given in Sections 3 and 5 illustrate the principles that govern Coulomb’s approach to the stability analysis of structures:
-
make a clear distinction between the imposed loads exerted on the structure under concern, and the resistances of the constituent materials that can be mobilized under the restrictions imposed by the limits of resistance;
-
acknowledge, as a necessary condition for stability, that equilibrium of the structure must be mathematically compatible with the constraints imposed by the constituent materials resistance;
-
expressing this necessary condition, most often in a weaker form, derive constraints to be imposed on the imposed loads as necessary conditions for the stability of the considered structure;
-
consequently, use optimization processes to tighten these constraints.
An important point to be underscored at this stage is that dealing only with necessary conditions, even if it were possible to reach the tightest ones, does not provide a full guarantee for the structure stability, which, actually, depends on various other parameters. It is also worth recalling that no energy concept is involved in the principles stated above.
Leaving aside applications to the design of vaults, masonry structures, etc., and focusing our attention onto soil mechanics issues, these principles have been extensively implemented, especially within the framework of continuum mechanics, once the concepts of stress vector, stress tensor and strength criterion had been introduced. Practically, various authors followed the same purely statical reasoning path as Coulomb, testing and checking a necessary equilibrium/resistance compatibility condition for surfaces with various shapes, which, apart from some specific cases, call for complementary statical hypotheses.
7.1.2 An energy balance viewpoint
Other applications of the principles recalled above proceed from the remark that checking a global equilibrium equation is equivalent to writing that the work by the “driving” forces exerted on the structure can be balanced by the work of resisting forces in the dual rigid body motion, under the constraints imposed by the material limit of resistance. As an example, checking the balance equation for moments is equivalent to writing the balance of works in a rigid body rotational motion. This opened the way to introducing an energy-balance, or “kinematical”, viewpoint in the approach, whose implementation often met with difficulties in expressing the work of resisting forces and could even lead to contradictory results. In fact, examples of problems addressed through such kinematical methods have shown that, in the case of constituent materials whose resistance can be properly described by a Tresca yield criterion, they can be implemented without any ambiguity. Problems arise when constituent materials with such a yield criterion as Coulomb’s criterion are concerned.
Taylor’s paper16 published in 1937 includes a review of the many solutions proposed up until that time, including Fellenius’ slip-circle17 and Taylor’s ϕ-circle methods, together with various methods of slices. They all follow statical rationales and, except for Rendulic’s (1935) log-spiral method, require complementary assumptions to make the problem statically determinate as regards the expression of the mobilized resisting forces. An extensive review of the difficulties encountered can be found in the introduction to Brinch-Hansen (1953)’s book Earth Pressure Calculation.
7.2 A theory of yield design
These difficulties can be explained and overcome through the theory of yield design18 that only refers to the basic principles of Coulomb’s analyses as listed in Section 7.1.1 and makes use of the principle of virtual work to implement a “kinematical approach” that fully complies with the fundamental laws of mechanics. It comes out then that the work of resisting forces in a potential collapse mechanism, or virtual velocity field, can be expressed and maximised unambiguously, only when this potential collapse mechanism is “orthogonal” to the resistance criterion of the constituent material19. Such virtual mechanisms or velocity fields are called “relevant” for the kinematical approach. They are the only potential collapse mechanisms in which the work by resisting forces is assigned a finite upper-bound by the resistance criterion of the constituent material. This concept of relevant virtual velocity fields in the theory of yield design is purely mathematical, only derived from the resistance criterion of the constituent material. The normality rule that defines them has nothing to do with a constitutive equation for the constituent material.
As a first example, for a purely cohesive material (Tresca’s criterion), only virtual velocity fields that induce no volume change and whose velocity jumps are tangent to the corresponding jump surfaces, are relevant. It so happens that collapse mechanisms derived from experimental intuition that are implemented in classical energy-balance kinematical approaches meet with these conditions and are relevant. This explains why they can be implemented successfully without any complementary assumption.
In the case of a material with friction and cohesion (Coulomb’s criterion), the conclusion is quite different. Relevant virtual velocity fields must comply with a condition depending on ϕ expressed on their dilatancy and their velocity jumps that must make an angle β ≥ ϕ with their jump surfaces. Such conditions are somewhat counterintuitive in view of experimental observations. In particular, they exclude the possibility of a slip-circle kinematical method being efficient without complementary assumptions. They also explain why Rendulic’s log-spiral method (that includes Coulomb’s triangular wedge method as a particular case) does not call for any complementary assumption.
It is now necessary to cast a look at the mathematical theory of plasticity and recall that, independently of the yield design rationale, it was initiated by Tresca’s Memoirs20 and built up and developed by eminent scholars with the introduction of two fundamentals concepts: the plastic yield criterion and the plastic flow rule. These concepts were associated to each other through the theory of plastic potential by Von Mises (1928) and, 20 years later, by Hill’s maximum plastic work principle (Hill, 1948, 1950). Within this framework, the plastic flow rule, as part of a constitutive equation, is derived by a normality rule from the yield criterion and said to be “associated”. The well-known lower-bound and upper-bound theorems of the theory of limit loads (limit theorems) come as direct consequences of this corpus of hypotheses.
Hence, it must be no surprise that the similarity between the mathematical formulations of the theory of yield design and the plastic theory of limits loads sometimes resulted in confounding them, e.g., (Chen, 1975), while it is worth noting that Sokolovski, when dealing with soil or granular media (Sokolovski, 1960, 1965), did not refer to the Theory of Plasticity (Sokolovski, 1955) or limit theorems, but only to Statics, thus implicitly following Coulomb’s viewpoint and Macquorn Rankine’s (1856) and Lévy’s (1867) analyses. Obviously, the confusion is of no consequence in what concerns practical applications but, unfortunately, it sometimes induces to disregard the yield design theory, which provides upper bound stability assessments, upon the argument that its relevance would depend on the physical validity of the associated flow rule as a constitutive equation. This would amount to forgetting about the basic principles of the yield design approach, which, pragmatically, is only concerned with the limit of resistance of the constituent material, whatever its physical origin and related yielding mode.
8 Conclusion
Although it is fair to say that, as a scientist, Coulomb is most widely renowned for his studies and discoveries in the fields of electricity and magnetism, the contribution to the design of structures that he presented in his first publication to the French Academy of sciences in 1773 still deserves and receives much attention from engineers and scholars in civil and construction engineering, even sometimes unbeknownst to them.
It being reminded that, whatever its sophistication, a model or method shall not be interpreted beyond its limits of relevance, this caveat can be taken into account through the introduction of well-defined safety factors properly assessed on the basis of field observations. It shall not overshadow the many merits of the yield design approach initiated from Coulomb’s insight in his 1773-Memoir. Provided the geometry of the considered structure is given and can be considered unchanged, this approach is independent of many data that often remain unknown in practice, such as the initial state of internal forces in the structure, its loading process history and, even, the complete knowledge of the behaviour of its constituent materials through constitutive equations, while all these data are required and should be available for a proper elastic or elastoplastic analysis for instance. Therefore, it is no surprise that the yield design approach still plays an important role in many design codes, e.g., as a fundamental basis of Ultimate Limit State Design (ULSD)21.
As an example, the distinction, made clear by Coulomb, between active and resisting forces may appear as a trivial issue but, in fact, it is still a major point to be addressed and correctly solved in such circumstances as the design of structures with reinforcement. Depending on the nature of the reinforcement, i.e., active or passive, its resistance shall be taken into account either in the active or the resisting term of the balance equation and the safety coefficient imposed on the nominal value of the corresponding resistance will proceed from completely different uncertainties in one case or the other. In addition, if a global safety coefficient is defined for assessing the stability of the structure, its numerical value will obviously be affected by an inappropriate assignment.
References
- Amontons G. 1699. Moyen de substituer commodement l’action du feu, à la force des hommes et des chevaux pour mouvoir les machines. Mémoires de l’Académie Royale des sciences, année 1699, pp. 112–126. https://gallica.bnf.fr/ark:/12148/bpt6k35013/f265.image.langEN. [Google Scholar]
- Brinch-Hansen J. 1953. Earth pressure calculation. Copenhagen: Danish Technical Press. [Google Scholar]
- Cauchy AL. 1823. Recherches sur l’équilibre et le mouvement intérieur des corps solides ou fluides, élastiques ou non élastiques. Bulletin de la Société Philomatique, 9–13; Œuvres complètes d’Augustin Cauchy publiées sous la direction scientifique de l’Académie des sciences…, Gauthier-Villars, Paris, 1882, 2, 2, pp. 300–304. [Google Scholar]
- Chen WF. 1975. Limit analysis and soil plasticity. Amsterdam (The Netherlands): Elsevier Scientific Publishing Company. [Google Scholar]
- Coulomb C-A. 1773. Essai sur une application des règles de maximis et minimis à quelques problèmes de statique, relatifs à l’architecture. Mémoires de Mathématique et de Physique présentés à l’Académie Royale des Sciences et lus dans ses Assemblées, vol. 7, 1776, pp. 343–382. Reprinted in Théorie des machines simples, Bachelier, Paris, 1809 & 1821. (English translation: Note on an application of the rules of maximum and minimum to some statical problems, relevant to architecture, Heyman [10], pp. 41–74). [Google Scholar]
- Delambre J-B. 1807. Éloge historique de M. Coulomb. Histoire de la classe des sciences, pp. 206–223. [Google Scholar]
- Fellenius W. 1926. Jordstatiska beräkningar med friktion of kehesion och under antagande av cirkulärcylindriska glidytor. Kungliga Väg-och Vatten-byggnadskåren 1851–1926, Festskrift, Stockholm, pp. 79–127. [Google Scholar]
- Fellenius W. 1927. Erdstatische Berechnungen mit Reibung und Kohäsion, Adhäsion, und unter Annahme kreiszylindrischer Gleitflächen. Berlin: W. Ernst und Sohn, 1939. [Google Scholar]
- Galileo Galilei. 1638a. Discorsi e dimostrazioni matematiche intorno à due nuove scienze. Leyden: Elsevier. [Google Scholar]
- Galileo Galilei. 1638b. Crew H, Salvio A, transl. Dialogues concerning two new sciences. New York: Dover, 1954. [Google Scholar]
- Hernández Morales F. 1988. Charles A. Coulomb. Mexico: Noriega Editores. [Google Scholar]
- Heyman J. 1972. Coulomb’s Memoir on Statics: an Essay in the History of Civil Engineering. Cambridge (UK). [Google Scholar]
- Hill R. 1948. A variational principle of maximum plastic work in classical plasticity. Q J Mech Appl Math 1: 18–28 [CrossRef] [Google Scholar]
- Hill R. 1950. The mathematical theory of plasticity. Oxford (G.B.): Clarendon Press. [Google Scholar]
- Hooke R. 1676. A description of helioscopes and some other instruments made by Robert Hooke, printed by T.R. for John Martyn, Printer to the Royal Society, at the Bell in St. Paul’s Church-Yard, London, p. 31. [Google Scholar]
- Hooke R. 1678. Lectures De Potentia restitutiva or of Spring, explaining the power of springing bodies, John Martyn, Printer to the Royal Society, at the Bell in St. Paul’s Church-Yard, London, p. 1. [Google Scholar]
- Kerisel J. 1973. Bicentenary of the 1773 paper of Charles Augustin Coulomb. Proceediings 8th International Conference of Soil Mechanics. and Foundation Engineering, Moscow, pp. 1–26. [Google Scholar]
- Lagrange J-L. 1788. Méchanique Analitique. À Paris, chez la Veuve Desaint, rue du Foin S. Jacques. [Google Scholar]
- Lagrange J-L. 1797. Sur le principe des vitesses virtuelles. Journal de l’École polytechnique. Ve cahier, Tome II, prairial an VI. Paris : Imprimerie de la République, pp. 115–118. [Google Scholar]
- Lagrange J-L. 1888. Œuvres complètes, vol. 11. Paris : Gauthier-Villars. [Google Scholar]
- Lévy M. 1867. Essai sur une théorie rationnelle de l’équilibre des terres fraîchement remuées et ses applications sur le calcul de la stabilité des murs de soutènement. Comptes rendus des séances de l’académie des sciences, Paris 68: 1456–1458. [Google Scholar]
- Macquorn Rankine WJ. 1856. On the stability of loose Earth. Phil Trans Roy Soc, 1857-01-01.147, pp. 9–27. [Google Scholar]
- Massarsch KR, Fellenius BH. 2012. Early Swedish Contributions to Geotechnical Engineering. ASCE GeoInstitute Geo-Congress, Oakland, March 25–29, 2012. In: Hussein MH, Massarsch KR, Likins GE, Holtz RD, eds. Full-scale Testing in Foundation Design, State of the Art and Practice in Geotechnical Engineering, Geotechnical Special Publication 227, ASCE, Reston, VA, pp. 239–256. [CrossRef] [Google Scholar]
- Musschenbroek P van. 1748. Institutiones Physicae conscriptae in usus academicos. Leyden: Lugduni Batavorum apud Samuelem Luchtmans et filium. [Google Scholar]
- Provost S. 1995. Charles Coulomb, La précision de l’ingénieur. In: Dhombres J, ed. Aventures scientifiques : Savants en Poitou-Charentes, du XVIe au XXe siècle. Les éditions de l’Actualité Poitou-Charente, pp. 72–85. [Google Scholar]
- Rendulic L. 1935. Ein Beitrag zur Bestimmung der Gleitsicherheit. Der Bauingenieur 19-20: 230–233. [Google Scholar]
- Salençon J. 1983. Calcul à la rupture et analyse limite. Paris : Presses de l’école nationale des ponts et chaussées. [Google Scholar]
- Salençon J. 2013. Yield design. London, New York: ISTE Ltd and John Wiley & Sons. [CrossRef] [Google Scholar]
- Salençon J. 2021. About Tresca’s Memoirs on the fluidity of solids (1864–1870). C R Mec 349: 1–7. [Google Scholar]
- Schofield A. 1998. The “Mohr-Coulomb” error. In: Proceedings Colloquium “Mécanique et géotechnique”, 19 May, 1998, Paris. [Google Scholar]
- Sokolovski VV. 1955. Theorie der Plastizität. Berlin: VEB Verlag Technik. [Google Scholar]
- Sokolovski VV. 1960. Statics of soil media. London: Butterworths scient. Publ. [Google Scholar]
- Sokolovski VV. 1965. Statics of granular media. Oxford: Pergamon Press. [Google Scholar]
- Taylor DW. 1937. Stability of Earth slopes. J Boston Soc Civil Eng 24(3): 337–386. [Google Scholar]
- Tresca H. 1864a. Mémoire sur l’écoulement des corps solides. Mémoires présentés par divers savants à l’Académie royale des sciences (1864), Paris, 18, 1868, pp. 733–799. [Google Scholar]
- Tresca H. 1864b. Mémoire sur l’écoulement des corps solides soumis à de fortes pressions. Comptes rendus des séances de l’académie des sciences, Paris 59: 754–758. [Google Scholar]
- Tresca H. 1867a. Mémoire sur l’écoulement des corps solides. Mémoires présentés par divers savants à l’Académie royale des sciences, Paris (1867), 20, 1872, pp. 75–135. [Google Scholar]
- Tresca H. 1867b. Sur l’écoulement des corps solides soumis à de fortes pressions. Comptes rendus des séances de l’académie des sciences, Paris 64: 809–812. [Google Scholar]
- Tresca H. 1867c. Applications de l’écoulement des corps solides au laminage et au forgeage. Mémoires présentés par divers savants à l’Académie royale des sciences, Paris (1867), 20, 1872, pp. 137–183. [Google Scholar]
- Tresca H. 1867d. Sur les applications de l’écoulement des corps solides au laminage et au formage. Comptes rendus des séances de l’académie des sciences, Paris 64: 1132–1136. [Google Scholar]
- Tresca H. 1869a. Écoulement des corps solides. Mémoire sur le poinçonnage des métaux. Mémoires présentés par divers savants à l’Académie royale des sciences (1869), Paris, 20, 1872, pp. 617–838. [Google Scholar]
- Tresca H. 1869b. Mémoire sur le poinçonnage et la théorie mécanique de la déformation des métaux. C. R. Ac. Sc., Paris 68: 1197–1201. [Google Scholar]
- Tresca H. 1870. Mémoire complémentaire sur le poinçonnage des métaux et des matières plastiques. C. R. Ac. Sc., Paris 70, 27–31. [Google Scholar]
- Tresca H. 1872. Complément au mémoire sur l’écoulement des corps solides. Mémoires présentés par divers savants à l’Académie royale des sciences, Paris, 20, pp. 281–286. [Google Scholar]
- Von Mises R. 1928. Mechanik der Festen Körper im plastisch deformablen Zustand. Göttingen Nachrichten Mathematik und Physik 1: 582–592. [Google Scholar]
- Varignon P. 1725. Nouvelle mécanique ou statique, vol. II. Paris : Claude Jombert. [Google Scholar]
Note on an application of the rules of maximum and minimum to some statical problems, relevant to architecture. Cf. (Heyman, 1972).
Cf. (Delambre, 1807), (Hernández Morales, 1988), (Provost, 1995).
(Varignon, 1725), II, ix, p. 176.
(Lagrange, 1788, 1797, 1888).
Preliminary proposition VIII: « Je suppose ici que l’adhérence oppose une égale résistance, soit que la force soit dirigée parallèlement ou perpendiculairement au plan de rupture ». This assumption is of no consequence as regards the validity of the reasoning implemented in this section of the Memoir.
« Jusqu’ici nous avons supposé que la surface qui produit la plus grande pression était une surface triangulaire ; la simplicité des résultats que donne cette supposition, la facilité de leur application à la pratique, le désir d’être utile et entendu des Artistes, sont les raisons qui nous ont décidé ; mais si l’on voulait déterminer d’une manière exacte la surface courbe qui produit la plus grande pression : voici, je crois comme on pourrait s’y prendre. »
(Taylor, 1937). It is worth noting that neither Macquorn Rankine’s paper (1856) nor Lévy’s contribution (1867) are mentioned, which both deal with the stress state within the soil mass.
(Fellenius, 1926, 1927), where earlier contributions by Petterson and Hultin are acknowledged (cf. Massarsch and Fellenius, 2012).
Cf. (Salençon, 1983, 2013).
Cf. (Salençon, 2021).
Cf. (Salençon, 2013).
Cite this article as: Jean Salençon. The Coulomb’s Essai Legacy in Soil Mechanics. Rev. Fr. Geotech. 2022, 170, 1.
All Figures
 |
Fig. 1 Charles Augustin Coulomb (1736–1806)4. Charles Augustin Coulomb (1736–1806). |
| In the text | |
 |
Fig. 2 Defining friction and cohesion in Coulomb’s Memoir. Définition du frottement et de la cohésion dans le Mémoire de Coulomb. |
| In the text | |
 |
Fig. 3 Resistance of a masonry pillar. Résistance d’un pilier en maçonnerie. |
| In the text | |
 |
Fig. 4 Bearing capacity of a cantilever beam (Galileo, 1638a, p. 114). Résistance d’une poutre console. |
| In the text | |
 |
Fig. 5 Coulomb’s analysis of a cantilever beam. Le problème de la poutre console dans le Mémoire de Coulomb. |
| In the text | |
 |
Fig. 6 Earth pressure on a retaining wall. Pression des terres sur un mur de soutènement. |
| In the text | |
 |
Fig. 7 Coulomb’s proposed method for determining the maximum pressure on CB. Méthode propose par Coulomb pour déterminer la pression maximale sur CB. |
| In the text | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




