| Issue |
Rev. Fr. Geotech.
Number 155, 2018
|
|
|---|---|---|
| Article Number | 2 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/geotech/2018006 | |
| Published online | 05 October 2018 | |
Revue / Review Article
Modélisation numérique des roches et fracturation : du continu au discontinu
Numerical rock modeling and fracturation: from continuous to discontinuous
Itasca Consultants SAS,
64 Chemin des Mouilles,
69130
Ecully, France
★ Auteur de correspondance : d.billaux@itasca.fr
Les massifs rocheux sont des milieux généralement discontinus et hétérogènes et souvent anisotropes. Leur comportement dépend aussi bien de la matrice rocheuse que des discontinuités initialement présentes dans le massif ou se formant au cours de leur histoire. La mécanique complexe qui en résulte est souvent difficilement prévisible sans l’apport des modèles numériques continus et/ou discontinus.
Abstract
Rock masses are discontinuous, heterogeneous, and often anisotropic media. Their behaviour depends as much on the rock matrix as on the discontinuities, both initially present in the rock mass or created during their evolution under any given perturbation. The resulting complex mechanics are difficult to predict without the help of continuous and/or discontinuous numerical models.
Mots clés : modélisation numérique / réseau de fractures / fragmentation / milieu continu équivalent
Key words: numerical modelling / fracture network / fragmentation / equivalent continuum
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2018
1 Introduction
Les roches, matériau cohésif dont la résistance à la compression simple est typiquement supérieure à 10 MPa (Martin et Saïtta, 2012), ont toujours été utilisées par l’homme pour ses constructions, qu’il s’agisse de grottes, creusées plusieurs dizaines de milliers d’années av. J.-C., ou plus récemment de grands travaux de génie civil (tunnels, galeries, fondations au rocher pour barrages et viaducs). L’augmentation de la taille et de la complexité des constructions du génie civil, et des exigences de sécurité de plus en plus fortes, requiert une connaissance de plus en plus fine de la roche et de son comportement pendant et après construction.
L’analyse de terrain, géologique, affleurement, carottage…, permet de connaître la structure et la composition de la roche en place, et les essais de laboratoire viennent compléter cette connaissance en mesurant les propriétés mécaniques et hydrauliques du matériau. La prédiction de son comportement durant les phases de construction et l’exploitation future ne peuvent souvent se faire qu’à l’aide d’outils numériques. Ainsi, les deux analyses, de terrain et numériques, sont complémentaires et ne peuvent être dissociées pour une compréhension complète du comportement de la roche dans son environnement.
Une bonne connaissance du comportement du massif rocheux n’est pas uniquement nécessaire dans le domaine du génie civil ; elle l’est tout autant en génie minier, en génie pétrolier et pour l’énergie au sens large du terme : géothermie, barrages hydroélectriques, stockage de CO2 et de déchets.
Nous passons ici en revue les différentes approches numériques (continues, fracturées et discrètes) permettant de traiter les problèmes à différentes échelles, et les avantages et inconvénients de chacune d’elles (Nikolić et al., 2016).
2 La roche : milieu continu équivalent
Un premier niveau d’analyse consiste à considérer la roche comme un matériau homogène continu équivalent. C’est l’approche la plus ancienne visant à la représentation du milieu rocheux fracturé sous une forme qui puisse se prêter à des calculs. Le choix du modèle de comportement et l’identification de ses paramètres sont alors des phases essentielles de la construction d’un modèle numérique, qui doivent s’appuyer sur des essais en laboratoire, des essais in situ ou des analyses inverses. Le modèle de comportement le plus utilisé dans ce contexte est celui dérivé des travaux de Hoek et Brown (1998). Des modèles de milieu continu anisotrope ont aussi été développés pour tenir compte de l’anisotropie créée par la présence de fractures.
Cette approche est suffisante dans de nombreux cas d’étude. Elle est adaptée, par exemple, à l’étude des convergences de galeries minières ou de tunnels (Fig. 1, Tran-Manh, 2014).
Les modélisations de type milieu continu équivalent (Fig. 2, Tran-Manh et al., 2015) permettent de tenir compte efficacement des grandes déformations différées et souvent anisotropes, de la ductilité des roches altérées présentes, des plans de stratification et des schistosités. Le développement de modèles de comportement spécifiques et le calage de leurs paramètres (Tran Manh et al., 2015) permettent d’approcher au plus près les mesures réalisées sur site (Fig. 3).
 |
Figure 1 Tunnel en terrain poussant. Tunnel in squeezing ground. |
 |
Figure 2 Maillage tridimensionnel FLAC3D. FLAC3D three-dimensional mesh . |
 |
Figure 3 Comparaison entre les convergences mesurées (symboles) et celles calculées (courbes). Comparison between measured (symbols) and calculated (lines) convergences. |
3 La roche dans son histoire : endommagement induit
La roche, soumise à des sollicitations diverses, s’endommage au cours de son histoire. Dans son comportement macroscopique, le matériau est endommagé lorsque la relation contrainte–déformation n’est plus linéaire. Sur la courbe contrainte–déformation classique d’un essai de compression (Fig. 4, Jaeger et Cook, 1979), quatre phases dans le comportement mécanique sont ainsi distinguées :
-
la phase de serrage, correspondant microscopiquement à la fermeture de fissures préexistantes (segment OA) ;
-
la phase pseudo-élastique où la courbe contrainte–déplacement est linéaire (segment AB) ;
-
la phase non linéaire pré-pic, ≪ endommagée », manifestation de la coalescence de fissures qui formeront les futures fractures macroscopiques (segment BC) ;
-
la phase post-pic, phase de propagation de la fracturation macroscopique.
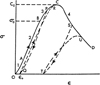 |
Figure 4 Courbe contrainte–déformation complète pour les roches. Complete stress-strain curve for rocks. |
3.1 Méthodes de résolution
Le comportement décrit ci-dessus peut être reproduit par un modèle de milieu continu équivalent muni d’une loi de comportement suffisamment sophistiquée, avec prise en compte de l’écrouissage positif (phase d’endommagement) et négatif (phase de rupture). La simulation permet alors de détecter la localisation des déformations et les débuts de la dislocation de la roche. Il est maintenant possible de s’affranchir des problèmes de sensibilité au maillage associés à de telles simulations, en utilisant des méthodes enrichies (XFEM, par exemple), qui restent néanmoins très onéreuses en temps de calcul.
La modélisation discrète, elle, décrit le massif rocheux, à l’échelle microscopique, comme un assemblage de particules. Celles-ci, sphériques ou polyédriques, sont liées par une loi de contact plus ou moins complexe (Potyondy et Cundall, 2004) qui permet de produire un comportement macroscopique émergeant, initialement continu, à partir de propriétés locales. La rupture des contacts cimentés permet ensuite de suivre la microfissuration. La coalescence des microfissures génère une fracture macroscopique qui entraîne la rupture de la roche. Le modèle gère ainsi intégralement l’évolution d’un milieu continu à un milieu divisé.
3.2 Exemples d’applications
3.2.1 Endommagement du massif autour de galeries d’un stockage
Le stockage de déchets ultimes de Wittelsheim (Alsace) se situe à une profondeur de 550 m, sous 300 m de sel gemme (Fig. 5, Camusso et Billaux, 2018). Les galeries ont été creusées selon la méthode des chambres et piliers, 24 m au-dessous d’un gisement de potasse exploité au siècle précédent. Des observations sur site ont montré un endommagement important, avec soufflage des murs, décollement de banc du toit, ainsi que de très fortes convergences de certaines allées, induites par la géométrie irrégulière des exploitations minières sus-jacentes et les concentrations de contraintes résultantes. Il s’agit ici d’évaluer l’endommagement de la roche autour de la zone excavée et ses conséquences, afin d’évaluer le fonctionnement du stockage tout au long de son exploitation : vérifier la tenue des soutènements, suivre l’évolution des perméabilités autour des galeries, anticiper les convergences des galeries pour évaluer la sûreté à long terme.
Le modèle numérique doit être capable de prendre en compte de nombreux aspects, tels que la méthode d’exploitation et le phasage des exploitations minières, mais également l’effondrement du toit de ces exploitations et la compaction des matériaux foudroyés. Ce dernier point a nécessité l’adaptation du modèle de comportement, en faisant varier le module de Young en fonction de l’état de compacité des matériaux et, par conséquent, de la porosité : le module tend à augmenter avec la diminution de la porosité de la zone. Le modèle numérique montre clairement un problème de tenue des galeries qui correspond aux observations sur site (Fig. 6, Camusso et Billaux, 2018).
 |
Figure 5 Modèle (exploitations supérieures et inférieures, et galeries de stockage). Model of upper and lower operations, and storage galleries. |
 |
Figure 6 Cartographie des convergences prédites dans les galeries du stockage. Convergence estimates in storage galleries. |
3.2.2 Fragmentation de la roche sous pression
La capacité de la modélisation discrète à suivre explicitement la propagation de la fissuration tout au long de la sollicitation permet d’analyser la fragmentation de la roche lors de l’interaction outils de coupe–roche (Rojek et al., 2011) ou lors de séquences d’explosion (Furtney, 2016), pour lesquelles la pression due à l’explosion provoque la déformation de la roche en contact avec l’explosif, et un écoulement de gaz dans les fractures nouvellement créées. La pression initiale est fonction du temps, avec une augmentation linéaire très rapide suivie d’une phase de décroissance exponentielle.
Après calage des paramètres de la loi de contact considérée, des modélisations numériques sont réalisées sur des cubes de roche de 25 cm de côté, percés d’une cavité cylindrique de 3,8 cm de diamètre et de 7,8 cm de longueur, dans laquelle l’explosion est initiée. La pression résultant de la réaction fragmente alors le bloc rocheux (Fig. 7, Furtney et al., 2016).
 |
Figure 7 Fracturation d’un bloc rocheux − modèle de 100 000 particules. Block fragments created in a 100,000-particles model. |
4 La roche, milieu fracturé
L’analyse du comportement mécanique, hydraulique ou hydromécanique d’un massif rocheux requiert une attention particulière à la caractérisation des discontinuités naturelles qui sont les zones de faiblesse du massif. Notons que leur présence peut être un atout pour la géothermie ou la production d’hydrocarbures pour lesquelles l’objectif est d’avoir une connectivité suffisante entre les fractures pour permettre une meilleure production.
La caractérisation de l’état de fracturation à partir des données brutes s’avère délicate : les informations sont soit précises mais très locales (données de puits et d’affleurements), soit globales mais peu précises (données sismiques). Deux catégories d’approches traitent ce problème :
-
des modèles numériques basés essentiellement sur des formulations mathématiques intégrant peu les connaissances géologiques disponibles. Ces modèles généralistes présentent un faible réalisme géologique ;
-
des études de terrain basées sur des observations très détaillées (uni- ou bidimensionnelles) dont la validité est souvent restreinte au site étudié.
La nature complexe et tridimensionnelle du problème implique le développement de techniques de caractérisation et de modélisation numériques spécifiques. Les exemples ci-dessous tirent profit de la caractérisation géométrique pour construire des modèles numériques aussi précis que possible. Après cette première étape, il est alors nécessaire de se pencher sur la caractérisation mécanique du réseau des fractures (élasticité, ouverture des fissures, frottement, cohésion…), qui influe fortement sur le comportement de la roche (Le Goc et al., 2014). Les réseaux de fractures discrètes (Discrete Fracture Networks [DFN]) sont utilisés différemment dans les applications minières et civiles (Lorig et al., 2015).
4.1 Exploitations minières
Dans le secteur minier, les DFN sont principalement utilisés dans le contexte des modèles de masse de roche synthétique (Synthetic Rock Mass [SRM]) pour estimer les propriétés macroscopiques de résistance et de déformation de la masse rocheuse à des fins d’analyse à l’échelle de la mine, souterraine ou à ciel ouvert. Les DFN sont également utilisés dans l’exploitation minière pour estimer les distributions de fragmentation, la stabilité des blocs du point de vue de la cinématique et l’écoulement des eaux souterraines dans les mines.
La figure 8 représente une masse rocheuse, modélisée comme un ensemble de blocs tétraédriques collés (mais détachables), séparés par des fractures secondaires. Des fractures primaires, plus persistantes, sont représentées sous la forme d’un réseau de fractures discrètes (DFN) superposé à cet assemblage. Ce type de modèle numérique permet de reproduire les phénomènes complexes qui surviennent lors de l’exploitation des cavernes (Garza-Cruz et al., 2014) par foudroyage : l’excavation progressive de la partie inférieure du massif-cible (Fig. 9, Mas Ivars et al., 2011) provoque la fragmentation et la chute contrôlées de la masse rocheuse sus-jacente. Il devient possible de gérer l’expansion progressive de la zone effondrée et la granulométrie des blocs soutirés.
 |
Figure 8 Modélisation 3DEC d’une masse rocheuse cohésive découpée par un réseau de fracture. 3DEC model of a cohesive rock mass cut by a DFN. |
 |
Figure 9 Schéma des zones de comportement de la roche dans l’exploitation de cavernes. A schematic of the mechanics of caving. |
4.2 Le rôle du fluide dans les roches − Génie civil et énergie
Les applications des DFN dans le génie civil traditionnel sont moins fréquentes que dans l’exploitation minière. Cependant, de larges recherches ont été effectuées dans le cadre du stockage des déchets nucléaires (Follin et Hartley, 2014 ; Follin et al., 2014). En effet, les propriétés hydrauliques des roches fracturées et les prévisions d’écoulement associées sont d’une importance cruciale pour le stockage des déchets nucléaires en milieu cristallin. La roche y est souvent considérée comme imperméable. L’écoulement ne se propage que dans les fractures, dont la connectivité joue alors un rôle fondamental.
En génie pétrolier et gazier, ou pour la géothermie, il est recherché de contrôler mais surtout d’améliorer les capacités d’écoulement de la roche, soit en augmentant l’ouverture des plans de fractures, soit en créant de nouvelles liaisons entre les fractures existantes par la fracturation hydraulique. Les modélisations fracturées de type 3DEC (Fig. 10, Damjanac et Cundall, 2016) sont les plus adaptées à ce genre d’analyse, car elles permettent de prendre en compte explicitement à la fois les zones de failles principales et le réseau de fractures secondaires.
 |
Figure 10 Plans de fracture connectés dans 3DEC (en haut) et contour de la pression hydraulique dans un plan de coupe horizontal lors d’une injection (en bas). Fractures in 3DEC: connected clusters (top), and fluid pressure distribution on a horizontal cross-section during an injection (bottom). |
5 Conclusions
L’ingénieur, quand il cherche à prédire le comportement d’un milieu rocheux, est confronté à la nature souvent discontinue du matériau, qui en rend la représentation plus ardue. L’expérience montre que si l’utilisation d’un ≪ milieu continu équivalent » donne des résultats réalistes dans de nombreuses circonstances, il est fondamental de repérer les situations dans lesquelles la prise en compte explicite des fractures est nécessaire pour des raisons géométriques (taille des blocs par rapport aux excavations) ou de contraintes (contraintes trop faibles pour empêcher les mouvements relatifs des blocs). L’ingénieur doit alors utiliser les méthodes discrètes pour prendre en compte la structure de l’assemblage.
Une difficulté supplémentaire survient lorsque la propagation de la fracturation, à partir d’un milieu qui peut déjà comporter des fractures naturelles, est un élément important du comportement du système étudié. C’est le cas lors de l’étude de la fragmentation (exploitation par foudroyage en masse, par exemple, ou étude de l’interaction entre roche et outil de coupe), ou pour la simulation de la fracturation hydraulique.
Les méthodes numériques permettent maintenant de simuler l’essentiel des phénomènes physiques survenant lors de l’exploitation des massifs rocheux. Il reste que, dans de nombreux cas, notre capacité de prédiction est limitée par la faible quantité de données disponibles, en regard de la complexité de ces phénomènes. Pour modéliser les roches, l’art de l’ingénieur reste basé sur un triptyque classique : faire le choix de la méthode la plus pertinente, la mettre en œuvre avec rigueur, et en interpréter les résultats de manière critique en fonction de ses limites.
Références
- Camusso M, Billaux D. 2018. Stockage de Wittelsheim. Étude de l’évolution de la subsidence en surface au-dessus du stockage. Rapport Itasca 18R-004 pour Stocamine. [Google Scholar]
- Damjanac B, Cundall P. 2016. Application of distinct element methods to simulation of hydraulic fracturing in naturally fractured reservoirs. Comput Geotech 71: 283–294. [CrossRef] [Google Scholar]
- Follin S, Hartley L. 2014. Approaches to confirmatory testing of a groundwater flow model for sparsely fractured crystalline rock, exemplified by data from the proposed high-level nuclear waste repository site at Forsmark, Sweden. Hydrogeol J 22 (2): 333–349. [CrossRef] [Google Scholar]
- Follin S, Hartley L, Rhen I, et al. 2014. A methodology to constrain the parameters of a hydrogeological discrete fracture network model for sparsely fractured crystalline rock, exemplified by data from the proposed high-level nuclear waste repository site at Forsmark, Sweden. Hydrogeol J 22 (2): 313–331. [CrossRef] [Google Scholar]
- Furtney J. 2016. PFC3D modeling of rock fragmentation by pressure pulse. Communication interne Itasca (technical memorandum 8528-03), 10 p. [Google Scholar]
- Furtney JK, Andrieux P, Hall AK. 2016. Applications for numerical modeling of blast induced rock fracture. In: Proceedings 50th US Rock Mechanics/Geomechanics Symposium, Alexandria, Virginia, ARMA- 2016–621. [Google Scholar]
- Garza-Cruz TV, Fuenzalida M, Pierce M, Andrieux P. 2014. A 3DEC-FLAC3D model to predict primary fragmentation distribution in cave mines. In: Proceedings, Third International Symposium on Block and Sublevel Caving, Santiago, Chile, pp. 146-158. [Google Scholar]
- Hoek E, Brown ET. 1998. Practical estimates of rock mass strength. Int J Rock Mech Min Sci 34(8): 1165–1186. [Google Scholar]
- Le Goc R, Darcel C, Davy P, Pierce M. 2014. Effective elastic properties of 3D fractured systems. In: Proceedings of the 1st International Conference on Discrete Fracture Network Engineering, Vancouver, Canada. [Google Scholar]
- Lorig LJ, Darcel C, Damjanac B, Pierce ME, Billaux D. 2015. Application of discrete fracture networks in mining and civil geomechanics. Min Technol 124 (4): 239–254. [CrossRef] [Google Scholar]
- Martin F, Saïtta A. 2012. Cours de travaux souterrains et de mécanique des roches. ENS Cachan, 88 p. [Google Scholar]
- Mas Ivars D, Pierce ME, Darcel C, et al. 2011. The synthetic rock mass approach for jointed rock mass modelling. Int J Rock Mech Min Sci 48(2): 219–244. [CrossRef] [Google Scholar]
- Nikolić M, Roje-Bonacci T, Ibrahimbegović A. 2016. Overview of the numerical methods for the modelling of rocks mechanics problems. Teh Vjesn 23 (2): 627–637. [Google Scholar]
- Jaeger JC, Cook NGW. 1979. Fundamentals of rocks mechanics. Chapman et Hall, 593 p. [Google Scholar]
- Potyondy DO, Cundall PA. 2004. A bonded-particle model for rock. Int J Rock Mech Min Sci 41 (8): 1329–1364. [CrossRef] [Google Scholar]
- Rojek J, Oñate E, Labra C, Kargl H. 2011. Discrete element simulation of rock cutting. Int J Rock Mech Min Sci 48 (6): 996–1010. [CrossRef] [Google Scholar]
- Tran-Manh H. 2014. Comportement des tunnels en terrain poussant. Thèse de doctorat de l’Université Paris-Est, 194 p. [Google Scholar]
- Tran-Manh H, Sulem J, Subrin D, Billaux D. 2015. Anisotropic time-dependent modeling of tunnel excavation in squeezing ground. Rock Mech Rock Eng 48 (6): 2301–2317. [CrossRef] [Google Scholar]
Citation de l’article : Daniel Billaux, Fabian Dedecker. Modélisation numérique des roches et fracturation : du continu au discontinu. Rev. Fr. Geotech. 2018, 155, 2.
Liste des figures
 |
Figure 1 Tunnel en terrain poussant. Tunnel in squeezing ground. |
| Dans le texte | |
 |
Figure 2 Maillage tridimensionnel FLAC3D. FLAC3D three-dimensional mesh . |
| Dans le texte | |
 |
Figure 3 Comparaison entre les convergences mesurées (symboles) et celles calculées (courbes). Comparison between measured (symbols) and calculated (lines) convergences. |
| Dans le texte | |
 |
Figure 4 Courbe contrainte–déformation complète pour les roches. Complete stress-strain curve for rocks. |
| Dans le texte | |
 |
Figure 5 Modèle (exploitations supérieures et inférieures, et galeries de stockage). Model of upper and lower operations, and storage galleries. |
| Dans le texte | |
 |
Figure 6 Cartographie des convergences prédites dans les galeries du stockage. Convergence estimates in storage galleries. |
| Dans le texte | |
 |
Figure 7 Fracturation d’un bloc rocheux − modèle de 100 000 particules. Block fragments created in a 100,000-particles model. |
| Dans le texte | |
 |
Figure 8 Modélisation 3DEC d’une masse rocheuse cohésive découpée par un réseau de fracture. 3DEC model of a cohesive rock mass cut by a DFN. |
| Dans le texte | |
 |
Figure 9 Schéma des zones de comportement de la roche dans l’exploitation de cavernes. A schematic of the mechanics of caving. |
| Dans le texte | |
 |
Figure 10 Plans de fracture connectés dans 3DEC (en haut) et contour de la pression hydraulique dans un plan de coupe horizontal lors d’une injection (en bas). Fractures in 3DEC: connected clusters (top), and fluid pressure distribution on a horizontal cross-section during an injection (bottom). |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




