| Issue |
Rev. Fr. Geotech.
Number 158, 2019
Fondations d'éoliennes offshore
|
|
|---|---|---|
| Article Number | 5 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/geotech/2019011 | |
| Published online | 06 September 2019 | |
Article de recherche / Research Article
Caractérisation des massifs rocheux pour le dimensionnement de pieux forés en mer
Characterization of rock masses for designing drilled and grouted offshore pile foundations
Fugro GeoConsulting,
Nanterre, France
★ Auteur de correspondance : a.puech@fugro.com
Les pieux forés et cimentés sont une solution envisagée comme fondations de structures marines dans les roches tendres à dures rencontrées au large des côtes françaises. Le dimensionnement des pieux au rocher est un exercice délicat. L’exécution de séries d’essais de cisaillement d’interface à rigidité constante (dits essais CNS) est considérée comme une approche réaliste pour estimer la résistance au cisaillement de l’interface roche-ciment sous chargements statiques et cycliques. Les essais CNS sont conditionnés par deux paramètres clés qui sont liés aux caractéristiques du massif rocheux : la rigidité du massif et la géométrie de l’interface roche-ciment. Cet article propose une approche méthodologique pour estimer ces paramètres.
Abstract
Drilled and grouted piles may be a feasible solution for founding offshore structures in weak to strong rock formations encountered offshore French coasts. Designing socket piles is a challenging task. Performing series of Constant Normal Stiffness (CNS) interface shearing tests is nowadays recognized as a suitable approach for assessing the rock-grout interface shear strength under static and cyclic loads. CNS tests require the determination of two key parameters which are linked to the rock mass properties: the rock mass stiffness and the rock-grout interface geometry. This paper focuses on a methodological approach for assessing these parameters.
Mots clés : massif rocheux / pieux ancrés au rocher / interfaces roche-coulis / essais d’interface à rigidité constante
Key words: rock masses / socket piles / rock-grout interface / CNS interface direct shear test
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2019
1 Introduction
Plusieurs sites d’implantation de fermes éoliennes au large des côtes françaises ont récemment fait l’objet de campagnes d’investigation. Les profondeurs d’eau sont de l’ordre de 15 à 60 m. Des formations rocheuses ont été rencontrées en surface ou à faible profondeur. Leur nature est très variée. Les formations composées de marnes, de calcarénites ou de craies sont généralement classifiées comme des roches très tendres à tendres sur la base de leurs résistances à la compression simple (1 < Rc < 10 MPa). Les formations de grès ou de schistes, les roches d’origine métamorphique, qui présentent des degrés d’altération et de fracturation divers sont classifiées dans les catégories de roches moyennement dures à dures (typiquement 10 < Rc < 100 MPa).
Sur les sites où la présence de roches modérément tendres à dures est prépondérante, le recours à des plates-formes métalliques (dites « jackets ») fondées sur pieux forés et cimentés est couramment envisagé pour supporter les éoliennes ou les ouvrages annexes (sous-stations, mâts météorologiques…). Les pieux sont constitués par des tubes métalliques de grand diamètre (Dext > 2 m). Ces tubes sont insérés dans des trous préforés, maintenus en position par des systèmes de centreurs et solidarisés à la roche par injection gravitaire d’un coulis de ciment dans l’annulaire. Ce type de réalisation permet de mobiliser des résistances élevées au niveau de l’interface coulis-roche et conduit à des pieux relativement courts et rigides. Leur dimensionnement est, à bien des égards, assimilable à celui des pieux terrestres ancrés au rocher. On supposera dans la suite de cet article que des dispositifs adéquats (du type « shear keys ») sont mis en place si nécessaire pour que la résistance à l’interface acier-coulis ne soit pas déterminante pour la capacité axiale du pieu.
Les méthodes récentes de dimensionnement de pieux ancrés au rocher conseillent le plus souvent de déterminer la résistance mobilisable à l’interface roche-coulis à partir d’une batterie d’essais de cisaillement d’interfaces réalisés sous rigidité normale constante (Seol et al., 2007). C’est notamment le cas des « Recommandations pour la conception et le dimensionnement des fondations d’éoliennes offshore » éditées en 2019 par le Comité français de mécanique des sols et de géotechnique (CFMS, 2019).
L’analogie entre un essai de cisaillement d’interface à rigidité constante (dit essai CNS pour Constant Normal Stiffness) et le comportement de la paroi d’un pieu ancré au rocher est discutée en section 2. La procédure utilisée pour conduire des essais CNS au laboratoire et des exemples de résultats obtenus au laboratoire 3S-R de l’université Joseph-Fourier de Grenoble sont présentés dans un article conjoint (Stavropoulou et al., 2019).
La représentativité des résultats issus d’un programme d’essais de laboratoire de type CNS requiert la détermination de deux paramètres essentiels :
-
d’une part, la géométrie de l’interface roche-coulis. Elle dépend de la nature de la roche, de la technique de forage et des caractéristiques de l’outil de forage ;
-
d’autre part de la rigidité du massif de roche. Celle-ci est fonction des propriétés mécaniques de la roche intacte mais également de la nature et de la fréquence des discontinuités à l’intérieur du massif.
L’objet de cet article est de proposer une approche méthodologique pour déterminer la géométrie de l’interface à reconstituer et la valeur de la rigidité normale à appliquer à l’échantillon en cours d’essai.
On notera qu’un troisième paramètre est requis pour conduire un essai CNS. Il s’agit de la contrainte normale initiale à appliquer à l’échantillon. Ce paramètre est généralement pris égal à la valeur de la pression moyenne appliquée par le coulis sur la paroi du tube avant prise. Il ne sera pas discuté par la suite.
Une version anglaise condensée du présent article peut être consultée dans les comptes-rendus du 17e Congrès européen de mécanique des sols et de géotechnique qui se tiendra à Reykjavik en septembre, 2019 (Puech et Quiterio-Mendoza, 2019).
2 Essais CNS de cisaillement pour simuler le comportement des interfaces roche-coulis
2.1 Essais de cisaillement d’interfaces sous contrainte normale constante
Lors d’un essai CNS, la rigidité normale appliquée sur l’interface roche-coulis est imposée comme condition aux limites.
En pratique, on maintient un rapport constant entre la contrainte normale et le déplacement normal pendant le cisaillement. Au démarrage de l’essai, une contrainte initiale σ0 (kPa) est appliquée à l’échantillon (généralement prise égale à la valeur de la pression moyenne appliquée par le coulis sur la paroi du tube avant prise). Il en résulte un déplacement normal u0 (mm). En cours de cisaillement, la contrainte normale σn est reliée au déplacement u (mm) par la relation :
 (1)
dans laquelle le paramètre k (kPa/mm) exprime la rigidité normale.
(1)
dans laquelle le paramètre k (kPa/mm) exprime la rigidité normale.
On s’attache à modifier en permanence la valeur de la contrainte normale σn de manière à maintenir la valeur de k constante et égale à une valeur présélectionnée.
On notera que les essais de cisaillement à contrainte normale imposée couramment utilisés (dits essais CNL pour Constant Normal Loading) sont des essais CNS particuliers pour lesquels la rigidité normale est nulle (k = 0) tandis que les essais à volume constant (CV) peuvent être considérés comme des essais à rigidité infinie (k→ ∞).
2.2 Analogie entre un essai CNS d’interface au laboratoire et la réponse d’une interface roche-coulis le long d’un pieu
L’interface roche-coulis entre la roche mère et le coulis de ciment peut être vue comme une discontinuité similaire à celle d’un joint rocheux. L’interface est sujette à des déplacements de cisaillement imposés par le chargement structural qui en raison de la rugosité des parois génèrent de la dilatation. Cette dilatation est contenue par la rigidité du massif environnant. Certains auteurs parlent alors de dilatance « empêchée ». Plus la rigidité du massif est grande, plus forte sera la contrainte associée à un déplacement normal donné.
Il est alors aisé de concevoir que la rupture du « joint » pourra prendre plusieurs formes dont les cas extrêmes sont :
-
le glissement relatif des parois par simple chevauchement de rigidités normales faibles ;
-
la rupture dans la roche mère dans le cas de rigidités normales fortes.
La figure 1 illustre l’analogie entre la réponse d’une interface roche-coulis le long d’un pieu et le comportement d’un échantillon cisaillé au laboratoire. Pour l’interface roche-coulis du pieu, la contrainte normale appliquée sur l’interface (c’est-à-dire la contrainte radiale le long de la paroi) est contrôlée par la rigidité radiale k du massif rocheux. Pour l’échantillon du laboratoire, la contrainte normale appliquée doit être contrôlée par la même valeur de rigidité k.
Le comportement global du système pieu-massif de roche peut être représenté par un modèle en déformation plane de l’expansion d’une cavité cylindrique dans un continuum élastique infini (Williams, 1980 ; Johnston et al., 1987). L’accroissement de contrainte normale Δσn sur l’interface roche-coulis peut s’exprimer par :
 (2)
avec :
(2)
avec :
r : rayon du forage (mm) ;
Δr : accroissement du rayon (mm) ;
Em : module élastique du massif rocheux (kPa) ;
Gm : module de cisaillement du massif rocheux ;
vm : coefficient de Poisson du massif rocheux (–) ;
L’équation (2) peut être recombinée pour faire apparaître la rigidité k (kPa/mm) :
 (3)
Dans la mesure où le rayon du forage r est très grand devant l’accroissement de rayon Δr et puisque le module élastique Em et le coefficient de Poisson vm caractérisent le massif rocheux, la rigidité normale k peut être considérée comme constante.
(3)
Dans la mesure où le rayon du forage r est très grand devant l’accroissement de rayon Δr et puisque le module élastique Em et le coefficient de Poisson vm caractérisent le massif rocheux, la rigidité normale k peut être considérée comme constante.
Une analogie avec l’essai d’expansion pressiométrique a été parallèlement proposée par Boulon et al. (1985).
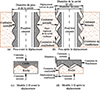 |
Fig. 1 Modèle de déplacement idéalisé d’un pieu ancré au rocher (adapté de Johnston et al., 1987). Idealized displacement behaviour of a pile socketed in rock (adapted from Johnston et al., 1987). |
3 Modélisation de la rugosité d’interface
La rugosité de l’interface roche-coulis est la conséquence de la géométrie de la cavité à la fin du forage. Cette géométrie peut être mesurée à l’aide d’outils de profilage et se présente sous la forme de profils irréguliers comme illustré sur la figure 2. La rugosité dépend de la technique de forage mise en œuvre, des caractéristiques de l’outil de forage, de la résistance de la roche et de l’état de fracturation du massif.
Convertir ces profils complexes en profils élémentaires pouvant permettre une transposition simple en laboratoire est un défi qui a fait et fait encore l’objet de développements théoriques.
Seidel et Haberfield (1995) ont introduit un modèle statistique fractal pour la caractérisation de la rugosité des joints rocheux (Fig. 3). Un profil de joint de longueur unitaire peut être caractérisé par N cordes de longueur constante r, chaque corde étant définie par sa longueur la et son inclinaison θ mesurée par rapport à l’horizontale. On suppose une distribution normale des angles des cordes avec une moyenne μθ et un écart type sθ.
Seidel et Collingwood (2001) ont poursuivi les travaux de Seidel et Haberfield (1995) sur les joints rocheux et proposé sur les mêmes bases le modèle de rugosité pour la prédiction du comportement des pieux ancrés au rocher dit de l’Université Monash (Fig. 4). Le modèle considère que la hauteur des aspérités Δr obéit à une distribution Gaussienne.
Plus récemment, Seol et al. (2007) ont mis en oeuvre de manière extensive le modèle de l’Université Monash et montré que le profil naturel irrégulier d’un forage pouvait être simplifié en un profil de rugosité régulier en dent de scie dont la hauteur équivalente des dents dépendait de la longueur de la corde.
Le tableau 1, reproduit d’après Seol et al. (2007), indique des valeurs de rugosité pour différentes natures et résistances de roches. Ces valeurs sont issues de mesures directes ou de retro-analyses d’essais de pieux bien documentés. Elles intéressent plusieurs méthodes de forage classiques. Les conclusions de Seol et al. (2007) sont que, selon sa base de données, la rugosité peut être représentée pas des dents de scie régulières avec une longueur de corde (la) de 25 mm et une hauteur d’aspérité (Δr) comprise entre 1 et 16,2 mm, ce qui corresponde à des angles de rugosité (i) compris entre 1,1° et 18,9° (Fig. 5).
On a, par ailleurs, observé que les forages en rotation mécanique réalisés en roches dures ont tendance à être relativement lisses (Kulhawy et Phoon, 1993) tandis que les forages en roches de dureté intermédiaire produiraient des rugosités plus prononcées et plus variables. Seidel et Collingwood (2001) ont réussi à proposer des limites hautes et basses pour les hauteurs d’aspérités en fonction de la dureté de la roche (Fig. 6).
Les essais CNS de cisaillement d’interface sont typiquement réalisés sur éprouvettes circulaires d’environ 100 mm de diamètre. Dans ce cas, on peut suggérer de travailler avec des longueurs de cordes de 12,5 mm permettant d’usiner quatre aspérités triangulaires sur la surface de l’échantillon de roche. Les aspérités varieront dans la fourchette de 0,5 à 3,5 mm (les angles correspondants étant compris entre 5° et 15°), ce qui permettra de couvrir les configurations de rugosité les plus courantes.
 |
Fig. 2 Relevé de rugosité sur une paroi de forage par profilage. Roughness profile of a borehole wall obtained from a caliper. |
 |
Fig. 3 Caractérisation d’un profil de longueur unité par des cordes de longueur r (Seidel et Haberfield, 1995). Characterization of a profile of unit length with chord length r (Seidel and Haberfield, 1995). |
 |
Fig. 4 Modèle de rugosité de l’université Monash. Monash University roughness model. |
Valeurs de rugosités obtenues lors du forage de cavités au rocher (Seol et al., 2007).
Quantified values of roughness for rock socket (Seol et al., 2007).
 |
Fig. 5 Profils de rugosité réguliers proposés pour les essais CNS. Regular roughness profile proposed for CNS tests. |
 |
Fig. 6 Limites empiriques de variations de la hauteur d’aspérité en fonction de la résistance à la compression simple. Empirical lower and upper limits of roughness height versus UCS. |
4 Évaluation de la raideur du massif rocheux
La rigidité normale k (kPa/mm) appliquée à l’échantillon au laboratoire doit représenter la rigidité radiale appliquée par le massif de roche à l’interface rocher-coulis. La rigidité normale est donnée par l’équation (3) dans laquelle Gm (kPa) est le module de cisaillement du massif de roche et D (mm) est le diamètre du pieu.
Les valeurs de k sont typiquement comprises entre 1000 kPa/mm pour des pieux de grands diamètres en roches tendres jusqu’à plus de 10 000 kPa/mm pour des pieux de faible diamètre en roches dures. On notera que de très fortes valeurs peuvent être obtenues pour des pieux d’essais de petit diamètre (D < 0,5 m).
Les valeurs des modules de cisaillement pour la roche intacte Gi sont relativement faciles à obtenir et ne seront pas discutées dans le cadre de ce papier. On rappelle simplement qu’elles sont accessibles par mesures directes (par exemple : essai de compression simple [Rc], essai triaxial avec ou sans mesure locale de déformations, essais Franklin, essai Brésilien) mais également par mesures indirectes (par exemple par mesure de la vitesse de propagation des ondes de cisaillement Vs, avec Gmax = f (Vs2)).
Les massifs de roche ne sont généralement pas constitués de roche intacte. Ils sont le plus souvent naturellement affectés par de l’altération et par des discontinuités (fissuration, fracturation) générées lors de l’histoire de leur formation (tectonique). Ces discontinuités peuvent faire significativement chuter la raideur apparente du massif par rapport à la rigidité de la roche intacte. Évaluer la rigidité d’un massif de roche demeure un défi pour le géotechnicien. On examine dans la suite du papier différentes approches permettant d’accéder à la valeur de Gm.
4.1 Utilisation de l’indice de qualité du la roche : RQD
L’indice de qualité de la roche (RQD) donne une estimation de la fréquence des fractures à partir de l’observation directe des carottes lors de leur extraction. Il se définit selon l’ASTM D6032-2 comme le pourcentage de roche intacte et saine récupérée dans un sondage, quelle que soit son orientation. Il s’exprime comme le rapport de la longueur cumulée de tous les morceaux de carottes intacts et sains égaux ou supérieurs à 100 mm à la longueur totale de la carotte.
Hobbs (1974) a proposé d’introduire un facteur de réduction de rigidité de masse j dont la valeur est fonction du RQD :
 (4)
(4)
Les valeurs de j sont données dans le tableau 2. Le facteur de masse chute fortement dès que le RQD devient inférieur à 75 %.
4.2 Utilisation des vitesses de propagation des ondes de compression Vs
Toujours selon Hobbs (1974), le facteur de masse peut être exprimé en fonction de la différence des vitesses de propagation des ondes de compression Vp dans le massif et sur échantillon au laboratoire. Si VF désigne la vitesse des ondes de compression mesurée in situ et VL la même vitesse mesurée longitudinalement sur un échantillon, j peut être commodément exprimé en fonction du carré du rapport VF / VL (Tab. 2). VF peut être obtenu par des mesures de sismique réfraction ou par des techniques de mesures d’ondes de surface (SASW, MASW). VL peut être mesuré au pundit ou par capteurs piezo-électriques (bender éléments).
 (5)
(5)
4.3 Utilisation des indices géologiques (RMR et GSI)
Le système de classification RMR (Rock Mass Rating) a été introduit par Bieniawski (1989). Six paramètres sont utilisés pour classifier un massif rocheux :
-
la résistance de la roche intacte telle que mesurée par exemple sur carottes à partir d’essais de compression simple (Rc) ou d’essais entre pointes (IS50) ;
-
l’indice de qualité RQD établi lors des relevés de carottage ;
-
l’espacement des discontinuités ;
-
les conditions de discontinuité ;
-
l’orientation des discontinuités ;
-
les conditions hydrogéologiques.
La classification RMR a été essentiellement développée pour être appliquée à l’ingénierie des tunnels. Les paramètres liés aux discontinuités sont assez bien accessibles en examinant des parois d’excavations de grandes dimensions. Leur détermination est plus difficile à partir de données de sondage, même si l’utilisation de techniques de logging (vidéo, ….) peut apporter des informations utiles.
L’indice GSI (Geological Strength Index) a été introduit par Hoek (1994). Il se base sur une description de la structure du matériau et des conditions de discontinuités en surface. Il se veut d’une utilisation plus générale que le RMR mais souffre lui aussi d’une difficulté de détermination sur la seule observation de parois de forage.
Le RMR ou le GSI peuvent être introduits dans des équations fournissant la valeur du module de déformation du massif Em, soit de manière directe, soit en combinaison avec d’autres paramètres tels que le module de la roche intacte Ei, la résistance à la compression simple Rc, ou encore le RQD. On donne une sélection d’équations dans le tableau 3. Le module de cisaillement du massif Gm peut être déduit de Em par l’équation (6) dans laquelle le coefficient de Poisson (v) a été mesuré ou a été dérivé de valeurs proposées par exemple par AASHTO (1989).
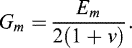 (6)
(6)
Équations permettant d’évaluer le module d’un massif rocheux.
Selection of rock mass modulus equations.
4.4 Utilisation de données dilatométriques (HPDT)
Les dilatomètres à haute pression (HPDT) sont des outils utilisés en trou de forage pour mesurer le module de cisaillement des massifs rocheux en place. Ils sont capables d’appliquer des pressions sur les parois du forage jusqu’à 20 MPa mais sont limités en expansion à un faible pourcentage de déformation de la cavité de sorte qu’ils ne permettent pas d’approcher la pression limite du milieu (comme c’est le cas des pressiomètres dans les sols). La technologie des membranes tissées semble permettre de réaliser des sondes monochambres capables d’atteindre voire dépasser les 20 MPa de pression tout en permettant des expansions de type pressiométrique (Cour et Lopes Dos Santos, 2018).
Lors d’un essai HPDT, une succession de phases de charge-décharge (boucles) est appliquée à la paroi du forage. Le module de cisaillement initial (de premier chargement) est représentatif de la réponse du massif (aux perturbations près du déchargement de la paroi dû au forage). Il intègre l’effet des discontinuités sur la rigidité d’ensemble à l’échelle de l’outil (métrique). La succession des boucles va provoquer des séries de fermetures/ouvertures des discontinuités dans le massif à proximité de la sonde. Il en résulte en général une augmentation des modules qui sont sensés tendre vers la module de la roche intacte au fur et à mesure que l’accroissement de pression « ferme » les discontinuités (Johnston et Haberfield, 1990). En pratique, il convient d’interpréter les résultats en relation avec le degré global de fracturation du massif. Certains essais peuvent être biaisés par un excès (ou un déficit) local de discontinuités à l’échelle de la sonde (Fig. 7).
 |
Fig. 7 Exemple d’essai au dilatomètre. Example of dilatometer test results. |
4.5 Évaluation à partir de sources combinées
Il n’y a pas de méthode idéale ou préférable pour la détermination de la rigidité des massifs de roche. Chaque méthode a ses limitations et doit être associée à un niveau d’incertitude élevé. C’est pourquoi il est fortement recommandé de combiner les résultats du plus grand nombre de méthodes, d’analyser les écarts, et de proposer ensuite des valeurs les plus probables encadrées par des estimations basses et hautes à partir d’un jugement d’expert articulé sur la géologie d’une part et sur les besoins de l’ingénierie, d’autre part.
Un exemple concret d’application de la philosophie décrite est illustré sur la figure 8. Cet exemple est issu d’une reconnaissance pour l’implantation d’éoliennes au large des côtes françaises.
Sur la figure 8a ont été reportées les valeurs des modules Gm obtenus dans la section haute de trois sondages groupés sur une position caractérisée par des grès durs et un degré de fracturation faible. La dispersion des valeurs est raisonnable. Elle provient à la fois des variations naturelles des propriétés du massif de roche et des écarts entre sources utilisées. Il est intéressant de noter que les mesures HPDT se situent près de la borne haute des données, ce qui suggère que les propriétés estimées se rapprochent de celles de la roche intacte. La valeur la plus probable (meilleure estimation) pour ce jeu de données est caractérisée par Gma tandis que les estimations basses et hautes ont été proposées à respectivement 0,5 Gma et 1,67 Gma (les valeurs réelles ne sont pas indiquées pour des raisons de confidentialité).
La figure 8b rassemble des données similaires obtenues sur le même site dans une zone où le grès présente des caractéristiques de résistance intacte très voisines mais un degré de fracturation nettement plus élevé. On constate que les caractéristiques de rigidité du massif sont nettement affectées. Le module de cisaillement moyen du massif chute d’environ 60 % (Gm ∼ 0.4 Gma). Cette fois, les mesures HPDT se situent vers la borne inférieure des données et on note que les modules mesurés ont tendance à croître avec le nombre de boucles de charge-décharge, suggérant une fermeture progressive des fractures avec l’augmentation de la pression appliquée sur les parois de la cavité.
 |
Fig. 8 Modules de cisaillement de masse pour des roches dures (Gma = meilleure estimation de Gm pour la formation à faible niveau de fracturation). Shear mass moduli for strong rock (Gma = best estimate of Gm for the slightly fractured formation). |
5 Conclusions
Le dimensionnement de pieux forés et cimentés ancrés dans des massifs rocheux est un exercice complexe. Des applications de cette technique sont attendues dans le cadre du développement des éoliennes marines au large des côtes françaises.
Les essais de cisaillement monotones d’interfaces roche-coulis réalisés sous conditions de rigidité normale constante sont consensuellement reconnus comme susceptibles d’apporter des éléments pertinents et fiables pour aider à la détermination du frottement ultime des pieux forés et cimentés au rocher. Un papier conjoint (Stavropoulou et al., 2019) présente des exemples de résultats obtenus au laboratoire 3SR de l’université Grenoble-Alpes qui dispose d’une machine particulièrement bien adaptée à ce type d’essai.
Le présent papier s’est focalisé sur la description des procédures destinées à fournir les paramètres clés pour la spécification des essais de cisaillement d’interface de type CNS : d’une part quelle rugosité doit-on reproduire sur les échantillons de roche au laboratoire, et d’autre part quelle valeur de rigidité normale faut-il appliquer sur l’interface roche-coulis.
Au terme des analyses sur les conditions de rugosité, il ressort un manque de données sur la rugosité réelle des parois du trou après forage. Il est vivement recommandé de collecter un maximum de données de manière à mieux cerner les effets de la nature de la roche, de la méthode de forage mise en œuvre et des caractéristiques des outils utilisés sur la rugosité du trou avant mise en place du pieu.
L’expérience acquise à ce jour permet de penser qu’il est possible de déterminer de manière réaliste la valeur du module de cisaillement de massifs de roches en prenant en compte leurs caractéristiques de fracturation. Il est recommandé de mettre en œuvre le maximum de techniques possibles pour parvenir à un jeu de données suffisamment fourni, ce qui suppose une planification efficace des opérations de reconnaissance. Un jugement d’expert restera nécessaire pour interpréter ces données sur le plan géologique et sans perdre de vue les implications en termes d’ingénierie des fondations.
La dégradation des interfaces roche-coulis sous chargements cycliques est un domaine qui reste encore largement à explorer.
Références
- AASHTO. 1989. Standard specifications for Highway Bridges. 14th edition. [Google Scholar]
- ASTM D 6032-2 Standard test method for determining rock quality designation (RQD) of Rock Core. [Google Scholar]
- Bieniawski ZT. 1989. Engineering rock mass classifications. New York: Wiley. [Google Scholar]
- Boulon M, Plytas C, Foray P. 1985. Interface behavior prediction of the lateral shaft friction along piles and anchors. Rev Fr Geotech 34. [Google Scholar]
- CFMS. 2019. Recommandations pour la conception et le dimensionnement des fondations d’éoliennes offshore. Disponible sur www.cfms-sols.org. [Google Scholar]
- Cour F, Lopes Dos Santos A. 2018. Sonde monocellulaire innovante pour la réalisation d’essais d’expansion de cavité cylindrique. In : Journées nationales de géotechnique et de géologie de l’ingénieur. Champs-sur-Marne. [Google Scholar]
- Diederichs MS, Kaiser PK. 1999. Stability of large excavations in laminated hard rock masses. Int J Rock Mech Mining Sci 36: 97–117. [CrossRef] [Google Scholar]
- Gardner WS. 1987. Design of drilled piers in the Atlantic Piedmont. Foundations and excavations in decomposed rock of the Piedmont province. New York, UK: ASCE. pp. 62–86. [Google Scholar]
- Hobbs NB. 1974. Factors affecting the prediction of settlements of structures on rock. Settlement of structures. Conference organised by British Geotechnical Society, Cambridge held. pp. 590–596. [Google Scholar]
- Hoek E. 1994. Strength of rock and rock masses. ISRM News J 2(2): 4–16. [Google Scholar]
- Hoek E, Brown ET. 1997. Practical estimates of rock mass strength. Int J Rock Mech Mining Sci Geomech 34(8): 1165–1186. [CrossRef] [Google Scholar]
- Hoek E, Diederichs MS. 2006. Empirical estimation of rock mass modulus. Int J Rock Mech Mining Sci 43: 203–215. [CrossRef] [Google Scholar]
- Johnston IW, Haberfield CM. 1990. Pressuremeter interpretation for weak rock. Proceedings 24th Annual Conference Engineering Group of the Geological Society, pp. 85–90. [Google Scholar]
- Johnston IW, Lam TSK, Williams AF. 1987. Constant normal stiffness direct shear testing for socketed pile design in weak rock. Geotechnique 37: 83–89. [CrossRef] [Google Scholar]
- Kulhawy FH, Phoon KK. 1993. Drilled shaft side resistance in clay soil to rock. Proceedings of the Conference on Des. and Perform. of Deep Found. 38. [Google Scholar]
- Lee MH, Cho CH, Yoo HK, Known HK. 2004. A study on the surface roughness of drilled shaft into rock in Korea. In: Proceedings of the Korean Society of Geotechnical Engineering Conference. Seoul 2003. [Google Scholar]
- Mitri HS, Edrissi R, Henning J. 1994. Finite element modeling of cablebolted stopes in hard rock ground mines. SME annual meeting. Albuquerque, USA. pp. 94–116. [Google Scholar]
- Nam MS. 2004. Improved design for drilled shafts in rock. PhD dissertation. University of Houston. [Google Scholar]
- Nicholson GA, Bieniawski ZT. 1990. A nonlinear deformation modulus based on rock mass classification. Int J Min Geol Eng 8(3). [Google Scholar]
- Puech A, Quiterio-Mendoza B. 2019. Characterization of rock masses for designing drilled and grouted offshore pile foundations, Proceedings of the 17th European Conference on Soil Mechanics and Geotechnical Engineering, Reykjavik. [Google Scholar]
- Seidel JP, Collingwood B. 2001. A new socket roughness factor for prediction of rocket socket shaft resistance. Can Geotech J 38: 138. [CrossRef] [Google Scholar]
- Seidel JP, Haberfield CM. 1995. Towards an understanding of joint roughness. Int J Rock Mech Rock Eng. [Google Scholar]
- Seol H, et al. 2007. Shear load transfer for rock-socketed drilled shafts based on borehole roughness and geological strength index. Int J Rock Mech Mining Sci 45: 848–861. [CrossRef] [Google Scholar]
- Serafim JL, Pereira JP. Consideration of the geomechanical classification of Bieniawski. In: Proceedings of International symposium on Engineering Geology and Underground Construction, vol. 1. Rotterdam: A.A. Balkema, 1983, II, pp. 3–44. [Google Scholar]
- Sonmez H, Gokceoglu C, Ulusay R. 2004. Indirect determination of the modulus of deformation of rock masses based on the GSI system. Int J Rock Mech Mining Sci 41(5): 849–857. [CrossRef] [Google Scholar]
- Stavropoulou E, Sharma A, Dano C, Boulon M, Briffaut M, Emeriault F, Puech A. 2019. Characterization of rock grout interfaces for foundations of offshore wind turbines. Proceedings of the XVII European Conference on Soil Mechanics and Geotechnical Engineering. Reykjavik. [Google Scholar]
- Stavropoulou E, Dano C, Boulon M, Briffaut M, Sharma A, Puech A. 2019. Résistance au cisaillement d’interfaces roche-coulis représentatives de pieux offshore. Rev Fr Geotech 158: 6. [CrossRef] [Google Scholar]
- Williams AF. 1980. The design and performance of piles socketed into weak rock. Ph.D. Thesis. Melbourne: Monash University. [Google Scholar]
- Zhang L, Einstein HH. 2004. Using RQD to estimate the deformation modulus of rock masses. Int J Rock Mech Mining Sci 41(2): 337–341. [CrossRef] [Google Scholar]
Citation de l’article : Alain Puech, Bibiana Quiterio-Mendoza. Caractérisation des massifs rocheux pour le dimensionnement de pieux forés en mer. Rev. Fr. Geotech. 2019, 158, 5.
Liste des tableaux
Valeurs de rugosités obtenues lors du forage de cavités au rocher (Seol et al., 2007).
Quantified values of roughness for rock socket (Seol et al., 2007).
Équations permettant d’évaluer le module d’un massif rocheux.
Selection of rock mass modulus equations.
Liste des figures
 |
Fig. 1 Modèle de déplacement idéalisé d’un pieu ancré au rocher (adapté de Johnston et al., 1987). Idealized displacement behaviour of a pile socketed in rock (adapted from Johnston et al., 1987). |
| Dans le texte | |
 |
Fig. 2 Relevé de rugosité sur une paroi de forage par profilage. Roughness profile of a borehole wall obtained from a caliper. |
| Dans le texte | |
 |
Fig. 3 Caractérisation d’un profil de longueur unité par des cordes de longueur r (Seidel et Haberfield, 1995). Characterization of a profile of unit length with chord length r (Seidel and Haberfield, 1995). |
| Dans le texte | |
 |
Fig. 4 Modèle de rugosité de l’université Monash. Monash University roughness model. |
| Dans le texte | |
 |
Fig. 5 Profils de rugosité réguliers proposés pour les essais CNS. Regular roughness profile proposed for CNS tests. |
| Dans le texte | |
 |
Fig. 6 Limites empiriques de variations de la hauteur d’aspérité en fonction de la résistance à la compression simple. Empirical lower and upper limits of roughness height versus UCS. |
| Dans le texte | |
 |
Fig. 7 Exemple d’essai au dilatomètre. Example of dilatometer test results. |
| Dans le texte | |
 |
Fig. 8 Modules de cisaillement de masse pour des roches dures (Gma = meilleure estimation de Gm pour la formation à faible niveau de fracturation). Shear mass moduli for strong rock (Gma = best estimate of Gm for the slightly fractured formation). |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




