| Issue |
Rev. Fr. Geotech.
Number 171, 2022
|
|
|---|---|---|
| Article Number | 4 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/geotech/2022005 | |
| Published online | 21 July 2022 | |
Article de recherche / Research Article
Une méthode d'interprétation des essais effectués sur site sur des boulons à ancrage réparti sollicités en traction
A method for interpreting field tests on fully grouted bolts under tension
Cerema Méditerranée, 30 rue Albert Einstein, CS 70499, 13593 Aix-en-Provence, France
* Auteur de correspondance: jean-francois.serratrice@cerema.fr
Les boulons à ancrage réparti sont utilisés dans le domaine des soutènements et des renforcements des sols et des roches. Leur comportement s'étudie au moyen d'essais d'arrachement ou par auscultation de boulons instrumentés. Une méthode d'interprétation de ces différents types d'essais est proposée. Fondée sur un calcul au module de réaction, elle met en jeu un boulon pris individuellement et sollicité dans sa direction axiale. La méthode a été appliquée à l’interprétation d'une dizaine d'essais d'arrachement et de cinq boulons radiaux instrumentés mis en place en tunnel ou dans une paroi clouée, d'après des données issues de la littérature. L'article présente une partie des résultats de cette étude en commençant par un aperçu des travaux de recherche effectués dans ce domaine. La méthode de calcul est ensuite présentée. Les exemples d'interprétation de deux essais d'arrachement sont commentés alors, pour lesquels trois lois de réaction sont mises en œuvre (bilinéaire, exponentielle et trilinéaire). Deux procédures sont proposées pour effectuer le choix de la loi de réaction et l'identification de ses paramètres. La méthode a été appliquée ensuite à un boulon radial instrumenté mis en place en tunnel.
Abstract
Fully grouted bolts are used as reinforcement elements in rock or soil masses. Their behaviour is studied by means of pull-out tests or instrumented bolt monitoring. A method is proposed to analyse these different types of tests. It is based on a reaction modulus calculation and involves a single axially loaded bolt. The method was applied to the interpretation of ten pull-out tests and five instrumented radial bolts installed in a tunnel or in a nailed wall, based on data from the literature. The paper presents some of the results of this study, starting with an overview of the research work done in this area. The calculation method is then presented. The interpretation of two pull-out tests is then commented on, for which three reaction laws are implemented (bilinear, exponential and trilinear). Two procedures are proposed for choosing the reaction law and identifying its parameters. The method was then applied to an instrumented radial bolt installed in a tunnel.
Mots clés : boulon à ancrage réparti / essai d'arrachement / boulon instrumenté / loi de réaction / tunnel
Key words: fully grouted bolt / pull-out test / instrumented bolt / reaction law / tunnel
© CFMS-CFGI-CFMR-CFG, 2022
1 Introduction
Les boulons à ancrage réparti constituent des éléments de renforcement des massifs rocheux ou des massifs de sols. Ils ont fait leur apparition dans le domaine minier il y a une centaine d'années. Leur utilisation s'est progressivement étendue dans divers domaines du génie civil pour composer le soutènement de parois d'excavations ou assurer la stabilisation de pentes. Ils figurent parmi les techniques essentielles de soutènement des tunnels réalisés par les méthodes conventionnelles. Ils sont à la base des techniques de clouage des sols. Ils servent aussi d'ancrage pour maintenir les dispositifs de protection contre les chutes de blocs.
Les recommandations GT6R4F1 « Technologie du boulonnage » (AFTES, 2014) décrivent des configurations technologiques des boulons à ancrage réparti et de leur scellement dans le domaine des tunnels. Ce type de boulonnage consiste à sceller des barres métalliques (ou autres) sur toute leur longueur dans un trou de forage. Le produit de scellement est généralement de la résine, du mortier de ciment ou du coulis. Les recommandations GT30R1F1 « Conception et guide de dimensionnement du boulonnage radial en tunnel » (AFTES, 2017) complètent les précédentes et proposent des méthodes d'analyse et de calcul applicables aux travaux souterrains.
La norme européenne NF EN 14490 « Exécution des travaux géotechniques spéciaux – Clouage » (AFNOR, 2010) énonce les principes généraux pour la construction, les essais, le suivi et les contrôles d'exécution des ouvrages en sol cloué et son domaine d'application (stabilisation des pentes anciennes ou récentes et de leurs parements dans les sols ainsi que des ouvrages de soutènement anciens, des talus, des parois de tunnels anciens et nouveaux). Les clous y sont définis comme des dispositifs de renforcement mis en place dans le terrain par forage et injection d'un coulis de scellement et qui mobilisent un frottement sur toute leur longueur.
Pour schématiser, le terme de clou est employé dans les renforcements des sols, alors que celui du boulon s'entend plutôt dans les renforcements des roches et des roches tendres, en particulier dans le domaine des tunnels. Les éléments constitutifs de ces clous ou ces boulons et le terrain sont séparés par deux interfaces: l'interface tige-scellement et l'interface scellement-terrain. À part les cas particuliers de rupture du terrain, du produit de scellement ou de la tige, la capacité de renforcement des boulons ou des clous tient aux performances des interfaces et en particulier de l'interface la moins résistante, en relation avec la nature du terrain encaissant ou la nature du produit de scellement (Li et Stillborg, 1999).
Des essais réalisés sur les ouvrages servent à mesurer les caractéristiques des boulons à ancrage réparti ou servent à vérifier leurs capacités mécaniques. Cette étude est dédiée à l'interprétation de tels essais, qu'il s'agisse d'essais d'arrachement, de boulons instrumentés en tunnel, boulons radiaux ou boulons de front, ou d'inclusions disposées dans les parois clouées. L'étude se place au niveau de l'interprétation de données expérimentales recueillies au moyen d'essais de boulons ou de clous dans le cadre du renforcement des massifs pour des ouvrages de soutènement. Elle ne vise pas à modifier les pratiques opératoires en usage pour mener à bien la réalisation des essais (normes d'essais NF P 94-242-1 ou XP P 94-444). Elle ne vise pas à changer les pratiques de conception des ouvrages telles que décrites dans les textes GT30R1F1 (AFTES, 2017) ou NF EN 14490 (AFNOR, 2010). Sur le plan expérimental, la méthode d'interprétation proposée vise à donner une description plus détaillée de la réponse d'un boulon, au-delà de la courbe effort-déplacement mesurée en tête. Il s'agit en particulier de décrire la déformée de la tige au cours des chargements, ou de décrire les réponses sous différents types de chargements.
La méthode d'interprétation des essais s'appuie sur une modélisation du comportement des boulons sollicités en traction, qui est fondée sur un calcul au module de réaction. Une solution numérique est recherchée. Ce type de calcul a été privilégié car il permet de modéliser divers modes de sollicitation du boulon. Plusieurs lois de réaction sont envisagées (loi bilinéaire, exponentielle ou trilinéaire).
Pour mener à bien ce travail, la méthode a été appliquée à l’interprétation d'une dizaine d'essais d'arrachement et de cinq boulons radiaux instrumentés mis en place en tunnel ou dans une paroi clouée, d'après les travaux de différents auteurs. La tâche n'est pas aisée, car les données disponibles dans la littérature sont très rares et peu documentées. Elles sont diverses, comme en témoigne la nature des tiges mises en œuvre (barres, câbles, torons, fibres) et scellées sur toute leur longueur. En vue d'accompagner l'identification des paramètres de la loi de réaction axiale, deux méthodes « tangentes » ont été développées, qui s'appuient sur la solution élastique du problème. Ces deux méthodes s'accordent au fait que, dans les essais d'arrachement, une partition des réponses s'opère en fonction de l'amplitude du déplacement en pied.
L'article commence par une brève revue des travaux publiés dans la littérature. Puis, les principaux items de la méthode calcul sont exposés. Les exemples d'interprétation de deux essais d'arrachement sont présentés et commentés. Les deux procédures d'aide pour le choix de la loi de réaction et l'identification de ses paramètres sont décrites. Puis, la méthode est appliquée au calcul de la réponse d'un boulon radial instrumenté mis en place en tunnel.
2 Boulons à ancrage réparti sollicités en traction
La réalisation d'un boulon à ancrage réparti consiste à effectuer un trou par forage dans le terrain, puis insérer la tige du boulon dans ce trou et la fixer au moyen d'un produit de scellement. Ce produit est un coulis de ciment ou une résine. Il est injecté dans l'espace annulaire entre la tige et le terrain sur toute la longueur de la tige. Il se place ainsi entre deux interfaces: l'interface tige-scellement et l'interface scellement-terrain. La tige est constituée par une barre pleine ou un câble en acier ou une barre en fibre de verre. Un autre procédé consiste à foncer une tige métallique creuse dans le terrain puis injecter le produit de scellement par l'intérieur de ce tube (boulon autoforeur). Selon la nature du boulon et sa fonction, la tige est accompagnée par divers accessoires disposés en tête qui prennent part au soutènement (plaque d'appui, écrou). D'autres accessoires servent à la mise en place de la tige (gaine géotextile, centreurs, canules d'injection, évents).
Dans les applications en tunnel ou dans les parois clouées, les boulons sont sollicités par les déplacements du massif auxquels ils doivent s'opposer. Dans ce mouvement de convergence du massif vers l'excavation, quand l'axe du boulon est dirigé dans la direction principale des déplacements, la tige est sollicitée majoritairement en traction et les cisaillements transversaux sont faibles. Quand ce mouvement n'est pas hétérogène (en l'absence de discontinuités), le terrain a tendance à expulser le boulon côté tête et le terrain retient le boulon côté pied, assurant le double ancrage du boulon dans sa partie proche de la paroi ainsi qu'en profondeur (Freeman, 1978). Ces deux longueurs d'ancrage sont séparées par un point neutre. La contribution de ces deux tronçons est assurée par des cisaillements qui sont mobilisés le long des interfaces ou dans le scellement. Un exemple est commenté au paragraphe 6. Pour simplifier, la solution du problème est recherchée en combinant l'équilibre des efforts linéiques de cisaillement et des efforts de traction dans la tige avec une loi d'interface longitudinale, ou loi de réaction, qui établit le rapport entre les cisaillements et le déplacement relatif du boulon et du terrain.
Les propriétés de la loi de réaction sont obtenues au moyen d'essais d'arrachement réalisés dans le site et dans des conditions représentatives du fonctionnement du boulon. Ces essais s'exécutent en appliquant un effort ou un déplacement contrôlé en tête jusqu'à atteindre la rupture du scellement, si possible (AFNOR, 1993, 2002), pour aboutir à la courbe donnant l'effort de traction en fonction du déplacement axial en tête. La rupture s'explique par un processus de décohésion qui gagne progressivement le long de l'interface en partant de la tête du boulon dans les boulons de longueur courante (Li et Stillborg, 1999). Au début du chargement, les tractions dans la tige et les cisaillements sur l'interface décroissent de la tête du boulon vers son extrémité (Farmer, 1975). Puis, avec la progression de la décohésion, la répartition des contraintes de cisaillement sur l'interface, les déplacements et les efforts dans le boulon continuent à évoluer au fil du chargement avec le même profil décroissant depuis la tête. À ce titre, les boulons courts présentent un comportement différent des boulons longs.
Les mécanismes à l'œuvre pendant le chargement des boulons mettent en jeu de nombreux paramètres: nature, état et comportement du terrain, état des contraintes environnant, champ des déplacements du terrain, caractéristiques du boulon (longueur, diamètre, diamètre du forage), nature et comportement des constituants du boulon, conditions de mise en place (pression d'injection, temps de prise), le temps, etc., sans compter l'hétérogénéité, l'anisotropie et la variabilité du terrain. Les essais d'arrachement sur site présentent toujours une très grande dispersion (Freeman, 1978; Zhang et al., 2009; Salcher et Bertuzzi, 2018). Par la suite, différents facteurs agissent sur les propriétés des boulons, qui sont liés à la progression des travaux (poursuite de l'excavation, modification des chargements ou qui apparaissent à long terme (corrosion, vieillissement, fatigue, fluage, etc.).
Pour simplifier, l'étude du comportement du boulon peut être ramenée aux contributions de la tige et celle de l'interface active (l'interface tige-scellement dans les terrains de type roche et l'interface scellement-terrain dans les terrains de type sol). Généralement, le comportement de la tige est supposé linéaire élastique (Farmer, 1975; Stille et al., 1989; et d'autres ensuite). Puis, en tous points, le comportement de l'interface est gouverné par la contrainte de cisaillement τ et la pression normale σ, auxquelles sont associées les déformations γ et ε (Cai et al., 2004a) ou des déplacements u et v (Blanco-Martin et al., 2013). Toutefois, la compréhension du comportement du boulon ne peut être acquise sans une connaissance précise de la distribution de la contrainte de cisaillement sur l'interface et des efforts dans la tige à toutes les étapes du chargement.
En pratique, les paramètres comportementaux caractéristiques de l'interface ne sont pas directement accessibles à la mesure sans l'aide d'une instrumentation spécifique. La recherche d'une représentation des courbes effort-déplacement (u, N) mesurées en tête pendant les essais d'arrachement demeure sous-déterminée. La courbe d'arrachement ne permet pas d'identifier tous les paramètres de la loi de réaction axiale. Aussi, différentes démarches ont été entreprises pour améliorer la connaissance du comportement des boulons à ancrage réparti à partir des comportements de leurs éléments constitutifs et de leurs interfaces. Ren et al. (2010), Blanco-Martin et al. (2013, 2016), Chen et al. (2015), Chen et al. (2019) retracent l'historique de ces travaux expérimentaux et théoriques. En associant les réponses normales et tangentielles autour de l'interface, les travaux récents appellent à suivre une démarche combinée expérimentale, analytique et numérique et développer des dispositifs expérimentaux spéciaux (Blanco-Martin et al., 2013, 2016; Bost et al., 2018).
À défaut de mettre en œuvre des lois d'interface complètes avec des relations cisaillement-glissement de la forme τ(σ, u, v), de nombreuses analyses du comportement des boulons à ancrage réparti ont porté sur des lois empiriques τ(u) réduites à la seule composante tangentielle de l'interface (Farmer, 1975; Li et Stillborg, 1999; Ren et al., 2010; Zhu et al., 2011). Diverses formes de loi ont été proposées (bilinéaires, exponentielles, hyperboliques, etc.). Parmi celles-ci figure une relation cisaillement-glissement τ(u) trilinéaire associant trois phases successives: (1) élastique, (2) de décohésion de l'interface, suivie par (3) un palier de résistance résiduelle portant la marque d'un frottement résiduel (Benmokrane et al., 1995; Cai et al., 2004a; Guan et al., 2007; Xiao et Chen, 2008; Ren et al. 2010; Blanco-Martin et al., 2011; Liu et al., 2017; Chen et al., 2019). D'autres formulations se fondent sur une description explicite des courbes τ(u) mesurées sur des tronçons courts en laboratoire (Ma et al., 2013; Chen et al., 2020).
D'autres approches préconisent l'intégration du boulon dans un champ de déplacement calculé autour d'un tunnel (Stille et al., 1989; Indraratna et Kaiser, 1990; Oreste et Peila, 1996; Li et Stillborg, 1999; Cai et al., 2004b; Jiang et al., 2004; Guan et al., 2007; Oreste, 2008; Carranza-Torres, 2009; Jalalifar, 2011; Wen et al., 2014; Ranjbarnia et al., 2016; Nguyen et al. 2018; Wang et al., 2020). Avec ces méthodes analytiques ou numériques, un calcul sans boulonnage fournit le déplacement libre du massif, puis, après boulonnage, le calcul fournit la réponse des boulons et celle du massif renforcé.
D'autres travaux concernent le clouage des sols (Schlosser et Guilloux, 1981; Recommandations Clouterre, 1991; plus récemment, Zhang et al., 2009; Sivakumar-Babu et Singh, 2010; Zhu et al. 2011; Zhao et al., 2014; Moayed et Namaei, 2020; et d'autres). Le frottement commande pour l'essentiel le comportement de l'interface scellement-terrain. Il prend plus d'importance dans les sols granulaires grossiers que dans les sols argileux, en lien avec les effets de dilatance et de confinement du sol. La résistance s'exprime avec le frottement latéral unitaire limite qs dont la mesure repose sur des essais d'arrachement (Norme NF P 94-270 « Calcul géotechnique – Ouvrage de soutènement – Remblais renforcés et massifs en sol cloué »; AFNOR, 2020). Ce paramètre intègre les conditions de mise en place, l’état de contrainte initiale dans le sol et la géométrie de l’inclusion et du forage. L'expérience montre une augmentation du diamètre initial du forage et une diffusion du coulis dans le sol environnant lorsque le coulis est injecté sous une forte pression. Enfin, plus encore qu'avec les massifs rocheux, les inclusions sont disposées pour fonctionner en groupe. Dans les sols cloués, la mobilisation du frottement latéral sol-clou s'effectue souvent au moyen d'une loi bilinéaire (Frank et Zhao, 1982; Clouterre, 1991).
Dans la pratique des projets, les essais standards servent à mesurer l'effort d'arrachement ultime au moyen de chargements menés à la rupture (AFNOR, 1993, AFNOR, 2002), ce qui répond aux objectifs des études. Néanmoins, une description de la déformée de la tige au cours des chargements élargit la base d'interprétation d'un essai. Dans ce sens, l'étude du comportement des boulons en situation réelle conserve un intérêt, comme en témoigne la littérature à laquelle il est fait référence ici. Dans la suite, une méthode de calcul est proposée pour décrire la courbe d'arrachement d'un boulon à ancrage réparti et décrire la déformée de la tige à chaque étape du chargement, à partir des mesures recueillies à l'aide d'un essai réalisé sur site. Deux procédures sont proposées pour accompagner l'identification des paramètres en jeu.
3 Comportement des boulons sollicités en traction
3.1 Méthode de calcul
Il est proposé de simuler le comportement des boulons sollicités en traction au moyen d'une méthode de calcul au module de réaction axial. Scellé au terrain, le boulon à ancrage réparti est chargé dans la direction de son axe par des efforts extérieurs. La direction axiale est notée x. La tige en acier ou en fibre de verre de diamètre da (ou de section Aa) et de longueur L est scellée dans un forage de diamètre ds. Dans cette approche simplifiée, l'interaction entre le boulon et le terrain se calcule en exprimant les déformations de la tige et l'équilibre des forces qui s'exercent dans la direction x. (Farmer, 1975; Cai et al., 2004a, 2004b; Zhu et al., 2011; Jalalifar, 2014; Wen et al., 2014; Chen et al., 2019; et d'autres).
À l'abscisse x de la tige, le déplacement axial et l'effort normal sont notés ux et Nx. En supposant que le comportement de la tige est linéaire élastique et Ea son module d'Young, la déformation axiale εx = dux/dx est proportionnelle à la contrainte normale σx = Nx/Aa, soit εx = σx/Ea. D'où: (1)
(1)
Le long d'un tronçon infinitésimal du boulon, l'équilibre des forces se traduit par l'égalité dNx = ‐Fx dx, où l'accroissement de l'effort normal Nx s'oppose à l'effort de cisaillement linéique Fx développé sur la longueur dx du scellement (Farmer, 1975; Li et Stillborg, 1999). Ainsi: (2)
(2)
Cet effort linéique Fx est une fonction du glissement relatif Δu, qui apparaît sur l'interface active (entre le boulon scellé et le terrain ou entre la tige et le produit de scellement) et qui est égal à Δu = ur – ux, où ur est le déplacement du terrain. Il est défini par la loi de réaction axiale qui régit l'interaction entre le boulon et le terrain sur cette interface active et qui porte les paramètres comportementaux du problème: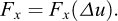 (3)
(3)
Enfin, le déplacement du massif ur est une fonction de l'abscisse x: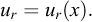 (4)
(4)
Les chargements s'appliquent aux deux extrémités de la tige sous la forme de conditions aux limites en force ou en déplacement et sous la forme de charges réparties le long de l'interface de scellement. Les variables x, ux et Nx s'expriment sous les formes normalisées X = x/L, Y1 = ux/L et Y2 = Nx/(AaEa) pour aboutir au système d'équations: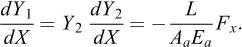 (5)
(5)
Après avoir établi les conditions aux limites, le déplacement du terrain et la loi de réaction, le système d'équations (5) est résolu par une méthode de calcul numérique (méthode de tirs multiples; module BVPMS de la bibliothèque logicielle IMSL (2014) qui est intégrable dans différents outils de calculs numériques). L'annexe A rappelle les principaux éléments de la solution élastique représentant un essai d'arrachement.
3.2 Lois de réaction
La loi de réaction (3) est choisie parmi différentes expressions empiriques. Le choix dépend principalement de la nature du terrain dans lequel est scellé le boulon (sol ou roche). Elle s'exprime en fonction du glissement relatif Δu: en contrainte de cisaillement sous la forme τx = τx(Δu) ou en effort de cisaillement linéique sous la forme Fx = Fx(Δu). Dans le premier cas la courbe a pour caractéristiques génériques la pente Gs qui est un coefficient de réaction (en kN/m3) et le frottement latéral unitaire limite qs (en kPa). Dans le second cas la courbe a pour caractéristiques génériques le module de réaction ks (en kN/m2) et la résistance Fs (en kN/m). Ainsi: ks = π ds Gs et Fs = π ds qs.
Les différentes expressions sont indiquées sur la figure 1 pour leur partie positive. En réalité elles sont impaires et les courbes de réaction qui les représentent sont continues et symétriques par rapport à l'origine des diagrammes (Δu, τx) et (Δu, Fx). Une première expression de la loi de réaction est bilinéaire avec écrouissage (en fait trilinéaire, Fig. 1a). Elle s'utilise dans le domaine du renforcement des sols par clouage (Clouterre, 1991). Elle possède quatre paramètres. Dans le domaine des sols et des roches tendres, une expression de forme exponentielle et de deux paramètres est utilisée aussi (Fig. 1b; Annexe B), telle l'expression proposée par Zhu et al. (2011). Zheng et al. (2020) réunissent diverses fonctions de ce type sous une forme générique. La troisième expression est trilinéaire et possède quatre paramètres (Fig. 1c). Elle est utilisée dans le domaine des roches pour représenter le comportement de l'interface entre la tige et le coulis de scellement qui constituent le boulon (Benmokrane et al., 1995; Cai et al., 2004b; Guan et al., 2007; Xiao and Chen, 2008; Ren et al., 2010; Blanco-Martin et al., 2011). Chen et al. (2019) proposent une étude paramétrique de la loi trilinéaire.
 |
Fig. 1 Courbes de réaction utilisées pour le calcul des boulons à ancrage réparti: (a) Loi bilinéaire; (b) Loi exponentielle; (c) Loi trilinéaire. Reaction curves used for the calculation of fully grouted bolts: (a) bilinear law; (b) exponential law; (c) trilinear law. |
3.3 Chargements
Les chargements sont définis par des conditions aux limites aux deux extrémités du boulon et par les déplacements du massif. Deux cas particuliers sont privilégiés. Le premier représente un essai d'arrachement. Un effort NxL ou un déplacement uxL est appliqué par paliers successifs à l'extrémité libre de la tige (où x = L), un effort nul est appliqué à l'autre extrémité (où x = 0) et le déplacement du massif est nul (ur = 0). Le second représente un boulon radial scellé en paroi d'un tunnel, parmi d'autres boulons identiques, dans un profil situé immédiatement en arrière du front. Les efforts sont nuls aux extrémités de la tige (néanmoins, un effort ou un déplacement pourraient être appliqués en tête). Le chargement du boulon provient du déplacement radial du terrain consécutif à l'avancement du front (convergence). Ce déplacement ur(x) est fourni par un extensomètre. Le problème peut être étendu au cas d'un boulon de front scellé dans un « champ » de déplacement simplifié décrit par les mesures produites par un extrusomètre. Ce second cas se trouve aussi dans les parois clouées où le chargement des clous des rangées supérieures découle de l'excavation des passes successives suivantes.
4 Application à des essais d'arrachement
4.1 Exemple 1
Les courbes d'arrachement d'une dizaine d'essais réalisés sur site ont fait l'objet d'une interprétation avec la méthode proposée. Ces données sont issues de la littérature (Clouterre, 1991; England, 2012; Wang et al., 2001 [dans Zheng et al., 2020]; Zhu et al., 2011; Bai et al., 2015 [dans Chen et al., 2019]; Stillborg, 1984 [dans Chen et al., 2019]; Chen et Ren, 2008 [dans Ren et al., 2010]; Rong et al., 2004 [dans Ren et al., 2010]; Thevenin et al., 2016). Il s'agit de clous, de câbles et de boulons. Les tiges sont en acier ou en fibre de verre. Deux de ces exemples sont commentés ici.
L'exemple 1 porte sur deux essais d'arrachement de deux boulons à ancrage réparti (clou) réalisés pour tester la faisabilité d'une utilisation de tiges en fibre de verre en vue d'une application au clouage des sols (exemple 1, tableau 1; Zhu et al., 2011). Les boulons de 3,4 m de longueur sont scellés au coulis de ciment dans des forages de diamètre 120 mm inclinés à 20° dans un massif granitique complètement décomposé. Les tiges en fibre de verre ont un diamètre da = 40,7 mm et sont prolongées par une longueur libre en acier de 0,2 m. Des mesures locales des déformations axiales sont recueillies pendant le chargement au moyen de différents types de capteurs disposés sur les tiges.
La simulation des essais d'arrachement est réalisée avec une loi de réaction bilinéaire appliquée à l'interface scellement-sol et deux jeux de paramètres. Le chargement est effectué en six paliers. Les paramètres de calcul sont indiqués dans le tableau 2 (calculs 1a et 1b). Les calculs sont effectués en déplacement (le déplacement uxL est imposé en tête à chaque palier). Les courbes calculées de l'exemple 1b sont reportées sur les figures 2 et 3. Les déplacements uxL appliqués en tête sont indiqués dans la légende. La figure 2 compare la courbe d'arrachement calculée (points rouges) aux deux courbes mesurées (triangles bleus). Le calcul peut être prolongé jusqu'à atteindre l'asymptote du frottement latéral unitaire limite qs représentée ici par l'effort limite Ns = 214 kN. À ce stade, le clou adopte un mouvement de translation (Fig. 2 et 3b). L'instrumentation locale des tiges montre que les déformations axiales affichent une distribution quasi-linéaire avec l'abscisse x, ce qui est bien reproduit par la simulation, d'après les courbes (x, Nx) donnant les efforts axiaux en fonction de l'abscisse x sur la figure 3a.
Caractéristiques des boulons à ancrage réparti soumis à un essai d'arrachement.
Characteristics of fully grouted bolts subjected to a pull-out test.
Paramètres de calcul pour les essais d'arrachement.
Calculation parameters for pull-out tests.
 |
Fig. 2 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 1b). Effort de traction en fonction du déplacement axial. Données de Zhu et al. (2011). Simulation of a pull-out test of a fully grouted bolt (calculation 1b). Tensile force versus axial displacement. Data from Zhu et al. (2011). |
 |
Fig. 3 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 1b). Représentation en fonction de l'abscisse: (a) Effort de traction dans la tige; (b) Déplacement axial; (c) Contrainte de cisaillement sur l'interface. Simulation of a pull-out test of a fully grouted bolt (calculation 1b). Representation as a function of the abscissa: (a) Tensile force in the rod; (b) Axial displacement; (c) Shear stress on the interface. |
4.2 Exemple 2
Ren et al. (2010) proposent une interprétation d'un essai d'arrachement réalisé par Chen et Ren (2008). La tige est un toron en acier scellé à la résine époxy, de longueur L = 5 m et de diamètre da = 15,3 mm (Tab. 1). L'interprétation est effectuée avec la loi de réaction trilinéaire agissant sur l'interface tige-scellement (ainsi ds = da). Les paramètres sont ceux préconisés par les auteurs après transformation dans les notations utilisées ici. Ils sont reportés dans le tableau 2 (calcul 2a). Le chargement est effectué en six paliers. L'interprétation de cet essai d'arrachement est reprise par Blanco Martin et al. (2011) avec une loi de réaction trilinéaire dotée de paramètres différents. Ces paramètres sont identifiés à l'aide d'une méthode analytique originale qui s'appuie sur la courbe d'arrachement prise dans son ensemble (Blanco Martin (2012). La réponse théorique de l'essai d'arrachement peut être calculée alors. Ces paramètres sont reportés dans le tableau 2 (calcul 2b) après transformation dans les notations utilisées ici.
Les courbes obtenues avec le calcul 2b sont reproduites sur les figures 4 et 5. Les efforts NxL appliqués en tête sont indiqués dans la légende. La courbe d'arrachement calculée (uxL, NxL) en tête (points rouges) est à comparer aux données expérimentales (triangles bleus). Elle présente un coude marqué vers NxL = 160 kN, en lien avec le faible rapport de la résistance résiduelle par rapport à la résistance de pic (paramètre c = 0,18). Ce contraste se traduit par les distributions des contraintes de cisaillement le long de l'interface tige-scellement représentées sur la figure 5c. Les calculs reproduisent l'interprétation des auteurs. Les deux jeux de paramètres 2a et 2b diffèrent surtout par la résistance de pic qs et la pente b. La première est fortement réduite (de 2300 à 1620 kPa) alors que la seconde a pour effet d'allonger la phase de radoucissement après le pic (b de 0,512 à 0,103). Les courbes calculées (x, Nx), (x, ux) et (x, τx) dans les deux solutions sont peu différentes. Néanmoins, la réponse (uxL, NxL) en tête de la solution 2b présente une courbure plus progressive et plus représentative des données expérimentales (Fig. 4). Cet exemple montre que l'interprétation des courbes d'arrachement n'aboutit pas automatiquement à une solution unique du fait de l'interdépendance des paramètres. L'incertitude des mesures et la variabilité des propriétés des terrains apportent un flou supplémentaire qui pénalise la recherche d'un jeu de paramètres. En vue d'améliorer cette recherche, une méthode d'accompagnement à l'identification des paramètres de la loi de réaction est proposée au paragraphe suivant.
 |
Fig. 4 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 2b). Effort de traction dans la tige en fonction du déplacement axial. Données de Chen et Ren (2008) dans Blanco Martin et al. (2011). Simulation of a pull-out test of a fully grouted bolt (calculation 2b). Tensile force versus axial displacement. Data from Chen et Ren (2008) in Blanco Martin et al. (2011) |
 |
Fig. 5 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 2b). Représentation en fonction de l'abscisse: (a) Effort de traction dans la tige; (b) Déplacement axial; (c) Contrainte de cisaillement sur l'interface. Simulation of a pull-out test of a fully grouted bolt (calculation 2b). Representation as a function of the abscissa: (a) Tensile force in the rod; (b) Axial displacement; (c) Shear stress on the interface. |
5 Identification des paramètres des lois de réaction
5.1 Loi de réaction trilinéaire
Il n'existe pas de méthode explicite qui permette d'identifier les quatre paramètres de la loi de réaction trilinéaire à partir d'une courbe d'arrachement donnant le déplacement et l'effort en tête du boulon (uxL, NxL). Au-delà des méthodes par tirs et essais successifs et d'ajustement optimal aux données expérimentales, diverses démarches ont été proposées pour obtenir ces paramètres. Partant des solutions analytiques, les méthodes s'appuient sur des points caractéristiques de la courbe d'arrachement (Ren et al., 2010; Chen et al., 2019) ou sur des calculs paramétriques (Chen et al., 2015, 2020). Toutefois, l'interprétation des essais dépend du choix de la méthode utilisée, sans garantie d'obtenir une solution unique. Blanco Martin (2012) et Blanco Martin et al. (2011) ont développé une procédure analytique d'identification des paramètres.
Une autre méthode est proposée ici. Elle consiste à faire intervenir la pente (ΔNx/Δux)L de la courbe d'arrachement (uxL, NxL) en quelques points de cette courbe depuis son origine jusqu'à la fin du chargement (de six à douze ou quinze points). Cette pente est déterminée graphiquement à partir de la tangente à la courbe d'arrachement en chacun de ces points (méthode A). Des itérations supplémentaires sont possibles pour affiner l'identification des paramètres. La méthode s'applique à des boulons longs et des scellements résistants quand le déplacement en pied (x = 0) reste faible (ux0 ≈ 0). Dans ce cas, à l'abscisse L, la pente (dNx/dux)L de la courbe représentant la déformée du boulon pendant un palier de chargement s'avère proche de la pente (ΔNx/Δux)L de la courbe d'arrachement dans sa forme globale, comme le montre la figure 4 par exemple. Ainsi, en assimilant la pente (ΔNx/Δux)L à (dNx/dux)L en tête (x = L) et d'après (1) et (2), la force linéique de cisaillement sur l'interface prend la forme:
 (6)
(6)
produit de la pente (dNx/dux)L par la déformation élastique de l'extrémité de la tige (NxL/AaEa)L. La contrainte de cisaillement τxL en tête se déduit alors de FxL par la relation τxL = FxL/(πds).
Ainsi, la contrainte de cisaillement τxL est déduite du couple {NxL, (dNx/dux)L} pour chacun des paliers de chargement. Puis elle est associée au déplacement uxL. La démarche est illustrée sur la figure 6 pour l'exemple 2. La courbe d'arrachement (uxL, NxL) est représentée par quelques points et les tangentes à la courbe sont déterminées graphiquement en ces points (Fig. 6a). Les couples (uxL, τxL) calculés à partir des tangentes sont représentés alors (Fig. 6b).
Sur la figure 6b sont indiquées les deux courbes de réaction trilinéaires utilisées pour effectuer les calculs et dont les paramètres sont reportés dans le tableau 2 avec la solution proposée par Ren et al. (2010) (calcul 2a en vert) et celle proposée par Blanco Martin et al. (2011) (calcul 2b en rouge). Malgré le caractère discret des données (six paliers de chargement), les contraintes de cisaillement évaluées à partir des tangentes semblent mieux représentées par la solution 2b, pour aboutir à une meilleure description de la courbe d'arrachement expérimentale (Fig. 4).
La méthode A a été appliquée à d'autres essais d'arrachement interprétés avec la loi de réaction trilinéaire (données de Rong et al., 2004; Ren et al., 2010; Thevenin et al., 2016). Elle donne un moyen d'accès rapide à un jeu pertinent de paramètres de cette loi. Toutefois, l'identification des quatre paramètres de la loi conserve un certain degré d'incertitude, ce qui appelle l'utilisateur à opérer un choix. Aussi, cette méthode doit être vue comme une aide à l'interprétation des essais d'arrachement de boulons à ancrage réparti dans une approche globale pour aboutir à la meilleure interprétation des essais.
 |
Fig. 6 Identification des paramètres de la loi de réaction trilinéaire à partir de la courbe d'arrachement (exemple 2, méthode A): (a) Courbe d'arrachement et ses tangentes; Données de Chen et Ren (2008) dans Blanco Martin et al. (2011); (b) Contraintes de cisaillement sur l'interface et lois de réaction (calculs 2a et 2b). dentification of the trilinear reaction law parameters from the pull-out curve (example 2, method A): (a) Pull-out curve and its tangents; Data from Chen et Ren (2008) in Blanco Martin et al. (2011) (b) Shear stresses on the interface and reaction laws (calculations 2a and 2b). |
5.2 Loi de réaction bilinéaire
L'expérience montre que la loi de réaction bilinéaire convient mieux pour décrire le comportement des clous scellés dans les sols. Une méthode d'identification des paramètres de cette loi à partir de la seule courbe d'arrachement mesurée en tête (uxL, NxL) a été recherchée, devant l'impossibilité d'appliquer la méthode A en raison des forts déplacements qui se produisent en pied du boulon.
En appliquant la solution élastique de Farmer (1975) sous une forme tangente, il est possible de trouver un encadrement de la force de cisaillement linéique en tête FxL, puis de la contrainte de cisaillement τxL (Annexe C, méthode B): (7)
(7)
La borne inférieure τxLu revient à considérer que le cisaillement est uniformément réparti le long du scellement, traduisant ainsi la saturation du frottement latéral unitaire à chaque pas du chargement. La contrainte de cisaillement tangente τxLt, qui constitue la borne supérieure, s'obtient en calculant la longueur de transfert Ltxt associée à la pente de la tangente Mt = ΔNxL/ ΔuxL à chaque pas du chargement. Cette pente décroît progressivement en partant de sa valeur initiale Ms au début de l'essai.
En pratique, la pente Ms de la tangente à l'origine de la courbe d'arrachement doit être évaluée au préalable pour en déduire le coefficient de réaction axial Gs. Puis le frottement latéral unitaire limite qs s'obtient au stade de l'arrachement du boulon quand τxLu = qs. Les deux paramètres Gs et qs déterminent directement la loi de réaction exponentielle (Annexe B). Pour la loi bilinéaire, le calcul des deux bornes de l'encadrement (7) est effectué alors en chaque point de la courbe d'arrachement (uxL, NxL). La droite intermédiaire définie par les deux paramètres a et b (Fig. 1a) doit être choisie à l'intérieur de cet encadrement. Les deux paramètres a et b sont identifiés ainsi.
La démarche est illustrée sur la figure 7 pour l'exemple 1 commenté au paragraphe précédent. La courbe d'arrachement (uxL, NxL) est représentée par neuf points sur la figure 7a. Elle est accompagnée par sa tangente à l'origine de pente Ms = 17 MN/m et son asymptote d'ordonnée Ns = 214 kN, qui ont été identifiés graphiquement. Après calcul, les courbes enveloppes (uxL, τxLu) et (uxL, τxLc) sont représentées sur la figure 7b. Les deux lois bilinéaires définies par les jeux de paramètres de l'exemple 1 (calculs 1a et 1b, Tab. 2) sont reportées aussi, avec un léger avantage à la solution 1b (en rouge). Les deux paramètres Ms et qs permettent de définir directement la loi de réaction exponentielle. Toutefois, la représentativité de cette loi n'est recevable que si la courbe de réaction s'inscrit entre les enveloppes. Enfin, le calcul des contraintes de cisaillement par la méthode A (croix grises) justifie d'écarter la loi trilinéaire pour interpréter l'essai.
L'interprétation de plusieurs essais d'arrachement a montré que la méthode B fournit une aide pour effectuer le choix d'une loi de réaction et identifier ses paramètres. L'encadrement constitué par les courbes enveloppes (uxL, τxLu) et (uxL, τxLc) n'est pas toujours très resserré, ce qui confirme la relative liberté de choix des paramètres de la loi bilinéaire autour d'un jeu optimal. L'écart entre les courbes enveloppes semble en rapport avec la longueur l au début de l'essai (l est définie dans l'annexe C). Il est faible quand l < 1. Ici, L = 3,4 m, Ltx = 3,10 m et l = 1,10.
 |
Fig. 7 Identification des paramètres de la loi de réaction bilinéaire à partir de la courbe d'arrachement (exemple 1, méthode B): (a) Courbe d'arrachement;); (b) Contraintes de cisaillement sur l'interface et lois de réaction (calculs 1a et 1b). Identification of the bilinear reaction law parameters from the pull-out curve (example 1, method B): (a) Pull-out curve; (b) Shear stresses on the interface and reaction laws (calculations 1a and 1b). |
6 Application au boulonnage en place. Eléments radiaux en tunnel
Cinq essais portant sur des boulons radiaux instrumentés ont fait l'objet d'une interprétation avec la méthode proposée. Les résultats des essais sont issus de la littérature (Li et Stillborg, 1999; Jiang et al., 2004; Cai et al., 2004b; Oreste et Peila, 1996; Robit et al., 2014)). Il s'agit de boulons radiaux mis en place en tunnel et d'un élément d'une paroi clouée. Les tiges sont en acier. Les exemples sont incomplètement documentés, ce qui amène à formuler des hypothèses supplémentaires pour décrire les résultats.
L'exemple commenté ici est rapporté par Cai et al. (2004b). Le boulon radial de 4 m est scellé à partir de la paroi d'un tunnel dans une roche tendre. L'essai fournit les efforts axiaux en six points de la tige. Les contraintes de cisaillement sur l'interface tige-scellement sont évaluées dans les intervalles entre ces points. L'interprétation de l'essai est effectuée à l'aide des trois lois de réaction bilinéaire, exponentielle et trilinéaire. Les paramètres sont reportés dans le tableau 3 (calculs 3a, 3b et 3c). Le chargement du massif est effectué en deux étapes à titre d'illustration. Le déplacement du massif est exprimé sous la forme exponentielle ur = ur0 exp(-x/x0) avec une amplitude en paroi ur0 égale à 15 et 40 mm (convergence) et x0 = 0,4 m.
Les résultats sont reportés sur la figure 8 pour le calcul 3c (loi trilinéaire). Les calculs reproduisent bien les données expérimentales en matière d'effort axial, de point neutre (qui est situé vers 1,1 m) et de répartition des contraintes de cisaillement. Le déplacement du massif à l'étape 2 aboutit à la résistance au cisaillement limite qs sur l'interface active. Toutefois, la répartition des contraintes de cisaillement paraît mieux décrite par la loi de réaction bilinéaire et la loi exponentielle (Fig. 9).
D'autres exemples d'interprétation des essais sur sites sont présentés dans le cadre du clouage des sols (Serratrice, 2022a) ou du boulonnage en tunnel (Serratrice, 2022b).
Paramètres de calcul pour les boulons radiaux et trois lois de réaction.
Calculation parameters for radial bolts and three reaction laws.
 |
Fig. 8 Simulation du chargement d'un boulon radial à ancrage réparti. Loi de réaction trilinéaire (calcul 3c). Représentation en fonction de l'abscisse: (a) Déplacement du massif et déplacement axial; (b) Effort axial; (c) Contrainte de cisaillement sur l'interface. Simulation of the loading of a radial fully grouted bolt. Trilinear reaction law (calculation 3c). Representation as a function of the abscissa: (a) Soil mass displacement and axial displacement; (b) Axial force; (c) Shear stress at the interface. |
 |
Fig. 9 Simulation du chargement d'un boulon radial à ancrage réparti. Contrainte de cisaillement sur l'interface en fonction de l'abscisse: (a) Calcul 3a, loi bilinéaire; (b) Calcul 3b, loi exponentielle. Simulation of the loading of a radial fully routed bolt. Shear stress at the interface as a function of abscissa: (a) Calculation 3a, bilinear law; (b) Calculation 3b, exponential law. |
7 Conclusion
L'interprétation d'une dizaine d'essais d'arrachement a permis de montrer différents aspects du comportement des boulons à ancrage réparti (évolution des principales variables en fonction de l'abscisse, allure des déformées des tiges, répartition des contraintes de cisaillement sur l'interface active et forme des courbes d'arrachement). Il apparaît que le déplacement évalué en pied de boulon départage les réponses calculées, en accord avec le contexte du site (nature du massif renforcé, ouvrage), pour ces chargements monotones croissants. En présence de faibles déplacements, la méthode d'identification des paramètres de la loi de réaction fait intervenir les pentes des tangentes à la courbe d'arrachement (méthode A). Ces pentes sont à déterminer graphiquement. La méthode convient au cas des scellements dans les roches auxquels s'applique plutôt la loi de réaction trilinéaire.
Les pentes de la courbe d'arrachement et de la déformée de la tige ne coïncident plus quand l'essai aboutit à un arrachement du boulon avec une translation importante du pied, situation qui se rencontre le plus souvent dans les sols. Une méthode d'interprétation a été proposée alors, qui fournit un encadrement dans lequel peuvent être recherchés les paramètres de la loi de réaction bilinéaire (méthode B). Ces approches globales, qui portent sur l'ensemble de la courbe d'arrachement, donnent un moyen d'accès rapide à un jeu pertinent de paramètres parmi divers jeux possibles, avant de passer au calcul de la courbe théorique.
La méthode d'interprétation a été appliquée à des boulons instrumentés placés dans un champ de déplacement continu. Ces données ont été recueillies par différents auteurs en tunnel ou dans une paroi clouée. L'interprétation de l'essai appelle à connaître les paramètres de la loi de réaction axiale, les conditions appliquées aux limites du boulon, mais aussi les déplacements du massif autour du boulon. Ici, une forme exponentielle a été utilisée pour décrire ces déplacements à partir des quelques informations disponibles. Mais, en principe, il est recommandé d’obtenir ces déplacements par des mesures en place au moyen d'extensomètres. L'allure des déplacements du massif détermine directement la réponse du boulon. L'interprétation des essais analysés ici montre que les trois lois de réaction mises en œuvre aboutissent à des résultats comparables, avec un avantage à la loi de réaction bilinéaire et la loi exponentielle.
La méthode proposée s'adresse à l'interprétation des essais réalisés sur site concernant des boulons à ancrage réparti (essais d'arrachement ou boulons instrumentés) et elle ne vise pas une utilisation dans le cadre des méthodes de conception des ouvrages, compte-tenu des hypothèses restrictives adoptées. Les méthodes d'interprétation conventionnelles des essais (basée sur l'effort d'arrachement) ne sont pas remises en cause, pas plus que les méthodes de dimensionnement des ouvrages qui répondent à des normes. Par contre, la description des réponses des tiges, et notamment le calcul d'un déplacement en pied, peuvent aider à mieux évaluer la consistance de l'essai d'arrachement dans son contexte. Le comportement des inclusions sollicitées en cisaillement n'est pas couvert dans cette approche. Enfin, il faut rappeler que l'étude porte sur des données trop rares et peu documentées. D'autres données expérimentales seraient à recueillir encore sur des boulons en situations réelles et diverses.
Annexe A: Solution élastique pour un essai d'arrachement.
Les déplacements axiaux du boulon produits sous l'effort NxL appliqué en tête à l'abscisse x = L pendant un essai d'arrachement en phase élastique sont donnés par Farmer (1975) sous la forme: (A1-1)
(A1-1)
où Ltx = 1/α est la longueur de transfert axiale (Clouterre, 1991): (A1-2)
(A1-2)
qui exprime un rapport de rigidité entre le boulon et le terrain (Ltx en m). Une barre courte de longueur inférieure à Ltx (L < Ltx) présente un comportement quasi rigide (quasi indéformable) vis à vis du terrain, contrairement à un barre longue (souple). Dans ce cadre: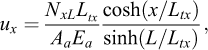 (A1-3)
(A1-3)
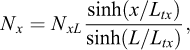 (A1-4)
(A1-4)
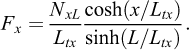 (A1-5)
(A1-5)
Divers paramètres sont déduits de ces relations. Ainsi, la pente initiale élastique Ms de la courbe d'arrachement (uxL, NxL) mesurée en tête vaut (en kN/m): (A1-6)
(A1-6)
Annexe B: Loi de réaction exponentielle.
Exprimée en contrainte de cisaillement sous la forme τx = τx(Δu), la loi de réaction exponentielle prend la forme: (A2-1)
(A2-1)
où interviennent les deux paramètres Gs et qs (Fig. 1b).
Annexe C: Encadrement de la contrainte de cisaillement dans la méthode B.
En introduisant le paramètre H = (Aa Ea)/(Ms L) dans (A1-6), puis en effectuant le changement de variable l = L/Ltx (sans dimension) et après transformation, il vient: (A3-1)
(A3-1)
La solution l de cette équation permet d'obtenir une longueur de transfert Ltxc = L/l connaissant la pente Ms.
L'expression FxL de Fx en tête (x = L) donnée par (A1-5) s'écrit: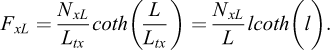 (A3-2)
(A3-2)
Dans cette expression, l coth(l) > 1,0. l et l coth(l) décroissent progressivement pendant un essai d'arrachement. Quand l > 2, l coth(l) ≈ l (barre souple) et quand l < 1/2, l coth(l) ≈ 1,0 (barre rigide). L'expression (A3-2) montre que FxL > NxL/L. L'effort de cisaillement en tête est plus grand que le cisaillement uniformément réparti le long de la tige FxLu > NxL/L.
En admettant que la pente Ms est représentée par la pente Mt de la tangente à la courbe d'arrachement (uxL, NxL), la solution de l'équation (A3-1) conduit à calculer lt, Ltxt et FxLt et: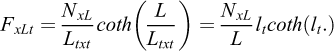 (A3-3)
(A3-3)
La tangente de pente Mt constitue une enveloppe de la courbe d'arrachement (uxL, NxL) monotone croissante et asymptotique, si bien que Ltxt < Ltx, lt > l et lt coth(lt) > l coth(l). D'où FxLt > FxL. Ainsi: (A3-4)
(A3-4)
En conséquence, la force de cisaillement linéique produite à l'extrémité L du boulon est encadrée par le cisaillement uniforme FxLu et le cisaillement tangent FxLt. Un tel encadrement s'applique alors à la contrainte de cisaillement pendant la progression des paliers de chargement. Aussi, en notant τxLu = NxLu/(π ds L) et τxLt = FxLt/(π ds) quand l décroît progressivement et tend vers 0: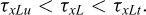 (A3-5)
(A3-5)
Références
- AFNOR (Association Française de Normalisation). 1993. Renforcement des sols – Essai statique d'arrachement de clou soumis à un effort axial de traction – Essai à vitesse de déplacement constante. Norme NF P 94-242-1 , 13 p. [Google Scholar]
- AFNOR (Association Française de Normalisation). 2002. Roches – Essai statique d'arrachement, sous un effort axial de traction, d'un ancrage scellé dans un massif rocheux – Essai par paliers. Norme XP P 94-444, 12 p. [Google Scholar]
- AFNOR (Association Française de Normalisation). 2010. Exécution des travaux géotechniques spéciaux – Clouage. Norme NF EN 14490, 66 p. [Google Scholar]
- AFNOR (Association Française de Normalisation). 2020. Calcul géotechnique – Ouvrage de soutènement – Remblais renforcés et massifs en sol cloué. Norme NF P 94-270, 186 p. [Google Scholar]
- AFTES (Association Française des Tunnels et de l'Espace Souterrain). 2014. Technologie du boulonnage. Recommandations GT6R4F1. Tunnels et Espace Souterrains 241: 14–31. [Google Scholar]
- AFTES (Association Française des Tunnels et de l'Espace Souterrain). 2017. Conception et guide de dimensionnement du boulonnage radial en tunnel. Recommandations GT30R1F1, 70 p. [Google Scholar]
- Bai X, Zhang M, Yan N 2015. Field contrast test and mechanism analysis on anchorage performance of antifloating anchors with two different materials. China Civil Eng J 48(8): 38–59. [Google Scholar]
- Benmokrane B, Chennouf A, Mitri HS. 1995. Laboratory evaluation of cement-based grouts and grouted rock anchors. Int J Rock Mech Min Sci Geomech Abstr 32(7): 633–642. [CrossRef] [Google Scholar]
- Blanco Martín L, Tijani M, Hadj-Hassen F. 2011. A new analytical solution to the mechanical behaviour of fully grouted rockbolts subjected to pull-out tests. Constr Build Mater 25: 749–755. [CrossRef] [Google Scholar]
- Blanco Martín L. 2012. Étude théorique et expérimentale du boulonnage à ancrage réparti sous sollicitations axiales. Mémoire de thèse, MINES-ParisTech, Paris, France. [Google Scholar]
- Blanco Martin L, Tijani M, Hadj-Hassen F, Noiret A. 2013. Assessment of the bolt-grout interface behaviour of fully grouted rockbolts from laboratory experiments under axial loads. Int J Rock Mech Min Sci 63: 50–61. [CrossRef] [Google Scholar]
- Blanco Martin L, Tijani M, Hadj-Hassen F Noiret, A. 2016. Boulonnage à ancrage réparti: étude de l’interface barre-scellement sous sollicitations axiales. Rev Fr Geotech 146: 2. [CrossRef] [EDP Sciences] [Google Scholar]
- Bost M, Ho DA, Pruvost C, et al. 2018. Étude paramétrique de la résistance a l'arrachement d’un ancrage passif scellé au rocher. In: Journées Nationales de Géotechnique et de Géologie de l’Ingénieur, JNGG 2018, Champs-sur-Marne, France, 8 p. [Google Scholar]
- Cai Y, Esaki T, Jiang Y. 2004a. A rock bolt and rock mass interaction model. Int J Rock Mech Min Sci 41(7): 1055–1067. [CrossRef] [Google Scholar]
- Cai Y, Esaki T, Jiang Y. 2004b. An analytical model to predict axial load in grouted rock bolt for soft rock tunnelling. Tunn Undergr Space Technol 19(6): 607–618. [CrossRef] [Google Scholar]
- Carranza-Torres C. 2009. Analytical and numerical study of the mechanics of rockbolt reinforcement around tunnels in rock masses. Rock Mech Rock Eng 42: 175–228. [CrossRef] [Google Scholar]
- Chen WW, Ren FF. 2008. Mechanical behavior of the bamboo-steel composite rockbolt. Report 2006BAK30B02. Dunhuang Academy & Cultural Relics Protection Center of Lanzhou University. [Google Scholar]
- Chen J, Saydam S, Hagan PC. 2015. An analytical model of the load transfer behavior of fully grouted cable bolts. Constr Build Mater 101: 1006–1015. [CrossRef] [Google Scholar]
- Chen J, Yang S, Zhao H, Zhang J, He F, Yin S. 2019. The analytical approach to evaluate the load-displacement relationship of rock bolts. Adv Civil Eng 2019: 19. [Google Scholar]
- Chen J, He F, Zhang S. 2020. A study of the load transfer behavior of fully grouted rock bolts with analytical modelling. Int J Min Sci Technol 30: 105–109. [CrossRef] [Google Scholar]
- Clouterre. 1991. Recommandations pour la conception, le calcul, l'exécution et le contrôle des soutènements réalisés par clouage des sols. Presses de l'École Nationale des Ponts et Chaussées, 268 p. [Google Scholar]
- England M. 2012. On the subject of piles in tension. Proceeding of Conference on Full-scale Testing and Foundation Design, GeoCongress 2012, Oakland, California, pp. 680–693. [Google Scholar]
- Farmer IW. 1975. Stress distribution along a resin grouted rock anchor. Int J Rock Mech Min Sci Geomech Abstr 12(11): 347–351. [CrossRef] [Google Scholar]
- Frank R, Zhao SR 1982. Estimation des paramètres pressiométriques de l'enfoncement sous charge axiale de pieux forés dans les sols fins. Bulletin de liaison des laboratoires des Ponts et Chaussées 119: 17–24. [Google Scholar]
- Freeman TJ. 1978. The behavior of fully-bonded rock bolts in the Kielder experimental tunnel. Tunn Tunn Int 10(5): 37–40. [Google Scholar]
- Guan Z, Jiang Y, Tanabasi Y, Huang H 2007. Reinforcement mechanics of passive bolts in conventional tunnelling. Int J Rock Mech Min Sci 44: 625–636. [CrossRef] [Google Scholar]
- Indraratna B, Kaiser PK. 1990. Analytical model for the design of grouted rock bolts. Int J Numer Anal Meth Geomech 14(4): 227–251. [CrossRef] [Google Scholar]
- IMSL. 2014. International Mathematics and Statistics Library User's Manual, Version 7.0. Rogue Wave Software, Inc. [Google Scholar]
- Jalalifar H. 2011. An analytical solution to predict axial load along fully grouted bolts in an elasto-plastic rock mass. J South Afr Inst Min Metall 111: 809–814. [Google Scholar]
- Jiang Y, Tanabashi Y, Cai Y, Esaki T. 2004. Analytical model for grouted rock bolts. Rep Fac Eng, Nagasaki Univ 34(62): 97–102. [Google Scholar]
- Li C, Stillborg B 1999. Analytical models for rock bolts. Int J Rock Mech Min Sci 36(8): 1013–1029. [CrossRef] [Google Scholar]
- Liu G, Xiao M, Chen J, Zhou H. 2017. Study on mechanical characteristics of fully grouted rock bolts for underground caverns under seismic loads. Hindawi, Math Probl Eng 2017: 12. [Google Scholar]
- Ma S, Nemcik J, Aziz N. 2013. An analytical model of fully grouted rock bolts subjected to tensile load. Constr Build Mater 49: 519–526. [CrossRef] [Google Scholar]
- Moayed RZ, Namaei A. 2020. Evaluation of the pullout resistance of soil nails in Tehran alluvium by considering the overburden pressure effect. Geotech Geol Eng 38: 743–754. [CrossRef] [Google Scholar]
- Nguyen QP, Nguyen VM, Nguyen KT. 2018. A new design concept of fully grouted rock bolts in underground construction. Earth Environ Sci 143: 012017. [Google Scholar]
- Oreste PP, Peila D. 1996. Radial passive rockbolting in tunnelling design with a new convergence-confinement model. Int J Rock Mech Min Sci Geomech Abstr 33(5): 443–454. [CrossRef] [Google Scholar]
- Oreste P 2008. Distinct analysis of fully grouted bolts around a circular tunnel considering the congruence of displacements between the bar and the rock. Int J Rock Mech Min Sci 45(7): 1052–1067. [CrossRef] [Google Scholar]
- Ranjbarnia M, Fahimifar A, Oreste P. 2016. New analytical approaches for evaluating the performance of systematic pre-tensioned fully grouted rockbolts in tunnel stabilization. Arch Min Sci 61(4): 823–852. [Google Scholar]
- Ren FF, Yang ZJ, Chen JF, Chen WW. 2010. An analytical analysis of the full range behaviour of grouted rockbolts based on a tri-linear bond-slip model. Constr Build Mater 24(3): 361–370. [CrossRef] [Google Scholar]
- Robit P, Rajot JP, Limam A. 2014. Paroi clouée AD/OC – Une alternative au béton projeté qui renforce le drainage et limite les émissions de CO2 . Journées Nationales de Géotechnique et de Géologie de l’Ingénieur, JNGG 2014, Beauvais, France, 10 p. [Google Scholar]
- Rong G, Zhu HC, Zhou CB. 2004. Testing study on working mechanism of fully grouted bolts of thread steel and smooth steel. Chin J Rock Mech Eng 23(3): 469–475. [Google Scholar]
- Salcher M, Bertuzzi R. 2018. Results of pull tests of rock bolts and cable bolts in Sydney sandstone and shale. Tunn Undergr Space Technol 74: 60–70. [CrossRef] [Google Scholar]
- Schlosser F, Guilloux A. 1981. Le frottement dans les sols. Rev Fr Geotech 16: 65–77. [CrossRef] [EDP Sciences] [Google Scholar]
- Serratrice JF. 2022a. Une interprétation du comportement des boulons à ancrage reparti sollicités en traction dans les sols. Journées Nationales de Géotechnique et de Géologie de l’Ingénieur, JNGG 2022, Lyon, France, 8 p. [Google Scholar]
- Serratrice JF. 2022b. Une interprétation du comportement des boulons à ancrage reparti sollicités en traction pour application en tunnel. Tunnels et Espace Souterrain, à paraître. [Google Scholar]
- Sivakumar Babu GL, Singh VP. 2010. Soil nails field pullout testing: evaluation and applications. Int J Geotech Eng 4: 3–21. [Google Scholar]
- Stillborg B. 1984. Experimental investigation of steel cables for rock reinforcement in hard rock. Lulea, Sweden: Lulea University. [Google Scholar]
- Stille H, Holmberg M, Nord G. 1989. Support of weak rock with grouted bolts and shotcrete. Int J Rock Mech Min Sci Geomech Abstr 26(1): 99–113. [CrossRef] [Google Scholar]
- Thevenin I, Jahangir E, Hadj Hassen F, Schleifer J, Rodriguez P. 2016. Analyse expérimentale de l'effet du confinement sur l'arrachement des boulons de front. Journées Nationales de Géotechnique et de Géologie de l’Ingénieur, JNGG 2016, Nancy, pp. 770–777. [Google Scholar]
- Wang XN, Ye R, Zhou FJ. 2001. Proposals for the selection of failure criteria in soil float-resisting achor rod test. J Geol Hazards Environ Preserv 12(3): 73–77. [Google Scholar]
- Wang M, Zhang X, Tong J, Yi W, Wang Z, Liu D. 2020. A new semi-analytical method for elasto-plastic analysis of a deep circular tunnel reinforced by fully grouted passive bolts. Appl Sci 10: 4402. [CrossRef] [Google Scholar]
- Wen JZ, Su HT, Tan XQ, Ning DB, Zhang CY 2014. An analytical model for fully grouted rock bolts in soft rock tunnel. EJGE 19: 2829–2839. [Google Scholar]
- Xiao SJ, Chen CF. 2008. Mechanical mechanism analysis of tension type anchor based on shear displacement method. J Centr South Univ Technol 15(1): 106–111. [CrossRef] [Google Scholar]
- Zhang LL, Zhang LM, Tang WH. 2009. Uncertainties of field pullout resistance of soil nails. J Geotech Geoenviron Eng 135(7): 956–972. [Google Scholar]
- Zhao K, You CA, Du W, Lv XP, Li YY. 2014. Pullout mechanism and failure characteristics of soil anchor. EJGE 19: 17701–17711. [Google Scholar]
- Zheng B, Zhang J, Feng T, Cao M 2020. Predicting the ultimate bearing capacity of bolts with an optimized function model. Hindawi Publishing Corporation, Adv Civil Eng 2020: ID 4934260, 9 p. [Google Scholar]
- Zhu HH, Yin JH, Yeung AT, Jin W. 2011. Field pullout testing and performance evaluation of GFRP soil nails. J Geotech Geoenviron Eng 137(7): 633–642. [CrossRef] [Google Scholar]
Citation de l’article: Jean-François Serratrice. Une méthode d'interprétation des essais effectués sur site sur des boulons à ancrage réparti sollicités en traction. Rev. Fr. Geotech. 2022, 171, 4.
Liste des tableaux
Caractéristiques des boulons à ancrage réparti soumis à un essai d'arrachement.
Characteristics of fully grouted bolts subjected to a pull-out test.
Paramètres de calcul pour les essais d'arrachement.
Calculation parameters for pull-out tests.
Paramètres de calcul pour les boulons radiaux et trois lois de réaction.
Calculation parameters for radial bolts and three reaction laws.
Liste des figures
 |
Fig. 1 Courbes de réaction utilisées pour le calcul des boulons à ancrage réparti: (a) Loi bilinéaire; (b) Loi exponentielle; (c) Loi trilinéaire. Reaction curves used for the calculation of fully grouted bolts: (a) bilinear law; (b) exponential law; (c) trilinear law. |
| Dans le texte | |
 |
Fig. 2 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 1b). Effort de traction en fonction du déplacement axial. Données de Zhu et al. (2011). Simulation of a pull-out test of a fully grouted bolt (calculation 1b). Tensile force versus axial displacement. Data from Zhu et al. (2011). |
| Dans le texte | |
 |
Fig. 3 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 1b). Représentation en fonction de l'abscisse: (a) Effort de traction dans la tige; (b) Déplacement axial; (c) Contrainte de cisaillement sur l'interface. Simulation of a pull-out test of a fully grouted bolt (calculation 1b). Representation as a function of the abscissa: (a) Tensile force in the rod; (b) Axial displacement; (c) Shear stress on the interface. |
| Dans le texte | |
 |
Fig. 4 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 2b). Effort de traction dans la tige en fonction du déplacement axial. Données de Chen et Ren (2008) dans Blanco Martin et al. (2011). Simulation of a pull-out test of a fully grouted bolt (calculation 2b). Tensile force versus axial displacement. Data from Chen et Ren (2008) in Blanco Martin et al. (2011) |
| Dans le texte | |
 |
Fig. 5 Simulation d'un essai d'arrachement d'un boulon à ancrage réparti (calcul 2b). Représentation en fonction de l'abscisse: (a) Effort de traction dans la tige; (b) Déplacement axial; (c) Contrainte de cisaillement sur l'interface. Simulation of a pull-out test of a fully grouted bolt (calculation 2b). Representation as a function of the abscissa: (a) Tensile force in the rod; (b) Axial displacement; (c) Shear stress on the interface. |
| Dans le texte | |
 |
Fig. 6 Identification des paramètres de la loi de réaction trilinéaire à partir de la courbe d'arrachement (exemple 2, méthode A): (a) Courbe d'arrachement et ses tangentes; Données de Chen et Ren (2008) dans Blanco Martin et al. (2011); (b) Contraintes de cisaillement sur l'interface et lois de réaction (calculs 2a et 2b). dentification of the trilinear reaction law parameters from the pull-out curve (example 2, method A): (a) Pull-out curve and its tangents; Data from Chen et Ren (2008) in Blanco Martin et al. (2011) (b) Shear stresses on the interface and reaction laws (calculations 2a and 2b). |
| Dans le texte | |
 |
Fig. 7 Identification des paramètres de la loi de réaction bilinéaire à partir de la courbe d'arrachement (exemple 1, méthode B): (a) Courbe d'arrachement;); (b) Contraintes de cisaillement sur l'interface et lois de réaction (calculs 1a et 1b). Identification of the bilinear reaction law parameters from the pull-out curve (example 1, method B): (a) Pull-out curve; (b) Shear stresses on the interface and reaction laws (calculations 1a and 1b). |
| Dans le texte | |
 |
Fig. 8 Simulation du chargement d'un boulon radial à ancrage réparti. Loi de réaction trilinéaire (calcul 3c). Représentation en fonction de l'abscisse: (a) Déplacement du massif et déplacement axial; (b) Effort axial; (c) Contrainte de cisaillement sur l'interface. Simulation of the loading of a radial fully grouted bolt. Trilinear reaction law (calculation 3c). Representation as a function of the abscissa: (a) Soil mass displacement and axial displacement; (b) Axial force; (c) Shear stress at the interface. |
| Dans le texte | |
 |
Fig. 9 Simulation du chargement d'un boulon radial à ancrage réparti. Contrainte de cisaillement sur l'interface en fonction de l'abscisse: (a) Calcul 3a, loi bilinéaire; (b) Calcul 3b, loi exponentielle. Simulation of the loading of a radial fully routed bolt. Shear stress at the interface as a function of abscissa: (a) Calculation 3a, bilinear law; (b) Calculation 3b, exponential law. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




