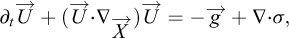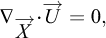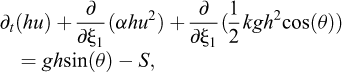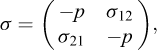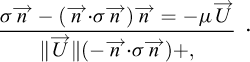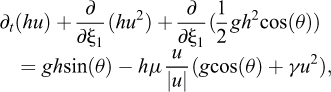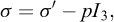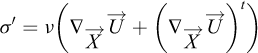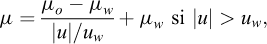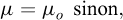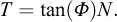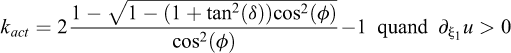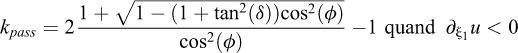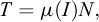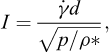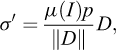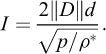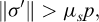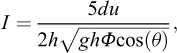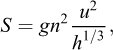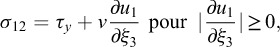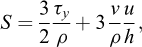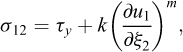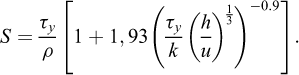Simulation des écoulements gravitaires avec les modèles d’écoulement en couche mince : état de l’art et exemple d’application aux coulées de débris de la Rivière du Prêcheur (Martinique, Petites Antilles)

Marc Peruzzetto; Gilles Grandjean; Anne Mangeney; Clara Levy; Yannick Thiery; Benoit Vittecoq; François Bouchut; Fabrice R. Fontaine; Jean-Christophe Komorowski

doi:10.1051/geotech/2023020

Home

Home (en)

All issues

No 176 (2023)

Rev. Fr. Geotech., 176 (2023) 1

Full HTML

Free Access

Review

Issue		Rev. Fr. Geotech. Number 176, 2023


Article Number		1
Number of page(s)		18
DOI		https://doi.org/10.1051/geotech/2023020
Published online		07 November 2023

Rev. Fr. Geotech. 2023, 176, 1

Revue / Review Article

Simulation des écoulements gravitaires avec les modèles d’écoulement en couche mince : état de l’art et exemple d’application aux coulées de débris de la Rivière du Prêcheur (Martinique, Petites Antilles)

Simulating gravitational flows with thin-layer models: state-of-the-art and application to debris flow modelling in the Prêcheur river (Martinique, Lesser Antilles).

Marc Peruzzetto¹^,2^*, Gilles Grandjean¹, Anne Mangeney², Clara Levy¹, Yannick Thiery¹, Benoit Vittecoq³, François Bouchut⁴, Fabrice R. Fontaine⁵ et Jean-Christophe Komorowski²

¹ BRGM, 45060 Orléans, France
² Université Paris Cité, Institut de physique du globe de Paris, CNRS, F-75005 Paris, France
³ BRGM, 97200 Fort-de-France, Martinique
⁴ Laboratoire d’analyse et de mathématiques appliquées (UMR 8050), CNRS, Univ. Gustave Eiffel, UPEC, 77454 Marne-la-Vallée, France
⁵ Observatoire volcanologique et sismologique de la Martinique, Institut de physique du globe de Paris, 97250 Fonds-Saint-Denis, France

^* Auteur de correspondance : m.peruzzetto@brgm.fr

Résumé

La quantification de la propagation des glissements de terrain est une étape clé de l’analyse des risques gravitaires. Dans ce contexte, les modèles d’écoulement en couche mince sont de plus en plus utilisés pour simuler la dynamique d’écoulements gravitaires comme les coulées de débris. Ils sont plus souples d’utilisation et moins coûteux en temps de calcul que des modèles 3D plus complexes, et fournissent des informations plus précises sur les vitesses et les épaisseurs des écoulements que des méthodes purement empiriques. Dans cette revue de la littérature, nous présentons les principales rhéologies utilisées pour modéliser des écoulements gravitaires homogènes, et donnons un exemple d’application pratique avec la Rivière du Prêcheur (Martinique, Petites Antilles). Nous discutons ensuite les principales pistes de développements permettant d’utiliser ces modèles dans le cadre d’études opérationnelles d’analyse d’aléas et de risques.

Abstract

Quantifying the propagation of landslides is a key step for analyzing gravitational risks. In this context, thin-layer models have met a growing success over the past years to simulate the dynamics of gravitational flows, such as debris flows. They are easier to use and require less computing ressources than 3D models, and provide more detailed estimations of flow thicknesses and velocities than purely empirical methods. In this literature review, we present the main rheologies used to model homogeneous gravitational flows, and describe a practical case study with debris flow modeling in the Prêcheur River (Martinique, Lesser Antilles). Then, we discuss possible developments for operational hazard and risk assessment with thin-layer models.

Mots clés : glissement de terrain / simulation / couche mince / aléas gravitaires / coulée de débris / risques

Key words: landslide / simulation / thin-layer / gravitational hazards / debris flow / risks

Note to the reader: The translated English title has been added on 9 February 2024.

© CFMS-CFGI-CFMR-CFG, 2023

Introduction

D’après Petley (2012) et Froude et Petley (2018), 55 000 personnes ont été tuées dans le monde par des mouvements de terrain entre 2004 et 2016, sans compter les mouvements déclenchés par des séismes. Les mouvements de terrain peuvent également avoir un impact économique significatif. Par exemple, en Espagne, les coûts directs (réparation et remplacement des infrastructures ou bâtiments affectés) sont estimés à 200 millions de dollars par an (Kjekstad et Highland, 2009). En France, le glissement du Chambon en 2015 a provoqué la fermeture de la route reliant Grenoble à Briançon pendant 2 ans (Dubois et al., 2016). Si les zones montagneuses sont les plus touchées par ces phénomènes, les régions côtières et les reliefs moins escarpés peuvent aussi être affectés. Ainsi, les coteaux de la vallée de la Marne et de la Montagne de Reims connaissent régulièrement des déstabilisations qui endommagent les axes de communication ainsi que des parcelles cultivées (e.g. Den Eeckhaut et al., 2010).

Compte tenu de ces enjeux économiques et humains, la communauté internationale (Fell et al., 2008 ; Corominas et al., 2014) préconise une stratégie 4 étapes pour analyser l’aléa puis évaluer les risques associés :

caractérisation du type de mouvements de terrain pouvant se produire sur le site d’étude. Cela passe souvent par la constitution d’un inventaire ;
établissement d’une carte de susceptibilité par type de phénomène, intégrant la probabilité spatiale d’occurrence des événements (i.e., identification des zones susceptibles de générer des mouvements de terrain) et la probabilité d’atteinte compte tenu des zones de départ identifiées. Dans la littérature, la notion de susceptibilité se rapporte parfois seulement à la probabilité spatiale d’occurrence ;
établissement d’une carte d’aléa (par type de phénomène ou pour tous les types de mouvements de terrains), qui intègre les probabilités spatiales et temporelles d’occurrence des phénomènes, selon leur magnitude (e.g. volume) et/ou leur intensité (e.g. vitesse) ;
analyse des risques, c’est-à-dire de l’impact des mouvements de terrain sur les enjeux (population, bâtiments, infrastructures). Cette analyse se base sur la quantification des aléas faite à l’étape précédente.

Les méthodes utilisées dépendent de la taille du site d’étude, des objectifs (e.g. cartes informatives ou réglementaires) et des données disponibles. Nous nous intéressons ici plus particulièrement à l’étape de caractérisation de la propagation, pour des analyses d’aléas et/ou de risques à l’échelle du site, où les zones sources sont bien identifiées. Nous considérons par ailleurs seulement la propagation des écoulements gravitaires, c’est-à-dire des mouvements de matériaux solides (terre/débris/roche/glace) et/ou liquides sous l’effet de la gravité et dont la dynamique est semblable à celle d’écoulements. Les écoulements gravitaires peuvent se propager à de grandes distances de leur zone d’initiation. C’est le cas notamment des avalanches de blocs qui parcourent parfois plusieurs kilomètres (e.g. Korup et al., 2013 ; Lucas et al., 2014). De même, les écoulements chargés en eau comme les coulées de débris et les laves torrentielles peuvent se propager sur plusieurs kilomètres ou dizaines de kilomètres (e.g. Coussot et Meunier, 1996 ; Thouret et al., 2020). Les vitesses associées atteignent parfois plusieurs dizaines de km hr⁻¹, ce qui rend ces écoulements dangereux pour les populations, les infrastructures et les bâtiments (Givry et Peteuil, 2011 ; Santi et al., 2011). La quantification de la propagation des écoulements gravitaires (distance de parcours, épaisseur et vitesse de l’écoulement, débit, ...) permet donc de mieux estimer les potentiels dégâts, et donc les risques associés. Cette quantification peut être réalisée de manière purement empirique à partir de bases de données d’observations. Par exemple, Mitchell et al. (2019) ont établi une loi puissance reliant la distance de parcours au volume d’avalanches de blocs (voir aussi, par exemple, Lucas et al., 2007 ; Corominas, 1996). Une approche similaire est utilisée par Rickenmann (1999) et Berti et Simoni (2014) pour estimer le débit, la distance de parcours et les zones inondées par des coulées de débris. Pour obtenir des résultats plus détaillés, des méthodes numériques à base physique résolvant les équations de la dynamique sont nécessaires.

Dans cette perspective, les modèles d’écoulement en couche mince sont de plus en plus utilisés. Ils simulent l’épaisseur de l’écoulement et la vitesse moyennée sur l’épaisseur. Ils sont ainsi plus faciles à mettre en oeuvre que des modèles 3D qui modélisent la dynamique de chaque particule solide et/ou de chaque volume élémentaire de fluide. Ces modèles 3D sont en effet coûteux en temps de calcul, nécessitent souvent la calibration de nombreux paramètres, et ne modélisent qu’un ou deux des processus physiques contrôlant la dynamique des écoulements gravitaires (Andreotti et al., 2013 ; Delannay et al., 2017). À l’inverse, les paramètres des modèles d’écoulement en couche mince sont généralement empiriques, mais moins nombreux. Cela simplifie leur calibration et l’analyse de sensibilité : dans le cas le plus simple, la mobilité de l’écoulement peut n’être contrôlée que par un seul paramètre (par exemple, un coefficient de friction basale).

Dans cette revue de la littérature, nous donnons les principales rhéologies utilisées dans les modèles monophasiques d’écoulement en couche mince (i.e., les matériaux s’écoulant sont supposés homogènes), sans prise en compte de l’érosion. Nous montrons ensuite comment un modèle d’écoulement en couche mince, SHALTOP, peut être utilisé pour une étude d’aléa, en prenant l’exemple de la rivière du Prêcheur, en Martinique. Nous discutons enfin de plusieurs axes de recherches actuels visant à améliorer les modèles existants, et à développer leur utilisation pour l’analyse d’aléas et de risques.

1 Les modèles d’écoulement en couche mince

1.1 Les principales rhéologies de modèles monophasiques : approche historique

Le principe de dérivation des équations d’écoulement en couche mince est d’intégrer les équations locales de conservation de la masse et des moments, perpendiculairement à la topographie, sur l’épaisseur (supposée petite) de l’écoulement. Les équations locales sont données par :

$\partial_{t} \vec{U} + (\vec{U} \cdot \nabla_{\vec{X}}) \vec{U} = - \vec{g} + \nabla \cdot σ,$ (1)

$\nabla_{\vec{X}} \cdot \vec{U} = 0,$ (2)

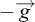où $\vec{U} (\vec{X})$ est le champ de vitesse en 3 dimensions, $- \vec{g}$ est la gravité et σ est le tenseur des contraintes. En supposant notamment que l’épaisseur de l’écoulement est faible par rapport à son étendue spatiale, et que la vitesse moyennée sur l’épaisseur est parallèle à la topographie, l’intégration des équations permet de réduire la dimension du problème. Cette approche a été initialement développée par Barré de Saint-Venant (1871), puis a été adaptée pour des applications hydrauliques (e.g. Dressler, 1978). La méthode a ensuite été reprise par Savage et Hutter (1989) pour modéliser des écoulements gravitaires secs. Depuis les années 2000, les modèles d’écoulement en couche mince sont de plus en plus utilisés pour des applications opérationnelles (e.g. McDougall, 2017 ; Pastor et al., 2018a). Plusieurs outils numériques commerciaux et académiques existent, comme RAMMS (Christen et al., 2010), DAN3D (McDougall et Hungr, 2004), FLO-2D (O’Brien et al., 1993 ; Jakob et al., 2013), r-avaflow (Mergili et al., 2017), Volcflow (Kelfoun et Druitt, 2005) ou SHALTOP (Bouchut et al., 2003 ; Bouchut et Westdickenberg, 2004 ; Mangeney et al., 2007).

Nous donnons ici les équations pour des écoulements homogènes, sans érosion basale. Ces équations sont en effet les plus simples à utiliser pour des applications pratiques : les modèles plus complexes nécessitent des informations parfois compliquées à obtenir en pratique comme la fraction liquide ou les épaisseurs érodables. Une étape clé de l’obtention des équations est l’écriture des équations locales de conservation dans un référentiel lié à la topographie, l’intégration devant en effet se faire perpendiculairement à la topographie. Le changement de référentiel est particulièrement complexe sur des topographies 2D quelconques Z = b(X,Y) à cause des dérivées spatiales de deuxième ordre (Bouchut et Westdickenberg, 2004 ; Luca et al., 2009). Une dérivation correcte est toutefois nécessaire pour bien décrire les effets de la courbure de la topographie, notamment pour les écoulements rapides (Peruzzetto et al., 2021).

Par simplicité, nous donnerons seulement les équations d’écoulement en couche mince pour des topographies 1D, avec Z = b(X) (Fig. 1). Considérant un système de coordonnées curvilignes associé (ξ₁,ξ₂) (ξ₁ le long de la topographie, ξ₂ dans la direction normale à la topographie), les équations d’écoulement en couche mince ont la forme générale suivante (Savage et Hutter, 1991 ; Peruzzetto, 2021b) :

$\partial_{t} h + \frac{\partial h u}{\partial ξ_{1}} = 0,$ (3)

$\partial_{t} (h u) + \frac{\partial}{\partial ξ_{1}} (α h u^{2}) + \frac{\partial}{\partial ξ_{1}} (\frac{1}{2} k g h^{2} \cos (θ)) = g h \sin (θ) - S,$ (4)

avec h l’épaisseur de l’écoulement, u la vitesse moyennée sur l’épaisseur de l’écoulement, θ la pente de la topographie (positive pour db/dX<0), g le coefficient de gravité, α un facteur de forme associé à des profils de vitesse non linéaires (on prend en général α = 1), et k un coefficient introduit pour prendre en compte la friction interne. Le terme source S intègre les effets dissipatifs d’énergie qui ralentissement l’écoulement, par exemple par friction, turbulence et/ou viscosité. Son expression dépend donc de la rhéologie choisie, comme expliqué dans les paragraphes suivants.

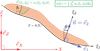Fig. 1

Notations pour les équations d’écoulement en couche mince sur une topographie 1D Z = b(X).

Notations for thin-layer equations on a 1D topography Z = b(X).

1.1.1 Modèle hydrostatique avec friction basale

La méthode la plus simple pour obtenir les équations d’écoulement en couche mince est de considérer que dans le référentiel lié à la topographie (ξ₁,ξ₂) (voir Fig. 1) le tenseur des contraintes est donné (toujours pour un écoulement sur une topographie Z = b(X)) par :

$σ = (\begin{array}{c} - p & σ_{12} \\ σ_{21} & - p \end{array}),$ (5)

avec σ₁₂ = σ₂₁ et p la pression hydrostatique. On peut alors introduire une condition de friction à la base de l’écoulement (rhéologie de Coulomb) :

$σ \vec{n} - (\vec{n} \cdot σ \vec{n}) \vec{n} = - μ \frac{\vec{U}}{‖ \vec{U} ‖} (- \vec{n} \cdot σ \vec{n}) +,$ (6)

μ = tan(δ) est le coefficient de friction basale, et δ l’angle de friction basale associé. Au premier ordre (en négligeant les effets d’inertie et de gradients d’épaisseurs), l’écoulement accélère s’il se propage sur des pentes tan(θ)>μ, et ralentit et s’arrête autrement. L’intégration des équations de conservation de la masse et des moments donne alors (Savage et Hutter, 1991 ; Peruzzetto, 2021b) :

$\partial_{t} (h u) + \frac{\partial}{\partial ξ_{1}} (h u^{2}) + \frac{\partial}{\partial ξ_{1}} (\frac{1}{2} g h^{2} \cos (θ)) = g h \sin (θ) - h μ \frac{u}{| u |} (g \cos (θ) + γ u^{2}),$ (7)

où γ = 1/R est la courbure de la topographie (R est le rayon de courbure). La généralisation de ces équations à des topographies 2D Z = b(X,Y) n’est pas simple. Pour conserver le formalisme mathématique tout en arrivant à une expression similaire à (7), Bouchut et Westdickenberg (2004) choisissent

$σ = σ^{'} - p I_{3},$ (8)

avec I₃ la matrice identité et

$σ^{'} = ν (\nabla_{\vec{X}} \vec{U} + {(\nabla_{\vec{X}} \vec{U})}^{t})$ (9)

où ν est la viscosité dynamique, qui est supposée très petite et disparaît dans les équations finales. Cela revient à considérer des écoulements laminaires pour lesquels les termes dominant de σ′ sont les dérivées de la vitesse dans la direction normale à la topographie. Cela permet d’introduire formellement la condition à la base de l’écoulement (6), ce qui ne serait possible si on avait simplement σ = −pI₃.

En réécrivant l’équation (7) dans le référentiel cartésien (X,Z) et en prenant en compte les approximations faites pour obtenir l’équation (4) (pour plus de détails, voir Bouchut et Westdickenberg, 2004 ; Bouchut et al., 2022), l’équilibre est obtenu pour :

$u = 0 et | \partial_{X} (\cos (θ) h + Z) | \leq μ = \tan (δ)$ (10)

Autrement dit, la masse reste stable tant que l’inclinaison de sa surface libre reste inférieure à δ. Introduit formellement comme un coefficient de friction basale, μ traduit donc également la résistance interne des matériaux. En pratique, il est compliqué de relier μ à des propriétés géotechniques des matériaux s’écoulant, d’autant plus que ces propriétés peuvent varier lors de la propagation (par exemple par fracturation, incorporation d’eau ou variation de la nature de la surface de propagation). Ainsi, la modélisation d’écoulements gravitaires à l’échelle du terrain nécessite une étape de calibration : μ est déterminé empiriquement, et traduit tous les processus de dissipation d’énergie au sein de l’écoulement, par friction basale mais aussi, notamment, par friction/collision entre grains solides et/ou par viscosité.

Il faut par exemple μ = tan(2°) = 0,03 pour modéliser des coulées de débris particulièrement mobiles (Frimberger et al., 2021 ; Peruzzetto et al., 2022b). La modélisation d’avalanches rocheuses et d’avalanches de débris nécessite un coefficient de friction d’autant plus faible que le volume mobile est important (typiquement, de μ = tan(30°) = 0,58 pour un volume de 10³ m³, à μ = tan(10°) = 0,18 pour un volume de 10⁹ m³, Lucas et al., 2014). Plusieurs études montrent néanmoins qu’un coefficient de friction variable, fonction de la vitesse et de l’épaisseur de l’écoulement, permet de mieux reproduire les observations. Lucas et al. (2014) proposent ainsi une loi empirique de diminution du coefficient de friction avec la vitesse, pour reproduire la mobilité importante des grands glissements de terrain :

$μ = \frac{μ_{o} - μ_{w}}{| u | / u_{w}} + μ_{w} si | u | > u_{w},$ (11)

$μ = μ_{o} sinon,$ (12)

avec u la vitesse de l’écoulement, u_w une vitesse seuil déterminée empiriquement, et μ_о et μ_w deux coefficients de friction atteints respectivement pour |u| ≤ u_w et |u| → +∞. Lucas et al. (2014) montrent que μ_о = tan(40°) = 0,84, μ_w = tan(6^_°) = 0,11 et u_w = 4,1 m s⁻¹ permettent de reproduire la propagation d’écoulements gravitaires notamment sur Terre et sur Mars.

À l’inverse, une augmentation du coefficient de friction pour des vitesses importantes et/ou de faibles épaisseurs permet de simuler la chenalisation d’écoulements granulaires secs (Mangeney et al., 2007 ; Edwards et al., 2017). Cette approche a été développée suite à des expériences de laboratoire (Pouliquen et Forterre, 2002), et a été ensuite théorisée avec la rhéologie μ(I) qui modélise la friction à l’intérieur d’écoulements granulaires (voir Sect. 1.1.3 pour les détails de cette rhéologie).

Mais, avant le développement de la rhéologie μ(I), une approche géotechnique a d’abord été utilisée pour distinguer la friction se produisant à l’intérieur de l’écoulement de la friction à la base de l’écoulement, au contact de la topographie.

1.1.2 La friction interne : une approche géotechnique

Dans leurs premiers travaux, Savage et Hutter (1989, 1991) ont déduit les équations (3) et (4) pour des écoulements granulaires secs, et ont ainsi introduit une rhéologie frictionnelle à laquelle ils associent deux angles de friction : l’angle de friction interne Φ et l’angle de friction basal δ.

Dans leurs calculs, Savage et Hutter (1991) reprennent ainsi la condition de friction basale, comme dans le paragraphe précédent. Ils supposent aussi que, pendant l’écoulement, le critère de rupture de Mohr-Coulomb est constamment vérifié. En chaque point du fluide, il existe alors un élément planaire pour lequel les contraintes normales N et tangentielles T vérifient :

$T = \tan (Φ) N .$ (13)

L’hypothèse de friction basale implique que les contraintes tangentielles (T_b) et normales (N_b) à la topographie vérifient :

$T_{b} = - \frac{u}{| u |} \tan (δ) N_{b},$ (14)

où le signe dépend de la direction de la vitesse. Les relations (13) et (14) étant vérifiées toutes les deux à la base de l’écoulement, l’utilisation des diagrammes de Mohr-Coulomb permet d’identifier géométriquement deux états de contraintes possibles : un état "passif" lors de la contraction de l’écoulement, et un état "actif" lors de sa dilatation. Le coefficient k de l’équation (4) peut prendre alors deux valeurs (Savage et Hutter, 1991) :

$k_{a c t} = 2 \frac{1 - \sqrt{1 - (1 + \tan^{2} (δ)) \cos^{2} (ϕ)}}{\cos^{2} (ϕ)} - 1 quand \partial_{ξ_{1}} u > 0$ (15)

$k_{p a s s} = 2 \frac{1 + \sqrt{1 - (1 + \tan^{2} (δ)) \cos^{2} (ϕ)}}{\cos^{2} (ϕ)} - 1 quand \partial_{ξ_{1}} u < 0$ (16)

Ce sont les coefficients de poussées, classiquement utilisés en mécanique des sols. Cette approche permet de reproduire en partie la géométrie de dépôts expérimentaux (e.g. avec δ = 30° et Φ = 40°, Gray et al., 1999 ; Pirulli et al., 2007). L’extension des équations à des topographies quelconques Z = b(X,Y) est toutefois difficile car l’utilisation des cercles de Mohr ne suffit plus. Dans ces situations, des simplifications sont nécessaires pour avoir une expression de la friction interne invariante par rotation (Christen et al., 2010 ; Kelfoun et Druitt, 2005), ou il faut au contraire déterminer toutes les composantes du tenseur de contraintes, ce qui est beaucoup plus complexe (Denlinger et Iverson, 2004). Par ailleurs, l’utilisation d’un critère de stabilité statique (angle de friction interne Φ) pour décrire un comportement dynamique peut être discuté, d’autant plus qu’il implique dans les équations (15) et (16) que Φ soit supérieur à l’angle de friction basale δ.

La rhéologie μ(I), présentée dans le paragraphe suivant, propose une approche plus générale avec un coefficient de friction interne variable.

1.1.3 La rhéologie μ(I) pour des écoulements granulaires

Depuis le début des années 2000, la rhéologie de μ(I) est de plus en plus utilisée pour étudier les écoulements granulaires. Grâce à des arguments dimensionnels et des simulations numériques, GDR MiDi (2004) et Jop et al. (2006) ont montré que pour des écoulements 1D (i.e. sur des topographies Z = b(X)) en régime permanent,

$T = μ (I) N,$ (17)

$I = \frac{\overset{}{γ} d}{\sqrt{p / ρ *}},$ (18)

où T et N sont les contraintes tangentielles et normales à la direction de l’écoulement, p la pression, I le nombre d’inertie, $\dot{γ}$ le taux de cisaillement, d le diamètre des grains, ρ* la masse volumique des grains et μ(I) un coefficient de friction variable, fonction du nombre d’inertie I. Le nombre d’inertie I, sans dimension, est le rapport du temps caractéristique de réarrangement des grains, sur le temps caractéristique de la déformation de l’écoulement granulaire (GDR MiDi, 2004). Des valeurs élevées de I correspondent donc à des écoulements dominés par les déformations macroscopiques par cisaillement. L’équation (17) peut être vue comme une généralisation de l’équation (13), avec un coefficient de friction μ(I) dépendant de la dynamique de l’écoulement. Une forme tensorielle des équations (17) et (18) a été donnée par Jop et al. (2006) et Gray et Edwards (2014) pour exprimer le déviateur σ′ du tenseur de contraintes (voir équation (8)) :

$σ^{'} = \frac{μ (I) p}{‖ D ‖} D,$ (19)

$I = \frac{2 ‖ D ‖ d}{\sqrt{p / ρ^{*}}} .$ (20)

En notant 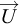$\vec{U}$ le champ de vitesses en coordonnées cartésiennes, 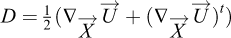$D = \frac{1}{2} (\nabla_{\vec{X}} \vec{U} + {(\nabla_{\vec{X}} \vec{U})}^{t})$ et $‖ D ‖ = \sqrt{\frac{1}{2} t r (D^{2})}$ . Ces équations sont cohérentes avec une friction solide de Coulomb, car lorsque I → 0, l’écoulement se produit seulement si :

$‖ σ^{'} ‖ > μ_{s} p,$ (21)

où μ_s est un coefficient de friction donné (Jop et al., 2006).

La rhéologie de μ(I) a été utilisée pour dériver les équations d’écoulement en couche mince sur des topographies 1D par Gray et Edwards (2014), en supposant des écoulements en régime permanent :

$\partial_{t} (h u) + \frac{\partial}{\partial ξ_{1}} (h u^{2}) + \frac{\partial}{\partial ξ_{1}} (\frac{1}{2} g h^{2} \cos (θ)) = g h \sin (θ) - S,$ (22)

avec

$S = μ (I) g h \cos (θ) \frac{u}{| u |} - \frac{\partial}{\partial ξ_{1}} (v h^{\frac{3}{2}} \frac{\partial u}{\partial ξ_{1}}) .$ (23)

S fait apparaître un terme frictionnel avec un coefficient de friction μ(I) dépendant du nombre d’inertie, et un terme "visqueux" introduisant le paramètre v (qui peut être formellement relié à I et à la pente locale de la topographie). L’étude expérimentale d’écoulements granulaires donne (Jop et al., 2006) :

$μ (I) = μ_{1} + (μ_{2} - μ_{1}) \frac{1}{\frac{I_{o}}{I} + 1},$ (24)

où I_о, μ₁ et μ₂ sont des constantes et où la valeur du nombre d’inertie intégrée sur l’épaisseur de l’écoulement est :

$I = \frac{5 d u}{2 h \sqrt{g h Φ \cos (θ)}},$ (25)

avec Φ la fraction solide volumique. Ionescu et al. (2015) utilisent par exemple μ₁ = tan(25,5°) = 0,48, μ₂ = tan(36°) = 0,73 et I_о = 0,279. L’équation (24) n’est néanmoins valide que pour des écoulements permanents (plus précisément, pour des nombres de Froude élevés). Elle doit donc être adaptée pour les faibles vitesses (e.g. Pouliquen et Forterre, 2002 ; Edwards et al., 2017).

Notons que pour obtenir les équations (22) et (23), Gray et Edwards (2014) supposent un écoulement sans glissement basal et utilisent (19) : il n’y a donc pas de friction basale dans les équations initiales. Toutefois, à l’exception des termes visqueux, les équations (22) et (23) peuvent aussi être obtenues en considérant la condition limite de friction basale de l’équation (6), en choisissant μ(I) comme coefficient de friction basale, et sans imposer de contrainte sur la vitesse basale. Le coefficient μ(ɪ) peut donc à la fois être vu comme un coefficient de friction interne dynamique, et un coefficient de friction basal. Comme dans le cas d’un coefficient de friction basale constant (voir Sect. 1.1.1), sa valeur reste donc empirique. Les limitations de la rhéologie μ(ɪ) sont évoquées plus en détail par Delannay et al. (2017) ; ces limites incluent, entre autre, le fait que la rhéologie μ(ɪ) ne soit pas reliée par une analyse théorique aux interactions à l’échelle des grains. Par ailleurs, les formulations existantes de la rhéologie ne sont pas mathématiquement bien posées. Cela peut conduire à des instabilités numériques dans les simulations pour des valeurs de I trop élevées ou trop faibles. Enfin, l’extension des équations d’écoulement en couche mince avec la rhéologie μ(ɪ) à des topographies 2D Ζ = b(X,Y) n’a été faite que pour le cas d’un plan incliné Ζ(X,Y) = tan(θ)X (Baker et al., 2016).

Malgré ces limites, l’utilisation empirique de la rhéologie μ(I) avec la formulation présentée plus haut sur des topographies quelconques donne de meilleurs résultats qu’un coefficient de friction constant. La rhéologie μ(I) permet en effet de mieux reproduire les dépôts de glissements de terrain aériens (e.g. Guimpier et al., 2021) et sous-marins (Brunet et al., 2017), l’auto-chenalisation des écoulements (Mangeney et al., 2007 : Mangold et al., 2010), et l’augmentation de la distance de parcours lors de la présence d’un lit érodable (Fernández-Nieto et al., 2016).

2.2.3 Modèles hydrauliques et visco-plastiques

Des approches hydrauliques sont aussi parfois utilisées, en particulier pour la modélisation des coulées de débris. Par exemple, la rhéologie associant les lois de Darcy-Weisbach et Manning donne pour S dans l’équation (4) (Chow, 1959 ; O’Brien et al., 1993 ; Jakob et al., 2013) :

$S = g n^{2} \frac{u^{2}}{h^{1 / 3}},$ (26)

où n en s m^−1/3 est le coefficient de Manning associé à la rugosité de la topographie (e.g. n = 0,02 à n = 0,1 dans Jakob et al., 2013). Cette équation a été déduite empiriquement pour des écoulements permanents dans des chenaux ouverts.

La modélisation des écoulements chargés en eau avec une fraction solide argileuse (comme certaines laves torrentielles) nécessite l’utilisation de rhéologies visco-plastiques (e.g. Coussot et al., 1993 ; Laigle et Coussot, 1997). La loi de Bingham décrit ainsi des écoulements visqueux à seuil. Pour un écoulement sur une topographie 1D Z = b(X), elle donne l’expression de la contrainte de cisaillement (toujours dans le référentiel (ξ₁, ξ₂) lié à la topographie) :

$σ_{12} = τ_{y} + v \frac{\partial u_{1}}{\partial ξ_{3}} pour | \frac{\partial u_{1}}{\partial ξ_{3}} | \geq 0,$ (27)

$σ_{12} \leq τ_{y} pour | \frac{\partial u_{1}}{\partial ξ_{3}} | = 0,$ (28)

où τ_y est la contrainte de rupture ("yield stress" en anglais) et ν est la viscosité dynamique. Dans la partie supérieure de l’écoulement, la contrainte de cisaillement est inférieure à τ_y et la vitesse est constante. Dans la partie inférieure, la vitesse présente un profil parabolique. Suivant les travaux de Pastor et al. (2004), la contrainte basale est alors liée à la vitesse moyenne de la colonne de fluide par une équation du troisième degré (voir aussi Peruzzetto, 2021b). Une solution simplifiée pour S est donnée par :

$S = \frac{3}{2} \frac{τ_{y}}{ρ} + 3 \frac{v}{ρ} \frac{u}{h},$ (29)

avec ρ la masse volumique. La contrainte basale augmentant pour des vitesses élevées et des petites épaisseurs (comme pour la rhéologie μ(ɪ)), la rhéologie de Bingham permet de reproduire l’auto-chenalisation et la formation de levées sur les côtés des écoulements (Coussot et al., 1993). Des formes plus complexes que la loi de Bingham ont été proposées. Par exemple, la loi de Herschel-Bulkley permet de modéliser des comportements non linéaires (Laigle et Coussot, 1997 ; Remaître et al., 2005) :

$σ_{12} = τ_{y} + k {(\frac{\partial u_{1}}{\partial ξ_{2}})}^{m},$ (30)

où k est le facteur de consistance (Pa s ^m ) et correspond à une viscosité pour m = 1, et m est l’indice de rhéofluidification, sans unité. L’analyse rhéométrique d’échantillons montre que m = 1/3 peut souvent être utilisé pour les coulées de débris visqueuses (Remaître et al., 2005). Pour une masse volumique ρ = 1800 kg m⁻³, τ_y varie typiquement entre 30 et 1000 Pa, et k entre 8 et 200 Pa s^−m (Remaître et al., 2005). Par l’analyse des équations et la comparaison avec des expériences, Coussot (1994) montre que pour des écoulements permanents sur des plans infinis, et pour m = 1/3, on obtient :

$S = \frac{τ_{y}}{ρ} [1 + 1, 93 {(\frac{τ_{y}}{k} {(\frac{h}{u})}^{\frac{1}{3}})}^{- 0.9}]$ (31)

Si τ_y = 0, Pastor et al. (2015) calculent :

$S = \frac{k}{ρ} {(\frac{1 + 2 m}{m})}^{m} {(\frac{u}{h})}^{m} .$ (32)

En particulier, en prenant m = 2 et en ajoutant un terme de friction, on obtient :

$S = g h \cos θ \tan δ + \frac{25 k}{4 ρ} \frac{u^{2}}{h^{2}} .$ (33)

Cette expression peut être reliée à la loi empirique de Voellmy (Voellmy, 1955), couramment utilisée pour modéliser des avalanches et des coulées de débris (McDougall, 2017) :

$S = g h \cos θ \tan δ + g \frac{u^{2}}{ξ},$ (34)

où ξ est un paramètre empirique appelé le coefficient de turbulence, généralement choisi entre 100 et 500 m s⁻² (Zimmermann et al., 2020).

Les différentes rhéologies présentées plus haut sont résumées dans le tableau 1. Elles sont toutes empiriques, dans la mesure où les paramètres associés sont difficiles à relier aux propriétés physiques des matériaux. Les paramètres sont en effet soit fondamentalement empiriques (comme le coefficient de friction de Voellmy), soit complexes à mesurer (comme la viscosité de coulées de débris : Sosio et al., 2007). Les paramètres des modèles d’écoulement en couche mince doivent donc être calibrés en reproduisant des événements connus, avec la difficulté d’avoir à disposition des données pour caractériser ces événements (par exemple, volumes mobilisés, vitesses et épaisseurs des dépôts). Notons par ailleurs que, à notre connaissance, aucun modèle ne permet de combiner une description rhéologique complexe des écoulements avec une dérivation rigoureuse des équations sur des topographies quelconques. L’approche la plus générale est donnée par Luca et al. (2009), mais elle-même nécessite des hypothèses sur les profils de vitesse au sein de l’écoulement. Par ailleurs, les équations de Luca et al. (2009) n’ont pas été implémentées dans un modèle numérique.

Ainsi, il peut être préférable d’utiliser des rhéologies plus simples nécessitant la calibration de moins de paramètres, tout en utilisant des équations décrivant le plus précisément possible la géométrie de topographies complexes. C’est cette approche qui a été choisie pour le code SHALTOP.

Tableau 1

Principales rhéologies pour les modèles monophasiques d’écoulement en couche mince . Les notations en gras sont les paramètres à choisir dans les simulations. Leur description est donnée dans le corps de l’article. Des comparaisons de simulations avec différentes rhéologies peuvent par exemple être trouvées dans McArdell et al. (2003) ou Pirulli et Mangeney (2008).

Main rheologies for homogeneous thin-layer models. Bold symbols are the parameters to be chosen in simulations. Their description is given in the main body of the article. Comparisons of simulations with different rheologies can be found, for instance, in McArdell et al. (2003) and Pirulli et Mangeney (2008).

1.2 SHALTOP

Le modèle SHALTOP modélise la propagation d’écoulements homogènes, sans érosion, sur des topographies complexes (Bouchut et al., 2003 ; Bouchut et Westdickenberg, 2004 ; Mangeney et al., 2007). Il a été testé pour modéliser des expériences de laboratoire (Mangeney-Castelnau et al., 2005) et des avalanches de débris ou de roches (e.g. Lucas et al., 2014 ; Moretti et al., 2015). Contrairement à la majorité des autres codes d’écoulement en couche mince, SHALTOP prend en compte précisément la courbure de la topographie dans les équations. Peruzzetto et al. (2021) ont montré que la courbure de la topographie peut avoir une influence significative sur la dynamique des écoulements rapides, en particulier pour modéliser les débordements d’écoulements chenalisés.

Pour des topographies 1D Z = b(X), les équations résolues par SHALTOP sont celles données par les équations (3) et (7). Sur des topographies 2D Z = b(X,Y), leur forme est plus complexe. Les équations incluent notamment le tenseur de courbure de la topographie. Par souci de simplicité, nous ne les donnons pas ici. Elles peuvent être trouvées dans Mangeney et al. (2007). La dérivation précise des équations est expliquée par Bouchut et Westdickenberg (2004), et la méthodologie est expliquée plus succinctement par Peruzzetto et al. (2021).

Dans sa forme la plus simple, SHALTOP n’utilise qu’une rhéologie frictionnelle de Coulomb avec un coefficient de friction μ_s constant. Néanmoins, le code permet d’utiliser des coefficients de friction non constants, dépendant par exemple de la vitesse de l’écoulement, et d’autres rhéologies (comme celles de Bingham ou de Voellmy). Dans la section suivante, nous montrons comment SHALTOP peut être utilisé pour modéliser des coulées de débris et quantifier l’exposition d’un village à ces coulées. Nous prenons le cas d’étude de la Rivière du Prêcheur, en Martinique (Petites Antilles).

2 Exemple d’application : les coulées de débris de la rivière du Prêcheur (Martinique, Petites Antilles)

Nous présentons ici une étude réalisée dans le cadre d’une thèse (Peruzzetto, 2021b ; Peruzzetto et al., 2022b) et d’un projet d’appui aux politiques publiques (Peruzzetto, 2021a). L’objectif de ces travaux était d’analyser les aléas associés à des avalanches de blocs générées par la déstabilisation d’un escarpement rocheux, et aux coulées de débris générées par la remobilisation dans une rivière des dépôts des avalanches de blocs. Pour ce cas d’étude en Martinique (Petites Antilles), SHALTOP a été utilisé pour modéliser la propagation des avalanches de blocs et des coulées de débris. SHALTOP ayant déjà été utilisé à plusieurs reprises pour modéliser des avalanches de blocs ou de débris (e.g. Lucas et al., 2014), nous nous concentrons ici sur la modélisation des coulées de débris.

Après avoir présenté le site d’étude, nous détaillons les différentes étapes de l’utilisation de SHALTOP : (i) la collecte de données de terrain pour caractériser les phénomènes modélisés et définir les scénarios de simulation, (ii) la calibration du modèle en reproduisant un événement historique, et (iii) la simulation directe d’événements possibles pour l’analyse de risques. Les deux premiers points sont détaillés dans Peruzzetto et al. (2022b), tandis que l’analyse de risques a été faite dans Peruzzetto (2021a).

2.1 Présentation du site

Le bassin versant de la Rivière du Prêcheur (Fig. 2) est situé sur le versant Ouest de la Montagne Pelée en Martinique (Petites Antilles). Le principal affluent de la rivière du Prêcheur est la rivière Samperre, dont la source est située au pied de la Falaise Samperre. 7 km séparent la Falaise Samperre de l’embouchure de la rivière, avec une pente moyenne du lit comprise entre 7° et 12° dans la partie amont, et entre 3° et 4° sur les 4 derniers kilomètres. La Falaise Samperre est difficilement accessible, ce qui rend sa caractérisation géologique et géotechnique difficile. En complétant la littérature par l’analyse de photos aériennes et orthophotographies historiques, et de modèles numériques de terrain, Peruzzetto et al. (2022a) montrent que cet escarpement est essentiellement constitué (sur 100 à 200 m) de dépôts pyroclastiques indurés de granulométries variables, contenant des blocs métriques à pluri-métriques, et probablement mis en place entre 36 et 25 ka.

La Falaise Samperre est relativement récente : elle a été formée entre 1951 et 1980 par des éboulements successifs affectant principalement les formations pyroclastiques évoquées précédemment. Au moins cinq épisodes de déstabilisations majeures se sont produits en 1980, 1997–1998, 2009–2010 et 2018 (Aubaud et al., 2013 ; Clouard et al., 2013 ; Peruzzetto et al., 2022a). Par exemple, Clouard et al. (2013) estiment le volume effondré entre mars et mai 2010 à 2,1 × 10⁶ m³. Entre mai 2010 et août 2018, le volume effondré est estimé à 4,9 × 10⁶ m³, avec une phase paroxysmale d’effondrement début 2018 (Peruzzetto et al., 2022b). La crête de l’escarpement rocheux a ainsi reculé de 250 m entre 1988 et 2018. Peruzzetto et al. (2022a) suggèrent que ces déstabilisations sont liées à la vidange d’une paléo-vallée comblée par les dépôts pyroclastiques à partir de 36 ka. La surface de la paléo-vallée favorise les écoulements d’eau souterrains et fragilise progressivement la base de l’unité pyroclastique, conduisant à sa rupture et à des déstabilisations régressives (pour une discussion plus détaillée, voir Peruzzetto et al., 2022a).

Les éboulements associés ne menacent pas directement des zones habitées qui sont situées beaucoup plus en aval. En revanche, le réservoir de débris constitué en pied de falaise peut être remobilisé par l’eau sous forme de coulées de débris ou d’écoulements hyper-concentrés se propageant parfois jusqu’à l’embouchure de la rivière, avec une ou plusieurs vagues (ou bouffées) successives. Ces deux types d’écoulements, regroupés sous le terme générique de lahar en contexte volcanique, se différencient par la fraction solide et la manière dont elle est transportée. Les coulées de débris présentent une fraction solide supérieure à 60 % et les phases liquides et solides sont mélangées de manière homogène. À l’inverse, les écoulements hyper-concentrés ont une fraction solide comprise en 20 % et 60 %, et la fraction solide est transportée à la base de l’écoulement (Thouret et al., 2020).

Les lahars, et plus spécifiquement les coulées de débris, menacent le village du Prêcheur à l’embouchure de la rivière, 7 km en aval de la Falaise Samperre. Ainsi en juin 2010, une coulée de débris a inondé la rive droite de la rivière et détruit le pont permettant d’accéder à cette rive. Un nouveau pont a depuis été construit, mais des lahars importants pourraient le détruire à nouveau, isolant environ 420 personnes (INSEE, 2015). Dans les travaux de Peruzzetto (2021a) et Peruzzetto et al. (2022b), une approche conservative a été choisie : seuls les phénomènes les plus dangereux pour le village du Prêcheur sont considérés. Il s’agit des coulées de débris générées par une remobilisation rapide voire instantanée du réservoir de matériaux situé au pied de la Falaise Samperre.

Fig. 2

Le bassin versant du Prêcheur. (a) Carte générale du site d’étude (Modèle numérique de Terrain IGN Lito3D), avec la localisation des échantillons récupérés dans le lit de la rivière (PR-XX). La localisation du site aux Antilles et en Martinique est indiquée sur les deux cartes supérieures. (b) Vue du village du Prêcheur (30/03/2021, Carige). (c) Vue de la Falaise Samperre (02/02/2018, OVSM/IPGP) Adapté de Peruzzetto et al. (2022b).

Prêcheur river catchment. (b) Map of the study site (Digital Elevation Model IGN Lito3D), with the location of sampling sites (PR-XX). The location of the study site in the Caribbean and in Martinique island is given by the maps above. (c) Aerial view of the Prêcheur village (30/03/2021, Carige Company). (d) Photograph of the Samperre cliff (02/02/2018, OVSM/IPGP). Adapted from Peruzzetto et al. (2022b).

2.2 Caractérisation des phénomènes et rhéologie

La caractérisation des événements passés a pour but d’extraire des observations quantifiées qui pourront être comparées avec les résultats des simulations lors de l’étape de calibration. Dans le cas des coulées de débris de la rivière du Prêcheur, deux types d’observations sont disponibles : les zones affectées par les coulées de débris, et les temps de passage des écoulements à différents points de la rivière. Les zones affectées par les débordements au niveau du village du Prêcheur sont identifiées par des photos aériennes prises juste après les événements. Les temps de passage sont déduits des enregistrements de géophones ("Acoustic Flow Monitoring systems", ou AFMs) installés le long de la rivière et maintenus par l’Observatoire Volcanologique et Sismologique de Martinique (OVSM). En Martinique ils sont utilisés pour déclencher automatiquement des alarmes dans le village du Prêcheur lorsque le débit de la rivière augmente rapidement.

Le choix de la rhéologie pour modéliser des coulées de débris est intrinsèquement lié à la granulométrie de la fraction solide. Peruzzetto et al. (2022b) ont ainsi analysé la granulométrie de 11 échantillons de dépôts de lahars dans la rivière du Prêcheur (Fig. 3). L’absence d’argiles (moins de 4 % de silts et d’argiles) indique que la dynamique des écoulements est plus contrôlée par la collision et la friction entre les particules solides, que par des forces visqueuses (Dumaisnil et al., 2010). Ainsi une rhéologie visco-plastique n’est pas appropriée pour modéliser les coulées de débris de la rivière du Prêcheur, et des rhéologies frictionnelles sont préférables (loi de Coulomb et/ou rhéologie de Voellmy). Pour caractériser plus finement les matériaux solides des coulées de débris, il faudrait échantillonner les matériaux au pied de la Falaise Samperre, mais l’accès à cette zone est trop dangereux. Par ailleurs, la comparaison des échantillons ne permet pas non plus d’identifier une variation systématique de la granulométrie en fonction de la distance à la source. Cela peut être expliqué par le fait que les dépôts de plusieurs coulées de débris ont été échantillonnés. Compte tenu du nombre de coulées de débris qui se sont produites en 2018, l’étude de terrain de 2019 n’a pas permis d’isoler les dépôts d’un même événement sur tout le linéaire de la rivière.

Fig. 3

Étude des dépôts de lahars dans la Rivière du Prêcheur. (a) Exemple de site de prélèvement, avec distinction de deux types de dépôts. (b) Courbes granulométriques des 11 échantillons prélevés dans la rivière du Prêcheur (PR-01 à PR-11, de l’amont à l’aval, voir Figure 2 pour les localisations). Les fuseaux granulométriques de Dumaisnil et al. (2010) sont ajoutés. Les noms en gras correspondent aux échantillons visibles en (a). Adapté de Peruzzetto et al. (2022b).

Granulometric analysis and lahars deposits in the Prêcheur River. (a) Example of sampling site, with the distinction between two deposits types. (b) Granulometric curves of the 11 samples taken in the Prêcheur River (PR-01 to PR-11, from upstream to downstream, see Figure 2 for locations). Granulometric ranges of Dumaisnil et al. (2010) are also given. Samples in bold are the samples from (a). Adapted from Peruzzetto et al. (2022b).

2.3 Calibration du modèle

Peruzzetto (2021a) et Peruzzetto et al. (2022b) ont reproduit la coulée de débris du 19 juin 2010 pour calibrer le modèle SHALTOP. Cette coulée de débris fait suite à un épisode important de déstabilisations de la Falaise Samperre le 11 mai 2010, qui génère un réservoir de matériaux en pied de falaise. La coulée de débris du 19 juin 2010 a lieu entre 7h30 et 12h00 TU (Temps Universel), après une onde tropicale d’intensité non exceptionnelle (11 mm pendant 1h40 avant le début du lahar : Aubaud et al., 2013). Sa bouffée principale a lieu entre 8h30 et 9h00 TU après 30 mm de précipitations sur une heure. La propagation de l’écoulement est alors particulièrement rapide : il parcourt 1,5 km dans la partie amont de la rivière en seulement 2 à 3 min (soit une vitesse de 30 à 45 km hr⁻¹).

Cette vitesse considérée comme très rapide (voir la classification des vitesses de Cruden et Varnes, 1996) et la vidange complète du réservoir suggèrent que la coulée de débris a été initiée par une remobilisation instantanée du réservoir, peut-être par liquéfaction statique (c’est à dire une perte soudaine de résistance de matériaux lâches non drainés, par une mise en charge conduisant au cisaillement, à la compaction des matériaux et donc à une augmentation de la pression de pore, Lalubie, 2013). Malheureusement, aucun relevé topographique ne permet de reconstruire la géométrie de ce réservoir. Ainsi, Peruzzetto et al. (2022b) ont utilisé des relevés topographiques réalisés en 2018 sur lesquels un autre réservoir est identifiable, et qui est donc utilisé comme proxy du réservoir de matériaux remobilisé en juin 2010. Compte tenu des incertitudes associées à l’estimation du volume, Peruzzetto et al. (2022b) ont testé plusieurs volumes pour reproduire la coulée de débris. Ils ont aussi montré qu’une initiation progressive, avec une remobilisation progressive des matériaux et non instantanée, ne permettait pas d’améliorer significativement les résultats de la calibration.

Le meilleur accord entre les observations et les résultats de simulation est ainsi obtenu pour un volume de 0,65 × 10⁶ m³ remobilisé instantanément. La figure 4 présente les résultats des simulations avec la rhéologie de Coulomb et la rhéologie de Voellmy. Les meilleurs résultats sont obtenus avec Coulomb et μ = tan(2^°) : les zones inondées rive gauche sont surestimées, mais la zone inondée rive droite est correctement reproduite. Le temps de parcours simulé entre les stations RPRE et CPMA est de 4 minutes, ce qui est cohérent avec le temps de parcours estimé à partir des enregistrements des AFMS.

Ainsi, le choix d’une rhéologie simple de Coulomb, semi-emprique, n’utilisant qu’un seul paramètre, permet de reproduire les caractéristiques principales d’une coulée de débris de forte intensité. C’est donc cette rhéologie qui a été utilisée pour réaliser une analyse d’aléas puis de risques.

Fig. 4

Résultat de la calibration de SHALTOP pour reproduire la coulée de débris du 19 juin 2010 (0,65 × 10⁶ m³). (a) Épaisseur maximale avec la rhéologie de Voellmy, μ_S= tan(2^°) et ξ = 500 m s⁻², (b) avec la rhéologie de Coulomb et μ_S = tan(3^°), et (c) avec la rhéologie de Coulomb et μ_S = tan(2^°). Chaque point dans (d), (e), (f), et (g) est un résultat de simulation, avec le coefficient de friction donné par la couleur de la ligne et le coefficient de turbulence donné par l’abcisse. Les points à gauche de la ligne hachurée sont les résultats avec Voellmy, ceux à droite les résultats avec la rhéologie de Coulomb. (d) et (e) : surfaces inondées sur les rives gauches et droites, dans les zones habitées. (f) et (g) : durée de parcours entre RPRE et CPMA (1,6 km), et RPRE et le pont (4,3 km). Les zones grisées correspondent aux observations, en prenant en compte les incertitudes.

Simulation results for the June 19, 2010 debris flow (0.65 × 10⁶ m³). (a) Maximum flow thickness with the Voellmy rheology, μ_S= tan(2^°) and ξ = 500 m s⁻², (b) with the Coulomb rheology and μ_S = tan(3^°), and (c) with the Coulomb rheology and μ_S = tan(2^°). Each point in (d), (e), (f) and (g) is a simulation result, with friction coefficient given by line color and turbulence coefficient given by the x-coordinate. Left of hatches is for the Voellmy rheology, right is for the Coulomb rheology. (d) and (e) : Area flooded on the left and right riverbank, within inhabited areas. (f) and (g) : Flow travel duration between RPRE and CPMA (about 1.6 km), and between RPRE and the Prêcheur bridge (about 4.3 km). Grey patches are observations, taking into account uncertainties.

2.4 Modélisation directe et analyse de risques

Des coulées de débris de volumes variés (de 0,05 × 10⁶ m³ à 2 × 10⁶ m³) ont été modélisées par Peruzzetto (2021a), avec différentes géométries du lit de la rivière dans son dernier kilomètre. Plusieurs configurations sont considérées, avec un comblement, un creusement et/ou un élargissement du lit de la rivière préalablement à l’occurrence de la coulée de débris. Des merlons de protection de différentes longueurs sont également simulés. Dans chaque cas, l’exposition du village du Prêcheur est quantifiée en terme de nombres de bâtiments impactés. Pour des coulées de débris de volumes supérieurs à 1,5 × 10⁶ m³, les différentes configurations ne changent pas l’exposition du village du Prêcheur, dans la mesure ou des débordements majeurs se produisent de toute façon. En revanche, pour des volumes inférieurs à 1,0 × 10⁶, le maintien du lit de la rivière à son niveau le plus bas et l’installation d’un merlon de protection rive gauche permet de réduire de 50 % le nombre de bâtiments impactés (Fig. 5).

Ce pourcentage dépend néanmoins des dimensions du merlon, et des volumes considérés. Les simulations numériques permettent en effet de mettre en évidence que l’augmentation de la longueur du merlon n’améliore pas systématiquement la protection du village. Peruzzetto (2021a) analyse ainsi l’efficacité de 3 merlons de 5 mètres de haut mis en place sur la rive gauche : un merlon court (175 m de long), un merlon intermédiaire (400 m de long) et un merlon long (575 m). Par exemple, le merlon intermédiaire protège moins le village que le merlon le plus court, pour une coulée de débris de 0,65 × 10⁶ m³. En effet, l’allongement du merlon concentre la coulée dans la rivière et engendre des débordements plus importants en aval. De même, le merlon de 575 m de long engendre plus de débordements rive droite que le merlon intermédiaire. Dans d’autres contextes, ces résultats pourraient être utilisés pour identifier les potentielles zones d’épandage, où les coulées de débris seraient en partie déviées. Mais pour la rivière du Prêcheur, les contraintes topographiques et l’urbanisation autour de l’embouchure de la rivière empêchent, en l’état, de définir de telles zones d’épandage.

L’utilisation de SHALTOP permet ainsi d’analyser l’exposition du village du Prêcheur, et d’aider à dimensionner les ouvrages de protection. Ces résultats doivent néanmoins être pris avec prudence, car toute la complexité des phénomènes n’est pas modélisée. Dans la section suivante, nous identifions trois axes de recherches pour améliorer l’utilisation opérationnelle des codes d’écoulement en couche mince.

Fig. 5

Étude de l’influence d’un merlon sur l’exposition du village du Prêcheur aux coulées de débris. L’échelle de couleur donne les zones impactées en fonction du volume des coulées de débris. (a) Cas de référence, avec la topographie d’août 2018 (DEAL Martinique/Helimap). (b) Avec un merlon de 175 m de long. (c) Avec un merlon de 400 m de long. (c) Avec un merlon de 575 m de long. (e) Dimensions du merlon. Adapté de Peruzzetto (2021a).

Analysis of the influence of protection walls on the vulnerability of the Prêcheur village to debris flows. The colorscale indicates which areas are affected by debris flows, depending on their volumes. (a) Reference case, with the topography of August 2018 (DEAL Martinique/Helimap). (b) With a 175 m protection wall. (c) With a 400 m protection wall. (d) With a 575 m protection wall. (e) Dimensions of the protection wall. Adapted from Peruzzetto (2021a).

3 Perspectives de développement et d’utilisation des modèles d’écoulement en couche mince

3.1 Développements rhéologiques et numériques

Dans la plupart des cas, les applications opérationnelles (comme celle présentée ci-dessus) considèrent des écoulements monophasiques et homogènes. Des développements récents s’intéressent à la modélisation d’écoulements biphasiques (Bouchut et al., 2016 ; Pastor et al., 2018b ; Iverson et George, 2014 ; Mergili et al., 2017). Dans le cas de la rivière du Prêcheur, de tels modèles pourraient aider à mieux modéliser l’initiation des coulées de débris (avec l’intégration progressive de matériaux solides dans une phase liquide) et leur arrêt (sédimentation progressive de la fraction solide). De même, des modèles multicouches (Fernández-Nieto et al., 2016 ; Fernández-Nieto et al., 2018) peuvent être utilisés pour analyser plus précisément les variations de vitesses verticales au sein d’une colonne de fluide, et tenter de modéliser des écoulements hyper-concentrés (avec une fraction solide/liquide variable sur une même verticale). Toutefois, comme évoqué précédemment, de tels modèles peuvent être complexes à calibrer et/ou ne sont pas encore adaptés à des rhéologies complexes.

Une autre piste de recherche largement étudiée depuis plusieurs années est la modélisation de l’érosion basale et latérale (voir Iverson et Ouyang (2015) pour une revue de la littérature). Celle-ci peut changer significativement le volume des coulées de débris : par exemple, le volume de la coulée de débris de Tsing Shan (Hong-Kong, 2000) a été multiplié par 10 entre son initiation et son arrêt (Pirulli et Pastor, 2012). Toutefois, la prise en compte de l’érosion dans les équations d’écoulement en couche mince est difficile à concilier, d’un point de vue méthodologique, avec la contrainte de conservation de l’énergie (Bouchut et al., 2016 ; Pudasaini et Fischer, 2020). Une possibilité est d’utiliser un modèle multicouche avec une zone initialement à l’arrêt à la base de l’écoulement (Fernández-Nieto et al., 2016), mais il n’existe pas d’approche unifiée (Pirulli et Pastor, 2012 ; Lusso et al., 2021). Par ailleurs, les résultats des simulations dépendent fortement d’une connaissance experte des zones et des épaisseurs érodables, ce qui peut être compliqué à estimer en pratique. Dans les cas où l’érosion se produit essentiellement près de la zone source, l’augmentation du volume qui en découle peut être prise en compte, dans une première approximation, en faisant simplement varier le volume initial (Peruzzetto et al., 2022b). Mais dans d’autres cas où l’érosion peut avoir lieu sur toute la zone de propagation (par exemple, lorsque des dépôts de coulées de débris non consolidés sont remobilisés par une nouvelle coulée de débris), la prise en compte de l’érosion devient nécessaire (Reid et al., 2016).

3.2 Analyse des aléas et des risques

Actuellement en France, la cartographie des aléas pour les Plans de Prévention des Risques est faite principalement de manière experte (Thiery et al., 2020). Des méthodes empiriques quantitatives peuvent être utilisées pour quantifier de manière objective et répétable la propagation à l’échelle locale et régionale (échelle 1 :5 000 à 1 :250 000, e.g. Mergili et al., 2019 ; Guyomard et al., 2021). Les modèles d’écoulement en couche mince sont plutôt utilisés, à l’heure actuelle, pour des études sur des sites plus petits, avec des zones sources identifiées. Quelques exemples d’utilisation des modèles d’écoulement en couche mince pour quantifier la propagation à l’échelle régionale existent toutefois. Par exemple Bout et al. (2018) modélisent la rupture superficielle de versants et les coulées de débris associées dans une même simulation. Ils ne considèrent toutefois qu’un seul scénario, et ne proposent pas de méthodologie pour obtenir une carte d’aléa.

Une analyse de risques détaillée nécessite de relier l’intensité des phénomènes aux dommages des infrastructures et bâtiments. Par exemple, pour les coulées de débris, il n’existe pas de consensus sur la définition d’un indicateur d’intensité. Un indicateur classique (car facilement observable sur le terrain) est la hauteur de l’écoulement (e.g. Papathoma-Köhle et al., 2015). Mais d’autres indicateurs sont parfois utilisés comme la vitesse (Dikau et al., 1996), la pression d’impact (Scheidl et al., 2013 ; Givry et Peteuil, 2011), ou un critère combiné sur la vitesse et l’épaisseur (Givry et Peteuil, 2011 ; Hürlimann et al., 2008). Dans tous les cas, l’obtention de courbes d’endommagement (degré de dommage en fonction de l’intensité du phénomène) pour un type de bâti est associée à de fortes incertitudes car les indicateurs d’intensité sont difficiles à estimer, en particulier ceux associés à la dynamique de l’écoulement, comme la pression d’impact (e.g. Jakob et al., 2012). La simulation d’événements passés avec les modèles d’écoulement en couche mince pourrait permettre de mieux caractériser le lien entre les dommages des bâtiments et infrastructures, et l’intensité des phénomènes. En effet, les relevés de terrain réalisés après les événements ne donnent qu’une vision parcellaire de la dynamique de l’écoulement, alors que la simulation numérique permet d’estimer, en chaque point, l’évolution des vitesses et des épaisseurs.

Pour obtenir des résultats précis, l’interaction entre l’écoulement et les bâtiments doit être modélisée. Cette interaction est parfois prise en compte de manière implicite en considérant les zones urbaines comme des zones poreuses (Sanders et al., 2008), ou de manière explicite en délimitant les bâtiments (Ouro et al., 2016). Ces méthodes sont souvent utilisées en hydraulique, mais ne sont à notre connaissance pas, ou très rarement, adaptées aux modèles d’écoulement en couche mince sur des topographies quelconques, impliquant notamment de fortes pentes.

3.3 Utilisation des modélisations pour l’alerte en temps réel

Les modèles d’écoulement en couche mince permettent de réaliser des simulations avec des temps de calcul plus courts que des modèles 3D. Toutefois, ces temps de calcul restent trop importants pour envisager des modélisations en temps réel. Une possibilité pour utiliser les résultats des simulations pour de l’alerte est donc de construire une base de données de simulations pour différentes zones sources, volumes et paramètres rhéologiques. En fonction des informations disponibles pour préciser l’aléa (par exemple, le volume et la localisation des effondrements à partir d’enregistrements sismiques (e.g. Durand et al., 2018), et/ou les prévisions de précipitations), les experts et acteurs pourraient alors avoir directement accès à la carte de propagation correspondante.

Peruzzetto et al. (2020) proposent une démarche de ce type pour estimer les distances de parcours, en déterminant des lois puissances spécifiques à trois sites d’étude, donnant la distance de parcours en fonction du volume des glissements. Des méthodes plus poussées existent pour extrapoler les résultats de simulations, pour des paramètres d’entrée non testés dans la base de données de simulations. Rohmer (2014) analyse ainsi avec des "méta-modèles" la dynamique d’un glissement de terrain en fonction de variations de la pression de pore. Plus récemment, Navarro et al. (2018) utilisent une approche similaire pour calibrer des simulations de coulées de débris.

Ces méthodes pourraient potentiellement être utilisées pour des applications opérationnelles de surveillance et d’alerte, comme c’est le cas actuellement pour les tsunamis (Titov et al., 2005). Toutefois des développements méthodologiques restent nécessaires du fait de la complexité et des processus contrôlant le déclenchement et la propagation des mouvements de terrain.

4 Conclusion

Les modèles d’écoulement en couche mince permettent de quantifier la propagation des écoulements gravitaires. À l’échelle d’un site où les zones sources sont identifiées, ils offrent le bon équilibre entre facilité d’utilisation (temps de calcul acceptable, peu de paramètres à calibrer) et précision des résultats (épaisseurs et vitesses de l’écoulement en fonction du temps). En particulier, le code SHALTOP utilise des rhéologies simples, semi-empiriques, mais décrit finement les interactions géométriques entre l’écoulement et la topographie pour modéliser les interactions avec des obstacles. SHALTOP permet ainsi de reproduire les caractéristiques principales d’écoulements gravitaires secs (e.g. avalanches de blocs) et hydro-gravitaires non visqueux (e.g. coulées de débris granulaires). Cela n’est toutefois possible qu’après la récupération et l’analyse de données de terrain pour calibrer le modèle et définir des scénarios de simulation réalistes.

Il existe de nombreuses pistes de recherches pour améliorer et développer l’utilisation opérationnelle des modèles d’écoulement en couche mince, comme le développement des modèles pour intégrer de manière robuste et fiable des processus comme l’érosion. D’autres axes de recherches concernent les développements méthodologiques pour la cartographie de l’aléa et des risques, et l’utilisation des modèles pour des systèmes d’alerte et de surveillance en temps réel.

Remerciements

Les auteurs remercient le Ministère de la Transition Ecologique et Solidaire, le BRGM, L’Université de Paris (ANR-18-IDEX-0001), l’Institut de Physique du Globe de Paris (IPGP), la DEAL Martinique et l’ERC (ERC-CG-2013-PE10-617472 SLIDEQUAKES) pour le financement des travaux présentés ici. Les équipes du BRGM de Martinique, du BRGM de Guadeloupe, et de l’Observatoire Volcanologique et Sismologique de Martinique de l’IPGP ont également contribué à la collecte et à l’interprétation des données de terrain dans la Rivière du Prêcheur.

Références

Andreotti B, Forterre Y, Pouliquen O. 2013. Granular media: between fluid and solid. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139541008. [CrossRef] [Google Scholar]
Aubaud C, Athanase JE, Clouard V, Barras AV, Sedan O. 2013. A review of historical lahars, floods, and landslides in the Prêcheur river catchment (Montagne Pelee volcano, Martinique island, Lesser Antilles). Bull Soc Géol Fr 184(1–2): 137–154. https://doi.org/10.2113/gssgfbull.184.1-2.137. [CrossRef] [Google Scholar]
Baker JL, Barker T, Gray JMNT. 2016. A two-dimensional depth-averaged mu(I)-rheology for dense granular avalanches. J Fluid Mech 787: 367–395. https://doi.org/10.1017/jfm.2015.684. [CrossRef] [Google Scholar]
Barré de Saint-Venant AJC. 1871. Théorie du mouvement non permanent des eaux, avec application aux crues des rivières et à l’introduction des marées dans leur lit. C R Hebd Séances Acad Sci LXXIII. Sous la dir. d’A. des sciences. [Google Scholar]
Berti M, Simoni A. 2014. DFLOWZ: A free program to evaluate the area potentially inundated by a debris flow. Computers & Geosciences 67: 14–23. https://doi.org/10.1016/j.cageo.2014.02.002. [CrossRef] [Google Scholar]
Bouchut F, Delgado-Sánchez J, Fernández-Nieto E, Mangeney A, Narbona-Reina G. 2022. A bed pressure correction of the friction term for depth-averaged granular flow models. Applied Mathematical Modelling 106: 627–658. https://doi.org/10.1016/j.apm.2022.01.034. [CrossRef] [Google Scholar]
Bouchut F, Fernández-Nieto ED, Mangeney A, Lagrée PY. 2008. On new erosion models of Savage-Hutter type for avalanches. Acta Mechanica 199(1–4): 181–208. https://doi.org/10.1007/s00707-007-0534-9. [CrossRef] [Google Scholar]
Bouchut F, Fernández-Nieto ED, Mangeney A, Narbona-Reina G. 2016. A two-phase two-layer model for fluidized granular flows with dilatancy effects. Journal of Fluid Mechanics 801: 166–221. https://doi.org/10.1017/jfm.2016.417. [CrossRef] [Google Scholar]
Bouchut F, Mangeney-Castelnau A, Perthame B, Vilotte P. 2003. A new model of Saint Venant and Savage-Hutter type for gravity driven shallow water flows. Comptes Rendus Mathématique 336(6): 531–536. https://doi.org/10.1016/S1631-073X(03)00117-1. [CrossRef] [Google Scholar]
Bouchut F, Westdickenberg M. 2004. Gravity driven shallow water models for arbitrary topography. Communications in Mathematical Sciences 2(3): 359–389. [CrossRef] [Google Scholar]
Bout B, Lombardo L, van Westen C, Jetten V. 2018. Integration of two-phase solid fluid equations in a catchment model for flashfloods, debris flows and shallow slope failures. Environmental Modelling & Software 105: 1–16. https://doi.org/10.1016/j.envsoft.2018.03.017. [CrossRef] [Google Scholar]
Brunet M, Moretti L, Le Friant A, Mangeney A, Fernández Nieto ED, Bouchut F. 2017. Numerical simulation of the 30–45 ka debris avalanche flow of Montagne Pelée volcano, Martinique : from volcano flank collapse to submarine emplacement. Natural Hazards 87(2): 1189–1222. https://doi.org/10.1007/s11069-017-2815-5. [CrossRef] [Google Scholar]
Chow VT. 1959. Open-channel hydraulics. Caldwell, NJ: McGraw Hill Book Company. [Google Scholar]
Christen M, Kowalski J, Bartelt P. 2010. RAMMS: Numerical simulation of dense snow avalanches in three-dimensional terrain. Cold Regions Science and Technology 63(1–2): 1–14. https://doi.org/10.1016/j.coldregions.2010.04.005. [CrossRef] [Google Scholar]
Clouard V, Athanase JE, Aubaud C. 2013. Physical characteristics and triggering mechanisms of the –2010 landslide crisis at Montagne Pelee volcano, Martinique : implication for erosional processes and debris-flow hazards. Bulletin de la Société Géologique de France 184(1–2): 155–164. https://doi.org/10.2113/gssgfbull.184.1-2.155. [CrossRef] [Google Scholar]
Corominas J. 1996. The angle of reach as a mobility index for small and large landslides. Canadian Geotechnical Journal 33(2): 260–271. https://doi.org/10.1139/t96-005. [CrossRef] [Google Scholar]
Corominas J, van Westen C, Frattini P, Cascini L, Malet JP, Fotopoulou S, et al. 2014. Recommendations for the quantitative analysis of landslide risk. Bulletin of Engineering Geology and the Environment 73(2): 209–263. https://doi.org/10.1007/s10064-013-0538-8. [Google Scholar]
Coussot P. 1994. Steady, laminar, flow of concentrated mud suspensions in open channel. Journal of Hydraulic Research 32(4): 535–559. https://doi.org/10.1080/00221686.1994.9728354. [CrossRef] [Google Scholar]
Coussot P, Leonov AI, Piau JM. 1993. Rheology of concentrated dispersed systems in a low molecular weight matrix. Journal of Non-Newtonian Fluid Mechanics 46(2): 179–217. https://doi.org/10.1016/0377-0257(93)85046-D. [CrossRef] [Google Scholar]
Coussot, P, Meunier M. 1996. Recognition, classification and mechanical description of debris flows. Earth-Science Reviews 40(3–4): 209–227. https://doi.org/10.1016/0012-8252(95)00065-8. [CrossRef] [Google Scholar]
Cruden D, Varnes D. 1996. Landslide types and processes. Landslides: investigation and mitigation. Special report 247. Transportation research board, US National Research Council, pp. 36–75. [Google Scholar]
Delannay R, Valance A, Mangeney A, Roche O, Richard P. 2017. Granular and particle-laden flows: from laboratory experiments to field observations. Journal of Physics D: Applied Physics 50(5): 053001. https://doi.org/10.1088/1361-6463/50/5/053001. [CrossRef] [Google Scholar]
Den Eeckhaut MV, Marre A, Poesen J. 2010. Comparison of two landslide susceptibility assessments in the Champagne-Ardenne region (France). Geomorphology 115(1): 141–155. https://doi.org/10.1016/j.geomorph.2009.09.042. [CrossRef] [Google Scholar]
Denlinger RP, Iverson RM. 2004. Granular avalanches across irregular three-dimensional terrain: 1. Theory and computation. Journal of Geophysical Research: Earth Surface 109(F1). https://doi.org/10.1029/2003JF000085. [Google Scholar]
Dikau R, Brunsden D, Schrott L, Ibsen ML, eds. 1996. Landslide recognition: identification, movement and causes. Wiley. New York, 210 p. [Google Scholar]
Dressler RF. 1978. New Nonlinear Shallow-Flow Equations with Curvature. Journal of Hydraulic Research 16(3): 205–222. https://doi.org/10.1080/00221687809499617. [CrossRef] [Google Scholar]
Dubois L, Dauphin S, Rul G. 2016. Le glissement du Chambon : évolution du phénomène et gestion de crise. Revue Française de Géotechnique 148(148): 2. https://doi.org/10.1051/geotech/2016010. [CrossRef] [EDP Sciences] [Google Scholar]
Dumaisnil C, Thouret JC, Chambon G, Doyle EE, Cronin SJ, Surono. 2010. Hydraulic, physical and rheological characteristics of rain-triggered lahars at Semeru volcano, Indonesia. Earth Surface Processes and Landforms 35(13): 1573–1590. https://doi.org/10.1002/esp.2003. [CrossRef] [Google Scholar]
Durand V, Mangeney A, Haas F, Jia X, Bonilla F, Peltier A et al. 2018. On the link between external forcings and slope instabilities in the Piton de la Fournaise summit crater, Reunion Island. Journal of Geophysical Research: Earth Surface 123(10): 2422–2442. https://doi.org/10.1029/2017JF004507. [CrossRef] [Google Scholar]
Edwards, AN, Viroulet S, Kokelaar BP, Gray JMNT. 2017. Formation of levees, troughs and elevated channels by avalanches on erodible slopes. Journal of Fluid Mechanics 823: 278–315. https://doi.org/10.1017/jfm.2017.309. [CrossRef] [Google Scholar]
Fell R, Corominas J, Bonnard C, Cascini L, Leroi E, Savage WZ. 2008. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Engineering Geology. Landslide Susceptibility, Hazard and Risk Zoning for Land Use Planning 102(3): 85–98. https://doi.org/10.1016/j.enggeo.2008.03.022. [Google Scholar]
Fernández-Nieto ED, Garres-Díaz J, Mangeney A, Narbona-Reina G. 2016. A multilayer shallow model for dry granular flows with the μ(I)-rheology: application to granular collapse on erodible beds. Journal of Fluid Mechanics 798: 643–681. https://doi.org/10.1017/jfm.2016.333. [CrossRef] [Google Scholar]
Fernández-Nieto E, Garres-Díaz J, Mangeney A, Narbona-Reina G. 2018. 2D granular flows with the μ(I)-rheology and side walls friction: A well-balanced multilayer discretization. Journal of Computational Physics 356: 192–219. https://doi.org/10.1016/j.jcp.2017.11.038. [CrossRef] [Google Scholar]
Frimberger T, Andrade SD, Weber S, Krautblatter M. 2021. Modelling future lahars controlled by different volcanic eruption scenarios at Cotopaxi (Ecuador) calibrated with the massively destructive 1877 lahar. Earth Surface Processes and Landforms 46(3): 680–700. https://doi.org/10.1002/esp.5056. [CrossRef] [Google Scholar]
Froude MJ, Petley D. 2018. Global fatal landslide occurrence from 2004 to 2016. Natural Hazards and Earth System Sciences 18(8): 2161–2181. https://doi.org/10.5194/nhess-18-2161-2018. [CrossRef] [Google Scholar]
GDR MiDi. 2004. On dense granular flows. The European Physical Journal E14(4): 341–365. [CrossRef] [Google Scholar]
Givry M, Peteuil C. 2011. Construire en montagne, la prise en compte du risque torrentiel. 5086-D-12/E/295. Ministère de l’Écologie, du Développement durable, des Transports et du Logement. [Google Scholar]
Gray J, Wieland M, Hutter K. 1999. Gravity-driven free surface flow of granular avalanches over complex basal topography. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 455: 1841–1874. [CrossRef] [Google Scholar]
Gray JMNT, Edwards AN. 2014. A depth-averaged μ(I)-rheology for shallow granular free-surface flows. Journal of Fluid Mechanics 755: 503–534. https://doi.org/10.1017/jfm.2014.450. [CrossRef] [Google Scholar]
Guimpier A, Conway SJ, Mangeney A, Lucas A, Mangold N, Peruzzetto M, et al. 2021. Dynamics of recent landslides (<20 My) on Mars : Insights from high-resolution topography on Earth and Mars and numerical modelling. Planetary and Space Science 206: 105303. https://doi.org/10.1016/j.pss.2021.105303. [CrossRef] [Google Scholar]
Guyomard Y, Mengin M, Colas B, Thiery Y, Mardhel V, Monge O. 2021. L’aléa naturel glissements de terrain en Nouvelle-Calédonie. Géologues–Géosciences et société. La Nouvelle-Calédonie 209. [Google Scholar]
Hürlimann M, Rickenmann D, Medina V, Bateman A. 2008. Evaluation of approaches to calculate debris-flow parameters for hazard assessment. Engineering Geology 102(3–4): 152–163. https://doi.org/10.1016/j.enggeo.2008.03.012. [CrossRef] [Google Scholar]
INSEE. 2015. Données carroyées – Niveau naturel. Disponible sur : https://www.insee.fr/fr/statistiques/4176281?sommaire=4176305 (dernière consultation: 2022/28/02). [Google Scholar]
Ionescu IR, Mangeney A, Bouchut F, Roche O. 2015. Viscoplastic modeling of granular column collapse with pressure-dependent rheology. Journal of Non-Newtonian Fluid Mechanics 219: 1–18. https://doi.org/10.1016/j.jnnfm.2015.02.006. [CrossRef] [Google Scholar]
Iverson RM, George DL. 2014. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. I. Physical basis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 470(2170): 20130819. https://doi.org/10.1098/rspa.2013.0819. [CrossRef] [Google Scholar]
Iverson RM, Ouyang C. 2015. Entrainment of bed material by Earth-surface mass flows: Review and reformulation of depth-integrated theory. Reviews of Geophysics 53(1): 27–58. https://doi.org/10.1002/2013RG000447. [CrossRef] [Google Scholar]
Jakob M, Stein D, Ulmi M. 2012. Vulnerability of buildings to debris flow impact. Natural Hazards 60(2): 241–261. https://doi.org/10.1007/s11069-011-0007-2. [CrossRef] [Google Scholar]
Jakob M, McDougall S, Weatherly H, Ripley N. 2013. Debris-flow simulations on Cheekye River, British Columbia. Landslides 10(6): 685–699. https://doi.org/10.1007/s10346-012-0365-1. [CrossRef] [Google Scholar]
Jop P, Forterre Y, Pouliquen O. 2006. A constitutive law for dense granular flows. Nature 441(7094): 727–730. https://doi.org/10.1038/nature04801. [NASA ADS] [CrossRef] [Google Scholar]
Kelfoun K, Druitt TH. 2005. Numerical modeling of the emplacement of Socompa rock avalanche, Chile. Journal of Geophysical Research 110(B12). https://doi.org/10.1029/2005JB003758. [CrossRef] [Google Scholar]
Kjekstad O, Highland L. 2009. Economic and social impacts of landslides. In: Sassa K, Canuti P. Landslides-Disaster Risk Reduction. Sous Berlin, Heidelberg: Springer, pp. 573–587. https://doi.org/10.1007/978-3−540-69970-5_30. [CrossRef] [Google Scholar]
Korup O, Schneider D, Huggel C, Dufresne A. 2013. Long-Runout Landslides. In: Treatise on geomorphology. T. 7. San Diego, CA: Academic Press, pp. 183–199. https://doi.org/10.1016/B978-0-12-374739-6.00164-0. [CrossRef] [Google Scholar]
Laigle D,Coussot P. 1997. Numerical modeling of mudflows. Journal of Hydraulic Engineering 123(7): 617–623. https://doi.org/10.1061/(ASCE)0733-9429(1997)123:7(617). [CrossRef] [Google Scholar]
Lalubie G. 2013. Les lahars et les laves torrentielles historiques aux Antilles françaises : un risque hydro-volcano-géomorphologique majeur. Physio-Géo. Géographie physique et environnement 7(7): 83–109. https://doi.org/10.4000/physio-geo.3479. [Google Scholar]
Luca I, Hutter K, Tai YC, Kuo CY. 2009. A hierarchy of avalanche models on arbitrary topography. Acta Mechanica 205(1–4): 121–149. https://doi.org/10.1007/s00707-009-0165-4. [CrossRef] [Google Scholar]
Lucas A, Mangeney A, Bouchut F, Bristeau MO, Mège D. 2007. Benchmarking exercises for granular flows. The 2007 International Forum on Landslide Disaster Management. Hong Kong: Ho & Li. [Google Scholar]
Lucas A, Mangeney A, Ampuero JP. 2014. Frictional velocity-weakening in landslides on Earth and on other planetary bodies. Nature Communications 5: 3417. https://doi.org/10.1038/ncomms4417. [CrossRef] [PubMed] [Google Scholar]
Lusso C, Bouchut F, Ern A, Mangeney A. 2021. Explicit solutions to a free interface model for the static/flowing transition in thin granular flows. ESAIM: M2AN(55): S369– S395. https://doi.org/10.1051/m2an/2020042. [CrossRef] [EDP Sciences] [Google Scholar]
Mangeney A, Bouchut F, Thomas N, Vilotte JP, Bristeau MO. 2007. Numerical modeling of self-channeling granular flows and of their levee-channel deposits. Journal of Geophysical Research 112(F2): F02017. https://doi.org/10.1029/2006JF000469. [CrossRef] [Google Scholar]
Mangeney-Castelnau A, Bouchut F, Vilotte JP, Lajeunesse E, Aubertin A, Pirulli M. 2005. On the use of Saint Venant equations to simulate the spreading of a granular mass: numerical simulation of granular spreading. Journal of Geophysical Research: Solid Earth 110(B9): B09103. https://doi.org/10.1029/2004JB003161. [Google Scholar]
Mangold N, Mangeney A, Migeon V, Ansan V, Lucas A, Baratoux D, et al. 2010. Sinuous gullies on Mars: Frequency, distribution, and implications for flow properties. Journal of Geophysical Research 115(E11): E11001. https://doi.org/10.1029/2009JE003540. [CrossRef] [Google Scholar]
McArdell BW, Zanuttigh B, Lamberti A, Rickenmann D. 2003. Systematic comparison of debris-flow laws at the Illgraben torrent, Switzerland. In: Debris-Flow Hazards Mitigation. Mechanics, Prediction, and Assessment. Proc. of the third Int. Conf. on Debris-Flow Hazards Mitigation. Third Int. Conf. on Debris-Flow Hazards Mitigation. Davos, Switzerland: Millpress, pp. 11. [Google Scholar]
McDougall S. 2017. 2014 Canadian Geotechnical Colloquium: Landslide runout analysis – current practice and challenges. Canadian Geotechnical Journal 54(5): 605–620. https://doi.org/10.1139/cgj-2016-0104. [CrossRef] [Google Scholar]
McDougall S, Hungr O. 2004. A model for the analysis of rapid landslide motion across three-dimensional terrain. Canadian Geotechnical Journal 41(6): 1084–1097. https://doi.org/10.1139/t04-052. [CrossRef] [Google Scholar]
Mergili M, Fischer JT, Krenn J, Pudasaini SP. 2017. r.avaflow v1, an advanced open source computational framework for the propagation and interaction of two-phase mass flows. Geoscientific Model Development Discussions 10: 553 –569. https://doi.org/10.5194/gmd-10-553-2017. [CrossRef] [Google Scholar]
Mergili M, Schwarz L, Kociu A. 2019. Combining release and runout in statistical landslide susceptibility modeling. Landslides 16(11): 2151–2165. https://doi.org/10.1007/s10346-019-01222-7. [CrossRef] [Google Scholar]
Mitchell A, McDougall S, Nolde N, Brideau MA, Whittall J, Aaron JB. 2019. Rock avalanche runout prediction using stochastic analysis of a regional dataset. Landslides 17: 777–792. https://doi.org/10.1007/s10346-019-01331-3. [Google Scholar]
Moretti L, Mangeney A, Capdeville Y, Stutzmann E, Huggel C, Schneider D, et al. 2012. Numerical modeling of the Mount Steller landslide flow history and of the generated long period seismic waves. Geophysical Research Letters 39(16). https://doi.org/10.1029/2012GL052511. [CrossRef] [Google Scholar]
Moretti L, Allstadt K, Mangeney A, Capdeville Y, Stutzmann E, Bouchut F. 2015. Numerical modeling of the Mount Meager landslide constrained by its force history derived from seismic data. Journal of Geophysical Research : Solid Earth 120(4): 2579–2599. https://doi.org/10.1002/2014JB011426. [CrossRef] [Google Scholar]
Navarro M, Le Maître OP, Hoteit I, George DL, Mandli KT, Knio OM. 2018. Surrogate-based parameter inference in debris flow model. Computational Geosciences 22(6): 1447–1463. https://doi.org/10.1007/s10596-018-9765-1. [CrossRef] [Google Scholar]
O’Brien JS, Julien PY, Fullerton WT. 1993. Two-dimensional water flood and mudflow simulation. Journal of hydraulic engineering 119(2): 244–261. [CrossRef] [Google Scholar]
Ouro P, Cea L, Ramírez L, Nogueira X. 2016. An immersed boundary method for unstructured meshes in depth averaged shallow water models. International Journal for Numerical Methods in Fluids 81(11): 672–688. https://doi.org/10.1002/fld.4201. [CrossRef] [Google Scholar]
Papathoma-Köhle M, Zischg A, Fuchs S, Glade T, Keiler M. 2015. Loss estimation for landslides in mountain areas − An integrated toolbox for vulnerability assessment and damage documentation. Environmental Modelling & Software 63: 156–169. https://doi.org/10.1016/j.envsoft.2014.10.003. [CrossRef] [Google Scholar]
Pastor M, Quecedo M, González E, Herreros MI, Merodo JAF, Mira P. 2004. Simple approximation to bottom friction for Bingham fluid depth integrated models. Journal of Hydraulic Engineering 130(2): 149–155. https://doi.org/10.1061/(ASCE)0733-9429(2004)130:2(149). [CrossRef] [Google Scholar]
Pastor M, Martin Stickle M, Dutto P, Mira P, Fernández Merodo JA, Blanc T, et al. 2015. A viscoplastic approach to the behaviour of fluidized geomaterials with application to fast landslides. Continuum Mechanics and Thermodynamics 27(1–2): 21–47. https://doi.org/10.1007/s00161-013-0326-5. [CrossRef] [Google Scholar]
Pastor M, Soga K, McDougall S, Kwan JSH. 2018a. Review of benchmarking exercise on landslide runout analysis 2018. Proceedings of the Second JTC1 Workshop on Triggering and Propagation of Rapid Flow-like Landslides. Hong Kong, pp. 65. [Google Scholar]
Pastor M, Yague A, Stickle M, Manzanal D, Mira P. 2018b. A two-phase SPH model for debris flow propagation. International Journal for Numerical and Analytical Methods in Geomechanics 42(3): 418– 448. https://doi.org/10.1002/nag.2748. [CrossRef] [Google Scholar]
Peruzzetto M. 2021a. Modélisation de scénarios de déstabilisation de la Falaise Samperre et de propagation des lahars. Rapport final BRGM/RP-71149-FR. Orléans, France: BRGM, pp. 88. [Google Scholar]
Peruzzetto M. 2021b. Numerical modeling of dry and water-laden gravitational flows for quantitative hazard assessment. Université de Paris. [Google Scholar]
Peruzzetto M, Mangeney A, Grandjean G, Levy C, Thiery Y, Rohmer J, et al. 2020. Operational estimation of landslide runout: comparison of empirical and numerical methods. Geosciences 10(11): 424. https://doi.org/10.3390/geosciences10110424. [CrossRef] [Google Scholar]
Peruzzetto M, Mangeney A, Bouchut F, Grandjean G, Levy C, Thiery Y, et al. 2021. Topography curvature effects in thin-layer models for gravity-driven flows without bed erosion. Journal of Geophysical Research: Earth Surface 126(4): e2020JF005657. https://doi.org/10.1029/2020JF005657. [CrossRef] [Google Scholar]
Peruzzetto M, Legendre Y, Nachbaur A, Dewez TJB, Thiery Y, Levy C, et al. 2022a. How volcanic stratigraphy constrains headscarp collapse scenarios : the Samperre cliff case study (Martinique island, Lesser Antilles). Natural Hazards and Earth System Sciences 22(12): 3973–3992. https://doi.org/10.5194/nhess-22-3973-2022. [CrossRef] [Google Scholar]
Peruzzetto M, Levy C, Thiery Y, Grandjean G, Mangeney A, Lejeune AM, et al. 2022b. Simplified simulation of rock avalanches and subsequent debris flows with a single thin-layer model: Application to the Prêcheur river (Martinique, Lesser Antilles). Engineering Geology 296: 106457. https://doi.org/10.1016/j.enggeo.2021.106457. [CrossRef] [Google Scholar]
Petley D. 2012. Global patterns of loss of life from landslides. Geology 40(10): 927–930. https://doi.org/10.1130/G33217.1. [CrossRef] [Google Scholar]
Pirulli M, Mangeney A. 2008. Results of Back-Analysis of the Propagation of Rock Avalanches as a Function of the Assumed Rheology. Rock Mechanics and Rock Engineering 41(1): 59–84. https://doi.org/10.1007/s00603-007-0143-x. [CrossRef] [Google Scholar]
Pirulli M, Bristeau MO, Mangeney A, Scavia C. 2007. The effect of the earth pressure coefficients on the runout of granular material. Environmental Modelling & Software 22(10): 1437–1454. https://doi.org/10.1016/j.envsoft.2006.06.006. [CrossRef] [Google Scholar]
Pirulli M, Pastor M. 2012. Numerical study on the entrainment of bed material into rapid landslides. Géotechnique 62(11): 959–972. https://doi.org/10.1680/geot.10.P.074. [CrossRef] [Google Scholar]
Pouliquen O, Forterre Y. 2002. Friction law for dense granular flows : application to the motion of a mass down a rough inclined plane. Journal of Fluid Mechanics 453. https://doi.org/10.1017/S0022112001006796. [Google Scholar]
Pudasaini SP, Fischer JT. 2020. A mechanical model for phase separation in debris flow. International Journal of Multiphase Flow 129: 103292. https://doi.org/10.1016/j.ijmultiphaseflow.2020.103292. [CrossRef] [Google Scholar]
Reid ME, Coe JA, Brien DL. 2016. Forecasting inundation from debris flows that grow volumetrically during travel, with application to the Oregon Coast Range, USA. Geomorphology 273: 396–411. https://doi.org/10.1016/j.geomorph.2016.07.039. [CrossRef] [Google Scholar]
Remaître A, Malet JP, Maquaire O, Ancey C, Locat J. 2005. Flow behaviour and runout modelling of a complex debris flow in a clayshale basin. Earth Surface Processes and Landforms 30(4): 479–488. https://doi.org/10.1002/esp.1162. [CrossRef] [Google Scholar]
Rickenmann D. 1999. Empirical relationships for debris flows. Natural Hazards 19(1): 47–77. [CrossRef] [Google Scholar]
Rohmer J. 2014. Dynamic sensitivity analysis of long-running landslide models through basis set expansion and meta-modelling. Natural Hazards 73(1): 5–22. https://doi.org/10.1007/s11069-012-0536-3. [CrossRef] [Google Scholar]
Sanders BF, Schubert JE, Gallegos HA. 2008. Integral formulation of shallow-water equations with anisotropic porosity for urban flood modeling. Journal of Hydrology 362(1): 19–38. https://doi.org/10.1016/j.jhydrol.2008.08.009. [CrossRef] [Google Scholar]
Santi PM, Hewitt K, VanDine DF, Barillas Cruz E. 2011. Debris-flow impact, vulnerability, and response. Natural Hazards 56(1): 371–402. https://doi.org/10.1007/s11069-010-9576-8. [CrossRef] [Google Scholar]
Savage SB, Hutter K. 1989. The motion of a finite mass of granular material down a roughincline. Journal of Fluid Mechanics 199(1): 177. https://doi.org/10.1017/S0022112089000340. [CrossRef] [Google Scholar]
Savage SB, Hutter K. 1991. The dynamics of avalanches of granular materials from initiation to runout. Part I: Analysis. Acta Mechanica 86(1): 201–223. [CrossRef] [Google Scholar]
Scheidl C, Chiari M, Kaitna R, Müllegger M, Krawtschuk A, Zimmermann T, et al. 2013. Analysing Debris-Flow Impact Models, Based on a Small Scale Modelling Approach. Surveys in Geophysics 34(1): 121–140. https://doi.org/10.1007/s10712-012-9199-6. [CrossRef] [Google Scholar]
Sosio R, Crosta GB, Frattini P. 2007. Field observations, rheological testing and numerical modelling of a debris-flow event. Earth Surface Processes and Landforms 32(2): 290–306. https://doi.org/10.1002/esp.1391. [CrossRef] [Google Scholar]
Thiery Y, Terrier M, Colas B, Fressard M, Maquaire O, Grandjean G, et al. 2020. Improvement of landslide hazard assessments for regulatory zoning in France: STATE-OF-THE-ART perspectives and considerations. International Journal of Disaster Risk Reduction 47: 101562. https://doi.org/10.1016/j.ijdrr.2020.101562. [CrossRef] [Google Scholar]
Thouret JC, Antoine S, Magill C, Ollier C. 2020. Lahars and debris flows: Characteristics and impacts. Earth-Science Reviews 201: 103003. https://doi.org/10.1016/j.earscirev.2019.103003. [CrossRef] [Google Scholar]
Titov VV, Gonzalez FI, Bernard EN, Eble MC, Mofjeld HO, Newman JC, et al. 2005. Real-Time Tsunami Forecasting: Challenges and Solutions. Natural Hazards 35(1): 35–41. https://doi.org/10.1007/s11069-004-2403-3. [CrossRef] [Google Scholar]
Voellmy A. 1955. Uber die Zerstorungskraft von Lawinen. Schweizerische Bauzeitung, Jahrg 73: 159–162, 212–217, 246–249, 280–285. [Google Scholar]
Zimmermann F, McArdell BW, Rickli C, Scheidl C. 2020. 2D Runout Modelling of Hillslope Debris Flows, Based on Well-Documented Events in Switzerland. Geosciences 10(2): 70. https://doi.org/10.3390/geosciences10020070. [CrossRef] [Google Scholar]

Citation de l’article : Marc Peruzzetto, Gilles Grandjean, Anne Mangeney, Clara Levy, Yannick Thiery, Benoit Vittecoq, François Bouchut, Fabrice R. Fontaine, Jean-Christophe Komorowski. Simulation des écoulements gravitaires avec les modèles d’écoulement en couche mince : état de l’art et exemple d’application aux coulées de débris de la Rivière du Prêcheur (Martinique, Petites Antilles). Rev. Fr. Geotech. 2023, 176, 1.

Liste des tableaux

Tableau 1

Principales rhéologies pour les modèles monophasiques d’écoulement en couche mince . Les notations en gras sont les paramètres à choisir dans les simulations. Leur description est donnée dans le corps de l’article. Des comparaisons de simulations avec différentes rhéologies peuvent par exemple être trouvées dans McArdell et al. (2003) ou Pirulli et Mangeney (2008).

Main rheologies for homogeneous thin-layer models. Bold symbols are the parameters to be chosen in simulations. Their description is given in the main body of the article. Comparisons of simulations with different rheologies can be found, for instance, in McArdell et al. (2003) and Pirulli et Mangeney (2008).

Dans le texte

Liste des figures

Fig. 1

Notations pour les équations d’écoulement en couche mince sur une topographie 1D Z = b(X).

Notations for thin-layer equations on a 1D topography Z = b(X).

Dans le texte

Fig. 2

Le bassin versant du Prêcheur. (a) Carte générale du site d’étude (Modèle numérique de Terrain IGN Lito3D), avec la localisation des échantillons récupérés dans le lit de la rivière (PR-XX). La localisation du site aux Antilles et en Martinique est indiquée sur les deux cartes supérieures. (b) Vue du village du Prêcheur (30/03/2021, Carige). (c) Vue de la Falaise Samperre (02/02/2018, OVSM/IPGP) Adapté de Peruzzetto et al. (2022b).

Prêcheur river catchment. (b) Map of the study site (Digital Elevation Model IGN Lito3D), with the location of sampling sites (PR-XX). The location of the study site in the Caribbean and in Martinique island is given by the maps above. (c) Aerial view of the Prêcheur village (30/03/2021, Carige Company). (d) Photograph of the Samperre cliff (02/02/2018, OVSM/IPGP). Adapted from Peruzzetto et al. (2022b).

Dans le texte

Fig. 3

Étude des dépôts de lahars dans la Rivière du Prêcheur. (a) Exemple de site de prélèvement, avec distinction de deux types de dépôts. (b) Courbes granulométriques des 11 échantillons prélevés dans la rivière du Prêcheur (PR-01 à PR-11, de l’amont à l’aval, voir Figure 2 pour les localisations). Les fuseaux granulométriques de Dumaisnil et al. (2010) sont ajoutés. Les noms en gras correspondent aux échantillons visibles en (a). Adapté de Peruzzetto et al. (2022b).

Granulometric analysis and lahars deposits in the Prêcheur River. (a) Example of sampling site, with the distinction between two deposits types. (b) Granulometric curves of the 11 samples taken in the Prêcheur River (PR-01 to PR-11, from upstream to downstream, see Figure 2 for locations). Granulometric ranges of Dumaisnil et al. (2010) are also given. Samples in bold are the samples from (a). Adapted from Peruzzetto et al. (2022b).

Dans le texte

Fig. 4

Résultat de la calibration de SHALTOP pour reproduire la coulée de débris du 19 juin 2010 (0,65 × 10⁶ m³). (a) Épaisseur maximale avec la rhéologie de Voellmy, μ_S= tan(2^°) et ξ = 500 m s⁻², (b) avec la rhéologie de Coulomb et μ_S = tan(3^°), et (c) avec la rhéologie de Coulomb et μ_S = tan(2^°). Chaque point dans (d), (e), (f), et (g) est un résultat de simulation, avec le coefficient de friction donné par la couleur de la ligne et le coefficient de turbulence donné par l’abcisse. Les points à gauche de la ligne hachurée sont les résultats avec Voellmy, ceux à droite les résultats avec la rhéologie de Coulomb. (d) et (e) : surfaces inondées sur les rives gauches et droites, dans les zones habitées. (f) et (g) : durée de parcours entre RPRE et CPMA (1,6 km), et RPRE et le pont (4,3 km). Les zones grisées correspondent aux observations, en prenant en compte les incertitudes.

Simulation results for the June 19, 2010 debris flow (0.65 × 10⁶ m³). (a) Maximum flow thickness with the Voellmy rheology, μ_S= tan(2^°) and ξ = 500 m s⁻², (b) with the Coulomb rheology and μ_S = tan(3^°), and (c) with the Coulomb rheology and μ_S = tan(2^°). Each point in (d), (e), (f) and (g) is a simulation result, with friction coefficient given by line color and turbulence coefficient given by the x-coordinate. Left of hatches is for the Voellmy rheology, right is for the Coulomb rheology. (d) and (e) : Area flooded on the left and right riverbank, within inhabited areas. (f) and (g) : Flow travel duration between RPRE and CPMA (about 1.6 km), and between RPRE and the Prêcheur bridge (about 4.3 km). Grey patches are observations, taking into account uncertainties.

Dans le texte

Fig. 5

Étude de l’influence d’un merlon sur l’exposition du village du Prêcheur aux coulées de débris. L’échelle de couleur donne les zones impactées en fonction du volume des coulées de débris. (a) Cas de référence, avec la topographie d’août 2018 (DEAL Martinique/Helimap). (b) Avec un merlon de 175 m de long. (c) Avec un merlon de 400 m de long. (c) Avec un merlon de 575 m de long. (e) Dimensions du merlon. Adapté de Peruzzetto (2021a).

Analysis of the influence of protection walls on the vulnerability of the Prêcheur village to debris flows. The colorscale indicates which areas are affected by debris flows, depending on their volumes. (a) Reference case, with the topography of August 2018 (DEAL Martinique/Helimap). (b) With a 175 m protection wall. (c) With a 400 m protection wall. (d) With a 575 m protection wall. (e) Dimensions of the protection wall. Adapted from Peruzzetto (2021a).

Dans le texte

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.