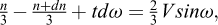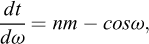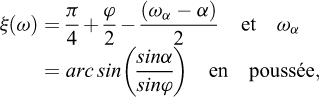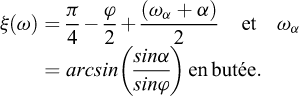© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2023

1 Introduction

La détermination des coefficients de poussée et de butée constitue encore un enjeu majeur pour le dimensionnement des murs et des écrans de soutènement. Il est d’usage de calculer les contraintes de poussée et de butée en appliquant un principe de superposition conduisant, au moyen du théorème des états correspondants (Caquot, 1934), à considérer trois types de coefficients : un coefficient de poussée K_aγ ou de butée K_pγ pour les milieux pesants, un coefficient de poussée K_aq ou de butée K_pq pour les milieux non pesants surchargés uniformément et un coefficient de poussée K_ac ou de butée K_pc pour les milieux cohérents.

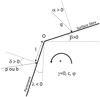
Afin de faciliter la lecture et la compréhension, les notations des tables de Kerisel et Absi (1990) sont utilisées (Fig. 1) : les angles δ, β et λ désignent respectivement l’obliquité (l’inclinaison) de la contrainte de poussée ou de butée sur le parement, notée respectivement p et b, la pente de la surface libre et le fruit de l’écran. La charge sur la surface libre est notée q et son inclinaison par rapport à la normale notée α (cet angle désigne de manière plus générale l’inclinaison du vecteur de contrainte sur tout plan radial partant du point 0). Le terrain est caractérisé par son poids volumique γ, son angle de frottement φ et sa cohésion c.

En fonction de la longueur l le long du parement, les contraintes de poussée et de butée sont évaluées selon les relations suivantes : $$p=K_{a\gamma }\gamma l+K_{aq}q-K_{ac}c,$$ $$b=K_{p\gamma }\gamma l+K_{pq}q+K_{pc}c.$$

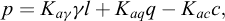
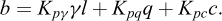
Les coefficients K_aq ou K_pq permettent de calculer les contraintes de poussée et de butée transmises par une surcharge uniforme q disposée sur la surface libre du terrain et peuvent être déterminés analytiquement selon les équations présentées par L’Herminier et Absi (1962). L’application du théorème des états correspondants, en supposant que la cohésion s’apparente à une contrainte de confinement c/tanφ permet par la suite de déterminer les coefficients K_ac et K_pc (l’Annexe A détaille le calcul de ces coefficients).

Les coefficients K_aγ et K_pγ qui dépendent seulement de l’angle de frottement φ du terrain considéré peuvent être déterminés au moyen des équations proposées par Boussinesq (1876). Caquot et Kerisel (1948) ont proposé une première méthode globale de résolution de ces équations aboutissant à la publication de tables de valeurs en 1948 actualisées en 1966, en 1972 et en 1990. D’autres approches avaient été proposées par Resal (1903) et Ravizé (1945) notamment. Des écarts, certes négligeables dans la pratique, existent entre les différentes versions de ces tables traduisant implicitement les incertitudes de résolution du système d’équations différentielles : par exemple, dans l’état de butée, pour un écran vertical, une surface libre horizontale, une obliquité δ égale à −φ et une valeur φ égale à 30°, les valeurs suivantes peuvent être lues : 6,42 en 1948, 6,56 en 1966 et 6,50 en 1990. Par ailleurs, les valeurs de ces coefficients peuvent être comparées à celles proposées par Sokolowski (1965) obtenues au moyen de la théorie des lignes de glissement (ou des lignes caractéristiques, Salençon, 1974 : Absi, 1984) et d’une méthode par différences finies : pour le présent exemple, une valeur égale à 6,55 est indiquée.

L’objectif visé est de revenir sur la résolution du système d’équations différentielles rendant compte des équilibres de Boussinesq et de Rankine. Cet objectif relève essentiellement de motivations visant à aborder un problème dont les sources sont de plus en plus rarement présentées alors que l’utilisation des solutions de ce problème par les ingénieurs est quotidienne. Malgré la fiabilité largement éprouvée des valeurs de ces coefficients, il paraît nécessaire que les ingénieurs utilisant ces solutions puissent avoir une idée même très partielle de leur origine (à ce titre, les Annexes B et C donnent des formules d’interpolation numériques des coefficients de poussée et de butée de 1948 très peu disponibles dans la littérature). Cet article participe ainsi à une vulgarisation de ce problème et renvoie pour plus de détails à l’œuvre originale de Caquot et Kerisel (1949).

L’intérêt est aussi de pouvoir apprécier les approximations faites par Caquot et Kerisel d’une part et Sokolowski d’autre part. Il s’agit enfin de proposer une méthode a priori plus simple dans sa présentation en tirant parti de la puissance de calcul actuelle des ordinateurs qui permettent un traitement plus direct de la résolution du système d’équations différentielles ainsi qu’une visualisation des résultats plus aisée. Bien que largement plus élégantes, les techniques de résolution décrites notamment par Caquot et Kerisel (1949) sont aussi largement plus complexes du fait de l’absence presque totale de moyens de calculs numériques à l’époque.

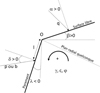Fig. 1 Notations. Notations.

2 Équilibre de Boussinesq

L’équilibre de Boussinesq (1876) conduit à considérer l’équilibre statique du volume élémentaire OMN à l’arrière du parement de poids V par unité de longueur tel que représenté sur la figure 2. L’équilibre en termes de moments autour du point O donne l’équation (1) et l’équilibre en termes de forces projetées sur le segment [ON] donne l’équation (2) (voir Caquot et Kerisel, 1949 pour plus détails). Cet équilibre est traduit par le système d’équations différentielles suivantes : 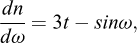$$\frac{dn}{d\omega }=3t-sin\omega ,$$(1)

obtenue de : 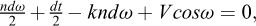$\frac{n}{3}-\frac{n+dn}{3}+td\omega =\frac{2}{3}Vsin\omega ,$ $$\frac{dt}{d\omega }=nm-cos\omega ,$$(2)

obtenue de : $\frac{nd\omega }{2}+\frac{dt}{2}-knd\omega +Vcos\omega =0,$

avec : m = 2k − 1, $m=1+4ta{n}^2\varphi \pm \frac{4}{cos\varphi }\sqrt{ta{n}^2\varphi -ta{n}^2\alpha }$ et $V=\frac{d\omega }{2}$

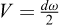
où ω désigne l’angle entre le plan vertical fictif et un plan radial quelconque et α l’inclinaison du vecteur de contrainte sur la normale des plans radiaux avec n la composante normale et t la composante tangentielle : $$\tan \alpha =\frac{t}{n}.$$

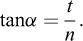
Le paramètre m assure que l’état de contraintes respecte le critère de Mohr–Coulomb défini uniquement par l’angle de frottement φ du terrain considéré et décrit une ellipse en fonction de la variable tanα : la partie supérieure de l’ellipse (associé au signe +) traduit l’état de poussée tandis que la partie inférieure (associée au signe −) traduit l’état de butée. L’inclinaison du vecteur de contrainte α est limitée à ± φ.

Le système d’équations différentielles obtenu est donc du 1^er ordre et non linéaire du fait de la présence du paramètre m qui dépend des deux variables à déterminer n et t en fonction de l’angle ω par rapport au parement. Les conditions initiales sont précisées ci-après. Boussinesq a démontré que le système d’équations différentielles n’est pas intégrable analytiquement. Par conséquent, il faut utiliser des approximations numériques pour le résoudre. Les techniques de résolution de ces équations sont traitées en détail dans le cadre de la théorie des lignes caractéristiques qui s’est développée surtout après 1945 (voir par exemple, Absi, 1984) et qui s’inscrit dans la recherche de charges acceptables vis-à-vis des approches statiques par l’intérieur (voir par exemple, Salençon, 1974). Des logiciels comme Rido (2022) mettent en œuvre des méthodes de résolution similaires sans toutefois fournir de détails.

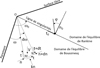Fig. 2 Équilibre d’un volume élémentaire (d’après Caquot et Kerisel, 1949). Equilibrium for an elementary volume (from Caquot and Kerisel, 1949).

3 Principe de résolution

La résolution débute en remarquant que le premier plan de glissement à partir de la surface libre dans l’équilibre de Rankine tel que représenté sur la figure 2 constitue une ligne de singularités qui peut être utilisée comme conditions initiales (voir Ravizé, 1945 d’après Caquot et Kerisel, 1949 ¹). Ce constat conduit à considérer deux équilibres de part et d’autre de cette ligne de singularités : un équilibre de Rankine entre cette ligne et la surface libre où l’état de contraintes est donc connu et un équilibre de Boussinesq entre cette ligne et le parement de l’écran pour lequel il s’agit de résoudre les équations différentielles (1) et (2).

Sur ce premier plan de glissement de Rankine séparé d’un angle ω₀ du parement fictif vertical, le vecteur de contrainte est nécessairement incliné d’un angle φ en poussée et −φ en butée puisqu’il respecte l’équilibre de Rankine. Il s’ensuit que les domaines où règnent les équilibres de Rankine et Boussinesq ne sont pas identiques en poussée et en butée.

Les valeurs de la composante normale n₀ et de la composante tangentielle t₀ du vecteur de contrainte correspondent à l’équilibre de Rankine sur ce plan et sont des conditions initiales définies par les relations suivantes au moyen de considérations dans le cercle de Mohr :

• pour l’état de poussée :

$$n_0=\frac{co{s}^2\phi sin{\omega }_{\beta }cos\left(\beta -{\omega }_0\right)}{sin\left({\omega }_{\beta }+\beta \right)}\mathrm{e}\mathrm{t}{t}_0=\frac{cos\phi sin\phi sin{\omega }_{\beta }cos\left(\beta -{\omega }_0\right)}{sin\left({\omega }_{\beta }+\beta \right)},$$

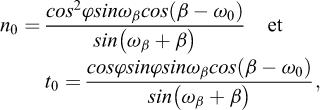
avec : 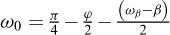${\omega }_0=\frac{\pi }{4}-\frac{\varphi }{2}-\frac{\left({\omega }_{\beta }-\beta \right)}{2}$ et ${\omega }_{\beta }=arcsin\left(\frac{sin\beta }{sin\varphi }\right),$

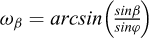
• pour l’état de butée :

$$n_0=\frac{co{s}^2\phi sin{\omega }_{\beta }cos\left(\beta -{\omega }_0\right)}{sin\left({\omega }_{\beta }-\beta \right)}\mathrm{e}\mathrm{t}{t}_0=-\frac{cos\phi sin\phi sin{\omega }_{\beta }cos\left(\beta -{\omega }_0\right)}{sin\left({\omega }_{\beta }-\beta \right)},$$

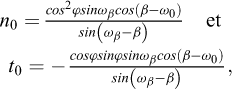
avec : 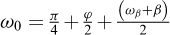${\omega }_0=\frac{\pi }{4}+\frac{\varphi }{2}+\frac{\left({\omega }_{\beta }+\beta \right)}{2}$ et ${\omega }_{\beta }=arcsin\left(\frac{sin\beta }{sin\varphi }\right),$

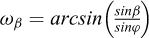
L’angle ω₀ est compté positivement à partir du parement vertical fictif.

La figure 3 indique la position du premier plan de glissement tant en poussée qu’en butée pour 3 configurations qui sont analysées tout au long de cet article :

• φ = 30°, β = 0°, λ = 0° (cas 1) ;

• φ = 20°, β = 12°, λ = −20° (cas 2) ;

• φ = 40°, β = −16°, λ = 10° (cas 3).

Ces trois configurations permettent d’examiner les états de poussée et de butée pour trois angles différents entre la surface libre et le parement.

La résolution du système d’équations différentielles par intégration directe en considérant les conditions initiales sur le premier plan de glissement de Rankine ne permet pas de choisir l’obliquité de la contrainte de poussée ou de butée sur le parement : celle-ci est en fait entièrement déterminée par les conditions initiales sur le premier plan de glissement. Sa résolution sert toutefois de repère lors des étapes suivantes et permet de définir un cheminement 1 (on utilise ici un terme souvent mentionné par Caquot et Kerisel) qui parcourt le massif depuis le premier plan de glissement de Rankine défini par ω = ω₀ jusqu’au parement défini par ω = λ. Une méthode d’intégration explicite de type Runge–Kutta d’ordre 4 (RK4) a été utilisée.

Les figure 4–7 montrent pour des états de poussée et de butée les cheminements de type 1 pour les 3 cas considérés précédemment en fonction des angles ω et α. Pour les figures 4 et 6, le vecteur de contrainte varie bien entre l’inclinaison du premier plan de glissement de Rankine défini par l’angle ω₀ et le parement du mur défini par son fruit λ. Il est important de remarquer que la distance angulaire entre le parement et le premier plan de glissement est nettement plus faible pour les états de poussée que pour les états de butée : par conséquent, il sera plus difficile de résoudre les équations pour les états de poussée notamment si des obliquités négatives sont imposées sur le parement (la variation d’inclinaison du vecteur de contrainte étant alors beaucoup plus rapide). Pour les figures 5 et 7, la valeur de l’angle α au niveau du premier plan de glissement de Rankine est bien égal à φ en poussée et −φ en butée. Comme déjà indiqué, l’inclinaison du vecteur de contrainte sur le parement du mur n’est pour l’instant pas fixée car elle dépend uniquement des conditions initiales sur le premier plan de glissement de Rankine. En poussée, elle vaut −8,21°, −13,14°, 9,18° respectivement pour les cas 1, 2 et 3. En butée, elle vaut 2,94°, 19,50° et −20,83° respectivement pour les cas 1, 2 et 3. Les valeurs des coefficients de poussée et de butée obtenues à ce stade correspondent donc respectivement à ces inclinaisons.

En fait, comme indiqué par Salençon (1974) et d’autres auteurs, le système défini par les équations différentielles (1) et (2) avec les conditions initiales sur le premier plan de glissement de Rankine est indéterminé. Il s’agit donc de trouver une solution à ce problème, à savoir de résoudre le système d’équations différentielles pour n’importe quelle valeur de l’obliquité sur le parement du mur ou de l’écran.

Afin de choisir l’obliquité souhaitée sur le parement, dans la méthode proposée, le système d’équations différentielles est intégré depuis le parement jusqu’au premier plan de glissement en fixant l’obliquité à la valeur souhaitée : pour le cas 1, avec une obliquité de 2/3φ en poussée et −2/3φ en butée et une valeur φ de 35°, un cheminement 2 est alors obtenu selon des valeurs de ω croissant tel que le présentent les figures 8–11 (le cheminement est 1 est déterminé selon les valeurs de ω décroissant). L’amplitude de la contrainte de poussée ou de butée est modifiée au niveau du parement de manière itérative de sorte à assurer un état de contraintes n₀ et t₀ sur le premier plan de glissement : les cheminements 1 et 2 se rejoignent donc avec le même état de contraintes au niveau du premier plan de glissement de Rankine. Pour ce faire, une procédure de dichotomie sur l’amplitude de la contrainte au niveau du parement est utilisée de telle sorte que les cheminements 1 et 2 donnent bien le même état de contraintes n₀ et t₀ (et donc la même inclinaison α) sur le premier plan de glissement de Rankine. Le système d’équations différentielles selon le cheminement 2 est résolu jusqu’à atteindre une convergence acceptable toujours selon une méthode explicite de type Runge–Kutta d’ordre 4 (RK4).

Différents auteurs dont Ravizé (1945) ou Salençon (1974) expliquent que la solution ainsi déterminée est bien unique quoique l’obliquité imposée sur le parement puisse apparaître comme une condition aux limites surabondante. Cette étape du calcul des coefficients de poussée et de butée est traitée par Caquot et Kerisel (1949) en proposant des techniques de résolution avec lesquelles il est possible de considérer près du parement des équilibres sans poids et avec poids permettant indirectement de choisir une obliquité quelconque de la poussée ou de la butée au niveau de ce dernier. Il est par ailleurs intéressant de noter que les techniques de résolution utilisées par Caquot et Kerisel diffèrent pour le traitement des états de poussée et de butée, ce qui n’est pas le cas ici.

Sur les figures 8–11, pour le cas 1 avec une obliquité égale à 2/3φ en poussée et −2/3φ en butée et une valeur φ de 35°, les cheminements 1 et 2 se rejoignent bien sur le même point au niveau du premier plan de glissement de Rankine. Les cheminements de type 2 varient entre φ ou −φ et la valeur de l’angle α correspondant à 2/3φ ou −2/3φ au niveau du parement, soit environ ± 23,33°.

Le coefficient de butée obtenu est égal à 7,77. Il est intéressant de noter que les tables de Caquot et Kerisel donnent 8,0 dans leur version de 1990 et 8,24 dans leur version de 1948. Les coefficients obtenus par une méthode d’analyse limite (Soubra et Macuh, 2002) et confirmés en termes de tendance par des logiciels comme Talren (2022) dans lequel une approche cinématique par l’extérieur est implémentée indiquent une valeur comprise entre 7,90 et 7,95. Comme cette approche est supposée donner une borne supérieure du coefficient de butée, la valeur probable de ce dernier est sans doute comprise entre 7,77 et 7,90. Ces différentes valeurs du coefficient de butée traduisent ainsi certaines incertitudes inhérentes à la résolution du système d’équations différentielles établies par Boussinesq (1876), qui demeurent toutefois négligeables en pratique. Le coefficient de poussée obtenu vaut 0,247, c’est-à-dire la même valeur que celle fournie par les tables de 1990.

Fig. 3 Vue des 3 cas avec la première ligne de glissement de Rankine pour les états de poussée et de butée. First Rankine slip line for the active and passive states for the three cases under consideration.

Fig. 4 Cheminement 1 – Variation du coefficient de poussée en fonction de ω. Path 1 – Active earth pressure variation according to ω.

Fig. 5 Cheminement 1 – Variation du coefficient de poussée en fonction de α. Path 1 – Active earth pressure variation according to α.

Fig. 6 Cheminement 1 – Variation du coefficient de butée en fonction de ω. Path 1 – Passive earth pressure variation according to ω.

Fig. 7 Cheminement 1 – Variation du coefficient de butée en fonction de α. Path 1 – Passive earth pressure variation according to α.

Fig. 8 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.

Fig. 9 Variation du coefficient de poussée en fonction de α. Active earth pressure variation according to α.

Fig. 10 Variation du coefficient de butée en fonction de ω. Passive earth pressure variation according to ω.

Fig. 11 Variation du coefficient de butée en fonction de α. Passive earth pressure variation according to α.

4 Quelques résultats

Les cas 1 à 3 précédemment présentés sont traités pour différentes inclinaisons (obliquités) afin d’illustrer l’approche développée. Seules les variations du vecteur de contrainte en fonction de l’angle α sont représentées. Il est aussi possible de représenter l’enveloppe des lignes de glissement qui détermine implicitement le mécanisme de rupture considéré. La première partie des lignes de glissement qui traduit l’équilibre de Boussinesq entre le parement et le premier plan de glissement de Rankine est proche d’une spirale logarithmique, sans en être formellement une. Elle peut être définie au moyen de considérations dans le cercle de Mohr et de la théorie des lignes caractéristiques (Absi, 1984) par les relations suivantes en prenant un rayon r égal à 1,0 au niveau du parement : $$r=e^{-\int tan\xi \left(\omega \right).d\omega }$$

avec : $$\xi \left(\omega \right)=\frac{\pi }{4}+\frac{\phi }{2}-\frac{\left({\omega }_{\alpha }-\alpha \right)}{2}\mathrm{e}\mathrm{t}{\omega }_{\alpha }=\mathit{a}\mathit{r}\mathit{c}\mathit{s}\mathit{i}\mathit{n}\left(\frac{sin\alpha }{sin\phi }\right)\mathrm{e}\mathrm{n}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{s}\mathrm{s}\mathrm{é}\mathrm{e},$$ $$\xi \left(\omega \right)=\frac{\pi }{4}-\frac{\phi }{2}+\frac{\left({\omega }_{\alpha }+\alpha \right)}{2}\mathrm{e}\mathrm{t}{\omega }_{\alpha }=\mathit{a}\mathit{r}\mathit{c}\mathit{s}\mathit{i}\mathit{n}\left(\frac{sin\alpha }{sin\phi }\right)\mathrm{e}\mathrm{n}\mathrm{b}\mathrm{u}\mathrm{t}\mathrm{é}\mathrm{e}\mathrm{.}$$

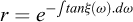
ξ(ω) désigne l’angle entre la ligne de glissement et la normale à un plan radial quelconque. Au niveau du parement, pour une obliquité nulle (α = 0 et ω_α = 0), on remarque que les inclinaisons des lignes de glissement sont égales à π/4 ± φ/2 en poussée et en butée. Pour une inclinaison α sur le parement correspondant à un rapport δ/φ respectivement égal à 1 en poussée et −1 en butée, la ligne de glissement est bien inclinée à φ ou −φ sur le parement (α = ± φ et ω_α = ± π/2). La seconde partie au-delà du premier plan de glissement est une droite correspondant au mécanisme de Rankine. La possibilité de visualiser rapidement les mécanismes de poussée et de butée permet d’apprécier les volumes de terrain mis en jeu et de contrôler, notamment en présence d’une pente ou d’un talus, si le calcul du coefficient de poussée ou de butée est licite.

Pour les états de poussée, les lignes de glissement sont globalement des droites ce qui explique le faible écart avec la théorie de Coulomb. Pour les états de butée, en revanche, il n’est plus du tout possible d’assimiler les lignes de glissement à des droites (sauf évidemment pour certains cas particuliers, par exemple celui d’une obliquité nulle sur un parement vertical). On remarque que la ligne de glissement change de concavité selon l’obliquité considérée sur le parement.

4.1 Cas 1 (φ = 30°, β = 0, λ = 0)

Les figures 12 et 13 présentent les résultats du cas 1. Le tableau 1 compare les coefficients obtenus par la méthode présentée à ceux indiqués dans les tables de Kerisel et Absi (1990) et ceux de Coulomb (uniquement en poussée). Les différences sont négligeables sauf sur un cas : en poussée, pour δ/φ = −1, un écart significatif de l’ordre de 10 % est mis en évidence qui peut être justifié par le fait que le mécanisme de rupture associé est extrêmement réduit. Le choix d’une telle obliquité est néanmoins très peu usuel en pratique (on retient en général des valeurs positives pour la poussée). La convergence obtenue avec la méthode développée n’est pas satisfaisante (Fig. 12) : l’inclinaison sur le premier plan de glissement de Rankine n’est pas égale à φ, elle atteint seulement 25,27° (au lieu de 30°), ce qui montre que la qualité de la résolution n’est pas suffisante. La valeur donnée par les tables de Caquot et Kerisel peut être approchée en modifiant légèrement la méthode proposée dans cet article : cette méthode (2) modifiée (Fig. 14 et 15) permet d’assurer des inclinaisons à −φ et φ respectivement sur le parement et le premier plan de glissement de Rankine et donne un coefficient de poussée de 0,965 (contre 0,981 pour la méthode Caquot et Kerisel). En revanche, elle ne permet plus d’obtenir une amplitude correcte des contraintes sur le premier plan de glissement de Rankine. La méthode (1) utilisée dans cet article garantit sur ce cas quant à elle la continuité avec le cheminement 1 en termes de contraintes sur le premier plan de glissement de Rankine mais pas en termes d’inclinaison du vecteur de contrainte. Les méthodes développées fournissent toutefois une valeur du coefficient de poussée supérieure à celle obtenue par la méthode de Coulomb qui constitue une borne inférieure du coefficient de poussée (Caquot et Kerisel, 1949).

L’enveloppe des lignes de glissement (Fig. 16 et 17) est conforme à des résultats présentés par Sokolowski (1965). Pour une inclinaison nulle sur le parement, il est facile de vérifier que la longueur du plan radial sur la surface libre vaut : tan(π/4 − φ/2) en poussée soit 0,577 et tan(π/4 + φ/2) en butée soit 1,732.

Fig. 12 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.

Fig. 13 Variation du coefficient de butée en fonction de α. Passive earth pressure variation according to α.

Fig. 14 Comparaison de deux méthodes d’estimation du coefficient de poussée en fonction de ω (δ/φ = −1). Comparison of two methods for assessing the earth pressure coefficient according to ω (δ/φ = −1).

Fig. 15 Comparaison de deux méthodes d’estimation du coefficient de poussée en fonction de α (δ/φ = −1). Comparison of two methods for assessing the earth pressure coefficient according to α (δ/φ = −1).

Fig. 16 Enveloppe des lignes de glissement en poussée. Envelope of slip lines for the active state.

Fig. 17 Enveloppe des lignes de glissement en butée. Envelope of slip lines for the passive state.

4.2 Cas 2 (φ = 20°, β = 12°, λ = −20°)

Les figures 18–21 présentent les résultats du cas 2. Le tableau 2 compare les coefficients obtenus par la méthode présentée à ceux indiqués dans les tables de Kerisel et Absi (1990) et à ceux de Coulomb (uniquement en poussée). Les différences sont négligeables sauf sur un cas : pour δ/φ = −1, un écart significatif de l’ordre de 10 % est toutefois mis en évidence sans réelle explication : la convergence semble bien être assurée pour la méthode présentée. À nouveau, le fait que le mécanisme de rupture est extrêmement réduit comme le montre la figure 20 peut expliquer un tel écart. En poussée, pour δ/φ = −2/3, le cheminement 1 et le cheminement 2 sont quasiment confondus (Fig. 18) ce qui est normal puisque l’inclinaison de la contrainte sur le parement pour le cheminement 1 vaut −13,25°, c’est-à-dire déjà quasiment −2/3φ = −13,33°. La même observation peut être faite en butée pour δ/φ = 1 (Fig. 19) où l’inclinaison de la contrainte sur le parement pour le cheminement 1 vaut 19,64°, c’est-à-dire déjà quasiment φ = 20°. La forme de l’enveloppe des lignes de glissement en poussée renseigne aussi indirectement sur l’écart entre la théorie de l’équilibre de Boussinesq et l’équilibre de Coulomb. Pour δ/φ = −2/3 en poussée (Fig. 20), l’enveloppe est visuellement rectiligne, ce qui apparaît clairement au niveau des 3 coefficients qui sont bien égaux et valent 0,533.

Fig. 18 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.

Fig. 19 Variation du coefficient de en butée en fonction de α. Passive earth pressure variation according to α.

Fig. 20 Enveloppe des lignes de glissement en poussée. Envelope of slip lines for the active state.

Fig. 21 Enveloppe des lignes de glissement en butée. Envelope of slip lines for the passive state.

4.3 Cas 3 (φ = 40°, β = −16°, λ = 10°)

Les figures 22–25 présentent les résultats du cas 3. Le tableau 3 compare les coefficients obtenus par la méthode présentée à ceux indiqués dans les tables de Kerisel et Absi (1990) et à ceux de Coulomb (uniquement en poussée). Les différences sont négligeables sauf sur un cas : en poussée, pour δ/φ = −1, un écart significatif de l’ordre de 10 % est toutefois mis en évidence : comme précédemment, le fait que le mécanisme de rupture est extrêmement réduit comme le montre la figure 24 peut expliquer un tel écart. Par ailleurs, la convergence obtenue avec la méthode développée n’est pas satisfaisante : l’inclinaison sur le premier plan de glissement de Rankine n’est pas égale à φ, elle atteint seulement 18,95°, ce qui montre que la qualité de la résolution n’est pas suffisante (Fig. 22). En butée (Fig. 23), pour δ/φ = −2/3, une solution a pu être obtenue avec la méthode proposée alors que les tables n’en fournissent pas : néanmoins, la solution obtenue n’est pas correcte dans la mesure où elle ne permet pas de garantir la continuité avec l’état de Rankine sur le premier plan de glissement. En butée, pour δ/φ = 0, la continuité entre les cheminements 1 et 2 n’est pas parfaitement assurée : néanmoins, la méthode proposée donne une valeur très proche des tables de 1990 : 1,52 contre 1,55. Ces résultats montrent que la détermination des coefficients de poussée ou de butée peut prêter à discussion.

Fig. 22 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.

Fig. 23 Variation du coefficient de butée en fonction de α. Passive earth pressure variation according to α.

Fig. 24 Enveloppe des lignes de glissement en poussée. Envelope of slip lines for the active state.

Fig. 25 Enveloppe des lignes de glissement en butée. Envelope of slip lines for the passive state.

4.4 Courbe enveloppe des contraintes

La courbe enveloppe des contraintes agissant sur les plans radiaux permet de visualiser les mécanismes mis en jeu car elle renseigne sur l’angle entre la normale aux plans radiaux et le vecteur de contrainte. Ces courbes sont représentées pour le cas 1 (Fig. 26 et 27) pour différentes obliquités tant en poussée qu’en butée. L’équation de ces courbes est définie par la relation suivante au moyen de considérations dans le cercle de Mohr en prenant un rayon r égal à 1,0 au niveau du parement : $$r=e^{-\int \tan \alpha \left(\omega \right).d\omega }.$$

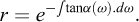
Elles sont comparées à une courbe en forme de spirale logarithmique pour laquelle l’inclinaison du vecteur de contrainte est inclinée à φ ou −φ respectivement en poussée et en butée. Les variations d’inclinaisons du vecteur de contrainte permettent d’apprécier l’amplitude de la poussée ou de la butée sur le parement. La spirale logarithmique fournit visuellement une borne inférieure ou supérieure de la poussée ou de la butée : en poussée, plus la courbe enveloppe des contraintes s’éloigne de la spirale logarithmique, plus celle-ci est forte ; en butée, c’est l’inverse.

Fig. 26 Courbe enveloppe des contraintes en poussée pour le cas 1. Envelope of stresses for the active state in case 1.

Fig. 27 Courbe enveloppe des contraintes en butée pour le cas 1. Envelope of stresses for the passive state in case 1.

4.5 Autres commentaires

La méthode proposée fonctionne globalement bien avec des temps de calcul extrêmement faibles (moins d’une seconde) qui pourraient permettre une résolution directe en pratique plutôt que l’utilisation des tables avec toutes les interpolations qu’elles nécessitent. Afin de montrer la bonne fiabilité de la méthode présentée, l’annexe D comprend une comparaison sur d’autres cas que ceux traités avec les valeurs coefficients de poussée et de butée estimés à partir des tables de Kerisel et Absi (1990) et des tables présentées par Sokolowski (1965).

Pour les états de poussée, les approches de Coulomb d’une part, de Caquot et Kerisel d’autre part et celle décrite dans le présent article sont très analogues. Pour les états de butée, l’approche de Coulomb ne peut plus être utilisée dès lors que la ligne de glissement n’est plus une droite. Les écarts entre l’approche de Caquot et Kerisel et l’approche décrite dans le présent article sont négligeables en pratique. De manière plus générale, au-delà des différences entre chaque méthode, l’incertitude prépondérante réside essentiellement dans le choix de l’angle de frottement et de l’obliquité.

La représentation de l’enveloppe des lignes de glissement ou de l’enveloppe des contraintes agissant sur les plans radiaux permet de comprendre pourquoi toutes les configurations géométriques ne peuvent pas être traitées et donnent une image des mécanismes de rupture mis en jeu avec les volumes de terrain associés : ainsi, il est plus facile de donner un sens physique aux coefficients de poussée ou de butée.

5 Conclusions

Cet article revient sur les méthodes de résolution du système d’équations différentielles rendant compte des équilibres de Boussinesq et de Rankine à l’arrière d’un mur ou d’un écran de soutènement. La méthode présentée pour la résolution de ces équations différentielles permet d’aborder la manière dont Caquot et Kerisel (1949) ont considéré le même problème en 1949. La technique de résolution proposée est différente mais elle permet de retrouver les mêmes résultats en pratique.

La fiabilité des coefficients étant largement éprouvée par la pratique et par différents travaux théoriques antérieurs, l’objectif de l’article n’était d’ailleurs pas celui-là : il s’agissait comme indiqué en introduction de présenter à nouveau ce problème en apportant dans la mesure du possible un éclairage original et vulgarisé afin d’assurer la diffusion de cette théorie au sein de la profession géotechnique.

Ce travail trouve aussi son intérêt dans les travaux normatifs en lien avec le nouvel Eurocode 7, en Europe et en France, durant lesquels il est toujours important de pouvoir réévaluer le travail réalisé par les scientifiques des générations précédentes.

Annexe A Coefficient K_aq, K_pq, K_ac et K_pc

Il a paru utile en complément de présenter les formules analytiques des coefficients K_aq et K_pq pour les milieux non pesants. Seule la relation de base est rappelée, c’est-à-dire celle où la spirale logarithmique est encadrée par deux équilibres de Rankine. Pour accéder à l’ensemble des relations, il convient de se reporter à la publication suivante : L’Herminier et Absi (1962).

Les coefficients K_aq et K_pq sont déterminés selon les relations suivantes : $$K_{aq}=\frac{cos\delta -sin\varphi cos{\omega }_{\delta }}{cos\alpha +sin\varphi cos{\omega }_{\alpha }}{e}^{-2{\psi }_{a}tan\varphi },$$ $$K_{pq}=\frac{cos\delta +sin\varphi cos{\omega }_{\delta }}{cos\alpha -sin\varphi cos{\omega }_{\alpha }}{e}^{2{\psi }_{p}tan\varphi },$$ $$sin{\omega }_{\delta }=\frac{sin\delta }{sin\varphi },$$ $$sin{\omega }_{\alpha }=\frac{sin\alpha }{sin\varphi },$$ $${\psi }_a=\frac{{\omega }_{\alpha }+\alpha }{2}+\frac{{\omega }_{\delta }-\delta }{2}+\beta -\lambda ,$$ $${\psi }_p=\frac{-{\omega }_{\alpha }+\alpha }{2}-\frac{{\omega }_{\delta }+\delta }{2}+\beta -\lambda .$$

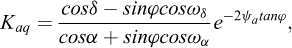
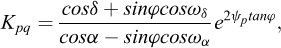
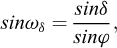
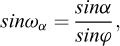
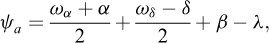
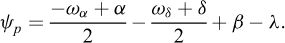
Pour un chargement vertical, il convient de prendre α = −β.

Les coefficients K_ac et K_pc nécessaires pour la prise en compte de la cohésion peuvent être déterminés par les relations suivantes par application du théorème des états correspondants :

• $K_{ac}=\frac{1}{tan\varphi }\left(\frac{1}{cos\delta }-K_{aq,\alpha =0}\right)$ avec K _aq,α=0 la valeur de K_aq calculée pour α = 0 ;

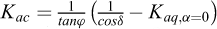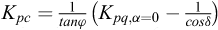• $K_{pc}=\frac{1}{tan\varphi }\left(K_{pq,\alpha =0}-\frac{1}{cos\delta }\right)$ avec K _pq,α=0 la valeur de K_pq calculée pour α = 0.

Ces expressions reposent sur le fait que l’adhérence entre le parement et l’écran est prise égale à : $$\frac{a}{c}=\frac{\tan \delta }{\tan \varphi }.$$

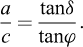
Annexe B Formules d’interpolation du coefficient de poussée

Le coefficient de poussée K_aγ peut être obtenu à partir des relations suivantes (Caquot et Kerisel, 1948, 1949) qui permettent de déterminer les valeurs présentées dans les tables de 1990 : $$k_a=\frac{co{s}^2\left(\lambda -\varphi \right)}{cos\left(\lambda +\delta \right){\left(1+\sqrt{\frac{sin\left(\varphi +\delta \right)sin\left(\varphi -\beta \right)}{cos\left(\lambda +\delta \right)cos\left(\beta -\lambda \right)}}\right)}^2}$$

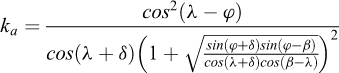
(Coefficient de Coulomb pour l’état de poussée)

K_aγ = ρk_a où ρ est un paramètre correctif défini par : $$ln\left(\rho \right)=-\left(2-\frac{ta{n}^2\beta +ta{n}^2\delta }{2ta{n}^2\varphi }\right)\sqrt{sin\varphi }ln\left[\left(1-0,9{\zeta }^2-0.1{\zeta }^4\right)\left(1-0,3{\zeta }^3\right)\right],$$ $$\zeta =\frac{\lambda -{\lambda }_0}{\lambda +{\lambda }_0+\pi -2\varphi },$$ $${\lambda }_0=\frac{\eta }{2}+\frac{\beta -{\omega }_{\beta }}{2}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}{\omega }_{\beta }=\frac{sin\beta }{sin\phi },$$ $$\left|tan\frac{\eta }{2}\right|=\frac{\left|1/tan\delta \right|-\sqrt{{\left(1/tan\delta \right)}^2-{\left(1/tan\varphi \right)}^2}}{1+1/sin\varphi }.$$

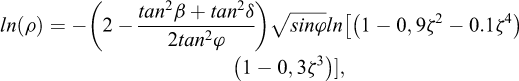
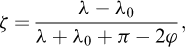
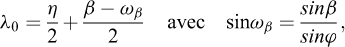
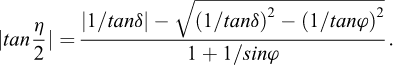
Le signe de η est celui de δ.

Il est intéressant de noter que le paramètre ρ est toujours supérieur à 1, ce qui traduit la simplification faite par Coulomb de supposer une surface de rupture plane.

Annexe C Formules d’interpolation du coefficient de butée

Dans le cadre de cet article, il a paru intéressant de rappeler les formules d’interpolation publiées par Caquot et Kerisel (1948, 1949). Bien que limitées dans leurs applications, elles permettent, au moyen d’un simple tableur, le calcul du coefficient de butée en milieu pesant. Ces formules rendent compte des valeurs présentées dans les tables de 1948. Comme indiqué précédemment, elles peuvent faire l’objet d’écarts parfois importants avec les valeurs des tables de 1990.

Les formules sont valables pour :

0 < φ < 60°, −φ < β < φ, −45° < λ < 45°

• (1) On détermine les fonctions φ_i suivantes de φ :

$${\Phi }_0=1,10tan\varphi +0,275{\left(tan\varphi \right)}^{5/3}$$	$${\Phi }_1=co{s}^6\varphi$$
$${\Phi }_2=1,135{\left(tan\varphi \right)}^{9/8}$$	$${\Phi }_3=\frac{sin\varphi }{2}$$
$${\Phi }_4=0,463sin\varphi +0,426si{n}^6\varphi$$	$${\Phi }_5={\Phi }_0-{\Phi }_4-log\left(co{s}^2\varphi \right)$$
$${\Phi }_6=0,07tan\left(\varphi \right)\left(1-0,7tan\left(\varphi \right)\right)$$	$${\Phi }_7=\frac{0,34sin\varphi }{0,1+sin\varphi +si{n}^2\varphi }$$

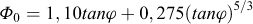
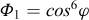
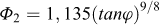
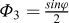
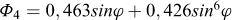
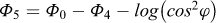
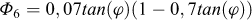
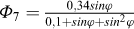
• (2) On détermine les fonctions λ_i suivantes de λ :

$${\lambda }_1=-log\left(cos\lambda \right)$$	$${\lambda }_2=sin\lambda$$
$${\lambda }_3=si{n}^3\lambda$$	$${\lambda }_7=1-cos\lambda +0,62sin\lambda$$

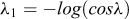
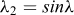
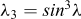
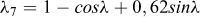
• (3) On détermine les fonctions β_i suivantes de β/φ :

$${\beta }_4=ta{n}^2\left(\frac{19\pi }{60}\frac{\beta }{\varphi }\right)$$	$${\beta }_5=1,124sin\left(\frac{\pi }{4}\frac{\beta }{\varphi }\right)+1,16si{n}^5\left(\frac{\pi }{4}\frac{\beta }{\varphi }\right)$$
$${\beta }_6=sin\left(\pi \frac{\beta }{\varphi }\right)$$	$${\beta }_7=1-{\left(1-\frac{\beta }{\varphi }\right)}^{2.5}$$

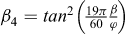
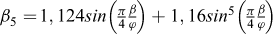
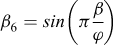
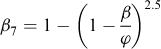
• (4) On calcule les valeurs des fonctions F_i suivantes de deux variables :

$${\text{F}}_1={\Phi }_1{\lambda }_1+{\Phi }_2{\lambda }_2+{\Phi }_3{\lambda }_3$$

$${\text{F}}_2=-0,422{\Phi }_4{\beta }_4+{\Phi }_5{\beta }_5-{\Phi }_6{\beta }_6+2,5\left(1+\frac{\beta }{\varphi }\right)sin2\varphi {.10}^{-6\left(1+\frac{\beta }{\varphi }\right)}$$

$${\text{F}}_7=sin\left(\frac{\pi }{360}\left(80+17{\left(\frac{\beta }{\varphi }\right)}^3-25{\left(\frac{\beta }{\varphi }\right)}^4-\varphi \right)\right)\left(\text{en degrés pour\hspace{0.17em}}\beta \text{\hspace{0.17em}et\hspace{0.17em}}\phi \right)$$

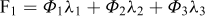
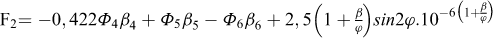
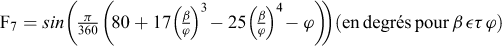
• (5) La composante normale de la butée n est obtenue par :

$$log\left(n\right)={\Phi }_0-{\text{F}}_1+{\text{F}}_2+{\text{F}}_7{\Phi }_7{\lambda }_7{\beta }_7.$$

La composante de la butée b inclinée à −φ est donnée par : $$b\left(-\varphi \right)=n/\cos \varphi .$$

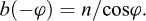
La composante de la butée b inclinée à δ est donnée par : $$b\left(\delta \right)=b\left(-\varphi \right)\frac{n\left(\delta \right)}{n\left(-\varphi \right)}\frac{\cos \varphi }{\cos \delta }.$$

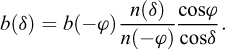
où n(δ) est la contrainte normale de la butée dans l’équilibre de Rankine et n(−φ) est la composante de la butée inclinée à −φ pour un parement vertical (λ = 0) et une inclinaison de la surface libre β = δ.

Exemples :

Le tableau ci-dessous présente, pour les cas 1, 2 et 3, les étapes permettant de calculer le coefficient de butée b(δ) selon la méthode proposée par Caquot et Kerisel (1949). On note des écarts significatifs avec les valeurs numériques dans les tables de Kerisel et Absi (1990).

Annexe D Comparaison sur d’autres cas avec les tables de Kerisel et Absi (1990) et les valeurs fournies par Sokolowski (1965)

La comparaison porte, pour l’état de poussée, sur des obliquités positives ou nulles (ce qui est le choix usuel) et, pour l’état de butée, sur des obliquités négatives ou nulles (ce qui est le choix usuel). Tant en poussée qu’en butée, les écarts entre les trois méthodes ne sont pas significatifs.

Références

Liste des tableaux

Liste des figures

	Fig. 1 Notations. Notations.
Dans le texte

	Fig. 2 Équilibre d’un volume élémentaire (d’après Caquot et Kerisel, 1949). Equilibrium for an elementary volume (from Caquot and Kerisel, 1949).
Dans le texte

	Fig. 3 Vue des 3 cas avec la première ligne de glissement de Rankine pour les états de poussée et de butée. First Rankine slip line for the active and passive states for the three cases under consideration.
Dans le texte

	Fig. 4 Cheminement 1 – Variation du coefficient de poussée en fonction de ω. Path 1 – Active earth pressure variation according to ω.
Dans le texte

	Fig. 5 Cheminement 1 – Variation du coefficient de poussée en fonction de α. Path 1 – Active earth pressure variation according to α.
Dans le texte

	Fig. 6 Cheminement 1 – Variation du coefficient de butée en fonction de ω. Path 1 – Passive earth pressure variation according to ω.
Dans le texte

	Fig. 7 Cheminement 1 – Variation du coefficient de butée en fonction de α. Path 1 – Passive earth pressure variation according to α.
Dans le texte

	Fig. 8 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.
Dans le texte

	Fig. 9 Variation du coefficient de poussée en fonction de α. Active earth pressure variation according to α.
Dans le texte

	Fig. 10 Variation du coefficient de butée en fonction de ω. Passive earth pressure variation according to ω.
Dans le texte

	Fig. 11 Variation du coefficient de butée en fonction de α. Passive earth pressure variation according to α.
Dans le texte

	Fig. 12 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.
Dans le texte

	Fig. 13 Variation du coefficient de butée en fonction de α. Passive earth pressure variation according to α.
Dans le texte

	Fig. 14 Comparaison de deux méthodes d’estimation du coefficient de poussée en fonction de ω (δ/φ = −1). Comparison of two methods for assessing the earth pressure coefficient according to ω (δ/φ = −1).
Dans le texte

	Fig. 15 Comparaison de deux méthodes d’estimation du coefficient de poussée en fonction de α (δ/φ = −1). Comparison of two methods for assessing the earth pressure coefficient according to α (δ/φ = −1).
Dans le texte

	Fig. 16 Enveloppe des lignes de glissement en poussée. Envelope of slip lines for the active state.
Dans le texte

	Fig. 17 Enveloppe des lignes de glissement en butée. Envelope of slip lines for the passive state.
Dans le texte

	Fig. 18 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.
Dans le texte

	Fig. 19 Variation du coefficient de en butée en fonction de α. Passive earth pressure variation according to α.
Dans le texte

	Fig. 20 Enveloppe des lignes de glissement en poussée. Envelope of slip lines for the active state.
Dans le texte

	Fig. 21 Enveloppe des lignes de glissement en butée. Envelope of slip lines for the passive state.
Dans le texte

	Fig. 22 Variation du coefficient de poussée en fonction de ω. Active earth pressure variation according to ω.
Dans le texte

	Fig. 23 Variation du coefficient de butée en fonction de α. Passive earth pressure variation according to α.
Dans le texte

	Fig. 24 Enveloppe des lignes de glissement en poussée. Envelope of slip lines for the active state.
Dans le texte

	Fig. 25 Enveloppe des lignes de glissement en butée. Envelope of slip lines for the passive state.
Dans le texte

	Fig. 26 Courbe enveloppe des contraintes en poussée pour le cas 1. Envelope of stresses for the active state in case 1.
Dans le texte

	Fig. 27 Courbe enveloppe des contraintes en butée pour le cas 1. Envelope of stresses for the passive state in case 1.
Dans le texte

Dans le texte

Dans le texte

Dans le texte