| Numéro |
Rev. Fr. Geotech.
Numéro 151, 2017
|
|
|---|---|---|
| Numéro d'article | 4 | |
| Nombre de pages | 15 | |
| DOI | https://doi.org/10.1051/geotech/2017010 | |
| Publié en ligne | 10 juillet 2017 | |
Revue / Review Article
Sols structurés sous sollicitation dynamique : des métamatériaux en géotechnique
Structured soils under dynamic loading: the metamaterials in geotechnics
1
Ménard,
91260
Nozay, France
2
Aix-Marseille Univ, CNRS, Centrale Marseille,
13013
Marseille, France
★ Auteur de correspondance : stephane.brule@menard-mail.com ; stephanebrule@orange.fr
Les fondations profondes et les éléments verticaux constitutifs du renforcement de sol en zone urbaine peuvent être considérés comme des structures enterrées interférant avec les vibrations et certaines composantes du signal sismique se propageant dans les milieux à faible vitesse. Dans ces milieux artificiels anisotropes constitués de sol et d'éléments géométriques pleins ou vides, les phénomènes physiques provoqués sont les interférences des ondes diffractées sur les surfaces et les objets. Les effets de l'anisotropie sont renforcés par les résonances locales des éléments insérés dans le sol et par le dimensionnement issu des techniques d'élasticité transformationnelle et du morphing pouvant conduire théoriquement jusqu'aux capes d'invisibilité qui détournent les ondes autour d'une zone protégée. Dans ces milieux périodiques ou non, les effets désirés sont la réflexion totale (effet de Bragg), les bandes interdites à basse fréquence par résonances locales, le contrôle du cheminement des ondes par le jeu de la physique transformationnelle, l'atténuation par dissipation d'énergie, etc.
Abstract
The deep foundations and vertical elements used for ground reinforcement techniques in urban area, could be considered as buried interfering structures with vibrations and a part of the seismic signal propagating in low velocity media. In these artificial and anisotropic media made of geometrical empty or full elements, the underlying physical phenomenon is interference of waves scattering on surfaces and objects. The anisotropic effects are enhanced by local resonances of implemented elements in the soil and by the design inherited from transformation elastodynamics and morphing tools that could theoretically lead to an ideal cloak detouring waves around a protected area. In these periodic or non-periodic media, the desired effects are total reflection (Bragg's effect), low frequency band gaps by local resonances, wave-path control via transformational physics, attenuation by energy-dissipation, etc.
Mots clés : sols structurés / métamatériau / cristal phononique / fondation profonde / miroir de Bragg / physique transformationnelle / matériaux auxétiques
Key words: structured soils / metamaterial / phononic crystal / deep foundation / Bragg's mirror / transformational physics / auxetic materials
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2017
1 Introduction : pourquoi des métamatériaux en géotechnique ?
La notion de sols structurés n'est pas nouvelle. Si nous entendons par cette définition, la création de sols rendus composites par l'action de l'Homme, avec des agencements périodiques ou non d'éléments introduits dans le sous-sol, constitués de vide ou remplis par un matériau (béton, sable, gravier, métal, etc.) alors les fondations spéciales d'un bâtiment, un maillage d'inclusions rigides, un réseau de cellules parallélépipédiques avec parois en béton de sol pour s'opposer à la liquéfaction des sols ou encore tout ensemble de structures enterrées à l'échelle d'une ville peut satisfaire à cette définition (Fig. 1)
Les techniques de fondations profondes (pieux, barrettes, parois moulées, etc.), d'amélioration de sol (compactage dynamique, vibrocompactage, etc.) et de renforcement de sol (inclusions rigides, inclusions souples, etc.) évoluent vers l'augmentation des longueurs des éléments constitutifs avec des records de 50 à 70 m pour des pieux ou inclusions rigides par exemple (Soil Magazine, 2016). D'autre part, une amélioration de l'industrialisation de ces procédés permet d'envisager un degré croissant de densification des éléments incorporés dans le sol hôte. Ainsi, le taux de substitution du sol, défini comme le rapport des volumes Vinclusions / Vsol soit le volume des inclusions sur le volume de sol est croissant au point de rechercher à définir les propriétés mécaniques de ce nouveau milieu « composite ». Le plus souvent, le renforcement répond à la question de la portance sous chargement monotone (rarement examiné sous chargement cyclique ou sous véritable situation sismique) et à la déformation verticale du sol sous charges de service, c'est-à-dire une gamme de déformations de l'ordre de 10−3 pour des ouvrages de surface.
Cependant, ces milieux composites sont aussi le plus souvent structurés, c'est-à-dire avec une distribution spatiale non aléatoire des inclusions, que nous définissons comme tout élément mis en place dans le sol, quelle que soit sa géométrie, ou du sol modifié (sol densifié, sol imprégné d'un coulis ou d'une résine, etc.). Cette structuration par l'action de l'Homme renvoie à la notion de « métamatériaux », qui sont des matériaux artificiels nés de l'électromagnétisme avant de faire leur apparition ces dernières années dans le domaine des ondes sismiques. Les métamatériaux sont souvent périodiques avec une périodicité a très inférieure à la longueur λ du signal les sollicitant et offrent des propriétés « exotiques » et inexistantes à l'état naturel. Il s'agit notamment d'un indice de réfraction négatif ne répondant pas à la loi de Snell-Descartes applicable à l'optique géométrique (Fig. 6).
Dans le cas d'inclusions verticales en béton dans le sol, il est fréquent de voir des maillages réguliers avec une maille carrée ou triangulaire dans le plan horizontal (O, x, y), rappelant les arrangements ioniques dans les structures cristallines (structure 2D). Des structures tridimensionnelles peuvent aussi être imaginées en superposant, par exemple, des alvéoles comme celle décrite en Figure 1 (à droite) à plusieurs profondeurs.
Pour illustrer ce changement de paradigme sur les sols structurés, examinons le cas d'une structure 1D, constituée d'un sol initialement homogène devenant, par exemple, artificiellement stratifié horizontalement par « rigidification » comme illustré en Figure 2. Cette rigidification peut être le résultat d'une densification ou d'une imprégnation du sol par une substance injectée de type coulis ou résine. Ce « nouveau » sol s'apparentant à une structure bicouche après travaux peut offrir de nouvelles propriétés de propagation des vibrations et ondes sismiques. Nous pouvons aussi illustrer cette influence sur la réponse dynamique en surface avec un autre exemple : faisons l'hypothèse d'un modèle de sol non chargé en surface, composé d'un milieu élastique bicouche, c'est-à-dire un sol caractérisé par son épaisseur h1, sa vitesse d'onde de cisaillement initial Vs1 initial = 200 m/s et d'une masse volumique ρ = 1800 kg.m−3, reposant sur substratum sismique tel que Vs substratum > 800 m/s. Pour ce modèle, nous considérons, comme pour la majorité des modèles utilisés en génie parasismique, une onde sismique incidente strictement verticale, en phase avec l'onde réfléchie en surface (Fig. 3), la fonction de transfert H(ω) où ω est la fréquence angulaire (en rad.s−1), se définit comme le rapport du déplacement en surface et à la base de la couche de sol, et s'exprime selon l'équation (1) en l'absence de tout amortissement matériel. Nous sommes dans le cas d'un nouveau sol structuré, de type 1D mais constitué d'une seule maille élémentaire a. Les maxima de cette fonction, autrement dit les modes résonants, sont donnés pour tout entier n strictement positif par ωh1/Vs1 = (n + 1)π /2. La fréquence fondamentale en Hertz pour le premier mode est f = Vs1/4 h1.
 (1)
(1)
Cette fonction est toujours supérieure à l'unité et n'a pas de borne supérieure, imposant, en raison de la formulation du phénomène physique, une amplification systématique du mouvement en surface. En introduisant un amortissement dans le sol, par l'intermédiaire d'un modèle visco-élastique plus réaliste de la rhéologie des sols (Verruijt, 2010), la fonction de transfert peut aussi prendre des valeurs comprises entre 0 et 1 (Fig. 3).
Cet exemple de sol structuré simple, constitué de deux couches, sans répétition périodique du motif a, offre déjà des propriétés intéressantes car il permet de montrer la modification des modes fondamentaux. La « rigidification » du sol conduit à l'augmentation de la valeur des fréquences fondamentales mais l'amortissement ζ, toutefois difficile à mesurer in situ, peut également être modifié, à la baisse (accroissement de l'amplitude du déplacement en surface). Pour des déformations de l'ordre de 10−6 à 10−4 l'amortissement est de quelques pour cents pour les sols (Iwasaki et al., 1978 ; Srbulov, 2010).
Comme illustré par cet exemple de sol bicouche 1D, l'intérêt des sols structurés est de rechercher une approche complémentaire à la seule modification des caractéristiques mécaniques d'un sol pour réaliser des dimensionnements par des méthodes « statiques » en assimilant l'action sismique à un chargement « pseudo-statique ». En effet, l'objectif est de solliciter des propriétés mises en évidence par les disciplines des milieux condensés. Ces propriétés sont les bandes interdites, l'atténuation, la réflexion de Bragg, le contrôle du cheminement des ondes.
Nous allons montrer dans cet article que les sols structurés, dont ceux considérés comme des métamatériaux, peuvent faire l'objet d'une exploration théorique et potentiellement appliquée. Nous posons d'abord les hypothèses concernant les signaux sismiques étudiés (Sect. 2) avant de rappeler les propriétés remarquables apportées par les cristaux photoniques, cristaux phononiques et métamatériaux dont nous présentons la définition (Sect. 3). La Section 4 est un regard sur les sols structurés en géotechnique dans le cadre des applications en approche pseudo-statique. La physique des milieux périodiques est abordée dans la Section 5 pour illustrer les phénomènes de diffraction, diffusion multiple, miroir de Bragg et de résonateurs. La nécessité de faire appel à des outils d'analyse spécifique est expliquée dans la Section 6. La puissance du formalisme de la physique transformationnelle est abordée dans la Section 7, l'illustration des similitudes multi-échelle à partir d'expérience en laboratoire ou in situ fait l'objet des Sections 7 et 8 avant de conclure par les perspectives concernant ces matériaux d'un nouveau genre (Sect. 9).
 |
Fig. 1 À gauche : sols structurés constitués de pieux et micropieux (Brûlé et al., 2015a). À droite : principe de cellules dans le sol, ici avec des colonnes de sol-mixing pour augmenter la résistance au cisaillement des sols lors de séismes (Aznavourian et al., 2016). Left: structured soils made of piles and micropiles (Brûlé et al., 2015a). Right: principle of cells into the soil, here the case of soil-mixing columns to increase the shear strength of the soil during earthquakes (Aznavourian et al., 2016). |
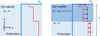 |
Fig. 2 Exemple de stratification horizontale artificielle de sols initialement homogènes par densification ou rigidification (structure 1D). Le profil des vitesses des ondes de cisaillement est modifié (à droite) après travaux de densification par compactage dynamique, vibrocompactage ou injection de coulis (ligne rouge pleine). Example of artificial horizontal stratification of initially homogeneous soil by means of densification or reinforcement (1D structure). The shear wave velocity profile is modified (right) after dynamic compaction, vibrocompaction works or grout injection (solid red line). |
 |
Fig. 3 Illustration de l'évolution de la fonction de transfert T(ω) avant (ligne pleine grise) et après densification du sol (ligne discontinue grise) dans l'hypothèse d'un modèle bicouche sans amortissement. h1 = 20 m, Vs1 initial = 200 m/s, Vs1 final = 260 m/s, soit 30 % d'amélioration. Les courbes noires prennent en compte un amortissement théorique ζ = 0,05 (ligne noire pleine) avant densification et, par exemple, ζ = 0,04 (ligne noire discontinue) après densification. Evolution of the transfer function T(ω) before (solid grey line) and after ground densification (dashed grey line) in case of a two layers model without damping. h1 = 20 m, Vs1 initial = 200 m/s, Vs1 final = 260 m/s, that is 30% of increase. Black lines represent cases with a theoretical damping ζ = 0.05 (solid black line) before soil densification and, for example, ζ = 0.04 (dashed black line) after works. |
2 Caractérisation du signal sismique
Nous faisons l'hypothèse des petites déformations sous sollicitations sismiques, c'est-à-dire que les conditions de l'analyse supposent d'être éloigné de toute faille active pouvant occasionner de fortes non-linéarités dans un proche périmètre.
L'amplitude des ondes sismiques incidentes peut être amplifiée par les sols « mous » de surface en raison du contraste d'impédance de ces matériaux de couverture avec le substratum sismique, ou encore par les effets de piégeage des ondes dans des bassins remplis de sédiments détritiques peu consolidés. La vitesse des ondes de cisaillement dans ces matériaux peut être inférieure à 100 m/s. Nous considèrerons des sols dont la vitesse est comprise entre 100 et 350 m/s, c'est-à-dire des sols pouvant faire l'objet de fondations spéciales de type pieux ou renforcement de sol à base d'inclusions rigides. Dans ces conditions, le rapport des modules d'Young Einclusion/Esol > 100, ce qui rentre dans le cadre de modèles mathématiques dits de fort contraste pour lesquels des théories d'homogénéisation non classiques ont été développées [e.g. en électromagnétisme, un fort contraste sur la permittivité conduit au magnétisme artificiel (Bouchitté et Felbacq, 2004)]. Pour les sols structurés à fort contraste, sont trouvés des effets similaires sur des coefficients élastiques effectifs fortement dispersifs en fréquence (Chesnais et al., 2011).
Considérant ces vitesses et une plage de fréquences comprise entre 0,1 et 50 Hz au sens large et 1 et 10 Hz au sens restreint pour les signaux sismiques incidents, dans le second cas, les longueurs d'ondes sont de quelques dizaines à centaines de mètres, c'est-à-dire du même ordre de grandeur que la majorité des ouvrages de surface (Betbeder-Matibet, 2003a,b). Dans ces conditions, les effets de l'interaction du sol avec la structure sont à prendre en considération, voire les effets de résonance de l'ouvrage avec le signal sismique.
Nous considérons des ondes de surface de type Rayleigh ou encore des ondes de volume à incidence oblique arrivant en surface (Fig. 4). Si le rapport largeur sur profondeur d'une vallée sédimentaire est important alors la simplification à un modèle de sol 1D pour traduire les effets de site avec des ondes stationnaires à incidence verticalisée est envisageable. En dehors de ces conditions, les effets de site 2D et 3D se manifestent (Hobiger, 2011) avec notamment pour conséquence des angles variables d'incidence des ondes en surface.
Le signal sismique est de nature « transitoire », allant de quelques secondes à quelques minutes pour les séismes majeurs, en comparaison avec matériaux testés en laboratoire avec des signaux entretenus conduisant à la recherche d'un état stationnaire illustrant les propriétés spécifiques avec des matériaux structurés.
 |
Fig. 4 Ondes de volume (pression P et cisaillement S) avec réfractions multiples dans un milieu stratifié et ondes de surface (Rayleigh R et Love L) apparaissant à l'interface libre sol-air. Body waves (pressure P and shear S) with multiple refractions in a stratified medium and surface waves (Rayleigh R and Love L) appearing at the air-soil free interface. |
3 Des « cristaux » aux propriétés remarquables
3.1 Cristaux photoniques et phononiques
Les cristaux photoniques (John, 1987 ; Yablonovitch, 1987), sont des nanostructures périodiques diélectriques (« isolantes ») ou métallo-diélectriques qui affectent la propagation des ondes électromagnétiques. Les longueurs d'onde pouvant se propager dans la structure s'appellent les modes. Les groupes de modes autorisés : les bandes. L'absence de propagation des ondes électromagnétiques pour une plage de fréquence : bande interdite (band gap). Les bandes interdites peuvent être prédites (élaboration d'un diagramme de dispersion). C'est Lord Rayleigh qui montre pour la première fois en 1887 (Rayleigh, 1888) la possibilité de produire des « bandes interdites ». La forme la plus simple de cristal photonique est une structure périodique à une dimension (1D) composée d'un empilement multicouche (« miroir de Bragg »). Un empilement de couches d'indices optiques différents créant des interférences constructives, sur le principe des réflexions et déphasage aux interfaces. De manière analogue, un cristal phononique est une structure périodique composée de matériaux de propriétés élastiques distinctes, conçue pour modifier la propagation des ondes acoustiques (Économou et Sigalas, 1993) et élastiques. L'avènement des cristaux phononiques traduit le passage de longueurs d'onde nanométriques aux longueurs d'ondes micrométriques à centimétriques. En Figure 2, une structure périodique réalisée avec des trous (voir aussi Benchabane et al., 2015 ; Laude, 2015) est présentée à l'échelle micrométrique (Fig. 5).
 |
Fig. 5 Cristal phononique dans une plaque de silicium. Diamètre des trous : 6 μm, profondeur 100 μm, bande interdite complète autour de 500 MHz (Laboratoire Femto de Besançon : http://www.femto-st.fr/). Silicon phononic crystal plate. Diameter of the holes: 6 μm, 100 μm of depth, complete stop band around 500 MHz (Courtesy of Femto laboratory at Besançon: http://www.femto-st.fr/). |
3.2 Les métamatériaux
En 2001, le terme « métamatériau » a été proposé par ; Walser (2001) avec la définition suivante : « macroscopic composite having a manmade, three-dimensional, periodic cellular architecture designed to produce an optimized combination, not available in nature, of two or more responses to specific excitation ». La traduction littérale peut être comme suit : « matériau composite macroscopique présentant une architecture cellulaire périodique tridimensionnelle façonnée par l'Homme en vue de produire une combinaison, non rencontrée dans la nature, de deux ou trois réponses à une sollicitation spécifique ».
Typiquement, la dimension des éléments constitutifs est inférieure à la longueur d'onde du signal entrant et les effets obtenus sont les conséquences d'une dispersion non conventionnelle comme l'indice de réfraction négatif, intervenant dans les concepts d'invisibilité (Guenneau et al., 2015).
Pour expliquer la notion d'indice de réfraction négatif, revenons en premier lieu sur la notion de lentille plate convergente, du théoricien soviétique Veselago (1968) pour les ondes électromagnétiques, revisitée et popularisée par le physicien anglais Sir John Pendry à partir de 2000 (Pendry, 2000; Guenneau et Gralak, 2006).
Veselago constate qu'avec un matériau d'indice négatif (n < 0), la relation de Snell-Descartes suggère qu'une lame plane se comporterait comme une lentille sphérique de verre. Après avoir traversé la surface de la lame, les rayons émis par un objet convergeraient d'abord en son centre, formant une image « fantôme ». Puis, sortant du matériau d'indice n = −1, ils convergeraient une seconde fois pour former une image identique à la source (Fig. 6). Pour réaliser un matériau avec de telles propriétés, les physiciens ont commencé dans les années 1990, à envisager et réaliser des microstructures périodiques capables d'induire la réponse électromagnétique souhaitée. Smith et ses collaborateurs de l'université de Californie réalisent en 2000 le premier matériau possédant un indice de réfraction négatif (Smith et Kroll, 2000 ; Smith et al., 2004), en s'inspirant des travaux de John Pendry sur les résonateurs en anneaux fendus (Guenneau et Gralak, 2006).
L'analogie des sols structurés avec ces microstructures peut paraître lointaine, cependant, comme nous le montrons dans les paragraphes suivants, les conditions peuvent être réunies pour observer des phénomènes physiques similaires.
En effet, à l'échelle d'un sol intéressant un ouvrage de surface, ces phénomènes ne sont pas forcément étudiés et donc non nécessairement mesurés avec les outils adaptés (réseaux adaptés de capteurs, méthodes d'analyse, etc.). Par exemple, la sismologie quantitative (Aki et Richards, 2002), fondée sur les enregistrements de sismographes distants de quelques dizaines à centaines de kilomètres sur l'ensemble de la planète, recherche la caractérisation des structures internes de la Terre. L'exploration pétrolière utilise quant à elle de nombreux récepteurs distants de quelques mètres en multipliant les tirs sismiques avec pour objectif d'améliorer le rapport signal sur bruit (stacking, common mid-point, etc.) pour une meilleure imagerie des structures réservoirs, gommant ainsi les effets de dispersion dans les sols hétérogènes, altérés ou sous-consolidés situés en proche surface.
C'est justement la portée de ces interactions des ondes élastiques avec les sols de faibles vitesses et structurés par l'Homme, que nous essayons de mettre en relief ici.
 |
Fig. 6 Principe de la lentille plate : la réfraction négative (n = −1). L'image est la réplique exacte de la source, translatée d'une distance double de celle de l'épaisseur e du milieu traversé. Ceci peut être vu comme un repliement d'espace, le plan image étant appliqué sur le plan source (Ramakrishna et al., 2002). Principle of flat lens: negative refraction (n = −1). The image is an exact replica of the source, translated to a distance twice that of the thickness e of the medium traversed. This can be interpreted as a space folding, source and image are overlapping (Ramakrishna et al., 2002). |
4 Géotechnique et sols structurés
4.1 Approche pseudo-statique des sols structurés
Dans le domaine de la géotechnique, les sols composites étudiés en condition pseudo-statique font l'objet d'une attention spécifique notamment quand il s'agit d'obtenir une augmentation du module de cisaillement du sol initial pour limiter la déformation du massif sol-fondations profondes. En dimensionnement des structures, le problème dynamique est souvent converti en problème statique équivalent (analyse pseudo-statique), à partir d'un chargement temporel ou d'un spectre.
Pour obtenir ces nouvelles propriétés, deux approches sont identifiables. La première consiste à renforcer un sol initial plutôt « mou » avec adjonction d'éléments verticaux plus « rigides », souvent cylindriques, en béton, mortier, métal voire en bois (AFPS et CFMS, 2012). À ce titre, les travaux de De Buhan ont été précurseurs sur la qualification de ces matériaux renforcés (De Buhan, 1986) avec des applications remarquables en génie civil comme les fondations du pont Rion-Antirion dans le Golfe de Corinthe (Pecker et Teyssandier, 2009). Ces avancées ont été poursuivies par des recherches récentes en conditions de chargement statique et dynamique (Guéguin, 2014 ; Nguyen, 2014). La caractérisation du matériau équivalent fait appel à des techniques d'homogénéisation.
La seconde approche consiste à augmenter les propriétés mécaniques des sols dans leur masse par densification (AFPS et CFMS, 2012 ; Bitri et al., 2013 ; Brûlé et al., 2010 ; Brûlé et Duquesnoy, 2016), ce qui peut offrir à la fois la possibilité de contraindre l'intensité de l'amplification du signal sismique dans le cas d'un modèle bi-couche, avec rai sismique incident verticalisé et polarisation des ondes de cisaillement dans le plan horizontal, et d'obtenir une meilleure résistance mécanique des sols ainsi densifiés (voir Sect. 1).
4.2 Analyse temporelle et spectrale des sols structurés sous chargement dynamique
Selon notre approche, la finalité de sols structurés consiste à rechercher des effets complémentaires à leur rôle traditionnellement recherché, à savoir s'opposer à un effort ou à un déplacement imposé avec de nouvelles propriétés mécaniques. Le regard nouveau proposé est d'essayer d'agir sur la propagation géométrique du signal lui-même et sur son contenu fréquentiel : infléchir le trajet d'un rai sismique, filtrer certaines fréquences du signal, guider, etc. Nous distinguerons donc les matériaux structurés de nature « composite » soumis à des sollicitations monotones, des « métamatériaux » offrant des propriétés inédites en sollicitations dynamiques. Dans les deux cas, il s'agit de structurer les sols mais le positionnement des éléments additionnels peut être ajusté spécifiquement dans le cas des métamatériaux.
4.3 Historique et récentes avancées
Venant du domaine de l'optique et de l'acoustique et en particulier depuis une quinzaine d'années (Ma et Sheng, 2016 ; Sheng, 2014), des travaux de recherche portant sur l'optique transformationnelle (Nicolet et al., 2004), les modèles de plaque (Colombi et al., 2015 ; Farhat et al., 2009) et les ondes hydrodynamiques à la surface de l'eau (Berraquero et al., 2013 ; Dupont et al., 2015 ; Farhat et al., 2008) ont contribué à la transposition aux ondes mécaniques sismiques avec des expérimentations sur site avec des réseaux de forages verticaux vides sollicités à 50 Hz et entre 3 et 12 Hz (Brûlé et al., 2014 ; Brûlé et al., 2016).
Les études théoriques sur les dispositifs anti-vibration relatifs aux sources telles le trafic routier ou ferroviaire sont abondantes cependant les expériences réalisées en vraie grandeur sont plus rares. En 2004, pour valider le principe d'homogénéisation des milieux hétérogènes pour des conditions déterminées, des sols rendus artificiellement hétérogènes, constitués d'une planche d'essai horizontale avec cinq unités de matériaux, alternant un sol homogène et un sol constitué rangés de briques ont été testés par émissions d'ondes de surface sur des modèles réduits (Abraham et al., 2004). Le signal, de fréquence comprise entre 80 et 1000 Hz, était généré par la chute d'une masse métallique de 2,5 cm de diamètre impactant le sol après quelques centimètres de hauteur de chute. Les résultats, notamment exprimés sous forme de courbe de dispersion (vitesse de phase fonction de la fréquence), montrent une nette différenciation des courbes des milieux hétérogènes (19 et 35 % de briques) par rapport au cas homogène sur la plage de fréquence comprise entre 90 et 140 Hz.
Semblat et Pecker (Semblat et Pecker, 2009) reportent les travaux réalisés in situ par Woods (1968) sur des barrières anti-vibratiles circulaires ou linéaires, testées avec des sources produisant des fréquences allant de 200 à 350 Hz. Ces travaux montrent une réduction d'amplitude du signal en fonction des caractéristiques géométriques de la barrière. Citons également les travaux plus récents sur la mesure in situ du trafic ferroviaire (Semblat et al., 2011) couplé avec une caractérisation dynamique des sols en laboratoire ainsi que des essais sur des palplanches (Dijckmans et al., 2016).
Très récemment, des liens indirects avec les réseaux cristallins, dont celui du graphène (Aznavourian et al., 2016) sont identifiables dans la littérature comme les cellules d'abeille décrites par Takemiya et Shimabuku en 2002 et dont le principe est reproduit en Figure 7, montrant des pieux au centre des structures hexagonales faites de colonnes jointives de sol-ciment. L'objectif était plutôt d'améliorer la raideur de l'ensemble du massif « sol et pieux » et d'utiliser ces colonnes comme dissipatrice d'énergie à la faveur de leur endommagement lors de forts séismes.
 |
Fig. 7 Principe du réseau de cellules hexagonales en nid d'abeille (honeycomb) de colonnes jointives en sol-ciment (en bleu) décrit par Takemiya pour la protection des fondations de pieux (en noir au centre des cellules) des piles de viaduc (Takemiya et Shimabuku, 2002). Principle of honeycomb network made of contiguous soil-cement columns (blue circles) described by Takemiya for the protection of deep foundations (black circles in the cells) of a viaduct (Takemiya et Shimabuku, 2002). |
5 Physique des ondes dans les milieux périodiques
5.1 Structures diffractives
Les phénomènes en jeu pour la propagation des ondes élastiques dans les milieux hétérogènes sont la réfraction, la diffraction et la diffusion (Brillouin, 1946). Pour les ondes sismiques se propageant dans la croûte terrestre, les sismologues ont mis en avant la possibilité d'obtenir de l'information dans le champ produit par la diffusion multiple liée aux « objets » de répartition aléatoire, rencontrés lors de la propagation du signal. Pour la Terre interne, il a été montré notamment que la coda sismique (Aki et Richards, 2002) met en jeu des ondes multiplement diffusées (Campillo et Paul, 2003). En proche surface terrestre, l'illustration de cette diffusion multiple a été faite par des expériences de sismique de surface (Larose et al., 2004).
Dans le cas de la rencontre d'un objet unique dans le milieu de propagation, si la longueur d'onde λ est inférieure à la largeur de l'objet (situation haute fréquence), il apparaît une zone d'ombre derrière l'objet. Lorsque λ est proche des dimensions de l'objet, la diffraction se traduit par la reconstruction d'un signal derrière l'obstacle (Fig. 8). Pour des longueurs d'onde bien plus importantes (situation basse fréquence) l'onde continue sa propagation comme si l'obstacle n'existait pas, il n'y a plus « d'ombre » derrière l'objet et il devient « invisible » pour ces ondes. Dans le cas du passage à travers une fente seule, l'onde incidente est peu perturbée par une ouverture L grande devant λ. En revanche, si l'ouverture L est inférieure ou égale à la longueur d'onde alors l'ouverture se comporte comme une nouvelle source quasi-circulaire, que l'onde incidente soit plane ou circulaire.
À la différence des milieux terrestres considérés à l'échelle crustale, les sols structurés par l'Homme vont présenter une répartition non aléatoire des inclusions. Ainsi, pour un nombre fini N de cavités cylindriques, une approche par la théorie modale de la diffusion multiple par des cavités cylindriques permet d'exprimer le champ de déplacement total (incident et diffusé). Par exemple, il est possible de considérer le cas de la propagation d'une onde élastique, transverse horizontale (« antiplane ou hors-plan »), harmonique, dans un milieu solide avec N cavités (Caléap, 2009). Sachant que les ondes considérées (type SH) ne génèrent pas de conversion de mode à la surface libre, le déplacement associé et les champs de contrainte vont être gouvernés par une seule équation scalaire.
La direction de propagation de l'onde incidente est perpendiculaire à l'axe z des cavités (Fig. 8), ainsi le problème reste bidimensionnel et les composantes du champ spatial sont telles que : ux = uyn= 0 et vérifient dans le domaine fréquentiel l'équation de Helmholtz :
 (2)
(2)
Avec uT, le déplacement pour tout point P Є R3, pour tout t > 0. kt = ω / cT est le nombre d'onde de l'onde transverse horizontale de vitesse cT et le terme de droite de (2) est le terme source. Les ondes considérées ici ne générant pas de conversion de mode à la surface libre, le déplacement associé et les champs de contrainte sont gouvernés par une seule équation scalaire aux dérivées partielles avec des coefficients qui peuvent être scalaires ou matriciels mais avec une inconnue qui est un champ scalaire.
 |
Fig. 8 Illustration de la diffraction par l'optique géométrique appliquée à une onde élastique plane rencontrant un objet cylindrique rigide de section circulaire (longueur d'onde λ petite par rapport au diamètre de l'objet diffractant). À gauche, représentation sous forme de rai et à droite, représentation du front d'onde incident (bleu) et réfracté (en rouge). D'après Bleistein, 1984. Illustration of the diffraction by the geometrical optics theory applied to an elastic plane wave encountering a rigid cylindrical body of circular section (the wavelength is small compared to the diameter of the diffractive object). At left, ray-tracing method and at right, representation of the incident wave front (blue) and refracted wave (in red). Inspired from Bleistein, 1984. |
5.2 Le miroir de Bragg
Pour illustrer à présent le cas des milieux structurés, examinons les cristaux phononiques agissant sur la propagation des ondes acoustiques et élastiques. Les cristaux phononiques sont des structures périodiques 1D, 2D ou 3D composées d'au moins deux matériaux ayant des propriétés élastiques différentes. Leur propriété la plus importante est l'existence potentielle de bandes interdites (band gap) traduisant l'absence de modes propagatifs des ondes dans de telles structures, dans une plage de longueurs d'ondes donnée.
L'apparition de bandes interdites n'est possible que sous des conditions spécifiques dépendant du choix des matériaux et des paramètres géométriques des structures. Les ondes diffractées apparaissent à partir d'une certaine fréquence qui dépend du pas de réseau, du contenu de la cellule élémentaire et des propriétés des milieux. La diffraction génère de nouvelles ondes à partir de l'onde incidente, à partir des réflexions ou diffusions multiples dans le réseau. Ce phénomène apparaît en général au-dessus d'une certaine fréquence de coupure, qui devient donc une borne supérieure limitant le domaine où la diffraction se manifeste de celui où elle ne le peut pas. La première bande interdite de Bragg (Fig. 9) apparaît de façon générale à des fréquences légèrement inférieures à la fréquence de coupure de la diffraction.
La bande interdite peut donc être caractérisée par l'atténuation introduite, mais également par son effet sur la phase de l'onde incidente. En effet, dans le gap, il est possible d'observer une inversion de la pente de la vitesse de phase fonction de la fréquence ce qui est caractéristique d'une dispersion anormale (Gralak et al., 2000).
Le miroir de Bragg est un phénomène se produisant pour des longueurs d'onde proches du pas de la structure, ce qui ne permet pas d'obtenir des effets pour une large bande de fréquences du signal incident. Pour y parvenir, il est nécessaire de recourir à la résonance des éléments enterrés.
 |
Fig. 9 Structure composée d'un empilement multicouche avec explication de l'effet « miroir de Bragg » (d'après Yablonovitch, 2001). Onde incidente sur une structure 1D (a), avec réflexion en phase sur chaque interface (b) et onde résultante stationnaire ne se propageant pas dans la structure (c). Structure consisting of a multilayer stack with explanation of the “Bragg mirror” effect (from Yablonovitch, 2001). Incident wave on a 1D structure (a). The reflected waves are in phase and reinforce one another (b). They combine with the incident wave to produce a standing wave (c) that does not travel through the material. |
5.3 Résonances locales et réseaux sub-longueur d'onde
Pour les cristaux phononiques, les physiciens (Achaoui et al., 2013 ; Liu et al., 2000), considèrent que l'origine des bandes interdites peuvent avoir deux origines : l'interférence de Bragg des ondes diffusées et l'hybridation des résonances locales, c'est-à-dire un couplage entre l'onde se propageant et les modes résonants.
D'autre part, une approche complémentaire pour créer des bandes interdites à basse fréquence par rapport aux gaps de Bragg est l'utilisation des résonances locales pour constituer des structures avec un pas de réseau inférieur à la longueur d'onde du signal incident (structure sub-longueur d'onde). En 2000, l'équipe de P. Sheng a introduit le concept de cristaux à résonance locale en considérant, en laboratoire, des inclusions constituées d'un cœur dur enrobé d'un polymère mou dans une matrice solide. Depuis, ces cristaux ont été intégrés dans l'ensemble des métamatériaux acoustiques qui peuvent présenter, autour des fréquences de résonances, des propriétés effectives négatives comme la masse et/ou la compressibilité (Larabi, 2011).
Toujours en laboratoire ou en simulation numérique, il est également envisagé par certains auteurs (Dubois et al., 2013) d'utiliser des trous dans des plaques, traversant ou non (dits alors « borgnes »), comme éléments résonateurs de base pour des structures acoustiques 2D complexes. À la différence du trou traversant qui ne présente pas de résonance basse fréquence, un trou borgne, bien que de géométrie très simple, est un résonateur remarquable.
En guise de résonateur, examinons le cas d'une inclusion, assimilable à une poutre de longueur L de section rectangulaire, d'épaisseur e et de largeur l, oscillant en mode de flexion. Les pulsations ωn pour les n modes sont données par l'équation (3) où E et ρ sont respectivement le module et la masse volumique du matériau considéré. La même expression pour les modes en élongation est donnée par (4). Le paramètre λn traduit les conditions aux limites de la poutre : libre ou encastrée (Tab. 1). La sollicitation d'un tel réseau de résonateurs est illustrée en Figure 10.
 (3)
(3)
 (4)
(4)
Pour un contenu fréquentiel d'un signal sismique incident compris entre 0.1 à 50 Hz, le Tableau 1 montre que la résonance des colonnes en flexion peut être provoquée pour le premier mode fondamental et la première harmonique (2,5 et 16 Hz). Un couplage entre le signal incident, la résonance du modèle bicouche et les modes locaux est ainsi envisageable. En effet, sur la base des hypothèses de la Section 1 sur les vitesses Vs = 200 m.s−1 pour un sol bicouche, la fréquence fondamentale du sol serait de 5 Hz (f = Vs/4H). D'autre part, comme évoqué dans la Section 2, le rapport des modules d'Young Einclusion/Esol est supérieur à 100, laissant la possibilité d'une résonance effective.
Paramètres λn pour une poutre de section rectangulaire (e = 0,5 m, l = 0,5 m) en conditions d'encastrement en une extrémité et de liberté à l'autre, pour modes de flexion et d'élongation. Pulsation ωn et fréquences fn correspondantes pour éléments de 10 m de longueur (L) en béton (E = 25 000 MPa, ρ = 2500 kg.m−3).
Parameters λn for a clamped-free beam of rectangular cross section (e = 0.5 m, l = 0.5 m), for bending and stretching modes. Pulsation ωn and frequency fn correspond to 10 m long elements (L) made of concrete (E = 25 000 MPa, ρ = 2500 kg.m−3).
 |
Fig. 10 Schémas de principe de la sollicitation d'éléments verticaux encastrés dans un sol plus raide en profondeur (sol 2). À gauche (a), modes de flexion et à droite (b), modes d'élongation (compression). Principle of the solicitation of vertical elements embedded in a stiffer soil in depth (soil 2). Left (a), bending modes and right (b) stretching (compressional) modes. |
5.4 Vers des résonateurs « haute performance »
Ce dernier paragraphe est plus exploratoire mais illustre les travaux les plus récents sur la recherche de caractérisation de propriétés effectives des milieux terrestres.
L'onde sismique résulte de la propagation d'un ébranlement mécanique dans un solide (matériaux terrestres) que nous pouvons considérer comme élastique en première approximation. Dans un solide élastique, contrainte σ et déformation ε sont reliées par les constantes élastiques exprimées par un tenseur Cijkl d'ordre 4 tel que : σij = Cijkl εkl. Le milieu solide avec ses inclusions, sphériques par exemple, peut être modélisé par une discrétisation 3D de l'espace comme illustré en Figure 11a, où les éléments sont reliés par des liaisons élastiques. Il est possible d'aller plus loin en considérant l'inclusion, pas seulement avec une masse, mais avec une masse imbriquée (Achaoui et al., 2016, Krodel et al., 2015).
En interprétant ρ non pas comme une masse divisée par un volume (nécessairement positif) mais comme un coefficient de proportionnalité entre la force subie par un système et son accélération (d'après le principe fondamental de la dynamique), il est possible de chercher à construire un système dont l'accélération s'oppose à la force appliquée. C'est le cas pour des masses imbriquées avec une liaison élastique interne. En assemblant un nombre important de ces éléments sous la forme d'une chaîne (Fig. 11b), avec une liaison élastique de raideur K1 entre chaque élément, est construit un modèle de matériau à une dimension avec une masse linéïque effective meff/L qui peut devenir négative au voisinage de la résonance.
Pour illustrer cette idée de valeur effective « négative », considérons par exemple le cas d'un système constitué d'une seule masse m1 avec à l'intérieur, une masse imbriqué m2, reliée à la masse m1 par un ressort de raideur K2 (Fig. 11c). Le système est soumis à un chargement dynamique monodirectionnel, par une force extérieure, selon y. Ce système peut être considéré comme équivalent à une masse effective (dispersive en fréquence) unique (Fig. 11c).
Les équations du mouvement sans frottement des deux masses m1 et m2 avec un ressort de raideur K2, s'expriment comme ci-dessous, avec y1 et y2 les déplacements du centre de gravité des masses dans le repère (O,x,y,z) :
 (5)
(5)
 (6)
(6)
La résolution de ce système conduit à :
 (7)
(7)
Nous choisissons une masse effective telle que ci-dessous et nous déterminons meff :
 (8)
(8)
 (9)
(9)
Avec  la pulsation propre de l'oscillateur interne constitué de la masse m2 et du ressort de raideur K2. Pour une oscillation de la force extérieure proche de la résonance de l'oscillateur interne (ω ≈ ω0), et en particulier pour
la pulsation propre de l'oscillateur interne constitué de la masse m2 et du ressort de raideur K2. Pour une oscillation de la force extérieure proche de la résonance de l'oscillateur interne (ω ≈ ω0), et en particulier pour  , la masse effective devient négative (Lee et al., 2017). Notons par ailleurs que (8) se généralise aisément au cas de milieux anisotropes pour lesquels une matrice de masse effective est construite avec des ressorts dont les masses et constantes de raideurs sont différentes suivant les directions (Milton, 2002).
, la masse effective devient négative (Lee et al., 2017). Notons par ailleurs que (8) se généralise aisément au cas de milieux anisotropes pour lesquels une matrice de masse effective est construite avec des ressorts dont les masses et constantes de raideurs sont différentes suivant les directions (Milton, 2002).
En considérant un tel modèle mais en trois dimensions avec des liaisons élastiques internes, il est possible de construire une masse volumique effective négative pour une certaine bande de fréquences proche de la fréquence de résonance des oscillateurs internes. Ces propriétés permettent de concevoir des bandes interdites dans le diagramme de dispersion. Dans le même objectif d'améliorer le contrôle des bandes interdites, certains auteurs (Ungureanu et al., 2016) explorent les matériaux à coefficient de Poisson négatif (matériaux auxétiques), pour obtenir une « compressibilité négative ».
 |
Fig. 11 À gauche (a), modélisation d'un solide élastique isotrope 3D. À droite (b), modélisation du milieu de propagation constitué d'une chaîne d'oscillateurs à masses imbriquées (1D). En bas (c), illustration de la mono-masse m1 avec masse m2 imbriquée équivalente à une masse unique de masse effective meff. Le système est soumis à un chargement dynamique monodirectionnel F(t) selon y. D'après Milton et al. (2006). Left (a), modeling a 3D isotropic elastic solid. Right (b), modeling the propagation medium consisting of a chain of oscillators with nested masses (1D). Below (c), illustration of a single mass m1 with an imbricated mass m2. The set is equivalent to a unique mass meff. The system is under a dynamic loading F(t) in y direction. From Milton et al. (2006). |
6 Nécessité d'adapter les outils d'analyse
Un des principaux sauts conceptuels est de transposer les outils des ondes électromagnétiques, régies par les équations de Maxwell, dans les milieux anisotropes aux ondes mécaniques (acoustiques et élastiques). Citons notamment la construction du diagramme de bandes définissant les bandes interdites d'une structure périodique (1D, 2D ou 3D) et d'identifier les modes guidés ou de surface. Pour une direction de propagation définie par le vecteur d'onde incident, on reporte un nombre donné de modes propres qui peuvent se propager dans la structure. Les modes propres sont des solutions fréquentielles des équations des ondes. Ce diagramme s'appelle diagramme de bandes ou diagramme de dispersion. Pour des raisons de périodicité dans le matériau, il suffit que le vecteur nombre d'onde couvre le domaine irréductible de Brillouin.
En Figure 12, les droites représentent la relation de dispersion pour un milieu homogène, constitué d'un seul matériau. Les courbes rouges correspondent à un matériau constitué d'un empilement périodique tel que décrit à gauche. La région centrale [−π/a, π/a] est la première zone de Brillouin en 1D, et l'intervalle [0, π/a] est la zone irréductible de Brillouin. Cette notion de dispersion n'est pas exactement la même que celle utilisée en sismologie ou en prospection sismique. En effet, il est plutôt question de courbes de dispersion, traduisant la variation de la vitesse ou de la phase des ondes de surface en fonction de la fréquence. Cependant, en méthode d'analyse des ondes de surface (SASW, MASW), la dispersion est bien reliée au caractère stratifié du milieu (anisotropie selon z).
 |
Fig. 12 À gauche, succession régulière de deux matériaux terrestres (ρ1, E1, ρ2, E2) en couches horizontales, avec une périodicité a. À droite, principe du diagramme de dispersion pour une structure 1D constituée d'une alternance de deux matériaux (d'après Brûlé et al., 2015b). Left, regular succession of two earth layered materials (ρ1, E1, ρ2, E2), with a periodicity a. Right, principle of dispersion diagram for a 1D structure consisting of an alternation of two materials (from Brûlé et al., 2015b). |
7 La physique transformationnelle
Dans ce paragraphe nous proposons une introduction au formalisme de la physique transformationnelle ayant beaucoup contribué au développement du concept « d'invisibilité », terme qu'il est important de démystifier. En effet un objet est « invisible » s'il ne modifie pas, ou peu, le champ d'onde dans lequel il est placé. Soit l'objet lui-même détient ces propriétés de reconstruction du champ d'onde comme s'il n'était pas présent dans l'espace considéré (alors il est question de « transparence »), soit il est entouré d'un dispositif (une « cape ») offrant ce même avantage. L'objet peut aussi être situé à côté du dispositif et il s'agit alors de « cape externe ». En prospection sismique, la présence des objets (couches géologiques, failles, plis, structures diapir, cavités) est déduite de la modification du signal produit en surface ou en puits et enregistré sur réseau de capteurs en surface. Si l'objet est « invisible », cela signifie qu'aucune « signature » de sa présence ne serait décelable sur les sismogrammes.
Pour se fixer les idées sur la puissance du formalisme de la physique transformationnelle, considérons une équation des ondes (10) dans un système de coordonnées (x,y,z,t) où les trois premières variables sont pour l'espace et la quatrième pour le temps. Un opérateur linéaire L avec un coefficient à valeurs scalaires m(x,y,z,t) qui dépend des coordonnées d'espace et de temps agit sur une inconnue u qui dépend elle-même des coordonnées (x,y,z,t). Cette inconnue peut être un champ scalaire de pression (ondes sonores dans l'air, un fluide), de cisaillement (e.g. hors-plan dans un milieu solide « cylindrique »), une élévation d'eau sur une interface libre air-liquide, de flexion dans une plaque, etc. Dans le cas des ondes de pression et cisaillement dans les solides, L est l'opérateur de Navier et u le champ vectoriel de déplacement. Dans le membre de droite de l'équation, nous avons un terme source S. Avec quelques hypothèses sur la coercivité de m, et des conditions d'onde sortante, nous pouvons montrer l'existence et l'unicité de la solution de cette équation [en faisant appel au théorème de Lax et Milgram (Duvaut et Lions, 1976)].
 (10)
(10)
Si nous faisons un changement de coordonnées (x,y,z,t) → (x',y',z',t) avec x', y' et z' fonctions des variables x, y, z, l'équation précédente prend en général la forme (11) :
 (11)
(11)
Où M, dans le cas de l'électromagnétisme, est un coefficient à valeurs matricielles (appelé permittivité) qui se déduit en général d'un produit de matrice Jacobienne de la transformation avec sa transposée, divisée par son déterminant (Nicolet et al., 1994).
Toujours dans le cas électromagnétique, le passage d'une équation avec un coefficient scalaire m à un tenseur d'ordre 2 M s'interprète physiquement comme de l'apparition d'anisotropie dans l'équation transformée. Pour ce qui concerne le cas élastodynamique, m est un tenseur d'élasticité d'ordre 4 isotrope symétrique, alors que M est un tenseur d'ordre 4 anisotrope et sans les symétries mineures (Brun et al., 2009). Alternativement, il est possible de préserver la symétrie du tenseur M, mais cela induit des termes supplémentaires (des tenseurs d'ordre 3) dans l'équation transformée (11), qui est dite de Willis modifiée (Milton et al., 2006). Cette difficulté inhérente au cas des ondes mécaniques provient du fait que l'opérateur de Navier ne s'écrit pas sous forme covariante, contrairement à l'opérateur de Maxwell qui se prête bien aux transformations de coordonnées. L'élastodynamique transformationnelle est donc moins naturelle à mettre en œuvre que l'optique transformationnelle.
Tout le secret du contrôle de la trajectoire des ondes réside dans ce changement de paradigme : le passage d'un milieu homogène (ou hétérogène) isotrope à un milieu hétérogène anisotrope induit des trajectoires courbes pour les ondes dont le plus court chemin d'un point A à un point B n'est plus une droite mais une géodésique. Il s'avère que les métamatériaux sont caractérisés par des coefficients anisotropes (et très dispersifs en fréquences) donc permettant de réaliser ce tour de « passe-passe ».
À titre d'exemple, le physicien Pendry a proposé en 2006 (Pendry et al., 2006) d'appliquer à l'équation de Maxwell des ondes électromagnétiques un changement de coordonnées qui applique un disque de rayon R2 sur une couronne de rayons R1 et R2, ce qui conduit à la matrice M diagonalisée suivante en coordonnées cylindriques (12) :
 (12)
(12)
Notons que sur le bord intérieur de la couronne en r' = R1, les première et troisième valeurs propres sont nulles, alors que la seconde est infinie. La « cape d'invisibilité » proposée par Pendry requiert donc un milieu avec une anisotropie localement infinie, ce qui est difficilement réalisable en pratique. Cette difficulté provient de la nécessité d'accélérer l'onde autour de la zone d'invisibilité au centre de la cape, afin qu'elle puisse « rattraper » une onde qui se déplacerait dans l'espace libre en l'absence de cape. En pratique, l'impossibilité de dépasser la vitesse de la lumière dans le vide induit un déphasage qui sera détecté par un observateur situé derrière la cape.
L'invisibilité pour les ondes mécaniques ne fait pas face à cette limitation de vitesse, comme évoqué plus haut, mais d'autres problèmes émergent tels que l'apparition de termes sensoriels supplémentaires dans l'équation de Navier transformée (Milton et al., 2006) ou d'un tenseur d'élasticité sans les symétries mineures (Brun et al., 2009). Notons l'extension au cas 3D traité par Diatta et Guenneau (2014).
Pour conclure ce paragraphe, nous citerons McCall ayant proposé d'étendre le concept de « cape d'invisibilité » pour faire « disparaître » des évènements dans des systèmes de coordonnées minkowskiens (McCall et al., 2011), ce qui revient à prendre des coordonnées x,y,z et x',y',z' elles-mêmes dépendantes du temps dans les équations (5) et (6), ce qui a donné lieu à une preuve expérimentale de ce concept (Lukens et al., 2013).
8 Expériences en laboratoire illustrant l'analogie avec les matériaux terrestres
Considérons un milieu composite à deux dimensions avec une structuration périodique de cylindres, tel que décrit en Figure 13. Pour le cas d'un objectif de bandes interdites, examinons ce qui a été étudié par certains auteurs à l'échelle millimétrique en termes de contraste de propriété entre la matrice et les éléments verticaux incorporés (Kushwaha, 1997, Vasseur et al., 1998).
Prenons le cas de cylindres de duralium dans une matrice en résine époxy (Vasseur et al., 1998). Le duralium est un alliage à base d'aluminium (> 90 %), de cuivre (3–5 %), de magnésium et de manganèse. Les caractéristiques de ces matériaux sont rappelées dans le Tableau 2. Ces deux matériaux ont été choisis pour le contraste de leurs caractéristiques. Le modèle physique contenant les éléments verticaux est un cube de 10 cm de côté.
Pour des matériaux terrestres, type argile, de consistance moyenne à bonne en termes géotechniques, ainsi que pour un béton altéré de résistance initiale à la compression Rc = 12 MPa, les caractéristiques élastiques sont détaillées en Tableau 2. La relation entre les ondes longitudinales et transversales est donnée par (Cl/Ct)2 = 2 (1−ν) / (1−2ν), permettant de calculer les coefficients de Poisson du duralium et de l'epoxy. Le rapport des modules E est donné par : Eduralium/Eepoxy = Gduralium(1 + νduralium)/ Gepoxy(1 + νepoxy).
Nous obtenons un rapport Eduralium/Eepoxy = 17,65 à comparer avec Ebéton/Esol = 40. Les rapports de module Eduralium/Eepoxy et Ebéton/Esol sont du même ordre de grandeur pour les valeurs choisies pour le sol (Tab. 3).
Les dimensions des éléments sont également à comparer. Le dispositif millimétrique est composé de cylindres de duralium de 16 mm de diamètre (d) pour un entraxe a de 20 mm. Avec une notion de substitution par rapport à la matrice, à savoir le rapport des surfaces inclusion/maille, πd2/a2, il faut comparer la valeur de 50 % obtenue pour les cylindres de duralium à ce qui peut se faire par exemple en renforcement de sol. Les inclusions en béton ont des diamètres compris entre 0,3 et 0,5 m, pour des entraxes de l'ordre de deux à trois diamètres, c'est-à-dire des substitutions de 4,9 à 8,7 %, ce qui est beaucoup pour la seconde valeur.
La source utilisée dans cette expérience pouvait aller jusqu'à 500 kHz. Le vecteur déplacement élastique u est perpendiculaire à l'axe des cylindres. En raison des valeurs de vitesse des matériaux considérés, la plage de fréquence utilisée permet de couvrir une gamme de longueur d'onde très supérieure à inférieure à l'entraxe a. Dans le cas de la maille carrée, deux bandes de fréquences interdites ont été observées : 55 à 85 kHz et 115 à 125 kHz. À ces fréquences l'entraxe a est plus faible que les longueurs d'onde émises : 0,43 < a/λ < 0,97 en considérant la vitesse de propagation longitudinale dans la résine d'époxy.
Revenons à présent sur la géotechnique des fondations profondes ou du renforcement des sols avec éléments cylindriques verticaux dans le sol, sachant que les fréquences enregistrées pour les sollicitations sismiques sont comprises entre 0,1 et 10 Hz et que les vitesses des ondes de cisaillement Vs des sols non rocheux de surface sont inférieures à 800 m/s (NF EN 1998-5, 2005). En faisant l'hypothèse de milieux élastiques, toutes proportions gardées, si un rapport a/λ ∼ 0,5 est recherché avec un maillage carré d'inclusions verticales à entraxe de l'ordre du mètre, il faut nécessairement considérer des sols pour lesquels la vitesse de propagation des ondes est très faible (Vs < 150 m/s) pour espérer observer des bandes de fréquences interdites.
 |
Fig. 13 Schéma d'un cristal phononique à deux dimensions avec, en plan (O,x,y), une maille carrée d'entraxe a. Diagram of a 2D phononic crystal ordered in a square mesh in the (O,x,y) plan. a is the spacing. |
Masses volumiques ρ, vitesses longitudinales, vitesses transversales (Cl et Ct), module M d'onde de compression et module G de cisaillement pour le duralium et la résine époxy (Vasseur et al., 1998).
Densities ρ, longitudinal and transverse wave velocities (Cl and Ct), longitudinal wave modulus M and the shear modulus G for duralium and epoxy resin (Vasseur et al., 1998).
Masses volumiques ρ, vitesses longitudinales, vitesses transversales (Cl et Ct), module M d'onde de compression et module G de cisaillement pour une argile et du béton altéré.
Densities ρ, longitudinal and transverse wave velocities (Cl and Ct), longitudinal wave modulus M and the shear modulus G for clay and altered concrete (Vasseur et al., 1998).
9 Expériences en vraie grandeur sur les sols structurés
Pour observer expérimentalement (tests en vraie grandeur ou modèles réduits en centrifugeuse) les phénomènes décrits par les diagrammes de dispersion (réflexion de Bragg, résonance), il faut pouvoir disposer de sources générant des signaux à fréquences variables et contrôler la polarisation des ondes émises afin d'être conforme aux simulations numériques. Les tests déjà réalisés in situ (Brûlé et al., 2014, Brûlé et al., 2016) peuvent être à sources monochromatiques, fréquence fixe ou variable (vibreur cylindrique dans le sol ou plaque vibrante), ou polychromatiques (impact en surface, tir en forage) comme peut l'être un signal sismique provenant d'un phénomène tellurique.
Ces tests avec des sources proches de la surface génèrent des ondes de volumes et de surface et, de fait, le signal propagé contient, en proportions variables selon la source, les composantes du déplacement dans les trois directions de l'espace. À ce jour, les tests en vraie grandeur réalisés sur des sols avec des « trous » ont mis en évidence un phénomène de réflexion comme pour le miroir de Bragg (Brûlé et al., 2014), de la concentration d'énergie dans le sol structuré ou encore une influence des éléments verticaux sur le rapport de composante horizontale et verticale du mouvement sismique (Brûlé et Duquesnoy, 2016 ; Brûlé et al., 2016), notamment une réduction relative de la composante horizontale du signal.
Les tests réalisés en laboratoire sur des plaques avec des trous ou avec des inclusions (cylindres, billes, etc.) permettent de recourir à des outils de mesure (balayage laser, etc.) permettant de recueillir l'intégralité du champ de déplacement avec le pas d'échantillonnage souhaité. Sur les tests réalisés sur le terrain, le nombre de capteurs est nécessairement limité même si les technologies récentes sans fils permettent d'en envisager un nombre 10 à 100 fois plus important que pour les réseaux habituels. Au même titre que le pas d'échantillonnage en temps est déterminant sur le pas de fréquence espéré après transformation discrète de Fourier, le pas d'échantillonnage spatial 2D est déterminant pour l'établissement d'un diagramme de dispersion dans l'espace réciproque (kx, ky) et pour voir apparaître, le cas échéant, les bandes interdites fines.
De plus, les sols ayant des comportements rhéologiques parfois difficiles à quantifier (visco-élasticité, non-linéarités), les mesures in situ, sur la durée de l'expérimentation ou pérennes, demeurent certes une nécessité mais ne permettent pas les possibilités de paramétrage qu'offrent les modèles physiques à échelle réduite, embarqués en centrifugeuse.
10 Conclusions et perspectives
Les sols structurés sont déjà une réalité dans l'Acte de Construire. En comparant les ordres de grandeurs des contrastes de propriétés mécaniques des différents éléments et en examinant les longueurs d'onde sismiques, nous constatons que des similitudes existent entre les cristaux phononiques venant du domaine de l'Acoustique et un sol contenant des cylindres verticaux constitués d'un matériau beaucoup plus rigide. Pour rester dans les conditions des expérimentations en laboratoire (sur plaques ou cubes), il est nécessaire que les ondes sismiques aient une composante horizontale importante. Seront donc considérées soient les ondes de surface se propageant dans les remplissages alluvionnaires, soient les ondes de volume à fort angle d'incidence par rapport à la verticale (effets 2D/3D liés à la morphologie des bassins). Sur des maillages réguliers carrés ou en « nid d'abeille », la densité des inclusions verticales est significative et plus importante que celle correspondant à du renforcement de sol utilisé pour améliorer la portance des sols ou réduire leur tassement sous ouvrage. Dans un premier temps, de tels métamatériaux pourront voir le jour si, par exemple, un traitement plus classique pour le renforcement des sols est déjà prévu pour la portance et le tassement. D'autre part, les appuis parasismiques en élastomère fretté sont efficaces dans le rôle d'abaissement de la fréquence fondamentale d'un ouvrage (Betbeder-Matibet, 2003b).
Avec ces matériaux structurés, les effets suivants sont recherchés : créer de bandes fréquentielles interdites pour les premiers modes de vibration des ouvrages, influencer la distribution d'énergie sismique en faveur de la construction, agir sur la diminution de la composante horizontale du signal, nuisible aux structures, etc. En ce sens, les pistes à explorer sont probablement à rechercher dans les maillages non réguliers, faisant appel à l'optique transformationnelle et l'anisotropie finement dimensionnée (Guenneau et al., 2015), voir Figure 14, et dans les taux de substitution importants (cellules en paroi sol-béton, en réseau 2D, voire 3D). Les sols considérés ayant des comportements rhéologiques parfois difficiles à quantifier (visco-élasticité, non-linéarités), les mesures in situ, sur la durée de l'expérimentation ou pérennes, demeurent une nécessité avec, probablement l'utilisation aussi, de modèles physiques à échelle réduite, embarqués en centrifugeuse (Semblat, 1995 ; Chazelas, 1999).
Ces travaux sur les métamatériaux sismiques ouvrent une piste complémentaire dans le domaine de l'étude de l'interaction sol-structure (ISS), montrant que les structures enterrées peuvent interagir sur le signal sismique lui-même. Ces sols structurés mettent à nouveau en perspective le rôle des résonateurs. Ainsi, il est aussi intéressant de se rappeler des travaux de Wirgin et Bard (1996), Guéguen et al. (2000), cités par Betbeder-Matibet (2003a), soulignant que les bâtiments de taille importante avec une forte densité d'implantation, peuvent être susceptibles de « modifier significativement le signal sismique par rapport à celui que l'on observerait dans une zone non bâtie ». Il s'agit bien dans ce cas, de résonateurs de surface dont l'action peut être complémentaire avec celle des résonateurs enterrés.
 |
Fig. 14 Simulation numérique d'onde de surface générée par une source sismique (en haut, à droite) dans un milieu argileux. L'onde se propage à travers une « cape sismique » (centre de la figure) constituée de couches concentriques de sols de densité et module de Young hétérogènes. L'onde contourne le disque au centre, qui est protégé des ondes. Modelling numerically a surface wave propagating in a clayey soil with a seismic source located in the top right part of the picture. The wave propagates through a "seismic cloack" (center of the figure) consisting of heterogeneous (E, ρ) concentric layers of soil. |
Références
- Abraham O, Chammas R, Cote PH, Pedersen HA, Semblat JF. 2004. Mechanical characterization of heterogeneous soils with surface waves: experimental validation on reduced-scale physical models. Near Surf Geophys 2(4): 249–258. [CrossRef] [Google Scholar]
- Achaoui Y, Laude V, Benchabane S, Khelif A. 2013. Local resonances in phononics crystals and in random arrangements of pillars on a surface. J Appl Phys 114: 104503. [CrossRef] [Google Scholar]
- Achaoui Y, Ungureanu B, Enoch S, Brûlé S., Guenneau S. 2016. Seismic waves damping with arrays of inertial resonators. Extrem Mechan Lett 8: 30–37. [Google Scholar]
- AFPS, CFMS. 2012. Procédés d'amélioration et de renforcement de sols sous action sismique. Guide technique. Presses des Ponts. [Google Scholar]
- Aki K, Richards PG. 2002. Quantitative seismology: theory and methods. California: University Science Books, ed. 2. [Google Scholar]
- Aznavourian R, Puvirajesinghe T, Brûlé S, Enoch S, Guenneau S. 2016. Bio-inspired seismic metamaterials with transformed elastic crystals. J Phys Condens Matter. Available from https://arxiv.org/ftp/arxiv/papers/1611/1611.00867. [Google Scholar]
- Benchabane S, Gaiffe O, Salut R, Ulliac G, Laude V, Kokkonen K. 2015. Guidance of surface waves in a micron-scale phononic crystal line-defect waveguide. Appl Phys Lett 106(8): 81903. [CrossRef] [Google Scholar]
- Berraquero CP, Maurel A, Petitjeans P, Pagneux V. 2013. Experimental realization of a water-wave metamaterial shifter. Phys Rev E 88: 051002. [CrossRef] [Google Scholar]
- Betbeder-Matibet J. 2003a. Génie parasismique. Phénomènes sismiques. Cachan : Hermes Science Publications − Lavoisier, Vol. 1, 318 p. [Google Scholar]
- Betbeder-Matibet J. 2003b. Génie parasismique. Prévention parasismique. Cachan : Hermes Science Publications − Lavoisier, Vol. 1, 318 p. [Google Scholar]
- Bitri A, Samyn K, Brûlé S, Javelaud EH. 2013. Assessment of ground compaction using multi-channel analysis of surface wave data and cone penetration tests. Near Surf Geophys 11: 683–690. [CrossRef] [Google Scholar]
- Bleistein N. 1984. Mathematical methods for wave phenomena. New York Academic Press, Inc. [Google Scholar]
- Bouchitté G, Felbacq D. 2004. Homogenization near resonances and artificial magnetism from dielectrics. Comptes Rendus Math Elsevier 339(5): 377–382. [Google Scholar]
- Brillouin L. 1946. Wave propagation in periodic structures. McGraw-Hill Book Company Inc. [Google Scholar]
- Brûlé S, Duquesnoy S. 2016. Change of ground type by means of dynamic compaction: Consequences on the calculation of seismic loadings. Innov Infrastruc Solut 1: (39). Doi: 10.1007/s41062-016- 0037-4. [Google Scholar]
- Brûlé S, Javelaud EH, Ohmachi T, Nakamura Y, Inoue S. 2010. H/V method used to qualify the modification of dynamic soil characteristics due to ground improvement work by means of heavy compaction process. A case study: the former Givors's glass factory area. 7th International Conference on Urban Earthquake Engineering and 5th International Conference on Earthquake Engineering in Tokyo, Japan 02-026, 451–455. [Google Scholar]
- Brûlé S, Javelaud EH, Enoch S, Guenneau S. 2014. Experiments on seismic metamaterials: molding surface waves. Physi Rev Lett 112: 133901. [Google Scholar]
- Brûlé S, Enoch S, Guenneau S. 2015a. Seismic holes for controlling surface waves. Proceedings of META'15, The 6th International Conference on Metamaterials, Photonic Crystals and Plasmonics, 4 to 7 july 2015, New-York, USA. [Google Scholar]
- Brûlé S, Bretschneider A, Djeran-Maigre I, Thorel L. 2015b. Métamatériaux sismiques et essais en centrifugeuses. 9ème Colloque national de l'AFPS, du 30 novembre au 2 décembre 2015. Session spéciale métamatériaux sismiques. Marne La Vallée, France. [Google Scholar]
- Brûlé S, Javelaud E, Enoch S, Guenneau S. 2016. Flat lens for seismic waves. Sci Rep Nat. Available from https://arxiv.org/abs/1602.04492. [Google Scholar]
- Brun M, Guenneau S, Movchan AB. 2009. Achieving control of in-plane elastic waves. Appl Phys Lett 94: 061903. [Google Scholar]
- Caleap M. 2009. Modélisation de la propagation d'ondes élastiques anti-planes dans les milieux multifissurés. Thèse de l'université de Bordeaux 1. [Google Scholar]
- Campillo M, Paul A. 2003. Long-range correlations in the diffuse seismic coda. Sci 299: 547. [CrossRef] [PubMed] [Google Scholar]
- Chazelas JL. 1999. Quinze ans de simulation sismique en centrifugeuse dans le monde, Colloque national de génie parasismique, Cachan, France. [Google Scholar]
- Chesnais C, Boutin C, Hans S. 2011. Structural dynamics and generalized continua, in mechanics of generalized continua. In Altenbach H, Maugin V, Erofeev V, eds. Advanced structured materials. Berlin Heidelberg: Springer, 7. [Google Scholar]
- Colombi A, Roux P, Guenneau S, Rupin M. 2015. Directional cloaking of flexural waves in a plate with a locally resonant metamaterial. Journal Acoust Soc Am 137: 1783–1789. [Google Scholar]
- De Buhan P. 1986. Approche fondamentale du calcul à la rupture des ouvrages en sols renforcés. Thèse de doctorat d'État, université Pierre et Marie Curie, Paris 6. [Google Scholar]
- Diatta A, Guenneau S. 2014. Controlling solid elastic waves with spherical cloaks. Appl Phys Lett 105(2): 021901. [Google Scholar]
- Dijckmans A, Ekblad A, Smekal A, Degrande G, Lombaert G. 2016. Efficacy of a sheet pile wall as a wave barrier for railway induced ground vibration. Soil Dyn Earthq Eng 84: 55–69. [CrossRef] [Google Scholar]
- Dubois M, Farhat M, Bossy E, Enoch S, Guenneau S, Sebbah P. 2013. Flat lens for pulse focusing of elastic waves in thin plates. Appl Phys Lett 103: 071915. [CrossRef] [Google Scholar]
- Dupont G, Kimmoun O, Molin B, Guenneau S, Enoch S. 2015. Numerical and experimental study of an invisibility carpet in a water channel. Phys Rev E 91: 023010. [CrossRef] [Google Scholar]
- Duvaut G, Lions JJ. 1976. Inequalities in Mechanics and Physics. Berlin: Springer, ISBN: 978-3-642-66167-9. [Google Scholar]
- Economou EN, Sigalas MM. 1993. Classical wave propagation in periodic structures: Cermet versus network topology. Phys Rev B 48: 13434–13438. [CrossRef] [Google Scholar]
- Farhat M, Enoch S, Guenneau S, Movchan AB. 2008. Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys Rev Lett 101: 1345011. [Google Scholar]
- Farhat M, Guenneau S, Enoch S. 2009. Ultrabroadband elastic cloacking in thin plates. Phys Rev Lett 103: 024301. [Google Scholar]
- Gralak B, Enoch S, Tayeb G. 2000. Anomalous refractive properties of photonic crystals. J Opt Soc Am A 17: 1012–1020. [CrossRef] [Google Scholar]
- Gueguen P, Bard PY, Semblat JF. 2000. From soil-structure interaction to site-city interaction. 12th World Conference on Earthquake Engineering, Auckland, New-Zeland. [Google Scholar]
- Guenneau S, Gralak B. 2006. Un matériau pour une lentille parfaite. La Recherche 401: 58. [Google Scholar]
- Guenneau S, Enoch S, Brûlé; S. 2015. Invisibilité en physique transformationnelle. Actes de la conférence AFPS'15, 30 novembre au 2 décembre 2015, Marne La Vallée, France. [Google Scholar]
- Guéguin M. 2014. Approche par une méthode d'homogénéisation du comportement des ouvrages en sols renforcés par colonnes ou tranchées. Thèse de l'université Paris Est. [Google Scholar]
- Hobiger M. 2011. Polarization of surface waves: characterization, inversion and application to seismic hazard assessment. Thèse de l'université de Grenoble. [Google Scholar]
- Iwasaki T, Tatsuoka F, Takagi Y. 1978. Shear moduli of sands under cyclic torsional shear loading. Soils Found. Jpn Soc Soil Mech Found Eng. 18(1): 39–56. [Google Scholar]
- John S. 1987. Strong localization of photons in certain disordered dielectric superlattices. Phys Rev Lett 58(23): 2486–2489. [Google Scholar]
- Krodel S, Thome N, Daraio C. 2015. Wide band-gap seismic metastructures. Extreme Mech Lett 4: 111–117. [Google Scholar]
- Kushwaha MS. 1997. Stop-bands for periodic metallic rods − sculptures that can filter the noise. Appl Phys Lett 70(24): 3218–3220. [CrossRef] [Google Scholar]
- Larabi H. 2011. Cristaux phononiques et métamatériaux acoustiques. Applications aux domaines du guidage, filtrage et de l'isolation phonique. Thèse de l'université de Lille 1 sciences et technologies. [Google Scholar]
- Larose E, Margerin L, Van Tiggelen BA, Campillo M. 2004. Weak localization of seismic waves. Appl Phys Lett 93: 048501. [Google Scholar]
- Laude V. 2015. Phononic crystals. Artificial crystals for sonic, acoustic, and elastic waves. Berlin, Boston: De Gruyter Studies in Mathematical Physics 26. [CrossRef] [Google Scholar]
- Laude V, Khelif A, Benchabane S. An introduction to phononic crystals. Available from http://www.femto-st.fr/en/Popularization/An-introduction-to-phononic-crystals.php (last consult: 01/06/2016). [Google Scholar]
- Lee D, Nguyen DM, Rho J. 2017. Acoustic wave science realized by metamaterials. Nano Converg 4: 3. [CrossRef] [Google Scholar]
- Liu Z, Zhang X, Mao Y, et al. 2000. Locally resonant sonic materials. Sci 289(5485): 1734–1736. [CrossRef] [Google Scholar]
- Lukens JM, Leaird DE, Weiner AM. 2013. A temporal cloak at telecommunication data rate. Nature 498: 205–208. [CrossRef] [Google Scholar]
- Ma G, Sheng P. 2016. Acoustic metamaterials: From local resonances to broad horizons. Sci Adv 2(2): e1501595. [Google Scholar]
- McCall MW, Favaro A, Kinsler P, Boardman A. 2011. A spacetime cloak, or a history editor. J Opt 13: 029501. [CrossRef] [Google Scholar]
- Milton GW. 2002. The theory of composites. Cambridge: Cambridge University Press. [Google Scholar]
- Milton GW, Briane M, Willis JR. 2006. On cloaking for elasticity and physical equations with a transformation invariant form. New J Phys 8: 248. [Google Scholar]
- NF EN 1998-5, 2005. Eurocode 8–Calcul des structures pour leur résistance aux séismes − Partie 5 : fondations, ouvrages de soutènement et aspects géotechniques. [Google Scholar]
- Nguyen V. 2014. Analyse sismique des ouvrages renforcés par inclusions rigides à l'aide d'une modélisation multiphasique. Thèse de l'université Paris Est. [Google Scholar]
- Nicolet A, Remacle JF, Meys B, Genon A, Legros W. 1994. Transformation methods in computational electromagnetics. J Appl Phys 75(10): 6036–6038. [CrossRef] [Google Scholar]
- Nicolet A, Zolla F, Guenneau S. 2004. Modelling of twisted optical waveguides with edge elements. Eur Phys J Appl Phys 28: 153. [CrossRef] [EDP Sciences] [Google Scholar]
- Pecker A, Teyssandier P. 2009. Conception parasismique du pont de Rion-Antirion. 19ème Congrès français de mécanique à Marseille, 24–28 août 2009. [Google Scholar]
- Pendry JB. 2000. Negative refraction makes a perfect lens. Phys Rev Lett 85, 3966–3969. [Google Scholar]
- Pendry JB, Schurig D, Smith DR. 2006. Controlling Electromagnetic Fields. Sci 312(5781): 1780–1782. [Google Scholar]
- Ramakrishna SA, Pendry JB, Schurig D, Smith DR. 2002. The asymmetry lossy near-perfect lens. J Mod Opt 49(10): 1747–1762. [CrossRef] [Google Scholar]
- Rayleigh JWS. 1888. On the remarkable phenomenon of crystalline reflexion described by Prof. Stokes. Philos Mag 26: 256–265. [CrossRef] [Google Scholar]
- Semblat JF. 1995. Sols sous sollicitations dynamiques et transitoires : réponses dynamiques aux barres de Hopkinson, propagation d'ondes en milieu centrifugé. Laboratoire des Ponts et Chaussées. Série géotechnique GT 60. [Google Scholar]
- Semblat JF, Pecker A. 2009. Waves and vibrations in soils: earthquakes, traffic, shocks, construction works. Pavia: Fondazione Eucentre. [Google Scholar]
- Semblat JF, Lenti L, Jacqueline D, Leblond JJ, Grasso E. 2011. Vibrations induites dans les sols par le trafic ferroviaire : expérimentations et isolation. Rev Fr Géotech 134–135: 23–26. [Google Scholar]
- Sheng P. 2014. Viewpoint: A Step towards a seismic cloak. Physics 7, 34. [CrossRef] [Google Scholar]
- Smith DR, Kroll N. 2000. Negative refractive index in left-handed materials. Phys Rev Lett 85: 2933. [Google Scholar]
- Smith DR, Pendry JB, Wiltshire MCK. 2004. Metamaterials and negative refractive index. Sci 305: 788–792. [Google Scholar]
- Soil Magazine. 2016. Revue interne de Solétanche-Bachy et Ménard. n° 2 de février 2016. [Google Scholar]
- Srbulov M. 2010. Ground vibration engineering. Geotechnical, Geological and Earthquake Engineering. Netherlands: Springer. [CrossRef] [Google Scholar]
- Takemiya H, Shimabuku J. 2002. Application of soil-cement columns for better seismic design of bridge piles and mitigation of nearby ground vibration due to traffic. J Struc Eng JSCE 48A: 437–444. [Google Scholar]
- Ungureanu B, Achaoui Y, Enoch S, Brûlé S, Guenneau S. 2016. Auxetic-like metamaterials as novel earthquake protections. Eur Phys J Appl Metamater 2, 17. [Google Scholar]
- Vasseur JO, Deymier PA, Frantziskonis G, Hong G, Djafari-Rouhani B, Dobrzynski L. 1998. Experimental evidence for the existence of absolute acoustic band gaps in two-dimensional periodic composite media. J Phys Condens Matt 10: 6051–6064. [CrossRef] [Google Scholar]
- Verruijt A. 2010. Theory and Applications of Transport in Porous Media,Volume 24. Netherlands: Springer. [Google Scholar]
- Veselago VG. 1968. The electrodynamics of substances with simultaneously negative values of ε and µ. Sov Phys Uspekhi 10(4): 509–514. [Google Scholar]
- Walser RM. 2001. Electromagnetic metamaterials. Paper presented at the International Society for Optical Engineering (SPIE), San Diego, USA 4467: 1–165. [Google Scholar]
- Wirgin A, Bard P-Y. 1996. Effects of buildings on the duration and amplitude of ground motion in Mexico City. Bull Seismol Soc Am 86: 914–920. [Google Scholar]
- Woods RD. 1968. Screening of surface waves in soils. University of Michigan. Tech. Rep. IP- 804. [Google Scholar]
- Yablonovitch E. 1987. Inhibited spontaneous emission in solid-state physics and electronics. Phys Rev Lett 58: 2059. [CrossRef] [Google Scholar]
- Yablonovitch E. 2001. Photonic crystals: semi-conductors of light. Scientific American. [Google Scholar]
Citation de l'article : Stéphane Brûlé, Stefan Enoch, Sébastien Guenneau. Sols structurés sous sollicitation dynamique : des métamatériaux en géotechnique. Rev. Fr. Geotech. 2017, 151, 4.
Liste des tableaux
Paramètres λn pour une poutre de section rectangulaire (e = 0,5 m, l = 0,5 m) en conditions d'encastrement en une extrémité et de liberté à l'autre, pour modes de flexion et d'élongation. Pulsation ωn et fréquences fn correspondantes pour éléments de 10 m de longueur (L) en béton (E = 25 000 MPa, ρ = 2500 kg.m−3).
Parameters λn for a clamped-free beam of rectangular cross section (e = 0.5 m, l = 0.5 m), for bending and stretching modes. Pulsation ωn and frequency fn correspond to 10 m long elements (L) made of concrete (E = 25 000 MPa, ρ = 2500 kg.m−3).
Masses volumiques ρ, vitesses longitudinales, vitesses transversales (Cl et Ct), module M d'onde de compression et module G de cisaillement pour le duralium et la résine époxy (Vasseur et al., 1998).
Densities ρ, longitudinal and transverse wave velocities (Cl and Ct), longitudinal wave modulus M and the shear modulus G for duralium and epoxy resin (Vasseur et al., 1998).
Masses volumiques ρ, vitesses longitudinales, vitesses transversales (Cl et Ct), module M d'onde de compression et module G de cisaillement pour une argile et du béton altéré.
Densities ρ, longitudinal and transverse wave velocities (Cl and Ct), longitudinal wave modulus M and the shear modulus G for clay and altered concrete (Vasseur et al., 1998).
Liste des figures
 |
Fig. 1 À gauche : sols structurés constitués de pieux et micropieux (Brûlé et al., 2015a). À droite : principe de cellules dans le sol, ici avec des colonnes de sol-mixing pour augmenter la résistance au cisaillement des sols lors de séismes (Aznavourian et al., 2016). Left: structured soils made of piles and micropiles (Brûlé et al., 2015a). Right: principle of cells into the soil, here the case of soil-mixing columns to increase the shear strength of the soil during earthquakes (Aznavourian et al., 2016). |
| Dans le texte | |
 |
Fig. 2 Exemple de stratification horizontale artificielle de sols initialement homogènes par densification ou rigidification (structure 1D). Le profil des vitesses des ondes de cisaillement est modifié (à droite) après travaux de densification par compactage dynamique, vibrocompactage ou injection de coulis (ligne rouge pleine). Example of artificial horizontal stratification of initially homogeneous soil by means of densification or reinforcement (1D structure). The shear wave velocity profile is modified (right) after dynamic compaction, vibrocompaction works or grout injection (solid red line). |
| Dans le texte | |
 |
Fig. 3 Illustration de l'évolution de la fonction de transfert T(ω) avant (ligne pleine grise) et après densification du sol (ligne discontinue grise) dans l'hypothèse d'un modèle bicouche sans amortissement. h1 = 20 m, Vs1 initial = 200 m/s, Vs1 final = 260 m/s, soit 30 % d'amélioration. Les courbes noires prennent en compte un amortissement théorique ζ = 0,05 (ligne noire pleine) avant densification et, par exemple, ζ = 0,04 (ligne noire discontinue) après densification. Evolution of the transfer function T(ω) before (solid grey line) and after ground densification (dashed grey line) in case of a two layers model without damping. h1 = 20 m, Vs1 initial = 200 m/s, Vs1 final = 260 m/s, that is 30% of increase. Black lines represent cases with a theoretical damping ζ = 0.05 (solid black line) before soil densification and, for example, ζ = 0.04 (dashed black line) after works. |
| Dans le texte | |
 |
Fig. 4 Ondes de volume (pression P et cisaillement S) avec réfractions multiples dans un milieu stratifié et ondes de surface (Rayleigh R et Love L) apparaissant à l'interface libre sol-air. Body waves (pressure P and shear S) with multiple refractions in a stratified medium and surface waves (Rayleigh R and Love L) appearing at the air-soil free interface. |
| Dans le texte | |
 |
Fig. 5 Cristal phononique dans une plaque de silicium. Diamètre des trous : 6 μm, profondeur 100 μm, bande interdite complète autour de 500 MHz (Laboratoire Femto de Besançon : http://www.femto-st.fr/). Silicon phononic crystal plate. Diameter of the holes: 6 μm, 100 μm of depth, complete stop band around 500 MHz (Courtesy of Femto laboratory at Besançon: http://www.femto-st.fr/). |
| Dans le texte | |
 |
Fig. 6 Principe de la lentille plate : la réfraction négative (n = −1). L'image est la réplique exacte de la source, translatée d'une distance double de celle de l'épaisseur e du milieu traversé. Ceci peut être vu comme un repliement d'espace, le plan image étant appliqué sur le plan source (Ramakrishna et al., 2002). Principle of flat lens: negative refraction (n = −1). The image is an exact replica of the source, translated to a distance twice that of the thickness e of the medium traversed. This can be interpreted as a space folding, source and image are overlapping (Ramakrishna et al., 2002). |
| Dans le texte | |
 |
Fig. 7 Principe du réseau de cellules hexagonales en nid d'abeille (honeycomb) de colonnes jointives en sol-ciment (en bleu) décrit par Takemiya pour la protection des fondations de pieux (en noir au centre des cellules) des piles de viaduc (Takemiya et Shimabuku, 2002). Principle of honeycomb network made of contiguous soil-cement columns (blue circles) described by Takemiya for the protection of deep foundations (black circles in the cells) of a viaduct (Takemiya et Shimabuku, 2002). |
| Dans le texte | |
 |
Fig. 8 Illustration de la diffraction par l'optique géométrique appliquée à une onde élastique plane rencontrant un objet cylindrique rigide de section circulaire (longueur d'onde λ petite par rapport au diamètre de l'objet diffractant). À gauche, représentation sous forme de rai et à droite, représentation du front d'onde incident (bleu) et réfracté (en rouge). D'après Bleistein, 1984. Illustration of the diffraction by the geometrical optics theory applied to an elastic plane wave encountering a rigid cylindrical body of circular section (the wavelength is small compared to the diameter of the diffractive object). At left, ray-tracing method and at right, representation of the incident wave front (blue) and refracted wave (in red). Inspired from Bleistein, 1984. |
| Dans le texte | |
 |
Fig. 9 Structure composée d'un empilement multicouche avec explication de l'effet « miroir de Bragg » (d'après Yablonovitch, 2001). Onde incidente sur une structure 1D (a), avec réflexion en phase sur chaque interface (b) et onde résultante stationnaire ne se propageant pas dans la structure (c). Structure consisting of a multilayer stack with explanation of the “Bragg mirror” effect (from Yablonovitch, 2001). Incident wave on a 1D structure (a). The reflected waves are in phase and reinforce one another (b). They combine with the incident wave to produce a standing wave (c) that does not travel through the material. |
| Dans le texte | |
 |
Fig. 10 Schémas de principe de la sollicitation d'éléments verticaux encastrés dans un sol plus raide en profondeur (sol 2). À gauche (a), modes de flexion et à droite (b), modes d'élongation (compression). Principle of the solicitation of vertical elements embedded in a stiffer soil in depth (soil 2). Left (a), bending modes and right (b) stretching (compressional) modes. |
| Dans le texte | |
 |
Fig. 11 À gauche (a), modélisation d'un solide élastique isotrope 3D. À droite (b), modélisation du milieu de propagation constitué d'une chaîne d'oscillateurs à masses imbriquées (1D). En bas (c), illustration de la mono-masse m1 avec masse m2 imbriquée équivalente à une masse unique de masse effective meff. Le système est soumis à un chargement dynamique monodirectionnel F(t) selon y. D'après Milton et al. (2006). Left (a), modeling a 3D isotropic elastic solid. Right (b), modeling the propagation medium consisting of a chain of oscillators with nested masses (1D). Below (c), illustration of a single mass m1 with an imbricated mass m2. The set is equivalent to a unique mass meff. The system is under a dynamic loading F(t) in y direction. From Milton et al. (2006). |
| Dans le texte | |
 |
Fig. 12 À gauche, succession régulière de deux matériaux terrestres (ρ1, E1, ρ2, E2) en couches horizontales, avec une périodicité a. À droite, principe du diagramme de dispersion pour une structure 1D constituée d'une alternance de deux matériaux (d'après Brûlé et al., 2015b). Left, regular succession of two earth layered materials (ρ1, E1, ρ2, E2), with a periodicity a. Right, principle of dispersion diagram for a 1D structure consisting of an alternation of two materials (from Brûlé et al., 2015b). |
| Dans le texte | |
 |
Fig. 13 Schéma d'un cristal phononique à deux dimensions avec, en plan (O,x,y), une maille carrée d'entraxe a. Diagram of a 2D phononic crystal ordered in a square mesh in the (O,x,y) plan. a is the spacing. |
| Dans le texte | |
 |
Fig. 14 Simulation numérique d'onde de surface générée par une source sismique (en haut, à droite) dans un milieu argileux. L'onde se propage à travers une « cape sismique » (centre de la figure) constituée de couches concentriques de sols de densité et module de Young hétérogènes. L'onde contourne le disque au centre, qui est protégé des ondes. Modelling numerically a surface wave propagating in a clayey soil with a seismic source located in the top right part of the picture. The wave propagates through a "seismic cloack" (center of the figure) consisting of heterogeneous (E, ρ) concentric layers of soil. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




