| Numéro |
Rev. Fr. Geotech.
Numéro 155, 2018
|
|
|---|---|---|
| Numéro d'article | 3 | |
| Nombre de pages | 27 | |
| DOI | https://doi.org/10.1051/geotech/2018005 | |
| Publié en ligne | 20 novembre 2018 | |
Article d’ingénierie / Engineering Article
Détermination de la fenêtre de pilotage de la pression de confinement d’un tunnelier fermé dans un sol cohérent-frottant ou purement cohérent
Definition of confinement pressure operation range for a closed TBM in cohesive-frictional or purely cohesive soil
ARCADIS ESG,
9 avenue Réaumur,
92354
Le Plessis-Robinson cedex, France
★ Auteur de correspondance : guillaume.champagnedelabriolle@arcadis.com ; gdelabriolle@gmail.com
Reçu :
7
Juin
2018
Accepté :
20
Août
2018
La détermination de la fenêtre de pilotage de la pression de confinement lors de la conception et de l’exécution d’un tunnel au tunnelier est essentielle afin de garantir la sécurité des travaux, l’intégrité des avoisinants, et la qualité de la mise en œuvre. Dans cet article est d’abord présentée une méthodologie mettant l’accent sur la relation entre le contexte réglementaire de l’Eurocode 7, puis les différents types de calcul à mettre en œuvre. L’article présente par la suite une amélioration des méthodes analytiques existantes vis-à-vis de la stabilité du front de taille. Dans la continuité des nombreux travaux de recherche sur ce thème, on montre que notre approche est à la fois plus adaptée aux conditions rencontrées (tunnel circulaire, conditions multicouches, conditions drainées ou non drainées) et plus robuste théoriquement (nouveau choix pour le coefficient de poussée latéral, comparaison vis-à-vis des méthodes de type analyse limite définissant des bornes théoriques) tout en étant cohérente avec l’allure des mécanismes de rupture réellement observés in situ ou en laboratoire.
Abstract
Definition of confinement pressure operational range for the design and execution of TBM built tunnel is essential, in order to guarantee personal safety, neighbourhood integrity, and top quality at the end. In this article is firstly introduced a methodology, insisting on the relation between norms context and justifications to produce. Several improvements of existing analytical methods are presented and demonstrated about front stability. Regarding this existing bibliography on this thema, we show that our new approach is better adapted to realistic situations (circular tunnel, multilayer case, drained or undrained conditions), theoretically more robust (new choice for lateral coefficient pressure, comparison with well-known limit analysis that provide theoretical bounds), and is geometrically coherent with failure mechanism observed in situ or in laboratory.
Mots clés : tunnelier / stabilité du front de taille / blow-out / méthode analytique / pression de consigne
Key words: tunnel boring machine / face stability / blow-out / analytical method / operational confinement pressure
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2018
1 Démarche pour la définition de la pression de consigne au tunnelier
1.1 Introduction
La maîtrise de la stabilité du front de taille au cours du creusement d’un tunnel est essentielle pour garantir la sécurité des travaux, l’intégrité des avoisinants, et la qualité de la mise en œuvre du soutènement et du revêtement.
Dans cet article, nous allons nous concentrer sur le creusement au tunnelier à confinement [pression de boue (Slurry en anglais selon AFTES, 2013), pression de terre (Earth Pressure Balance, EPB), à densité variable (Variable Density, VD)], mais l’analyse réglementaire/calculatoire que nous menons peut s’étendre avec peu d’adaptation à un creusement en méthodes conventionnelles où la pression de confinement est apportée par un boulonnage de front de taille. En méthodes conventionnelles, cependant, les règles de l’art et l’expérience ont une part plus grande que les calculs dans la définition des opérations à mener au cours de chaque cycle d’avancement.
Nous allons proposer une démarche qui clarifie l’aspect réglementaire et améliore et étend le cadre d’application des méthodes analytiques usuellement utilisées, pour définir la fenêtre de pilotage du tunnelier, c’est-à-dire l’intervalle de pression de confinement minimale et maximale au front de taille dans lequel le pilote doit s’inscrire impérativement. Le choix de la pression de consigne située dans cet intervalle dépend principalement de l’expérience de l’entreprise en charge du pilotage et de la maîtrise du confinement.
1.2 Démarche réglementaire et organisation des chapitres
Pour définir la pression de confinement à maintenir lors du creusement au tunnelier, permettant par la suite de dimensionner les anneaux de voussoirs et la poussée à installer sur le tunnelier (AFTES, 1998 ; Maidl et al., 2012), il est nécessaire d’évaluer 5 types de pression de confinement à l’axe du tunnelier (cf. notations Tab. 1) :
-
pression de confinement minimale au front de taille pour assurer l’étanchéité à l’avancement : pfront, min, ELU HYD
-
méthode analytique, vérification de type ELU HYD. Cette vérification se fait en compensant la pression d’eau pw dans le terrain, en fonction du mode de confinement (γM poids volumique du matériau dans la chambre, h hauteur du tunnel) :

-
pression de confinement minimale au front de taille pour éviter sa rupture : pfront, min, ELU GEO
-
thème abordé dans la section 2 – méthode analytique, vérification de type ELU GEO. La majorité de l’article va s’intéresser à ce thème, afin de présenter diverses améliorations par rapport aux méthodes existantes actuelles ;
-
pression de confinement maximale au front de taille pour éviter le phénomène de blow-out : pfront, max, ELU
-
thème abordé dans la section 3 – méthode analytique, vérification de type ELU GEO ;
-
pression de confinement minimale de calcul pour respecter les critères de tassement : pfront, min, ELS
-
non abordé dans cet article, cf. section 1.3 – méthode numérique, vérification de type ELS ;
-
pression de confinement maximale de calcul pour éviter le soulèvement de la surface ou d’un ouvrage proche du tunnel : pfront, max, ELS
-
non abordé dans cet article, cf. section 1.3 – méthode numérique, vérification de type ELS.
Soit finalement, pour une section donnée, les pressions minimale et maximale nécessaires pour assurer la stabilité sont les suivantes :

Pour le terme pfront, min, ELU, sa détermination dépend du cas de figure :

Il ne reste plus qu’à prendre en compte la variabilité v de la pression de confinement en fonction du mode de confinement : on retient généralement v = ± 10 kPa en mode pression de boue et v = ± 30 kPa en mode pression de terre avec chambre pleine (appelé mode full EPB en anglais ; GEO report No. 249, 2009 ; GEO report No. 298, 2014). La pression de confinement est plus finement contrôlée avec un tunnelier à pression de boue ou à densité variable grâce à un pilotage via une bulle d’air déportée (non en contact avec le front de taille), bien que son pilotage soit moins aisé car ce mode agit différemment sur la contrainte hydrostatique et sur la contrainte effective ; en effet, un pression de terre agit directement sur la contrainte totale.
La plage autorisée de variation de pression de confinement au front de taille, que l’on appelle fenêtre de pilotage, est alors comprise entre les deux bornes suivantes (cf. Fig. 1 où les notations ont été reportées) :

Bien sûr, il est ensuite recommandé de retenir une pression de confinement de pilotage qui s’approche au plus de la valeur de pfront, avance, min, afin de minimiser les moyens mobilisés au niveau du tunnelier.
Attention, même si l’on aboutit à un domaine possible de pression de confinement (borne minimale plus faible que la borne maximale), il faut également vérifier que le tunnel ne sera pas soumis au risque de flottaison (ELU UPL), qui devient rapidement possible sous faible couverture. Ce thème sera abordé dans la section 4. Finalement, quelques abaques de synthèse ainsi que deux exemples de fenêtre de pilotage seront présentés dans la section 5.
Concernant les coefficients partiels à l’ELU, nous retenons l’approche 3 de l’Eurocode 7 (jeu de coefficients partiels ≪ A2 + M2 + R3 »), qui consiste à pondérer uniquement les paramètres de sol (1.25 sur les paramètres drainés et 1.4 sur les paramètres non drainés). Ils ne seront pas explicitement affichés dans ce texte : on suppose que ceux-ci ont déjà été appliqués.
 |
Fig. 1 Définition de la fenêtre autorisée de pilotage – inspiré de (ITA/AITES/DAUB, 2016). Operation range definition – inspired from (ITA/AITES/DAUB, 2016). |
1.3 Focus sur les vérifications de type ELS
Bien que les vérifications ELS ne soient pas abordées dans cet article (régulièrement dimensionnantes en site urbain pour la pression de confinement minimale), il est cependant nécessaire de rappeler qu’elles ne sont pas obtenues via le même moyen que les vérifications ELU. Il faut donc veiller à avoir une grande rigueur afin de transformer des pressions de calcul utilisées dans des modèles numériques 2D, en pression de confinement (minimale ou maximale) ELS au front de taille du tunnelier.
La pression de calcul pour les modèles numériques 2D doit prendre en compte la contribution à la maîtrise des tassements du confinement au front de taille, autour du bouclier et de la jupe (selon le mode de confinement retenu), et de l’injection du produit de bourrage. On remonte à la pression équivalente de calcul au front de la manière suivante :
-
quel que soit le mode de confinement, à partir de Aristaghes et Autuori (2001), on propose de retenir les coefficients de contribution suivants (pouvant être affinés selon le contexte via une modélisation 3D) :

-
quel que soit le mode de confinement, pour des raisons de qualité de mise en œuvre, on a :
pbourrage = pfront + psécurité (= pfront + 100 kPa en général)
-
en fonction du mode de confinement, s’il y a une pression autour de la jupe :
pbouclier/jupe = pfront
-
soit, finalement, dans le cas où :
-
il n’y a pas de bentonite autour de la jupe (mode pression de terre chambre pleine) :

-
il y a de la bentonite autour de la jupe (mode pression de boue ou mode pression de terre chambre pleine amélioré) :

On peut alors comparer les valeurs obtenues entre les calculs numériques à l’ELS et les calculs analytiques à l’ELU.
2 Étude de la stabilité du front de taille
2.1 Principes généraux
L’étude de la stabilité du front de taille vis-à-vis d’un effondrement lors de l’excavation d’un tunnel via des expressions analytiques sur la base du mécanisme de rupture du silo (Janssen, 1895) associé à un dièdre (Horn, 1961) a été développée de manière approfondie pour la première fois dans les années 1990 (Jancsecz et Steiner, 1994 ; Anagnostou et Kovári, 1994).
Les étapes de la méthode sont les suivantes :
-
utiliser la démarche 2D pour le calcul des contraintes verticales (Terzaghi, 1951) pour calculer la contrainte verticale 3D dans le silo ;
-
établir un bilan des forces dans le dièdre pour un angle donné d’inclinaison, moyennant plusieurs hypothèses fortes sur lesquelles nous reviendrons plus loin ;
-
faire varier l’angle d’inclinaison du dièdre jusqu’à trouver l’inclinaison la plus défavorable, c’est-à-dire celle correspondant au mécanisme de rupture probable donnant la pression de confinement la plus élevée.
Les hypothèses associées à la résolution analytique usuelle de ce mécanisme de rupture (Fig. 2) sont les suivantes :
-
sol homogène et uniforme sur toute la hauteur ;
-
choix empirique du coefficient de poussée latéral ;
-
aucun décousu pris en compte ;
-
nappe située dans le silo (au-dessus du tunnel) ou tunnel hors nappe ;
-
excavation de forme rectangulaire ;
-
répartition linéaire du frottement sur les faces latérales du dièdre ;
-
pression de confinement uniforme sur le front de taille.
Dans la pratique, cette approche est utilisée uniquement dans les terrains cohérents-frottant car les nombreux travaux sur le nombre de stabilité en terrains purement cohérents (cf. Broms et Bennermark, 1967 ; Davis et al., 1980 ; Gunn, 1980 ; Kimura et Mair, 1981), ont montré qu’elle donnait à la fois des valeurs cibles de pression de confinement bien trop faibles par rapport à ces approches très reconnues, et à des angles de rupture non réalistes.
En effet, afin d’être cohérente avec les observations, les expérimentations et approches théoriques usuelles (cf. Fig. 3 ; Chambon et Corté, 1989 ; Leca et Dormieux, 1990 ; Messerli et al., 2010), le mécanisme le plus défavorable obtenu doit afficher un angle d’ouverture w :
-
inférieur à 45° dans les terrains cohérents-frottant (en général dans la plage 15–35°, proche du 45°-φ/2) ;
-
supérieur à 45° dans les terrains purement cohérents (en général dans la plage 45–60°).
C’est dans ce contexte qu’il a été proposé récemment par Perazzelli et Anagnostou (2017) de modifier le mode de calcul de la contrainte verticale transmise au toit du dièdre pour passer d’un mécanisme de silo à des mécanismes de type analyse limite statiquement admissible tels que proposés par Gunn (1980).
Cette adaptation nous permettra d’associer les deux pratiques les plus répandues (Silo & Dièdre pour les terrains cohérents-frottant, d’une part, nombre de stabilité pour les terrains purement cohérents, d’autre part) pour combiner les avantages de chacune : nous verrons toutes les améliorations possibles au modèle de référence exposé, que l’on pourra étendre aux terrains purement cohérents tout en garantissant une continuité de la rigueur d’analyse dans ces terrains par rapport à la pratique existante.
 |
Fig. 2 Mécanisme de rupture 3D. 3D failure mechanism. |
 |
Fig. 3 À gauche : Mécanisme en terrain cohérent-frottant. À droite : mécanisme en terrain purement cohérent (Leca, 2007). Left: Face collapse in dry granular soils. Right: Face collapse in cohesive ground soils (Leca, 2007). |
2.2 Solution dans le silo
2.2.1 Mise en place du problème usuel de Terzaghi (2D)
Dans le cadre d’un calcul en 2D transversal (Fig. 4), on considère une tranche de sol infiniment fine de cohésion c, avec un angle de frottement interne φ (voir l’ensemble des notations dans le Tab. 1).
L’objectif est d’obtenir la contrainte verticale au toit du tunnel, en intégrant sur toute la hauteur de couverture une équation différentielle qui caractérise la répartition des charges sur la tranche de sol.
En faisant un bilan à l’équilibre des forces verticales sur la tranche :

Usuellement, on suppose que σh, la contrainte horizontale sur les faces latérales de la tranche vaut σh = K*σv. Avec le critère de Mohr-Coulomb :

En remplaçant les termes respectifs :

Comme σv(z = 0) = q, alors on obtient l’expression suivante :

Ainsi, pour z grand devant B/2 pour un angle ϕ non nul, la contrainte verticale tend de manière asymptotique vers la valeur suivante :

On rappelle que, comme cette approche 2D est utilisée principalement pour le calcul des revêtements définitifs, on saisit l’occasion de rappeler les règles de l’art : il est recommandé par AFTES (1976) et Széchy (1970), de retenir, pour un tunnel de couverture inférieure à 2,5 B, une charge égale au poids volumique multiplié par la plus petite valeur entre la couverture T et la largeur de la voûte de décharge B.
 |
Fig. 4 Bilan des forces sur une tranche de sol. Forces equilibrium in a ground soil slice. |
2.2.2 Lien entre la contrainte verticale et la contrainte horizontale
D’un point de vue théorique, la valeur de K n’est pas vraiment le coefficient de poussée des terres au repos K0, et n’est pas non plus le coefficient de poussée Ka (il est situé entre les deux). Comme il n’y a pas d’unanimité sur ce coefficient, il semblerait recommandé, conformément à ce qui aurait été observé par Terzaghi (1951) sur des mesures en laboratoire, de prendre K = 1. Ce choix a été retenu également par Anagnostou (2012, 2013), bien que l’on ait pu trouver dans Anagnostou et Kovári (1994) et Peila (1994) une valeur de 0,4 ou 0,8, ou dans Handy (1985) une expression similaire à la formule de Jaky (1944) pour le coefficient de poussée des terres au repos (K = 1,06* (1 − sin(φ))). On peut se reporter également au chapitre 6 du rapport ITA/AITES/DAUB (2016) qui aborde également cette difficulté et ce que la bibliographie propose.
La valeur de K reste donc sujette à discussion car le choix de retenir 1 quel que soit le cas de figure reste quelque peu arbitraire. C’est pourquoi nous proposons ci-dessous une approche purement théorique telle que proposée par Sequeira Nunes Antao (1997), utilisant le fait que l’on est sur un plan de rupture au niveau des parois du mécanisme.
Le cercle de Mohr du problème est représenté (Fig. 5), où la contrainte verticale σv est obtenu par rotation de 90° par rapport à σh, c’est-à-dire 180° dans le plan de Mohr.
En égalisant les expressions de r, rayon du cercle de Mohr, on peut obtenir la relation suivante :

On appelle λ et Kc le couple de coefficients définissant le lien entre σv et σh. On retrouve dans le tableau 2 quelques valeurs pour ce couple de coefficients.
Dans cette approche, on n’a donc posé aucune autre hypothèse sur le lien entre σ1 et σ3, que le fait que le critère de rupture est vérifié en paroi, ce qui est l’hypothèse de base du mécanisme étudié. On remarque que si φ tend vers 0, alors on obtient σv = σh.
Dans ce cas, par résolution de l’équation différentielle, on obtient :

La valeur à l’infini devient :

Par comparaison aux valeurs obtenues si l’on pose K = 1, cette expression donne des résultats assez similaires. En effet, elle est à la fois un peu plus conservative en minimisant l’importance de la cohésion, et un peu moins conservative en réduisant l’influence de la profondeur.
 |
Fig. 5 Cercle de Mohr correspondant à la situation aux surfaces de rupture. Mohr circle at collapse plane. |
Valeurs du couple définissant le lien entre la contrainte horizontale et verticale.
Values for the coefficient defining the link between horizontal and vertical stress.
2.2.3 Largeur de la voûte de décharge
Concernant la largeur de la tranche, on a deux cas de figures géométrique : le tunnel en fer à cheval, et le tunnel circulaire, où l’hypothèse principale est que l’angle de rupture par rapport à la verticale vaut π/4−φ/2. En fonction de la forme du tunnel, on a (AFTES, 1980) :

Pour un tunnel avec une section en fer à cheval, la démonstration se fait dans la figure 6.
Pour un tunnel avec une section circulaire, la démonstration se fait à l’aide de la figure 7 et de deux changements de variables (poser α = π/4 + φ/2 puis t = tan(α/2)) et de quelques règles trigonométriques.
 |
Fig. 6 Largeur de la voûte de décharge – tunnel en fer à cheval. Arching vault – U-shaped tunnel. |
 |
Fig. 7 Largeur de la voûte de décharge– tunnel circulaire. Arching vault – circular tunnel. |
2.2.4 Prise en compte d’une nappe ou de plusieurs couches différentes
Dans ce cas, il suffit de réécrire la solution à partir de la même équation différentielle, mais en modifiant les conditions aux limites. Supposons que l’on a le problème tel qu’illustré (Fig. 8).
En partant de l’hypothèse que c’est la couche n qui dicte la largeur de la voûte de décharge, on calcule donc B selon l’expression suivante :

Puis, il s’agit de calculer successivement la contrainte verticale à la base de chaque couche de sol :

 |
Fig. 8 Problème multicouche. Multilayer case. |
2.2.5 Adaptation de la solution au problème 3D
On réécrit le bilan que l’on avait établi en 2D dans la section 2.2.1, pour l’adapter au problème 3D (Fig. 2). On a alors :

Où S est la surface du silo et P son périmètre. Soit :

Ainsi, B/2 en 2D correspond à S/P en 3D. Pour éviter les confusions, on note R = S/P. Cette solution peut donc s’adapter à n’importe quelle forme de silo. En particulier, pour un silo de forme rectangulaire :

En 3D, la valeur de R est bien plus faible que la valeur de B associée à la 2D. Il en résulte qu’il est fréquent d’obtenir une contrainte négative. Ceci n’ayant aucun sens, il faut veiller à s’assurer d’avoir une valeur supérieure ou égale à 0. Cette prudence est d’autant plus importante en multicouche.
Ainsi, la contrainte verticale en clef du tunnel vaut :


On peut utiliser les adaptations nécessaires détaillées au chapitre précédent si on a plusieurs couches et/ou s’il y a la présence d’une nappe.
En particulier, si on a une seule couche de terrain et une nappe en conditions drainées (jugement soumis au cas par cas à l’ingénieur) :



2.2.6 Prise en compte d’un décousu
Le décousu est la distance non soutenue depuis le front de taille (Fig. 9). Ce concept est utile pour des tunnels réalisés en méthodes conventionnelles. Sur la proposition de Anagnostou et Perazzelli (2013), on modifie alors l’expression de R issue du silo pour prendre en compte une forme rectangulaire allongée du décousu ≪ e » dans le sens longitudinal :
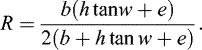
Pour faire le lien avec les futures conditions aux limites au toit du dièdre, on pose les définitions suivantes, Vsilo représentant la force verticale transmise par le silo et qui sera à équilibrer par le dièdre :
 où σz(h) est la contrainte verticale au toit du dièdre. C’est-à-dire :
où σz(h) est la contrainte verticale au toit du dièdre. C’est-à-dire :

 |
Fig. 9 Définition du décousu. Unsupported span. |
2.2.7 Calcul de la contrainte verticale en clef dans un terrain purement cohérent
On réutilise les formules obtenues par Perazzelli et Anagnostou (2017) aux pages 5 et 6, équations 21 à 25. Elles traduisent la contrainte obtenue en clef pour 3 mécanismes d’analyse limite statiquement admissibles (borne sécuritaire en termes de pression de confinement). Il faut retenir le plus défavorable en fonction de l’angle w d’ouverture du dièdre.
Où Qs et Us sont tels que pour un w, ils donneront la valeur maximale de V :


Leurs résultats permettent de prendre en compte une augmentation de la cohésion avec la profondeur, ce qui est la seule option ici pour introduire de manière moyennée le cas multicouche. Il faut toutefois rester prudent quant à son utilisation dans le cas multicouche car ces expressions n’ont pas été déterminées dans ce but. Par ailleurs, il n’est pas fréquent que soient pris en compte sur les projets réels des valeurs de cohésion qui varient avec la profondeur. C’est pourquoi dans la suite nous proposerons une autre approche.
2.3 Solution dans le dièdre
2.3.1 Résolution historique : méthode d’équilibre des forces
Dans cette approche, il s’agit de faire un bilan des forces sur le dièdre (Fig. 10), où en particulier S est la force à apporter au front pour assurer l’équilibre du dièdre.
Si la force S obtenue est nulle ou négative, le dièdre est en équilibre : il n’y aura pas d’effondrement en l’absence de confinement. On note que si la cohésion est nulle, on a de toute façon instabilité du front. Trois forces peuvent être déterminées aisément. On a :

Puis on établit le bilan des efforts selon deux axes Ox et Oy opportunément choisis :

En injectant le bilan selon Oy dans l’expression de TN, le bilan selon Ox devient :

Soit, après transformation trigonométrique :

Pour déterminer Ts, l’hypothèse usuelle est la suivante : la contrainte en clef décroit linéairement sur la hauteur du dièdre. Comme la largeur du triangle sur lequel on doit intégrer varie avec la hauteur, et vaut z*tan(w) :

Il s’agit donc de maximiser la valeur de S en faisant varier w.
On peut réécrire la solution en contraintes, sous une forme régulièrement utilisée dans la littérature pour l’analyse de la stabilité du front de taille :

Mais on retiendra plutôt une notation proche de celle utilisée par Anagnostou (2012). Après substitution :


Ce passage en contraintes suppose que l’excavation est rectangulaire, de largeur b et de hauteur h. Pour un tunnel circulaire, il a été proposé de retenir b et h tels que (Anagnostou, 2012) :

On aboutit donc à une réduction fictive de la section de calcul, ce qui diminue la pression de confinement obtenue par rapport à une section carrée. Attention cependant à l’incidence sur le calcul de la pression d’eau qui elle, ne devra pas être réduite (si le diamètre vaut 10, alors il y aura 98,1 kPa à prendre en compte, et non π0,5/2*98,1 = 86,9 kPa).
 |
Fig. 10 Équilibre des forces sur le dièdre. Forces equilibrium on the wedge. |
2.3.2 Améliorations du modèle par Anagnostou (2012, 2013)
2.3.2.1 Méthode des tranches
La méthode des tranches consiste à faire un bilan de forces infinitésimales dans le dièdre, comme dans le silo. Cette méthode diffère donc de la méthode historique qui fait un bilan de forces globales sur le dièdre. Cette méthode, plus fastidieuse à mettre en œuvre, permet de s’affranchir de l’hypothèse simpliste pour obtenir le frottement sur les faces latérales (Ts). Le problème, résolu la première fois par Anagnostou (2012), est illustré (Fig. 11).
La largeur de la tranche vaut z*tan(w), la hauteur vaut dz, et la hauteur en biais vaut dz/cos(w). Ainsi, la surface latérale de la tranche dA vaut :

En négligeant le second ordre, on obtient :

Nous allons utiliser cette approche qui nous permettra par la suite d’extrapoler aisément au cas de figure ≪ multicouche ».
 |
Fig. 11 Méthode des tranches (Anagnostou, 2012). Method of slices (Anagnostou, 2012). |
2.3.2.2 Pression de confinement variable sur le front de taille
Lors du process de creusement au tunnelier, en fonction des conditions de creusement (sous nappe ou hors nappe), il est fréquent d’appliquer une pression de confinement qui varie linéairement sur le front de taille.
Cette variation est dû au poids volumique moyen du matériau dans la chambre qui est différent du poids volumique du terrain, quel que soit le mode de confinement (pression de boue, pression de terre, pression d’air). Si saxe est la pression de confinement au centre, et δs la variation entre le radier et la voûte, on peut alors poser :


2.3.2.3 Limites de ces améliorations
Les approches de calcul considèrent alors les hypothèses suivantes :
-
sol homogène et uniforme sur toute la hauteur ;
-
choix empirique du coefficient de poussée latéral ;
-
nappe située dans le silo (au-dessus du tunnel) ou tunnel hors nappe ;
-
excavation de forme rectangulaire ;
-
répartition linéaire de la pression de confinement sur le front de taille.
Par rapport à la liste d’hypothèse du premier chapitre, seulement 2 hypothèses ont été levées (prise en compte décousu et plus de choix de la répartition du frottement latéral), et une 3e améliorée (pression de confinement variant linéairement plutôt qu’uniforme).
2.3.3 Améliorations proposées par l’auteur
Nous allons intégrer aux solutions de Anagnostou et Perazzelli (2013) les améliorations suivantes, en reprenant les mêmes notations :
-
coefficient de poussée latéral déterminé de manière théorique, comme présenté dans la section 2.2.2 :

-
tunnel de section elliptique de largeur β et de hauteur D.
Pour prendre en compte cette géométrie de manière explicite, alors la largeur b qui est utilisée dans les équations différentielles doit varier avec la hauteur, en respectant les conditions aux limites suivantes :

-
répartition quelconque de la pression de confinement sur la hauteur du front
En effet, une répartition linéaire suppose qu’en particulier, aucun des cas suivants ne survient : la nappe intercepte le front, le tunnel est excavé dans un front mixte, une opération de maintenance est menée [mode de confinement partiellement à l’air, voir Gugliemetti et al. (2008)], ou encore on met en œuvre un boulonnage au front de taille [les résultats de ce chapitre ayant vocation à s’étendre à l’étude de la stabilité du front de taille en méthodes conventionnelles – voir les différences d’approches entre Peila (1994) et Anagnostou et Serafeimidis (2007)].
Prendre en compte une répartition quelconque suppose déjà de prendre en compte le cas ≪ multicouche » ;
-
prise en compte d’un dièdre plus petit que la hauteur du tunnel.
Dans le cas d’un front mixte, il peut s’avérer que la couche supérieure soit de bien plus mauvaise qualité que le terrain sous-jacent : il est alors tout à fait pertinent d’étudier la rupture de la partie supérieure seulement plutôt que l’ensemble du front.
2.3.4 Nouvelle formulation semi-analytique généralisée
Dans notre approche, on présuppose la répartition de la pression de confinement sur la hauteur du front en fonction du mode de confinement retenu, pour vérifier ensuite si on assure l’équilibre vis-à-vis de la contrainte en clef du tunnel et issue du calcul dans la couverture.
On peut donc supposer que la pression de confinement est constante sur chaque tranche infinitésimale k de hauteur dz et comprise entre les cotes zk et zk+1 (Serafeimidis et al., 2007). Soit :

De la même manière, on suppose que tous les paramètres de sol sont constants dans chaque couche k, ce qui permet de simplifier la prise en compte du cas ≪ multicouche ».
À partir de la figure 11, par analogie avec la méthode de démonstration utilisée dans la méthode d’équilibre des forces, on établit le bilan suivant sur une tranche dz du dièdre :

Par ailleurs, pour z inclus dans une couche k (c’est-à-dire zk−1 < z < zk), on a :

Par la même stratégie de substitution que dans la méthode d’équilibre des forces, on obtient l’équation différentielle suivante :


On présente toutes les étapes de la démonstration mathématique pour obtenir V(zk) = Vk en annexe 1. On réécrit l’expression obtenue en annexe 1 pour obtenir une écriture similaire à celle de Anagnostou (2012) :


Il est intéressant de noter que Vk ne dépend que de Vk − 1. Afin de calculer de proche en proche la valeur de Vk, il suffit de poser le fait que V0, force verticale en pied du dièdre, vaut 0. Ainsi, on obtient tous les Vk de bas en haut jusqu’à obtenir V(D) qui est la force verticale au toit du dièdre.
Si V(D), force verticale au toit du dièdre, est supérieure ou égale à Vsilo, force verticale obtenue à la base du silo, alors l’équilibre est assuré. Dans le cas contraire, la répartition retenue de la pression de confinement n’est pas suffisante (cf. Fig. 12 où l’on présente un exemple pour un tunnel de 9 m de diamètre pour une couverture de 9 m).
On présente en annexe 2 une comparaison terme à terme entre notre résultat qui prend en compte explicitement une forme circulaire et la correction a priori proposée dans la littérature pour transformer les résultats associés à une forme rectangulaire (cf. dernier paragraphe de la Sect. 2.3.1).
On note par ailleurs qu’avec une discrétisation suffisante (tous les 10 cm par exemple), l’approche détaillée permet de mener des calculs quelle que soit la variation de la largeur b(z) sur la hauteur du tunnel.
Il y a une particularité lors d’un creusement avec un tunnelier à pression de boue. Ce mode de confinement est associé à une pénétration plus ou moins profonde de la boue (cake), fonction de la surpression de confinement (pression effective). Cela implique que la boue située au-delà du dièdre en pied de tunnel ne contribue pas à la stabilité. Pour avoir une estimation de la taille du cake, on peut se référer à Anagnostou et Kovári (1994), Broere (2001), Aristaghes et Autuori (2001), AFTES (2002) et ITA/AITES/DAUB (2016).
On corrige la surpression de confinement de la manière suivante (Lmax(z) profondeur du cake à la cote z) :

Si on souhaite tronquer le dièdre à la cote zref, alors il faut utiliser les cotes suivantes, sans changer D ou β :

De plus, pour le calcul dans le silo, on a (sachant que l’angle optimal w pourra être différent) :
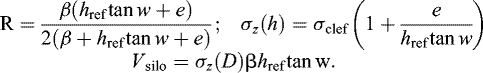
 |
Fig. 12 Répartition des forces verticales dans le dièdre et dans le silo pour 3 modes de confinement (pression d’air, pression de boue, pression de terre chambre pleine). À gauche : répartition de pression de confinement insuffisante. À droite : répartition de pression de confinement suffisante. Shape of vertical forces in wedge and silo for 3 confinement modes (air, slurry, full EPB). Left: insufficient confinement pressure. Right: sufficient confinement pressure. |
2.3.5 Nouvelle formulation analytique simplifiée : terrain cohérent frottant
À des fins de comparaison avec les méthodes existantes, mais aussi en vue de mettre au point des abaques, nous proposons une solution simplifiée où l’on considère des paramètres de sol uniformes sur le front du tunnel et dans la couverture, avec une variation linéaire de la pression de confinement sur le front de taille, soit :

Où δs est le gradient de pression de confinement entre la voûte et le radier et saxe la pression de confinement à l’axe.
En conservant les mêmes notations en faisant disparaître l’indice k, on part de la même stratégie qu’au chapitre précédent. On a alors l’équation différentielle suivante :

On présente toutes les étapes de la démonstration mathématique pour obtenir V(D) en annexe 1 (stratégie similaire à celle du chapitre précédent).
Les conditions aux limites suivantes s’appliquent à l’expression de V(D) :

Finalement, dans le cadre de ces hypothèses simplifiées, on peut obtenir de manière directe la pression de confinement nécessaire :


2.3.6 Nouvelle formulation analytique simplifiée : terrain purement cohérent (Trappe & Dièdre)
Sur la base des mêmes hypothèses que la section 2.3.5, on cherche la limite les coefficients  à
à  pour φ tendant vers 0. On obtient obtient les limites suivantes :
pour φ tendant vers 0. On obtient obtient les limites suivantes :

On remarque que la variation linéaire de la pression de confinement n’a plus d’influence sur le résultat.
Finalement, pour la pression de confinement à l’axe :

Si on injecte la valeur obtenue à partir de la couverture :

Si la cohésion non drainée et le poids volumique sont les mêmes toute hauteur :

Dans le cas où le décousu est nul, on obtient :


Dans le cas où D/β = 1 (comme w ≥ 45° pour un sol purement cohérent, ici Qs2 < Qs1) :


En faisant une équivalence avec l’approche de type ≪ nombre de stabilité », on propose pour un tunnel circulaire :

2.4 Comparaison et vérifications théoriques
2.4.1 Terrain cohérent-frottant
On souhaite donc comparer les résultats de Anagnostou (2012) pour un décousu nul avec une couverture relative égale à 1, une pression de confinement constante sur le front et aucun décousu (cf. Fig. 13). On le fait via un graphe qui présente, pour 4 valeurs de φ (20, 25, 30 ou 35°), la pression de confinement relative nécessaire pour stabiliser le front de taille en fonction de la cohésion relative du sol.
Sur cette figure, on y compare également l’approche de Mollon et al. (2010), basée sur des mécanismes complexes en forme de corne Subrin et Wong (2002), qui théoriquement fournit les pressions de confinement minimales certaines. Cette approche améliore les recherches antérieures de Vermeer et al. (2002), basées sur un calage numérique par c-ϕ réduction, qui elle améliorait déjà légèrement l’approche cinématique de Leca et Dormieux (1990). On a calé l’abaque de Mollon et al. (2010), sur le même type d’écriture intéressante retenue par Vermeer et al. (2002) :

Comme illustré (Fig. 13), et c’est également le cas si l’on avait choisi T/h = 2 ou plus, notre nouvelle approche est plus sécuritaire. L’impact de l’amélioration des caractéristiques est atténué dans notre approche, un peu comme cela l’avait été noté dans la section 2.2.2.
On remarque également que les calculs issus de notre approche donnent des résultats qui sont bien toujours supérieurs aux valeurs fournies par Mollon et al. (2010), ce qui est cohérent théoriquement.
Par ailleurs, on note que les valeurs ci-dessus de Anagnostou (2012) pour ϕ = 30 et 35° sont plus faibles que Mollon et al. (2010), ce qui démontre qu’elles sont sous estimées : notre approche tend donc à corriger cette limite. Ceci a déjà été observé par Mollon et al. (2010), sur la base de Anagnostou et Kovári (1996).
En plus de ce qui est présenté ci-dessus, nous avons comparé notre nouvelle solution avec les approches cinématiques et statiques de Atkinson et Potts (1977) pour un terrain purement frottant avec φ = 30° ou 35° (respectivement à gauche et à droite sur la Fig. 14) (NB : l’approche statique de Leca et Panet (1988) est meilleure pour T/h < 0,8). Notre solution doit être encadrée par ces deux bornes : cela est effectivement bien le cas, tant que T/h > 0,5 (couverture très faible), contrairement à celle de Anagnostou (2012). Par ailleurs, on saisit l’occasion pour montrer que les formules de Piaskowski et Kowalewski (1965) et celles de Carranza-Torres (2004) et Carranza-Torres et al. (2013) ne présentent pas non plus cette cohérence théorique dans les milieux purement frottant.
Ceci confirme donc que notre approche pour le coefficient de poussée latéral selon le cercle de Mohr associé à la prise en compte d’un tunnel explicitement elliptique est une approche plus robuste théoriquement que les méthodes existantes.
 |
Fig. 13 Comparaison nouvelle formulation simplifiée (trait plein & marqueur) / (Anagnostou, 2012) avec λ = 1 (trait plein) / Mollon et al. (2010) (pointillés). Comparison between the new simplified solution (full line & dots) / (Anagnostou, 2012) with λ = 1 (full line) / Mollon et al. (2010) (dashed line). |
 |
Fig. 14 Terrain purement frottant. À gauche : φ = 30°. À droite : φ = 35°. Comparaison nouvelle formulation simplifiée / limites supérieures et inférieures de Atkinson et Potts (1977) / formules de Piaskowski et Kowalewski (1965), Carranza-Torres (2004) et Carranza-Torres et al. (2013). Purely frictional soil ground. Left: φ = 30°. Right: φ = 35°. Comparison between the new simplified solution / upper and lower bound from Atkinson and Potts (1977) / formulas from Piaskowski and Kowalewski (1965), Carranza-Torres (2004) and Carranza-Torres et al. (2013). |
2.4.2 Terrain purement cohérent
Pour justifier la pertinente de cette nouvelle approche (que l’on appelle Trappe & Dièdre) pour le calcul des contraintes verticales dans la couverture pour un terrain purement cohérent, ces résultats ont été comparés au nombre de stabilité, indicateur utilisé communément dans les terrains purement cohérents, et ayant été validé par l’expérience des travaux et les expérimentations en laboratoire (cf. Sect. 1) :

On dispose de valeurs théoriques qui donnent une limite plus précise de Ns en fonction de la profondeur grâce aux travaux de Davis et al. (1980). Ces limites sont présentées (Fig. 15).

Si on inverse cette relation, la pression de confinement pour assurer la stabilité vaut :
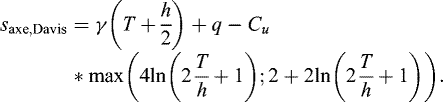
D’autre part, la méthode de Carranza-Torres (2004) et Carranza-Torres et al. (2013), basée sur un calcul en symétrie sphérique, est bien adaptée dans une seule couche de terrain purement cohérent pour un tunnel de section circulaire. Cette méthode est en fait une extension de la méthode bien connue de Caquot et Kerisel (1966) qui était établi en symétrie cylindrique. Dans ce contexte, la formule est la suivante :

On peut inverser cette relation pour obtenir le nombre de stabilité associé à cette méthode (c’est le seul cas où le nombre de stabilité dépend de Cu – pour les figures 17 et 18, on a retenu Cu = 50 kPa) :

Enfin, on a combiné l’approche Trappe & Dièdre avec la prise en compte d’un tunnel de section circulaire pour une seule couche de sol, afin de comparer le nombre de stabilité équivalent que l’on obtient.
On compare le nombre de stabilité ciblé en fonction de la couverture relative sur la figure 16 et la pression de confinement relative nécessaire sur la figure 17, pour chacune des 5 méthodes mentionnées pour les terrains purement cohérents : (Broms et Bennermark, 1967 ; Davis et al., 1980 ; Carranza-Torres, 2004 ; Carranza-Torres et al., 2013), Trappe & Dièdre pour une section carrée, Trappe & Dièdre pour une section circulaire. On présente également le résultat obtenu pour la formule de Piaskowski et Kowalewski (1965), afin de montrer que son application n’est pas recommandée dans les terrains purement cohérents.
Partout, notre nouvelle approche est sensiblement égale à la méthode de Carranza-Torres (2004) et Carranza-Torres et al. (2013), tout en étant un peu moins sécuritaire que la méthode usuellement utilisée de Davis et al. (1980). Sur l’ensemble de la plage de variation, la méthode Trappe & Dièdre de Perazzelli et Anagnostou (2017) pour un tunnel carré est un peu moins sécuritaire que les trois autres approches.
En comparant les pressions de confinement obtenues pour un Cu fixé, on retrouve bien les mêmes conclusions.
Il est donc justifié que la méthode Trappe & Dièdre introduite par Perazzelli et Anagnostou (2017) et améliorée dans cet article permet d’élargir son cadre d’application.
On ajoute qu’avec cette méthode on obtient des angles de mécanisme de rupture de l’ordre de 45 à 60°, contrairement à l’approche Silo & Dièdre adaptée aux terrains purement frottant donnant des angles de rupture de l’ordre de 15 à 35°.
Enfin, Davis et al. (1980) obtiennent, pour un ratio Cu/γh < 1/10,96 = 0,091, un mécanisme assuré d’instabilité locale du front. Néanmoins, ce ratio implique une valeur très faible de Cu (15 kPa dans l’exemple de la Fig. 17), pour laquelle on prévoit dans tous les cas qu’une pression de confinement est nécessaire pour stabiliser le front.
On ajoute ici une prudence concernant le concept de nombre de stabilité qui s’étend mal à des cas de figure avec décousu (utile en creusement en méthodes conventionnelles). Un abaque assez répandu (Kimura et Mair, 1981) propose un nombre de stabilité cible en fonction du décousu (e/h = 0, 0,5, 1,0, 2,0 ou l’infini). D’une part, cet abaque n’est pas cohérent avec les résultats désormais bien connus pour e/h = 0, et, d’autre part, l’application à quelques exemples montrent qu’il vaut mieux étudier ces situations au cas par cas.
 |
Fig. 15 Limites supérieures et inférieures du nombre de stabilité (Davis et al., 1980). Upper and Lower bound for Ns (Davis et al., 1980). |
 |
Fig. 16 Terrain purement cohérent – nombre de stabilité cible obtenus. Purely cohesive soil – targeted Ns. |
 |
Fig. 17 Terrain purement cohérent – pressions de confinement obtenues. Purely cohesive soil – confinement pressure required. |
3 Étude du phénomène de blow-out
3.1 En avant du front de taille
L’approche retenue par la pratique usuelle pour prévenir le phénomène de blow-out consiste à retenir l’objectif suivant : la pression de confinement au front en voûte ne doit pas dépasser la contrainte in situ. Ceci permet d’éviter des pertes de boue sous pression, ou de claquer le terrain dans le cas d’un tunnelier à pression de terre. Ainsi, plus le gradient de pression est élevé dans la chambre d’abattage, plus on est sécurisé vis-à-vis de ce risque : c’est le principe du mode de confinement à boue lourde, utilisable sur les tunneliers à densité variable. Le coefficient de sécurité réglementaire est de 1,1 (Eurocode 7 – annexe A, 2005).
En retenant des poids volumiques usuels de matériau dans la chambre (γM = 11 kN/m3 pour le pression de boue et 15 kN/m3 pour le pression de terre), on obtient une condition dont le résultat varie avec le diamètre du tunnel et le poids volumique moyen retenu pour le sol (Fig. 18). Sur cette figure on représente également le tunnelier à densité variable (VD TBM) en mode de confinement boue lourde. On a retenu une précision de type pression de boue (v = ± 10 kPa) pour un poids volumique de matériau dans la chambre de 18 kN/m3 (cas extrême). Ceci permet d’observer l’impact intéressant généré par ce mode de confinement sur le blow-out.
Si l’on souhaite aller plus loin dans la compréhension de ce phénomène, il est important de noter que le blow-out ne consiste pas en une rupture du terrain par excès de compression. En effet, si l’on considère un mécanisme de rupture similaire à celui évoqué au chapitre sur la stabilité du front, mais cette fois-ci vers le haut (gravité favorable dans ce cas) et que l’on redémontre l’ensemble des expressions, on obtient des pressions limites de l’ordre de 5 à 20 fois la contrainte in situ (voir annexe 3). Ceci rejoint par ailleurs les résultats de l’approche cinématique de Leca et Dormieux (1990) sur le blow-out dont les valeurs sont largement au-delà de ce que recommande la pratique.
D’après nous, le phénomène de blow-out s’apparente plutôt à de la fracturation hydraulique : le process de confinement, par une pression trop importante, finit par générer un claquage par une rupture en traction du terrain. Ceci est d’autant plus critique si le terrain présente une orientation préférentielle de discontinuités (dans ce cas, des vérifications pour un terrain non continu sont à mener).
La pratique de la fracturation hydraulique est généralement orientée vers la reconnaissance du champ de contraintes dans le massif, son anisotropie et la direction de la contrainte horizontale majeure. En se référant au chapitre dédié à la fracturation hydraulique dans Jaeger et al. (2007), on obtient alors :

Ce nouveau critère peut être à la fois plus ou moins pénalisant, et coïncide avec le critère usuel pour K0 = 2/3.
On suggère, par précaution, de considérer le plus faible des deux critères :

 |
Fig. 18 Pression de consigne maximale à l’axe. Blow-out values. |
3.2 En arrière de la jupe du tunnelier
Des travaux récents (Vu et al., 2015) proposent de prendre en compte le risque d’occurrence du blow-out au moment de l’introduction du produit de bourrage, dans un calcul 2D (Fig. 19). Dans ce calcul, le produit de bourrage est considéré comme étant un fluide de Bingham. En effet, il reste fluide pendant un certain temps (environ 16 h pour un mortier semi-actif, 3 h pour un mortier actif), et pourrait générer un risque. Dans cette approche est pris en compte le frottement du terrain, contrairement aux expressions ci-dessus.
Nous avons donc redémontré leur expression en utilisant le coefficient de poussée latéral tel que nous l’avons défini dans la section 2.2.2.
Le poids de sol est donné par :

NB : Le poids volumique de sol à prendre est le poids volumique moyen entre celui que l’on a au-dessus de la nappe et sa valeur déjaugée sous la nappe.
Les forces de frottement sont :

En décrivant le produit de bourrage comme un fluide de Bingham, on obtient un gradient entre la voûte et le radier plus faible que seul le poids volumique :

Avec δp le gradient de pression, ρb la masse volumique du bourrage, τy le seuil de cisaillement et db le vide annulaire. La pression d’injection du produit de bourrage a donc pour expression :

Son intégration sur la partie supérieure de l’anneau donne :

Le coefficient réglementaire étant 1,1, on obtient :

On illustre dans la figure 20 un exemple d’application en terrain cohérent frottant, pour un exemple type de paramètres de produit de bourrage, et psécurité = 100 kPa . (cf. annexe 4 où l’on propose une réflexion sur psécurité).
Plus le tunnelier est petit, plus ce critère est pénalisant. En terrain cohérent-frottant, ce critère est plutôt pénalisant pour les faibles couvertures (T/h < 1), mais peut l’être quelle que soit la couverture dans un terrain purement cohérent.
 |
Fig. 19 Blow-out à l’introduction du produit de bourrage. Blow-out at injection of the grouting. |
 |
Fig. 20 Pression de consigne maximale à l’axe – critère sur le produit de bourrage. Blow-out values – grouting criterion. |
4 Justification de la non-flottaison
Cet aspect est essentiel pour les tunnels superficiels sous nappe car il peut être dimensionnant pour l’épaisseur des anneaux de voussoirs (en particulier pour les tunnels sous-fluviaux). Le cas échéant, il faudra trouver un moyen d’alourdir la couverture (remblai additionnel en surface) ou bien d’alourdir le tunnel (remblai dans le tunnel juste derrière le tunnelier). Le coefficient de sécurité réglementaire est de 1,1 (Eurocode 7 – annexe A, 2005).
Il y a 3 efforts à évaluer pour vérifier qu’un tunnel sous nappe ne va pas se mettre à flotter sous la poussée d’Archimède :
-
WL : Poids linéique de l’anneau de voussoirs

-
WS : Poids déjaugé de la couverture entièrement submergée (à adapter le cas échéant si tunnel non entièrement sous nappe)

-
PA : Poussée d’Archimède sous le tunnel

Le résultat est présenté dans la figure 21, pour un tunnel où le niveau de nappe coïncide avec le TN (terrain naturel) et un ratio d’épaisseur relative classique d’anneau de voussoirs t/D = 1/20 (AFTES, 1998 ; Van der Waart van Gulik, 2010).
 |
Fig. 21 Couverture relative minimale pour éviter la flottaison. Minimal relative overburden to avoid bouyancy. |
5 Abaques de synthèse
5.1 Résultats théoriques sur l’étude de la stabilité du front de taille
5.1.1 Terrains cohérents-frottant – méthode Silo & Dièdre
Dans la figure 22, on présente la cohésion relative nécessaire pour avoir un front stable sans appliquer de pression de confinement, en fonction de la couverture, pour diverses valeurs de l’angle de frottement interne (15 à 35°). Le graphe de gauche présente les résultats pour un décousu nul et celui de droite pour un décousu e/h = 1/5. On a fixé la surcharge en surface à q = 0. Bien sûr si on est sous nappe, une pression de confinement sera nécessaire pour contrer la pression d’eau (cf. clarifications de la Sect. 1.2).
Dans la figure 23, on présente la pression de confinement relative nécessaire à l’axe pour avoir un front stable, pour diverses valeurs de cohésion relative c/γh et un décousu nul. Sur chacun des 4 graphes, l’angle de frottement interne est fixé (20, 25, 30 ou 35°). On a fixé la surcharge en surface à q = 0. Bien sûr si on est sous nappe, ces graphes ne donnent que la pression de confinement effective, et une pression de confinement supplémentaire sera nécessaire pour contrer la pression d’eau (cf. clarifications de la Sect. 1.2).
Ces abaques permettent de donner rapidement le curseur de la problématique du projet étudié. Les deux premières (Fig. 22) nous disent si l’on est stable (sous la courbe) ou non (au-dessus de la courbe). Les quatre suivantes (Fig. 23) nous donnent l’ordre de grandeur de la pression de confinement nécessaire.
On note que sur ces deux figures, comme cela avait été observé avec la formule de Terzaghi en 2D, on obtient toujours des courbes qui tendent vers une asymptote, qui ici est quasiment atteinte dès T/h = 2. C’est l’effet silo qui typique des sols cohérents-frottant qui se met en place progressivement avec la profondeur et qui écrête les actions à une valeur limite. Si l’on se place au cas le plus défavorable illustré, soit φ = 20°, c/γh = 0, T/h = 3, on a ≪ seulement » s/γh = 0,42, soit 76 kPa si γh = 180 kPa.
 |
Fig. 22 Terrain cohérent frottant – cohésion relative nécessaire pour avoir un front stable. Cohesive-frictional soil – minimal relative cohesion to avoid face collapse. |
 |
Fig. 23 Terrain cohérent frottant – pression de confinement relative nécessaire pour avoir un front stable. Cohesive-frictional soil – minimal relative confinement pressure to avoid face collapse. |
5.1.2 Terrains purement cohérents – méthode Trappe & Dièdre
Dans la figure 24, on présente la pression de confinement nécessaire à l’axe pour avoir un front stable, pour diverses valeurs de cohésion relative Cu/γh. Le graphe de gauche présente les résultats pour un décousu nul et celui de droite pour un décousu e/h = 1/5. On a fixé la surcharge en surface à q = 0. Ces deux abaques ont une applicabilité moins générale que ceux du chapitre précédent, car ils dépendent de la valeur de γh, la pression de sol en place sur la hauteur du tunnel.
Contrairement aux sols cohérents-frottant, on n’observe aucune asymptote avec l’accroissement de la profondeur, avec des valeurs de pression de confinement nécessaires largement plus élevées (environ 230 kPa pour Cu = 50 kPa et T/h = 3).
Ici, on a alors un critère qui peut être discriminant selon la valeur de pression de confinement pouvant être mise en œuvre en fonction des technologies existantes :
-
< 100 à 150 kPa en méthodes conventionnelles sur la contrainte effective (aucune action sur l’eau) selon la géométrie de la section et le frottement mobilisable entre le coulis et le terrain ;
-
< 300 kPa (contrainte totale) en mode pression d’air en terrain étanche à l’air ;
-
< 600 kPa (contrainte totale) en mode pression de terre avec chambre pleine en terrain de faible perméabilité ;
-
< 1800 kPa (contrainte totale) en mode pression de boue (record à l’heure actuelle) en terrain avec un faible potentiel de colmatage.
Au-delà d’une certaine couverture, pour de faibles valeurs de Cu (< 40 kPa), on observe une accélération de l’augmentation de la pression de confinement nécessaire. On se situe donc dans un domaine qu’il semble préférable d’éviter car s’il y a un problème particulier de stabilité ELU, cela peut se retrouver également du côté des déformations estimées à l’ELS.
 |
Fig. 24 Terrain purement cohérent – pression de confinement relative nécessaire pour avoir un front stable Purely cohesive soil – minimal relative confinement pressure to avoid face collapse. |
5.2 Exemples de fenêtre de pilotage de la pression de confinement
Dans la figure 25, on présente la fenêtre de pilotage pour un tunnelier à pression de boue de 15 m de diamètre dans un terrain cohérent-frottant. On a considéré une situation où le tunnel est sous-fluvial, ce qui explique les pressions de confinement importantes. Pour le blow-out on a utilisé le critère usuel au front de taille uniquement. On rappelle que les pressions de confinement de type ELS ne sont pas prises en compte : celles-ci doivent être intégrées en fonction des avoisinants spécifiques à chaque projet.
Sur cette figure on retrouve bien sûr la tendance remarquée sur les abaques de la section 5.1. En terrain cohérent-frottant, la surpression de confinement en plus de celle nécessaire pour contrer la pression hydrostatique est modeste (< 50 kPa sur cet exemple, même avec une cohésion nulle). Avec c/γh = 0,16, pour φ = 30°, la surpression de confinement nécessaire est nulle, et donc la limite inférieure correspond uniquement à la pression minimale à appliquer pour contrer la pression hydrostatique.
Bien qu’on observe qu’il soit possible de piloter le tunnelier pour une couverture relative entre 0,6 et 1, il est fortement recommandé d’attirer son attention sur ce type de situation car il existe de nombreux cas de blow-out. De manière générale, il vaut mieux prévoir en phase conception d’avoir au moins une couverture relative de 1.
Dans la figure 26, on présente la fenêtre de pilotage pour un tunnelier à pression de terre de 10 m de diamètre dans un terrain purement cohérent. Pour le blow-out et l’ELS, on reconduit les remarques associées à la figure précédente. Aucun minimum associé à la présence d’une nappe n’a été introduite, ceci est à étudier en fonction du contexte hydrogéologique et ne peut pas faire partie d’une approche calculatoire ≪ systématique » (cf. Sect. 1.2 pour la démarche réglementaire).
Sur cette figure on a un graphe très proche de l’abaque de gauche de la figure 24 car on a la même valeur de γh (180 kPa), où l’ensemble des aspects associés au pilotage ont été introduits. On a ajouté une valeur minimale qui correspond au mode pression de terre avec chambre pleine. Ce mode est important car c’est le seul qui garantit la maîtrise du confinement en terrain non étanche à l’air, mais aussi celui qui permet d’introduire un confinement actif supplémentaire autour de la jupe du tunnelier, pouvant être essentiel dans le cadre de la maîtrise des tassements.
 |
Fig. 25 Terrain cohérent frottant – fenêtre de pilotage d’un pression de boue de 15 m de diamètre. Purely cohesive soil – minimal relative confinement pressure to avoid face collapse. |
 |
Fig. 26 Terrain purement cohérent – pressions de confinement obtenues. Purely cohesive soil – confinement pressure required. |
6 Conclusion et perspectives
Après avoir clarifié la démarche réglementaire à mettre en œuvre pour définir la fenêtre de pilotage d’un tunnel au tunnelier à confinement, nous avons rappelé la pratique usuelle puis proposé plusieurs améliorations notables en vue de rendre plus robuste théoriquement les méthodes analytiques (relation entre la contrainte verticale et horizontale, tunnel explicitement circulaire, répartition quelconque de la pression sur le front, comparaison avec les approches statiquement et cinématiquement admissibles du calcul à la rupture…) et d’élargir leur cadre d’application (cas multicouche quel que soit le niveau de la nappe…). Après quelques réflexions sur le blow-out et le risque de flottaison, nous avons présenté des abaques et deux exemples d’application concrets.
L’approche que nous proposons est directement opérationnelle pour une application en phase de conception ou d’exécution, et sécurise réglementairement la démarche de l’ingénieur, tout en lui permettant de faire soit une analyse globale via les formules simplifiée (une seule couche), soit une analyse détaillée grâce à la formulation multicouche, souvent recherchée en phase d’exécution.
Par ailleurs, nous avons sciemment écarté les phénomènes de couplage hydromécanique, qui ont été étudiés en particulier par Anagnostou et Kovári (1994), Bezuijen et Talmon (2008), Perazzelli et Anagnostou (2014) et Perazzelli et al. (2014). Néanmoins, les forces d’écoulement défavorables significatives n’interviennent qu’à partir du moment où la pression hydrostatique n’est pas contrée complètement dans un sol de perméabilité suffisamment grande. D’une part, ceci a été écarté de notre analyse via l’approche réglementaire que nous avons établie dans la section 1.2 (cf. ELU HYD, quand ce n’est pas pour des raisons d’impact environnemental qu’il faut le proscrire), et, d’autre part, ceci n’est pas souhaitable dans les sols car cela génère des tassements très défavorables. Bien sûr, notre article concerne les sols, rencontrés principalement en site urbain, et non à grande profondeur où égaliser la pression hydrostatique peut être inutile ou inatteignable technologiquement. Dans tous les cas, il est recommandé de suivre l’analyse hydrogéologique du site étudié pour étudier la pertinence de prendre en compte des dispositions complémentaires à celles exposées dans cet article.
Si la stratigraphie rencontrée comporte des terrains qui, au vu de la cadence d’avancement envisagée, ont un comportement purement cohérent pour certains et cohérent-frottant pour d’autres, il peut s’avérer non aisé de savoir quelle expression analytique utiliser. On peut essayer de rechercher un Cu équivalent à c’ et φ’ en fonction de la contrainte initiale (par exemple en égalisant le taux de déconfinement à l’apparition de la plasticité en symétrie sphérique – voir la méthode convergence-confinement) (Panet, 1995), mais il faut faire attention à ce type de passerelle : l’expérience du géotechnicien spécialisé dans les ouvrages souterrains doit impérativement se greffer à la détermination de la fenêtre de pilotage, qui ne peut être de toute façon en aucun cas un calcul automatique sans hauteur de vue.
Concernant le blow-out, nous avons proposé une nouvelle approche basée sur le phénomène de fracturation hydraulique qui appellera certainement des échanges au sein de la communauté : c’est l’objectif premier de ce chapitre. Ce thème mérite des développements complémentaires.
L’avènement du Grand Paris Express avec 200 km de métro dans la géologie parisienne est une occasion unique de confirmer l’expérience acquise depuis 25 ans avec des tunneliers de tout diamètre à pression de boue et à pression de terre, d’exploiter les évolutions technologiques, mais aussi de mettre en œuvre un retour d’expérience à grande échelle qui permettrait d’apprendre et de capitaliser pour l’avenir.
Remerciements
Je remercie l’encadrement technique et managérial d’Arcadis, qui m’a fourni les moyens de progresser sans relâche, en particulier Olivier Givet, Pascal Guedon, Hichem Ouffroukh, Martin Doll, Alain Bernardet, Jacques Robert, Philippe Autuori. Enfin, je remercie Georgios Anagnostou pour ses encouragements afin de publier ce travail.
Annexe 1 . Démonstration mathématique des résultats des sections 2.3.4 et 2.3.5
Dans la section 2.3.4, on a obtenu l’équation différentielle suivante :

On propose ci-dessous la démonstration mathématique du résultat.
En substituant b(z) par son expression (cf. Sect. 2.3.3) :

À l’aide d’un logiciel en ligne de mathématiques formelles1, on obtient la solution implicite suivante :

Avec la condition aux limites en zk−1 :


On note I(zk − 1,z) l’intégrale encore indéterminée dans l’expression de V(z). On a donc :

Pour résoudre cette intégrale, on propose le changement de variable suivant :

On obtient les correspondances suivantes :

Après injection, l’intégrale peut se réécrire de la manière suivante :

On sépare le problème en 3 intégrales distinctes J1, J2 et J3, telles que :

Pour simplifier l’écriture des résultats, on pose :

Par intégrations par parties successives, les 3 intégrales donnent :

Dans la section 2.3.5, on a obtenu l’équation différentielle suivante :

Par le même mode de résolution, avec la condition aux limites V(0) = 0 (la constante d’intégration est alors nulle), et ε un nombre proche de 0 :

On réutilise alors les solutions obtenues plus haut. En faisant tendre ε vers 0 et z vers D :

On obtient ainsi progressivement tous les termes nécessaires à l’évaluation de V(z) en z = D. En effet :

Annexe 2 . Comparaison termes à termes circulaire/carrée
Ce résultat nous permet de vérifier dans quelle mesure la correction de section pour passer d’un calcul sur une section carrée à une section circulaire est-il pertinent. Pour cela, on réécrit les coefficients f1 à f4 obtenus par Anagnostou et Perazzelli (2013) avec une section rectangulaire pour faciliter l’identification.

Alors on a les équivalences suivantes pour chacun des 4 coefficients :

Pour quelques exemples typiques de paramètres de sol et de géométrie de tunnel, les rapports h/b équivalents obtenus sont les suivants (processus par dichotomie) :

Cela signifie que la correction arbitraire n’était pas une approximation rigoureuse car le changement de géométrie induit des effets différents sur l’influence des paramètres du problème :
-
l’effet de la gravité est amoindri (valeur proche de 0,85 pour le rapport h/b équivalent) ;
-
l’effet de la cohésion est augmenté, dans un rapport inverse d’impact supérieur à celui sur la gravité (valeur proche de 1,30 pour le rapport h/b équivalent) ;
-
l’effet de la surcharge sur le dièdre n’a pas d’évolution claire en fonction des cas de figure ;
-
l’effet du gradient de pression de confinement est amoindri dans le même ordre de grandeur que celui de la gravité (valeur proche de 0,85 pour le rapport h/b équivalent).
Annexe 3 . Blow-out par excès de compression ?
On reproduit ci-dessous la démonstration qui permet d’obtenir les expressions aboutissant à des valeurs de blow-out de 5 à 20 fois la contrainte initiale. Ce qui démontre que la rupture par excès de compression n’est pas le phénomène dimensionnant lors de l’excavation d’un tunnel.
Démonstration dans la couverture (2D)
Le blow-out survient si la pression active en souterrain dépasse la résistance du sol et entraîne un soulèvement.
On utilisera donc notre mode de rupture 2D à l’envers.
Pour préparer ce cas de figure, on résout ici en 2D l’équation où le cisaillement est cette fois-ci dirigé vers le bas. De plus, la condition initiale est au niveau du tunnel et pas au niveau du sol : le sens de σv et σv + dσv sont inversés également (cf. Sect. 2.2.1).
En faisant un bilan à l’équilibre des forces verticales sur la tranche :

Avec le critère de Mohr-Coulomb :

Et la relation selon le cercle de Mohr :

Comme σv(z = −T) = ps, une pression verticale appliquée depuis le tunnel, alors :


Finalement, en surface (z = 0) :

Pour une profondeur très importante (T >> B), on a alors une expression toujours négative – il y a donc toujours équilibre :

Si l’on souhaite connaître la pression de soutènement Ps telle que la contrainte verticale en surface est non nulle, alors il faut que la pression de soutènement soit au moins égale à :


Démonstration dans le silo (3D)
En adaptant en 3D l’expression obtenue ci-dessus, on a alors la contrainte suivante comme critère en surface au toit du silo :


Démonstration dans le dièdre
Il s’agit donc de trouver la pression de confinement minimale telle que cette valeur en clef soit atteignable.
Par rapport à la méthode des tranches évoquée dans la section 2.3.2.1, on a le même mécanisme mais avec dTs et dT inversés. On obtient le bilan suivant :

Les expressions de chacun des termes étant les mêmes, par la même stratégie de démonstration, on obtient l’équation différentielle suivante :
Puis, comme l’équation obtenue est de forme identique, avec les mêmes conditions aux limites :


Comme on n’a pas de décousu au tunnelier, on peut poser :

Ce type de phénomène d’ensemble due à une compression excessive du massif à l’avant du tunnelier n’est donc a priori pas à redouter. Ce mode de rupture semble donc être très loin de ce qui a pu être observé sur divers chantiers, comme l’apparition de bulles sous les fleuves lors de l’utilisation de pression de boue ou le claquage du terrain avec un pression de terre.
Annexe 4 . Réflexions sur la surpression de sécurité appliquée au produit de bourrage
Généralement, il est retenu une pression de bourrage supérieure de 100 kPa à la pression de confinement au front.
Pour éviter tout désordre, la pression du produit de bourrage ne doit être en aucun cas inférieure à la pression de confinement autour du bouclier.
On représente la situation pour un tunnelier en mode pression de terre chambre pleine avec bentonite autour de la jupe (Fig. 27).
 |
Fig. 27 Répartition des pressions de fluides de confinement autour du tunnelier. Shape of confinement pressures around TBM. |
Il faut donc que les pressions en voûte soient au moins égales, en tenant compte de la variabilité propre à chaque injection (chambre, bouclier/jupe, bourrage) :

Pour les valeurs indiquées sur la figure 20, un diamètre de 10 m et en supposant une variabilité d’injection de mortier de 30 kPa, on obtient :

On retrouve ainsi la valeur classique de 100 kPa généralement retenue.
Références
- AFTES. 1976. Réflexions sur les méthodes usuelles de calcul du revêtement des souterrains. Tunnels et Ouvrages Souterrains, mars/avril, pp. 139–164. [Google Scholar]
- AFTES. 1980. Réflexions sur les méthodes usuelles de calcul du revêtement des souterrains, mai/juin, pp. 153–187. [Google Scholar]
- AFTES. 1998. Recommandations pour la conception, le dimensionnement et l’exécution des revêtements en voussoirs préfabriqués en béton armé installés à l’arrière d’un tunnelier. Tunnels et Ouvrages Souterrains, mai/juin, pp. 153–187. [Google Scholar]
- AFTES. 2002. Recommandations sur la boue de forage à usage des boucliers à pression de boue. Tunnels et Ouvrages Souterrains, novembre/décembre, pp. 465–467. [Google Scholar]
- AFTES. 2013. Recommandation : Nomenclature simplifiée des tunneliers. Tunnels et Ouvrages Souterrains, mai/juin, pp. 141–161. [Google Scholar]
- Anagnostou G. 2012. The contribution of horizontal arching to tunnel face stability. Geotechnik 35(1): 34–44. [CrossRef] [Google Scholar]
- Anagnostou G, Kovári K. 1994. The face stability of slurry shield-driven tunnels. Tunn Undergr Space Technol 9(2): 165–174. [CrossRef] [Google Scholar]
- Anagnostou G, Kovári K. 1996. Face stability in slurry and EPB shield tunneling. Geotechnical aspects of underground construction in soft ground. Rotterdam: Balkema, pp. 453–458. [Google Scholar]
- Anagnostou G, Perazzelli P. 2013. The stability of a tunnel face with a free span and a non-uniform support. Geotechnik 36(1): 40–50. [CrossRef] [Google Scholar]
- Anagnostou G, Serafeimidis K. 2007. The dimensioning of tunnel face reinforcement. In: Barták J, Hrdina I, Romancov G, Zlámal J, eds. Underground Space – the 4th Dimension of Metropolises. ITA World Tunnel Congress, Prague, pp. 291–296. [Google Scholar]
- Aristaghes P, Autuori P. 2001. Calcul des tunnels au tunnelier. Rev Fr Géotech 97: 31–40 [Google Scholar]
- Atkinson JH, Potts DM. 1977. Stability of a shallow circular tunnel in cohesionless soil. Géotechnique 27(2): 203–215. [CrossRef] [Google Scholar]
- Bezuijen A, Talmon AM. 2008. Processes around a TBM. In: Geotechnical Aspects of Underground Construction in Soft Ground - 6th International Symposium, Shanghai, China. [Google Scholar]
- Broere W. 2001. Tunnel face stability and new CPT applications. PhD thesis, Delft University of Technology. [Google Scholar]
- Broms BB, Bennermark H. 1967. Stability of clay at vertical openings. J Soil Mech Found Div Am Soc Civ Eng 93(SM1): 71–94. [Google Scholar]
- Caquot A, Kerisel J. 1966. Traité de mécanique des sols, 4e édition. Paris : Gauthier-Villars. [Google Scholar]
- Carranza-Torres C. 2004. Computation of factor of Safety for Shallow Tunnels using Caquot’s Lower Bound Solution. Minneapolis: Itasca Consulting Group. [Google Scholar]
- Carranza-Torres C, Reich T, Saftner D. 2013. Stability of shallow circular tunnels in soils using analytical and numerical models. In: Proceedings of the 61st Minnesota Annual Geotechnical Engineering Conference. University of Minnesota, St. Paul Campus. February 22, 2013. [Google Scholar]
- Chambon P, Corté JF. 1989. Stabilité du front de taille d’un tunnel faiblement enterré : modélisation en centrifugeuse. Colloque international Tunnels et Microtunnels en terrain meuble : du chantier à la théorie, Paris, pp. 307–315. [Google Scholar]
- Davis EH, Gunn MJ, Mair RJ, Seneviratne HN. 1980. The stability of shallow tunnels and underground openings in cohesive material. Géotechnique 30(4): 397–416. [CrossRef] [Google Scholar]
- Eurocode 7. 2005. NF EN 1997-1, Calcul géotechnique, Partie 1 : Règles générales. AFNOR. [Google Scholar]
- GEO report No. 249. 2009. Ground control for slurry TBM tunnelling. Hong Kong: Geotechnical Engineering Office, 57 p. [Google Scholar]
- GEO report No. 298. 2014. Ground control for EPB TBM tunnelling. Hong Kong: Geotechnical Engineering Office, 82 p. [Google Scholar]
- Gugliemetti V, Grasso P, Mahtab A, Xu S. 2008. Mechanized tunneling in urban areas. London: Taylor & Francis. [Google Scholar]
- Gunn MJ. 1980. Limit analysis of undrained stability problems using a very small computer. Proc., Symp. on Computer Applications to Geotechnical Problems in Highway Engineering, Cambridge Univ., Cambridge, UK, pp. 5–30. [Google Scholar]
- Handy LH. 1985. The Arch in Soil Arching. J Geotech Eng 111(3): 302–318. [Google Scholar]
- Horn M. 1961. Horizontaler Erddruck auf senkrechte Abschlussflächen von Tunneln. In: Landeskonferenz der ungarischen Tiefbauindustrie (Deutsche Überarbeitung durch STUVA, Düsseldorf). [Google Scholar]
- ITA/AITES/DAUB. 2016. Recommandations for face support pressure Calculations for shield tunnelling in soft ground, p. 64. [Google Scholar]
- Jaeger JC, Cook NGW, Zimmerman RW. 2007. Fundamentals of rock mechanics. 4th edition. Oxford: Blackwell publishing Ltd. [Google Scholar]
- Jaky J. 1944. The coefficient of earth pressure at rest. J Soc Hungarian Arch Eng: 355–358. [Google Scholar]
- Jancsecz S, Steiner W. 1994. Face support for large mix-shield in heterogeneous ground conditions. London: Tunneling, p. 94. [Google Scholar]
- Janssen HA. 1895. Versuche über Getreidedruck. In: Silozellen. Zeitschrift des Vereines Deutscher Ingenieure, p. 1045. [Google Scholar]
- Kimura T, Mair RJ. 1981. Centrifugal testing of model tunnels in soft clay. Proc. Xth Int. Conf. SMFE, Stockholm. Vol. 2. [Google Scholar]
- Leca E. 2007. Settlements induced by tunneling in soft ground. Tunn Undergr Space Technol 22: 119–149. [Google Scholar]
- Leca E, Dormieux L. 1990. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Géotechnique 40(4): 581–606. [CrossRef] [Google Scholar]
- Leca E, Panet M. 1988. Application du calcul à la rupture à la stabilité du front de taille d’un tunnel. Rev Fr Géotech 43: 5–19. [CrossRef] [Google Scholar]
- Maidl B, Herrenknecht M, Maidl U, Wehrmeyer G. 2012. Mechanised Shield Tunnelling. Berlin: Ernst & Sohn, A Wiley Company. [Google Scholar]
- Messerli J, Pimentel E, Anagnostou G. 2010. Experimental study into tunnel face collapse in sand. In: 7th International Conference on Physical Modelling in Geotechnics, Zurich, Switzerland. [Google Scholar]
- Mollon G, Dias D, Soubra A-H. 2010. Face stability analysis of circular tunnels driven by a pressurized shield. J Geotech Geoenviron Eng (ASCE) 136(1): 215–229. [Google Scholar]
- Panet M. 1995. Le calcul des tunnels par la méthode convergence confinement. Paris : Presses de l’ENPC. [Google Scholar]
- Peila D. 1994. A theoretical study of reinforcement influence on the stability of a tunnel face. Geotech Geol Eng 12: 145–168. [CrossRef] [Google Scholar]
- Perazzelli P, Anagnostou G. 2014. A limit equilibrium method for the assessment of the tunnel face stability taking into account seepage forces. World Tunnel Congress 2013, Geneva, pp. 715–722. [Google Scholar]
- Perazzelli P, Anagnostou G. 2017. Analysis Method and Design Charts for Bolt Reinforcement of the Tunnel Face in purely Cohesive Soils. J Geotech Geoenviron Eng 143(9). [Google Scholar]
- Perazzelli P, Leone T, Anagnostou G. 2014. Tunnel face stability under seepage flow conditions. Tunn Undergr Space Technol 43: 459–469. [Google Scholar]
- Piaskowski A, Kowalewski Z. 1965. Application of thixotropic clay suspensions for stability of vertical sides of deep trenches without strutting. Proc. Of 6th Int. Conf. On Soil Mech. And Found. Eng., Montreal, Vol. 111. [Google Scholar]
- Sequeira Nunes Antao AM. 1997. Analyse de la stabilité des ouvrages souterrains par une méthode cinématique régularisée. Thèse, ENPC. [Google Scholar]
- Serafeimidis K, Ramoni M, Anagnostou G. 2007. Analysing the stability of reinforced tunnel faces. Geotechnical engineering in urban environments, XIV European conference on soil mechanics and geotechnical engineering. Madrid: Millpress Science Publishers Rotterdam, Vol. 2, pp. 1079–1084. [Google Scholar]
- Subrin D, Wong H. 2002. Stabilité du front d’un tunnel en milieu frottant : un nouveau mécanisme de rupture 3D. C R Mécanique 330: 513–519. [CrossRef] [Google Scholar]
- Széchy K. 1970. Traité de construction des tunnels. Paris : Dunod. [Google Scholar]
- Terzaghi K. 1951. Mécanique théorique des sols. Paris : Dunod. [Google Scholar]
- Van der Waart van Gulik TG. 2010. Snap through of large shield driven tunnels, Reserved capacity. PhD Thesis, TU Delft. [Google Scholar]
- Vermeer PA, Ruse N, Marcher T. 2002. Tunnel heading stability in drained ground. Felsbau 6: 8–18. [Google Scholar]
- Vu MN, Broere W, Bosch J. 2015. The impact of shallow cover on tunnelling in soft soil. World Tunnel Congress 2015. Dubrovnik. [Google Scholar]
Citation de l’article : Guillaume Champagne de Labriolle. Détermination de la fenêtre de pilotage de la pression de confinement d’un tunnelier fermé dans un sol cohérent-frottant ou purement cohérent. Rev. Fr. Geotech. 2018, 155, 3.
Liste des tableaux
Valeurs du couple définissant le lien entre la contrainte horizontale et verticale.
Values for the coefficient defining the link between horizontal and vertical stress.
Liste des figures
 |
Fig. 1 Définition de la fenêtre autorisée de pilotage – inspiré de (ITA/AITES/DAUB, 2016). Operation range definition – inspired from (ITA/AITES/DAUB, 2016). |
| Dans le texte | |
 |
Fig. 2 Mécanisme de rupture 3D. 3D failure mechanism. |
| Dans le texte | |
 |
Fig. 3 À gauche : Mécanisme en terrain cohérent-frottant. À droite : mécanisme en terrain purement cohérent (Leca, 2007). Left: Face collapse in dry granular soils. Right: Face collapse in cohesive ground soils (Leca, 2007). |
| Dans le texte | |
 |
Fig. 4 Bilan des forces sur une tranche de sol. Forces equilibrium in a ground soil slice. |
| Dans le texte | |
 |
Fig. 5 Cercle de Mohr correspondant à la situation aux surfaces de rupture. Mohr circle at collapse plane. |
| Dans le texte | |
 |
Fig. 6 Largeur de la voûte de décharge – tunnel en fer à cheval. Arching vault – U-shaped tunnel. |
| Dans le texte | |
 |
Fig. 7 Largeur de la voûte de décharge– tunnel circulaire. Arching vault – circular tunnel. |
| Dans le texte | |
 |
Fig. 8 Problème multicouche. Multilayer case. |
| Dans le texte | |
 |
Fig. 9 Définition du décousu. Unsupported span. |
| Dans le texte | |
 |
Fig. 10 Équilibre des forces sur le dièdre. Forces equilibrium on the wedge. |
| Dans le texte | |
 |
Fig. 11 Méthode des tranches (Anagnostou, 2012). Method of slices (Anagnostou, 2012). |
| Dans le texte | |
 |
Fig. 12 Répartition des forces verticales dans le dièdre et dans le silo pour 3 modes de confinement (pression d’air, pression de boue, pression de terre chambre pleine). À gauche : répartition de pression de confinement insuffisante. À droite : répartition de pression de confinement suffisante. Shape of vertical forces in wedge and silo for 3 confinement modes (air, slurry, full EPB). Left: insufficient confinement pressure. Right: sufficient confinement pressure. |
| Dans le texte | |
 |
Fig. 13 Comparaison nouvelle formulation simplifiée (trait plein & marqueur) / (Anagnostou, 2012) avec λ = 1 (trait plein) / Mollon et al. (2010) (pointillés). Comparison between the new simplified solution (full line & dots) / (Anagnostou, 2012) with λ = 1 (full line) / Mollon et al. (2010) (dashed line). |
| Dans le texte | |
 |
Fig. 14 Terrain purement frottant. À gauche : φ = 30°. À droite : φ = 35°. Comparaison nouvelle formulation simplifiée / limites supérieures et inférieures de Atkinson et Potts (1977) / formules de Piaskowski et Kowalewski (1965), Carranza-Torres (2004) et Carranza-Torres et al. (2013). Purely frictional soil ground. Left: φ = 30°. Right: φ = 35°. Comparison between the new simplified solution / upper and lower bound from Atkinson and Potts (1977) / formulas from Piaskowski and Kowalewski (1965), Carranza-Torres (2004) and Carranza-Torres et al. (2013). |
| Dans le texte | |
 |
Fig. 15 Limites supérieures et inférieures du nombre de stabilité (Davis et al., 1980). Upper and Lower bound for Ns (Davis et al., 1980). |
| Dans le texte | |
 |
Fig. 16 Terrain purement cohérent – nombre de stabilité cible obtenus. Purely cohesive soil – targeted Ns. |
| Dans le texte | |
 |
Fig. 17 Terrain purement cohérent – pressions de confinement obtenues. Purely cohesive soil – confinement pressure required. |
| Dans le texte | |
 |
Fig. 18 Pression de consigne maximale à l’axe. Blow-out values. |
| Dans le texte | |
 |
Fig. 19 Blow-out à l’introduction du produit de bourrage. Blow-out at injection of the grouting. |
| Dans le texte | |
 |
Fig. 20 Pression de consigne maximale à l’axe – critère sur le produit de bourrage. Blow-out values – grouting criterion. |
| Dans le texte | |
 |
Fig. 21 Couverture relative minimale pour éviter la flottaison. Minimal relative overburden to avoid bouyancy. |
| Dans le texte | |
 |
Fig. 22 Terrain cohérent frottant – cohésion relative nécessaire pour avoir un front stable. Cohesive-frictional soil – minimal relative cohesion to avoid face collapse. |
| Dans le texte | |
 |
Fig. 23 Terrain cohérent frottant – pression de confinement relative nécessaire pour avoir un front stable. Cohesive-frictional soil – minimal relative confinement pressure to avoid face collapse. |
| Dans le texte | |
 |
Fig. 24 Terrain purement cohérent – pression de confinement relative nécessaire pour avoir un front stable Purely cohesive soil – minimal relative confinement pressure to avoid face collapse. |
| Dans le texte | |
 |
Fig. 25 Terrain cohérent frottant – fenêtre de pilotage d’un pression de boue de 15 m de diamètre. Purely cohesive soil – minimal relative confinement pressure to avoid face collapse. |
| Dans le texte | |
 |
Fig. 26 Terrain purement cohérent – pressions de confinement obtenues. Purely cohesive soil – confinement pressure required. |
| Dans le texte | |
 |
Fig. 27 Répartition des pressions de fluides de confinement autour du tunnelier. Shape of confinement pressures around TBM. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.