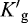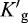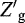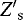| Numéro |
Rev. Fr. Geotech.
Numéro 159, 2019
|
|
|---|---|---|
| Numéro d'article | 4 | |
| Nombre de pages | 20 | |
| DOI | https://doi.org/10.1051/geotech/2019017 | |
| Publié en ligne | 15 janvier 2020 | |
Article de recherche / Research Article
Interprétation des essais de sensibilité des sols compactés à l’imbibition d’après la méthode d’interprétation des essais de gonflement en parallèle
Interpretation of sensivity tests of compacted soils to wetting according to the method of interpretation of multiple specimens swelling tests
Cerema Méditerranée,
30 rue Albert Einstein CS 70499,
13593
Aix-en-Provence, France
★ Auteur de correspondance : jean-francois.serratrice@cerema.fr
Au laboratoire, l’essai de sensibilité est réalisé en visant à mesurer l’amplitude des déformations de gonflement et de tassement provoquées par l’imbibition d’un sol compacté et chargé sous différents niveaux de contraintes totales dans des cellules œdométriques indépendantes. Le sol est compacté par compactage statique. Des indices de sensibilité à l’imbibition servent à décrire la réponse du sol point par point en fonction des charges appliquées. Dans cette étude, une méthode d’analyse globale est proposée pour interpréter les essais de sensibilité portant sur une vingtaine de sols compactés dans différents états. L’interprétation se fonde sur la loi semi-logarithmique de compressibilité des sols qui est mise en œuvre habituellement pour exploiter les essais de gonflement en parallèle. La méthode est présentée sur des exemples de courbes expérimentales, à partir desquelles sont identifiés les principaux paramètres caractéristiques : compressibilités, pression de gonflement, rapport de gonflement. Un regard particulier est porté à la pression de gonflement, définie et attachée à cette procédure d’essai, en comparaison de la contrainte de compactage. Mais il faut faire appel à une contrainte de reprise du compactage pour interpréter les tassements observés pendant le chargement et avant l’imbibition du sol compacté. Cet éclairage offre une base intéressante pour expliquer la variété des réponses observées au cours des essais de sensibilité et poser les limites d’application de cette approche globale et complémentaire de l’approche originale.
Abstract
In the laboratory, the sensitivity test is performed aiming at measuring the amplitude of swelling and settling deformations caused by the imbibition of compacted soil loaded under different levels of total stress in independent œdometric cells. The soil is compacted by static compaction. Wetting sensitivity indices to imbibition are used to describe the soil response point by point depending on the loads applied. In this study, a global method of analysis is proposed to interpret sensitivity tests performed on about twenty soils compacted in different states. The interpretation is based on the semi-logarithmic soil compressibility law that is usually implemented to exploit multiple specimens swelling tests. The method is presented on examples of experimental curves, from which the main characteristic parameters are identified: compressibilities, swelling pressure, swelling ratio. A particular attention is given to the swelling pressure, defined and linked to this test procedure, in comparison with the compaction pressure. However, a yield pressure must be used to interpret the settlements observed during loading and before wetting the compacted soil. This insight provides an interesting basis for explaining the variety of responses observed during sensitivity tests and to set the limits for the application of this comprehensive and complementary approach to the original approach.
Mots clés : sols compactés / gonflement / pression de gonflement / essais œdométriques / sensibilité
Key words: compacted soils / swelling / swelling pressure / œdometer tests / sensivity
© CFMS-CFGI-CFMR-CFG, 2020
1 Introduction
Les variations de teneur en eau engendrent des déformations volumiques dans les sols fins compactés. Très tôt dans l’histoire des recherches consacrées aux sols compactés, des études ont été menées en laboratoire pour caractériser et quantifier ces déformations (Lambe, 1958 ; Ladd, 1960 ; Seed et al., 1962 ; Komornik et David, 1969 ; Nayak et Christensen, 1971 ; Jennings et al., 1973 ; Sridharan et al., 1986 ; Basma, 1993 ; Cerato et al., 2009 ; Rosenbalm, 2013). La plupart des procédures d’essais se fondent sur des essais œdométriques. Pour beaucoup d’entre elles, souvent qualifiées d’essai de gonflement, la sollicitation hydrique consiste en l’imbibition complète du sol dans différentes conditions de chargement. Ces essais montrent que les déformations différées résultent de mécanismes souvent interdépendants de consolidation, gonflement, tassement, effondrement, retrait, fluage, qui héritent du caractère non saturé du sol compacté et des interactions physico-chimiques des particules argileuses avec l’eau. D’un point de vue macroscopique, la sensibilité d’un sol compacté, placé dans un état donné, traduit son aptitude à se déformer plus ou moins en fonction des variations de sa teneur en eau.
Les procédures d’essais de gonflement en parallèle consistent à charger plusieurs éprouvettes œdométriques identiques d’un sol sous des charges indépendantes, puis à comparer les déformations mesurées avant et après imbibition du sol. Ces procédures apparaissent dans les années 1980. Elles s’appliquent aux sols argileux (ISSMFE, 1989) ou aux roches argileuses (ISRM, 1989). Elles sont transcrites sous une forme normalisée avec la méthode A de la norme D4546-08 (ASTM, 2008) ou la norme expérimentale XP P94-091 (AFNOR, 1995), par exemple. Noorany (1992) propose d’appliquer ce type de procédures aux sols compactés. Les essais en parallèle visent ainsi à évaluer l’effet de l’imbibition sur le sol compacté soumis à des contraintes totales constantes, en termes de tassements et de gonflements. La procédure d’essai de sensibilité proposée par Mieussens (1993) reprend ce principe. L’essai porte sur six éprouvettes d’un sol compacté dans un état donné. Les résultats s’expriment sous la forme d’indices de sensibilité qui sont définis en fonction des charges appliquées.
Cette procédure d’essais de sensibilité a été appliquée à des sols différents dans le cadre de projets d’ouvrages en terre et dans le cadre d’études du comportement des sols compactés au laboratoire (Serratrice, 2013). Dans l’article « Les essais de sensibilité appliqués aux sols compactés » (Serratrice et al., 2019), la récapitulation des essais de sensibilité a donné l’occasion de présenter ces résultats expérimentaux, de montrer l’influence de la nature du sol et de son état, de préciser le domaine de variation des indices de sensibilité et les tendances observées. Les éprouvettes sont préparées par compactage statique. Les courbes contrainte-déformation, qui décrivent la densification du sol foisonné, sont enregistrées pendant cette phase préliminaire d’essai (Serratrice, 2018). Les contraintes de compactage sont déduites de ces courbes et servent à l’interprétation des essais de sensibilité.
La présente étude a pour objectif d’appliquer aux essais de sensibilité une méthode d’interprétation globale qui se fonde sur la pratique des essais de gonflement en parallèle, puis de montrer à la fois les limites et l’intérêt de cette approche. La méthode s’appuie sur l’hypothèse classique d’une variation linéaire de la déformation axiale avec le logarithme de la contrainte axiale en condition œdométrique. La loi s’applique dans le domaine pseudo-élastique du sol, qui prend corps après son compactage. Elle se caractérise par une pression de gonflement et un rapport de gonflement, qui sont à identifier sur les courbes d’essai. En se rapportant à la teneur en eau, l’indice des vides et la contrainte axiale totale, la méthode présente l’avantage de mobiliser un nombre réduit de paramètres qu’il est aisé de déterminer avec des essais conventionnels et elle s’inscrit dans une démarche de valorisation de telles pratiques (Islam et Kodikara, 2016 ; Kodikara et al., 2016 ; Li et al., 2016). Les différents aspects de cette proposition sont commentés à partir de l’examen des courbes expérimentales et sont discutés. En complément de l’interprétation des essais de sensibilité, des essais œdométriques issus de la littérature sont exploités dans ce sens. Les caractéristiques déduites des essais sont comparées entre elles et elles sont analysées en lien avec l’état des sols compactés.
2 Approche globale de la sensibilité
2.1 Essais de gonflement en parallèle
Au laboratoire, l’œdomètre se place en outil privilégié pour mesurer les déformations des sols sous l’effet des chargements et des variations de teneur en eau. De nombreuses méthodes d’essais œdométriques ont vu le jour. Quelques procédures sont normalisées. Pour beaucoup, souvent qualifiées d’essai de gonflement, la sollicitation hydrique consiste en l’imbibition complète du sol dans différentes conditions de chargement. Ces méthodes ont fait l’objet d’études comparatives de leurs performances (Brackley, 1973 ; Sridharan et al., 1986 ; Schreiner et Burland, 1991 ; Basma et al., 1995 ; Serratrice et Soyez, 1996 ; Feng et al., 1998 ; Attom et Barakat, 2000 ; Fityus et al., 2005 ; Thompson et al., 2006 ; Sun et al., 2007 ; Nagaraj et al., 2009 ; Soundara et Robinson, 2009 ; Kayabali et Demir, 2011 ; Singhal et al., 2011 ; Abbaszadeh et al., 2016). Une des conclusions souvent rapportée fait état de la dépendance des pressions de gonflement avec les procédures d’essai.
La méthode du double œdomètre sert à tester les sols gonflants, c’est-à-dire les sols dont les particules argileuses réagissent avec l’eau en produisant une augmentation de volume du sol (Jennings et Knight, 1957 ; Kayabali et Demir, 2011). Elle sert aussi à caractériser les sols effondrables, c’est-à-dire les sols non saturés qui possèdent une structure ouverte métastable (Dudley, 1970 ; Barden et al., 1973 ; Lutenegger et Saber, 1988 ; Lawton et al., 1989, 1992 ; Sun et al., 2007 ; Leong et al., 2013 ; Li et al., 2016). L’essai porte sur une paire d’éprouvettes identiques et soumises à des paliers de chargements successifs afin de comparer les réponses du sol, une éprouvette étant maintenue dans son état naturel, l’autre étant préalablement soumise à une phase de gonflement libre sous imbibition. La comparaison porte ainsi sur les déformations enregistrées pendant deux chemins de chargement mécaniques et hydriques différents. Une pratique différente consiste à charger plusieurs éprouvettes identiques sous des contraintes différentes et indépendantes, avant de soumettre ces éprouvettes à l’imbibition et comparer les déformations aux différents stades de l’essai, comme l’a proposé Noorany (1992). La méthode relève du principe des essais de gonflement en parallèle consacrés aux sols naturels (ISSMFE, 1989 ; ISRM, 1989 ; AFNOR, 1995 ; ASTM, 2008). La procédure des essais de sensibilité proposée par Mieussens (1993) reprend ce principe et vise à évaluer l’effet de l’imbibition sur un sol compacté soumis à des charges constantes.
2.2 Essai de sensibilité
L’essai de sensibilité sert à mesurer l’amplitude des déformations de gonflement et de tassement provoquées par l’imbibition d’un sol compacté et chargé sous différents niveaux de contraintes totales dans des cellules œdométriques indépendantes. L’essai se veut simple et rapide. Le sol est compacté dans un état donné, en référence à l’optimum Proctor normal, par exemple. Six éprouvettes œdométriques identiques sont chargées sous des contraintes axiales totales σa distribuées en série géométrique de raison deux, ente 25 et 800 kPa, puis elles sont mises en imbibition. Les déformations axiales εa des six éprouvettes sont enregistrées pendant ces différentes étapes.
Les schémas de la figure 1 donnent une image simplifiée du chargement subi par le sol compacté au cours d’un essai de sensibilité portant sur quatre éprouvettes. Les réponses sont représentées dans le plan (log(σa), εa) en échelles semi-logarithmiques. Les éprouvettes sont préparées par compactage statique, qui est schématisé par la courbe en pointillés. La contrainte de compactage du sol σacmp est la pression maximale atteinte au cours du processus de densification du sol. Après déchargement, le sol compacté se trouve dans son état initial avec un indice des vides initial e0 sous la contrainte unité σa0 = 1 kPa (rond). Puis, les éprouvettes sont chargées sous les contraintes axiales comprises entre σamin et σamax et elles trouvent leur équilibre aux points 1, 2, 3 et 4 indiqués par des carrés. L’imbibition sous ces charges produit des déformations de gonflement ou de tassement (flèches verticales) avant d’aboutir aux points d’équilibre représentés par des triangles. Sous chacune des charges σa(i), les déformations sont pointées sur les courbes d’essai avant imbibition εaavi(i) et après imbibition εaapi(i), pour obtenir l’écart Δϵa(i) = ϵaapi(i) − ϵaavi(i). Les indices de sensibilité sont obtenus à partir de ces mesures.
Des indices sont identifiés sur les courbes d’essai (εa, log(σa)) et servent à caractériser la sensibilité du sol (Mieussens, 1993 ; Serratrice et al., 2019). Les indices C1 et C2 représentent les coefficients de compressibilité du sol avant et après imbibition dans chacun des intervalles de la série des contraintes axiales appliquées, comme indiqué dans la figure 1a. L’indice de sensibilité Csg exprime le rôle combiné de la déformabilité du sol et de l’effet de l’eau (Csg = [C2/C1] Δϵa). Il est négatif pour les gonflements. Ces paramètres sont fonction de la contrainte verticale σa et ne sont définis que pour une valeur donnée de cette charge. Une pression de gonflement σag peut être identifiée comme la pression sous laquelle l’imbibition ne provoque pas de déformation axiale. La série des charges appliquées doit encadrer la pression de gonflement si possible.
 |
Fig. 1 Paramètres issus d’un essai de sensibilité exprimé en déformation axiale. États d’équilibre de quatre éprouvettes avant et après imbibition. a : interprétation en indices de sensibilité C1, C2 et Δεa (Mieussens, 1993 ; Serratrice et al., 2019) ; b : approche globale sous la forme d’une loi semi-logarithmique. Parameters derived from a sensitivity test expressed in axial strain. Equilibrium states of four specimens before and after wetting. a: sensibility indexes; b: semi-logatithmic law. |
2.3 Approche globale de la sensibilité
L’approche globale proposée vise à caractériser la réponse d’un sol compacté, mesurée pendant un essai de sensibilité, par un paramètre global indépendant du niveau de chargement statique. À l’image de l’exploitation des essais de gonflement en parallèle, cette approche fait appel à la loi de compressibilité semi-logarithmique des sols pour décrire les courbes contrainte-déformation mesurées avant et après imbibition. Une illustration de cette hypothèse de la linéarité des réponses mesurées avant et après imbibition dans le plan (log(σa), εa) est indiquée sur le schéma de la figure 1b. Les déformations axiales εa mesurées avant imbibition sont caractérisées par l’expression suivante (la notation « avi » signifie avant imbibition) :
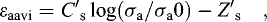 (1)
où σa la contrainte axiale totale,
(1)
où σa la contrainte axiale totale, 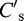 le coefficient de gonflement pseudo-élastique, σa0 la contrainte unité et
le coefficient de gonflement pseudo-élastique, σa0 la contrainte unité et 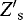 la déformation associée. Après imbibition, la déformation est donnée par l’expression (la notation « api » signifie après imbibition) :
la déformation associée. Après imbibition, la déformation est donnée par l’expression (la notation « api » signifie après imbibition) :
 (2)avec des notations semblables et
(2)avec des notations semblables et 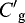 le coefficient de gonflement sous imbibition. La déformation due à l’imbibition s’obtient alors par différence :
le coefficient de gonflement sous imbibition. La déformation due à l’imbibition s’obtient alors par différence :
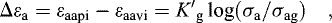 (3)où
(3)où 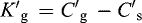 représente le rapport des déformations dues à l’imbibition et σag la pression de gonflement qui vaut
représente le rapport des déformations dues à l’imbibition et σag la pression de gonflement qui vaut  . Cette pression de gonflement correspond à une déformation nulle après la mise en imbibition du sol (Δεa = 0). Comme les pressions définies dans d’autres procédures, sa valeur reste attachée à la procédure d’essai mise en œuvre ici. Les notations C′ et K′ sont utilisées car elles expriment les variations de volume du sol au moyen des déformations axiales. Quand ces variations de volumes sont exprimées en indice des vides, les coefficients de compressibilité sont notés Cs (ou Cc) et
. Cette pression de gonflement correspond à une déformation nulle après la mise en imbibition du sol (Δεa = 0). Comme les pressions définies dans d’autres procédures, sa valeur reste attachée à la procédure d’essai mise en œuvre ici. Les notations C′ et K′ sont utilisées car elles expriment les variations de volume du sol au moyen des déformations axiales. Quand ces variations de volumes sont exprimées en indice des vides, les coefficients de compressibilité sont notés Cs (ou Cc) et  , où e0 est l’indice des vides initial du sol compacté. Le coefficient
, où e0 est l’indice des vides initial du sol compacté. Le coefficient 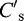 s’apparente à C1 mais il s’applique sur l’intervalle de plusieurs charges axiales. De même
s’apparente à C1 mais il s’applique sur l’intervalle de plusieurs charges axiales. De même  vis-à-vis de C2. Dans la norme XP P94-091 (AFNOR, 1995), la pression de gonflement σag est notée σg et le rapport
vis-à-vis de C2. Dans la norme XP P94-091 (AFNOR, 1995), la pression de gonflement σag est notée σg et le rapport 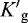 est noté Rg.
est noté Rg.
La qualité des paramètres 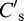 ,
, 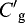 ,
,  et σag dépend de l’étendue de l’intervalle des charges axiales où la linéarité des relations (1) et (2) est avérée. Cet intervalle doit contenir la pression de gonflement σag si possible. L’identification de cette pression est explicite dans la plupart des essais d’après (3). Mais des difficultés se rencontrent dans les sols peu déformables et les sols non sensibles, pour lesquels l’écart est faible entre les déformations mesurées avant et après imbibition. La suite de l’étude est consacrée à l’identification des paramètres de gonflement-tassement de la loi de compressibilité semi-logarithmique d’après les courbes expérimentales recueillies au cours de quarante-cinq essais de sensibilité. Quelques essais œdométriques supplémentaires issus de la littérature sont exploités ensuite.
et σag dépend de l’étendue de l’intervalle des charges axiales où la linéarité des relations (1) et (2) est avérée. Cet intervalle doit contenir la pression de gonflement σag si possible. L’identification de cette pression est explicite dans la plupart des essais d’après (3). Mais des difficultés se rencontrent dans les sols peu déformables et les sols non sensibles, pour lesquels l’écart est faible entre les déformations mesurées avant et après imbibition. La suite de l’étude est consacrée à l’identification des paramètres de gonflement-tassement de la loi de compressibilité semi-logarithmique d’après les courbes expérimentales recueillies au cours de quarante-cinq essais de sensibilité. Quelques essais œdométriques supplémentaires issus de la littérature sont exploités ensuite.
3 Données expérimentales
3.1 Origine et nature des sols
Les données expérimentales examinées ici ont été recueillies dans le cadre de projets d’ouvrages en terre et dans le cadre de programmes consacrés à l’étude du comportement des sols compactés en laboratoire (Serratrice, 1995a, 1995b, 2013). Ces essais de sensibilité ont fait l’objet d’une première interprétation d’après la procédure originale sous la forme d’indices de sensibilité (Serratrice et al., 2019). Deux autres sources de données produites à l’aide de procédures œdométriques différentes ont été recueillies dans la littérature et exploitées à titre d’illustration (Ferber, 2005 ; Rosenbalm, 2013).
Le tableau 1 indique l’origine et la nature des vingt-trois sols testés au moyen de la procédure d’essai de sensibilité, puis le numéro d’essai de 1 à 45. Quelques essais sont définis dans un plan d’expérience en plusieurs points d’état. Les sites 15 et 16 ont fait l’objet d’un plan d’expérience plus étendu (argile de Bavent, limon de Goderville). Les sols testés sont essentiellement des sols fins déstructurés. Le tableau 2 indique les propriétés physiques des sols (wL et wP limites de consistance, Ip indice de plasticité, C2 teneur en particules de diamètres inférieurs à 2 μm, VB valeur au bleu de méthylène) et les caractéristiques de l’optimum Proctor normal (wOPN, ρdOPN). Quatre essais de sensibilité sont effectués sur des blocs extraits d’un remblai expérimental (site 15, argile de Bavent, essais no 29 à 32). Les sols sont représentés en majorité par les limons ou des argiles et des marnes peu plastiques. Ces terrains forment un ensemble de sols peu à moyennement actifs qui se classent en A1 et A2 d’après la classification GTR (LCPC-SETRA, 2000). Quelques sols se singularisent au contraire, qui proviennent des sites 7 (marne altérée de Calas), 15 (argile de Bavent) ou 17 (essais 42 à 45), et entrent dans les classes A2 ou A3.
Dans la suite, les caractéristiques d’état du sol sont définies par la teneur w en eau et la masse volumique sèche ρd ou l’indice des vides e, avec e = ρs/ρd − 1 et ρs la masse volumique des particules solides. Le degré de saturation du sol est Sr = (w ρs)/(e ρw) et la densité des particules solides est Gs = ρs/ρw, avec ρw la masse volumique de l’eau.
3.2 Réalisation des essais
L’exécution d’un essai de sensibilité se déroule en plusieurs étapes : préparation du sol, compactage statique des six éprouvettes, chargement, imbibition (Mieussens, 1993). Les détails pratiques de la réalisation des quarante-cinq essais de sensibilité sont donnés par Serratrice et al. (2019). En résumé, les sols sont déstructurés et écrêtés pour certains. Puis, ils sont portés à leur teneur en eau visée w0 = wvisée par humidification sans malaxage et conservés ainsi 24 heures au moins. Les six éprouvettes sont compactées dans leur cellule œdométrique pour atteindre la masse volumique sèche visée ρdvisée. Les éprouvettes compactées possèdent alors un diamètre d0 = 70 mm et une hauteur h0 = 24 mm. Le chemin de compactage s’effectue à la teneur en eau constante wvisée dans le plan d’état (w, e) avant d’aboutir à un état proche de la saturation. L’indice des vides minimal qu’il est possible d’atteindre à teneur en eau constante est 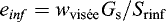 où le degré de saturation Srinf est proche de l’unité (Serratrice, 2018). Une compacité plus forte ne peut être obtenue (evisé < einf) avec la poursuite de la densification que si le drainage concomitant d’un volume d’eau est possible alors (w0 < wvisée).
où le degré de saturation Srinf est proche de l’unité (Serratrice, 2018). Une compacité plus forte ne peut être obtenue (evisé < einf) avec la poursuite de la densification que si le drainage concomitant d’un volume d’eau est possible alors (w0 < wvisée).
Les chargements des éprouvettes compactées s’effectuent sur six bâtis indépendants. Les contraintes axiales totales sont distribuées en série géométrique de 30 kPa jusqu’à la contrainte maximale σamax. Les contraintes σa = 30, 56, 107, 209, 412 et 820 kPa ont été appliquées pendant les essais no 1 à 41 et les contraintes σa = 30, 56, 132, 260, 580 et 1220 kPa pendant les suivants. Ces charges sont maintenues durant trois jours, puis, sauf exception pour les sols compactés gonflants, quatre jours supplémentaires après imbibition. Les déformations axiales sont enregistrées (positives pour les tassements, εa > 0 ; négatives pour les gonflements, εa < 0). Puis les éprouvettes sont démontées, pesées et séchées, ce qui permet d’obtenir les caractéristiques d’état du sol à l’issue de toutes les phases d’essai. Le tableau 3 indique les caractéristiques d’état des sols après compactage, avec w0 la teneur en eau, e0 l’indice des vides et Sr0 le degré de saturation à ce stade. Il rassemble aussi les paramètres de compactage et de gonflement définis précédemment et les paramètres ee et Es qui seront définis au paragraphe 3.1.
3.3 Courbes de compression statique
La figure 2 montre les courbes enregistrées pendant un essai de sensibilité consacré à une marne (essai no 21). L’indice des vides est représenté en fonction de la contrainte axiale totale en échelles semi-logarithmiques pendant les trois étapes principales de l’essai : compactage statique, chargement, imbibition. Dans ce plan (log(σa), e), les courbes de compression statique des six éprouvettes sont représentées par des croix. Une partie de la courbe est représentée schématiquement dans la figure 1 (courbe en pointillés). L’enregistrement de ces courbes permet de relier le compactage du sol, en particulier la contrainte de compactage σacmp, aux propriétés mécaniques qui seront mesurées ensuite sur le sol compacté, telles que la pression de gonflement (voir plus bas). Cette courbe est associée au chemin suivi dans le plan d’état (w, e) (Serratrice, 2018). En principe, il s’agit d’un chemin à teneur en eau constante w = wvisée, sauf si le compactage statique a provoqué un drainage du sol. Ici, la moyenne des contraintes de compactage des six éprouvettes est σacmp = 1983 kPa. Elle est supérieure à la contrainte maximale appliquée σamax = 820 kPa. Le chargement à l’étape suivante amène le sol dans les états représentés par des carrés. Cette courbe de rechargement coïncide jusqu’à σamax avec les courbes de déchargement du sol de l’étape de compactage. À l’étape 3, des gonflements se produisent sous les contraintes inférieures à 412 kPa et un tassement sous σamax.
Le graphique (log(σa), e) montre que le compactage, considéré comme histoire récente du sol compacté, confère à ce dernier un statut surconsolidé à basse pression, dans un domaine pseudo-élastique où s’applique la loi de compressibilité semi-logarithmique représentée par un coefficient de gonflement de la forme Cs = de/dlog(σa) et défini en contraintes totales.
 |
Fig. 2 Exemple de courbes de compression statique et de courbes de sensibilité. Marne, essai no 21. Example of compaction curves and sensitivity curves. Marl, test no. 21. |
3.4 Courbes d’essai
L’exploitation de l’essai commence par le report des déformations mesurées avant et après imbibition en fonction des contraintes axiales totales dans un plan (εa, σa) en échelles arithmétiques. La figure 3 montre l’exemple de trois essais réalisés sur des sols compactés différents (essais no 1, argile ; no 6, limon ; no 19, limon argileux). Bien qu’ils soient indépendants, les points ont été reliés entre eux pour faciliter la lecture des graphiques. Les déformations εaavi(i) enregistrées avant imbibition sont représentées par des figurés creux. Les déformations εaapi(i) enregistrées après imbibition sont représentées par des figurés pleins.
Globalement et comme attendu, les courbes présentent une allure exponentielle. Elles donnent un aperçu des compressibilités généralement observées dans les sols compactés, ici avant et après imbibition, pour chacun des essais de sensibilité. Mais des écarts apparaissent. Les premiers sont d’ordre expérimental et tiennent des erreurs systématiques qui affectent la mesure du zéro initial de la déformation axiale ne sont pas compensées d’une éprouvette à l’autre (Serratrice et al., 2019). L’interprétation globale des essais en parallèle permet d’amoindrir l’effet de ces erreurs, en portant sur un domaine plus étendu des charges axiales que l’intervalle situé entre deux charges consécutives.
D’autres écarts vis-à-vis d’une réponse de forme exponentielle sont de nature comportementale. Les essais de sensibilité ont pour intérêt de pointer ces écarts. En guise de référence, la réponse du limon d’Orly dans la figure 3 (site 3, essai no 6 ; carrés) montre deux courbes (εa, σa), avant et après imbibition, de forme exponentielle et superposées. Le limon compacté est insensible à l’imbibition, contrairement aux deux autres sols qui figurent sur le graphique. La réponse du limon argileux (site 11, essai no 19 ; pentagones) montre un fort gonflement sous les charges inférieures à 200 kPa, qui va jusqu’à −2,5 % sous 30 kPa. Le limon argileux est très fortement compacté sous une pression de 6,2 MPa qui lui confère un faible indice des vides initial e0 = 0,29, bien inférieur à l’indice des vides à l’optimum Proctor normal (eOPN = 0,38). En présence d’eau, il gonfle sous toutes les charges appliquées.
La réponse de l’argile du PK189 faiblement compactée (site 1, essai no 3 ; losanges) dans la figure 3 montre une réponse de forme exponentielle sous les faibles charges, avec un très léger gonflement. Mais, de forts tassements s’observent dès le chargement sous les charges de 412 et 820 kPa et avant imbibition. Puis, les tassements dus à l’imbibition, qui se dessinent vers 200 kPa, s’estompent ensuite sous les fortes charges. Les six éprouvettes ont été compactées en moyenne sous une contrainte σacmp = 649 kPa avec un degré de saturation Sr = 54 %. Un sol argileux dans un tel état faiblement compacté devrait montrer des déformations d’effondrement sous l’effet de l’imbibition. Mais ici, l’argile s’avère sous-compactée par rapport à la contrainte maximale appliquée σamax = 820 kPa, voire la contrainte de 412 kPa. En dépassant la contrainte de préconsolidation du sol apportée par le compactage, qui peut être estimée autour de 250 kPa, ces charges entraînent une densification supplémentaire du sol dès leur mise en place, sous la forme de déformations irréversibles. Ces tassements seront qualifiés de reprise du compactage dans la suite. Puis l’imbibition ne produit que des tassements mineurs additionnels pendant la seconde phase d’essai.
Les courbes de la figure 3 sont reproduites en échelles semi-logarithmiques dans la figure 4 dans le plan (log(σa), εa) (essais no 1, argile ; no 6, limon ; no 19, limon argileux). Sauf dans de rares exceptions qui concernent des sols fortement densifiés, la réponse des sols compactés montre à la fois des déformations de gonflement et des déformations de tassement de part et d’autre de la pression de gonflement. Mais la linéarité des courbes ne s’observent parfois que dans un intervalle limité des basses pressions. Cela concerne les sols peu compactés. Il convient alors d’abandonner les mesures obtenues pendant le chargement sous les charges les plus grandes, qui révèlent une reprise du compactage au-delà de la contrainte axiale totale qui sera notée σarcmp. Tel est le cas de l’argile (essai no 1, losanges) dans la figure 4, qui montre une reprise de compactage à partir de la contrainte σarcmp = 209 kPa, et du limon argileux à partir de la contrainte σarcmp = 413 kPa. De même, la linéarité n’est obtenue que dans un domaine limité des basses pressions après imbibition. La contrainte de reprise du compactage σarcmp borne par valeur supérieure le domaine de validité de la loi semi-logarithmique appliquée aux essais de sensibilité. Les charges axiales plus grandes sortent du domaine pseudo-élastique du sol compacté.
Les droites de pentes 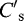 et
et  sont alors à identifier sur les courbes expérimentales, comme indiqué par les segments représentés dans la figure 4 (Éq. (1) et (2)). La pression σag et la pente
sont alors à identifier sur les courbes expérimentales, comme indiqué par les segments représentés dans la figure 4 (Éq. (1) et (2)). La pression σag et la pente 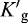 s’obtiennent par le calcul de l’intersection des deux droites, d’après (3). Les paramètres σag,
s’obtiennent par le calcul de l’intersection des deux droites, d’après (3). Les paramètres σag, 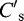 ,
, 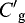 et
et  ainsi identifiés sont reportés dans le tableau 3. L’estimation de ces paramètres n’est pas possible dans les sols compactés non sensibles, tels que le limon indiqué dans la figure 4 (essai 6, carrés). Dans ce cas,
ainsi identifiés sont reportés dans le tableau 3. L’estimation de ces paramètres n’est pas possible dans les sols compactés non sensibles, tels que le limon indiqué dans la figure 4 (essai 6, carrés). Dans ce cas, 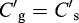 ,
, 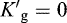 et la pression de gonflement est indéfinie. Une pression peut être fixée à σag = 30 kPa forfaitairement, pour tenir compte des petits gonflements souvent observés sous la charge minimale σamin appliquée. Les variations de ces paramètres seront examinées plus bas, après avoir exploité quelques essais issus de la littérature.
et la pression de gonflement est indéfinie. Une pression peut être fixée à σag = 30 kPa forfaitairement, pour tenir compte des petits gonflements souvent observés sous la charge minimale σamin appliquée. Les variations de ces paramètres seront examinées plus bas, après avoir exploité quelques essais issus de la littérature.
Les courbes (log(σa), εa) de la figure 5 montrent les réponses enregistrées sur l’argile de Bavent à partir de deux états différents (essais no 27, w = 15,5 %, e = 0,60, Sr = 71 %, losanges ; essai no 28, w = 14,8 %, e = 0,71, Sr = 58 %, pentagones). Les droites de pentes 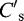 sont quasi confondues. Les contraintes de reprise de compactage, contraintes à partir desquelles la courbe de chargement s’écarte de la droite de pente
sont quasi confondues. Les contraintes de reprise de compactage, contraintes à partir desquelles la courbe de chargement s’écarte de la droite de pente 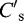 , sont respectivement égales à σarcmp = 413 et 209 kPa. Les droites de pente
, sont respectivement égales à σarcmp = 413 et 209 kPa. Les droites de pente 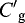 sont presque parallèles, mais décalées, ce qui aboutit à des pressions de gonflement σag = 229 et 79 kPa et des rapports
sont presque parallèles, mais décalées, ce qui aboutit à des pressions de gonflement σag = 229 et 79 kPa et des rapports  = 0,057 et 0,070 (Tab. 3). Le choix des droites de pentes
= 0,057 et 0,070 (Tab. 3). Le choix des droites de pentes 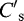 et
et  porte bien sur des portions linéaires des courbes (log(σa), εa) qui encadrent les pressions de gonflement. Tous ces paramètres sont en lien avec les contraintes de compactage, qui sont égales à σacmp = 1281 et 837 kPa. Avec des rapports σarcmp/σag = 1,8 et 2,6, il est clair que le compactage confère à l’argile une préconsolidation éphémère et largement mise à mal par l’imbibition sous les hautes pressions, qui produisent un effondrement de l’argile. Mais, à partir de σarcmp, ces tassements sont en partie réalisés dès le chargement. Il faut noter aussi les forts gonflements observés à basse pression, qui sont en lien avec l’état du sol, pour cette argile faiblement compactée.
porte bien sur des portions linéaires des courbes (log(σa), εa) qui encadrent les pressions de gonflement. Tous ces paramètres sont en lien avec les contraintes de compactage, qui sont égales à σacmp = 1281 et 837 kPa. Avec des rapports σarcmp/σag = 1,8 et 2,6, il est clair que le compactage confère à l’argile une préconsolidation éphémère et largement mise à mal par l’imbibition sous les hautes pressions, qui produisent un effondrement de l’argile. Mais, à partir de σarcmp, ces tassements sont en partie réalisés dès le chargement. Il faut noter aussi les forts gonflements observés à basse pression, qui sont en lien avec l’état du sol, pour cette argile faiblement compactée.
 |
Fig. 3 Exemples de courbes de sensibilité fournies par des sols compactés de natures différentes. Échelles linéaires. Examples of sensitivity curves given by different compacted soils. Linear scales. |
 |
Fig. 4 Exemples de courbes de sensibilité fournies par des sols compactés de natures différentes. Échelles semi-logarithmiques. Examples of sensitivity curves given by different compacted soils. Semi-logaritmic scales. |
 |
Fig. 5 Exemples de courbes de sensibilité fournies par deux essais consacrés à l’argile de Bavent. Échelles semi-logarithmiques. Examples of sensitivity curves given by two tests on Bavent clay. Semi-logaritmic scales. |
3.5 Exemple de quatre argiles
Les essais portent sur quatre argiles compactées étudiées à l’université d’Arizona (Rosenbalm, 2013). Les mesures de leurs propriétés physiques sont accompagnées par un essai Proctor normal. Ces caractéristiques sont indiquées dans le tableau 4. Ces argiles sont peu plastiques à très plastiques. Elles se classent en A2, A3 et A4 d’après la classification GTR (LCPC-SETRA, 2000). Les essais œdométriques sont réalisés selon la méthode A de la norme D4546-08 (ASTM, 2008). Les éprouvettes sont compactées à la dame dans un moule spécial, puis elles sont portées dans la bague œdométrique. La consigne de compactage est définie par rapport à l’optimum Proctor normal (wvisée = wOPN, ρdvisée = 0, 95 ρdOPN). Les contraintes axiales appliquées sont faibles, comprises entre σamin = 1 kPa et σamax = 140 ou 240 ou 380 kPa, et elles sont distribuées en sept ou huit points. Plusieurs éprouvettes sont testées en chaque point (1, 2 ou 3). L’auteur formule quelques propositions pour assurer une meilleure efficacité de la procédure (mettre en œuvre six éprouvettes par exemple, contre quatre au minimum d’après la norme). Il discute la validité de la loi semi-logarithmique pour interpréter les essais. L’exploitation de chacun des quatre essais commence par le calcul de l’état initial du sol compacté. Les propriétés ρs, wOPN et ρdOPN donnent cet état initial (wavi, ρdavi) et son indice des vides eavi avant imbibition. La courbe Proctor normal donne la pente dρd/dw de sa branche côté sec.
Le résultat de l’essai consacré à l’argile compactée du Colorado est représenté dans la figure 6, où la variation de la déformation axiale Δεa due à l’imbibition est donnée en fonction de la contrainte axiale en échelles semi-logarithmique (losanges). L’exploitation des courbes (log(σa), Δεa) constitue une variante par rapport à la démarche utilisée plus haut, qui préconise d’identifier les droites de pentes 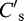 et
et  et apprécier ainsi les compressibilités du sol avant et après imbibition, puis d’évaluer la pression de gonflement σag et le rapport
et apprécier ainsi les compressibilités du sol avant et après imbibition, puis d’évaluer la pression de gonflement σag et le rapport  d’après la relation (3). Les données disponibles dans ces quatre exemples ne permettent pas d’évaluer les compressibilités
d’après la relation (3). Les données disponibles dans ces quatre exemples ne permettent pas d’évaluer les compressibilités  et
et  ni d’estimer la contrainte σarcmp de reprise du compactage. Par contre, elles aboutissent à identifier directement σag et
ni d’estimer la contrainte σarcmp de reprise du compactage. Par contre, elles aboutissent à identifier directement σag et 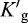 . Ces deux paramètres sont indiqués dans la figure 6 et sont reportés dans le tableau 5. À très basse pression, l’écart observé entre les mesures des gonflements et la loi logarithmique ne sont pas pris en compte ici. Ils s’expliquent en partie par des effets tridimensionnels du gonflement œdométrique (Serratrice, 2007).
. Ces deux paramètres sont indiqués dans la figure 6 et sont reportés dans le tableau 5. À très basse pression, l’écart observé entre les mesures des gonflements et la loi logarithmique ne sont pas pris en compte ici. Ils s’expliquent en partie par des effets tridimensionnels du gonflement œdométrique (Serratrice, 2007).
Propriétés physiques des argiles de l’exemple.
Physical properties of the clay in the example.
 |
Fig. 6 Essai de gonflement en parallèle. Argile compactée du Colorado. D’après Rosenbalm (2013). Multiple-specimens swelling test. Compacted clay from Colorado. |
3.6 Données du LCPC
Des programmes expérimentaux ont été réalisés au Laboratoire Central des Ponts et Chaussées (LCPC) dans le cadre des études du comportement des remblais routiers et ferroviaires. Plusieurs sols compactés ont été testés au moyen de différents types d’essais œdométriques (Ferber, 2005 ; Ferber et al., 2008). Parmi ces données, figurent les résultats recueillis sur une argile verte très plastique et sur le limon de Goderville. Ces données sont mises à profit pour illustrer l’utilisation de la méthode d’exploitation des essais de gonflement en parallèle appliquée aux essais de sensibilité. Les propriétés physiques de l’argile verte sont indiquées dans le tableau 6 (Berche et al., 2009). Celles du limon de Goderville ont été données dans le tableau 2 et sont reproduites ici. Les sols se classent en A2 et A4 d’après la classification GTR (LCPC-SETRA, 2000).
Différents types d’essais œdométriques ont été effectués. Parmi les essais réalisés figurent des essais de gonflement libre, où le sol compacté est mis en imbibition dans un œdomètre sous une contrainte axiale totale très faible correspondant au poids du piston (3 kPa), et des essais de gonflement en parallèle sous des contraintes axiales totales distribuées suivant la série 30, 100, 200, 400, 800, 1400 kPa (soit sept niveaux de contraintes). Les sols sont compactés dans la bague œdométrique à l’aide d’une dame miniaturisée. Ils sont préparés à différentes densités initiales pour une seule teneur en eau de l’argile verte (wvisée = 21,2 %) ou deux teneurs en eau du limon (wvisée = 13,8 et 18,2 %). Au total le programme compte 41 éprouvettes d’argile compactée et 63 éprouvettes de limon compacté (Tab. 7).
Pour mener à bien l’exploitation des résultats ici, les différentes éprouvettes sont regroupées dans des classes de densités, afin de former l’équivalent de quatre essais de sensibilité sur l’argile verte compactée et de six essais sur le limon compacté. Les bornes de ces classes sont définies en indices des vides et sont indiquées dans le tableau 7 (deux éprouvettes de limon sont écartées). Les caractéristiques d’état (w, ρd) mesurées aux différents stades des essais œdométriques individuels et qui constituent les données sont converties en teneur en eau, indice des vides et degré de saturation, mais aussi en déformation axiale εa (e = ρs/ρd − 1 ; e = e0 − (1 + e0) ϵa). Les sept contraintes axiales totales sont associées à ces déformations pour former autant d’essais œdométriques en parallèle que de classes (4 et 6 classes, respectivement).
La figure 7 montre les résultats des essais appartenant à la classe 2 de l’argile verte (0,95 < e0 < 1,05). Le chargement fait apparaître une reprise de compactage à partir de σarcmp = 200 kPa. Au-delà, les tassements s’accentuent fortement. Par contre, la part des tassements due à l’imbibition diminue. La droite de rechargement de pente 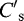 = 0,011 (carrés), puis la droite des déformations après imbibition de pente
= 0,011 (carrés), puis la droite des déformations après imbibition de pente 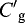 = 0,176 (triangles) sont identifiées entre 30 et 200 kPa. L’argile verte compactée présente une très forte sensibilité à l’imbibition, avec σag = 290 kPa et
= 0,176 (triangles) sont identifiées entre 30 et 200 kPa. L’argile verte compactée présente une très forte sensibilité à l’imbibition, avec σag = 290 kPa et  = 0,165. Les gonflements sont exceptionnels (−30 %). Les paramètres
= 0,165. Les gonflements sont exceptionnels (−30 %). Les paramètres  ,
, 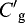 ,
, 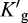 et σag ainsi identifiés sur les données expérimentales sont rassemblés dans le tableau 8 par classes homogènes.
et σag ainsi identifiés sur les données expérimentales sont rassemblés dans le tableau 8 par classes homogènes.
De même, la figure 8 montre les résultats des essais appartenant à la classe 2 du limon de Goderville (0,95 < e0 < 1,05). Le chargement fait apparaître une reprise de compactage à partir de σarcmp = 400 kPa. Au-delà, les tassements s’accentuent ; mais avec une amplitude moindre que l’argile verte. De même, la part des tassements due à l’imbibition diminue ensuite. La droite de rechargement de pente  = 0,012 (carrés), puis la droite des déformations après imbibition de pente
= 0,012 (carrés), puis la droite des déformations après imbibition de pente 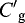 = 0,041 (triangles) sont identifiées entre 30 et 200 kPa. Le limon compacté présente une sensibilité à l’imbibition plus faible que l’argile, avec σag = 159 kPa et
= 0,041 (triangles) sont identifiées entre 30 et 200 kPa. Le limon compacté présente une sensibilité à l’imbibition plus faible que l’argile, avec σag = 159 kPa et 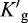 = 0,028. Les paramètres
= 0,028. Les paramètres  ,
,  ,
, 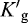 et σag ainsi identifiés sur les données expérimentales sont rassemblés dans le tableau 8 par classes homogènes.
et σag ainsi identifiés sur les données expérimentales sont rassemblés dans le tableau 8 par classes homogènes.
 |
Fig. 7 Essai de gonflement en parallèle. Argile verte compactée (classe 2). D’après Ferber (2005). Multiple-specimens swelling test. Compacted green clay. |
 |
Fig. 8 Essai de gonflement en parallèle. Limon de Goderville compactée (classe 2). D’après Ferber (2005). Multiple-specimens swelling test. Compacted silt. |
4 Récapitulation
4.1 Contraintes de compactage statique
Les six courbes de compression statique enregistrées pendant la préparation des éprouvettes d’un essai de sensibilité sont exploitées ensemble. Un exemple est donné dans la figure 2. Une contrainte de compactage moyenne σacmp en est déduite (ou pression de compactage), qui est utilisée ensuite pour exploiter l’essai. Cette pression de compactage est indiquée dans le tableau 3 avec la teneur en eau et l’indice des vides du sol compacté. Elle est représentée en fonction de ces caractéristiques d’état des sols compactés sur les graphiques des figures 9a et 9b en échelles semi-logarithmiques. Ces moyennes calculées sur les six éprouvettes sont proches de la consigne (wvisée, evisé), aux incertitudes près des mesures, sauf si un drainage s’est produit en tentant de compacter un sol trop humide. Quelques sols particuliers sont mis en évidence sur ces graphiques : argile du PK189, argile de Bavent, limon de Goderville et diverses marnes. Les carrés délimitent le domaine du plan d’expériences en neuf points qui a été consacré au limon de Goderville.
Les graphiques de la figure 9 montrent que les contraintes de compactage s’étalent sur deux ordres de grandeur, entre 0,1 et 10 MPa. Les sols ne sont pas tous compactés à l’optimum Proctor normal, ce qui explique en partie ce large éventail de réponses. Comme attendu, la contrainte de compactage diminue quand la teneur en eau visée et l’indice des vides visé augmentent. Des encadrements par des droites indiquent cette évolution pour le limon de Goderville, avec des pentes égales à –0,07 (% et kPa) et –2, et avec des ordonnées à l’origine égales à 3,5 et 17,4 MPa (0,50 < e < 0,85), puis 5,9 et 18,2 MPa (14 < w < 21 %). Sur cette base, une expression de la contrainte de compactage est donnée par :
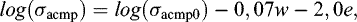 (4)
où σacmp0 est une constante qui dépend de la nature du sol, w est en % et σacmp en kPa. Ici, la constante σacmp0 = 174 MPa représente le compactage du limon de Goderville dans les conditions du plan d’expériences consacré à ce sol. Les contraintes de compactage calculées par cette relation à partir des caractéristiques d’état w et e du sol compacté sont reportées en fonction des contraintes mesurées dans la figure 10. Elles se placent effectivement sur la bissectrice. Les pentes –0,07 (% et kPa) et –2 et cette constante σacmp0 expliquent aussi le compactage de l’argile du PK189 approximativement (ronds). Mais ces paramètres ne permettent pas d’expliquer le compactage des autres sols dont les figurés s’écartent de la bissectrice du diagramme.
(4)
où σacmp0 est une constante qui dépend de la nature du sol, w est en % et σacmp en kPa. Ici, la constante σacmp0 = 174 MPa représente le compactage du limon de Goderville dans les conditions du plan d’expériences consacré à ce sol. Les contraintes de compactage calculées par cette relation à partir des caractéristiques d’état w et e du sol compacté sont reportées en fonction des contraintes mesurées dans la figure 10. Elles se placent effectivement sur la bissectrice. Les pentes –0,07 (% et kPa) et –2 et cette constante σacmp0 expliquent aussi le compactage de l’argile du PK189 approximativement (ronds). Mais ces paramètres ne permettent pas d’expliquer le compactage des autres sols dont les figurés s’écartent de la bissectrice du diagramme.
D’après la relation (4), chaque contrainte de compactage statique σacmp du limon de Goderville est associée à une droite de pente négative –0,035 /% dont l’équation dans le plan d’état (w, e) est de la forme e = C − Es w où C = 0, 5 log(σacmp0/σacmp) et la pente Es = − de/dw vaut Es = 0,035 /% et (w est en %). Cette droite représente approximativement la direction des branches des courbes Proctor du côté sec dans un domaine du plan d’état proche des optimums. Sa pente de/dw = − Es est reliée à la pente dρd/dw de ces courbes dans le plan (w, ρd) par la relation suivante :
 (5)
et d’après l’expression e = (w ρs)/(Sr ρw) = ρs/ρd − 1. Ainsi, Es = 3,5 = 0,035 /%, avec la pente dρd/dw = +0,033 Mg/m3/% des tangentes aux courbes Proctor du limon de Goderville et de l’argile du PK189, pour une masse volumique sèche ρd = 1,58 Mg/m3 environ. Avec d’autres droites parallèles dont σacmp0 est le paramètre, les droites de pente Es offrent un paramétrage des contraintes de compactage dans le plan d’état (w, e). Les pentes Es changent peu d’un sol à l’autre. Elles augmentent avec l’argilosité du sol. Obtenues à partir des courbes Proctor, elles sont arrondies et réparties en trois classes en fonction de la limite de liquidité du sol dans le tableau 3.
(5)
et d’après l’expression e = (w ρs)/(Sr ρw) = ρs/ρd − 1. Ainsi, Es = 3,5 = 0,035 /%, avec la pente dρd/dw = +0,033 Mg/m3/% des tangentes aux courbes Proctor du limon de Goderville et de l’argile du PK189, pour une masse volumique sèche ρd = 1,58 Mg/m3 environ. Avec d’autres droites parallèles dont σacmp0 est le paramètre, les droites de pente Es offrent un paramétrage des contraintes de compactage dans le plan d’état (w, e). Les pentes Es changent peu d’un sol à l’autre. Elles augmentent avec l’argilosité du sol. Obtenues à partir des courbes Proctor, elles sont arrondies et réparties en trois classes en fonction de la limite de liquidité du sol dans le tableau 3.
Ainsi, l’indice des vides es peut être défini pour représenter chacun des points d’état (w, e) du sol compacté :
 (6)
(6)
Associé au degré de saturation, il forme un couple de variables indépendantes (es, Sr) équivalent au couple (w, e) pour caractériser un état du sol compacté. De même, les droites parallèles à la droite de saturation du plan (w, e) possèdent une ordonnée à l’origine em :
 (7)
qui forment avec es un autre couple (em, es) de variables indépendantes et équivalent au couple (w, e). L’indice des vides em = 0 quand Sr = 100 %. La relation (4) s’écrit alors en fonction de es (les pressions sont en kPa) :
(7)
qui forment avec es un autre couple (em, es) de variables indépendantes et équivalent au couple (w, e). L’indice des vides em = 0 quand Sr = 100 %. La relation (4) s’écrit alors en fonction de es (les pressions sont en kPa) :
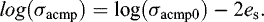 (8)
(8)
L’indice des vides es est attaché à une contrainte de compactage statique et plus généralement à une énergie de comptage. Ainsi par exemple, à un optimum Proctor normal wOPN = 15 % et ρdOPN = 1,8 Mg/m3 correspond les indices des vides eOPN = 0,5, esOPN = 1,02 et emOPN = 0,10 (avec Gs = 2,7 et Es = 3,5).
En s’appuyant sur des essais œdométriques conventionnel et les mesures des teneurs en eau, des indices des vides et des contraintes axiales totales, l’interprétation des essais de sensibilité s’inscrit dans la démarche proposée par Kodikara (2012), Islam et Kodikara (2016) et Kodikara et al. (2016), qui est désignée sous le nom de méthode MPK. Ces auteurs suggèrent, entre autres, d’adopter l’indice des vides ew = Gs w comme variable représentant la teneur en eau pour définir le plan d’état (ew, e) qui est équivalent au plan d’état (w, e). Le plan d’état (w, e) joue un rôle clé dans la compréhension du comportement des sols compactés, pendant le compactage statique (Serratrice, 2018), ou pendant les essais de sensibilité, comme ici, en donnant accès à la définition des paramètres es et Es d’après (6), pour porter une notion liée à l’énergie de compactage. Faute d’accès à la mesure ou au contrôle de la succion, l’instrumentation mise en œuvre ici pour enregistrer les courbes de sensibilité des sols compactés ne permet pas d’interpréter les réponses observées dans le cadre de la mécanique des sols non saturés. Aussi, l’approche envisagée veut se projeter dans la lignée de la méthode MPK qui, comme le suggèrent ses auteurs, vise à établir un lien direct entre l’étape de compactage et le comportement mécanique du sol compacté. Les développements qui suivent s’inscrivent dans cette optique.
 |
Fig. 9 Contrainte de compactage statique. a : en fonction de la teneur en eau ; b : en fonction de l’indice des vides du sol compacté. Static compaction pressure. a: versus water content; b: versus void ratio of compacted soil. |
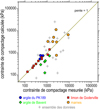 |
Fig. 10 Contrainte de compactage statique calculée comparée à la contrainte mesurée. Static compaction pressure calculated compared to the measured pressure. |
4.2 Contraintes caractéristiques
Parmi les charges appliquées pendant un essai de sensibilité, la contrainte de reprise de compactage σarcmp est la contrainte axiale totale à partir de laquelle des nouveaux tassements irréversibles se produisent dès le chargement, sans imbibition du sol. Cette contrainte est pointée sur la courbe expérimentale (log(σa), εa). Des exemples sont donnés dans les figures 4 et 5. Cette contrainte ne peut pas être évaluée plus précisément parmi ces charges, qui sont distribuées en série géométrique. Elle représente une borne inférieure de la pression de préconsolidation du sol compacté maintenu dans son état initial et à partir de laquelle la réponse (log(σa), εa) s’écarte de la forme semi-logarithmique attendue. Les contraintes σarcmp sont reportées dans le tableau 3. Elles sont représentées en fonction de la contrainte de compactage σacmp en échelles bi-logarithmiques dans la figure 11a. Quelques sols insensibles à l’imbibition sont écartés. Les segments indiqués ont pour pente l’unité. Ils expriment des rapports σarcmp/σacmp égaux à 100, 80, 50 et 10 %. D’après les données, les contraintes de reprise du compactage ne dépassent pas 80 % de la contrainte de compactage et peuvent descendre à 10 % de celle-ci dans les sols peu déformables et/ou fortement compactés.
Le tri des points expérimentaux de la figure 11 est effectué au moyen de la quantité pms = em (es − es0), qui est nulle lorsque Sr = 100 % et/ou es = es0). Il sera admis ici que, en première approximation, es0 ≈ 1 donne un ordre de grandeur de l’indice des vides es le long des branches Proctor normal côté sec. L’état du sol est compact et non saturé quand pms < –0,02 (triangles). Il est lâche et non saturé quand pms > +0,02 (pentagones). Dans les autres cas, il est quasi saturé (em ≈ 0) ou situé aux alentours de la branche des courbes Proctor normal côté sec (es ≈ es0 ≈ 1, losanges). Ici, les contraintes de reprises du compactage les plus basses s’observent dans les sols les plus lâches et non saturés (pentagones, Fig. 11a).
Comme indiqué plus haut, une pression de gonflement σag peut être définie pour une charge intermédiaire d’un essai de sensibilité où ne se produirait pas de déformation axiale pendant l’imbibition (Fig. 1). À l’exception de quelques essais où le sol s’est révélé insensible à l’imbibition ou gonflant jusqu’à 820 kPa, ces pressions sont identifiées par le calcul de l’intersection des droites d’équations (1) et (2) dans le plan (log(σa), εa), avant et après imbibition. Ces pressions de gonflement sont reportées dans le tableau 3. Elles sont représentées en fonction des contraintes de compactage σacmp sur le graphique de la figure 11b. Des segments de pente égale à l’unité sont indiqués aussi. Ils représentent des rapports σag/σacmp égaux à 100, 40 et 10 % respectivement. Quelques sols insensibles à l’imbibition sont écartés. Le graphique de la figure 11b montre une bande dans laquelle les rapports σag/σacmp se rangent en majorité entre 10 et 40 %. Cela signifie que des tassements dus à l’imbibition apparaissent fréquemment pour des charges qui dépassent à peine 10 % de σacmp et que de tels tassements voient le jour systématiquement sous les charges supérieures à 40 % de σacmp. Mais, dans cette bande, la pression de gonflement augmente globalement avec la contrainte de compactage, indiquant ainsi qu’une élévation de la contrainte de compactage favorise le développement des gonflements sous une charge donnée. La littérature est abondante sur ce sujet (Sridharan et al., 1986 ; Sridharan et Gurtug, 2004 ; Masin et Khalili, 2016 ; et d’autres). D’après le classement des données avec le produit pms, les sols les plus lâches et non saturés fournissent les plus faibles pressions de gonflement (pms > 0,02, pentagones).
La figure 11c montre la pression de gonflement σag en fonction de la contrainte de reprise de compactage σarcmp. Les segments reportés sur le graphique, de pente égale à l’unité, expriment des rapports σag/σarcmp égaux à 100, 50 et à 20 %. Le tri des données au moyen du produit pms prend ici tout son sens. Les sols les plus lâches et non saturés s’inscrivent sous des rapports σag/σarcmp inférieurs à 50 %, voire 20 % (pentagones). Autrement dit, les sols compactés dans ces états sont capables de supporter des charges de 2 à 5 fois supérieures à leur pression de gonflement avant imbibition. Mais, instables, l’imbibition provoque un effondrement de la structure qui les constitue. Au contraire, les sols quasi saturés de la classe intermédiaire (losanges) tassent pendant le chargement pour ne laisser qu’une faible part de tassement supplémentaire sous l’effet de l’imbibition. Dans l’approche originale de leur interprétation, les essais de sensibilité révèlent ces différentes formes de réponses au cas par cas. L’exploitation des essais à l’aide de la loi de compressibilité semi-logarithmique complète utilement cette interprétation des données.
 |
Fig. 11 Contraintes de compactage, contraintes de reprise de compactage et pressions de gonflement. a : σrcmp fonction de σacmp ; b : σag fonction de σacmp. c : σag fonction de σarcmp. Compaction pressures, yield pressure and swelling pressures. |
4.3 Amplitudes des déformations dues à l’imbibition
La récapitulation des paramètres de gonflement issus des essais de sensibilité montre une grande diversité de réponses. Les coefficients de compressibilité 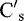 sont compris en majorité entre 0,008 et 0,016. Ils dépendent de la nature des sols compactés. Ils augmentent avec les indices des vides e0 et es, mais ils semblent indépendants de l’indice des vides em. Ils diminuent quand les contraintes de compactage augmentent. Les coefficients de compressibilité après imbibition
sont compris en majorité entre 0,008 et 0,016. Ils dépendent de la nature des sols compactés. Ils augmentent avec les indices des vides e0 et es, mais ils semblent indépendants de l’indice des vides em. Ils diminuent quand les contraintes de compactage augmentent. Les coefficients de compressibilité après imbibition  sont compris entre 0,01 et 0,09. Les plus grands s’observent dans les sols argileux, par opposition aux limons et aux marnes. De fait, les pressions de gonflement σag et les pentes
sont compris entre 0,01 et 0,09. Les plus grands s’observent dans les sols argileux, par opposition aux limons et aux marnes. De fait, les pressions de gonflement σag et les pentes 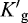 dépendent à la fois de la nature des sols compactés et de leur état. Néanmoins, il s’avère difficile de dégager des tendances.
dépendent à la fois de la nature des sols compactés et de leur état. Néanmoins, il s’avère difficile de dégager des tendances.
Les pressions de gonflement σag et les pentes 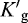 déduites des essais de sensibilité sont représentées en fonction de l’indice des vides es et en fonction du degré de saturation Sr avant imbibition sur les graphiques de la figure 12. Les segments parallèles du plan (es, log(σag)) de la figure 12a ont pour équations :
déduites des essais de sensibilité sont représentées en fonction de l’indice des vides es et en fonction du degré de saturation Sr avant imbibition sur les graphiques de la figure 12. Les segments parallèles du plan (es, log(σag)) de la figure 12a ont pour équations :
 (9)
avec A = 8, 28,5, 101, 360 et 3500 MPa qui dépend de la nature du sol. La pression de gonflement augmente quand es diminue (l’énergie de compactage augmente), comme attendu. Cette formulation découle d’une démarche analogue à celle qui a été proposée pour paramétrer la contrainte de compactage σacmp dans le plan d’état (w, e) avec la relation (8). Mais comme (8), il s’agit d’une allure générale dont il convient de déterminer expérimentalement les paramètres dans chaque cas particulier. De leur côté, les couples de données (Sr,
(9)
avec A = 8, 28,5, 101, 360 et 3500 MPa qui dépend de la nature du sol. La pression de gonflement augmente quand es diminue (l’énergie de compactage augmente), comme attendu. Cette formulation découle d’une démarche analogue à celle qui a été proposée pour paramétrer la contrainte de compactage σacmp dans le plan d’état (w, e) avec la relation (8). Mais comme (8), il s’agit d’une allure générale dont il convient de déterminer expérimentalement les paramètres dans chaque cas particulier. De leur côté, les couples de données (Sr, 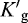 ) forment des alignements dont la pente augmente fortement dans les argiles plastiques (Fig. 12b). L’expression empirique suivante est proposée pour caractériser cette évolution (Sr en %) :
) forment des alignements dont la pente augmente fortement dans les argiles plastiques (Fig. 12b). L’expression empirique suivante est proposée pour caractériser cette évolution (Sr en %) :
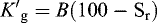 (10)avec B = 0,00020, 0,00077, 0,00200 et 0,00410 /% pour les segments indiqués. Pour un sol donné, la pente
(10)avec B = 0,00020, 0,00077, 0,00200 et 0,00410 /% pour les segments indiqués. Pour un sol donné, la pente 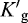 ne dépend pas de es mais elle dépend de Sr. L’expansion du sol compacté est amplifiée quand le sol est moins saturé. Cette sensibilité (la pente B) est exacerbée dans les argiles plastiques, ce qui renvoie aux nombreux travaux consacrés à ce sujet dans la littérature.
ne dépend pas de es mais elle dépend de Sr. L’expansion du sol compacté est amplifiée quand le sol est moins saturé. Cette sensibilité (la pente B) est exacerbée dans les argiles plastiques, ce qui renvoie aux nombreux travaux consacrés à ce sujet dans la littérature.
Dans l’exemple des quatre argiles présenté plus haut (Rosenbalm, 2013), les pentes dρd/dw sont issues des essais Proctor normal qui accompagnent les essais œdométriques. Elles sont reportées dans le tableau 4. Les pentes Es déduite de la relation (5) sont reportées dans le tableau 4. L’indice des vides es et le degré de saturation Sr sont associés à chacun des états des argiles après chargement. La relation (9) permet d’identifier A connaissant σag. Le paramètre B s’obtient ensuite en quelques itérations pour ajuster la réponse calculée à la courbe expérimentale (log(σa), Δεa), avec la relation (10). Les résultats sont donnés dans le tableau 5. Les paramètres A et B augmentent avec l’argilosité du sol.
Cette démarche est appliquée ensuite aux données du LCPC. Un essai Proctor normal réalisé sur l’argile verte permet d’identifier la pente dρd/dw côté sec de la courbe de compactage, voir le tableau 6 (Berche et al., 2009). Avec ρs = 2,71 Mg/m3, ρd = 1,58 Mg/m3, dρd/dw = 0,033 Mg/m3/% alors de/dw = –(2,71 / 1,552) × 0,031 = –0,035 /%. Cette pente de/dw = –0,035 /% est identique à celle du limon. Les paramètres  ,
, 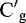 , σag et
, σag et 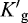 identifiés sur les courbes (log(σa), εa), comme dans les exemples des figures 7 et 8. Ils sont indiqués dans le tableau 8. Ils sont reportés dans les plans (es, log(σag)) et (Sr,
identifiés sur les courbes (log(σa), εa), comme dans les exemples des figures 7 et 8. Ils sont indiqués dans le tableau 8. Ils sont reportés dans les plans (es, log(σag)) et (Sr, 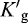 ) de la figure 12 (données LCPC) avec les données précédentes issues des essais de sensibilité (données LRPC). Un bon accord apparaît entre les diverses sources de données. L’argile verte très plastique sort du lot précédent, mais les paramètres mesurés s’inscrivent dans la même tendance. Les paramètres des essais LRPC et LCPC sur le limon sont en bon accord.
) de la figure 12 (données LCPC) avec les données précédentes issues des essais de sensibilité (données LRPC). Un bon accord apparaît entre les diverses sources de données. L’argile verte très plastique sort du lot précédent, mais les paramètres mesurés s’inscrivent dans la même tendance. Les paramètres des essais LRPC et LCPC sur le limon sont en bon accord.
 |
Fig. 12 Pressions de gonflement σag et pentes Swelling pressures σag and slopes |
4.4 Prévision de la déformation due à l’imbibition
Les relations précédentes sont utilisées pour calculer les déformations dues à l’imbibition d’après les différentes sources de données présentées plus haut. Connaissant la pente Es, l’indice des vides es est calculé avec la relation (6) à partir de l’état du sol après chargement et avant imbibition (wavi, eavi, Sravi), qui est donné sous chacune des six charges appliquées. La pression de gonflement σag et le rapport 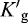 sont déduits de es et Sravi par les relations (9) et (10). Enfin, la déformation Δεa due à l’imbibition sous la charge σa est calculée à l’aide de la relation (3). Ces déformations calculées sont comparées aux mesures des déformations dues à l’imbibition pendant les essais de sensibilité dans la figure 13. Les quatre sols ou les familles de sols déjà mis en exergue plus haut sont pointés à nouveau sur le graphique. Les paramètres Es, A et B utilisés sont reportés dans le tableau 9. Des paramètres individuels sont utilisés pour les essais concernant l’argile de Bavent et la marne altérée très plastique (essai no 7). Sinon, un jeu unique de paramètres explique les déformations de l’argile du PK189, du limon de Goderville et des marnes. Ces couples de déformations s’alignent en majorité sur la bissectrice du diagramme et tout particulièrement les gonflements, preuve d’une bonne prévisibilité de la méthode. Mais cette formulation ne permet pas d’expliquer les tassements mesurés sur l’argile du PK189 et le limon de Goderville. Les déformations calculées sont nettement plus faibles que les déformations mesurées, ce qui explique la divergence des couples de déformations par rapport à la bissectrice. En privilégiant les déformations mesurées dans le domaine pseudo-élastique du sol compacté, la méthode d’exploitation ne permet pas de rendre compte des reprises de tassement et des tassements d’effondrement observés sous les hautes pressions.
sont déduits de es et Sravi par les relations (9) et (10). Enfin, la déformation Δεa due à l’imbibition sous la charge σa est calculée à l’aide de la relation (3). Ces déformations calculées sont comparées aux mesures des déformations dues à l’imbibition pendant les essais de sensibilité dans la figure 13. Les quatre sols ou les familles de sols déjà mis en exergue plus haut sont pointés à nouveau sur le graphique. Les paramètres Es, A et B utilisés sont reportés dans le tableau 9. Des paramètres individuels sont utilisés pour les essais concernant l’argile de Bavent et la marne altérée très plastique (essai no 7). Sinon, un jeu unique de paramètres explique les déformations de l’argile du PK189, du limon de Goderville et des marnes. Ces couples de déformations s’alignent en majorité sur la bissectrice du diagramme et tout particulièrement les gonflements, preuve d’une bonne prévisibilité de la méthode. Mais cette formulation ne permet pas d’expliquer les tassements mesurés sur l’argile du PK189 et le limon de Goderville. Les déformations calculées sont nettement plus faibles que les déformations mesurées, ce qui explique la divergence des couples de déformations par rapport à la bissectrice. En privilégiant les déformations mesurées dans le domaine pseudo-élastique du sol compacté, la méthode d’exploitation ne permet pas de rendre compte des reprises de tassement et des tassements d’effondrement observés sous les hautes pressions.
La prévision des déformations due à l’imbibition est envisagée ensuite pour les données recueillies dans la littérature. Concernant les quatre argiles du tableau 4, la coïncidence des déformations mesurées avec les prévisions calculées est implicite, car les paramètres Es, A et B ont été identifiés sur des essais individuels réalisés en un seul point d’état (Tab. 5). Concernant les données du LCPC, les paramètres de calcul issus des essais, dont les figures 7 et 8 donnent des exemples, sont reportés dans le tableau 10. La méthode de calcul aboutit à une bonne prévision des déformations de l’argile verte sous l’effet de l’imbibition (Fig. 14a). Ce n’est pas le cas du limon de Goderville pour lequel les amplitudes des déformations de reprise du compactage et d’effondrement sont ignorées par la méthode d’interprétation. Ainsi, seules les déformations calculées, qui représentent majoritairement des gonflements produits dans le domaine pseudo-élastique du limon compacté, s’accordent aux mesures (Fig. 14b).
 |
Fig. 13 Déformations calculées dues à l’imbibition en fonction des déformations mesurées d’après les essais en parallèle. Calculated déformations versus measured deformations from sensitivity tests. |
Paramètres pour le calcul des déformations pendant les essais d’imbibition.
Parameters for the calculation of deformations during soaking tests.
Paramètres pour le calcul des déformations pendant les essais LCPC.
Parameters for the calculation of deformations during LCPC tests.
 |
Fig. 14 Déformations calculées dues à l’imbibition en fonction des déformations mesurées d’après les essais œdométriques du LCPC. a : argile verte ; b : limon de Goderville. Calculated deformations versus measured deformations from œdometer tests of LCPC. a: green clay; b: Goderville silt. |
5 Conclusion
Ce travail s’appuie sur les résultats d’une série d’essais de sensibilité à l’imbibition réalisés sur une vingtaine de sols compactés dans différents états. La procédure d’essai prévoie de tester un sol à l’aide de six éprouvettes œdométriques compactées. Les éprouvettes sont chargées sous des contraintes indépendantes formant une série géométrique, avant d’être mises en imbibition. La description des courbes de déformation s’effectue point par point au moyen d’indices de sensibilité qui dépendent des charges appliquées. Les essais de sensibilité à l’imbibition constituent une forme particulière des essais de gonflement en parallèle. Afin d’interpréter des courbes de sensibilité sur un intervalle étendu des charges appliquées en s’inspirant de la méthode d’exploitation des essais de gonflement en parallèle, cette étude fait appel à la loi de compressibilité semi-logarithmique classique de variation des déformations œdométriques avec le logarithme de la contrainte axiale.
Selon cette méthode d’interprétation, cinq paramètres sont déduits des essais de sensibilité. Les quatre premiers sont identifiés directement sur les courbes : les compressibilités avant et après imbibition, une pression de gonflement et un rapport de gonflement. Le cinquième paramètre pointe la contrainte axiale de reprise du compactage pendant le chargement des éprouvettes compactées, et marque ainsi la déviation de la réponse mesurée par rapport à la loi de compressibilité semi-logarithmique. L’enregistrement des courbes de compression statique pendant la phase préliminaire des essais de sensibilité permet de pointer un autre paramètre important pour interpréter les essais, qui est la contrainte de compactage.
L’exploitation des essais de sensibilité montre rapidement que, dans les sols faiblement compactés, la loi de compressibilité semi-logarithmique ne s’applique que dans une plage limitée des contraintes axiales où n’apparaît pas de reprise de compactage ni des tassements d’effondrement. Ces charges appartiennent au domaine pseudo-élastique du sol dans son état initial compacté. L’imbibition produit néanmoins des gonflements et des tassements d’amplitudes plus ou moins grandes, qui sont caractérisées par une pression de gonflement et un rapport de gonflement. Ces paramètres dépendent de la nature du sol. Ils sont liés aux caractéristiques d’état du sol compacté par des relations empiriques gouvernées par l’argilosité. Ces relations offrent une bonne prévisibilité des déformations dans ce domaine des contraintes totales.
Cette restriction de l’usage de la loi de compressibilité semi-logarithmique se pose en contraste avec les indices de sensibilité de la procédure originale qui présentent l’intérêt de décrire la réponse expérimentale du sol point par point dans toutes les situations. En contrepartie, cette méthode d’interprétation des essais de gonflement en parallèle met en relief les différents aspects des effets de l’imbibition dans les sols compactés d’un point de vue macroscopique (gonflements, tassements, reprises de compactage, effondrements). D’après les données recueillies, les contraintes de reprise du compactage ne dépassent pas 80 % de la contrainte de compactage statique. Elles sont souvent bien inférieures à ce taux dans les sols peu compactés. De même, des tassements voient le jour systématiquement sous les charges supérieures à 40 % de la contrainte de compactage. A contrario, l’élévation de la contrainte de compactage favorise les gonflements. Enfin, les sols compactés dans des états non saturés lâches se trouvent en capacité de supporter des charges de 2 à 5 fois supérieures à leur pression de gonflement avant imbibition, en exhibant ainsi un risque d’instabilité à l’effondrement d’autant plus élevé.
Dans son domaine d’application, la loi de compressibilité semi-logarithmique offre une approche globale intéressante pour caractériser les déformations volumiques des sols compactés aux taux habituels de compactage pour les applications courantes. La méthode présente l’avantage de mettre en œuvre des essais œdométriques conventionnels réalisés en parallèle et de s’appuyer sur un nombre limité de paramètres. Elle doit être enrichie par le recueil de nouvelles données. Cette approche empirique ne cache pas le besoin d’affiner l’analyse des réponses des sols compactés sous l’effet de l’imbibition, qui relèvent du comportement des sols non saturés et des sols gonflants pour leurs interactions physico-chimiques des particules argileuses avec l’eau.
Principales notations
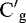 :
Coefficient de gonflement sous imbibition
:
Coefficient de gonflement sous imbibition
 :
Coefficient de gonflement pseudo-élastique
:
Coefficient de gonflement pseudo-élastique
e0 : Indice des vides initial du sol compacté
eapi : Indice des vides après imbibition
eavi : Indice des vides avant imbibition
em : Ordonnée à l’origine des droites parallèles à la droite de saturation du plan (w, e)
es : Ordonnée à l’origine des tangentes aux branches des courbes de compactage du côté sec ; es dépend de l’énergie de compactage
es0 : Ordonnée es pour une énergie Proctor normal (es0 ≈ 1 en première approximation)
Es : Pente des tangentes aux branches des courbes de compactage du côté sec
Gs : Densité des grains solides
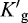 :
Rapport des déformations dues à l’imbibition
:
Rapport des déformations dues à l’imbibition
pms : pms = em (es − es0) paramètre donnant l’écart entre la branche des courbes Proctor normal côté sec et la droite de saturation dans le plan d’état (w, e)
w0 : Teneur en eau de compactage
Δεa : Déformation axiale due à l’imbibition
εa api : Déformation axiale après imbibition
εa avi : Déformation axiale après imbibition
σa0 : Contrainte axiale unité (σa0 = 1 kPa)
σacmp : Contrainte axiale maximale appliquée pour le compactage
σag : Pression de gonflement (pour cette procédure)
σamin, σamax : Plage des contraintes axiales appliquées
σarcmp : Contrainte axiale de reprise du compactage
Références
- Abbaszadeh S, Houston SL, Zapata CE. 2016. Effect of desiccation cracking on the swell and swell pressure of expansive clay. Proceedings of the Geotechnical and Structural Engineering Congress, Phoenix, US, pp. 2054–2065. [Google Scholar]
- AFNOR (Association française de normalisation). 1995. Sols : reconnaissance et essais – Essai de gonflement à l’œdomètre – Détermination des déformations par chargement de plusieurs éprouvettes. Norme XPP94-091, décembre 1995, 13 p. [Google Scholar]
- ASTM (American Society for Testing and Materials). 2008. Standard D4546-08. 2008. Standard test methods for one-dimensional swell or collapse of cohesive soils. West Conshohocken, PA: ASTM International. [Google Scholar]
- Attom MF, Barakat S. 2000. Investigation of three methods for evaluating swelling pressure of soils. Environ Eng Geosci VI(3): 293–299. [CrossRef] [Google Scholar]
- Barden L, Mc Gown A, Collins K. 1973. The collapse mechanism in partly saturated soil. Eng Geol 7(1): 49–60. [CrossRef] [Google Scholar]
- Basma AA. 1993. Prediction of expansion degree for natural compacted clays. Geotech Test J 16(6): 542–542. [CrossRef] [Google Scholar]
- Basma AA, Al-Homoud AS, Husein A. 1995. Laboratory assessment of swelling pressure of expansive soils. Appl Clay Sci 9(5): 355–368. https://doi.org/10.1016/0169-1317(94)00032-L. [CrossRef] [Google Scholar]
- Berche V, Jeanjean P, Rossigny P, Ferber V, Quibel A. 2009. Réutilisation d’argiles très plastiques en corps de remblais routiers: expérimentations sur le chantier de l’Autoroute A34 (Charleville-Réthel). Bull Lab Ponts Chaussées 274: 31–46. [Google Scholar]
- Brackley JJA. 1973. Swell pressure and free swell in compacted clay. Proceedings of 3rd International Conference on Expansive Soils, Haifa, 1, pp. 169–176. [Google Scholar]
- Cerato AB, Miller GA, Hajjat JA. 2009. Influence of clod-size and structure on wetting-induced volume change of compacted soil. J Geotech Geoenviron Eng 135(11): 1620–1628. [CrossRef] [Google Scholar]
- Dudley JH. 1970. Review of collapsile soils. J Soil Mech Found Div, ASCE 96(3): 925–945. [Google Scholar]
- Feng M, Gan KM, Fredlund DG. 1998. A laboratory study of swelling pressure using various test methods. Proceedings of the 2nd International Conference on Unsaturated Soils, Beijing, China, pp. 350–355. [Google Scholar]
- Ferber V. 2005. Sensibilité des sols fins compactés à l’humidification. Apport d’un modèle de microstructure. Thèse de doctorat. École Centrale de Nantes et Université de Nantes, 285 p. [Google Scholar]
- Ferber V, Auriol JC, Cui YJ, Magnan JP. 2008. Comportement des sols fins compactés à l’humidification. Apport d’un modèle de microstructure. Rev Fr Geotech 122: 13–24. [CrossRef] [Google Scholar]
- Fityus SG, Cameron DA, Walsh PF. 2005. The shrink swell test. Geotech Test J 28(1): 92–101. [Google Scholar]
- Islam T, Kodikara J. 2016. Interpretation of the loading-wetting behaviour of compacted soils within the “MPK” framework. Part I: Static compaction. Can Geotech J 53(5): 783–805. https://doi.org/10.1139/cgj-2014-0316. [CrossRef] [Google Scholar]
- ISRM (International Society for Rock Mechanics). 1989. Suggested methods for laboratory testing of argillaceous swelling rock. Int J Rock Mech Min Sci Geomech Abstr 26(5): 415–426. [CrossRef] [Google Scholar]
- ISSMFE (International Society for Soil Mechanics and Foundation Engineering). 1989. Draft standard for evaluation of swelling potential of expansive soils in laboratory. Report of Technical Committee on expansive soils (TC6). Publié dans: Rev Fr Geotech 56: 18–22. [Google Scholar]
- Jennings JE, Knight K. 1957. The prediction of total heave from the double œdometer test. Trans S Afr Inst Civ Eng 7(9): 13–19. Proceedings of the Symposium on Expansive Clays, Johannesburg, South Africa, pp. 13–19. [Google Scholar]
- Jennings JE, Firth RA, Ralph TK, Nagar N. 1973. An improved method for predicting heave using the œdometer test. Proceedings of International Conference of Expansive Soils, Haifa, Israel, pp. 149–154. [Google Scholar]
- Kayabali K, Demir S. 2011. Measurement of swelling pressure: Direct method versus indirect methods. Rev Can Geotech 48(3): 354–364. https://doi.org/10.1139/T10-074. [CrossRef] [Google Scholar]
- Kodikara J. 2012. New framework for volumetric constitutive behaviour of compacted unsaturated soils. Can Geotech J 49(11): 1227–1243. [CrossRef] [Google Scholar]
- Kodikara J, Islam T, Rajeev P. 2016. Interpretation of the loading–wetting behaviour of compacted soils within the “MPK” framework. Part II: Dynamic compaction. Can Geotech J 53(5): 806–827. [CrossRef] [Google Scholar]
- Komornik J, David A. 1969. Prediction of swelling potential of compacted clays. J Soil Mech Found Div, ASCE 95(1): 209–225. [Google Scholar]
- Ladd CC. 1960, Mechanism of swelling by compacted clay. Highw Res Board Bull 245: 10–26. [Google Scholar]
- Lambe TW. 1958. The engineering behaviour of compacted clay. J Soil Mech Found Div, ASCE 84(2): 1–35. [Google Scholar]
- Lawton EC, Fragaszy RJ, Hardcastle JH. 1989. Collapse of compacted clayey sand. J Geotech Eng 115(9): 1252–1267. https://doi.org/10.1061/(ASCE)0733-9410(1989)115:9(1252). [Google Scholar]
- Lawton EC, Fragaszy RJ, Hetherington MD. 1992. Review of wetting-induced collapse in compacted soil. J Geotech Eng 118(9): 1376–1394. https://doi.org/10.1061/(ASCE)0733-9410(1992)118:9(1376). [CrossRef] [Google Scholar]
- LCPC-SETRA. 2000. Guide technique pour les terrassements routiers (GTR). Réalisation des remblais et des couches de forme. Juillet 2000, 2e Édition. Fascicule I, Principes généraux, 98 p, Fascicule II, Annexes techniques, 102 p. [Google Scholar]
- Leong EC, Widiastuti S, Rahardjo H. 2013. Estimating wetting-induced settlement of compacted soils using œdometer test. Geotech Eng J SEAGS AGSSEA 44(1): 26–33. [Google Scholar]
- Li P, Vanapalli S, Li T. 2016. Review of collapse triggering mechanism of collapsible soils due to wetting. J Rock Mech Geotech Eng 8: 256–274. [CrossRef] [Google Scholar]
- Lutenegger AJ, Saber RT. 1988. Determination of collapse potential of soils. Geotech Test J 11(3): 173–178. [CrossRef] [Google Scholar]
- Masin D, Khalili N. 2016. Swelling phenomena and effective stress in compacted expansive clays. Can Geotech J 53(1): 134–147. [Google Scholar]
- Mieussens C. 1993. Détermination de la sensibilité des sols aux variations de teneur en eau en laboratoire. Essais à l’œdomètre sur les sols compactés. Projet de méthode LPC, Rapport du LRPC de Toulouse, 12 p. [Google Scholar]
- Nagaraj HB, Munnas MM, Sirdharan A. 2009. Critical evaluation of determining swelling pressure by swell-load method and constant volume method. Geotech Test J 32(4): 305–314. [Google Scholar]
- Nayak NV, Christensen RW. 1971. Swelling characteristics of compacted, expansive soils. Clays Clay Miner 19: 251–261. [CrossRef] [Google Scholar]
- Noorany I. 1992. Stress ratio effects on collapse of compacted clayey sand. Discussion de l’article de Lawton, Gragaszy et Hardcastle (1989). J Geotech Eng 118(9): 1472–1474. [CrossRef] [Google Scholar]
- Rosenbalm DC. 2013. Volume change behavior of expansive soils due to wetting and drying cycles. Thèse, Arizona State University, August 2013, 319 p. [Google Scholar]
- Schreiner HD, Burland JB. 1991. A comparison of the three swell test procedures. Proceedings of 10th Regional Conference for Africa on Soil Mechanics and Foundation Engineering. Maseru, Lesotho, pp. 259–266. [Google Scholar]
- Seed HB, Woodward RJ Jr, Lundgren R. 1962. Prediction of swelling potential for compacted clays. J Soil Mech Found Div, ASCE 88(3): 53–87. [Google Scholar]
- Serratrice JF. 1995a. Comportement d’une argile compactée. Bull Liaison Lab Ponts Chaussées 200: 13–24. [Google Scholar]
- Serratrice JF. 1995b. Comportement d’une craie compactée. Actes du Colloque « Colloquium Mundanum, Craies et schistes », Bruxelles, pp. 1.1.71–1.1.80. [Google Scholar]
- Serratrice JF. 2007. Retrait-gonflement des sols argileux et des marnes. Rev Fr Geotech 120–121: 1–14. [Google Scholar]
- Serratrice JF. 2013. Comportement d’un limon compacté. Bull Lab Ponts Chaussées 280–281: 105–122. [Google Scholar]
- Serratrice JF. 2018. Apport expérimental de la méthode de compactage statique des sols au laboratoire. Rev Fr Geotech 156: 1. https://doi.org/10.1051/geotech/2019001. [CrossRef] [Google Scholar]
- Serratrice JF, Soyez B. 1996. Les essais de gonflement. Bull Lab Ponts Chaussées 204: 65–85. [Google Scholar]
- Serratrice JF, Calissano H, Batilliot L. 2019. Les essais de sensibilité appliqués aux sols compactés. Rev Fr Geotech. https://doi.org/10.1051/geotech/2019016. [Google Scholar]
- Singhal S, Houston S, Houston WN. 2011. Effects of testing procedures on the laboratory determination of swell pressure of expansive soils. Geotech Test J 34(5): 476–488. [Google Scholar]
- Soundara B, Robinson RG. 2009. Influence of test method on swelling pressure of compacted clay. Int J Geotech Eng 3: 439–444. https://doi.org/10.3328/IJGE2009.03.03.439-444. [CrossRef] [Google Scholar]
- Sridharan A, Rao AS, Sivapullaiah PV. 1986. Swelling pressure of clays. Geotech Test J 9(1): 24–31. [CrossRef] [Google Scholar]
- Sridharan A, Gurtug Y. 2004. Swelling behaviour of compacted fine-grained soils. Eng Geol 72: 9–18. [CrossRef] [Google Scholar]
- Sun D, Sheng D, Xu Y. 2007. Collapse behaviour of unsaturated compacted soil with different initial densities. Rev Can Geotech 44(6): 673–686. https://doi.org/10.1139/t07-023. [CrossRef] [Google Scholar]
- Thompson RW, Perko HA, Raethamel WD. 2006. Comparison of constant volume swell pressure and œdometer load-back pressure. Proceedings of 4th International Conference of Unsaturated Soils. Carefree, Arizona, pp. 1382–1393. [Google Scholar]
Citation de l’article : Jean François Serratrice. Interprétation des essais de sensibilité des sols compactés à l’imbibition d’après la méthode d’interprétation des essais de gonflement en parallèle. Rev. Fr. Geotech. 2019, 159, 4.
Liste des tableaux
Propriétés physiques des argiles de l’exemple.
Physical properties of the clay in the example.
Paramètres pour le calcul des déformations pendant les essais d’imbibition.
Parameters for the calculation of deformations during soaking tests.
Paramètres pour le calcul des déformations pendant les essais LCPC.
Parameters for the calculation of deformations during LCPC tests.
Liste des figures
 |
Fig. 1 Paramètres issus d’un essai de sensibilité exprimé en déformation axiale. États d’équilibre de quatre éprouvettes avant et après imbibition. a : interprétation en indices de sensibilité C1, C2 et Δεa (Mieussens, 1993 ; Serratrice et al., 2019) ; b : approche globale sous la forme d’une loi semi-logarithmique. Parameters derived from a sensitivity test expressed in axial strain. Equilibrium states of four specimens before and after wetting. a: sensibility indexes; b: semi-logatithmic law. |
| Dans le texte | |
 |
Fig. 2 Exemple de courbes de compression statique et de courbes de sensibilité. Marne, essai no 21. Example of compaction curves and sensitivity curves. Marl, test no. 21. |
| Dans le texte | |
 |
Fig. 3 Exemples de courbes de sensibilité fournies par des sols compactés de natures différentes. Échelles linéaires. Examples of sensitivity curves given by different compacted soils. Linear scales. |
| Dans le texte | |
 |
Fig. 4 Exemples de courbes de sensibilité fournies par des sols compactés de natures différentes. Échelles semi-logarithmiques. Examples of sensitivity curves given by different compacted soils. Semi-logaritmic scales. |
| Dans le texte | |
 |
Fig. 5 Exemples de courbes de sensibilité fournies par deux essais consacrés à l’argile de Bavent. Échelles semi-logarithmiques. Examples of sensitivity curves given by two tests on Bavent clay. Semi-logaritmic scales. |
| Dans le texte | |
 |
Fig. 6 Essai de gonflement en parallèle. Argile compactée du Colorado. D’après Rosenbalm (2013). Multiple-specimens swelling test. Compacted clay from Colorado. |
| Dans le texte | |
 |
Fig. 7 Essai de gonflement en parallèle. Argile verte compactée (classe 2). D’après Ferber (2005). Multiple-specimens swelling test. Compacted green clay. |
| Dans le texte | |
 |
Fig. 8 Essai de gonflement en parallèle. Limon de Goderville compactée (classe 2). D’après Ferber (2005). Multiple-specimens swelling test. Compacted silt. |
| Dans le texte | |
 |
Fig. 9 Contrainte de compactage statique. a : en fonction de la teneur en eau ; b : en fonction de l’indice des vides du sol compacté. Static compaction pressure. a: versus water content; b: versus void ratio of compacted soil. |
| Dans le texte | |
 |
Fig. 10 Contrainte de compactage statique calculée comparée à la contrainte mesurée. Static compaction pressure calculated compared to the measured pressure. |
| Dans le texte | |
 |
Fig. 11 Contraintes de compactage, contraintes de reprise de compactage et pressions de gonflement. a : σrcmp fonction de σacmp ; b : σag fonction de σacmp. c : σag fonction de σarcmp. Compaction pressures, yield pressure and swelling pressures. |
| Dans le texte | |
 |
Fig. 12 Pressions de gonflement σag et pentes Swelling pressures σag and slopes |
| Dans le texte | |
 |
Fig. 13 Déformations calculées dues à l’imbibition en fonction des déformations mesurées d’après les essais en parallèle. Calculated déformations versus measured deformations from sensitivity tests. |
| Dans le texte | |
 |
Fig. 14 Déformations calculées dues à l’imbibition en fonction des déformations mesurées d’après les essais œdométriques du LCPC. a : argile verte ; b : limon de Goderville. Calculated deformations versus measured deformations from œdometer tests of LCPC. a: green clay; b: Goderville silt. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.