| Numéro |
Rev. Fr. Geotech.
Numéro 166, 2021
Modélisation Physique en Géotechnique - Partie 1
|
|
|---|---|---|
| Numéro d'article | 2 | |
| Nombre de pages | 17 | |
| DOI | https://doi.org/10.1051/geotech/2021003 | |
| Publié en ligne | 9 avril 2021 | |
Article de recherche / Research Article
Modélisation physique à 1 × g pour l’étude des conséquences de mouvements de terrain et des moyens de mitigation
1 × g physical modelling for studying the consequences of ground movements and means mitigation methods
1
Ineris, Parc technologique Alata,
F-60550
Verneuil-En-Halatte, France
2
Univ. Grenoble Alpes, CNRS, Grenoble INP, 3SR,
38041
Grenoble, France
* Auteur de correspondance : marwan.alheib@ineris.fr
Un modèle physique réduit à 1 × g de 6 m3 a été développé pour étudier les conséquences de mouvements de terrains, les mécanismes d’interactions entre les mouvements du sol et les ouvrages et les moyens de mitigation. Les mouvements de terrains sont reproduits à l’aide de vérins. Deux sols analogues (granulaire et cohésif) sont utilisés au-dessus de cavités ainsi reproduites. Cet article présente deux applications montrant la contribution de la modélisation physique. La première application concerne l’évaluation des dommages induits dans une structure en maçonnerie à l’aide de la corrélation d’images. La deuxième application concerne le dimensionnement d’un géosynthétique de renforcement au-dessus de cavités souterraines. Les deux applications montrent la capacité de la modélisation physique à combler le manque de données nécessaires à la validation des approches analytiques et empiriques.
Abstract
A 6 m3 1 × g physical model, has been developed to better assess the consequences and understand the interactions between ground movements, structure behavior and mitigation solutions. The ground movements are reproduced using jacks. Two analogous soils (granular and cohesive) are used over the cavity. The paper presents two applications to highlight the main contribution of this physical model. The first one concerns the qualification and quantification, using images correlation, of damage induced in a masonry structure and the improvement of the damage scale. The second application concerns the use of geosynthetic over shallow underground cavities as a method for hazard reduction. The two cases demonstrate the benefit of physical modeling to overcome the lack of data and in situ observations.
Mots clés : Cavités / mouvements de terrains / modélisation physique / interaction sol-structure
Key words: Cavity / ground movements / physical modelling / soil-structure interaction
© CFMS-CFGI-CFMR-CFG, 2021
1 Introduction et objectifs
La France comme beaucoup d’autres pays, regorge dans son sous-sol de nombreuses cavités naturelles et anthropiques (PNC, 2014). Elles présentent un aléa, à court ou/et à long terme, et un risque de mouvements de terrains. Les mouvements de terrains sont associés à la dégradation des cavités. Cette dégradation évolue vers la surface et finit par former un fontis ou un affaissement (Al Heib, 2008). Ces mouvements peuvent provoquer des dommages plus ou moins importants. Les ingénieurs sont confrontés à l’évaluation et à la prédiction de l’intensité de ces dommages. Ils disposent de peu d’observations documentées pour réaliser cette évaluation et préconiser des solutions de mitigation des risques. Il est également assez difficile de réaliser des corrélations directes entre la sollicitation et le dommage compte tenu des phénomènes complexes d’interaction entre les mouvements du sol et l’ouvrage. Le recours à l’expérimentation en grandeur réelle permet de développer la connaissance. Or, le coût de la réalisation d’une expérimentation à grande échelle est souvent élevé. La modélisation physique à une échelle réduite permet ainsi de surmonter cette limitation et d’offrir des informations utiles à l’expertise à coût maîtrisé. La modélisation physique permet de reproduire le comportement de prototypes (White et al., 2013 ; Green, 2014), de vérifier et de valider leur comportement dans des conditions réalistes, de disposer des données pour vérifier les résultats de modèles analytiques et numériques. Cet objectif est difficilement accessible par les approches théoriques notamment analytiques. À titre d’exemple, plusieurs modèles physiques ont été réalisés pour caractériser les mouvements du sol et la stabilité des ouvrages souterrains (Meguid et al., 2008). Pour améliorer le comportement du sol, des modèles physiques 1 × g ont été conçus pour simuler le comportement d’inclusions rigides et étudier les mécanismes de transfert de charge (e.g. Dinh, 2010 ; Houda et al., 2016).
L’objectif de cet article est de présenter les avantages d’un modèle physique (1 × g) réduit, développé pour simuler les mouvements de terrains. Deux applications sont choisies pour illustrer la capacité de cet outil à réaliser des expérimentations à une échelle réduite et reproduire le comportement des ouvrages soumis à des mouvements de terrains (structures en maçonnerie et remblais renforcés par géosynthétique). L’objectif est aussi d’apporter des observations permettant d’enrichir l’expertise et la compréhension des phénomènes d’interaction sol-structure et de renforcement du sol par un géosynthétique.
2 Simulateur de mouvements de terrains (1 × g)
La construction du modèle physique réduit nécessite le respect des lois de similitudes (Muir Wood, 2006). Le choix d’une modélisation réduite sous gravité terrestre (1 × g) impose que le facteur d’échelle de la pesanteur soit égal à un, i.e., g* = 1. Le tableau 1 permet de déduire les autres facteurs d’échelle tels que σ* = E* = c* = τ* = L* = 1/n. Cela signifie que le module de Young E et la cohésion c du modèle doivent être n fois plus petits que ceux du prototype.
Dans un objectif d’amélioration de la connaissance et de l’expertise, l’Ineris a développé un modèle physique (1 × g) de mouvements de terrains permettant ainsi d’évaluer les dommages induits sur les ouvrages existants et d’étudier des solutions de réduction de l’aléa et de mitigation du risque. L’approche expérimentale développée vise à accroître les observations et les mesures nécessaires à la validation des modèles théoriques numériques et analytiques. Le modèle physique se compose d’un bâti expérimental de dimensions 3 × 2 × 1 m3, équipé de 15 vérins mobilisant chacun une surface de 0,25 × 0,25 m2 (Fig. 1 et 2). Les vérins permettent de simuler la création d’une ou plusieurs cavités et la formation d’un mouvement de terrain en surface du sol. Les vérins peuvent être actionnés séparément à une vitesse contrôlée (plage de vitesse de 0,02 mm/s à 1 mm/min). Ce simulateur permet de reproduire les mouvements de terrain de type affaissement continu ou d’effondrement localisé (fontis) de différentes dimensions en fonction du nombre de vérins mobilisés, de l’épaisseur du recouvrement et de la nature du sol. L’amplitude maximale de mouvement en surface dépend de l’épaisseur de recouvrement, du sol utilisé et de la course maximale de vérins, qui est de 150 mm. Il permet également de reproduire des mouvements de terrain en présence de structures en surface. Les mouvements générés sont reproductibles en respectant un mode opératoire identique (vitesse de déplacement de vérins, nature du sol, etc.). Les résultats expérimentaux ont été validés par rapport aux modèles analytiques (Hor, 2012).
Deux types de sols ont été utilisés pour la réalisation des expérimentations. Le premier est un sol granulaire correspondant au sable de Fontainebleau NE34, un matériau de référence bien connu dans la modélisation physique en géotechnique (Garnier, 2002 ; Boussaid, 2005). Les propriétés mécaniques du sable ont été caractérisées par des essais de cisaillement direct, des essais triaxiaux sous faibles contraintes afin de traduire les conditions de la modélisation physique, une faible épaisseur du sol, et des essais œdométriques modifiés sans phase de déchargement (Hor, 2012). Le tableau 2 synthétise les caractéristiques de ce sable (noté SF). Il est caractérisé par sa densité relative qui dépend de l’état de compactage (lâche ou dense). Le deuxième sol utilisé est un sol cohésif correspondant à un mélange d’argile (30 % de kaolin) et de sable (70 %) de Fontainebleau (noté SK), la teneur en eau est fixée à 8 %. Ce mélange a montré un comportement élasto-plastique sans écrouissage.
Afin d’obtenir des caractéristiques reproductibles des sols avant la réalisation d’un essai, une procédure a été mise en place. Le sol est manuellement placé dans la cuve par couches d’épaisseur constante (15 cm pour le sable et 5 cm pour le sable-kaolin). Chaque couche est damée et piquetée afin de supprimer autant que possible tout historique micromécanique de mise en place et donc d’obtenir un certain niveau de densité répétable pour tous les essais. Cela est reproduit jusqu’à la hauteur désirée du massif de sol.
Le simulateur de mouvements de terrains est équipé de quatre caméras permettant de déterminer les déplacements et les déformations du sol et de la structure (Fig. 2) grâce à la technique de la corrélation d’images (DIC). Les capteurs utilisés sont de la marque Kodak-KAI-4022, 1,2 inches. Les images ont une résolution de 2048 × 2048 pixel2, 8 bits, correspondant à 7,4 µm par pixel. L’algorithme de corrélation ne peut théoriquement pas détecter des déplacements inférieurs à 2−8 pixels, soit une valeur minimale du déplacement détectable de 2−8 × 7,4 = 0,03 µm. En revanche, la précision globale de la mesure dans les conditions des essais a été évaluée de l’ordre de 0,02 mm (Nghiem, 2015). La calibration et l’analyse des images sont réalisées par le logiciel VIC-3D.
Conditions de similitude du modèle physique (1 × g).
Similitude conditions of (1 × g) physical model.
 |
Fig. 1 Représentation du simulateur de mouvements de terrain (1 × g) de l’Ineris : (a) vue générale ; (b) vue de l’ensemble des vérins et (c) vue en plan. Ineris ground movement physical model (1 × g): (a) general view; (b) view of the group of jacks and (c) plan view. |
 |
Fig. 2 Système de corrélation d’images (a) position des caméras exprimée en fonction des paramètres géométriques ; (b) Position de 4 caméras ; (c) caméras 1 et 2 observant le sol et la structure ; (d) caméras 3 et 4 observant une façade. Image correlation system (a) camera positions function of geometric parameters; (b) positions of the 4 cameras; (c) cameras 1 and 2 observing the soil and the structure; (d) cameras 3 and 4 observing a façade. |
Caractéristiques du sable de Fontainebleau NE34 et du mélange sable-kaolin.
Characterization of the NE34 Fontainebleau sand and of the sand-kaolin mix.
3 Première application : évaluation des dommages d’une structure soumise à un affaissement
L’évaluation des dommages des ouvrages soumis à des mouvements de terrains est habituellement basée sur la nature ou l’amplitude de mouvements du sol ou/et sur la typologie des ouvrages. Le niveau de dommages d’une structure en maçonnerie est estimé en fonction de la largeur des fissures induites par les mouvements du sol et leur nombre pour les classes D3 à D5 (Potts et Addenbrooke, 1997, Tab. 3). Cette évaluation a montré ses limites, notamment quant à l’estimation des déformations transmises à la structure qui définit principalement son niveau d’endommagement. Une évaluation plus juste et plus précise nécessite de prendre en compte le phénomène d’interaction sol-structure (ouvrage et sol) et les rigidités relatives entre sol et structure (Basmaji et al., 2019). L’interaction sol-structure modifie l’intensité (e.g. le nombre de fissures) et le type de dommage (traction, cisaillement, etc.) qui risque de se produire.
Classification des dommages typiques induits par le mouvement de terrains, (Potts et Addenbrooke, 1997).
Typical damage classification due to ground movement hazard (Potts and Addenbrooke, 1997).
3.1 Simulation de la structure en maçonnerie
Pour prendre en compte l’interaction sol-structure, le simulateur de mouvement de terrain est utilisé pour la génération de l’affaissement en présence d’une structure en maçonnerie permettant d’observer son endommagement en fonction de l’amplitude de l’affaissement. Les déformations de la structure sont transmises en fonction de la rigidité relative du sol et de la structure. Le prototype étudié est une maison en maçonnerie de deux étages, correspondant à un cas typique d’habitation d’une surface de 10 × 10 m2 (Fig. 3a et 3b). Les caractéristiques élastiques équivalentes de la structure sont : un module de Young EM = 6000 MPa et un coefficient de Poisson νM = 0,3. Les fondations sont du type semelles filantes en béton armé (module de Young EB = 30 000 MPa, coefficient de Poisson νB = 0,2). Une simplification du prototype initial a été réalisée pour étudier la réponse globale de la structure.
Pour simuler le comportement du prototype, trois modèles réduits de la structure ont été conçus sous forme d’une plaque réalisée dans différents matériaux. Le premier modèle est en polycarbonate avec des dimensions de 25 × 25 × 0,55 cm3 correspondant au prototype simplifié d’un radier en béton 10 × 10 × 0,25 m3, soumis à une charge répartie de 10 kPa. Le respect des lois de similitudes a été recherché en respectant les rigidités relatives. Deux types de rigidités ont été considérés : la rigidité relative en flexion, rf* = 16EI/(EsB4), et la rigidité relative axiale, ra* = 2EA/EsB (A, B, E et I : section, largeur, module de Young et inertie de la structure ; Es : module de Young du sol). Compte-tenu des dimensions de la structure et du modèle physique, un facteur d’échelle n de 40 est adopté. Le respect absolu des lois de similitudes n’est pas possible pour l’ensemble des grandeurs physiques (Tab. 4). Le modèle a été réalisé en polycarbonate représentant un radier, le poids total de la structure a été remplacé par des sacs de billes de plomb associés (Fig. 3d). Les résultats des premiers essais ont présenté plusieurs différences de comportement par rapport aux observations de dommages de structures réelles (Deck et al., 2002), notamment en termes de transfert du mouvement du sol à la structure (déflexion, mise en pente) à cause d’une rigidité axiale très élevée. Le deuxième modèle a été réalisé en silicone de dimensions 25 × 25 × 4 cm3, (Fig. 3e et 3f). Il correspond également à un radier. La comparaison des caractéristiques de ce modèle avec celui en polycarbonate est synthétisée dans le tableau 4. Le modèle en silicone a plus d’épaisseur mais son module de Young est plus petit que celui du polycarbonate. Ces propriétés traduisent moins de rigidité en flexion et de rigidité axiale que celle de la structure en polycarbonate (Tab. 4). Le modèle en silicone est élastique et plus flexible, notamment sa rigidité axiale relative : 2 et 9,6 × 10−3 respectivement pour les modèles en polycarbonate et en silicone. Lors des essais, les résultats obtenus (déformations et déplacements) ont été plus cohérents avec le comportement des ouvrages réels d’une maison individuelle. Le modèle en silicone apparaît donc comme une bonne solution pour l’étude de l’interaction sol-structure mais elle n’est pas représentative du prototype initial, i.e. d’une maison en maçonnerie.
Le troisième modèle correspond à une maison avec sa fondation, la fondation est en silicone et la maison est réalisée avec des blocs, parallélépipède rectangle, en bois dense (7 × 14 × 7 mm3) sans mortier permettant de simuler une structure en maçonnerie pour respecter les lois de similitude (Fig. 4).
La réalisation de l’expérimentation consiste à préparer le sol et déposer la structure sur une surface parfaitement horizontale avant d’actionner le déplacement du vérin, qui génère un déplacement du sol à une vitesse constante (0,15 mm/s). Grâce à la corrélation d’images, on peut obtenir les déplacements, x, y et z ainsi que les déformations de la structure et du sol.
 |
Fig. 3 Évolution des modèles de la structure : (a, b) plan horizontal et vertical de la structure prototype ; (c, d) modèle physique réduit de la structure en polycarbonate ; (e, f) modèle physique réduit de la structure en silicone. Les dimensions sont en mm. Evolution of the physical structure models: (a, b) section and plan of the prototype structure; (c, d) small physical model of the structure in polycarbonate; (e, f) small physical model of the structure in silicone. Dimensions are in mm. |
Comparaison des paramètres de modèles de structure carrée en polycarbonate, en silicone et murs en bois (Hor, 2012 ; Al Heib et al., 2013).
Comparison of the structure parameters of the structure model of polycarbonate, silicone and wood walls (Hor, 2012; Al Heib et al., 2013).
 |
Fig. 4 Modélisation physique d’une structure en maçonnerie soumise à un mouvement du sol. Physical modelling of masonry structure submitted to ground movement. |
3.2 Caractérisation de l’endommagement
Dans cette partie, un exemple d’essai sur le modèle 3 (fondation en silicone et maison en maçonnerie) est présenté. Les déplacements et les déformations de la structure sont obtenus grâce à la corrélation d’images. La figure 5 présente un exemple de la localisation de la déformation horizontale (extension et compression) de la structure à la suite du déplacement du sol. La déformation d’extension positive peut être assimilée à la création des fissures. Les zones de fortes déformations sont les zones de dommages maximaux.
La localisation de la déformation ne permet pas directement de déterminer l’ouverture des joints entre les blocs de la maçonnerie. Pour mieux caractériser l’endommagement de la structure en maçonnerie, un module (DIC-M) a été développé pour fournir le déplacement des joints entre les blocs. Un maillage régulier est généré pour l’identification des points sur les joints (Fig. 6). La longueur de joint est l’interface verticale ou horizontale entre deux blocs. Cette longueur est découpée en n éléments (Fig. 6). Chaque élément est associé à une longueur élémentaire (h) appartenant à l’interface entre deux blocs et associée au point de contact (j). Elle est égale à h pour les points intérieurs et égale à h/2 pour les points aux bords du mur (Fig. 6b). Pour ce point de l’interface, le déplacement du joint est calculé par la relation suivante :
 (1)
où u1, u2 sont les déplacements des blocs 1 et 2, n1 et n2 sont les vecteurs normaux de l’interface des blocs 1 et 2. Dans l’équation 1, une valeur négative de Δu correspond à une ouverture de fissure.
(1)
où u1, u2 sont les déplacements des blocs 1 et 2, n1 et n2 sont les vecteurs normaux de l’interface des blocs 1 et 2. Dans l’équation 1, une valeur négative de Δu correspond à une ouverture de fissure.
Le déplacement (Δu) de la longueur élémentaire h(j), en fonction de sa valeur, est associé à une classe de dommages (Di) (Tab. 3). Le ratio L*Di de la longueur cumulée est considéré comme indicateur de dommage de la structure. Il est déterminé, pour chaque classe de dommage Di, par la relation suivante :
 (2)
où «
(2)
où «  » est la longueur discrète associée au point de contact « j », et à la classe de dommages « Di ». L0 est la longueur totale cumulée des interfaces entre tous les blocs du mur. Les fissures sont classées en 6 catégories
» est la longueur discrète associée au point de contact « j », et à la classe de dommages « Di ». L0 est la longueur totale cumulée des interfaces entre tous les blocs du mur. Les fissures sont classées en 6 catégories 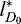 à
à  , la somme de celles-ci doit être égale à 1 :
, la somme de celles-ci doit être égale à 1 :
 (3)
(3)
Grâce à ce développement numérique et l’analyse des images (cf. Fig. 5 et 7), il est désormais possible de déterminer le niveau de dommage de la structure en fonction de la localisation des fissures et du comportement global de la structure.
 |
Fig. 5 Déformation horizontale du mur en maçonnerie, la fissuration potentielle correspond à la localisation de la déformation horizontale (valeurs positive–traction). Horizontal deformation of the masonry wall, the potential cracks correspond to the localisation of the tensile deformation (positive value–tension strain). |
 |
Fig. 6 (a) Interface entre deux blocs et discrétisation ; (b) définition de la longueur élémentaire de l’interface (h). (a) Interface between two blocks and mesh; (b) definition of the elementary length of the interface (h). |
 |
Fig. 7 Distribution des fissures pour des déplacements du vérin de (a) 10 mm ; (b) 20 mm et (c) 30 mm. Fissure distribution for jack displacement of (a) 10 mm; (b) 20 mm et (c) 30 mm. |
3.3 Résultats et discussion
Les résultats présentés ici correspondent à une cuvette d’affaissement en présence d’une structure en maçonnerie (modèle 3 : fondation en silicone et maison en maçonnerie). Les caractéristiques de l’essai sont présentées et comparées à celles du prototype (Tab. 5). Trois déplacements du vérin ont été analysés : 10, 20 et 30 mm. Le déplacement du toit de la cavité à l’échelle du prototype est de 0,4, 0,8 et 1,2 m. La structure est localisée au centre de la cuvette d’affaissement. La structure a la même dimension que la cavité (Tab. 5). Elle est donc soumise à des efforts de flexion combinés à une mise en compression (« sagging zone » en référence à la littérature internationale). L’amplitude de l’affaissement a été également mesurée en l’absence de la structure (Tab. 5).
La figure 7 représente la localisation des fissures de différentes classes de dommage et les ratios L*Di dans le cas où la structure est soumise respectivement à un déplacement de vérin de 10, 20 et 30 mm. Il est à noter que la localisation de la fissuration n’est pas symétrique malgré la symétrie de l’affaissement.
On note que les ratios L* des classes de dommages D2 et D3 augmentent avec l’augmentation du déplacement du vérin (Fig. 8). En revanche, celui de la classe (D0-1) diminue. Cette diminution correspond au fait qu’initialement il n’y a pas de fissures, ces ouvertures de joints sont probablement associées à la mise en place de la structure. Donc l’ouverture des fissures créées au démarrage de l’affaissement augmente. La présence des fissures même nombreuses de classe D0&1 et D2 n’affecte pas la stabilité de la structure. Pour un déplacement du sol compris entre 5 et 20 mm, les ratios de classes D3 et D4&5 augmentent notamment aux extrémités de la structure. À partir de 20 mm d’affaissement, le dommage de la structure n’évolue plus.
Grâce à cette modélisation physique, nous avons pu observer et quantifier les dommages de la structure dans le cas d’une structure en maçonnerie se trouvant au centre de la cuvette d’affaissement. D’autres configurations ont été modélisées pour améliorer l’évaluation de l’endommagement des ouvrages (Nghiem et al., 2015), notamment suivant le type de sollicitation en flexion et compression et/ou traction longitudinale suivant la position de la structure vis-à-vis du centre de la cuvette. La multiplication de configurations étudiées permettrait d’améliorer les modèles analytiques et les approches empiriques basées sur les observations visant à évaluer le niveau de dommage des ouvrages des zones de mouvements de terrains (Deck et al., 2002 ; Basmaji et al., 2019).
Caractéristiques géométriques de l’affaissement : prototype et modèle (facteur d’échelle 1/40).
Geometric characteristics of the subsidence: prototype and model (scale factor 1/40).
 |
Fig. 8 Évolution des indicateurs de dommage en fonction de déplacement vertical du vérin. Damage indicator evolution function of vertical displacement of the jack. |
4 Deuxième application : Formation d’une cavité sous une couche de sol renforcée par géosynthétique
La deuxième application présentée a pour objectif de montrer la capacité de la modélisation physique à rendre compte du comportement d’une couche de sol renforcée par géosynthétique soumise à un effondrement localisé et à participer à la validation des modèles analytiques de dimensionnement. Dans cette application, le rôle du renforcement géosynthétique est de réduire à des valeurs admissibles de service les tassements de surface en cas d’effondrement souterrain. La conception et le dimensionnement d’une nappe de géosynthétique au-dessus d’une cavité naturelle ou anthropique s’appuient sur plusieurs données géométriques et géotechniques telles que les dimensions de la cavité, la nature et la hauteur de la couche de sol (remblai) au-dessus de la cavité, le tassement maximal admissible en surface, etc. (Delmas et al., 2015). Dans les méthodes de dimensionnement, le modèle d’effondrement et l’action du sol sur le géosynthétique sont des paramètres importants qu’il convient de considérer avec attention. Pour les matériaux granulaires, le modèle de Terzaghi est souvent utilisé pour évaluer la charge sur la nappe géosynthétique (Villard et Briançon, 2008). Huckert (2014) a développé plus récemment un modèle analytique pour un sol cohésif. Afin de confronter les modèles analytiques à des données expérimentales, des expériences à échelle réduite ont été menées avec le simulateur de mouvements de terrains de l’Ineris. Les objectifs sont d’analyser les modes d’effondrement dans le cas des sols granulaires et cohésifs, d’observer les déplacements à la surface du sol, et de mesurer la déformée de la nappe géosynthétique et les contraintes transmises aux bords de la cavité.
4.1 Caractéristiques de l’essai d’effondrement et instrumentation mise en œuvre
Pour répondre à ces objectifs, une cavité carrée de B = 50 cm de côté, avec une épaisseur de sol H de 12,5 cm, est modélisée. Le rapport hauteur de sol/largeur de la cavité retenu est de H/B = 0,25. Le choix de ce rapport H/B permet d’étudier en particulier le comportement d’un géosynthétique posé sous faible couverture de sol. Les dimensions choisies représentent à la fois un cas réel d’une cavité de petites dimensions susceptible d’apparaître sous un remblai de faible épaisseur, et un cas d’effondrement plus conséquent si l’on considère les lois de similitude ; une échelle de 1/4 correspond à une cavité de 2 m se trouvant à 50 cm au-dessous de la surface. Deux types de sol ont été utilisés : le sable de Fontainebleau (SF) et le mélange sable-kaolin (SK). Le géosynthétique utilisé est un produit industriel bidirectionnel (deux directions de renforcement) commercialisé sous l’appellation PET200. Pour cette expérimentation, en plus du système de caméras utilisés pour déterminer les déplacements de surface, 7 capteurs de distance (radar) de type VL6180X (Flightsense), utilisant une technique de mesure laser (Fig. 9), ont été utilisés pour mesurer les déplacements verticaux de la portion de nappe géosynthétique située au droit de la cavité. Chaque radar est placé sous la nappe géosynthétique dans un boîtier de protection en plastique de 5 × 5 cm, dont la face supérieure est percée d’un trou circulaire de petit diamètre pour laisser passer le faisceau lumineux émis par le capteur. La précision de la mesure de distance est de 2 mm.
Les contraintes verticales en différentes positions du sol (Fig. 9) ont été mesurées par des cellules de pression de petite taille (C2 à C13) montées et assemblées à l’Ineris. Les cellules de pression utilisées sont des transducteurs qui convertissent la pression en un signal électrique. La cellule est placée dans un boîtier en aluminium de dimensions 62 × 62 × 26 mm. Le calibrage des cellules de pression a été réalisé avant le démarrage des essais en appliquant un poids connu. La précision de la mesure hors sol est de 0,5 % de la pression mesurée. Pour estimer le déplacement horizontal de la nappe géosynthétique en bordure de la cavité (points A et B), des câbles métalliques inextensibles coulissant dans des gaines rigides ont été fixés à l’une de leurs extrémités au géosynthétique (Fig. 10 et 11).
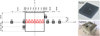 |
Fig. 9 Localisation des radars (R) et des capteurs de pression (C). Location of radars (R) and stress measurement cells (C). |
 |
Fig. 10 Câbles de mesure des déplacements horizontaux de la nappe de géosynthétique (GSY) aux bords de la cavité. Cables to measure the horizontal displacements of the geosynthetic (GSY) layer on the borders of the cavity. |
 |
Fig. 11 Étapes de préparation d’une expérimentation : (A) installation des instruments et du RG ; (B) installation du sol et localisation de la cavité; (C) chargement du sol. Steps of preparation of an experiment: (A) installation of instruments and the RG; (B) installation of soil and cavity position; (C) loading of the soil. |
4.2 Préparation et procédure d’essai
Deux essais ont été réalisés avec le sable de Fontainebleau (SF1 et SF2) et deux essais avec le mélange sable-kaolin (SK1 et SK2). Quatre vérins de 25 × 25 cm permettent de simuler la cavité de forme carrée de dimensions 50 × 50 cm (Fig. 1 et 11). Une nappe géosynthétique de 1,7 × 1 m est posée au fond du modèle, tendue manuellement, et fixée à sa périphérie dans la direction longitudinale, ce qui permet par la suite de faire l’hypothèse d’un renforcement monodirectionnel (Fig. 11). La préparation de l’essai consiste d’abord à installer les radars et les cellules de pression (Fig. 11a). On vient positionner la nappe de géosynthétique puis le sol est mis en place et compacté en une seule couche pour le sable et en couches successives de 5 cm pour le sol cohésif (sable-kaolin) (Fig. 11b). Les radars et les cellules de pression sont vérifiés et calibrés. Les mesures obtenues à cette étape sont les mesures initiales de référence. Les vérins sont actionnés à une vitesse de 0,03 mm/s pour atteindre l’amplitude du déplacement souhaitée, soit 90 mm pour les essais présentés. Un chargement de surface par des plaques métalliques est réalisé, après la descente de vérin de 90 mm, par palliers avec un temps de stabilisation entre les mesures de distance et de pression (Fig. 11c).
5 Résultats et discussion
5.1 Cas d’un sol granulaire
Les expérimentations, pour un même type du sol, fournissent des résultats très proches (Tab. 6). Dans le cas du matériau granulaire, la cuvette d’affaissement obtenue par photogrammétrie est symétrique (SF1, Fig. 12), la zone affectée par le déplacement des vérins s’étend en surface sur une zone de 56,5 × 58,8 cm soit une surface supérieure à celle de la cavité créée (50 × 50 cm), l’angle d’influence est de l’ordre de 30° en fin d’essai. Le déplacement vertical de surface (W) est maximal au centre de la cavité. Les déplacements horizontaux de surface (U et V) sont maximums au voisinage des bords de la cavité. Sur le pourtour de la cavité, le ratio des déplacements verticaux et horizontaux du sol de surface est de 0,4.
Le tableau 6 résume les valeurs des déplacements maximum du sol (horizontal : U, V et vertical : W) et du géosynthétique (f) pour les deux tests réalisés. Les profils de déplacement verticaux du géosynthétique, pour la phase d’ouverture de la cavité, sont comparés à ceux du sol de surface (Fig. 13). On constate (Tab. 6) qu’au centre de la cavité, les déplacements maximums du sol sont de 27,6 mm et 22,5 mm, ils atteignent 39,8 mm et 43 mm au niveau du géosynthétique ce qui traduit un phénomène de foisonnement. En considérant un affaissement de surface et une déformation de la nappe sous forme de paraboloïdes, les coefficients de foisonnement (Ce) calculés sont égaux à 1,05 et 1,08 en se basant sur la relation simple (Ce = 1 + (ΔS/2H)), avec ΔS = W−f (Briançon et Villard, 2006). Grâce au modèle physique, il est ainsi possible d’estimer le coefficient de foisonnement du sol, un paramètre souvent supposé a priori dans les calculs analytiques.
Les contraintes mesurées sont normalisées par la contrainte verticale géostatique γH = 1,92 kPa. Les capteurs positionnés de part et d’autre montrent, lors de la descente des vérins, un accroissement quasiment continu par rapport à la valeur initiale de référence (Fig. 14a). Cette augmentation est fonction de leur position par rapport à la cavité et de l’amplitude du déplacement des vérins (Fig. 14b). On note que les cellules proches de la cavité mesurent le transfert de charge le plus important (C13). Néanmoins, il est à noter que les contraintes mesurées par les capteurs, d’un essai à un autre, sont très hétérogènes. Ceci reflète la difficulté des mesures de contrainte dans un massif de sol (Adachi et al., 2003). Ces mesures de contraintes doivent être considérées comme qualitatives et en aucun cas quantitatives compte tenu des écarts observés par rapport à la contrainte géostatique avant la mobilisation des vérins.
La déformée de géosynthétique obtenue expérimentalement a été comparée à celle calculée analytiquement selon la méthode proposée par Villard et Briançon (2008), en supposant une distribution uniforme de la charge au-dessus du géosynthétique dont l’intensité σvg est calculée selon la formule de Terzaghi. Les paramètres géométriques (largeur de la cavité, hauteur de la couche de sol, etc.) et mécaniques (poids volumique, angle de frottement, etc.) utilisés dans le calcul analytique sont ceux de l’expérimentation. La raideur longitudinale du géosynthétique est de 170 kN/m pour une déformation de 1,7 %. La comparaison entre les résultats analytiques, pour une distribution uniforme classiquement utilisée pour le dimensionnement de la nappe de géosynthétique (analytique 1), montre un écart significatif avec les résultats expérimentaux (Fig. 15) notamment en termes de géométrie de la déformée de la nappe. Une distribution de charge tridimensionnelle en forme de pyramide inversée (Fig. 15, analytique 2) pour laquelle la charge est maximale (Q = 3/2 σvg) en bordure de la cavité et nulle au centre de la cavité a été testée à titre comparatif (Hassoun, 2019), elle correspond à un triangle inversé (DTI) pour une coupe passant au milieu de la cavité. Comme on peut le constater sur la figure 14, cette géométrie de charge permet de mieux rendre compte de la géométrie aplatie de la déformée de la nappe. On peut aussi noter que les mesures expérimentales sont comprises entre les deux courbes analytiques. Néanmoins les résultats de deux hypothèses sont, dans ce cas, très proches.
On peut conclure, en considérant les observations expérimentales, que la comparaison de la forme et l’amplitude de la déformée de géosynthétique a permis de montrer que globalement l’hypothèse d’une charge uniforme (analytique 1) est, pour cette géométrie de remblai, satisfaisante pour dimensionner le géosynthétique. Néanmoins, des améliorations du modèle analytique sont possibles pour mieux estimer l’intensité et la géométrie de la charge agissant sur le géosynthétique.
Après la formation de l’affaissement induit par la création de la cavité, l’expérience a été poursuivie, des surcharges localisées au centre de la zone effondrée ont été progressivement appliquées en surface (Fig. 11). Ces surcharges induisent principalement une augmentation de la flèche (f) du géosynthétique au centre de la cavité, les déplacements verticaux du géosynthétique sur le pourtour de la cavité sont moins affectés (Fig. 16). La phase finale, correspondant à un déchargement, s’est traduite par un soulèvement du géosynthétique (comportement élastique de celui-ci). La flèche du géosynthétique obtenue à la fin du déchargement reste plus importante que la valeur avant chargement, compte tenu, d’une part, de la présence de la couche de sol qui s’est effondrée sur le géosynthétique et dont le comportement n’est pas réversible et d’autre part à la suite des glissements du géosynthétique aux bordures de la cavité qui se traduisent par des déplacements horizontaux de l’ordre de 4 mm aux bords de la cavité.
Les contraintes augmentent pratiquement linéairement en fonction de la surcharge appliquée, notamment pour les capteurs les plus proches de la cavité (Fig. 17), malgré la faible épaisseur de la couche de sol, le géosynthétique ne reprend pas en totalité la charge appliquée en surface, une partie est transmise aux bords de la cavité. Ce résultat est très important pour le dimensionnement de géosynthétique, notamment en termes de transfert de charge appliquée au bord de la cavité et au modèle géométrique utilisé (distribution de la charge sur la nappe) pour estimer les contraintes agissantes sur la nappe de géosynthétique.
Déplacements (U, V, W), flèche (f) du géosynthétique (GSY) et coefficient de foisonnement (Ce) du sol pour les deux essais avec sable de Fontainebleau (SF).
Displacements (U, V, W), deflexion (f) of geosynthetic and bulking coefficient (Ce) for the two Fontainebleau sand experimentations (SF).
 |
Fig. 12 Essai avec le sable de Fontainebleau – déplacements verticaux et horizontaux de la surface du sol : (a) vue 3D du déplacement vertical W (mm) ; (b) déplacements horizontaux U et V (mm) selon X et Y. Experimentation with Fontainebleau sand – vertical and horizontal displacement: (a) 3D vertical displacement W (mm); (b) horizontal displacement U and V (mm) in X and Y directions. |
 |
Fig. 13 Essai avec sable de Fontainebleau (SF1 et SF2) – déformée du géosynthétique (GSY) et déplacements en surface (sol). Experimentation with Fontainebleau sand – (SF1 and SF2) geosynthetic (GSY) deformation and surface displacements (soil). |
 |
Fig. 14 Évolution des contraintes des essais avec le sable de Fontainebleau : (A) évolution des contraintes verticales ; (B) reports de charge verticale mesurées à la phase finale. Stress evolution for the tests carried out with Fontainebleau sand: (A) evolution of vertical stresses; (B) vertical stress measurements at final stage. |
 |
Fig. 15 Comparaison des déformées expérimentale et analytique (1 et 2) du géosynthétique (GSY) : (a) déformée de GSY ; (b) différentes distribution de la charge σvg et Q. Comparison between analytical and experimental results of the deformation of the geosynthetic (GSY): (a) deformation of the GSY; (b) different distributions of the load σvg et Q. |
 |
Fig. 16 Évolution de la déformée du géosynthétique (GSY) pendant les cycles du chargement et déchargement. Evolution of the deformation of the geosynthetic (GSY) during the loading and unloading phases. |
 |
Fig. 17 Évolution des contraintes en fonction des phases du chargement (15, 35 et 55 kg). Evolution of stresses during the loading phases (15, 35 et 55 kg). |
5.2 Cas d’un sol cohésif : mélange sable-kaolin
Deux essais avec le mélange sable–kaolin (SK1 et SK2), renforcé à sa base par le géosynthétique (PET 200) ont été réalisés. La démarche suivie est similaire à celle des essais avec le sable sauf pour le contrôle de la teneur en eau (8 %) qui est mesurée avant la mise en place du sol dans la cuve. Le déplacement du sol en surface est peu significatif après avoir abaissé verticalement les vérins de 90 mm. Il est de l’ordre de 2 mm. Les déplacements horizontaux U et V du sol de surface sont du même ordre de grandeur que la précision de la corrélation d’images ; soit de 0,02 mm. Dans ce cas, les conditions géométriques (H/B = 0,25) et les caractéristiques physiques et mécaniques (γ = 15,3 kN/m3 et c = 35 kPa) sont suffisantes pour assurer la stabilité du sol. Le déplacement vertical du géosynthétique résulte de son poids propre (de l’ordre de ± 5 mm). Aucune partie de sol ne s’est effondrée sur le géosynthétique. Les mesures enregistrées par les capteurs de contrainte dans les zones d’ancrage pendant le déplacement des vérins sont assez similaires pour les deux essais SK1 et SK2. Comme pour les essais avec le sol granulaire (sable de Fontainebleau), les valeurs initiales de référence de la contrainte à la base de la couche du sol ne sont pas toujours égales à γH = 2,05 kPa. Les capteurs les plus affectés par les augmentations de contrainte sont les plus proches de la cavité. La comparaison des mesures de contrainte d’un sol granulaire (SF) et cohésif (SK) est présentée sur la figure 18. Les reports de charge dans le cas d’un sol cohésif s’avèrent principalement localisés au voisinage de la cavité. En revanche, pour les capteurs les plus éloignés de la cavité, les reports de charge dans le cas du sol granulaire sont plus importants que ceux obtenus avec le sol cohésif. Par conséquent, les reports de charge sont moins importants et plus diffus dans le cas d’un sol granulaire, alors qu’ils sont plus intenses et fortement localisés aux bords de la cavité dans le cas d’un sol cohésif.
La déformation du géosynthétique a été mesurée uniquement en fin de chargement soit après une surcharge en surface de 55 kg. Les déplacements mesurés sont dus à la surcharge conduisant à l’effondrement du sol. Le déplacement vertical du géosynthétique pour les deux essais réalisés (SK1 et SK2) sont très proches (Fig. 19). Les observations issues des essais expérimentaux montrent que la forme et l’amplitude des déplacements sont différentes de celles observées avec un sol granulaire.
Le mécanisme d’effondrement en blocs de la couche de sol cohésive observé après le chargement de la surface (Fig. 11), est assez proche de celui observé par Huckert (2014). En se basant sur les observations expérimentales, une forme de pyramide tronquée est proposée pour décrire la géométrie du volume de sol effondré (Fig. 20). Celui-ci présente des fissures qui permettent de délimiter trois zones distinctes (A, B et C).
Pour comparer les résultats expérimentaux avec ceux du modèle analytique, pour le cas d’un sol cohésif, nous avons utilisé le modèle de Huckert (2014). Ce modèle considère que la nappe de géosynthétique est sollicitée localement par deux forces ponctuelles (2P) pour tenir compte de la forte rigidité des blocs effondrés sur la nappe. Cette hypothèse diffère sensiblement de l’hypothèse d’une charge uniforme repartie formulée dans le cas d’un sol granulaire. Les deux forces sont estimées en fonction du poids des blocs effondrés en se basant sur les observations du modèle physique. Pour estimer la charge supportée par la nappe de géosynthétique, les poids des deux blocs B et C sont supposés négligeables au regard de la charge de 55 kg appliquée au centre de la cavité. On considère que le poids du bloc A de sol effondré (4,5 kg) et la charge de surface à la rupture (55 kg) sont transmis au géosynthétique sans aucun report de charge. On admet également que la charge transmise au géosynthétique est supportée en totalité (hypothèse pessimiste) par une bande de renforcement de largeur 0,15 cm (nappe ancrée dans une seule direction) soit une charge totale par mètre de large de 59,5 × 9,81/0,15 = 3,9 kN/m. Le déplacement horizontal UA en bordure de cavité est supposé égal à sa valeur expérimentale moyenne mesurée aux bords A et B de la cavité (2 et 1,5 mm respectivement). La raideur du géosynthétique est de 170 kN/m. L’espacement des charges P est supposé égal à la taille de la dalle de chargement (15 cm). La figure 19 compare les déplacements verticaux obtenus expérimentalement et analytiquement selon le modèle de Huckert (2014), adapté selon les observations expérimentales, notamment pour les dimensions de blocs effondrés et le calcul des forces ponctuelles (2P). On observe que les courbes analytique et expérimentales sont très proches.
Pour conclure, cette deuxième application a permis de distinguer les mouvements induits dans le cas d’un sol granulaire et cohésif. Elle a fourni également les observations et les données nécessaires à la validation des modèles analytiques pour les deux types de sol testés.
 |
Fig. 18 Intensités des reports de charge dans le cas d’un sol granulaire (SF) et sol cohésif (SK). Intensity of load transfer ratio for sandy (SF) and cohesive soil (SK). |
 |
Fig. 19 Déformées expérimentale et analytique de géosynthétique, d’un sol cohésif (SK) – chargement 55 kg. Experimental and analytical deformation of the geosynthetic for cohesive soil (SK) – load 55 kg. |
 |
Fig. 20 Géométrie proposée du bloc de sol cohésif effondré sur le géosynthétique (GSY). Suggested geometry of collapsed soil over the geosynthetic (GSY). |
6 Conclusion
Cet article a présenté le modèle physique (1 × g) réduit développé pour simuler les mouvements de terrains. Il s’agit d’un modèle à la fois simple et efficace équipé de vérins pour simuler les mouvements de terrain, de caméras pour suivre les déplacements et les déformations, ainsi que de cellules de pression et de radars. Au travers des deux applications présentées, nous avons montré que l’utilisation du simulateur présente plusieurs avantages, notamment les faibles coût et temps de réalisation d’un essai à une échelle réduite par rapport à d’autres moyens d’investigation (ex. essais in situ). Les deux applications ont illustré la capacité de cet outil à réaliser des expérimentations à une échelle réduite et reproduire le comportement des ouvrages soumis à des mouvements de terrains (structures en maçonnerie et remblais renforcés par géosynthétique). L’interaction entre l’ouvrage et le sol a été prise en compte (utilisation de semelles dont les caractéristiques et les dimensions permettent de respecter les conditions de similitude et les mécanismes d’interaction) et des mesures de déformations des sols et de l’ouvrage ont été obtenues grâce à l’instrumentation et à la corrélation d’images. L’étude de l’endommagement d’une structure soumise à un mouvement de terrain a permis de mieux caractériser l’endommagement de la structure grâce au développement d’une méthode basée sur la corrélation d’images. Elle a également permis de localiser et quantifier les fissures induites et donc de mieux juger du niveau de dommages. Le simulateur de mouvements de terrains a également été utilisé pour étudier le rôle d’un renforcement par géosynthétique. Cette modélisation physique apporte des observations permettant d’enrichir l’expertise et la compréhension des phénomènes d’interaction entre le sol, le renfort géosynthétique et le remblai (cohésif ou granulaire). Les résultats obtenus sont analysés à la lumière des méthodes de dimensionnement analytiques actuelles. Ils ont notamment fait apparaître les différences de comportement des sols granulaire et cohésif en termes de type de rupture et de la sollicitation du géosynthétique. Ces résultats expérimentaux apportent également des compléments et des pistes d’amélioration pour le dimensionnement de la nappe géosynthétique.
Liste de notations
σvg : Charge repartie agissant sur le RG
Δu : Déplacement relative de l’interface entre deux blocs (joint)
A : Section de l’élément de la structure
B : Largeur de l’élément de la structure
Ce : Coefficient de foisonnement du sable
Di : Associée à la classe de dommages
Dr : Densité relative du sable
f : Flèche de la nappe de géosynthétique (déflection)
H : Hauteur du sol au-dessus de la cavité
h : Longueur élémentaire de l’interface
L0 : Longueur totale cumulée des interfaces entre tous les blocs du mur
 :
Longueur discrète associée au point de contact « j »
:
Longueur discrète associée au point de contact « j »
n1 et n2 : Vecteurs normaux de l’interface des blocs 1 et 2
n : Facteur de réduction des caractéristiques d’un prototype
p : Force ponctuelle agissante sur le géosynthétique
Q : Charge maximale en bordure de la cavité
U : Déplacement horizontal du sol selon x
UA : Déplacement horizontal de la nappe de GSY en bordure de la cavité
V : Déplacement horizontal du sol selon y
u1, u2 : Déplacements de blocs 1 et 2
W : Déplacement vertical du sol selon z
rf* : Rigidité relative en flexion
ra* : Rigidité relative axiale
Références
- Adachi T, Kimura M, Kishida K. 2003. Experimental study on the distribution of earth pressure and surface settlement through three-dimensional trapdoor tests. Tunnel Undergr Space Technol 18(2-3): 171–183. DOI: 10.1016/S0886-7798(03)00025-7. [Google Scholar]
- Al Heib M. 2008. State of the art of the prediction methods of short and long-term ground movements (subsidence and sinkholes) for mines in France. In: Michel T, Fournier H, eds. Coal geology research progress. ISBN:978-1-60456-596-6. New York: Nova Science Publishers Inc., pp. 53–76. [Google Scholar]
- Al Heib M, Emeriault F, Caudron M, Nghiem L, Hor B. 2013. Large-scale soil-structure physical model (1g)-assessment of structure damages. Int J Phys Model Geotech 13(4): 138–152. DOI: 10.1680/ijpmg.13.00007. [Google Scholar]
- Basmaji B, Deck O, Al Heib M. 2019. Analytical model to predict building deflections induced by ground movements. Eur J Environ Civil Eng 23(3): 409–431. DOI: 10.1080/19648189.2017.1282382. [Google Scholar]
- Boussaid K. 2005. Sols intermédiaires pour la modélisation physique : application aux fondations superficielles. Thèse de doctorat, École Centrale de Nantes et Université de Nantes. [Google Scholar]
- Briançon L, Villard P. 2006. Dimensionnement des renforcements géosynthétiques de plateformes sur cavités. Rev Fr Geotech 117: 51–61. DOI: https://doi.org/10.1051/geotech/2006117051. [CrossRef] [Google Scholar]
- Deck O, Al Heib M, Hommand F, Gueniffey Y, Wojtkowiak F. 2002. Méthode de prévision des dégradations des structures bâties en zone d’affaissement minier. Rev Fr Geotech 100: 15–33. DOI: 10.1051/geotech/2002100015. [Google Scholar]
- Delmas Ph, Villard P, Huckert A. 2015. Dimensionnement à court terme et long terme de structure renforcée par géosynthétique sur cavités potentielles : prise en compte de la sécurité. In: 10es Rencontres Géosynthétiques, 24–26 mars, La Rochelle, France, pp. 13–34. [Google Scholar]
- Dinh AQ. 2010. Étude sur modèle physique des mécanismes de transfert de charge dans les sols renforcés par inclusions rigides. Thèse de doctorat, École Nationale des Ponts et Chaussées. [Google Scholar]
- Garnier J. 2002. Properties of soil samples used in centrifuge models. Conference Proceedings. Phys Model Geotech, St John’s, Canada. ISBN: 9058093891. [Google Scholar]
- Green DL. 2014. Modelling geomorphic systems: Scaled physical models. In: Geomorphological Techniques, Chapter 5.3. British Society for Geomorphology, pp. 1–17. ISSN: 2047-0371. [Google Scholar]
- Hassoun M. 2019. Modélisation physique du renforcement par géosynthétique des remblais granulaires et cohésifs sur cavité. Thèse de doctorat de la Communauté Université Grenoble Alpes. [Google Scholar]
- Hor B. 2012. Evaluation et réduction des conséquences des mouvements de terrains sur le bâti : approches expérimentale et numérique. Thèse de doctorat, Institut National des Sciences Appliquées de Lyon. [Google Scholar]
- Houda M, Jenck O, Emeriault F. 2016. Massifs de sol renforcés par inclusions rigides : analyse de l’effet d’un chargement cyclique vertical quasi statique par expérimentation du modèle réduit et validation numérique. Rev Fr Geotech 147(2). DOI: 10.1051/geotech/2016006. [Google Scholar]
- Huckert A. 2014. Approches expérimentale et numérique du dimensionnement de renforcements géosynthétiques sur cavités et inclusions rigides. Thèse de doctorat, Université de Grenoble. [Google Scholar]
- Meguid MA, Saada O, Nunes MA, Mattar J. 2008. Physical modeling of tunnels in soft ground: A review. Tunnel Undergr Space Technol 23(2): 185–198. DOI: 10.1016/j.tust.2007.02.003. [Google Scholar]
- Muir Wood D. 2006. Physical modelling. In: Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Millpress Science Publishers/IOS Press, pp. 3639–3643. [Google Scholar]
- Nghiem L. 2015. Évaluation des dommages induits par des mouvements de terrain sur des structures en maçonnerie à l’aide de la modélisation physique. Thèse de doctorat, Université de Grenoble. [Google Scholar]
- Nghiem L, Al Heib M, Emeriault F. 2015. Method based on digital image correlation for damage assessment in masonry structures. Eng Struc 86: 1–15. DOI: 10.1016/j.engstruct.2014.12.021. [Google Scholar]
- PNC. 2014. Plan national pour la prévention des risques d’effondrements de cavités souterraines. Direction générale de la Prévention des risques. Ministère de l’Écologie, du Développement durable et de l’Énergie. [Google Scholar]
- Potts DM, Addenbrooke TI. 1997. A structure’s influence on tunnelling-induced ground movements. Proc Inst Civil Eng – Geotech Eng 125(2): 109–125. DOI: 10.1680/igeng.1997.29233. [Google Scholar]
- Villard P, Briançon L. 2008. Design of geosynthetic reinforcements for platforms subjected to localized sinkholes. Can Geotech J 45: 196–209. DOI: 10.1139/T07-083. [Google Scholar]
- White DJ, Gaudin C, Take WA. 2013. General Report for TC104, Physical Modelling in Geotechnics. In: Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, pp. 867–873. [Google Scholar]
Citation de l’article : Marwan Al Heib, Mouhamad Hassoun, Huu-Luyen Nghiem, Fabrice Emeriault, Pascal Villard. Modélisation physique à 1 × g pour l’étude des conséquences de mouvements de terrain et des moyens de mitigation. Rev. Fr. Geotech. 2021, 166, 2.
Liste des tableaux
Conditions de similitude du modèle physique (1 × g).
Similitude conditions of (1 × g) physical model.
Caractéristiques du sable de Fontainebleau NE34 et du mélange sable-kaolin.
Characterization of the NE34 Fontainebleau sand and of the sand-kaolin mix.
Classification des dommages typiques induits par le mouvement de terrains, (Potts et Addenbrooke, 1997).
Typical damage classification due to ground movement hazard (Potts and Addenbrooke, 1997).
Comparaison des paramètres de modèles de structure carrée en polycarbonate, en silicone et murs en bois (Hor, 2012 ; Al Heib et al., 2013).
Comparison of the structure parameters of the structure model of polycarbonate, silicone and wood walls (Hor, 2012; Al Heib et al., 2013).
Caractéristiques géométriques de l’affaissement : prototype et modèle (facteur d’échelle 1/40).
Geometric characteristics of the subsidence: prototype and model (scale factor 1/40).
Déplacements (U, V, W), flèche (f) du géosynthétique (GSY) et coefficient de foisonnement (Ce) du sol pour les deux essais avec sable de Fontainebleau (SF).
Displacements (U, V, W), deflexion (f) of geosynthetic and bulking coefficient (Ce) for the two Fontainebleau sand experimentations (SF).
Liste des figures
 |
Fig. 1 Représentation du simulateur de mouvements de terrain (1 × g) de l’Ineris : (a) vue générale ; (b) vue de l’ensemble des vérins et (c) vue en plan. Ineris ground movement physical model (1 × g): (a) general view; (b) view of the group of jacks and (c) plan view. |
| Dans le texte | |
 |
Fig. 2 Système de corrélation d’images (a) position des caméras exprimée en fonction des paramètres géométriques ; (b) Position de 4 caméras ; (c) caméras 1 et 2 observant le sol et la structure ; (d) caméras 3 et 4 observant une façade. Image correlation system (a) camera positions function of geometric parameters; (b) positions of the 4 cameras; (c) cameras 1 and 2 observing the soil and the structure; (d) cameras 3 and 4 observing a façade. |
| Dans le texte | |
 |
Fig. 3 Évolution des modèles de la structure : (a, b) plan horizontal et vertical de la structure prototype ; (c, d) modèle physique réduit de la structure en polycarbonate ; (e, f) modèle physique réduit de la structure en silicone. Les dimensions sont en mm. Evolution of the physical structure models: (a, b) section and plan of the prototype structure; (c, d) small physical model of the structure in polycarbonate; (e, f) small physical model of the structure in silicone. Dimensions are in mm. |
| Dans le texte | |
 |
Fig. 4 Modélisation physique d’une structure en maçonnerie soumise à un mouvement du sol. Physical modelling of masonry structure submitted to ground movement. |
| Dans le texte | |
 |
Fig. 5 Déformation horizontale du mur en maçonnerie, la fissuration potentielle correspond à la localisation de la déformation horizontale (valeurs positive–traction). Horizontal deformation of the masonry wall, the potential cracks correspond to the localisation of the tensile deformation (positive value–tension strain). |
| Dans le texte | |
 |
Fig. 6 (a) Interface entre deux blocs et discrétisation ; (b) définition de la longueur élémentaire de l’interface (h). (a) Interface between two blocks and mesh; (b) definition of the elementary length of the interface (h). |
| Dans le texte | |
 |
Fig. 7 Distribution des fissures pour des déplacements du vérin de (a) 10 mm ; (b) 20 mm et (c) 30 mm. Fissure distribution for jack displacement of (a) 10 mm; (b) 20 mm et (c) 30 mm. |
| Dans le texte | |
 |
Fig. 8 Évolution des indicateurs de dommage en fonction de déplacement vertical du vérin. Damage indicator evolution function of vertical displacement of the jack. |
| Dans le texte | |
 |
Fig. 9 Localisation des radars (R) et des capteurs de pression (C). Location of radars (R) and stress measurement cells (C). |
| Dans le texte | |
 |
Fig. 10 Câbles de mesure des déplacements horizontaux de la nappe de géosynthétique (GSY) aux bords de la cavité. Cables to measure the horizontal displacements of the geosynthetic (GSY) layer on the borders of the cavity. |
| Dans le texte | |
 |
Fig. 11 Étapes de préparation d’une expérimentation : (A) installation des instruments et du RG ; (B) installation du sol et localisation de la cavité; (C) chargement du sol. Steps of preparation of an experiment: (A) installation of instruments and the RG; (B) installation of soil and cavity position; (C) loading of the soil. |
| Dans le texte | |
 |
Fig. 12 Essai avec le sable de Fontainebleau – déplacements verticaux et horizontaux de la surface du sol : (a) vue 3D du déplacement vertical W (mm) ; (b) déplacements horizontaux U et V (mm) selon X et Y. Experimentation with Fontainebleau sand – vertical and horizontal displacement: (a) 3D vertical displacement W (mm); (b) horizontal displacement U and V (mm) in X and Y directions. |
| Dans le texte | |
 |
Fig. 13 Essai avec sable de Fontainebleau (SF1 et SF2) – déformée du géosynthétique (GSY) et déplacements en surface (sol). Experimentation with Fontainebleau sand – (SF1 and SF2) geosynthetic (GSY) deformation and surface displacements (soil). |
| Dans le texte | |
 |
Fig. 14 Évolution des contraintes des essais avec le sable de Fontainebleau : (A) évolution des contraintes verticales ; (B) reports de charge verticale mesurées à la phase finale. Stress evolution for the tests carried out with Fontainebleau sand: (A) evolution of vertical stresses; (B) vertical stress measurements at final stage. |
| Dans le texte | |
 |
Fig. 15 Comparaison des déformées expérimentale et analytique (1 et 2) du géosynthétique (GSY) : (a) déformée de GSY ; (b) différentes distribution de la charge σvg et Q. Comparison between analytical and experimental results of the deformation of the geosynthetic (GSY): (a) deformation of the GSY; (b) different distributions of the load σvg et Q. |
| Dans le texte | |
 |
Fig. 16 Évolution de la déformée du géosynthétique (GSY) pendant les cycles du chargement et déchargement. Evolution of the deformation of the geosynthetic (GSY) during the loading and unloading phases. |
| Dans le texte | |
 |
Fig. 17 Évolution des contraintes en fonction des phases du chargement (15, 35 et 55 kg). Evolution of stresses during the loading phases (15, 35 et 55 kg). |
| Dans le texte | |
 |
Fig. 18 Intensités des reports de charge dans le cas d’un sol granulaire (SF) et sol cohésif (SK). Intensity of load transfer ratio for sandy (SF) and cohesive soil (SK). |
| Dans le texte | |
 |
Fig. 19 Déformées expérimentale et analytique de géosynthétique, d’un sol cohésif (SK) – chargement 55 kg. Experimental and analytical deformation of the geosynthetic for cohesive soil (SK) – load 55 kg. |
| Dans le texte | |
 |
Fig. 20 Géométrie proposée du bloc de sol cohésif effondré sur le géosynthétique (GSY). Suggested geometry of collapsed soil over the geosynthetic (GSY). |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




