| Numéro |
Rev. Fr. Geotech.
Numéro 167, 2021
|
|
|---|---|---|
| Numéro d'article | 5 | |
| Nombre de pages | 15 | |
| DOI | https://doi.org/10.1051/geotech/2021018 | |
| Publié en ligne | 26 mai 2021 | |
Revue / Review Article
Calculs probabilistes des déplacements dus à la réalisation de tunnels à l’aide d’un modèle aux éléments finis
Finite element-based probabilistic analyses of displacements due to tunnel construction
1
Eiffage Génie Civil,
3-7 place de l’Europe,
78140
Vélizy-Villacoublay, France
2
iTEC, School of Engineering and Architecture (HEIA-FR), HES-SO, University of Applied Sciences Western Switzerland,
Pérolles 80,
CH-1700
Fribourg, Suisse
3
GeoMod SA,
Epinettes 32,
CH-1007
Lausanne, Suisse
* Auteur de correspondance : yi.zhang@eiffage.com
L’estimation des déplacements dus à la réalisation de tunnels est un sujet important pour les projets des travaux souterrains en sites urbains. Ces déplacements, plus particulièrement les tassements et gonflements, sont souvent l’origine d’endommagements pour les constructions avoisinantes et les ouvrages en cours de construction. Cet article présente le cadre d’une approche probabiliste à l’aide d’un modèle aux éléments finis permettant d’estimer ces déplacements. Cette approche permet de prendre en compte les incertitudes liées aux problèmes géotechniques (manque de données d’entrée, variabilité spatiale des sols, etc.). Une méthode pour la vérification probabiliste des déplacements est tout d’abord définie à l’aide du calcul de la probabilité de défaillance Pf (ou de l’indice de fiabilité β) en fonction des niveaux cibles de sécurité ou performance. Elle est ensuite appliquée à un tunnel réalisé en méthode conventionnelle grâce au couplage des outils ZSOIL et UQLab. Les évaluations de fiabilité (probabilité de défaillance et indice de fiabilité) de la fonction de sécurité basées sur les résultats des calculs aux éléments finis ont été réalisées avec succès à l’aide des méthodes FORM, AK-MCS et MCS. Cette approche probabiliste illustre l’évaluation de la fiabilité aux cas ELS selon les Eurocodes.
Abstract
The estimation of movements due to the construction of tunnels is an important subject for underground works projects in urban sites. These displacements, particularly settlements and swellings, may bring detrimental consequences to neighbouring buildings and structures under construction. This article presents the framework of a probabilistic approach using a finite elements model to estimate these displacements. It takes into account the uncertainties related to geotechnical problems (lack of input data, spatial variability of soils, etc.). Using the probability of failure Pf (or a reliability index β) as a function of the selected safety or performance levels, a method for the probabilistic evaluation of displacements is firstly defined. It is then applied to a tunnel constructed using the conventional method thanks to the coupling of the ZSOIL and UQLab tools. The reliability assessment (probability of failure and reliability index) of the safety function based on the results of finite elements model has been carried out successfully with FORM, AK-MCS and MCS methods. This probabilistic approach illustrates the reliability assessment for SLS (Serviceability Limit State) cases according to the Eurocodes.
Mots clés : fiabilité / calculs probabilistes / modèle aux éléments finis / quantification des incertitudes / tunnels / déplacements
Key words: reliability / probabilistic analyses / finite elements model / uncertainty quantification / tunnels / displacements
© CFMS-CFGI-CFMR-CFG, 2021
1 Introduction
La réalisation de tunnels induit inévitablement des déplacements du terrain dus au relâchement des contraintes naturelles lors du forage. Ces déplacements, plus particulièrement les tassements et les gonflements, sont souvent l’origine d’endommagements pour les constructions avoisinantes et les ouvrages en cours de construction (Leca et New, 2007 ; AFTES GT16R2F1, 2018 ; CFMS, 2018). Sur les sites urbains, la limitation de ces déplacements est un sujet important. Elle est souvent estimée à l’aide des solutions analytiques. Avec le développement des outils numériques, elle est de plus en plus calculée à l’aide de Modèle aux Eléments Finis (MEF) afin d’obtenir des résultats plus précis et complets. L’analyse par éléments finis non linéaires calcule les déplacements par la résolution numérique d’équations différentielles non linéaires, dans lequel les propriétés des sols, l’interaction entre les sols et les structures, ainsi que différentes phases de construction, sont prises en compte (Leca et New, 2007 ; Lees, 2016 ; AFTES GT16R2F1, 2018).
Pour réduire le risque associé à ces déplacements à un niveau acceptable, il est nécessaire de bien définir les hypothèses du calcul d’interaction sol-structure pour un phasage de construction établi. Le choix de la valeur caractéristique des paramètres géotechniques influe fortement sur les résultats des calculs (EN 1997, 2004 ; Fenton et al., 2015 ; Lees, 2016). Néanmoins, le manque de données, la variabilité spatiale des sols, et la sensibilité des résultats par rapport aux données d’entrée sont des sujets difficilement traités par un calcul déterministe, voire semi-probabiliste. Dans ce cas, le calcul probabiliste peut être une meilleure solution pour prendre en compte ces incertitudes et permet d’accéder à une probabilité de défaillance (Baecher et Christian, 2003 ; Phoon et Retief, 2016). L’approche probabiliste permet d’évaluer les effets combinés des incertitudes, elle fournit un moyen de distinguer les conditions où les incertitudes sont particulièrement élevées ou faibles. Cependant, il est clair qu’une approche probabiliste ne saurait remplacer un manque de données relatives, par exemple, aux propriétés géotechniques ou à la variabilité spatiale des sols, sujets vers lesquels doivent se concentrer les reconnaissances géologiques, hydrogéologiques et géotechniques.
Cet article présente des calculs probabilistes avec une évaluation de fiabilité à l’aide d’un MEF pour estimer les déplacements (tassements et gonflements) engendrés par la réalisation de tunnels. Ces calculs probabilistes sont ensuite associés aux niveaux cibles de sécurité ou performance avec les probabilités de défaillance et les indices de fiabilité correspondants, conformément à la norme ISO 2394 (ISO 2394, 2015) et aux Eurocodes (EN 1990, 2002).
2 Calculs probabilistes des déplacements dus à la réalisation de tunnels
2.1 Notion de base sur la fiabilité des ouvrages
Depuis quelques décennies, l’évaluation de la fiabilité des ouvrages est de plus en plus analysée grâce au développement de méthodes numériques pour résoudre les problèmes stochastiques (Fellin et al., 2005 ; Ang et Tang, 2007 ; Lemaire, 2009 ; Melchers et Beck, 2018). La notion de fiabilité couvre essentiellement la sécurité, l’aptitude au service, la durabilité et la robustesse des ouvrages. L’évaluation de la fiabilité des ouvrages s’appuie d’une part sur la probabilité de défaillance Pf, et d’autre part sur l’indice de fiabilité β, comme présenté par exemple dans le code modèle probabiliste JCSS (JCSS, 2001).
Dans la norme ISO 2394 (ISO 2394, 2015) et les Eurocodes (EN 1990, 2002), la fiabilité s’exprime en termes de probabilité cible de défaillance, qui est la probabilité qu’une défaillance se produise pendant une certaine durée. Trois classes de fiabilité RC1, RC2 et RC3 ont été définies dans l’EN 1990 (EN 1990, 2002). De plus, trois catégories géotechniques ont été également définies dans l’EN 1997 (EN 1997, 2004), à savoir GC1, GC2 et GC3. Pour la classe de fiabilité RC2, l’indice de fiabilité cible à l’état limite ultime (ELU) βELU est égal à 3,89 (Pf correspondante = 5 × 10−5 sur une durée de 50 ans) (EN 1990, 2002 ; Gulvanessian et al., 2012 ; Zhang et Toutlemonde, 2020). Par contre, l’indice de fiabilité cible à l’état limite de service (ELS) n’est pas explicitement exprimé dans les Eurocodes. Selon la littérature, l’indice de fiabilité cible à l’ELS βELS est de 1,5 (Pf correspondante = 6,7 × 10−2 sur une durée de 50 ans) (Gulvanessian et al., 2012), comme présenté dans le tableau 1. La méthode proposée dans cet article et ses résultats illustreront l’évaluation de la probabilité de défaillance aux cas ELS selon les Eurocodes.
En outre, la norme ISO 2394-2015 a ajouté une annexe D au sujet de la fiabilité des ouvrages géotechniques (ISO 2394, 2015 ; Phoon et Retief, 2016). Pour l’application de la théorie de la fiabilité à la géotechnique, l’estimation de la probabilité de défaillance est un sujet majeur. Les incertitudes sur les hypothèses et données d’entrée peuvent être traitées par l’approche probabiliste, en associant une probabilité de défaillance Pf et un indice de fiabilité β en fonction des niveaux de sécurité ou performance choisis (Baecher et Christian, 2003 ; Phoon et Retief, 2016).
Ainsi, dans l’application de l’approche probabiliste aux problèmes géotechniques (Zhang et Ng, 2005 ; Zhang et Goh, 2012 ; Xiao et al., 2016 ; Zevgolis et al., 2018), plutôt que de sélectionner des valeurs uniques pour le calcul, nous utilisons d’abord les résultats des sondages disponibles pour définir des distributions de probabilité des paramètres géotechniques. Ceci permet d’analyser statistiquement un sujet géotechnique. Ensuite, des séries de calculs peuvent être effectuées et conduisent à un calcul de fiabilité afin d’obtenir la probabilité de défaillance.
Probabilité cible de défaillance dans l’Eurocode.
Target probability of failure and reliability index in Eurocodes.
2.2 Calculs probabilistes de déplacements
L’approche probabiliste peut être appliquée à la géotechnique en utilisant le MEF (Roubos et al., 2020), dans lequel les distributions des paramètres géotechniques, considérés comme des variables probabilistes, sont générées selon les résultats des investigations géotechniques disponibles.
Nous pouvons adopter les étapes suivantes pour appliquer cette approche probabiliste aux analyses géotechniques (Fig. 1) à l’aide du MEF :
-
réaliser un modèle aux éléments finis à l’aide d’un logiciel comme ZSOIL (ZSOIL, 2018) ;
-
identifier les paramètres les plus impactants et définir les descriptions statistiques de ces paramètres (loi de probabilité, valeur moyenne, écart type ou coefficient de variation, etc.) ;
-
établir la formulation de la fonction de sécurité G(X) ;
-
calculer la probabilité de défaillance Pf et l’indice de fiabilité β en utilisant les méthodes de calcul de fiabilité comme FORM (First Order Reliability Method), MCS (Monte Carlo Simulation), AK-MCS (Adaptive Kriging Monte Carlo Simulation), etc.
De plus, si des mesures issues d’auscultations ou des observations sont disponibles, la comparaison entre les résultats numériques et les mesures en cours de réalisation est utile, voire nécessaire, pour vérifier les résultats des simulations numériques et orienter les choix techniques du projet via la méthode observationnelle, couplée à une analyse inverse (méthode Bayésienne).
Plus précisément, la fonction de sécurité G(X) peut être formulée comme suit pour les calculs des déplacements :
 (1)
où X est le vecteur des n variables probabilistes considérées : X = (X1, ...Xi, …Xn). E(X) est le déplacement calculé à l’aide du MEF, C(X) est le déplacement admissible, choisi en fonction des niveaux de sécurité ou performance et souvent contractualisé au marché.
(1)
où X est le vecteur des n variables probabilistes considérées : X = (X1, ...Xi, …Xn). E(X) est le déplacement calculé à l’aide du MEF, C(X) est le déplacement admissible, choisi en fonction des niveaux de sécurité ou performance et souvent contractualisé au marché.
De nombreux paramètres géotechniques sont susceptibles d’impacter le déplacement E(X), qui sont principalement :
-
Les conditions géologiques, hydrogéologiques et géotechniques ;
-
La géométrie et la profondeur du tunnel ;
-
Les charges provenant des ouvrages avoisinants ;
-
Les phasages et la méthode de réalisation du tunnel.
L’hypersurface de l’équation G(X) = 0 décrit la frontière entre le domaine de défaillance {G(X) ≤ 0} et le domaine de sécurité {G(X) > 0} (Fig. 2). La probabilité de défaillance Pf est calculée par :
 (2)
où g(x) correspond à la densité de probabilité, égale à la dérivée de la fonction de répartition ou de distribution cumulée. Il montre toutes les valeurs possibles qu’une variable probabiliste peut prendre et les probabilités relatives de ces valeurs. Ωd est le domaine de défaillance, Ωd = {x : g(x) ≤ 0}.
(2)
où g(x) correspond à la densité de probabilité, égale à la dérivée de la fonction de répartition ou de distribution cumulée. Il montre toutes les valeurs possibles qu’une variable probabiliste peut prendre et les probabilités relatives de ces valeurs. Ωd est le domaine de défaillance, Ωd = {x : g(x) ≤ 0}.
Différentes méthodes peuvent être utilisées pour évaluer la valeur de Pf, à savoir des méthodes d’approximation (FORM, SORM (Second Order Reliability Method), etc.), des méthodes de simulation (MCS, Importance Sampling, Subset Simulation, etc.) et des méthodes adaptatives basées sur un méta-modèle (AK-MCS, Polynomial Chaos Expansions (PCE), etc.) (Marelli et al., 2019).
Dans les méthodes de simulation et adaptatives, la probabilité de défaillance Pf est définie par :
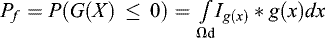 (3)
où Ig (x) est une fonction d’indicateur :
(3)
où Ig (x) est une fonction d’indicateur :  ;
; 
Pour un espace linéaire et normalisé, l’indice de fiabilité β est défini comme :
 (4)
où
(4)
où 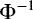 est l’inverse de la fonction de répartition de la distribution normale standard.
est l’inverse de la fonction de répartition de la distribution normale standard.
Pour un espace non linéaire et non normalisé, l’indice de fiabilité de Hasofer et Lind (Lemaire, 2009 ; Marelli et al., 2019 ; Zhang et Toutlemonde, 2020) est utilisé. Il permet de ramener un espace non normalisé et non linéaire dans un espace normalisé et linéaire :
 (5)
où βHL est l’indice de fiabilité de Hasofer et Lind.
(5)
où βHL est l’indice de fiabilité de Hasofer et Lind.
Dans les chapitres suivants, nous allons étudier les paramètres les plus influents sur les déplacements à travers un cas concret d’application. Cette analyse probabiliste à l’aide d’un MEF a été réalisée grâce au couplage entre ZSOIL (ZSOIL, 2018) et UQLab (Marelli et Sudret, 2014), et appliquée à un tunnel construit en méthode conventionnelle. L’incertitude inhérente au modèle numérique lui-même et la corrélation entre les variables d’entrée ne sont pas traitées dans cet article.
 |
Fig. 1 Description de l’approche probabiliste et comparaison avec l’approche déterministe ou semi-probabiliste. Logigramme retravaillé d’après (Marelli et Sudret, 2014). Probabilistic approach and comparison with the deterministic or semi-probabilistic approach. Flowchart reworked after (Marelli and Sudret, 2014). |
 |
Fig. 2 Schéma représentatif des domaines de sécurité et de défaillance. Representative diagram of safety and failure domains. |
3 Cas d’étude : simulations numériques à court terme et à long terme
3.1 Tunnel réalisé en méthode conventionnelle
À titre d’exemple, cette approche probabiliste a été appliquée au tunnel de la gare Maison Blanche dans le cadre du projet Grand Paris Express, le plus grand projet de métro en cours de construction en Europe.
Ce tunnel se situe à la future gare Maison Blanche sur la ligne 14 (Zhang et al., 2020a). Il est caractérisé d’une part par les enjeux géotechniques forts comme des argiles plastiques gonflantes, et d’autre part par un site urbain dense avec la proximité immédiate de bâtiments et ouvrages très sensibles et très vulnérables (Fig. 3).
Des investigations ont été effectuées lors des études géotechniques des missions G1, G2 et G3 conformément à la norme NF P 94-500. Au total, 25 sondages carottés, 13 sondages pressiométriques, 2 essais dilatomètres, 1 essai sismique cross-hole, 21 sondages destructifs et 5 sondages pénétrométriques (CPT) ont été réalisés sur une surface de 5690 m2, soit 1 sondage par 73 m2. De plus, de nombreux essais d’identification et de mesures des caractéristiques mécaniques ont été effectués au laboratoire (Zhang et al., 2020a, 2020b).
Ces études géotechniques ont mis en évidence les constats suivants (Fig. 4) :
-
Le calcaire grossier supérieur (Lutétien CGsup) est fortement altéré mais sans présence de carrières, le calcaire grossier moyen (Lutétien CGmoy) est plutôt marneux, le calcaire grossier inférieur (Lutétien CGinf) est raide mais fracturé ;
-
Les argiles plastiques (Sparnacien AP) sont saturées, mais elles sont sensibles à la variation de la teneur en eau, ce qui peut conduire à des effets comme le gonflement, la modification des caractéristiques mécaniques et la réduction des butées ;
-
Trois nappes ont été identifiées, à savoir : dans le calcaire grossier avec une surface piézométrique à environ 40 NGF, localement dans les sables d’Yprésien inférieur avec une surface piézométrique à environ 31 NGF (négligeable car majoritairement en dehors du chantier) et dans les craies (Campanien C) avec une surface piézométrique à environ 28 NGF. La nappe dans les craies est une nappe captive sous les Marnes de Meudon (Montien CMM) et présente souvent des flux ascendants à travers cette formation jusqu’aux argiles plastiques.
Pendant les études d’exécution, les incertitudes liées au taux de déconfinement (λ), au module (E) du calcaire grossier inférieur et à la pression de gonflement (pg’) des argiles plastiques, ont été identifiées comme ayant un fort impact sur les résultats des déplacements. Ainsi, ces trois paramètres ont été considérés comme des variables probabilistes. Des distributions lognormales ont été choisies car elles sont couramment utilisées dans le cadre de la représentation de paramètres associés à la résistance des matériaux.
Le taux de déconfinement λ avant pose du soutènement dans le modèle 2D peut être estimé grâce à la méthode convergence-confinement (formules de Corbetta-Panet) ou à l’aide d’un modèle 3D avec introduction explicite du phasage d’excavation, mètre par mètre, et de la pose du soutènement (cintres et béton projeté). Dans le cas présent, l’excavation a été réalisée en pleine section avec des passes de 1,0 m à 1,2 m. Le soutènement est du profilé HEB200 avec du béton projeté de 0,3 m d’épaisseur. La méthode convergence-confinement induit une valeur théorique de λ = 0,6 ou 60 %, le modèle 3D donnant plutôt une valeur proche de λ = 0,4 ou 40 % (calage du taux de déconfinement avant pose du soutènement dans le modèle 2D afin d’obtenir des déplacements équivalents en calotte et en surface dans le modèle 3D). Nous avons choisi d’effectuer les calculs avec une valeur moyenne de λ = 0,4 ou 40 % et un COV (coefficient de variation) de 25 %. De plus, nous avons réalisé une étude de sensibilité ainsi qu’une étude paramétrique sur le COV du taux de déconfinement dans le chapitre 4.
Selon les résultats des sondages et des essais géotechniques des missions G1, G2 et G3, la valeur moyenne du module E des calcaires grossiers inférieurs, déterminée à l’aide du logiciel ROCLAB à partir des résultats des essais en laboratoire (résistance et module mesurés sur échantillon) et de l’approche Hoek et Brown, est aux alentours de 400 MPa. Le COV est évalué à 0,25 en se basant sur les résultats des essais. De plus, nous avons réalisé une étude de sensibilité ainsi qu’une étude paramétrique sur le COV du module E des CGinf au chapitre 4.
Les essais de gonflement à l’œdomètre des argiles plastiques montrent une grande disparité. Les modèles 3D ont montré que la pression de gonflement (contrainte effective) appliquée au radier du revêtement varie entre 250 kPa et 350 kPa en fonction du temps de la mise en place du revêtement (épaisseur variable entre 0,4 m en calotte et 0,6 m en contre-voûte) et de la profondeur du radier, nous avons pris la fourchette haute 350 kPa comme valeur moyenne et un écart type relativement important, à savoir 50 %.
Le tassement de la couronne du tunnel, le tassement d’un bâtiment existant (très sensible et très vulnérable) ainsi que le gonflement des argiles plastiques au niveau du radier en contre-voûte du tunnel sont évalués par des calculs probabilistes. Le tableau 2 donne un aperçu des variables probabilistes considérées et de leurs fonctions de distribution.
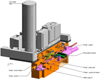 |
Fig. 3 Gare Maison Blanche en 3D avec ses ouvrages avoisinants très sensibles et très vulnérables. White House station in 3D with its very sensitive and vulnerable neighbouring structures. |
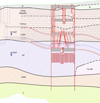 |
Fig. 4 Coupe géologique du site et ouvrages. Le tunnel est représenté par sa voûte et son radier (il traverse le calcaire grossier inférieur et les argiles plastiques). Geological section of construction site and works. The tunnel is represented by its vault and its base (it crosses the lower coarse limestone and plastic clays). |
Statistique des variables probabilistes.
Statistical characteristics of the selected parameters.
3.2 Modèles et lois de comportement
Le modèle 2D aux éléments finis a été réalisé à l’aide du logiciel ZSOIL (ZSOIL, 2018), comme l’illustre la figure 5. Le modèle utilisé pour appliquer l’approche probabiliste illustrée dans cet article est une simplification du modèle original : un axe de symétrie a été admis, le nombre d’éléments volumiques bilinéaires en formulation Enhanced Assumed Strains (EAS) est ainsi réduit à 2273 au lieu de 6873 dans le modèle original de calcul (incluant également la proximité de la ligne 7 du métro parisien). Le soutènement provisoire et le radier des bâtiments sont modélisés à l’aide d’éléments poutres, alors que le revêtement définitif est modélisé à l’aide d’éléments volumiques bilinéaires en formulation CFS (Continuum For Structures, une spécialisation des EAS).
Grâce à ce modèle, deux types d’études ont été menés :
-
une étude « Court Terme (CT) en condition non drainée » avec les paramètres CT des sols pour estimer les tassements de la couronne du tunnel et du radier du bâtiment existant ;
une étude « Long Terme (LT) en condition drainée » avec les paramètres LT des sols pour estimer le gonflement des argiles plastiques au radier du tunnel.
Pour le cas CT, calculé par une suite d’étapes permanentes, l’unité de temps est fictive, et n’est pas considérée dans le calcul. Par contre, pour le cas LT, le temps est réel, puisqu’il s’agit d’un calcul tenant compte du gonflement et du fluage des argiles plastiques.
Le choix des lois de comportement constitutives et la calibration des paramètres géomécaniques sont importants pour les résultats des calculs. Les lois constitutives et les paramètres géomécaniques retenus sont présentés dans le tableau 3. Ils sont basés sur les résultats des études géotechniques et vérifiés par les modèles 2D et 3D, ainsi que par les mesures issues des auscultations (Zhang et al., 2020b).
La loi de comportement Hardening Soil Model (HSM) a été choisie pour décrire le comportement élastoplastique avec écrouissage positif et la détente de certains sols (Remblai, Alluvion, Calcaire Grossier Supérieur fortement altéré, Argiles Plastiques). Par rapport à d’autres modèles fréquemment utilisés comme Mohr-Coulomb élasto-plastique (EPMC), le modèle HSM permet de mieux prédire les déplacements dans les travaux souterrains car il permet notamment de prendre en compte la dilatance avant rupture, la variation des modules E en fonction de l’état de contrainte et un module en déchargement différent de celui en chargement (Schanz et al., 1999 ; Hejazi et al., 2008). L’effet du gonflement hydrique des argiles plastiques a été implémenté dans le modèle à l’aide de la loi de comportement Huder et Amberg (HA) (Huder et Amberg, 1970). Les couches géologiques comme les Calcaires Grossiers moyen et inférieur, les Calcaires Marneux de Meudon et la Craie sont des formations rocheuses. Le modèle EPMC a été utilisé pour simuler leur comportement avec les paramètres (module et résistance au cisaillement c’, ϕ’) évalués par l’approche Hoek et Brown et les essais en laboratoire.
Dans le présent cas, il n’y a pas de dépendance des modules en fonction de l’état de contrainte puisque le paramètre m est pris égal à 0.
 |
Fig. 5 Maillage du modèle 2D aux éléments finis. Mesh of the 2D finite element model. |
Principaux paramètres géomécaniques des modèles constitutifs.
Main geomechanical parameters of the constitutive laws.
3.3 Étude à partir du modèle de comportement à court terme
Les phases principales de réalisation considérées dans le MEF à court terme du tunnel sont les suivantes :
-
Établissement d’un état initial en équilibre mais non déformé avant travaux ;
-
Excavation du tunnel (en pleine section avec passes d’excavation de 1 à 1,2 m) et mise en place du soutènement provisoire (profilé HEB200 avec béton projeté de 0,3 m) avec déconfinement partiel à 40 % (valeur moyenne, déterminée sur la base d’un modèle 3D auxiliaire) ;
-
Déconfinement à 100 % sur le soutènement provisoire.
Les calculs probabilistes sont effectués à l’aide du logiciel UQLab (Marelli et Sudret, 2014). Les méthodes numériques utilisées sont les méthodes FORM, AK-MCS et MCS. Le tableau 4 récapitule les principaux résultats des calculs probabilistes du modèle à court terme. Les 3 méthodes donnent des valeurs de la probabilité de défaillance assez proches. Les indices de fiabilité β estimés sont :
-
proches de 1,75 avec les trois méthodes considérées (FORM, AK-MCS et MCS) en ce qui concerne la probabilité que le déplacement vertical de la calotte du tunnel excède 10 mm ;
-
proches de 2,30 avec les trois méthodes considérées (FORM, AK-MCS et MCS) en ce qui concerne la probabilité que le tassement du bâtiment existant excède 10 mm.
Le nombre de calculs nécessaires est indiqué dans le tableau 4. En comparant le nombre d’évaluations exactes de la fonction de sécurité et le temps de calcul des trois méthodes de fiabilité (chaque appel à ZSOIL prenant approximativement 20 s), la méthode FORM s’avère être une méthode efficace conduisant à des résultats similaires à ceux obtenus par les méthodes MCS et AK-MCS. La méthode AK-MCS est plus générale et peut être considérée comme plus précise, elle présente également une meilleure performance en temps de calcul.
La figure 6 illustre le tassement de la calotte du tunnel et du bâtiment existant dans l’étude à court terme avec un taux de déconfinement égal à 40 %.
La figure 7 illustre les résultats des 1000 simulations MCS, où les couples (E, λ) conduisant à un tassement du bâtiment existant supérieur à 10 mm ont été identifiés. Sur les 1000 échantillons (calculs) réalisés par la simulation MCS, la figure 8 montre la densité de probabilité et l’histogramme du tassement du bâtiment existant.
Résultats de l’étude probabiliste à court terme.
Short-term probabilistic calculation results.
 |
Fig. 6 Tassements issus du modèle CT (λ = 40 %) – Courbes d’iso-déplacement vertical, valeurs exprimées en mètres. Settlements from the ST model (λ = 40%) – Vertical iso-displacement curves, values expressed in meters. |
 |
Fig. 7 Simulation MCS – Couples (E, λ) conduisant à un tassement du bâtiment > 10 mm. MCS simulation – Couples (E, λ) leading to the building settlement > 10 mm. |
 |
Fig. 8 Simulation MCS – Densité de probabilité et histogramme du tassement du bâtiment. MCS simulation – Probability density and histogram of the building settlement. |
3.4 Étude à partir du modèle de comportement à long terme
Les phases principales de réalisation considérées dans le MEF à long terme du tunnel sont les suivantes :
-
Établissement d’un état initial en équilibre mais non déformé avant travaux ;
-
Excavation du tunnel et mise en place du soutènement provisoire avec un déconfinement partiel à 40 % ;
-
Déconfinement à 100 % sur le soutènement provisoire ;
-
Mise en place du revêtement définitif avec E = 10 GPa, nappe Eaux Chantier (EC) ;
-
Disparition du soutènement provisoire et passage à la nappe Eaux Hautes (EH) ;
-
Application de la loi de gonflement dans les argiles plastiques sur plusieurs années.
Les calculs probabilistes sont effectués à l’aide du logiciel UQLab (Marelli et Sudret, 2014). La figure 9 illustre le déplacement vertical autour du tunnel après 5 ans. La figure 10 exprime le gonflement du nœud appartenant au radier définitif en fonction de la pression limite de gonflement de la loi de Huder et Amberg. À titre d’illustration, la probabilité que le gonflement du radier dépasse 1 cm après 5 ans est Pf = 37,3 % si l’on considère, pour la pression limite de gonflement, une valeur moyenne de 350 kPa avec un COV de 50 %. De même, la probabilité que le gonflement dépasse 1,2 cm après 5 ans est de 24,7 %, cette probabilité est réduite à 0 pour un gonflement cible de 1,3 cm.
 |
Fig. 9 Déplacement vertical à la fin de l’étude LT (après 5 ans) avec pg’ = 350 kPa et COV = 50 % – Courbes d’iso-déplacement vertical, valeurs exprimées en mètres. Vertical displacements from the LT model (after 5 years) with pg’ = 350 kPa and COV = 50%) – Vertical iso-displacement curves, values expressed in meters. |
 |
Fig. 10 Distribution du déplacement vertical du radier en fonction de la pression limite de gonflement. Distribution of the vertical displacement of tunnel base as a function of the swelling pressure. |
4 Analyse de sensibilité, étude paramétrique et mesures in-situ
4.1 Analyse de sensibilité
L’analyse de sensibilité consiste à quantifier l’importance relative de chaque paramètre probabilisé sur la variabilité du résultat considéré. Nous utilisons pour cela les indices de sensibilité de Sobol (Marelli et al., 2021). Dans le cadre probabiliste, l’utilisation de ces indices permet de décomposer la variance d’un des résultats (output) de notre modèle en fractions qui peuvent être attribuées aux variables d’entrée (input).
Les variables d’entrée sont le module élastique E et le taux de déconfinement λ. Nous souhaitons étudier leur influence sur le tassement du bâtiment existant. La figure 11 illustre cette analyse et indique une prédominance du taux de déconfinement λ (98 %) vis-à-vis du module E (2 %).
 |
Fig. 11 Analyse de sensibilité : indices de Sobol. Sensitivity analysis: Sobol index. |
4.2 Étude paramétrique
Les variables probabilistes ont été modélisées suivant une distribution log-normale avec des valeurs moyennes et des coefficients de variation présentés dans le tableau 2.
Les valeurs moyennes (µ) sont les résultats d’une étude géotechnique limitée qui a eu lieu sur le site. En l’absence de plus de données détaillées, les valeurs de COV sont présupposées, permettant ainsi, de façon arbitraire, d’introduire la variabilité des données dans l’analyse de sensibilité.
L’étude paramétrique des COV a donc été menée pour comprendre la sensibilité des calculs aux valeurs de COV (Tab. 5). L’augmentation du COV a pour conséquence d’augmenter Pf. Logiquement, au vu de l’analyse de sensibilité du paragraphe précédent, c’est le COV du taux de déconfinement qui a largement la plus grande influence sur Pf.
Afin de pouvoir lancer un grand nombre de calculs, la méthode dite « Polynomial Chaos Expansion » (ou PCE) a été utilisée. Cette méthode consiste à lancer un nombre raisonnable de simulations du MEF (ici 200 évaluations) puis, sur la base des résultats de ces simulations, de créer une série polynomiale qui approxime le MEF. Une fois ce méta-modèle construit, il est aisé de lancer un grand nombre d’évaluations en un temps minime et ainsi l’utilisation de la méthode MCS ou de la méthode FORM est à nouveau possible dans un laps de temps raisonnable.
La figure 12 illustre la quasi parfaite adéquation des densités de probabilité du tassement du bâtiment pour le MEF et pour son méta-modèle (PCE), et valide ainsi l’utilisation de ce dernier pour lancer une étude MCS sur 10 000 réalisations, afin de calculer la probabilité de défaillance lorsque le seuil acceptable du tassement varie (Fig. 13 : Pf = 15,4 % pour 5 mm, Pf = 1,05 % pour 10 mm, et Pf = 0,19 % pour 15 mm).
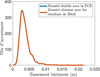 |
Fig. 12 Probabilité de densité pour le MEF et son méta-modèle (PCE). Probability density for the FEM and its meta-model (PCE). |
 |
Fig. 13 Illustration des Pf pour différents seuils de tassement acceptable (5, 10 et 15 mm). Illustration of Pf for different settlement thresholds (5, 10 and 15 mm). |
4.3 Comparaison des résultats numériques avec des mesures in-situ
Un système d’auscultation a été installé avant les travaux, il a permis de mesurer le comportement réel du terrain et des ouvrages en suivant notamment le tassement en surface, la pression de gonflement, la convergence du tunnel, etc. (Zhang et al., 2021).
Le tassement mesuré en surface est présenté dans la figure 14, la mesure se situe dans la fourchette des résultats des analyses probabilistes, elle est plus proche du résultat de calcul à court terme avec un taux de déconfinement à 60 %.
La pression de gonflement mesurée sous le radier est également présentée dans la figure 15, le décalage entre les courbes de mesure et de résultat de calcul à long terme provient du fait que la mesure part d’une pression à peu près nulle alors que dans le calcul on part d’une valeur entre 100 et 150 kPa car la pression n’est pas nulle en raison de la présence du soutènement et du revêtement.
Ces mesures in-situ permettent de vérifier les résultats numériques et d’ajuster certains paramètres de calcul si nécessaire. Couplée à une analyse inverse (méthode Bayésienne), cette méthode observationnelle permet également d’orienter les choix techniques pour la suite du projet.
 |
Fig. 14 Comparaison de tassements en surface. Comparison of settlements. |
 |
Fig. 15 Comparaison de pressions de gonflement sous le radier du tunnel. Comparison of swelling pressures under tunnel base. |
5 Discussion
Nous avons présenté au chapitre 2 le cadre de l’approche probabiliste avec les outils numériques ZSOIL et UQLab. Les chapitres 3 et 4 ont présenté l’application de cette approche probabiliste au calcul des déplacements (tassements et gonflements) d’un tunnel réalisé en méthode conventionnelle à l’aide d’un modèle aux éléments finis 2D.
Les données les plus influentes sur les déplacements, à savoir le taux de déconfinement λ, le module élastique E et la pression de gonflement pg’, ont été traités comme variables probabilistes avec la densité de probabilité, la valeur moyenne et le coefficient de variation appropriés. Selon les hypothèses admises à court terme pour les COV du module E des calcaires grossiers inférieurs (25 %) et du taux de déconfinement λ (25 %), la probabilité de défaillance calculée avec un tassement cible du bâtiment (très sensible et très vulnérable) à 10 mm avoisine 1 × 10−2, inférieure à la probabilité de défaillance de l’état limite de service indiquée comme cible par les Eurocodes, à savoir 6,7 × 10−2 sur une durée de 50 ans. Le soulèvement maximal du radier à long terme est estimé entre 1,2 et 1,3 cm avec une valeur moyenne de 350 kPa et un COV de 50 % pour la pression limite de gonflement.
L’étude de sensibilité a montré l’importance de taux de déconfinement λ sur les tassements et la probabilité de défaillance. En outre, la bonne qualité des sondages géotechniques réalisés et la bonne estimation de taux de confinement permettent de diminuer le COV des variables, et en conséquence de réduire la probabilité de défaillance.
L’application de l’approche probabiliste à la géotechnique permet de prendre en compte les incertitudes intrinsèques des problèmes géotechniques (données d’entrée limitées, variabilité spatiale des sols, sensibilité aux données d’entrée, etc.). La méthode présentée avec les outils numériques développés, illustre l’évaluation de la probabilité de défaillance à l’ELS dans les Eurocodes.
Néanmoins, cette approche ne constitue qu’une des nombreuses méthodes pour modéliser le monde réel complexe pour les applications d’ingénierie. Elle ne dispense nullement d’un bon jugement géotechnique de l’ingénieur, qui reste essentiel pour établir les bonnes lignes de recherche scientifique et technique, sélectionner les modèles et paramètres appropriés pour les calculs probabilistes et vérifier le caractère raisonnable des résultats.
Malgré toutes les prévisions fournies par les simulations numériques, il reste également indispensable d’évaluer les propriétés des sols (d’où l’importance des reconnaissances géologiques, hydrogéologiques et géotechniques) et d’observer le comportement de la construction en continu pendant la phase de travaux. Les ingénieurs recueillent des observations sur le terrain (par exemple des mesures de déformations, de contraintes ou d’autres données pertinentes) pour l’analyse afin d’identifier les bonnes hypothèses. Une bonne utilisation de la méthode observationnelle est indispensable, et permettrait d’une part d’adapter les choix techniques pendant les travaux, et d’autre part de limiter les COV au moyen d’analyses inverses (approche Bayésienne) appropriées.
6 Conclusions
Cet article présente les calculs des déplacements dus à la réalisation de tunnels selon une approche probabiliste appliquée à un modèle aux éléments finis. Un cadre pour la conception probabiliste associée à la limitation de ces déplacements a été proposé avec une application à un tunnel réalisé en méthode conventionnelle.
Les résultats principaux sont :
-
Les déplacements (tassements et gonflements) peuvent être estimés par les calculs probabilistes en considérant les paramètres de plus fort impact comme des variables probabilistes ;
-
La probabilité de défaillance et l’indice de fiabilité peuvent être déterminés avec un déplacement admissible choisi en fonction des niveaux cibles de sécurité ou performance ;
-
Les indices de fiabilité trouvés pour les situations critiques dans le cas d’application correspondent aux exigences des Eurocodes. L’approche probabiliste illustre ainsi l’évaluation de la probabilité de défaillance pour les cas ELS ;
-
Les évaluations de fiabilité (probabilité de défaillance et indice de fiabilité) basées sur les éléments finis ont été réalisées avec succès à l’aide des méthodes FORM, AK-MCS et MCS, qui convergent efficacement en tenant compte d’un certain nombre de variables probabilistes ;
-
La méthode FORM est une méthode efficace conduisant à des résultats similaires à ceux obtenus par les méthodes MCS et AK-MCS. La méthode AK-MCS est plus générale et précise avec une meilleure performance en temps de calcul.
De plus, l’approche probabiliste peut jouer un rôle complémentaire aux approches bien établies issues des bonnes pratiques géotechniques. La méthode observationnelle permet de cadrer cette approche probabiliste et d’orienter les bons choix techniques pour le projet.
En outre, il faut rappeler que ces méthodes sont d’autant plus performantes que les données de départ sont précises, celles-ci ne pouvant être apportées que par des campagnes de reconnaissance géologiques, hydrogéologiques et géotechniques de haute qualité.
Les simulations numériques et l’approche probabiliste permettent de mettre en évidence les paramètres de plus fort impact sur les résultats de calcul et d’orienter ainsi, de façon appropriée, les campagnes de reconnaissance géologiques et géotechniques, tout spécialement pour des travaux futurs.
Déclaration des conflits d’intérêt
Aucun conflit d’intérêt n’a été signalé par les auteurs.
Remerciements
Les auteurs souhaitent remercier Prof. Thomas Zimmermann ainsi que Prof. Bruno Sudret et Dr Stefano Marelli pour les nombreuses discussions autour de l’application des approches probabilistes au MEF, ainsi que l’équipe de GeoMod SA (en particulier Gil Jacot-Descombes et Marc Groslambert) qui a conduit la plupart des simulations avec ZSOIL et UQLab présentées dans cet article.
Les auteurs souhaitent également remercier Prof. Jean-Pierre Magnan, Dr François Toutlemonde et Prof. Jean-Armand Calgaro pour leur relecture de cet article et leur avis.
Références
- ISO 2394. 2015. General principles on reliability for structures. [Google Scholar]
- EN 1990. 2002. Eurocode 0: Basis of structural design. [Google Scholar]
- EN 1997. 2004. Eurocode 7: Geotechnical design. [Google Scholar]
- JCSS (Joint Committee on Structural Safety). 2001. JCSS Probabilistic Model Code. [Google Scholar]
- Comité Français de Mécanique des Sols et de Géotechnique. 2018. Recommandations sur la prise en compte du gonflement des terrains argileux dans le dimensionnement des ouvrages d’infrastructure (version provisoire V9). [Google Scholar]
- Recommandation de l’AFTES GT16R2F1. 2018. Prise en compte des effets induits par le creusement sur les constructions avoisinantes dans la conception et la réalisation des ouvrages souterrains. [Google Scholar]
- Ang AHS, Tang WH. 2007. Probability concepts in engineering: emphasis on applications to civil and environmental engineering, 2nd ed. Wiley. [Google Scholar]
- Baecher GB Christian JT. 2003. Reliability and statistics in geotechnical engineering. Wiley. [Google Scholar]
- Fellin W, Lessmann H, Oberguggenberger M, Vieider R (eds.). 2005. Analyzing uncertainty in civil engineering. Springer. [CrossRef] [Google Scholar]
- Fenton GA, Naghibi F, Dundas D, Bathurst RJ, Griffiths DV. 2015. Reliability-based geotechnical design in the 2014 Canadian Highway bridge design code. Can Geotech J 53(2): 236–251. [CrossRef] [Google Scholar]
- Gulvanessian H, Calgaro J-A, Holicky M. 2012. Designer’ guide to Eurocode: basis of structural design EN 1990, 2nd ed. ICE Publishing. [Google Scholar]
- Hejazi Y, Dias D, Kastner R. 2008. Impact of constitutive models on the numerical analysis of underground constructions. Acta Geotech 2008(3): 251–258. [CrossRef] [Google Scholar]
- Huder J, Amberg G. 1970. Quellung im Mergel, Opalinuston und Anhydrit. Schweiz Bauzeitung 43: 975–980. [Google Scholar]
- Leca E, New B. 2007. ITA/AITES Report 2006 on settlements induced by tunnelling in soft ground. Tunnel Undergr Space Technol 22: 119–149. [CrossRef] [Google Scholar]
- Lees A. 2016. Geotechnical finite element analysis – A practical guide. ICE Publishing. [CrossRef] [Google Scholar]
- Lemaire M. 2009. Structural reliability. Wiley. [CrossRef] [Google Scholar]
- Marelli S, Sudret B. 2014. UQLab: A framework for uncertainty quantification in MATLAB. In: 2nd International Conference on Vulnerability and Risk Analysis and Management (ICVRAM 2014), July 13–16, 2014, University of Liverpool, United Kingdom, pp. 2554–2563. [Google Scholar]
- Marelli S, Schobi R, Sudret B. 2019. UQLab User Manual – Structural reliability (rare event estimation), Report #UQLab-V1.3-107. ETH Zürich, Switzerland: Chair of Risk, Safety and Uncertainty Quantification. [Google Scholar]
- Marelli S, Lamas C, Konakli K, Mylonas C, Wiederkehr P, Sudret B. 2021. UQLab User Manual – Sensitivity analysis, Report #UQLab-V1.4-106. ETH Zurich, Switzerland: Chair of Risk, Safety and Uncertainty Quantification. [Google Scholar]
- Melchers RE, Beck AT. 2018. Structural reliability analysis and prediction, 3rd ed. Wiley. [Google Scholar]
- Phoon KK, Retief JV. 2016. Reliability of geotechnical structures in ISO 2394. CRC Press. [CrossRef] [Google Scholar]
- Roubos AA, Schweckendiek T, Brinkgreve RBJ, Steenbergen RDJM, Jonkman SN. 2020. Finite element-based reliability assessment of quay walls. Georisk: Assess Manage Risk Eng Syst Geohazards. DOI: 10.1080/17499518.2020.1756344. [Google Scholar]
- Schanz T, Vermeer PA, Bonnier PG. 1999. The hardening soil model: Formulation and verification. In: Beyond 2000 in Computational Geotechnics. Rotterdam: Balkema. [Google Scholar]
- Xiao J, Luo Z, Martin JR, Gong W, Wang L. 2016. Probabilistic geotechnical analysis of energy piles in granular soils. Eng Geol 209: 119–127. [CrossRef] [Google Scholar]
- Zevgolis IE, Deliveris AV, Koukouzas NC. 2018. Probabilistic design optimization and simplified geotechnical risk analysis for large open pit excavations. Comput Geotech 103: 153–164. [CrossRef] [Google Scholar]
- Zhang LM, Ng AMY. 2005. Probabilistic limiting tolerable displacements for serviceability limit state design of foundations. Géotechnique 55(2): 151–161. [CrossRef] [Google Scholar]
- Zhang W, Goh ATC. 2012. Reliability assessment on ultimate and serviceability limit states and determination of critical factor of safety for underground rock caverns. Tunnel Undergr Space Technol 32: 221–230. [CrossRef] [Google Scholar]
- Zhang Y, Toutlemonde F. 2020. Calibrating partial safety factors in line with required reliability levels for concrete structures. Eur J Environ Civil Eng. DOI: 10.1080/19648189.2020.1824820. [Google Scholar]
- Zhang Y, Commend S, Martin-Lavigne Q, Lacoste J. 2020a. The White House Station of the Grand Paris Express Project. Struct Eng Int 30(4): 460–467. DOI: 10.1080/10168664.2019.1701966. [CrossRef] [Google Scholar]
- Zhang Y, Commend S, Taherzadeh R, Sinagra O, Lacoste J. 2020b. Analysis, modelling and surveys of plastic clays − Feedback from the White House metro station. Tunnels et espace souterrain 271: 114–138. [Google Scholar]
- Zhang Y, Commend S, Taherzadeh R, Sinagra O, Lacoste J. 2021. Études expérimentales et simulations numériques des argiles plastiques – Cas de la L14 gare Maison Blanche. In: Congrès AFTES 2021, Paris, France. [Google Scholar]
- ZSOIL (User manual ZSoil.PC). 2018. Soil, rock and structural mechanics in dry or partially saturated media. Lausanne, Switzerland: ZACE Services Ltd, Software Engineering. [Google Scholar]
Citation de l’article : Yi Zhang, Stéphane Commend. Calculs probabilistes des déplacements dus à la réalisation de tunnels à l’aide d’un modèle aux éléments finis. Rev. Fr. Geotech. 2021, 167, 5.
Liste des tableaux
Probabilité cible de défaillance dans l’Eurocode.
Target probability of failure and reliability index in Eurocodes.
Statistique des variables probabilistes.
Statistical characteristics of the selected parameters.
Principaux paramètres géomécaniques des modèles constitutifs.
Main geomechanical parameters of the constitutive laws.
Résultats de l’étude probabiliste à court terme.
Short-term probabilistic calculation results.
Liste des figures
 |
Fig. 1 Description de l’approche probabiliste et comparaison avec l’approche déterministe ou semi-probabiliste. Logigramme retravaillé d’après (Marelli et Sudret, 2014). Probabilistic approach and comparison with the deterministic or semi-probabilistic approach. Flowchart reworked after (Marelli and Sudret, 2014). |
| Dans le texte | |
 |
Fig. 2 Schéma représentatif des domaines de sécurité et de défaillance. Representative diagram of safety and failure domains. |
| Dans le texte | |
 |
Fig. 3 Gare Maison Blanche en 3D avec ses ouvrages avoisinants très sensibles et très vulnérables. White House station in 3D with its very sensitive and vulnerable neighbouring structures. |
| Dans le texte | |
 |
Fig. 4 Coupe géologique du site et ouvrages. Le tunnel est représenté par sa voûte et son radier (il traverse le calcaire grossier inférieur et les argiles plastiques). Geological section of construction site and works. The tunnel is represented by its vault and its base (it crosses the lower coarse limestone and plastic clays). |
| Dans le texte | |
 |
Fig. 5 Maillage du modèle 2D aux éléments finis. Mesh of the 2D finite element model. |
| Dans le texte | |
 |
Fig. 6 Tassements issus du modèle CT (λ = 40 %) – Courbes d’iso-déplacement vertical, valeurs exprimées en mètres. Settlements from the ST model (λ = 40%) – Vertical iso-displacement curves, values expressed in meters. |
| Dans le texte | |
 |
Fig. 7 Simulation MCS – Couples (E, λ) conduisant à un tassement du bâtiment > 10 mm. MCS simulation – Couples (E, λ) leading to the building settlement > 10 mm. |
| Dans le texte | |
 |
Fig. 8 Simulation MCS – Densité de probabilité et histogramme du tassement du bâtiment. MCS simulation – Probability density and histogram of the building settlement. |
| Dans le texte | |
 |
Fig. 9 Déplacement vertical à la fin de l’étude LT (après 5 ans) avec pg’ = 350 kPa et COV = 50 % – Courbes d’iso-déplacement vertical, valeurs exprimées en mètres. Vertical displacements from the LT model (after 5 years) with pg’ = 350 kPa and COV = 50%) – Vertical iso-displacement curves, values expressed in meters. |
| Dans le texte | |
 |
Fig. 10 Distribution du déplacement vertical du radier en fonction de la pression limite de gonflement. Distribution of the vertical displacement of tunnel base as a function of the swelling pressure. |
| Dans le texte | |
 |
Fig. 11 Analyse de sensibilité : indices de Sobol. Sensitivity analysis: Sobol index. |
| Dans le texte | |
 |
Fig. 12 Probabilité de densité pour le MEF et son méta-modèle (PCE). Probability density for the FEM and its meta-model (PCE). |
| Dans le texte | |
 |
Fig. 13 Illustration des Pf pour différents seuils de tassement acceptable (5, 10 et 15 mm). Illustration of Pf for different settlement thresholds (5, 10 and 15 mm). |
| Dans le texte | |
 |
Fig. 14 Comparaison de tassements en surface. Comparison of settlements. |
| Dans le texte | |
 |
Fig. 15 Comparaison de pressions de gonflement sous le radier du tunnel. Comparison of swelling pressures under tunnel base. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




