| Numéro |
Rev. Fr. Geotech.
Numéro 170, 2022
|
|
|---|---|---|
| Numéro d'article | 3 | |
| Nombre de pages | 14 | |
| DOI | https://doi.org/10.1051/geotech/2022001 | |
| Publié en ligne | 8 février 2022 | |
Article de recherche / Research Article
Peut-on modifier l’effet de site sismique ?
Can seismic site effect be modified?
1
EDF-DI-TEGG,
905 av. du Camp de Menthe,
13097
Aix-en-Provence Cedex 02, France
2
IMSIA (UMR9219), CNRS, EDF, CEA, ENSTA Paris, Institut Polytechnique de Paris,
91120
Palaiseau, France
* Auteur de correspondance : emmanuel.javelaud@edf.fr
Réduire le mouvement sismique atteignant les ouvrages de surface par modification de l’effet de site sismique est une solution innovante pour contribuer à répondre aux objectifs de protection parasismique. Cela peut être obtenu par modification du sol dans la masse pour réduire l’effet de site lithologique ou bien par la mise en place de dispositifs d’atténuation des ondes de surfaces pour réduire l’effet de site géométrique. Des difficultés pratiques doivent encore être résolues, dont l’identification des situations où réduire le mouvement sismique peut être utile en lien avec le type d’ondes (de volume/de surface) concernées, la faisabilité pratique des travaux envisagés, et la nécessité d’intégrer le comportement non-linéaire du sol dans les études spécifiques d’effet de site sismique. Cet article propose un cadre permettant d’évaluer l’intérêt pratique d’une réduction de l’effet de site sismique. Il fait le lien entre les capacités à modifier les caractéristiques mécaniques des sols à l’échelle de petits bassins sédimentaires, et d’autre part les études spécifiques des effets de site lithologique 1D et géométriques 2D/3D. Dans les conditions restrictives d’une configuration tabulaire 1D ou d’un bassin de forme géométrique 2D simple, il explore, pour un chargement sismique donné, les possibilités de modification du mouvement sismique en surface. Quatre profils de sols types sont considérés : trois sols de caractéristiques mécaniques croissantes (module de Young effectif, amortissement effectif) et un quatrième profil comprenant la purge des formations superficielles. Les résultats permettent d’apprécier les effets respectifs d’une atténuation des ondes de surface se propageant horizontalement et des ondes de volume à propagation verticale.
Abstract
A reduction of the seismic movement that reaches surface structures by modification of the seismic site effect is an alternative way to ensure the seismic protection of structures. It can be obtained by soil improvement to reduce the lithologic seismic site effect or by installing engineered barriers to reduce the surface waves generated by 2D/3D geometric site effect. Some practical difficulties remain, including the identification of situations where a reduction of the seismic movement can be useful in relation to the wave types (body/surface waves) concerned, the practical feasibility of the site work, and the need to integrate the soil complex non-linear behavior (including damping) beyond elasticity for specific seismic site effect evaluation. This paper provides a framework for evaluating the practical usefulness of a reduction of the seismic site effect. It makes the link between the practical feasibility of modifying the soil mechanical characteristics on site, and specific evaluation of 1D lithologic and 2D/3D geometric seismic site effects. In the restrictive conditions of 1D tabular layers or of a 2D sedimentary basin of simple geometry, this paper investigates, for a given seismic input, the possibilities to modify the seismic motion on the surface. Four soil profiles are considered: three of increasing mechanical characteristics (effective Young modulus, effective damping) and a fourth profile where the superficial layer is removed. The results allow to discuss the respective effects of an attenuation of the surface waves travelling horizontally and of the body waves travelling vertically.
Mots clés : effet de site sismique / réduction / dynamique des sols / petites déformations / ondes de volume / onde de surface
Key words: seismic site effect / mitigation / soil dynamics / body waves / surface waves
© CFMS-CFGI-CFMR-CFG, 2022
1 Quel intérêt pratique à réduire l’effet de site sismique ?
La protection parasismique vise habituellement à dimensionner les ouvrages pour résister aux sollicitations provoquées par les séismes. Une autre façon de répondre aux objectifs de protection parasismique d’un ouvrage est d’agir directement sur le mouvement sismique auquel il est soumis. Cela peut être réalisé par traitement du sous-sol afin de modifier ses caractéristiques mécaniques et ainsi sa réponse sismique.
L’objectif d’une réduction de l’effet de site sismique est de réduire la demande sismique mais pas de la supprimer complètement. En terme de modification de l’effet de site sismique, la situation ultime serait de pouvoir remplacer totalement par du rocher les matériaux sédimentaires de sub-surface, afin que l’effet de site sismique ne se produise plus (cf. Fig. 1). L’effet de site sismique se produit par exemple en présence d’un bassin sédimentaire (passage de la Fig. 1a à la Fig. 1b). L’objectif ultime serait d’aboutir à une situation sans bassin sédimentaire (passage retour de la Fig. 1b à la Fig. 1a)
En pratique, il peut s’agir d’améliorer de manière substantielle les caractéristiques mécaniques des sols constituant la formation sédimentaire afin que le spectre de réponse (Fig. 2, gauche, trait pointillé) soit significativement diminué après réduction de l’effet de site (Fig. 2, gauche, trait continu fin) et couvert par le spectre de dimensionnement (Fig. 2, gauche, trait continu épais).
Cette diminution peut être économiquement avantageuse pour des projets d’ouvrages neufs construits de façon standardisée (c’est-à-dire avec une qualification des équipements et composants basée sur un spectre générique), afin d’éviter une reprise de la qualification pour un simple dépassement ponctuel du spectre de dimensionnement pour un site, ou dans le cas de la justification d’ouvrages ou d’équipement existants suite à une réévaluation à la hausse de l’aléa sismique. Sur la figure de principe (Fig. 2, droite), le spectre de réponse en accélération SRO (trait pointillé) dépasse ponctuellement le spectre de dimensionnement (trait continu épais) et il suffirait d’abaisser le pic pointé par la flèche pour que le spectre de réponse après réduction de l’effet de site (trait continu fin) soit couvert par le spectre de dimensionnement.
Différentes méthodes permettent de réduire l’effet de site sismique (Javelaud et Semblat, 2017). Il peut s’agir de réduire l’effet de site lithologique (Fig. 3a) par substitution des formations superficielles, par densification ou renforcement de sol (Fig. 3b), ou bien par purge (Fig. 3b). Dans les configurations géométriques de bassins 2D/3D pour lesquelles les ondes de surfaces générées en bordure du bassin se propagent horizontalement vers son centre (Fig. 3c), il peut s’agir de réduire l’amplitude de ces ondes par des dispositifs d’atténuation mis en place en périphérie des ouvrages à protéger (Fig. 3d).
D’autres méthodes alternatives incluent l’utilisation de l’interaction cinématique qui résulte de la différence de raideur, pour la partie située dans le sol, entre la structure et le sol, que ce soit par encastrement de l’ouvrage ou par la présence de pieux (AFCEN, 2017). Une dernière façon d’agir sur l’effet de site géométrique est par une organisation spatiale optimale des ouvrages qui constituent la ville (ville « hétérogène ») (Bard et al., 2005 ; Kham et al., 2006 ; Varone et al., 2021).
Cet article évalue l’efficacité d’une modification de l’effet de site sismique, à partir de deux exemples présentant des configurations géométriques simples de complexité croissante (configuration tabulaire 1D ; bassin 2D de géométrie trapézoïdale).
Dans cet article, la modification de l’effet de site sismique est évaluée pour un profil de sol réaliste simple, par densification, cimentation ou purge du sol pour la configuration tabulaire 1D, et l’effet complémentaire des ondes de surfaces générées en bord de bassin est estimé pour une configuration 2D.
Une première partie (Sect. 2) conduit à la définition de trois profils de sols de caractéristiques mécaniques croissantes. Elle présente dans un premier temps une synthèse des évolutions de caractéristiques mécaniques de sols obtenues in situ et au laboratoire (vitesse des ondes de cisaillement Vs), puis la faisabilité de travaux de grande ampleur à l’échelle de petits bassins sédimentaires. Pour notre cas d’étude, la section 3 s’intéresse plus particulièrement à la modification de l’effet de site lithologique 1D par densification, renforcement de sol ou purge. La section 4 s’intéresse quant à elle à une configuration géométrique de bassin 2D et au mouvement sismique complémentaire apporté par les ondes de surfaces générées en bordure de bassin.
 |
Fig. 1 Schéma de principe du développement et de la modification des effets de site sismiques dans les bassins sédimentaires : (a) situation de référence sans effet de site sismique ; (b) situation en présence d’un bassin sédimentaire avec effet de site sismique. |
 |
Fig. 2 Schéma de principe présentant l’effet de la réduction de l’effet de site sismique sur les positions relatives des spectres de réponse SRO en accélération et du spectre de dimensionnement. |
 |
Fig. 3 Principales configuration conduisant à un effet de site sismique dans les bassins sédimentaires : (a) effet de site lithologique ; (b) réduction de l’effet de site lithologique par amélioration de sol, renforcement de sol ou purge ; (c) effet de site géométrique 2D/3D de bassin ; (d) réduction de l’effet de site géométrique 2D/3D de bassin par modification des sols et barrières anti-vibratiles. |
2 Amélioration des caractéristiques mecaniques des sols : dans quelle gamme et de quels volumes ?
2.1 Augmentation de la vitesse des ondes de cisaillement Vs par traitement de sol
L’amélioration des caractéristiques mécaniques des sols en petites déformations lors de travaux d’amélioration ou de renforcements de sols s’apprécie au travers de l’évolution de la vitesse des ondes de cisaillement Vs.
2.1.1 Amélioration de sol par densification
2.1.1.1 Amélioration de sol in situ par compactage dynamique et vibrocompactage
Le retour d’expérience de chantiers de compactage dynamique montre que l’augmentation de vitesse des ondes de cisaillement liée aux travaux peut être supérieure à 30 %. À Givors (Brûlé et al., 2010), l’amélioration de matériaux de remblaiement de type grave sableuse a conduit à une augmentation moyenne de la vitesse des ondes de cisaillement sur les cinq premiers mètres de plus de 20 %, de 134 m/s à 163 m/s, mesurée par M.A.S.W. (Fig. 4). À Jackson (Sirles, 1988 ; Sirles et Viksne, 1990), des mesures par cross-holes montrent une augmentation moyenne de 28 % sur les dix mètres supérieurs, avec les plus fortes augmentations pouvant ponctuellement dépasser 40 %.
Le retour d’expérience de chantiers de vibrocompactage montre que l’augmentation de la vitesse des ondes de cisaillement Vs peut aller jusqu’au doublement. Au barrage de Péribonka (Karray et al., 2010), des sables lâches situés sous une ancienne paléo-rivière présentent une vitesse des ondes de cisaillement Vs allant de 150–175 m/s avant travaux, à 250–275 m/s après travaux (Fig. 4), mesurées par M.A.S.W. Au port d’El Musel, des remblais hydrauliques (niveau II) constitués de sables marins mis en place par déversement dans le cadre d’un projet d’extension du port, présentent une augmentation de la vitesse des ondes de cisaillement Vs (Jimenez et Roman, 2012) de 175 m/s avant travaux à 350 m/s après travaux (Fig. 4), mesurée par piézocône sismique SCPTu.
 |
Fig. 4 Synthèse de modifications de la vitesse des ondes de cisaillement Vs par densification ou renforcement de sols. Les valeurs initiales sont représentées par des disques noirs, celles après amélioration par des disques gris. |
2.1.1.2 Amélioration de sol au laboratoire par densification
Les expériences au laboratoire montrent que le module de cisaillement à très petite déformation G0 de sols sans cohésion, ou leur vitesse des ondes de cisaillement Vs, est contrôlé principalement par l’indice des vides e, la contrainte de confinement effective σ’0, et par la composition granulométrique, selon une relation de la forme :
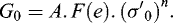
Par exemple pour le sable de Toyoura, les données expérimentales donnent une formule typique (Kokusho, 1980) :
 avec
avec  et G0 en kPa.
et G0 en kPa.
Pour un sol à une contrainte de confinement donnée, le module de cisaillement G0 varie quasi-linéairement de sa configuration la plus lâche (indice des vides emax ou densité relative Dr = 0) vers sa configuration la plus compacte (indice des vides emin ou densité relative Dr = 100 %).
Pour quatre sols granulaires, Karray et al. (2010) présente de façon synthétique l’évolution de la vitesse des ondes de cisaillement Vs entre les configurations les plus lâches (emax) et les plus compactes (emin) : à une contrainte de confinement de 100 kPa, elle augmente d’environ 40 à 70 %.
Mesurée au laboratoire par bender éléments sur du sable d’Ottawa C109 compacté à ses indices des vides minimum et maximum (Robertson et al., 1995), la vitesse des ondes de cisaillement présente une variation de l’ordre de 60 %, de Vs = 148 m/s (emax) à Vs = 236 m/s (emin) pour une contrainte de consolidation isotrope de 100 kPa. Pour un objectif de compaction in situ réaliste de Dr = 70 % (qui était par exemple l’objectif de compaction par vibrocompactage pour le site de Dakar présenté par Briançon et al., 2018), la vitesse des ondes de cisaillement de 209 m/s correspond à une augmentation de l’ordre de 40 %.
Pour le sable saturé de Toyoura (Kokusho, 1980), G0 varie de 88 à 120 MPa lorsque l’indice des vides varie de 0,8 à 0,64 ce qui correspond à une évolution de 15 % de la vitesse des ondes de cisaillement Vs lorsque l’indice des vides varie dans cette gamme.
Les mesures de module de cisaillement et d’amortissement en fonction de la distorsion réalisés à la colonne résonnante sur le sable saturé de Toyoura (Kokusho, 1980) présentent un décalage général, bien que limité, vers la droite quand le sol est en configuration plus dense, ce qui correspond à un amortissement plus faible et à une augmentation du module de cisaillement. Cette diminution de l’amortissement est aussi montrée par Yoshida (2015) sur du sable de Nevada.
2.1.2 Renforcement de sol in situ et au laboratoire par addition de ciment au sol
Le retour d’expérience de jet grouting montre que la vitesse des ondes de cisaillement Vs peut tripler. À Poti Railway (Alkaya et al., 2011), l’amélioration de sables limoneux (environnement 2) conduit à une augmentation moyenne de la vitesse des ondes de cisaillement Vs, de 113 m/s, à 341 m/s mesurée par sismique réfraction (Fig. 4). Au barrage de Tuttle Creek (Axtell et Stark, 2008), des mesures par cross-hole ont montré que la vitesse des ondes de cisaillement passe d’environ 120 m/s à plus de 200 m/s (Fig. 4).
Les essais au laboratoire montrent l’importance de la teneur en ciment et qu’il est possible, simplement en faisant varier la teneur en ciment, d’obtenir des matériaux sol-ciment qui vont d’une modification simple du sol compacté à un sol complètement rigidifié.
Pour le sable d’Osori (Consoli et al., 2013), la vitesse des ondes de cisaillement Vs augmente de 15 %, passant de 96 m/s à 110 m/s, lorsque la densité relative passe de 10 % à 90 % sans addition de ciment (Fig. 4). Elle évolue par ailleurs de 723 m/s à 900 m/s, 7 jours après que 7 % de ciment aient été ajoutés, lorsque la densité relative passe de 10 % à 90 %, ce qui correspond à une évolution de 24 % de la vitesse des ondes de cisaillement Vs (Fig. 4).
Pour le sable n°0 de Monterey, les résultats expérimentaux donnent la formule typique (Saxena et Reddy, 1987) suivante :
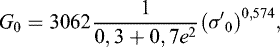 avec
avec 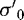 et G0 en kPa.
et G0 en kPa.
Entre les configurations de compaction minimum (Dr = 25 %) et maximum (Dr = 80 %) du matériau testé, la vitesse des ondes de cisaillement Vs augmente d’environ 13 %, passant de 148 m/s à 167 m/s à une pression de confinement de 49 kPa. L’addition de 8 % de ciment au matériau le plus lâche (Dr = 25 %) conduit à une vitesse des ondes de cisaillement de 755 m/s après 15 jours de cure (Fig. 4).
À une pression de confinement de 98 kPa, la vitesse des ondes de cisaillement augmente d’environ 21 % passant de 170 m/s à 205 m/s. L’addition de 2 % de ciment au matériau le plus lâche (Dr = 25 %) conduit à une vitesse des ondes de cisaillement de 291 m/s après 15 jours de cure (Fig. 4).
2.1.3 Renforcement de sol in situ et au laboratoire par biocalcification
Des procédés naturels microbiologiques peuvent également être utilisés pour améliorer les caractéristiques mécaniques des sols sans cohésion par précipitation de calcite.
Des expériences réalisées au laboratoire sur du sable d’Ottawa 50-70 (Dejong et al., 2006) montrent une augmentation de la vitesse des ondes de cisaillement Vs mesurée par bender éléments, passant d’environ 170 m/s à 540 m/s (augmentation par un facteur 3) à une contrainte de confinement de 50 kPa (Fig. 4), et passant d’environ 210 m/s à 540 m/s (augmentation par un facteur 2,5) à une contrainte de confinement de 100 kPa.
Une expérience de grande taille comprenant 100 m3 de sable saturé, et des techniques et moyens similaires à ceux qui seraient utilisés lors de potentielles applications, montre une augmentation de la vitesse in situ des ondes de cisaillement (Van Passen et al., 2010). À partir d’une vitesse initiale homogène des ondes de cisaillement Vs de 107 m/s, cette dernière atteint 16 jours après le traitement une valeur de 188 m/s au minimum (Vs de 188 à 395 m/s, diminuant lorsque la distance à la source augmente) (Fig. 4).
Cette synthèse d’évolutions de la vitesse de cisaillement Vs obtenues in situ et au laboratoire montre que des augmentations très fortes de vitesse des ondes de cisaillement (supérieures à 50 %, et jusqu’au doublement) peuvent être obtenues par densification des sols granulaires dans la masse, mais que de telles augmentations sont réservées aux sols initialement très lâches. En général, les augmentations atteignent au plus 20 % à 40 %. De façon générale, l’évolution de la vitesse des ondes de cisaillement Vs dans les sols dépend en particulier de la nature du sol, de la forme des grains (angulaire/sphériques), de la densité relative initiale du sol et de celle à laquelle il est porté. Le traitement des sols par ajout de ciment ou par biocalcification peut conduire à des vitesses des ondes de cisaillement Vs mesurées in situ de plusieurs centaines de mètres par seconde ; des vitesses dépassant 800 m/s ont été mesurées au laboratoire. Dans tous les cas, l’évolution potentielle de la vitesse des ondes de cisaillement Vs doit être déterminée par une étude spécifique pour chaque sol.
2.2 Capacité technique de traitement en place de petits bassins sédimentaires
Les techniques d’amélioration de sol dans la masse sont utilisées pour augmenter les caractéristiques mécaniques de matériaux granulaires sur de larges surfaces et profondeurs (Briançon et al., 2018).
Le vibrocompactage (Fig. 5a) consiste à densifier un sol granulaire en utilisant une aiguille vibrante. Les comptes-rendus de travaux montrent des améliorations de sols par vibrocompactage jusqu’à des profondeurs dépassant 65 m (Kirstein, 2012) et sur des surfaces excédant les 180 ha (Briançon et al., 2018). Comme chantier de très grande ampleur, Sigismond et al. (1983) cite des travaux d’amélioration d’environ un demi-million de mètres cube de sol par vibrocompactage lors de la construction du parc électronucléaire français. Briançon et al. (2018) mentionnent le chantier de la construction du parc Disneyland de Hong Kong pour lequel 40 millions de m3 de sable ont été vibrocompactés.
Le compactage dynamique (Fig. 5b) consiste quant à lui à faire tomber une masse sur le sol. Les comptes-rendus de travaux montrent des améliorations de sol par compactage dynamique jusqu’à des profondeurs de 30 m (Mitchell, 1981) et sur des surfaces dépassant les 480 ha (Hamidi et al., 2011). Chu et al. (2009) rapportent que les volumes traités par vibrocompactage et compactage dynamique lors de la construction d’îles artificielles à Dubai se comptent en centaines de millions et jusqu’à 1,3 milliard de mètres cubes de sols compactés.
En ce qui concerne les fondations profondes comme les pieux ou le renforcement de sol, ils peuvent être réalisés avec l’espacement choisi et à des profondeurs pouvant excéder les 75 m (Guilloux et al., 2009). Sigismond et al. (1983) cite des travaux d’injection de sol d’ampleur significative où quelques milliers de mètres cube de coulis ont été injectés.
La purge des sols consiste à retirer les sols de caractéristiques médiocres de la zone d’intérêt. Des travaux de purge de grande ampleur sont parfois réalisés. Sigismond et al. (1983) citent des travaux de purge de sols d’environ 2 millions de mètres cube de sol par réalisation de deux excavations d’environ 17,5 m de profondeur et formant un rectangle de 210 × 265 m de côté chacune.
Ces expériences de chantier montrent qu’il est techniquement possible d’améliorer dans la masse les sols de bassin sédimentaires de petites dimensions, ou de purger les formations superficielles jusqu’à un substratum sismique situé à faible profondeur.
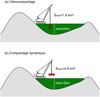 |
Fig. 5 Vue schématique de l’extension (surface, profondeur) de travaux d’amélioration de sols : (a) par vibrocompactage ; (b) par compactage dynamique. |
2.3 Sélection du cas d’étude
Nous avons sélectionné comme cas d’étude le sable de Monterey n°0 (Saxena et Reddy, 1987) car il est bien caractérisé dans un état de densité relative de 25 %, de densité relative de 80 %, et de densité relative de 25 % avec ajout de 8 % de ciment. Cela permet d’obtenir un profil réaliste de vitesse des ondes de cisaillement Vs avec la profondeur. De plus, les courbes de dégradations G-γ et D-γ disponibles pour les trois matériaux permettent d’évaluer les modules de cisaillement et l’amortissement intrinsèque du sol de façon réaliste, en fonction de la profondeur, dans la gamme de distorsion associée au chargement sismique considéré.
2.3.1 Matériaux
Trois profils de sol numérotés #1, #2 et #3 sont supposés constitués de 30 m de sable de Monterey n°0 (Saxena et Reddy, 1987). Les résultats expérimentaux réalisés au laboratoire par Saxena et Reddy (1987) sur ce matériau montrent qu’entre un état de compaction minimum (sol #1 avec un indice de densité de 25 %, c’est-à-dire présentant un indice des vides de 0,7775) à un état de compaction maximum (sol #2 avec un indice de densité de 80 %, c’est-à-dire présentant un indice des vides de 0,618), la vitesse des ondes de cisaillement Vs augmente d’environ 13 % en passant de 148 m/s à 167 m/s à une contrainte de confinement de 49 kPa.
Pour le sable de Monterey n°0, les données expérimentales donnent l’évolution du module de cisaillement G0 à très petites déformations, en fonction de la contrainte effective σ’0 et de l’indice des vides e (Saxena et Reddy, 1987), suivante :
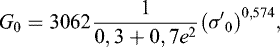 avec
avec  et G0 en kPa.
et G0 en kPa.
En terme de vitesse des ondes de cisaillement Vs sur les trente premiers mètres, cela correspond à une évolution de Vs,30 de 13 %, de 176 m/s (sol #1) à 199 m/s (sol #2), qui se situe dans la gamme basse des augmentations maximales possibles de vitesses des ondes de cisaillement Vs (cf. Sect. 2.1).
L’addition de 8 % de ciment au sol le plus lâche conduit à une vitesse des ondes de cisaillement de 755 m/s après 15 jours de cure (Saxena et Reddy, 1987). Ceci est cohérent avec les autres mesures in situ et au laboratoire réalisées sur des sols densifiés ou renforcés (cf. synthèse Fig. 4). Pour explorer complètement la gamme des caractéristiques mécaniques des bassins sédimentaires, nous avons choisi de façon conservative une vitesse des ondes de cisaillement intermédiaire et constante de 520 m/s pour le sol #3. En ce qui concerne les travaux d’imprégnation dans la masse, ils sont habituellement réalisés au droit des ouvrages concernés ; cette situation où l’ensemble du sol est traité constitue un cas limite. Enfin pour avoir une solution de référence en l’absence d’effet de site sismique, le bassin #4 est considéré constitué de rocher de référence dont la Vs est de 800 m/s. Le tableau 1 présente de façon synthétique les caractéristiques mécaniques des 4 profils de sol.
Synthèse des caractéristiques mécaniques retenues pour les quatre profils de sol.
2.3.2 Chargement sismique
Le chargement sismique est une onde incidente plane SV verticale. II s’agit d’un accélérogramme synthétique appliqué en condition de rocher affleurant (Fig. 6a, i).
Sa durée est cohérente avec un séisme de magnitude Mw 4,7 se produisant à une distance hypocentrale de 10 km (Bommer et al., 2009). L’accélérogramme synthétique est généré pour être conforme aux exigences de l’Eurocode 8-1 (2005) pour un sol de classe A et une accélération maximale de 0,35 m/s2, en utilisant le générateur de signaux synthétiques du code de calcul Code_Aster (Zentner, 2017). Il est convolué dans les fonctions de transfert des 4 colonnes de sols (Fig. 6a).
 |
Fig. 6 Réduction de l’effet de site lithologique par traitement de sol. (a) Gauche : accélération utilisée comme chargement sismique en condition de rocher affleurant ; Droite : accélérations calculées à la surface pour les quatre profils de sol de caractéristiques mécaniques croissantes par la méthode linéaire-équivalent ; (b) Caractéristiques non-linéaires des sols ; (c) Caractéristiques mécaniques effectives des sols (module de Young, amortissement intrinsèque) pour le chargement sismique considéré, ainsi que distorsion maximale calculée à chaque profondeur ; (d) Spectre de réponse en accélération à 5 % d’amortissement, du chargement sismique ainsi que des mouvements sismiques calculés en surface pour les quatre profils de sol. |
3 Modification de l’effet de site lithologique 1D
L’effet de site lithologique 1D est comparé entre une situation initiale où le sol est lâche (Dr25, Fig. 6a, ii) et les situations où le sol est dense (Dr80, Fig. 6a, iii), le cas limite où le sol est injecté (Dr25 cc 8 %, Fig. 6a, iv) et à la situation où le sol est purgé (Fig. 6a, i) ; la situation de référence pour évaluer la modification de l’effet de site lithologique 1D étant celle où le bassin est constitué de rocher identique au substratum (Fig. 6a, v).
3.1 Méthode
L’effet de site sismique est évalué par la méthode linéaire-équivalent : les caractéristiques mécaniques des sols (module de cisaillement, amortissement) sont ainsi sélectionnées en fonction de la gamme de distorsions auxquels les sols sont sollicités en relation avec le chargement sismique, et elles sont évaluées selon une discrétisation verticale métrique. Les simulations numériques 1D sont réalisées dans le domaine fréquentiel avec le code aux éléments finis Code_Aster (Devesa, 2015 ; Jacquet, 2016).
3.2 Calculs réalisés
Les analyses de réponse de site spécifiques sont réalisées pour les 4 profils de caractéristiques mécaniques croissantes : un rempli de sable lâche, deux remplis de sol améliorés (par compaction ou injection), et le quatrième étant constitué de rocher (Fig. 6a).
Le module de cisaillement normalisé G/G0-γ et l’amortissement D-γ des sols (Fig. 6b) #1, #2 et #3 à une pression de confinement de 49 kPa (Saxena et Reddy, 1987) sont utilisés conjointement à un coefficient de Poisson de 0,3 et à une densité de 1,93 pour les sols présentant une densité relative de 25 %, et à une densité de 2,02 pour les sols présentant une densité relative de 80 %. Le substratum rocheux représentant le substratum sismique est supposé avoir une vitesse des ondes de cisaillement de 800 m/s, une densité de 2,40 et un comportement quasi élastique : ses caractéristiques mécaniques correspondent à un amortissement de 0,5 % (Fig. 6b) et un coefficient de Poisson de 0,2. Pour le quatrième profil, le bassin sédimentaire est supposé constitué du même rocher que celui constituant le substratum sismique.
3.3 Résultats
Les résultats sont donnés en terme d’accélérations temporelles (Fig. 6a, ii, iii et iv) et de spectre de réponse en accélération à 5 % d’amortissement (Fig. 6d). Ils sont comparés à la situation de référence en l’absence d’effet de site sismique lorsque le bassin sédimentaire est constitué de rocher (Fig. 6a, v). La figure 6c présente la distorsion maximale des sols en fonction de la profondeur pendant le séisme ainsi que le module de Young effectif et l’amortissement effectif des sols pendant le séisme.
En termes d’accélérations enregistrées à la surface, l’accélération maximale (PGA) observée pour le profil #1 est de 0,89 m/s2. L’amplification est plus faible pour le sol densifié du profil #2 (PGA de 0,78 m/s2), et diminue drastiquement lorsque du ciment est ajouté (PGA de 0,39 m/s2 pour le profil de sol #3). Elle décroit encore dans le cas de la purge pour atteindre, en l’absence d’effet de site sismique, 0,35 m/s2. On retrouve naturellement la même accélération (PGA de 0,34 m/s2) pour le sol #4.
La densification du sol #1 en sol #2 conduit globalement à un spectre de réponse en accélération plus faible pour les structures dont la fréquence fondamentale va jusqu’à 10 Hz, avec des facteurs de réduction atteignant 1,3 à 1,5 pour les structures de fréquence fondamentale proche de 2,1 Hz, 5,1 Hz et 8,7 Hz. Il faut mentionner qu’autour de 2,8 Hz et 6,8 Hz, le sol densifié présente un spectre de réponse en accélération légèrement supérieur au cas du sol peu dense (sol #1).
Les modifications de sols plus prononcées conduisent à des évolutions marquées du spectre de réponse en accélération quelle que soit la fréquence : l’addition de ciment au sol #1 conduit au sol #3 pour lequel le spectre de réponse en accélération est drastiquement réduit quelle que soit la fréquence d’intérêt ; pour la situation où le bassin est purgé ou bien rempli de rocher (sol #4), il n’y a pas d’effet de site et le spectre de réponse en accélération est identique à celui du mouvement du rocher affleurant.
4 Modification de l’effet de site lithologique et de l’effet géométrique 2D
Pour un bassin de forme géométrique 2D simple, l’effet de site est comparé pour les quatre situations suivantes qui sont les mêmes que pour l’étude de l’effet de site lithologique 1D : sol lâche Dr25, sol dense Dr80, le cas limite où le sol est injecté (Dr25 cc 8 %) et à la situation où le sol est purgé. La particularité d’une géométrie 2D de bassin sédimentaire est qu’un mouvement sismique complémentaire est généré par la géométrie du bassin sédimentaire par rapport à la situation 1D où les couches de sols tabulaires ont une extension latérale infinie.
En pratique, les applications possibles sont restreintes aux capacités techniques de chantier à traiter les sols de petits bassins sédimentaires. Des bassins de grande largeur sont toutefois utilisés dans cette section pour caractériser le mouvement sismique complémentaire apporté par une configuration géométrique de bassin 2D par rapport à la situation 1D. Ils permettent en effet de séparer temporellement dans les modélisations les ondes de surfaces générées aux bords du bassin et à propagation horizontale, des ondes de volume 1D à propagation verticale, et de les étudier séparément.
4.1 Méthode
La propagation d’ondes sismiques dans un milieu semi-infini est réalisée avec le code aux éléments finis Code_Aster. Le maillage est constitué d’éléments quadrangles de 1 m de côté.
Les simulations 2D en déformation plane sont réalisées sur des modèles de 14 km de largeur. Des conditions de périodicité sur les faces latérales des modèles imposent des déplacements identiques pour les nœuds des faces gauche et droite situés en vis-à-vis. Pour les modèles 2D, des conditions de rocher infinies latéralement au bord du modèle sont ainsi modélisées, en dehors du bassin sédimentaire qui fait 13 km de largeur (en surface, le bassin sédimentaire fait 13 km de largeur et il y a 500 m de rocher de chaque côté). Au bas du modèle, un élément de frontière absorbante modélise le substratum comme un milieu infini élastique : ainsi, une partie des ondes est réfléchie sur cette interface, tandis qu’une autre est dissipée par amortissement radiatif.
Les modélisations sont dimensionnées pour être précises jusqu’à une fréquence d’au moins 15 Hz, afin d’inclure l’ensemble des fréquences d’intérêt pour le génie parasismique. La limitation apparaît pour la plus petite vitesse effective des ondes de cisaillement de 90 m/s près de la surface dans le cas du profil de sol #1 en considérant le maillage de 1 m de côté. Les simulations sont réalisées jusqu’à des fréquences de 50 Hz.
Les modélisations 2D sont effectuées dans le domaine fréquentiel. De longues durées de calculs de 81,92 s permettent aux ondes de surfaces d’être complètement dissipées avant la fin des simulations. La durée moyenne de calcul avec 8 processeurs est d’environ 8 h pour 924 000 degrés de liberté.
Le mouvement sismique est appliqué en condition de rocher affleurant à la base du modèle à la profondeur de −32 m. Le chargement sismique est une onde incidente plane SV verticale et le mouvement sismique utilisé est le même accélérogramme synthétique que pour les modélisations 1D (Fig. 6a, i).
Des bassins sédimentaires larges sont utilisés pour étudier l’effet de l’amélioration des caractéristiques mécaniques des sols sur les ondes de surfaces additionnelles générées par des géométries 2D. La largeur du bassin est ainsi choisie de telle manière que les ondes de surface générées aux bords du bassin arrivent en son milieu bien après que les ondes de volume 1D aient cessées. La géométrie du bassin est un simple trapèze symétrique de 13 km de large et de 30 m de profondeur. Soixante-sept récepteurs sont définis à sa surface, soixante-six de manière régulière entre les positions −6500 m et +6500 m avec une interdistance de 200 m, et un récepteur au centre du bassin. Les points situés à 6500 m du milieu du bassin marquent le début du bassin sédimentaire à la surface libre. Les côtés du bassin sédimentaires ont une pente de 3H/2V.
4.2 Cas sans amortissement
Les premières modélisations ont été réalisées sans ou quasiment sans amortissement (0,025 %) pour les profils de sols #1, #2 et #3 remplissant le bassin sédimentaire. Cela permet (Fig. 7) la visualisation à la fois des ondes de volumes se propageant verticalement, la génération des ondes de surface aux bords du bassin puis la propagation horizontale des ondes de surface à l’intérieur du bassin sédimentaire.
La figure 8 présente un zoom sur une partie de la figure 7 (sol #2). Sur le côté gauche de la figure 8, le récepteur situé à la position x = −6500 m est placé exactement au bord du bassin sédimentaire et il n’enregistre donc pas d’effet de site. À l’opposé de la figure, le récepteur situé trois kilomètres plus loin à la position x = −3500 m enregistre d’abord l’onde 1D se propageant vers le haut du modèle, puis les ondes de surface formées au bord du bassin et se propageant horizontalement.
Entre les deux, les ondes de surfaces sont tout d’abord complètement mêlées aux ondes 1D à la position x = −6300 m. En allant vers le centre du bassin aux positions x = −6100 m à x = −5700 m, la partie principale des ondes de surfaces arrivent progressivement une fois que les ondes 1D ont cessé : cela crée globalement une augmentation de la durée du mouvement sismique. Finalement, à la position x = −4500 m et ensuite jusqu’au centre du bassin, les ondes 1D et les ondes de surface arrivent séparément.
 |
Fig. 7 Représentation spatio-temporelle du mouvement sismique enregistré par la composante horizontale de chacun des 67 récepteurs situés à la surface le long d’une ligne de 13 km de longueur recoupant le bassin sédimentaire, pour les profils de sol #1, #2, #3, sans amortissement du sol (amortissement quasi-nul, réduit à 0,025 %). Le rectangle rouge montre les ondes à incidence verticale 1D de volume, tandis que les rectangles verts montrent les ondes de surface formées aux bords du bassin et qui se propagent horizontalement vers son centre. |
 |
Fig. 8 Zoom de la figure 7b montrant le mouvement sismique calculé pour la composante horizontale des seize premiers récepteurs placés le long d’une ligne recoupant en largeur le bassin sédimentaire constitué de sol #2, sans amortissement dans le sol (l’amortissement est quasi nul, réduit à 0,025 %). |
4.3 Cas avec amortissement
Des modélisations d’effet de site 2D sont réalisées pour trois bassins sédimentaires d’extension latérale finie et remplis des sols #1, #2 et #3 de caractéristiques mécaniques croissantes. Les caractéristiques mécaniques (module de Young, amortissement, densité, coefficient de Poisson) utilisés pour les bassins sédimentaires sont les propriétés effectives obtenues précédemment à la fin des calculs 1D et présentés sur la figure 6c. Des simulations 2D en déformation plane sont réalisées dans le domaine fréquentiel en utilisant le code aux éléments finis Code_Aster pour les trois modèles de bassins sédimentaires décrits ci-dessus.
Les résultats sont donnés en termes d’accélérations temporelles à chaque récepteur. La comparaison des accélérations obtenues par les modélisations 1D à la section précédente (Sect. 3) et au centre des bassins sédimentaires pour des sols ayant des caractéristiques mécaniques identiques montre une excellente concordance en termes d’amplitudes des ondes de volume 1D, ce qui correspond aux 15 premières secondes.
Les ondes de surfaces sont extraites des accélérogrammes enregistrés à chaque capteur situé aux positions −6300 m, −6100 m, −5900 m et −5700 m (Fig. 9a–9c) en soustrayant l’accélération enregistrée au centre du bassin. La figure 9d–9f présente les ondes de surface (accélérations temporelles) aux positions −6300 m à −5700 m, ainsi que leur contenu fréquentiel obtenu par transformée de Fourier (Fig. 9g–9i) ; les ondes de surfaces se déplacent du bord du bassin vers son centre, et leur amplitude diminue lorsqu’elles voyagent. Le contenu fréquentiel des ondes de surface est essentiellement de 2 à 10 Hz quelle que que soit la distance du bord du bassin, bien que leur diminution d’amplitude avec la distance est plus rapide pour les fréquences les plus hautes et les plus basses. Une quantification des ondes de surface est également envisageable par analyse temps-fréquence (Meza-Fajardo et al., 2015).
Les résultats sont également présentés en termes de spectre de réponse en accélération, calculés pour l’ensemble des accélérogrammes obtenus à différentes positions le long du bassin sédimentaire rempli des sols #1, #2 et #3 (Fig. 10). Des interférences importantes entre les ondes de volume et les ondes de surfaces peuvent se produire. Aux positions −6300 m, −6100 m et −5900 m pour les sols #1 et #2, les spectres de réponse en accélération sont plus élevés que pour les cas 1D en raison d’interférences constructives. Cet effet est plus prononcé pour les structures de fréquences propres situées entre 2 et 5 Hz pour les sols #1 et #2. Pour le sol #3, l’effet de site lithologique 1D est faible et par conséquent l’amplitude des ondes de surfaces générées en bord de bassin est faible également. Un amortissement plus fort contribue aussi à une plus forte atténuation des ondes de surface. Aux positions allant de −6300 m à −5900 m, cet amortissement n’induit pas de différences significatives entre les simulations 1D et 2D (Fig. 10).
 |
Fig. 9 Accélérations temporelles et contenu fréquentiel des ondes de surface à différentes positions le long des bassins #1, #2 et #3, au fur et à mesure de leur propagation vers leur centre. Les figures d–f montrent les accélérogrammes des ondes de surface générées au bord du bassin par les ondes SV d’incidence verticale ; les figures g–i montrent leur contenu fréquentiel. |
 |
Fig. 10 Spectres de réponses en accélération pour les accélérogrammes calculés à différentes positions le long des bassins sédimentaires remplis de sols #1, #2 et #3. |
5 Discussion et conclusion
Dans le cas de l’exemple présenté, une façon efficace de réduire l’effet de site sismique est d’agir sur les caractéristiques mécaniques du sol directement dans la masse. Ici, la densification des sols (augmentation de 13 % de la Vs,30 entre le profil #1 et le profil #2) entraine une diminution de l’ordre de 10 % de l’accélération maximale PGA en surface, et une diminution ponctuelle du spectre de réponse en accélération, qui peut toutefois être suffisante pour que le nouveau spectre de réponse en accélération soit couvert par le spectre de dimensionnement (cas de la Fig. 2, droite). L’injection d’imprégnation du sol dans la masse (profil #3) ou bien la purge des formations sédimentaires superficielles, entrainent une diminution de plus de 50 % de l’accélération maximale PGA en surface, et une diminution significative du spectre de réponse en accélération. Cela peut permettre d’assurer que le nouveau spectre de réponse en accélération soit couvert par le spectre de dimensionnement (cas de la Fig. 2, gauche).
Une façon efficace de réduire l’effet de site sismique est d’agir directement dans la masse sur les caractéristiques mécaniques du sol. La réduction peut parfois être drastique et conduire à supprimer l’effet de site (effet de site lithologique et par conséquence l’effet de site géométrique 2D/3D). Les travaux de purge ramènent dans le cas d’étude considéré au cas de référence sans effet de site sismique.
La contribution des ondes de surface au mouvement sismique total est quantifiée dans le cas de la configuration géométrique 2D. Les ondes de volume à propagation verticale, et les ondes de surfaces générées en bordure du bassin et à propagation horizontale, sont séparées en utilisant un bassin sédimentaire de grande largeur. Pour cette configuration de bassin trapézoïdale, les résultats montrent que les ondes de surface produisent un mouvement sismique additionnel qui s’ajoute au mouvement 1D des ondes de volumes à propagation verticale, ce qui conduit à un spectre de réponse en accélération plus élevé.
Dans l’exemple considéré, la prise en compte de l’effet géométrique 2D génère un mouvement sismique complémentaire. Ce dernier est significatif à l’abscisse −6300 m pour les sols #1 et #2, et il diminue ensuite rapidement avec la distance du bord du bassin en raison de l’amortissement intrinsèque du sol. Agir sur l’effet géométrique 2D par des dispositifs d’atténuation des ondes de surface disposés autour de l’ouvrage, en considérant le cas limite où ils permettent d’atténuer totalement ces ondes et revenir au cas 1D, permet de quantifier la diminution ponctuelle maximale ainsi atteignable du spectre de réponse en accélération. Celle-ci peut s’avérer suffisante pour que le nouveau spectre de réponse en accélération soit couvert par le spectre de dimensionnement (cas de la Fig. 2, droite).
Toutefois, pour les bassins, les dispositifs d’atténuation des ondes de surface disposés autour de l’ouvrage n’entraineront pas systématiquement une atténuation totale des ondes de surface. En perspective, la quantification de l’effet bénéfique sur les ondes de surface de différents dispositifs d’atténuation des ondes de surface pourra faire l’objet d’une analyse ultérieure, en utilisant les caractéristiques mécaniques effectives des sols (module de Young effectif, amortissement effectif) et le mouvement sismique (ondes de surface, ondes de volume) déterminés lors du séisme.
Pour cet exemple constitué d’un bassin sédimentaire de faible épaisseur, plusieurs possibilités de réduction de l’effet de site sismique existent (amélioration de sol dans la masse par densification ou par injection d’imprégnation ; purge ; atténuation des ondes de surface générées au bord du bassin). En fonction de l’objectif de réduction du mouvement sismique visé, elles permettent d’évaluer le type d’effet de site et d’ondes sur lesquels agir (ondes de surface à propagation horizontale ; onde de volume 1D à propagation verticale).
Références
- AFCEN. 2017. RCC-CW. Règles de conception et réalisation pour le génie civil des centrales électronucléaires. [Google Scholar]
- Alkaya D, Ҫobanoğlu I, Yeşil B, Yildiz MŞ. 2011. The evaluation of stone column and jet grouting soil improvement with seismic refraction method: Example of Poti (Georgia) railway. Int J Phys Sci 6(28): 6565–6571. [Google Scholar]
- Axtell PJ, Stark TD. 2008. Increase in shear modulus by soil mixing and jet grout methods. DFI J 2(1). [Google Scholar]
- Bard PY, Chazelas JL, Gueguen P, Kham M, Semblat JF. 2005. Chapter 5: Site-city interaction. Oliveira CS, Roca A, Goula X, eds. Assessing and Managing Earthquake Risk. Springer, 375 p. [Google Scholar]
- Bommer JJ, Stafford PJ, Alarcón JE. 2009. Empirical equations for the prediction of the significant, bracketed, and uniform duration of earthquake ground motion. Bull Seism Soc Am 99(6). [Google Scholar]
- Briançon L, Liausu P, Plumelle C, Simon B. 2018. Amélioration et renforcement des sols. Éditions Le Moniteur. [Google Scholar]
- Brûlé S, Javelaud E, Bitri A. 2010. Analyse de la réponse sismique sur un site après travaux d’amélioration des sols par compactage dynamique haute énergie. In: Conférence franco-maghrébine en ingénierie géotechnique, Tunis. [Google Scholar]
- Chu J, Varaksin S, Klotz U, Mengé P. 2009. State of the art report : procédés de constructions. In: 17th International Conference on Soil Mechanics and Geotechnical Engineering, 5–9 October 2009, Alexandrie, Egypte. [Google Scholar]
- Consoli NC, Fonini A, Maghous S, Schnaid F, Viana da Fonseca A. 2013. Experimental analysis of the mechanical properties of artificially cemented soils and their evolution in time. In: Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris. [Google Scholar]
- Dejong JT, Fritzges MB, Nüsslein K. 2006. Microbially induced cementation to control sand response to undrained shear. J Geotech Geoenviron Eng 132(11): 1381–1392. [CrossRef] [Google Scholar]
- Devesa G. 2015. Code_Aster, Documentation n°U4.84.31. Commande DEFI_SOL_EQUI (2015). https://www.code-aster.org/V2/doc/v12/fr/man_u/u4/u4.84.31.pdf. [Google Scholar]
- EN 1998-1:2005 (AFNOR). 2005. Eurocode 8 – Design of structures for earthquake resistance – Part 1: General rules, seismic actions and rules for buildings. [Google Scholar]
- Guilloux A, Berthelot P, Zaghouani K, Schlosser F. 2009. Les fondations du Pont de Radès-La Goulette (Tunisie) : reconnaissances, conception et essais de pieux. In: Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering. [Google Scholar]
- Hamidi B, Varaksin S, Nikraz H. 2011. Dynamic compaction for treating millions of square meters of sand. In: International Conference on Advances in Geotechnical Engineering, Perth, Australia. [Google Scholar]
- Jacquet M. 2016. Code_Aster, Documentation n°R4.05.06. Méthode linéaire-équivalente pour la propagation des ondes en 1D (2016). https://www.code-aster.org/V2/doc/v13/fr/man_r/r4/r4.05.06.pdf. [Google Scholar]
- Javelaud EH, Semblat J-F. 2017. Effets de site sismiques pour les ouvrages de surface. Techniques de l’Ingénieur, C260. [Google Scholar]
- Jimenez R, Roman F. 2012. A comparison of soil improvement achieved using different vibro methods. In: Proceedings of the International symposium on ground improvement IS-GI, Brussels. [Google Scholar]
- Karray M, Lefebvre G, Ethier Y, Bigras A. 2010. Assessment of deep compaction of the Péribonka dam foundation using “modal analysis of surface waves” MASW. Can Geotech J 47: 312–326. [CrossRef] [Google Scholar]
- Kham M, Semblat JF, Bard PY, Dangla P. 2006. Seismic site-city interaction: Main governing phenomena through simplified numerical models. Bull Seismolog Soc Am 96(5): 1934–1951. [CrossRef] [Google Scholar]
- Kirstein JF. 2012. General report, session 1: Vibro and impact compaction. International Symposium on Ground Improvement ISGI (2012). [Google Scholar]
- Kokusho T. 1980. Cyclic triaxial test of dynamic soil properties for wide range strain. Soils Found 20(2). [Google Scholar]
- Meza-Fajardo KC, Papageorgiou AS, Semblat JF. 2015. Identification and extraction of surface waves from three-component seismograms based on the Normalized Inner Product. Bull Seismolog Soc Am 105(1): 210–229. [CrossRef] [Google Scholar]
- Mitchell JK. 1981. Soil improvement: State-of-the-art. In: Proc Tenth Int Conf on Soil Mechs, Found Eng, June 1981, Stockholm, Sweden, 4, pp. 509–565. [Google Scholar]
- Robertson PK, Sasitharan S, Cunning JC, Sego DC. 1995. Shear-wave velocity to evaluate in situ state of Ottawa sand. J Geotech Eng 121(3): 262–273. [CrossRef] [Google Scholar]
- Saxena SK, Reddy RK. 1987. Mechanical behavior of cemented sands. Report n°IIT-CE-8701, Department of Civil Engineering, Illinois Institute of Technology. [Google Scholar]
- Sigismond M, Groupe de travail d’EDF/SEPTEN. 1983. The use of soil improvement techniques in the realization of the French Nuclear Power Programme. In: Proceedings of the Eighth European Conference on Soil Mechanics and Foundation Engineering, organized by the Finnish Geotechnical Society, 23–26 May 1983, Helsinki. [Google Scholar]
- Sirles PC. 1988. Case study: Shear wave velocity measurements before and after dynamic compaction of cohesionless soil deposits. In: 1988 SEG Annual Meeting, pp. 290–293. [Google Scholar]
- Sirles PC, Viksne A. 1990. Site-specific shear wave velocity determination for geotechnical engineering applications. Soc Explor Geophys Investig Geophys: 121–132. [Google Scholar]
- Van Passen LA, Ghose R, Van der Linen TJM, Van der Star WRL, Van Loosdrecht MCM. 2010. Quantifiying biomediated ground improvement by Ureolysis: Large-scale biogrout experiment. J Geotech Geoenviron Eng 136(12): 1721–1728. [CrossRef] [Google Scholar]
- Varone C, Lenti L, Martino S, Semblat JF. 2021. Spatial variability of the urban ground motion in a highly heterogeneous site-city configurations. Bull Earthq Eng 19: 27–45. [CrossRef] [Google Scholar]
- Yoshida N. 2015. Seismic ground response analysis. Geotechnical, Geological and Earthquake Engineering 36. Springer. [Google Scholar]
- Zentner I. 2017. Code_Aster, Documentation n°U4.36.04. Commande GENE_ACCE_SEISME (2017). https://www.code-aster.org/V2/doc/default/fr/man_u/u4/u4.36.04.pdf. [Google Scholar]
Citation de l’article: Emmanuel Javelaud, Jean-François Semblat. Peut-on modifier l’effet de site sismique ? Rev. Fr. Geotech. 2022, 170, 3.
Liste des tableaux
Synthèse des caractéristiques mécaniques retenues pour les quatre profils de sol.
Liste des figures
 |
Fig. 1 Schéma de principe du développement et de la modification des effets de site sismiques dans les bassins sédimentaires : (a) situation de référence sans effet de site sismique ; (b) situation en présence d’un bassin sédimentaire avec effet de site sismique. |
| Dans le texte | |
 |
Fig. 2 Schéma de principe présentant l’effet de la réduction de l’effet de site sismique sur les positions relatives des spectres de réponse SRO en accélération et du spectre de dimensionnement. |
| Dans le texte | |
 |
Fig. 3 Principales configuration conduisant à un effet de site sismique dans les bassins sédimentaires : (a) effet de site lithologique ; (b) réduction de l’effet de site lithologique par amélioration de sol, renforcement de sol ou purge ; (c) effet de site géométrique 2D/3D de bassin ; (d) réduction de l’effet de site géométrique 2D/3D de bassin par modification des sols et barrières anti-vibratiles. |
| Dans le texte | |
 |
Fig. 4 Synthèse de modifications de la vitesse des ondes de cisaillement Vs par densification ou renforcement de sols. Les valeurs initiales sont représentées par des disques noirs, celles après amélioration par des disques gris. |
| Dans le texte | |
 |
Fig. 5 Vue schématique de l’extension (surface, profondeur) de travaux d’amélioration de sols : (a) par vibrocompactage ; (b) par compactage dynamique. |
| Dans le texte | |
 |
Fig. 6 Réduction de l’effet de site lithologique par traitement de sol. (a) Gauche : accélération utilisée comme chargement sismique en condition de rocher affleurant ; Droite : accélérations calculées à la surface pour les quatre profils de sol de caractéristiques mécaniques croissantes par la méthode linéaire-équivalent ; (b) Caractéristiques non-linéaires des sols ; (c) Caractéristiques mécaniques effectives des sols (module de Young, amortissement intrinsèque) pour le chargement sismique considéré, ainsi que distorsion maximale calculée à chaque profondeur ; (d) Spectre de réponse en accélération à 5 % d’amortissement, du chargement sismique ainsi que des mouvements sismiques calculés en surface pour les quatre profils de sol. |
| Dans le texte | |
 |
Fig. 7 Représentation spatio-temporelle du mouvement sismique enregistré par la composante horizontale de chacun des 67 récepteurs situés à la surface le long d’une ligne de 13 km de longueur recoupant le bassin sédimentaire, pour les profils de sol #1, #2, #3, sans amortissement du sol (amortissement quasi-nul, réduit à 0,025 %). Le rectangle rouge montre les ondes à incidence verticale 1D de volume, tandis que les rectangles verts montrent les ondes de surface formées aux bords du bassin et qui se propagent horizontalement vers son centre. |
| Dans le texte | |
 |
Fig. 8 Zoom de la figure 7b montrant le mouvement sismique calculé pour la composante horizontale des seize premiers récepteurs placés le long d’une ligne recoupant en largeur le bassin sédimentaire constitué de sol #2, sans amortissement dans le sol (l’amortissement est quasi nul, réduit à 0,025 %). |
| Dans le texte | |
 |
Fig. 9 Accélérations temporelles et contenu fréquentiel des ondes de surface à différentes positions le long des bassins #1, #2 et #3, au fur et à mesure de leur propagation vers leur centre. Les figures d–f montrent les accélérogrammes des ondes de surface générées au bord du bassin par les ondes SV d’incidence verticale ; les figures g–i montrent leur contenu fréquentiel. |
| Dans le texte | |
 |
Fig. 10 Spectres de réponses en accélération pour les accélérogrammes calculés à différentes positions le long des bassins sédimentaires remplis de sols #1, #2 et #3. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




