| Issue |
Rev. Fr. Geotech.
Number 153, 2017
|
|
|---|---|---|
| Article Number | 3 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/geotech/2017017 | |
| Published online | 02 February 2018 | |
Article d’ingénierie / Engineering Article
Méthode d’estimation des tassements des sols fins sous les remblais d’infrastructures ferroviaires pour lignes à grande vitesse
Prediction of embankment settlement over soft soils in high-speed railway projects
1
Terrasol, Immeuble Central Seine,
42–52 quai de la Rapée,
75583
Paris cedex 12, France
2
École Nationale des Ponts et Chaussées (ENPC), Cité Descartes,
6–8 Avenue Blaise Pascal,
77455
Champs-sur-Marne, France
3
Institut Français des Sciences et Technologie des Transport de l’Aménagement et des Réseaux (IFSTTAR), Cité Descartes,
19–20 boulevard Newton,
77455
Champs-sur-Marne, France
★ Auteur de correspondance : philippe.reiffsteck@ifsttar.fr
Le besoin de maîtriser les déformations des sols sous les remblais destinés à recevoir les structures de lignes à grande vitesse, en fait un enjeu important pour ces projets. Toutefois, de nombreuses difficultés ont été soulevées liées principalement au grand nombre d’incertitudes qui entourent le phénomène. En effet, la caractérisation géologique et géotechnique dépend de sondages et d’essais où le risque de remaniement est important et dont l’interprétation est, souvent, délicate. Cet article présente une procédure de calcul qui permettrait en pratique d’évaluer le tassement sous remblai avec une bonne précision et qui a été validée sur un certain nombre d’ouvrages. Pour cela, des corrections sont introduites aux méthodes usuelles de calcul permettant d’approcher les valeurs mesurées sur chantier.
Abstract
Settlement of high-speed railway embankments is a major issue encountered in maintaining railway facilities and controlling settlements. The challenges mainly come from the large number of uncertainties related to this phenomenon. In fact, the geology and the geotechnical characterization of the ground depend on interpretations of in situ and laboratory tests that are influenced by soil disturbance during sampling and laboratory testing. Hence, this paper describes a design procedure that will insure, in practice, an acceptable error while evaluating embankment settlements. In this regard, some adjustments have been introduced to usual design methods. The results are comparable to the consolidation settlement measured in the field.
Mots clés : consolidation; remblai / coefficients de pression interstitielle A et B / cohésion non-drainée / surconsolidation / œdomètre / pressiomètre
Key words: consolidation / embankment / pore-pressure coefficients A and B / undrained shear strength / overconsolidation / œdometer / pressuremeter
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2018
1 Introduction
Les remblais font partie des ouvrages de génie civil les plus anciens et les plus courants (Leroueil et al., 1985). Si les critères de dimensionnement et de mise en œuvre (temps de consolidation et amplitude des tassements) étaient plus souples autrefois, ces trente dernières années ont vu ces critères se durcir avec les nouveaux projets de lignes à grande vitesse et, également, avec l’évolution du cadre socio-économique, politique et environnemental (Boutonnier et Guerpillon, 2005).
Ces critères particulièrement rigides se trouvent face à l’incertitude des prédictions des tassements et de leur évolution au cours du temps, résultat de l’incertitude sur les conditions initiales des sols, les tests en laboratoire et leurs interprétations et le respect des hypothèses de la théorie de la consolidation (SETRA et LCPC, 2000).
Lors de projets récents, les retours d’expérience montrent que les méthodes de calcul, utilisées dans la pratique, surestiment souvent les valeurs réelles du tassement et du temps de consolidation (Boutonnier et al., 2013 ; Coste et al., 2014). En conséquence, les dispositions constructives (purges, drains, préchargement) mises en œuvre dans le but d’atteindre les critères de dimensionnement se révèlent, a posteriori, exagérées. Toutefois, cela ne semble pas avoir été le cas par le passé (Bru et al., 1973).
Cette évolution soulève une question importante sur la justesse1 des méthodes dans la pratique actuelle de la géotechnique. Cet article présente les contextes géotechniques des trois sites analysés et les résultats des études d’exécution. Ensuite, sur la base d’une comparaison entre plusieurs procédures de calcul, une méthode de recalage permettant de prévoir avec une bonne précision les valeurs des tassements, sera validée sur les différents profils étudiés. Ce travail se veut une analyse critique des calculs usuellement pratiqués pour l’estimation des tassements des ouvrages en terre dans le cadre de projets linéaires.
2 Présentation du cadre géologique et géotechnique des sites étudiés
Cette analyse de tassement a été réalisée sur un certain nombre de profils de remblais issus des tracés des Lignes à Grande Vitesse (LGV) Bretagne Pays de la Loire (BPL) et Est Européenne (EE) et sur le remblai expérimental B de Cubzac-les-Ponts construit et instrumenté par les Laboratoires des Ponts et Chaussées (LPC). Ce dernier ouvrage se situe à proximité du tracé de la LGV Sud Europe Atlantique (SEA). Ces trois sites présentent des caractéristiques géotechniques différentes. Le tableau 1 récapitule les données de projet de ces différents ouvrages.
Localisé dans les méandres de la Dordogne, le remblai de Cubzac-les-Ponts repose sur un sol fortement compressible (Cc/(1 + e0) entre 0,25 et 0,40), à forte teneur en matière organique (MO entre 5 et 25 %), surconsolidé sur les trois premiers mètres et légèrement surconsolidé à normalement consolidé en profondeur. L’épaisseur de cette couche varie entre 9 et 10 m (Magnan et al., 1983).
Reliant Le Mans à Rennes, le tracé de la LGV BPL passe au-dessus de formations alluvionnaires et argileuses moyennement compressibles (Cc/(1 + e0) entre 0,07 et 0,2) et surconsolidées dont l’épaisseur varie selon les profils.
Situé entre la Lorraine et l’Alsace, le dernier tronçon de la LGV EE traverse des zones où les horizons rencontrés sont décrits dans les sondages comme des argiles à limons argileux posés sur des sables calcaires. Ils sont, globalement, faiblement compressibles (Cc/(1 + e0) entre 0,05 et 0,1) et plus fortement surconsolidés.
La figure 1 présente les valeurs de l’indice de compressibilité Cc/(1 + e0) en fonction de la teneur en eau de l’ensemble des essais œdométriques réalisés sur ces trois sites et qui sont superposées aux courbes de Lambe et Whitman (1969). La répartition des points confirme cette interprétation de sols surconsolidés en se plaçant au-dessus de la courbe supérieure.
Données des projets étudiés.
 |
Fig. 1 Indice de compressibilité en fonction de la teneur en eau. Variation of compressibility index with natural water content. |
3 Comparaison des valeurs estimées en EXE et des valeurs mesurées
L’ensemble des calculs réalisés suit les procédures présentées dans les notes méthodologiques rédigées dans le cadre de ces projets LGV (par exemple : Eiffage Rail Express, 2013). En phase d’études d’exécution (EXE), ces calculs sont réalisés par la méthode pressiométrique sauf pour les couches jugées fortement compressibles où le calcul est fait par la méthode œdométrique. En phase d’avant-projet (APD), les calculs sont réalisés, pour quelques ouvrages, uniquement par la méthode œdométrique.
Dans la figure 2 sont reportées les valeurs de tassement prévues par les calculs (en phase EXE et APD) en fonction des valeurs mesurées in situ. Chaque point correspond à un profil instrumenté différent ou à une phase de calcul différente. Ce même graphique tracé pour l’ensemble des remblais aurait donné des tendances identiques. Le rapport des valeurs de calcul aux valeurs de mesure est globalement assez élevé et l’est davantage lorsque la méthode appliquée est la méthode œdométrique pour les calculs en phase APD. Les valeurs de tassement prévu décroissent notablement en phase EXE.
La figure 3 montre l’histogramme du rapport tassement prévu/réel pour l’ensemble des valeurs calculées en phase EXE. De ces données, nous observons que l’amplitude du tassement a été :
-
dans 15 % des cas de calculs, estimée avec une erreur inférieure à 100 % ;
-
dans 78 % des cas (dont 20 % en phase APD pour les profils de la LGV BPL), surestimée de 100 à 700 % ;
-
et dans 7 % des cas de calculs, surestimée à plus de 1300 %.
 |
Fig. 2 Comparaison des tassements prévus et réels. Measured settlement vs. predicted. |
 |
Fig. 3 Histogramme du rapport tassement prévu/réel pour les différents points de la figure précédente. Distribution of measured settlement-to-predicted settlement ratio. |
4 Définition des procédures de calcul envisagées
Sur la base des différentes observations sur les méthodes de calcul usuelles, les théories et les constatations sur chantier, trois procédures de base ont pu être envisagées avec des sous-variantes pour le calcul œdométrique selon la correction à apporter :
4.1 Méthode pressiométrique (pressio)
Présenté dans la notice D60 (Ménard, 1963) sur l’utilisation des essais pressiométriques de Ménard, repris dans le fascicule 62 titre 5 et la norme NF P94-261 et dans l’ensemble des notes méthodologiques de calcul des remblais utilisées par les bureaux d’études impliqués dans ces projets de LGV, le tassement sous des fondations souples de grandes dimensions a été formulé en fonction du module pressiométrique EM par une approche dite « en condition œdométrique ». Il se calcule par l’intégration sur l’épaisseur de la couche compressible du rapport de la surcharge sur un module pris égal à EM/α, en prenant en compte le facteur d’influence dû à la diffusion de la charge (Ménard et Rousseau, 1962 ; Frank, 1999). Nous rappelons que cette approche suppose implicitement que les déformations produites sont essentiellement « volumiques » (déformations latérales négligées d’où des déformations verticales égales aux déformations volumiques).
4.2 Méthode œdométrique
Développée avec l’approche en contraintes effectives de Terzaghi (1925), la théorie de la consolidation concerne les matériaux sablo-argileux biphasiques (grains et eau). Cette dernière postule que le tassement des sols sous une charge donnée, correspond, sous certaines hypothèses, à la déformation d’un échantillon de sol dans un essai œdométrique. Elle a montré dans de nombreuses applications la pertinence de ses prédictions (Bru et al., 1973 ; Ladd et De Groot, 2003 ; Lavisse et Schmitt, 2004). Ceci dit, il est important de noter qu’une partie de ces hypothèses n’est pas toujours vérifiée dans la réalité (Leroueil et al., 1985).
Selon la correction apportée, quatre sous-variantes ont été testées avec pour base un calcul œdométrique. Toutefois, l’analyse des paramètres qui entrent dans le calcul reste similaire pour les quatre sous-variantes. Cette analyse consiste à valider les valeurs issues des essais en laboratoire par diverses corrélations afin d’éviter de considérer dans les calculs des valeurs aberrantes qui peuvent fausser les résultats de calcul du tassement.
4.2.1 Validation des paramètres de calcul
En effet, les essais œdométriques présentent de nombreux risques quant à la présence d’erreurs dans l’évaluation des paramètres. D’abord, le risque de remaniement de l’échantillon rend difficile l’interprétation de la courbe œdométrique et l’extraction de la valeur de la contrainte de pré-consolidation car les limites des domaines idéalement de recompression et de compression vierge ne sont pas toujours identifiables. Ensuite, le nombre d’essais réalisés est rarement assez élevé pour permettre une comparaison significative entre les différents paramètres résultants.
Pour valider les valeurs issues des essais, plusieurs critères sont utilisés. Par exemple, le rapport Cc/Cs doit être de l’ordre de 5 à 10. Des valeurs trop élevées seront comparées au fuseau de Lambe et Whitman (1969) afin d’identifier la valeur de Cc ou Cs à éliminer.
Les courbes de Lambe et Whitman (1969), en figure 1, relient l’indice de compressibilité Cc/(1 + e0) à la teneur en eau w. Ces courbes ont été tracées sur la base de résultats d’essais obtenus sur des éprouvettes d’argiles variées pour une grande gamme de chargements. Un fuseau a été défini permettant d’éliminer selon les auteurs les valeurs qui semblent atypiques.
4.2.2 Sous-variante 1 (œdo brute)
La première sous-variante correspond à l’application de la méthode œdométrique telle que préconisée par les notes méthodologiques des calculs d’exécution, c’est-à-dire un calcul œdométrique classique. Les paramètres introduits dans les calculs sont ceux validés par les corrélations listées au paragraphe précédent. Cette sous-variante est notée « œdo brute » dans les figures.
4.2.3 Sous-variante 2 (œdo, corrigée S-B)
L’hypothèse de la déformation unidimensionnelle de la méthode œdométrique ne correspondant pas à la réalité, une amélioration a été proposée par Skempton et Bjerrum (1957). Cette méthode, partie intégrante de la méthode œdométrique classique, figurait dans les notes méthodologiques mais a été systématiquement ignorée dans les études. Un facteur μ multiplicateur du tassement œdométrique permet de rendre compte de la déformation latérale accompagnant la déformation verticale. Ce facteur dépend du coefficient de pression interstitielle A (Fig. 4) et, dans ce cas, le tassement s’écrit :
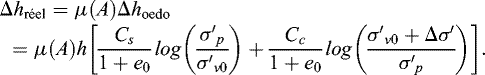 (1)
(1)
Avec : si  alors le terme en Cs n’existe pas ;
si
alors le terme en Cs n’existe pas ;
si  et
et  alors le terme en Cc n’existe pas ;si
alors le terme en Cc n’existe pas ;si  et
et  alors l’expression est considérée en entier.
alors l’expression est considérée en entier.
Où :
h : épaisseur de la couche considérée (m) ;
e0 : indice des vides initial ;
Cc : indice de compression ;
Cs : indice de gonflement ;
 : contrainte de pré-consolidation (kPa) ;
: contrainte de pré-consolidation (kPa) ;
 : contrainte verticale initiale dans le sol calculée au milieu de la couche considérée (kPa) ;
: contrainte verticale initiale dans le sol calculée au milieu de la couche considérée (kPa) ;
Δσ′ : surcharge à la profondeur z due au remblai (kPa). Cette valeur est atténuée en fonction de la profondeur pour tenir compte de l’effet de la diffusion de charge dans le sol, par exemple, en utilisant la méthode d’Österberg ou le modèle de Boussinesq.
La figure 4 montre la relation entre ces paramètres telle que présentée par Skempton et Bjerrum (1957) pour une semelle filante :
Ce résultat a été mis en évidence sur la base des travaux de Bishop et Henkel (1957), Henkel (1956) et Skempton (1954) sur la surpression interstitielle à partir de résultats obtenus lors d’essais triaxiaux non drainés CU + u. La surpression interstitielle due à une surcharge Δσ1 peut être exprimée par l’équation suivante :
 (2)
où :
(2)
où :
Δσ1 : variation de la contrainte verticale qui s’applique sur le sol (kPa) ;
Δσ3 : variation de la contrainte horizontale qui s’applique sur le sol (kPa) ;
A et B : coefficients de pression interstitielle qui dépendent de l’état du sol et sont calculés à partir des résultats d’un essai triaxial.
Le coefficient B dépend de l’état de saturation du sol et est égal à 1 lorsque le sol est totalement saturé. Quant au coefficient A, il a été démontré qu’il dépend de l’état de pré-consolidation du sol et que sa valeur varie entre −0,5 à 1,5 pour un OCR décroissant. La figure 5 montre les courbes lissées pour les argiles de Londres et de Weald. Ces courbes sont le résultat d’un ensemble d’essais triaxiaux réalisés par Henkel (1956) sur des éprouvettes préalablement chargées jusqu’à différents états de surconsolidation.
Ces courbes sont parfois appliquées à des sols intermédiaires, sans plus de discrimination. Une étude paramétrique a été menée sur des mélanges de sable et d’argile pour confirmer la validité de ces courbes pour notre cas. Des mélanges de 10, 50 et 90 % de sable de Fontainebleau avec une illite ont été préparés selon le protocole décrit par Henkel et utilisé pour l’argile de Londres et de Weald (Henkel, 1956). Une série d’éprouvettes a été cependant préparée par compactage statique à des fins de comparaison. La figure 5a compare les résultats de ces essais à ceux de Henkel. Une tendance similaire peut être observée. Les résultats obtenus sur des sols plus sableux se positionnent sur une courbe moins inclinée finissant aux plus fortes valeurs d’OCR au-dessus des argiles de Weald et Londres. Les éprouvettes préparées par compactage statique se placent sur une limite inférieure du fuseau.
Une analyse similaire a été réalisée sur l’argile « n7s-C1a » rencontrée sur le chantier de la LGV BPL et décrite en sondages comme des formations argileuses plus ou moins sableuses à des sables argilo-graveleux de l’Albien supérieur/Cénomanien inférieur.
Ainsi, à partir de 14 essais triaxiaux CU + u réalisés sur différents échantillons de cette argile prélevés à des profondeurs différentes et dans des endroits différents du tracé, nous avons calculé à partir des fiches d’essais des dossiers, d’une part, le coefficient de pression interstitielle A et, d’autre part, le rapport de surconsolidation de l’échantillon OCR.
Les résultats sont assez satisfaisants montrant une décroissance de même type pour cette argile. La vitesse de décroissance est néanmoins plus faible (Fig. 5b).
Nous allons cependant utiliser les courbes de Henkel (1956) (Fig. 5a) ou le tableau de synthèse proposé par Skempton et Bjerrum (1957) (Fig. 4) pour évaluer le coefficient A afin de rester cohérent avec le contexte des projets : application stricto sensu de la méthode de Skempton et Bjerrum préconisée par les notes méthodologiques.
L’effet de ce coefficient A sur la valeur du tassement a été mis en évidence, analytiquement et expérimentalement, à travers le facteur correcteur µ (Skempton et Bjerrum, 1957). Ce dernier a été exprimé par :
 (3)
(3)
Où α est un coefficient tabulé par les auteurs, qui dépend de la géométrie du problème : l’épaisseur de la couche « compressible » H et la largeur moyenne du chargement L (dans notre cas, du remblai).
Dans le cadre des projets, le rapport entre la largeur du remblai et l’épaisseur de sol compressible ayant été jugé toujours assez faible, le coefficient µ(A) avait été pris égal à 1 dans les notes méthodologiques.
 |
Fig. 4 Valeurs du facteur correcteur µ d’après Skempton et Bjerrum (1957). Values of µ factor (Skempton et Bjerrum, 1957). |
 |
Fig. 5 Valeurs moyennes des coefficients de pression interstitielle A en fonction de l’OCR pour différentes argiles. Variation of pore-pressure coefficient A with overconsolidation ratio OCR for different clays. |
4.2.4 Sous-variante 3 (œdo, corrigée  )
)
Quant à la troisième sous-variante, elle apporte une correction sur la valeur de la contrainte de pré-consolidation  . D’une part, l’essai œdométrique servant de référence pour le profil considéré est réalisé sur des échantillons prélevés plus en profondeur entraînant que la contrainte de pré-consolidation qui est en résulte n’est pas représentative des niveaux superficiels. D’autre part, comme dit précédemment, son évaluation est souvent accompagnée d’une erreur assez importante d’interprétation de la courbe œdométrique. L’impact de cette erreur est d’autant plus important que la valeur de
. D’une part, l’essai œdométrique servant de référence pour le profil considéré est réalisé sur des échantillons prélevés plus en profondeur entraînant que la contrainte de pré-consolidation qui est en résulte n’est pas représentative des niveaux superficiels. D’autre part, comme dit précédemment, son évaluation est souvent accompagnée d’une erreur assez importante d’interprétation de la courbe œdométrique. L’impact de cette erreur est d’autant plus important que la valeur de  détermine le domaine de consolidation du sol sous la charge du remblai. Une sous-évaluation peut conduire à des valeurs calculées de tassements très importantes non confirmées dans la réalité. À l’opposé, la valeur de la cohésion non drainée cu peut être estimée avec moins d’erreur à partir des essais in situ (scissomètre, pénétromètre, pressiomètre) (Cassan, 1978 ; Reiffsteck et al., 2012). En effet, en fonction des caractéristiques techniques propres aux essais : vitesse de pénétration du pénétromètre statique, longueur des pales du scissomètre ou de la sonde pour le pressiomètre, la segmentation du profil de sol varie, localisant plus ou moins précisément dans l’espace la position des horizons et leurs propriétés mécaniques. Ces techniques de reconnaissance diffèrent aussi par leurs erreurs d’observation. Si les erreurs de mesure peuvent être estimées comme assez faibles en règle générale − en tout cas, en ce qui concerne la part de l’appareil –, les erreurs de représentativité sont plus fortes pour le pénétromètre qui passe par un modèle de corrélation et non négligeables pour le pressiomètre et le scissomètre, vu la façon dont on calcule les caractéristiques géotechniques. Ainsi, l’avantage de l’obtention d’un profil continu de cu par les essais in situ par rapport aux essais de laboratoire est contrebalancé par l’utilisation de relations empiriques.
détermine le domaine de consolidation du sol sous la charge du remblai. Une sous-évaluation peut conduire à des valeurs calculées de tassements très importantes non confirmées dans la réalité. À l’opposé, la valeur de la cohésion non drainée cu peut être estimée avec moins d’erreur à partir des essais in situ (scissomètre, pénétromètre, pressiomètre) (Cassan, 1978 ; Reiffsteck et al., 2012). En effet, en fonction des caractéristiques techniques propres aux essais : vitesse de pénétration du pénétromètre statique, longueur des pales du scissomètre ou de la sonde pour le pressiomètre, la segmentation du profil de sol varie, localisant plus ou moins précisément dans l’espace la position des horizons et leurs propriétés mécaniques. Ces techniques de reconnaissance diffèrent aussi par leurs erreurs d’observation. Si les erreurs de mesure peuvent être estimées comme assez faibles en règle générale − en tout cas, en ce qui concerne la part de l’appareil –, les erreurs de représentativité sont plus fortes pour le pénétromètre qui passe par un modèle de corrélation et non négligeables pour le pressiomètre et le scissomètre, vu la façon dont on calcule les caractéristiques géotechniques. Ainsi, l’avantage de l’obtention d’un profil continu de cu par les essais in situ par rapport aux essais de laboratoire est contrebalancé par l’utilisation de relations empiriques.
Ce paramètre de cohésion non drainée permet, également, de renseigner sur la valeur de la contrainte de pré-consolidation  à travers la corrélation de Bjerrum (1973) en fonction de l’indice de plasticité IP (Fig. 6a). Cette corrélation a été validée pour différents types d’argiles par d’autres auteurs, cités par Leroueil et al. (1985). Cependant, cette corrélation n’est plus valable pour des teneurs en matière organique élevées.
à travers la corrélation de Bjerrum (1973) en fonction de l’indice de plasticité IP (Fig. 6a). Cette corrélation a été validée pour différents types d’argiles par d’autres auteurs, cités par Leroueil et al. (1985). Cependant, cette corrélation n’est plus valable pour des teneurs en matière organique élevées.
Par ailleurs, cette correction a été largement discutée par Boutonnier dans ses récentes publications (Boutonnier et al., 2013 ; Coste et al., 2014). Coste et al. (2014) et les notes méthodologiques suggèrent de prendre une valeur unique de 0,35 pour le rapport  . Cette proposition n’a pas été retenue dans nos corrections.
. Cette proposition n’a pas été retenue dans nos corrections.
La figure 6b représente les valeurs issues des projets fournies dans le tableau 1 et obtenues après correction. On observe que les valeurs d’indice de plasticité relativement faibles conduisent à utiliser un ratio  plutôt proche de 0,2.
plutôt proche de 0,2.
 |
Fig. 6 Relation entre le rapport de la cohésion non drainée cu sur la contrainte de pré-consolidation et l’indice de plasticité proposée par Bjerrum (1973) (a repris de Leroueil et al., 1985). Variation of undrained cohesion-to-preconsolidation pressure ratio with the plasticity index given by Bjerrum (1973) (a from Leroueil et al., 1985). |
4.2.5 Sous-variante 4 (œdo, corrigée S-B et  )
)
La quatrième sous-variante consiste à combiner les deux corrections des sous-variantes 2 et 3.
4.3 Méthode mixte (mixte brute)
Cette troisième méthode permet de s’affranchir de la limitation liée à l’hypothèse de la saturation parfaite du sol.
Lorsque la nappe phréatique est assez basse, une partie du terrain en surface se retrouve non saturée (Sr < 100 %). Cet état de non saturation est le résultat du cycle de dessèchement-humidification du sol selon les saisons. Cette zone du terrain présente plusieurs caractéristiques propres :
-
les vides sont remplis d’air et d’eau ;
-
une surconsolidation importante due à la fluctuation de la nappe et à la succion.
Le calcul du tassement induit dans cette couche de sol est difficile à déterminer. En effet, la méthode œdométrique qui correspond au chemin décrit par un échantillon dans l’essai œdométrique n’est plus valable car, lors de l’essai, l’échantillon est complètement saturé et n’est donc plus représentatif des conditions réelles du terrain.
Le tableau 2 introduit une analyse de l’effet de la non-saturation sur le tassement de consolidation et sur le temps de consolidation.
L’ambiguïté concernant l’effet de la non-saturation sur le tassement du sol et l’absence de mesure de la succion dans les couches concernées ne permettent pas de réaliser une analyse plus en détail du phénomène.
La solution retenue pour s’affranchir de cette limitation est d’effectuer un calcul pressiométrique pour les couches situées au-dessus de la nappe. En effet, une partie non négligeable du tassement se produit instantanément ce qui fait qu’un module obtenu pour un chargement rapide semble plus approprié pour rendre compte de l’amplitude du tassement. Alors que pour les couches situées en-dessous de la nappe, le tassement est calculé par la méthode œdométrique avec ses trois sous-variantes.
Cependant, il est à noter que, selon les travaux de Boutonnier (2007), un défaut de saturation peut être rencontré même sous le toit de la nappe, pouvant aller jusqu’à 6 à 16 m sous le toit de la nappe. Ce point mérite des approfondissements qu’il ne sera pas possible de traiter dans le présent article.
Par ailleurs, les mesures de surpressions sous les profils étudiés ont montré que son évolution en fonction de la montée du remblai (soit de la charge appliquée) est différente de l’hypothèse de la théorie de la consolidation unidimensionnelle Δu = Δσ. En effet, un constat général est que la surpression générée par l’ajout d’une surcharge est très faible (quelques pour cents). Ce résultat peut s’expliquer par la combinaison de deux facteurs. D’abord, les drains mis en place sont assez efficaces et alors les surpressions sont dissipées rapidement. Ensuite, le sol n’étant pas parfaitement saturé, la surcharge passe en grande partie directement au squelette solide. Cependant, il semble que l’effet du deuxième facteur soit prépondérant car la même observation a pu être faite sur des profils non équipés de drains.
En complément de la méthode mixte brute, les différentes corrections de la méthode œdométrique ont été appliquées donnant lieu aux calculs : mixte corrigée S-B, mixte corrigée  et mixte corrigée S-B et
et mixte corrigée S-B et  .
.
Tableau comparatif du comportement du sol dans des états de saturation parfaite et de non-saturation.
Comparison of soil behavior according to saturation state.
5 Présentation des résultats de calcul
Les figures 7 et 8 résentent l’ensemble des valeurs calculées en fonction des valeurs mesurées du tassement. Pour le remblai de Cubzac-les-Ponts (tassement approchant le mètre), la valeur maximale estimée par la méthode œdométrique est celle qui approche le mieux le tassement réel ce qui était prévisible au vu de la grande compressibilité des terrains sous-jacents au remblai (Magnan et al., 1983). Par contre, la méthode pressiométrique donne des valeurs très en-deçà du tassement réel même avec le calcul le plus défavorable. Le tassement dû à la consolidation de cette couche de sols organiques ne peut pas être évalué correctement par un calcul élastique.
Nous remarquons aussi l’intérêt d’introduire des corrections à la méthode œdométrique pour les profils des LGV BPL et EE. Les valeurs calculées se rapprochent davantage des valeurs mesurées in situ. En particulier, la correction de la contrainte de pré-consolidation proposée par Bjerrum (1973) semble amener aux meilleurs résultats.
La figure 9a présente l’écart « tassement prévu – tassement mesuré », vis-à-vis de seuils comme 5 et 10 cm. En effet, pour les valeurs du zoom de la figure 8, où l’amplitude des tassements est somme toute modérée, la différence en valeur absolue peut être un critère aussi valable que le rapport. Afin de rendre plus lisible la figure, nous n’avons conservé que les méthodes principales.
On observe que les méthodes de référence comme les méthodes œdométrique et pressiométrique se situent au-delà de la valeur de 10 cm. Le gain apporté par la correction de surconsolidation  appliquée à la méthode œdométrique permet dans la plupart des cas de descendre en dessous de 10 cm, voire en dessous de 5 cm. La correction supplémentaire de Skempton et Bjerrum apporte un gain significatif qui permet dans la plupart des cas de vérifier un seuil à 5 cm, ce qui n’est pas le cas de la méthode mixte.
appliquée à la méthode œdométrique permet dans la plupart des cas de descendre en dessous de 10 cm, voire en dessous de 5 cm. La correction supplémentaire de Skempton et Bjerrum apporte un gain significatif qui permet dans la plupart des cas de vérifier un seuil à 5 cm, ce qui n’est pas le cas de la méthode mixte.
La représentation sur la figure 9b de l’écart « tassement prévu – tassement mesuré », en fonction du rapport de l’épaisseur de sol compressible H et de la largeur du remblai L, permet de confirmer que la justesse de la méthode œdométrique croît avec l’épaisseur de la couche compressible considérée. Un rapport faible devrait selon toute logique, comme indiqué dans les notes méthodologiques, être plus représentatif des conditions œdométriques. Sans doute l’erreur faite sur le modèle géotechnique (attribution d’un caractère compressible à un horizon surconsolidé) devient alors prépondérante. Les corrections de la contrainte de pré-consolidation et de Skempton et Bjerrum gardent leur pertinence pour cette plage.
Une analyse statistique a été réalisée sur ces valeurs calculées, hormis les valeurs de Cubzac-les-Ponts – LGV SEA. Cette analyse permet de mieux apprécier l’efficacité des corrections dans l’estimation du tassement.
Les valeurs calculées sont classées selon la méthodologie de calcul appliquée, tel un échantillon de valeurs. La figure 10 montre les fonctions de répartitions de ces différents échantillons. Sur ce graphe, le point à approcher avec les différentes méthodes de calcul est le point de coordonnées (1 ; 50 %) correspondant à la meilleure probabilité d’avoir le résultat correct. Toutefois, il faut aussi s’assurer d’avoir un écart-type maîtrisé.
Une autre représentation des résultats peut être faite, en faisant l’hypothèse que ces échantillons de valeurs suivent une loi normale. Les moyennes et écarts-types des échantillons sont donnés dans le tableau 3. La figure 11 montre les fonctions de répartition de chaque méthode.
En corrigeant uniquement la valeur de la contrainte de pré-consolidation, la surévaluation des tassements peut être réduite de près de 360 % à 90 % ainsi que l’ont constaté Coste et al. (2014). Cette simple correction permet de ramener l’évaluation des tassements à un niveau (90 %) inférieur à celui de la méthode pressiométrique (158 %).
La correction de Skempton et Bjerrum appliquée seule réduit la surestimation du tassement à 249 % (soit une baisse de 25 %) ce qui reste toujours plus pessimiste que la méthode pressiométrique.
La méthode mixte brute, du fait des hypothèses conservatrices prises sur les positions de la nappe n’apporte pas de correction notable.
La méthode œdométrique à laquelle nous avons appliqué le coefficient correcteur de Skempton et Bjerrum (1957) et pour laquelle nous avons corrigé la contrainte de pré-consolidation représente donc la méthode la plus juste mais également la plus fidèle (surévaluation réduite à 47 %).
La méthode pressiométrique représente une limite inférieure aux évaluations de tassements œdométrique et mixte calculées sans la correction de la contrainte de pré-consolidation. Ceci justifie, finalement, le choix des ingénieurs lors des calculs d’exécution de ces remblais. De ce fait, on note la nécessité d’introduire la correction de la contrainte pour avoir des résultats corrects.
La procédure de calcul permettant d’avoir la valeur la plus proche de la réalité correspond à la méthode œdométrique doublement corrigée ; par le coefficient de Skempton et Bjerrum et par la corrélation entre la contrainte de pré-consolidation et la cohésion non drainée (courbe « œdo, corrigée S-B et  » dans les Fig. 10 et 11).
» dans les Fig. 10 et 11).
Avec cette correction, l’amplitude du tassement est en moyenne surestimée de 47 % par rapport à la valeur réelle. En effet, le rapport « tassement prévu/tassement réel » moyen est égal à 1,5 avec cette double correction de la méthode œdométrique. En outre, l’écart-type étant de 0,65 par rapport à la valeur moyenne, il montre une faible dispersion en comparaison aux dispersions établies pour le reste des méthodes de calcul (Tab. 3).
 |
Fig. 7 Comparaison des valeurs du tassement prévu et des valeurs du tassement réel. Measured settlement vs. predicted. |
 |
Fig. 8 Zoom de la figure 7 sur les résultats des LGV BPL et LGV EE. Zoom of figure 7 on LGV BPL and LGV EE results. |
 |
Fig. 9 Évolution de l’écart de tassement prédit en fonction du tassement réel et de la géométrie du remblai. Evolution of the over-predicted settlement as a function of the actual settlement and the geometry of the embankment. |
 |
Fig. 10 Courbes de répartition naturelle des échantillons de valeurs de tassement par méthode. Natural distribution curve for each prediction procedure. |
Moyennes et écart-types des rapports « tassement prévu/mesuré » pour chaque procédure de calcul classés par ordre croissant de la moyenne.
Mean and standard deviation of measured/predicted settlement ratio for each calculation procedure.
 |
Fig. 11 Fonctions de répartition caractérisant chaque procédure de calcul. Normal distribution curve for each calculation procedure. |
6 Conclusion
La prédiction des amplitudes de tassement est une tâche difficile. Les méthodes de calcul usuelles permettent d’avoir un ordre de grandeur du tassement du sol sous une charge de grandes dimensions avec des erreurs plus ou moins élevées. En effet, les observations sur les retours d’expériences montrent la divergence des calculs par rapport aux valeurs mesurées.
L’étude de cette problématique de tassement passe, d’abord, par l’identification des différents facteurs qui peuvent produire ces divergences tels que des erreurs d’interprétation des essais en laboratoire et in situ ou encore les hypothèses des théories sur lesquelles sont basées les différentes méthodes de calcul. En considérant toutes ces limitations, les procédures de calcul proposées ont essayé de s’affranchir de certains de ces éléments, tels que le remaniement de l’échantillon ou encore les conditions de saturation et la définition de la géométrie du profil de calcul.
Les résultats de cette étude comparative valident, donc, que la méthode œdométrique reste plus pertinente pour l’évaluation du tassement des sols sous des charges de grandes dimensions que la méthode pressiométrique. Toutefois, il faudrait, d’une part, prendre le soin nécessaire pour réaliser des essais en laboratoire corrects sur des échantillons bien conservés (depuis leur prélèvement jusqu’à la réalisation des essais en laboratoire). D’autre part, il faudrait introduire des corrections et des améliorations fonction du type et de la stratigraphie de sol rencontré. L’apport des essais in situ, comme l’essai de pénétration au cône, est sur ce point indéniable.
Ainsi, sur les sites où le sous-sol est moyennement compressible à raide (cas des LGV BPL et EE), la théorie œdométrique est valable. Cependant, les erreurs lors de la réalisation et de l’interprétation des essais rendent, généralement, indispensable l’introduction de la correction de la contrainte de pré-consolidation (Coste et al., 2014). Ceci dit, il faut s’assurer, d’abord, de la validité de la corrélation qui dépend de la teneur en matière organique.
D’autre part, en présence d’une épaisseur de couche compressible non négligeable devant la largeur moyenne du remblai, l’introduction du coefficient correcteur de Skempton et Bjerrum est indispensable, permettant de prendre en compte l’effet des déformations latérales.
Cette démarche a montré sa pertinence sur les 18 profils analysés de la LGV BPL et de la LGV EE. Par ailleurs, sur le site de Cubzac-les-Ponts, la spécificité du site et de l’argile rencontrée rend injustifiée la correction de la contrainte de pré-consolidation, toutefois cette dernière présente la particularité d’être bien estimée car les essais en laboratoire étaient de bonne qualité.
Références
- Bishop AW, Henkel DJ. 1957. The triaxial test. London: Arnold. [Google Scholar]
- Bjerrum L. 1973. Problems of soil mechanics and construction on soft clays and structurally unstable soils (collapsible, expansive and others). Proceeding 8th International Conference on Soil Mechanics and Geotechnical Engineering, Moscow, vol. 3, pp. 111–159. [Google Scholar]
- Boutonnier L. 2007. Comportement hydromécanique des sols fins proches de la saturation, cas des ouvrages en terre : coefficient B, déformations instantanées et différées, retrait/gonflement. Thèse de Doctorat, Institut National Polytechnique de Grenoble, 394 p. [Google Scholar]
- Boutonnier L, Guerpillon Y. 2005. Reconnaissances géotechniques et critères en déformation dans la conception des ouvrages en terre des lignes ferroviaires à grande vitesse. Géoline 2005, 8 p. [Google Scholar]
- Boutonnier L, Hajaoui F, Bacar Fadhuli N, Gandille D. 2013. LGV EST lot 41 : tassements calculés puis mesurés sous remblais. Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, pp. 1233–1237. [Google Scholar]
- Bru JP, Baguelin F, Goulet G, Jaeck G, Jézéquel J. 1973. Prévision du tassement au pressiomètre et constatations, Proceeding 8th International Conference on Soil Mechanics and Geotechnical Engineering, Moscow, vol 2, pp. 25–31 [Google Scholar]
- Cassan M. 1978. Les essais in situ en mécanique des sols. Tome1 : Réalisation et interprétation. Paris : Eyrolles, 458 p. [Google Scholar]
- Coste P, Deluzarche R, Boutonnier L, Hansen N, Chardard P. 2014. Tassements et temps de consolidation mesurés et calculés sur projets LGV. Journée Nationale de Géotechnique et de géologie de l’ingénieur JNGG 2014, Beauvais, 11 p. [Google Scholar]
- Eiffage Rail Express. 2013. Études d’exécution géotechniques : Note méthodologique pour les calculs de stabilité des ouvrages en terre. Phase T, numéro 10003, Indice 1, BPE, 40 p. [Google Scholar]
- Frank R. 1999. Fondations superficielles. Paris : Techniques de l’ingénieur, 31 p. [Google Scholar]
- Henkel DJ. 1956. The effect of overconsolidation on the behaviour of clays during shear. Géotechnique 4: 139–150. [CrossRef] [Google Scholar]
- Ladd C, De Groot DJ. 2003. Recommended practice for soft ground site characterization: Arthur Casagrande Lecture. In: 12th Panamerican conference on soil mechanics and geotechnical engineering. USA: Cambridge, 60 p. [Google Scholar]
- Lambe TW, Whitman RV. 1969. Soil Mechanics. Massachusetts Institute of Technology, New Jersey (USA): John Wiley & Sons, 553 p. [Google Scholar]
- Lavisse J, Schmitt P. 2004. Interprétation de mesures de tassements sous des remblais de préchargement au Port de Rouen. In : Dhouib, Magnan et Mestat, eds. Amélioration des sols en place. Paris : Presses de l’ENPC, pp. 437–445. [Google Scholar]
- Leroueil S, Magnan JP, Tavenas F. 1985. Remblais sur argiles molles – Technique et Documentation. Paris: Lavoisier, 360 p. [Google Scholar]
- Magnan JP, Mieussens C, Queyroi D. 1983. Étude d’un remblai sur sols compressibles : Le remblai B du site expérimental de Cubzac-les-Ponts – Paris : Rapport de recherche LPC no 127, 103 p. [Google Scholar]
- Ménard L. 1963. Règles de réalisation des essais pressiométriques Ménard et d’exploitation des résultats obtenus pour le dimensionnement des fondations (Notice D60). Saulx les Chartreux (France) : Techniques Louis Ménard, 50 p. [Google Scholar]
- Ménard L, Rousseau J. 1962. L’évaluation des tassements. Tendances Nouvelles. Sols Soil 1: 13–30. [Google Scholar]
- Reiffsteck P, Lossy D, Benoît J. 2012. Forages, sondages et essais in situ géotechniques. Les outils pour la reconnaissance des sols et des roches. Paris (France) : Presses des Ponts, ISBN : 978-2-85978-466-9, 800 p. [Google Scholar]
- SETRA, LCPC. 2000. Guide Technique : Étude et réalisation des remblais sur sols compressibles, 88 p. [Google Scholar]
- Skempton AW. 1954. The pore-pressure coefficients A and B. Géotechnique 4: 143–147 [CrossRef] [Google Scholar]
- Skempton AW, Bjerrum L. 1957. A contribution to the settlement analysis of foundations on clay. Géotechnique 7: 168–178. [CrossRef] [Google Scholar]
- Terzaghi K. 1925. Erdbaumechanik auf bodenphysikalischer Grundlage. Vienne: Franz Deuticke Verlag, 399 p. [Google Scholar]
Citation de l’article : Soukaina Said Alami, Philippe Reiffsteck, Fahd Cuira. Méthode d’estimation des tassements des sols fins sous les remblais d’infrastructures ferroviaires pour lignes à grande vitesse. Rev. Fr. Geotech. 2017, 153, 3.
Liste des tableaux
Tableau comparatif du comportement du sol dans des états de saturation parfaite et de non-saturation.
Comparison of soil behavior according to saturation state.
Moyennes et écart-types des rapports « tassement prévu/mesuré » pour chaque procédure de calcul classés par ordre croissant de la moyenne.
Mean and standard deviation of measured/predicted settlement ratio for each calculation procedure.
Liste des figures
 |
Fig. 1 Indice de compressibilité en fonction de la teneur en eau. Variation of compressibility index with natural water content. |
| Dans le texte | |
 |
Fig. 2 Comparaison des tassements prévus et réels. Measured settlement vs. predicted. |
| Dans le texte | |
 |
Fig. 3 Histogramme du rapport tassement prévu/réel pour les différents points de la figure précédente. Distribution of measured settlement-to-predicted settlement ratio. |
| Dans le texte | |
 |
Fig. 4 Valeurs du facteur correcteur µ d’après Skempton et Bjerrum (1957). Values of µ factor (Skempton et Bjerrum, 1957). |
| Dans le texte | |
 |
Fig. 5 Valeurs moyennes des coefficients de pression interstitielle A en fonction de l’OCR pour différentes argiles. Variation of pore-pressure coefficient A with overconsolidation ratio OCR for different clays. |
| Dans le texte | |
 |
Fig. 6 Relation entre le rapport de la cohésion non drainée cu sur la contrainte de pré-consolidation et l’indice de plasticité proposée par Bjerrum (1973) (a repris de Leroueil et al., 1985). Variation of undrained cohesion-to-preconsolidation pressure ratio with the plasticity index given by Bjerrum (1973) (a from Leroueil et al., 1985). |
| Dans le texte | |
 |
Fig. 7 Comparaison des valeurs du tassement prévu et des valeurs du tassement réel. Measured settlement vs. predicted. |
| Dans le texte | |
 |
Fig. 8 Zoom de la figure 7 sur les résultats des LGV BPL et LGV EE. Zoom of figure 7 on LGV BPL and LGV EE results. |
| Dans le texte | |
 |
Fig. 9 Évolution de l’écart de tassement prédit en fonction du tassement réel et de la géométrie du remblai. Evolution of the over-predicted settlement as a function of the actual settlement and the geometry of the embankment. |
| Dans le texte | |
 |
Fig. 10 Courbes de répartition naturelle des échantillons de valeurs de tassement par méthode. Natural distribution curve for each prediction procedure. |
| Dans le texte | |
 |
Fig. 11 Fonctions de répartition caractérisant chaque procédure de calcul. Normal distribution curve for each calculation procedure. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




