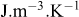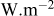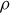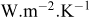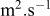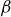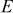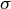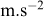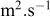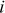| Issue |
Rev. Fr. Geotech.
Number 172, 2022
Jeunes Chercheurs
|
|
|---|---|---|
| Article Number | 1 | |
| Number of page(s) | 19 | |
| DOI | https://doi.org/10.1051/geotech/2022007 | |
| Published online | 05 September 2022 | |
Article de recherche / Research Article
Géostructures thermiques : verrous scientifiques et moyens d’étude
Energy geostructures: questions raised and analysis tools
1
GERS-SRO, Univ Gustave Eiffel, IFSTTAR, 77447 Marne-la-Vallée, France
2
Setec, Terrasol, 75583 Paris, France
3
ESIEE Paris, Univ Gustave Eiffel, 77447 Marne-la-Vallée, France
* Auteur de correspondance : jean.de-sauvage@univ-eiffel.fr
Alors que nous consommons toujours plus d’énergie pour le chauffage et la climatisation de nos lieux de vie, les impératifs de lutte contre le changement climatique et la croissance de la population urbaine mondiale rendent crucial le recours à des sources d’énergies renouvelables. Parmi elles, les géostructures thermiques associent au rôle mécanique pour lequel elles sont conçues un rôle énergétique en captant l’énergie du sol de faible profondeur à l’aide de tubes échangeurs de chaleur connectés à une pompe à chaleur. Elles apparaissent donc comme une solution décarbonée, non intermittente, locale, à faible risque pour l’homme, aisément intégrable dans le mix énergétique et au taux de retour sur investissement raisonnable. Pourtant, certaines questions quant à leur dimensionnement thermomécanique, notamment en présence d’un écoulement souterrain en freinent toujours le développement à large échelle. Après avoir dressé un état de l’art détaillé pour rappeler les points d’achoppement subsistant, un groupe de pieux géothermique au sein d’un écoulement est étudié sous l’angle de la modélisation numérique et de la modélisation physique centrifugée. Les différents outils à disposition de la communauté scientifique pour lever les verrous restant sont présentés.
Abstract
As we consume increasingly more energy to heat and cool our living places, the climate change and the growth of global urban population urge to use renewable energy. Among them, energy geostructures are promising. Their principle is to add to their initial mechanical role a thermal role by extracting energy from the shallow subsoil with the help heat exchanger pipes connected to a heat pump. They appear to be a very low carbon, local, non-intermittent solution with low risk for human beings, easily integrated in the energy mix and with a reasonable return investment rate. However, some questions regarding their thermomechanical design – notably within seepage – still inhibit their large scale implementation. After a detailed state of the art reminding the main stumbling blocks, an energy pile group within seepage is studied through numerical modelling and centrifuge modelling. The various tools available to the scientific community to remove the remaining obstacles are presented.
Mots clés : géostructures thermiques / dimensionnement / thermomécanique / éléments finis / centrifugeuse géotechnique
Key words: energy geostructures / design / thermomechanical / finite elements / centrifuge modelling
© CFMS-CFGI-CFMR-CFG, 2022
1 Introduction
Dans les profondeurs de la Terre règne une chaleur extrême qui réchauffe les roches de la croûte terrestre, ainsi que l’eau et la vapeur qu’elles contiennent. Ainsi, une quantité importante d’énergie thermique se trouve dans le sous-sol sous différentes formes :
celle dont la puissance est la plus élevée, la géothermie très profonde et à très haute température, réside dans l’eau liquide à haute température, entre 200 °C et 250 °C, dans des nappes entre 2000 m et 12 000 m de profondeur, souvent dans des régions volcaniques ou proche des failles tectoniques. Puisée grâce à des pompes, elle peut être utilisée pour produire de l’électricité, ou directement dans un circuit de chauffage ;
la géothermie profonde puise une eau entre 50 et 95 °C et entre 1000 m et 2000 m de profondeur ;
la géothermie à faible profondeur (moins de 300 m) et basse température, ne dépasse pas 40 °C.
Alors que le secteur de la construction représente environ 40 % de la consommation d’énergie globale (Nejat et al., 2015) dont 80 % sont dédiés au chauffage des volumes et de l’eau, les impératifs de lutte contre le changement climatique et la croissance de la population urbaine mondiale rendent crucial le recours à des sources d’énergies renouvelables. La géothermie apparaît comme une solution technologique décarbonée, non intermittente, présentant peu de risque pour l’homme et aisément intégrable dans le mix énergétique.
Différentes législations à travers le monde, internationalement reconnues et introduites localement, sont mises en place par les gouvernements pour veiller à la réduction des émissions de carbone dans un avenir proche et rendre la présence de l’humanité sur Terre plus durable. En effet, les réglementations thermiques qui régissent les constructions neuves en France sont de plus en plus strictes et la RT 2020, par exemple, a pour objectif de mettre en œuvre des constructions neuves à énergie positive, aussi appelées BEPOS, c’est-à-dire qui produisent plus d’énergie qu’elles n’en consomment. Des exemples de telles procédures de réglementation à travers le monde sont le protocole de Kyoto, le Climate Change Act 2008 au Royaume-Uni et de nombreuses politiques australiennes telles que « 2030 Emission Reduction Target ».
Les systèmes d’énergie géothermique traditionnels, requérant une interaction avec des roches se situant à plus d’un kilomètre de profondeur, permettent une production d’énergie à grande échelle mais leur coût et leur praticité ne sont pas adaptés à un développement à l’échelle d’un éco-quartier. Le développement de solutions de géothermie de faible profondeur a permis d’ajouter aux avantages déjà mentionnés le caractère local de l’énergie exploitée. Ces systèmes montrent un grand potentiel comparé aux systèmes traditionnels, en termes de durabilité à long terme, d’accès, de flexibilité et d’économie (De Moel et al., 2010).
Parmi les systèmes de faible profondeur, les géostructures thermiques permettent d’atteindre un bilan environnemental exceptionnel pour un TRI de 7 à 12 ans (CFMS et Syntec, 2017) et sans accroissement notable des contraintes de chantier. Leur principe consiste en effet à faire circuler un fluide caloporteur dans des tubes échangeurs en PEHD fixés directement sur les cages d’armature de fondations, tunnels ou soutènements. Grâce à une pompe à chaleur (PAC), ce fluide circule alors des fondations jusqu’aux radiateurs ou planchers chauffants. Il est alors possible d’injecter de la chaleur dans le sol en été pour refroidir le bâtiment ou d’en extraire en hiver pour le chauffer. Les géostructures thermiques remplissent donc un rôle énergétique en plus du rôle mécanique (portance, soutènement) pour lequel leur réalisation est, de toute façon, nécessaire (Fig. 1).
Cependant, si ce double rôle garantit un excellent bilan environnemental, il est aussi à l’origine de réticences quant à l’implémentation de tels systèmes. En particulier, l’impact des cycles thermiques sur leur comportement mécanique suscite de nombreuses préoccupations : modifications des efforts de service, des contraintes de cisaillement à l’interface sol-géostructure mais également modifications des déplacements en tête et en pied d’ouvrages. De plus, la présence d’écoulement d’eau dans le sol complique encore la question puisque les échanges thermiques qui impactent la mécanique des ouvrages sont très fortement sensibles à l’hydrologie. Le sol devient donc le théâtre de différents couplages entre hydrologie, thermique et mécanique.
Parmi les géostructures thermiques, les plus développées à l’heure actuelle sont les pieux géothermiques (Fig. 2). Relativement répandus dans des pays tels que l’Autriche, pionnier dans ce domaine1 (Brandl, 2006), ou le Royaume-Uni, où de nombreuses recherches les ont rendus populaires, ils restent peu utilisés en France par manque de connaissance. Toutefois le recours aux tunnels et parois moulées thermoactifs se développe également. En France, cette technique est aussi utilisée dans des projets de stations de métro à Paris et à Rennes (Di Donna et al., 2020). Bien que le comportement mécanique des géostructures thermiques et leurs performances aient été examinés et validés par de nombreuses études menant à des recommandations nationales (CFMS et Syntec, 2017), certains verrous en empêchent encore le développement à grande échelle.
Les changements dans le comportement mécanique du sol, l’influence du type de sol et la présence d’un ou plusieurs écoulements sont des phénomènes importants à prendre en compte dans la conception des géostructures thermiques. En vue du développement de ces solutions à grande échelle, de nombreuses questions sont particulièrement à élucider concernant les interactions entre les géostructures thermiques lors de la présence d’un écoulement d’eau dans le sol. Afin de lever les verrous identifiés, la communauté scientifique dispose de nombreux moyens d’études prometteurs présentés ici.
 |
Fig. 1 Illustration du double rôle des géostructures thermiques dans le cas d’un projet de métro (soutènements de type parois moulées et tunnel). Illustration of the dual role of energy geostructures in the case of a metro project (diaphragm wall type retaining walls and tunnel). |
 |
Fig. 2 Diffusion des géostructures énergétiques (a) dans différents pays et (b) depuis 1988. (Di Donna et al., 2020). Diffusion of energy geostuctures (a) in different countries and (b) since 1988. |
2 Couplages thermo-hydro-mécaniques
Comme précisé ci-dessus, l’étude des géostructures thermiques implique un couplage de phénomènes mécaniques, hydrauliques et thermiques qu’il convient de préciser ici.
2.1 Transferts de chaleur
Le sol étant un matériau multiphasique, il est le théâtre de mécanismes de transfert de chaleur divers incluant conduction (transfert d’agitation thermique entre atomes ou molécules voisins), convection (transfert de chaleur liée au mouvement d’un fluide2), rayonnement (interaction du rayonnement électromagnétique et de la matière) et changements d’états (vaporisation, condensation, congélation et décongélation). Le principal mécanisme est la conduction, suivie de la convection.
Dans l’hypothèse où la température du squelette granulaire est égale à celle de l’eau dans chaque volume élémentaire représentatif (approximation raisonnable dans le cas d’un écoulement lent tel que celui d’une nappe souterraine), le comportement thermique du sol peut être représenté par celui d’un corps monophasique équivalent. La prise en compte de tous les transferts thermiques conduit sa température à être régie par l’équation de diffusion générale suivante :
 (1)
(1)
S est un terme traduisant la création de chaleur et il est donc nul en tout point du sol. ctot est la capacité thermique équivalente du sol (J.m−3.K−1) et j est le flux thermique au point considéré (W.m−2).
La capacité thermique ne dépend pas de la microstructure et, dans la plupart des cas, il est acceptable de la calculer à partir de la porosité et de la saturation du sol (Andersland et Ladanyi, 2013) par la formule suivante :
 (2)
(2)
La capacité thermique volumique (utilisée ici) est reliée à la capacité thermique massique par la simple relation cvol = ρcmas et cette dernière vaut environ 920 J.kg−1.K−1 pour de l’argile et 800 J.kg−1.K−1 pour des limons ou du sable (Vasilescu, 2019).
Le flux thermique est la somme des flux décrits ci-dessous :
 est le flux de conduction. En l’absence d’autre transfert thermique, l’équation (1) devient l’équation de la chaleur classique. La conductivité thermique λ est déterminée expérimentalement par un test de réponse thermique (Cekerevac et Laloui, 2004) ou un test à l’aiguille (Delerablée, 2019) et varie de 0,15 à 4 W.m−1.K−1 en fonction de la nature et de la saturation du sol (Vasilescu, 2019). On a ainsi :
est le flux de conduction. En l’absence d’autre transfert thermique, l’équation (1) devient l’équation de la chaleur classique. La conductivité thermique λ est déterminée expérimentalement par un test de réponse thermique (Cekerevac et Laloui, 2004) ou un test à l’aiguille (Delerablée, 2019) et varie de 0,15 à 4 W.m−1.K−1 en fonction de la nature et de la saturation du sol (Vasilescu, 2019). On a ainsi :
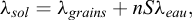 (3)
(3)
 est le flux d’advection le long de l’écoulement souterrain. VD est la vitesse de Darcy et non la vitesse réelle des particules d’eau (Delerablée, 2019).
est le flux d’advection le long de l’écoulement souterrain. VD est la vitesse de Darcy et non la vitesse réelle des particules d’eau (Delerablée, 2019). est le flux de convection entre un solide et un fluide à sa surface (de normale
est le flux de convection entre un solide et un fluide à sa surface (de normale  ). h est le coefficient de convection dont la détermination est décrite dans (Jannot, 2012). Ce terme de flux est nul dans le sol mais intervient dans l’évolution des températures au sein des géostructures.
). h est le coefficient de convection dont la détermination est décrite dans (Jannot, 2012). Ce terme de flux est nul dans le sol mais intervient dans l’évolution des températures au sein des géostructures.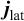 est le flux thermique lié à un éventuel changement d’état. Dans le cas des géostructures thermiques, il n’est pas à prendre en compte.
est le flux thermique lié à un éventuel changement d’état. Dans le cas des géostructures thermiques, il n’est pas à prendre en compte.
Notons tout de suite que ces transferts thermiques sont à l’origine de multiples couplages, les variations de température générant entre autres des variations de viscosité de l’eau ou de la teneur en eau du sol. Ces couplages peuvent être importants dans des sols non saturés (Lahoori et al., 2020) et/ou à forte porosité. Une évaluation correcte des propriétés thermiques du sol est donc d’une grande importance pour la conception de géostructures thermiques. En particulier la détermination de sa diffusivité thermique α = λ/ρc (m2.s−1) traduira la capacité du sol à égaliser les différences de température et à atteindre l’équilibre thermique. Le tableau 1 présente les caractéristiques thermiques des principaux types de sol. On notera que le paramètre le plus critique est la saturation et une connaissance fine du contexte hydraulique est nécessaire au bon dimensionnement d’un projet géothermique. La composition minéralogique et la granulométrie des sols sont également des critères prépondérants. Une base de donnée de plus de 400 échantillons est présentée par Dalla Santa et al. (2020).
Au sein des géostructures thermiques, une différence de température entre le fluide caloporteur et le sol produit le transfert de chaleur nécessaire au fonctionnement du système géothermique. Ce transfert implique une convection forcée entre le fluide caloporteur et le tube échangeur, une conduction à travers le sol, le matériau constituant la géostructure (béton, acier…) et la paroi des tubes échangeurs en PEHD ainsi qu’une convection dans le sol si le débit des eaux souterraines est supérieur à 0,5–1,0 m/jour. La figure 3 illustre ces mécanismes pour une géostructure de type pieu ou paroi dans sa partie fiche. Dans certains cas, il arrive qu’une seule face d’une paroi moulée soit en contact avec le sol, l’autre étant en contact avec l’atmosphère d’un parking souterrain par exemple.
Caractéristiques thermiques de certains sols (Fromentin et al., 1997)
Thermal characteristics of some soils.
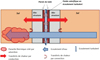 |
Fig. 3 Schéma de principe récapitulant les mécanismes de transfert de chaleur dans les géostructures thermiques. Schematic diagram summarizing the heat transfer mechanisms in energy geostructures. |
2.2 Comportement thermomécanique des sols
Le transfert de charges en toute sécurité de la structure au sol restant le rôle principal des géostructures thermiques, l’impact des variations de température sur le comportement des sols est un sujet d’attention particulier. Les variations thermiques induisant une migration de l’eau vers les zones plus froides (Brandl, 2006), cela peut provoquer une contraction dans les zones chaudes en particulier dans le cas des sols fins. De plus, l’augmentation de température accroît la pression de l’eau interstitielle et par conséquent diminue la contrainte effective du sol. La présence de constituants organiques augmente la sensibilité à la température des sols (en particulier des argiles). Si ces interactions sont généralement négligeables, elles doivent être prises en compte pour les ouvrages très sensibles aux tassements différentiels.
Le comportement thermomécanique des sols a fait l’objet de nombreuses études (Campanella et Mitchell, 1968 ; Cekerevac et Laloui, 2004 ; Abuel-Naga et al., 2009). Mentionnons en particulier Burghignoli et al. (2000) qui ont conduit une étude en laboratoire des sols argileux pour des températures variant de 20 °C à 60 °C à l’aide d’essais non isothermiques drainés et non drainés, et durant la consolidation thermique. Dans cette plage de températures, la déformabilité et la résistance du sol sont peu dépendantes de la température mais la rigidité du sol est augmentée par les cycles thermiques. L’impact de la température sur le processus de fluage dépend très fortement de l’histoire de contraintes du sol.
Les géostructures génèrent également des variations de température dans le sol qui peuvent induire une variation volumique des terrains et donc impacter l’interaction entre le sol et la géostructure. Cette variation volumique dépend du taux de surconsolidation. En effet, lorsque l’on chauffe des sols fins, une contraction quasiment irréversible apparaît s’ils sont normalement consolidés. Les sols fins sur-consolidés, eux, se dilatent lors d’un réchauffement, mais cette dilatation est quasi réversible (Cekerevac et Laloui, 2004).
Ainsi pour une argile avec un OCR de 12, on relève une déformation volumique thermiquement induite allant jusqu’à −1 % (dilatation) lorsque cette dernière est chauffée jusqu’à 50 °C. Au-delà de cette température, la déformation volumique se met à décroitre, le sol se contracte. Par ailleurs, pour les sables, les effets cycliques associés aux variations successives de température peuvent conduire à une contractance du sol (Ng et al., 2016).
La température peut également modifier les propriétés mécaniques des terrains comme l’angle de frottement de pic et le module élastique mais, au vu des gammes de températures que l’on considère en géothermie de très basse énergie, ces influences sont négligeables.
2.3 Interaction sol-structure
Les variations de température impactent le comportement du sol mais aussi celui des géostructures en elles-mêmes. Dans la gamme de température de fonctionnement, leur comportement reste thermoélastique mais cela n’est pas sans impact sur les interactions sol-structure. La technique la plus développée dans le monde étant celle des pieux, c’est sur ses ouvrages que l’étude a été la plus conséquente.
En notant β le coefficient de dilatation thermique d’un pieu, une variation de température ΔT entraînerait une déformation de ce dernier s’il était libre égale à :
 (4)
(4)
Afin de respecter la convention de signe géotechnique, le coefficient de dilatation thermique du béton est affecté d’un signe négatif. Il vaut entre −9 et −14,5 µε/°C selon la conception du mélange de béton et la minéralogie des granulats (Stewart et McCartney, 2012).
En réalité, les conditions aux limites et le sol environnant limitent les déformations axiales à une valeur  (Fig. 4). Les déformations ainsi empêchées induisent donc des contraintes d’origine thermique observées sur des pieux géothermiques instrumentés (Laloui et al., 2006 ; Bourne-Webb et al., 2009 ; McCartney et Murphy, 2012) et valant :
(Fig. 4). Les déformations ainsi empêchées induisent donc des contraintes d’origine thermique observées sur des pieux géothermiques instrumentés (Laloui et al., 2006 ; Bourne-Webb et al., 2009 ; McCartney et Murphy, 2012) et valant :
 (5)où E est le module de Young du pieu. À titre d’exemple, l’allongement libre d’un pieu en béton armé (E = 35 GPa, β = 10−5 °C−1) de longueur 25 m soumis à ΔT = 30 °C serait de 7,5 mm. Si ce même pieu était bloqué en tête et en pointe, la contrainte thermique développée serait de 10,5 MPa.
(5)où E est le module de Young du pieu. À titre d’exemple, l’allongement libre d’un pieu en béton armé (E = 35 GPa, β = 10−5 °C−1) de longueur 25 m soumis à ΔT = 30 °C serait de 7,5 mm. Si ce même pieu était bloqué en tête et en pointe, la contrainte thermique développée serait de 10,5 MPa.
Par ailleurs, sous l’effet d’une descente de charge, le pieu présente un état de déformation ɛm et un état de contraintes mécaniques associé :
 (6)
(6)
Sous l’effet combiné des actions mécaniques et thermiques l’état total du pieu est donc décrit par :
 (7)
(7)
Cette analyse simple permet de saisir comment la mobilisation du frottement sol-inclusion induit des perturbations de l’interaction sol-structure lors de cycles de chargement thermiques (Amatya et al., 2012 ; Delerablée et al., 2020). Dans la réalité, les conditions aux limites sont plus complexes (raideur de la connexion en tête, terme de pointe, fonctions de transfert sol-pieu…) mais le même type d’analyse peut être conduit.
Si les développements précédents étaient centrés sur les pieux, ils concernent également les ouvrages de type parois moulées et tunnels (Di Donna et al., 2020) pour lesquels certaines difficultés supplémentaires peuvent apparaître. Dans le cas des parois moulées, les variations de température génèrent principalement des variations de la poussée des terres dépendant des caractéristiques du sol (Maghsoodi, 2020). De même, les raideurs d’interface sol-paroi utilisables dans un calcul aux coefficients de réaction sont dépendantes de la température. Enfin, par principe, l’une des faces d’un soutènement (hors fiche) est en contact avec l’air et cela complique l’étude de son comportement thermomécanique.
Enfin, l’étude de l’impact des variations de température sur l’interaction sol-structure considère généralement que le comportement mécanique de l’interface n’est pas modifié. Maghsoodi (2020) a investigué cette hypothèse en étudiant d’une part un sable de Fontainebleau et d’autre part une argile kaolinique. Pour le sol grossier, l’effet est négligeable mais la cohésion de l’interface argile-structure a augmenté suite à la contraction thermique. Le chauffage a également permis d’augmenter le nombre de cycles jusqu’à la rupture.
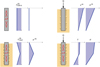 |
Fig. 4 Chargements thermiques et mécaniques d’un pieu. Thermal and mechanical loadings of a pile. |
2.4 Influence de la présence d’un écoulement dans le sol
Le couplage thermomécanique décrit précédemment dépend du champ de température dans le sol et donc de la présence d’eau dans le sol. En effet, comme présenté plus haut, les propriétés thermiques du sol sont nettement plus importantes lorsque ce dernier est saturé.
De surcroît, si l’eau est en mouvement, le terme de flux advectif  n’est plus nul et cela a pour conséquence de déplacer la chaleur en aval de l’écoulement. Cette variation du champ de température peut impacter le comportement thermomécanique des géostructures considérées mais aussi celui de tout ouvrage géotechnique immédiatement en aval.
n’est plus nul et cela a pour conséquence de déplacer la chaleur en aval de l’écoulement. Cette variation du champ de température peut impacter le comportement thermomécanique des géostructures considérées mais aussi celui de tout ouvrage géotechnique immédiatement en aval.
Lorsque la vitesse d’écoulement est très faible, le champ de température est principalement dicté par le phénomène de diffusion. À l’inverse, lorsque la vitesse d’écoulement est très élevée, les anomalies de température se déplacent « en translation » le long de l’écoulement. Dans les cas intermédiaires, on observe un panache de température dont l’étalement et le caractère évanescent dépendent de l’importance relative de l’advection et de la diffusion (Fig. 5). Cette importance relative est caractérisée par le nombre de Péclet :
 (8)
(8)
L est la dimension caractéristique de la source d’anomalie (le diamètre dans le cas d’un pieu perpendiculaire au plan de l’écoulement). Ce nombre adimensionnel caractérise le rapport entre l’énergie transmise par advection et celle transmise par conduction. Lorsque Pe >> 1, l’advection est majoritaire.
Enfin, si les pieux ne perturbent qu’à la marge l’écoulement souterrain, les tunnels ou les parois moulées, du fait de leur taille et/ou de leur géométrie, provoquent des perturbations non négligeables de l’écoulement (Delerablée et al., 2020). On parle en particulier d’effet barrage et il peut en découler de fortes variations du champ de vitesses (zones d’ombres hydrauliques, survitesses…).
 |
Fig. 5 Allure du panache thermique observé dans la simulation en éléments finis (CESAR-LCPC) du refroidissement d’un pieu pour Pe = 0 ; Pe = 5,4 et Pe = 10,8. Shape of the thermal plume observed in the finite elements modelling (CESAR-LCPC) of a cooled down pile for Pe = 0; Pe = 5.4 and Pe = 10.8. |
3 Performances énergétiques
Le principe des géostructures thermiques consiste (en mode chauffage) à extraire de la chaleur du sol pour chauffer des volumes à une température de l’ordre de 20 °C alors même que la température du sol, dans la zone considérée, est voisine de la température moyenne annuelle en surface, soit environ 14 °C en France métropolitaine.
3.1 Performances des pompes à chaleur géothermiques
Nous avons mentionné précédemment l’usage de pompes à chaleurs et les principes régissant leur comportement sont fondamentaux pour étudier les contraintes réelles d’implémentation de systèmes de captation d’énergie géothermique dans des conditions particulières. De la même manière qu’une pompe mécanique permet de faire circuler un fluide depuis une zone de faible charge hydraulique vers une zone de haute charge, donc contrairement au sens naturel, une pompe à chaleur permet de puiser de la chaleur dans une source froide pour la restituer dans un milieu de température plus élevée. Dans notre cas, en mode chauffage, la source froide est le sol environnant la géostructure et la source chaude, l’espace à chauffer (Fig. 6). Cela est rendu possible par l’apport d’un travail mécanique (compresseur) et la variation de l’enthalpie de changement d’état (chaleur latente) en fonction de la pression.
La figure 6 fait apparaître 3 cycles de circulation de fluide : un fluide caloporteur (généralement de l’eau glycolée) circule entre la géostructure thermique et la PAC, un autre circule entre la PAC et les radiateurs ou planchers chauffants et, au milieu, un fluide frigorigène circule au sein de la PAC.
Ce dernier est liquide et à basse pression en sortie du détendeur puis passe sous l’état de vapeur (basse pression) dans l’évaporateur, captant ainsi la chaleur latente de la source froide. Dans le compresseur, la vapeur devient à haute pression puis elle se liquéfie dans le condenseur à une température comparable à son évaporation grâce à la hausse de pression. Le fluide frigorigène délivre alors la chaleur latente stockée lors de son évaporation à la source chaude, et retourne dans le détendeur. L’ajout d’une vanne d’inversion de cycle permet de faire fonctionner la PAC en mode chauffage comme en mode refroidissement.
L’optimisation des performances des PAC passe donc par un choix judicieux du fluide frigorigène, un dimensionnement des échangeurs de chaleur et une sélection de compresseurs permettant d’atteindre des températures d’évaporation les plus élevées possibles et des températures de condensation les plus basses possible. Le choix du liquide frigorigène a toute son importance sur les performances de l’installation mais aussi sur d’autres critères comme la sécurité, la santé ou encore sur l’environnement. En effet, certains gaz comme les CFC et HCFC détruisent l’ozone et leur impact sur la couche d’ozone n’est plus à démontrer, d’autres comme le R717 et le R290 sont toxiques ou inflammable, ils nécessitent donc des précautions d’usage bien plus élevées.
La performance de la PAC est évaluée via le Coefficient de Performance (COP) défini comme le rapport entre la puissance transmise à la source chaude et la puissance mécanique à apporter au compresseur. Sa valeur théorique, déduite du cycle idéal de Carnot ne dépend que des températures (en °K) à l’entrée des échangeurs de chaleur Tchaud et Tfroid :
 (9)
(9)
On observe donc que le COP est maximisé lorsque la température du sol est au plus proche de la température de l’espace chauffé. Dans le cas d’une PAC géothermique (PACg), Tchaud et Tfroid sont les températures des fluides caloporteurs et le COP dépend donc des circuits secondaires. On observe que les performances d’une PAC sont nettement plus favorables pour une PACg que pour une PAC aéraulique (Fig. 7).
Le COPCarnotne rend pas compte de la réalité des PAC et il faut plutôt se référer au COP calculé en fonction des caractéristiques des composants et de la configuration d’usage ou mesuré. On en distingue plusieurs types :
le COP machine, donnant les performances de la PAC indépendamment du reste du système ;
le COP système, tenant compte des circulateurs, des pompes de relevage de l’eau et des accessoires annexes (affichage numérique, boîtier de commande…) ;
le COP annuel, prenant en compte l’usage dans des conditions réelles pendant une année complète. Il sera naturellement plus élevé si les variations de température entre source chaude et source froide sont plus faibles. La stabilité des températures du sol par rapport aux températures de l’air explique donc en partie les meilleures performances des PACg ;
le COP saisonnier (ou SCOP), calculé sur la saison de chauffe et tenant compte de plusieurs scénarios d’évolutions de la température extérieure.
Pour des géostructures thermiques dans des cas d’usage courants, le SCOP varie entre 3,8 et 4,3 (Vasilescu, 2019). Cela nécessite de limiter la température du circuit de chauffage à 40 °C environ et d’avoir donc recours à un autre mode de chauffage pour l’eau chaude sanitaire.
 |
Fig. 6 Schéma de principe d’une PAC géothermique en mode chauffage. Schematic diagram of a geothermal heat pump in heating mode. |
 |
Fig. 7 Comparaison des COP annuels d’une PAC aéraulique (gauche) et géothermique (droite) dans les conditions courantes au Royaume-Uni (Staffell et al., 2012). Comparison of annual COP of an air heat pump (left) and a geothermal heat pump (right) in the common conditions in UK. |
3.2 Stockage thermique et dérive thermique pluriannuelle
Le fonctionnement même des systèmes géothermiques tend à accroître la différence de température entre leurs sources et diminuent ainsi progressivement leurs performances. Toutefois, l’alternance des besoins entre été et hiver permet de pallier ce problème grâce au phénomène de stockage thermique : le refroidissement des bâtiments en été permet de stocker de la chaleur dans le sol qui pourra être captée en hiver. Si ce gain intersaison est supérieur aux pertes dues à la baisse du COP au cours de chaque saison, le stockage est favorable. Ce sera d’autant plus le cas que sa capacité thermique est grande et sa conductivité thermique faible (Tab. 1).
Cependant, si les besoins en fraicheur et en chaleur ne sont pas équilibrés sur l’année, comme c’est souvent le cas en France, une dérive thermique pluriannuelle peut avoir lieu (Delerablée, 2019). En présence d’un écoulement souterrain, le phénomène d’advection peut permettre d’éviter cette dérive. De manière générale, le contexte sera d’autant plus favorable que la conductivité thermique sera forte, que la vitesse d’écoulement de la nappe sera élevée et que l’état thermique du milieu sera proche de l’état naturel, ou, tout au moins, peu influencé par des facteurs anthropiques (CFMS et Syntec, 2017). Toutefois, dans le cas où les besoins sont équilibrés, la présence d’un écoulement rend le stockage sous-optimal (Di Donna et al., 2017). Dans tous les cas, l’équilibre du sol doit être recherché dans le long terme. Les dérives thermiques impactent négativement l’efficacité du système et une accumulation de chaleur est considérée par certaines agences de l’environnement comme étant une pollution (De Moel et al., 2010).
Une fois encore, il apparait essentiel de connaître finement le contexte hydraulique pour envisager le dimensionnement d’un projet géothermique. Si le tableau 1 ne fait pas apparaitre de très grandes différences entre sols fins et grossiers en ce concerne les caractéristiques thermiques statiques des sols, les différences de perméabilité entre argiles et graves induisent une forte variation des gradients hydrauliques et donc, in fine, de la capacité du terrain à atténuer les anomalies thermiques.
3.3 Puissances extraites
Dans le cas des pieux géothermiques, la puissance extractible du sol est estimée à l’aide du concept de résistance thermique Rth reliant la différence de température ΔT entre le sol environnant et le fluide caloporteur entrant dans la géostructure à la puissance ϕ extraite par mètre linéaire de pieu :
 (10)
(10)
Cette résistance thermique est la résultante de contributions diverses (cf. Fig. 3). Dans le cas d’un pieu géothermique classique, elle est la somme de la résistance en conduction du béton Rbet et de celle de la paroi du tube échangeur RPEHD ainsi que de la résistance due à la convection au sein du tube Rtube et de la résistance due à la convection à l’interface entre le pieu et l’écoulement souterrain Rsol. Si le tube échangeur était au milieu du pieu, elle s’écrirait :
 (11)
(11)
re et ri sont les rayons externes et internes du tube échangeur, rpieu le rayon du pieu, L la longueur de pieu activée, λbet et λPEHD les conductivités thermiques du béton et du PEHD. Enfin Stube et Ssol sont les surfaces sur lesquelles se déroulent les transferts convectifs tandis que htube et hsol sont les coefficients de convection correspondant. Ces derniers peuvent être estimés à l’aide de corrélations présentes dans la littérature reliant le nombre de Nusselt aux nombres de Reynolds et Prandtl (Jannot, 2012). Une fois connu le nombre de Nusselt, à l’aide d’une longueur caractéristique Lc et de la conductivité thermique du fluide on obtient le coefficient de convection :
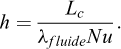 (12)
(12)
La détermination de cette résistance thermique en régime permanent ne dépend que des caractéristiques thermiques des matériaux constitutifs du pieu mais les conditions de fonctionnement des géostructures thermiques sont en général hors du régime permanent. De nombreux développements théorique ont permis d’affiner le calcul de Rth en régime stationnaire (Loveridge et Powrie, 2013 ; Maragna et Loveridge, 2018). On observe que la résistance thermique est d’autant plus faible que le recouvrement des tubes échangeurs est mince (Loveridge et al., 2014). À l’inverse, augmenter excessivement le nombre de tubes échangeurs favorisera l’interaction entre les tubes froids et chauds, réduisant le rendement de l’installation. Il existe donc un nombre optimal de tubes échangeurs en fonction du diamètre du pieu. Ces contraintes peuvent être réduites par l’utilisation de tubes hélicoïdaux (Fadejev et al., 2017) mais ce type de configuration n’est pas utilisé dans la pratique en France. On retiendra qu’en général, les pieux géothermiques peuvent échanger avec le sol entre 40 et 100 W/m de pieu (Di Donna et al., 2017).
Les ouvrages de type parois moulées et tunnels présentent l’avantage d’avoir une plus grande surface d’échange avec le sol et bénéficient ainsi d’un meilleur échange thermique. Ils ont donc un potentiel énergétique important. Néanmoins, il est difficile de généraliser quant à la quantité d’énergie récupérable puisque cette dernière dépend très fortement de la présence d’un écoulement et de sa vitesse le cas échéant. L’effet barrage mentionné plus haut complique la prédiction de l’impact de l’écoulement sur les performances énergétiques mais des abaques sont disponibles (Fig. 8). On observe également un espacement optimal des tubes échangeurs dans le cas des parois moulées (Fig. 9).
Afin d’illustrer le potentiel de puissance extractible par les géostructures thermiques, on peut noter que le projet de métro M3 à Lausanne pourrait permettre d’équiper 50 à 60 % du tracé et de chauffer ainsi l’équivalent de 1500 appartements de 80 m2, évitant 2 millions de tonnes de CO2 émis en comparaison d’un chauffage au gaz (Peltier, 2018). À cela pourrait s’ajouter les parois moulées thermoactives des stations de métro. De même, en Suisse, le terminal E de l’aéroport de Kloten mis en service en 2003 repose sur 350 pieux forés de 27 m de longueur dont 306 sont équipés énergétiquement, assurant 85 % du besoin en chaleur annuel (Pahud, 2002).
 |
Fig. 8 Abaques de puissances échangées par surface de paroi ou de tunnels en fonction des conditions de sol (Di Donna et al., 2020). Abacus giving the exchanged power per wall or tunnel surface for different soil conditions. |
 |
Fig. 9 Temps de retour sur investissement en fonction de l’espacement entre les tubes échangeurs dans le cas d’une paroi moulée thermoactive (Adam et Markiewicz, 2009). Time of return on investment as a function of the spacing between heat pipes in the case of an energy diaphragm wall. |
4 Dimensionnement des géostructures thermiques
Les géostructures thermiques ayant, avant tout, un rôle mécanique, leur dimensionnement est principalement piloté par des règles dépendantes des techniques de mise en œuvre. En France et en Europe, la majorité des pieux géothermiques sont mis en œuvre par la méthode des pieux forés mais on trouve également dans le monde des pieux géothermiques battus notamment au Japon et en Asie plus généralement (Ng et al., 2016). Il existe également des pieux en béton centrifugé, évidés en leur centre pour y placer facilement les tubes échangeurs. C’est le cas pour la technique dite Pilotherm® de l’entreprise suisse SACAC.
Toutefois, les sollicitations thermiques appliquées aux pieux, dépendant des besoins énergétiques à assurer, du temps de fonctionnement et des propriétés hydro-thermo-mécaniques du sol nécessitent des règles de dimensionnement supplémentaires adaptées (CFMS et Syntec, 2017). Les variations de température observées sont de l’ordre de ± 10 °C par rapport à la température du sol. En Autriche, où l’utilisation de géostructures thermiques est fortement développée, il ne semble pas exister de vérification supplémentaire liée à l’aspect énergétique de ces ouvrages. Toutefois en France, certaines vérifications sont faites en lien avec celles déjà existantes dans l’Eurocode (Delerablée et al., 2020).
4.1 Cas des pieux
Dans le dimensionnement d’un pieu, trois aspects interviennent et doivent donc être considérés : le comportement du sol, celui du pieu et celui de l’interaction entre les deux. Le premier n’est généralement pas pris en compte, conformément à l’impact négligeable évoqué plus haut.
La justification des pieux sous la charge thermique s’effectue en considérant chaque pieu totalement bloqué et en vérifiant sous différentes combinaisons de charges la variation d’effort normal, le déplacement en tête de pieu et la différence de résistance mobilisée. En effet, les chargements thermiques dus à l’activation du pieu sont considérés comme des charges variables statiques. Par exemple, lorsque l’on injecte de la chaleur dans le pieu en été, il apparaît une augmentation de la variation de l’effort normal et une diminution du tassement en tête. Les mêmes vérifications sont faites pour des pieux totalement libres de se déformer.
Dans la réalité, les pieux ne sont ni totalement bloqués, ni totalement libres de se déplacer. Les valeurs réelles sont donc situées à l’intérieur d’un intervalle formé par les valeurs calculées. Par conséquent, si les bornes supérieures et inférieures de ces intervalles respectent les critères considérés (ELU, ELS), alors la justification des pieux est acceptable. Cette méthode est simple et rapide à mettre en œuvre mais l’utilisation d’abaques tenant compte de la raideur en tête de pieu permettrait des résultats plus fins (Fig. 10).
À cet aspect mécanique du dimensionnement, il faut évidemment ajouter un aspect de dimensionnement thermique, essentiel dès la phase d’avant-projet afin de caractériser la rentabilité et le TRI du projet. La répartition des tubes échangeurs dans les pieux est un aspect essentiel de ce dimensionnement et met en œuvre les principes évoqués plus haut. On attirera l’attention sur le fait que l’objectif du dimensionnement thermique n’est pas uniquement de maximiser le flux thermique échangé mais également de maintenir le sol dans un état proche de son équilibre naturel afin de pérenniser l’exploitation du potentiel.
 |
Fig. 10 Diagramme d’analyse du comportement global en tête d’un pieu géothermique isolé en fonction de la raideur en tête kh (Mroueh et al., 2018). Diagram for the analysis of global head behaviour of an isolated energy pile as a function of the head stiffness kh. |
4.2 Cas des groupes de pieux
La plupart des projets pour lesquels le recours à des pieux géothermiques est envisageable font en réalité intervenir des radiers supportés par des groupes de pieux. Bien que l’étude de tels systèmes de fondations reste un sujet de recherche ouvert (voir section suivante), des recommandations existent déjà et elles illustrent le difficile découplage entre dimensionnement thermique et dimensionnement mécanique. En particulier, il est recommandé de ne pas placer des pieux géothermiques à proximité de pieux non géothermiques. En effet, selon la rigidité de la structure portée, les différences de dilatation thermique entre pieux activés et non activés peuvent générer des contraintes dans le radier.
Un exemple de justification d’un groupe de pieux géothermiques est donné à travers le retour de l’étude d’une station d’épuration située à Sept-Sorts (Borely et Okyay, 2017 ; Vasilescu, 2019). Un chargement mécanique axial de 430 kN est appliqué en tête des pieux et ceux activés thermiquement sont réchauffés de 10 °C puis refroidis de −20 °C. La loi de transfert sol-pieu proposée est celle de Frank et Zhao (1982) induisant un tassement en tête de 2 mm et des efforts verticaux de 430 kN si le pieu est libre en tête, 607 kN pour la rigidité calculée et 656 kN s’il est bloqué. Pourtant un calcul aux éléments finis, tenant compte des interactions entre pieux indiquent une variation d’effort normal 3 fois inférieure, illustrant le surdimensionnement conséquent qu’impliquent les méthodes simplifiées.
Concernant les efforts thermiquement induits dans un radier de type dalle sur longrines, il faut vérifier que les déformations restent inférieures à 1/1000 de la portée entre longrines. Pour un plancher champignon, un modèle aux éléments finis est recommandé même si la théorie des poutres ou la méthode des raideurs sont utilisables. Enfin, concernant les déplacements, la méthode classique consiste à vérifier que la rotation relative reste inférieure à 1/500.
4.3 Cas des écrans et des tunnels
Les parois thermoactives sont source de complexité supplémentaire puisque l’ajout d’une charge thermique à ces structures induit des problématiques mécaniques au niveau des déplacements et des efforts additionnels (Delerablée et al., 2020). En effet, la dilatation (ou la contraction) de la structure peut être contrainte par le terrain de la même façon que pour les pieux, mais également par la rigidité du radier et des panneaux adjacents non équipés. Ainsi, les résistances géotechnique et structurelle sont vérifiées à la fois à l’ELS et à l’ELU et les déplacements sont vérifiés à l’ELS ; comme pour les pieux géothermiques. Sous combinaisons d’actions à l’ELS, les déplacements horizontaux et verticaux sont obtenus ainsi que les différentes variations d’efforts. Cette fois, on considère non seulement les efforts verticaux mais également les efforts horizontaux et les moments thermiquement induits.
Quant aux tunnels, seuls ceux construits au tunnelier peuvent être équipés énergétiquement (échangeurs thermiques intégrés aux voussoirs en usine). Leur dimensionnement thermique est piloté par l’écoulement souterrain (Fig. 8) et les spécificités de leur dimensionnement mécanique liées à l’activation des voussoirs font encore l’objet de recherches même si les premiers résultats indiquent des efforts négligeables (Bourne-Webb et al., 2016).
5 Étude d’un groupe de pieux au sein d’un écoulement
Comme cela a été mentionné au sujet du dimensionnement, l’étude des groupes de pieux contenant des pieux activés thermiquement est un sujet de recherche ouvert même s’il a déjà fait l’objet de nombreuses études (Suryatriyastuti et al., 2016 ; Ng et Ma, 2019 ; Rotta Loria et Laloui, 2017). On peut mentionner les contraintes thermiques induites dans le radier déjà évoquées mais Ng et Ma (2019) font également part de l’inclinaison résiduelle d’un groupe de pieux soumis à une charge mécanique constante et dont un seul pieu est soumis à un chargement thermique cyclique. Cette inclinaison implique l’apparition d’un moment fléchissant additionnel en tête de pieu. Ce moment est calculé par l’auteur de l’article et est estimé à 15 % de la capacité maximale du connecteur.
De plus, on a vu que les contraintes thermiquement induites dans un pieu sont fortement dépendante de ses conditions de blocage en tête. Ces conditions sont particulièrement difficiles à évaluer dans le cas d’un groupe de pieux puisqu’elles sont en partie liées à la non-déformation des pieux non activés thermiquement.
Enfin, la présence d’un écoulement souterrain peut tendre à homogénéiser les variations de température entre les pieux et ainsi réduire les contraintes thermiquement induites. Cet aspect, très peu étudié dans la littérature est ici exploré dans le cas simple d’un groupe de 4 pieux en béton (diamètre 1 m, longueur 15,5 m) disposés selon une maille carrée de 3 m de côté. Les pieux sont enfouis sur 12,5 m dans une couche de 16,5 m de sable d’Hostun saturé reposant sur un substratum infiniment rigide. Ils sont reliés en tête par un chevêtre carré de 4,5 m de côté. L’écoulement est orienté selon l’un des côtés du chevêtre (Fig. 11). Seul le pieu numéroté 1 est activé thermiquement et uniquement dans la partie enterrée. L’étude comporte une modélisation numérique et une modélisation physique en centrifugeuse.
 |
Fig. 11 Représentation du groupe de pieux étudié (vue de côté et vue de dessus). Representation of the pile group studied (side and top views). |
5.1 Modélisation aux éléments finis
La modélisation aux éléments finis (FEM) permet de reproduire et prédire le comportement des structures pour différents problèmes physiques. Dans le cadre d’une structure géothermique, les FEM permettent de résoudre les problèmes d’hydrologie, de thermique et de mécanique. Suivant les possibilités des logiciels, il est possible de mettre en place un couplage entre les différents problèmes physiques afin de modéliser la complexité du problème. L’étude présentée ici est conduite à l’aide du logiciel de calcul par éléments finis Cesar-LCPC (Humbert et al., 2005). Une procédure de calcul adaptée permet de modéliser un couplage faible entre les trois phénomènes physiques. L’écoulement hydrologique est calculé en tenant compte des perturbations induites par la présence de la géostructure. Le problème thermique est ensuite résolu en tenant compte du flux advectif lié au champ de vitesse de l’eau souterraine. Le calcul du régime d’écoulement permanent est mené à l’aide du module DTNL de CESAR-LCPC. Le calcul des champs de température en régime transitoire utilise le module DTNL de CESAR-LCPC. L’intégration temporelle faite selon l’algorithme d’Euler implicite (Mestat, 2005). Les états de température successifs obtenus sont ensuite utilisés comme sollicitation thermomécanique transitoire du problème mécanique. À chaque étape du problème mécanique, l’état de contraintes et déformations est calculé selon l’équation quasi statique (Éq. (13)) à l’aide du module MCNL de CESAR-LCPC. Les modélisations hydro-géothermiques ont montré leur pertinence sur le cas expérimental du site de Sense-City (Badinier et al., 2020).
Afin de correspondre au prototype (équivalent 1 g) du modèle réduit centrifugé présenté ensuite, les pieux du modèle numérique sont constitués de ciment et on étudiera l’impact de la réalisation du chevêtre en aluminium ou en PVC. Les pieux seront numérotés comme indiqué sur la figure 11 et les coins du chevêtre suivront la même numérotation.
Le système est initialement dans un équilibre mécanique et thermique à 13 °C. Au début de la modélisation, l’un des pieux est chauffé en son centre par une différence de température imposée de +20° (33 °C). Le calcul est mené sur 100 pas de calcul de 86 400 s (1 jour), ce qui s’est montré être un découpage temporel suffisamment fin pour assurer la précision du modèle numérique. Le modèle complet comporte 80 701 nœuds pour 58 133 éléments. Dans le cadre de cette étude simple, le comportement de l’ensemble du modèle est thermoélastique linéaire et isotrope. Les équations qui gouvernent le comportement mécanique du modèle sont donc les équations élastiques linéaires de Hooke (Éq. (13)) et l’influence du chargement thermique peut être vue comme un chargement volumique isotrope fonction du coefficient de dilatation thermique β (Éq. (14)) (Salençon, 2002). Les caractéristiques des matériaux sont présentés dans le tableau 2. De même pour la simplicité de ce modèle les interfaces sol-pieux sont considérées comme adhérentes.
 (13)
(13)
Dans cette équation, λ correspond au coefficient de Lamé et non au coefficient de conduction thermique.
 (14)
(14)
Cinq cas de figure sont étudiés. Un premier cas où le chevêtre est en aluminium, un second où le chevêtre est en PVC et un troisième ou le matériau représenté dispose des propriétés mécanique de l’aluminium et des propriétés thermiques du PVC afin de simuler la réalisation d’un modèle avec chevêtre en aluminium isolé thermiquement des pieux. Pour ces trois premiers cas aucun mouvement de nappe n’est imposé. Dans les deux derniers cas, le chevêtre est en aluminium et un mouvement de nappe est alors imposé avec une vitesse de 0,05 m/j pour le cas 4 et une vitesse de 0,50 m/j pour le cas 5. Ces vitesses d’écoulement correspondent à des nombre de Péclet de Pe = 2.8 et Pe = 28 respectivement.
Les résultats thermiques préliminaires permettent de constater que le chauffage d’un seul pieu ne permet pas de chauffer de façon significative l’intégralité du groupe. Le profil de température est globalement homogène dans la hauteur du pieu sur toute sa partie enterrée (Fig. 12). Pour les trois premiers cas, l’observation de la température en fonction de la distance depuis le centre du pieu 1 (actif) ne montre pas de différence. Après 99 h d’activité le sol atteint une température 16,6 °C en périphérie du pieu 1 et la température décroît ensuite avec la distance (Fig. 12). Dans le cas 4 où la nappe est en mouvement à une vitesse relativement faible (Pe = 2.8), la transmission de la température dans le sol est beaucoup plus importante dans la direction d’écoulement et on observe une différence d’environ 0,5 °C à 5 m. En revanche, l’influence thermique du pieu actif dans les autres directions est bien moins importante. Enfin dans le cas 5, la transmission de chaleur en aval du pieu actif est également plus importante que pour les trois premiers cas. Cependant, l’importance du phénomène d’advection thermique (Pe = 28) permet de limiter l’échauffement du pieu 1 à une température de 14,9 °C en périphérie du pieu et d’homogénéiser les variations de température entre les pieux.
La transmission de chaleur vers le chevêtre est très limitée. La température finale au coin 1 est de 13,41 °C dans le cas d’un chevêtre avec la propriété thermique du PVC et 13,10 °C dans le cas de l’aluminium. On remarque que dans les cas d’un chevêtre en aluminium la température dans le chevêtre est très homogène au contraire des cas PVC. Cela peut s’expliquer d’une part par la capacité calorifique de l’aluminium qui est supérieure et nécessite donc d’avantage d’énergie pour atteindre des températures équivalentes, et d’autre part par la pauvre conductivité thermique du PVC conduisant à un effet de localisation de la chaleur dans le chevêtre. Ceci étant, la faible transmission dans le chevêtre y rend négligeables les déformations thermo-induites en comparaison de celles des pieux et, dans les conditions de fonctionnement étudiées, il apparaît que le matériau du chevêtre a peu d’influence.
Ainsi, la déformation globale du système est majoritairement gouvernée par la dilatation du pieu 1 (Fig. 13). Cette déformation se traduit par un phénomène classique d’extension du pieu selon un profil symétrique autour d’un point neutre immobile (voir Fig. 4). Cela entraîne donc une rotation du chevêtre autour de l’axe formé par les têtes des pieux 2 et 3. Plus précisément, on observe une déformation en flexion du chevêtre. La flexion principale se produit logiquement entre les coins 1 et 4. Celle-ci se met assez rapidement en place puis progresse quasi linéairement avec le temps (Fig. 13).
Dans les cas 4 et 5 le phénomène d’advection permet d’augmenter la transmission de chaleur vers le pieu 3 en aval du pieu 1. Cela a pour effet d’une part de produire un échauffement plus important du pieu 3 accompagné d’une dilatation plus importante. D’autre part, cela a pour effet de limiter l’échauffement du pieu 1 conduisant alors à une réduction de sa dilatation. La réduction des déformations thermo-induites dans le cas d’un écoulement souterrain est donc confirmée. L’augmentation de la température du pieu aval et sa dilatation accrue entraine une seconde flexion perpendiculaire à la première. En comparaison du cas 1, le déplacement vertical du coin 3 augmente et, en réaction, celui du coin 2 diminue. Cela est illustré par la divergence des courbes « Coin 2, cas 4 » et « Coin 3, cas 4 » de leur courbe de référence « Coin 3, cas 1 ». Pour le cas 5, le phénomène le plus impactant est la limitation sensible de l’augmentation de température du pieu. Cela conduit à une dilation moindre et à un déplacement vertical final du coin 1 de seulement 0,35 mm.
On notera toutefois que le chevêtre en PVC (cas 2) résiste moins à la flexion et le déplacement observé au coin 1 est nettement supérieur (0,70 mm). Cela tend à proscrire pour la modélisation physique l’usage d’un chevêtre en PVC quand bien même cela serait pertinent sur le plan thermique.
La déformation du chevêtre se traduit assez rapidement par le développent de contraintes de cisaillement en son sein. La figure 14 montre la contrainte de Tresca calculée le long de la diagonale entre les coins 1 et 4. L’évolution de cette contrainte dans le cas 1 montre qu’une fois mis en flexion le chevêtre ne se déforme que très peu et que la contrainte de cisaillement n’évolue alors que marginalement. Dans ce premier cas les contraintes de Tresca obtenues atteignent 0,11 MPa, ce qui représente 0,1 % de la résistance en traction d’un alliage d’aluminium faible. Dans le cas 2, le module de Young du PVC étant moins important que celui de l’aluminium, la contrainte de cisaillement développée lors de la flexion est alors moins importante. Dans les cas 2 et 3, le comportement thermique du chevêtre (celui du PVC) conduisant à une accumulation de chaleur au niveau du pieux actif (et donc une localisation des déformations), les plus fortes contraintes de cisaillement se développent au niveau de la jonction entre le pieu et le chevêtre. Ce phénomène est amplifié dans le cas 3 par l’importance du module de Young de l’aluminium. Dans le cadre d’un modèle réduit centrifugé, une attention particulière sera alors portée à la jonction mécanique et thermique entre le chevêtre et le pieux.
D’autres codes de calcul sont aujourd’hui capables de modéliser des comportements couplés. Le logiciel FEFLOW permet par exemple de modéliser le déplacement des anomalies thermiques (Russo et al., 2014). De même FLAC 3D permet un couplage hydro-thermique (Delerablée, 2019). Mentionnons également Comsol Multiphysics, logiciel spécialisé dans la modélisation des problèmes multiphysiques, qui permet des couplages thermo-hydro-mécaniques de différents niveaux avec des couplages faible ou fort (interaction entre les problèmes dans les deux sens). Les modélisations couplée hydro-thermo-mécaniques aujourd’hui possible avec le logiciel Cesar-LCPC sont toutefois prometteuse bien que ne représentant qu’un couplage faible (pas d’interactions du modèle thermique sur le modèle hydrologique par exemple). À l’avenir, la complexification des modèles devrait permettre de tenir compte de comportements plus complexes, par exemple les comportements non linéaires. Il reste cependant des points qui seront complexes à traiter par une approche actuelle, tels que l’évolution des lois de comportement en fonction de la température (Maghsoodi, 2020).
Caractéristiques thermiques et mécaniques des matériaux modélisés.
Thermal and mechanical characteristics of the modelled materials.
 |
Fig. 12 Répartition de la température dans le modèle (cas 1 à gauche et cas 4 à droite) et température en fonction de la distance à l’axe du pieu 1 dans le sens de l’écoulement. Repartition of temperature in the model (case 1 on left and case 4 on right) and temperature as a function of the distance to the centre of pile 1 along the seepage. |
 |
Fig. 13 Déformation totale du groupe (cas 1 à gauche et cas 4 à droite) et déplacements verticaux aux coins supérieurs du chevêtre. Total strains of the group (case 1 on left and case 4 on right) and vertical displacements at the corners of the raft. |
 |
Fig. 14 Contrainte de Tresca le long de la diagonale en surface du chevêtre. Tresca stress along the diagonal of the raft surface. |
5.2 Modélisation en centrifugeuse
Les études en centrifugeuse se sont développées dans les années 1980 dans le domaine de la géotechnique et permettent de modéliser certains comportements d’ouvrages grâce à des modèles de tailles réduites. Les propriétés du modèle et des couches de sol peuvent être choisies de façon pertinente, il est possible de charger les structures modèles jusqu’à la rupture et il est plus aisé de les instrumenter pour mesurer la température ou des grandeurs mécaniques. De plus, les propriétés du modèle et du sol étudiés sont contrôlées et différentes configurations peuvent alors être considérées rapidement et pour de plus bas coûts. Par rapport à un simple modèle réduit, le modèle centrifugé présente l’avantage de soumettre les matériaux aux mêmes contraintes qu’au sein d’un ouvrage réel correspondant et les comportements thermomécaniques, même complexes, peuvent donc être observés.
Enfin, comme on le verra plus bas, sur un modèle réduit d’un facteur n, les phénomènes de diffusion s’observent sur un temps réduit d’un facteur n2 et une année peut être modélisée en une journée, accélérant ainsi l’observation des interactions thermomécaniques. La modélisation en centrifugeuse apparaît donc comme un moyen judicieux pour étudier le comportement des fondations géothermiques à condition de s’assurer de la similitude entre les phénomènes observés sur le modèle réduit et sur son équivalent en grandeur réelle (appelé prototype).
Goode et McCartney (2015) ont ainsi démontré l’augmentation de la capacité portante d’un pieu chauffé lorsqu’il est mis en œuvre dans du limon (pieux modèles en béton armé de 34 et 53 cm soumis à une accélération centrifuge de 24 g). Cette augmentation n’apparaît pas dans le cas où la mise en œuvre se fait dans du sable. Par ailleurs, le chauffage des pieux modèles a induit un déplacement de la tête du pieu de l’ordre du millième du diamètre, et les contraintes axiales mesurées sur les pieux étaient plus fortes dans le cas où le sol était du limon compacté que dans le cas du sable.
Ng et al. (2016) ont utilisé des pieux modèles en aluminium de 42 cm recouvert d’une couche d’époxy. Ils ont pu prouver en appliquant une accélération de 40 g et une charge thermique cyclique sur ces pieux modèles qu’un tassement avait lieu au cours des cycles mais à un taux de plus en plus faible. De plus, le déplacement est plus fort lorsque le sol est de l’argile légèrement consolidée que lorsqu’il est surconsolidé. Enfin, l’auteur impute ce tassement à la réduction de contrainte causée par une contraction plastique de l’argile.
Le comportement des sols étant généralement complexe et non linéaire, on cherche à utiliser le même sol entre le modèle et le prototype. Pour s’assurer simplement de la similitude, on choisit de conserver les températures, les déformations et les contraintes. La conservation de ces dernières nécessite d’augmenter la gravité. En effet, dans un sol en équilibre géostatique, une particule située à une profondeur prototype zp sera soumise à une contrainte verticale σp = ρgzp. Dans le modèle réduit, cette même particule sera située à une profondeur zm = zp/n et subira une contrainte verticale σm = ρgmzm, ρ étant inchangé par conservation du sol. Alors la conservation des contraintes impose :
 (15)
(15)
Ainsi, un modèle réduit 100 fois est centrifugé sous une accélération de 100 g afin que la contrainte sous 10 m de sol dans le prototype soit la même que celle sous 10 cm de sol dans le modèle réduit. Concrètement, le modèle réduit est placé dans une nacelle reliée par une liaison pivot au bras de la centrifugeuse afin que l’accélération centrifuge agisse sur lui comme l’accélération de la pesanteur sur le prototype (Fig. 15).
Afin de pouvoir comparer les observations entre modèle et prototype, il faut déterminer pour toute grandeur x en jeu le facteur d’échelle constant x* = xm/xp reliant la grandeur modèle à la grandeur prototype. À titre d’exemple, la conservation des contraintes (σ* = 1) et la réduction des longueurs (L* = 1/n) imposent le facteur d’échelle des forces : F* = σ*L*2 = 1/n2. Les facteurs d’échelle principaux sont présentés dans le tableau 3.
On peut en particulier, retrouver le facteur d’échelle du temps caractéristique de diffusion à l’aide de l’équation (1). Dans le cas purement diffusif unidimensionnel elle impose :
 (16)
(16)
Comme vu précédemment, l’étude des géostructures thermiques fait intervenir, en plus du phénomène de diffusion, le phénomène d’advection. Il est essentiel que leur importance relative soit conservée entre le modèle et le prototype. Ainsi le nombre de Péclet doit être conservé et l’équation (8) impose alors  . Ainsi le facteur d’échelle du temps caractéristique d’advection est
. Ainsi le facteur d’échelle du temps caractéristique d’advection est 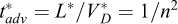 . L’égalité de
. L’égalité de  et
et  permettra d’observer des profils de température similaires aux profils prototypes. Dans le contraire, il aurait été nécessaire de modifier les propriétés du fluide afin de conserver le nombre de Péclet tout en respectant l’égalité des temps d’observation.
permettra d’observer des profils de température similaires aux profils prototypes. Dans le contraire, il aurait été nécessaire de modifier les propriétés du fluide afin de conserver le nombre de Péclet tout en respectant l’égalité des temps d’observation.
Ces deux règles de similitudes concernant les temps caractéristiques de diffusion et d’advection ont été vérifiées numériquement sur des modèles 1D. En considérant pour des modèles de taille réduite n fois, des vitesses n fois plus grandes et des temps n2 fois plus courts, les évolutions du champ de température étaient identiques entre modèle à échelle réelle et modèle à échelle réduite.
La diffusion et la conduction sont les deux principaux phénomènes thermiques en jeu dans le fonctionnement d’une géostructure thermique. Il existe cependant d’autres phénomènes thermiques qui entrent en jeu en second plan tels que la convection naturelle. En réalité, elle est négligeable dans le prototype et le reste dans le modèle. Le calcul du nombre de Grashof permet de s’en assurer.
Comme pour les phénomènes mécaniques et thermiques, les phénomènes hydrauliques doivent respecter des règles de similitude afin de pouvoir interpréter correctement les observations. Elles sont répertoriées dans le tableau 3 et découlent de la loi de Darcy si l’on garde à l’esprit que la conductivité hydraulique dépend de l’accélération de la pesanteur et de caractéristiques du fluide ou du milieu poreux :
 (17)
(17)
Ces règles de similitudes ont été vérifiées expérimentalement (Khalifa et al., 2000) mais un point de vigilance est à retenir : en accroissant la vitesse de l’écoulement, il est possible de sortir du domaine de validité de la loi de Darcy. Dans ce cas, la similitude serait rompue entre le modèle et le prototype. Les contraintes liées à l’utilisation de pompes en vol conduisent à envisager la mise en place de l’écoulement à l’aide de réservoirs à hauteur d’eau constante imposant une différence de charge hydraulique entre aval et amont.
L’ensemble des développements précédents a permis, dans le cadre d’une collaboration actuellement en cours avec le Schofield Center de l’Université de Cambridge (Royaume-Uni), la mise en place d’une première série d’expériences visant à modéliser le groupe de pieu décrit dans la figure 11. Pour des raisons pratiques, les pieux prototypes en béton ont été modélisés par des pieux réalisés en ciment, bien que cela en impacte les propriétés thermiques (Leung et al., 2019). Pour simuler au mieux le chargement thermique du groupe de pieux prototypes, de l’eau est circulée à l’aide d’une pompe à diaphragme dans un circuit incluant une boucle en U au sein du pieu activé et un module thermoélectrique à effet Peltier permettant de la chauffer ou de la refroidir (Fig. 16). L’instrumentation, constituée de capteurs de température de type Pt100 et capteurs de forces est présentée sur la figure 17.
Les capteurs de forces sont de forme cylindrique (20 mm de diamètre et 12 mm de hauteur) et constitués d’une vis à chaque extrémité pour pouvoir être fixés au pieu d’une part et au raft de l’autre. Selon les données du constructeur, ils peuvent être utilisés dans une gamme de température allant de −20 °C à 80 °C et leur capacité maximale est de 250 N (environ 4 fois plus que la charge qui leur est appliquée durant l’expérience). Enfin, ils possèdent une précision dite de classe C3 (la plus commune), qui correspond à une précision de 0,023 % et lors de leur calibration, les coefficients de corrélation étaient tous supérieurs à 0,99.
Les Pt100 sont des capteurs passifs dans la mesure où ils correspondent à une résistance (faite de Platine) dont la valeur évolue avec la température (elle vaut 100 Ohms à 0 °C). Ils ont été câblés, étanchéifiés, puis reliés à un pont de Wheatstone pour améliorer leur précision. Avant le test, la calibration de ces capteurs, faite à l’aide d’un thermomètre numérique, a pu attester de leur précision puisque les coefficients de corrélation étaient tous supérieurs à 0,997.
La première série d’expériences a été réalisée sans écoulement et a permis de comparer le cas d’un sol sec et celui d’un sol saturé. Les profils de température obtenus et leur évolution dans le temps sont comparables aux résultats du modèle numérique. Les variations d’effort mesurées en tête de pieu (Fig. 18) présentent également des évolutions en accord avec la modélisation numérique (compression des pieux 1 et 4 et traction des pieux 2 et 3 lors du chauffage). On note en particulier la différence d’inertie entre le sol saturé et le sol sec. Cependant, la somme de ces variations d’efforts devrait être nulle et constante au cours du temps et ce n’est pas le cas. Cela peut s’expliquer par des efforts parasites dus à la jonction chevêtre-pieu.
 |
Fig. 15 Schéma de principe du fonctionnement de la centrifugeuse géotechnique. Schematic diagram of principles of a geotechnical centrifuge. |
Principaux facteurs d’échelle pour la modélisation en centrifugeuse (Garnier et al., 2007).
Main scaling factors for centrifuge modelling.
 |
Fig. 16 Modèle réduit centrifugé et système géothermique associé. Centrifuge model and associated geothermal system. |
 |
Fig. 17 Schéma d’instrumentation du modèle réduit centrifugé. Monitoring scheme of the centrifuge model. |
 |
Fig. 18 Variation des efforts en tête de pieu au cours de cycles thermique sur le modèle réduit centrifugé. Variations of forces on pile heads during the thermal cycles on the centrifuge model. |
6 Perspectives pour l’étude des géostructures thermiques
Bien qu’elles aient fait l’objet de nombreuses études, les géostructures thermiques soulèvent encore des questions quant à leur dimensionnement et ces questions sont autant de verrous qui limitent leur développement à large échelle. En particulier, le comportement thermomécanique des groupes de pieux géothermiques n’est pas suffisamment caractérisé et les incertitudes que cela génère peuvent tendre à induire un surdimensionnement susceptible de grever l’intérêt économique initial d’une solution combinant rôle structurel et rôle énergétique.
L’interaction des écoulements souterrains avec les géostructures thermiques est un autre aspect sur lequel le manque de connaissance est dommageable. En plus des implications thermomécaniques de cette inconnue, on peut noter deux questions liées dont la résolution participera à la large implémentation de ces infrastructures productrices d’énergies :
Quel est l’impact de l’hétérogénéité de l’écoulement ou des incertitudes liées à sa reconnaissance sur l’évaluation du rendement énergétique des géostructures thermiques ?
Quelles interactions positives ou négatives, l’écoulement souterrain peut-il générer entre géostructures voisines ?
Pour répondre à ces questions, la communauté géotechnique dispose d’un panel complet d’outils :
la modélisation numérique bénéficie aujourd’hui d’une multitude de codes de niveaux de complexification variables et un recensement des performances et plages de validité de chacun est à faire. En particulier, il semble nécessaire de produire des approches simplifiées pour l’ingénieur qui permettent des dimensionnements moins conservatifs ;
la modélisation physique, que ce soit sur modèles réduits centrifugés ou sur modèles physiques 1 g en semi-grandeur (de Sauvage et al., 2020) est une voie prometteuse dans le sens où elle permet d’obtenir des résultats expérimentaux difficilement accessibles sur ouvrages réels ;
enfin, l’instrumentation d’ouvrages réels tels que la station de Sept-Sorts ou la station Jules Ferry du métro de Rennes ainsi que leur suivi sur le long terme sont essentiels.
Table des sigles
| CFC | Chlorofluorocarbure |
| CFMS | Comité Français de Mécanique des Sols |
| HCFC | Hydro chlorofluorocarbure |
| COP | Coefficient de Performance |
| ELS | État Limite de Service |
| ELU | État Limite Ultime |
| FEM | Finite Elements Method (Méthode des éléments finis) |
| OCR | Overconsolidation Ratio (Rapport de Consolidation) |
| PEHD | Polyéthylène Haute Densité |
| PAC | Pompe à chaleur |
| PACg | Pompe à chaleur géothermique |
| Pe | Nombre de Péclet |
| PVC | Polychlorure de Vinyle |
| RT | Réglementation thermique |
| R717 | Ammoniac |
| R290 | Propane |
| SCOP | Seasonal Coefficient of Performance, Coefficient de performance saisonnier |
| Syntec | Syndicat des sociétés d’études et de conseils |
| TRI | Temps de retour sur investissement |
Table des notations
Remerciements
Les auteurs souhaitent exprimer leurs remerciement envers le Ministère de la Transition Ecologique et Solidaire pour le financement des travaux de thèse de Badr Ouzzine au cours de laquelle ont eu lieu certains des développements présentés ici. Nos profonds remerciements vont également aux membres du Schofield Center de l’Université de Cambridge, et en particulier à Gopal Madabhushi et Giulia Viggiani, pour leur collaboration.
Références
- Abuel-Naga HM, Bergado DT, Bouazza A, Pender M. 2009. Thermomechanical model for saturated clays. Géotechnique 59(3): 273–278. [CrossRef] [Google Scholar]
- Adam D, Markiewicz R. 2009. Energy from earth-coupled structures, foundations, tunnels and sewers. Géotechnique 59(3): 229–236. [CrossRef] [Google Scholar]
- Amatya BL, Soga K, Bourne-Webb PJ, Laloui L. 2012. Thermo-mechanical performance of energy piles. Géotechnique 62(6): 503–519. [CrossRef] [Google Scholar]
- Andersland OB, Ladanyi B. 2013. An introduction to frozen ground engineering. Springer Science & Business Media. [Google Scholar]
- Badinier T, de Sauvage J, Szymkiewicz F, Benitez BR. 2020. Groupe de pieux thermoactifs dans un écoulement aquifère : modélisation physique et numérique. In: JNGG 2020, Journées Nationales de Géotechnique et de Géologie de l’Ingénieur, pp. 8. [Google Scholar]
- Borely C, Okyay US. 2017. Structure énergétiques : interaction Pieu-Sol-Structure. In: Journée technique « Guide Géostructures énergétiques ». [Google Scholar]
- Bourne-Webb PJ, Amatya B, Soga K, Amis T, Davidson C, Payne P. 2009. Energy pile test at Lambeth College, London: geotechnical and thermodynamic aspects of pile response to heat cycles. Géotechnique 59(3): 237–248. [CrossRef] [Google Scholar]
- Bourne-Webb P, Burlon S, Javid S, Kuerten S, Loveridge F. 2016. Analysis and design methods for energy geostructures. Renew Sustain Energy 65: 402–419. [CrossRef] [Google Scholar]
- Brandl H. 2006. Energy foundations and other thermo-active ground structures. Géotechnique 56(2): 81–122. [CrossRef] [Google Scholar]
- Burghignoli A, Desideri A, Miliziano S. 2000. A laboratory study on the thermomechanical behaviour of clayey soils. Can Geotech J 37(4): 764–780. [CrossRef] [Google Scholar]
- Campanella RG, Mitchell JK. 1968. Influence of temperaturevariations on soil behavior. J Soil Mech Found Div, ASCE 94(3): 709–734. [CrossRef] [Google Scholar]
- Cekerevac C, Laloui L. 2004. Experimental study of thermal effects on the mechanical behaviour of a clay. Int J Num Anal Meth Geomech 28(3): 209–228. [CrossRef] [Google Scholar]
- CFMS, Syntec. 2017. Recommandations pour la conception, le dimensionnement et la mise en œuvre des géostructures thermiques. Rev fr Geotech 149. [Google Scholar]
- Dalla Santa G, Galgaro A, Sassi R, et al. 2020, An updated ground thermal properties database for GSHP applications. Geothermics 85: 101758. [CrossRef] [Google Scholar]
- De Moel M, Bach PM, Bouazza A, Singh RM, Sun JO. 2010. Technological advances and applications of geothermal energy pile foundations and their feasibility in Australia. Renew Sustain Energy Rev 14(9): 2683–2696. [CrossRef] [Google Scholar]
- Delerablée Y. 2019. Intégration thermique et mécanique des géostructures thermiques : de l’échelle du bâtiment à l’échelle de la cité. Thèse de doctorat, Université Paris Est. [Google Scholar]
- Delerablée Y, Habert J, Burlon S. 2020. Géostructures thermiques – Présentation du fonctionnement thermique et mécanique. Techniques de l’ingénieur: C264 V1. [Google Scholar]
- Di Donna A, Barla M, Amis T. 2017. Energy geostructures: Analysis from research and systems installed around the World. In: DFI 42nd Annual Conference on Deep Foundations. [Google Scholar]
- Di Donna A, Emeriault F, Demongodin L, Gobichon JF. 2020. Aspects géotechniques et énergétiques des géostructures thermoactives : application à un cas d’étude réel. Rev fr Géotech 164: 4. [CrossRef] [EDP Sciences] [Google Scholar]
- Fadejev J, Simson R, Kurnitski J, Haghighat F. 2017. A review on energy piles design, sizing and modelling. Energy 122: 390–407. [CrossRef] [Google Scholar]
- Frank R, Zhao SR. 1982. Estimation par les paramètres pressiométriques de l’enfoncement sous charge axiale de pieux forés dans des sols fins. Bulletin de Liaison des Laboratoires des Ponts et Chaussées 119: 387–421. [Google Scholar]
- Fromentin A, Pahud D, Jaquier C, Morath M. 1997. Recommandations pour la réalisation d’installations avec pieux échangeurs. Empfehlungen für Energiepfahlsysteme. Rapport final. Rapport d’étude n°120.104. Lausanne, Suisse: Office Fédéral de l’Énergie, 79 p. [Google Scholar]
- Garnier J, Gaudin C, Springman SM, et al. 2007. Catalogue of scaling laws and similitude questions in geotechnical centrifuge modelling. Int J Phys Model Geotech 7(3): 01–23. [Google Scholar]
- Goode, III. JC, McCartney JS. 2015. Centrifuge modeling of end-restraint effects in energy foundations. J Geotech Geoenviron Eng 141(8): 04015034. [CrossRef] [Google Scholar]
- Humbert P, Dubouchet A, Fezans G, Remaud D. 2005. CESAR-LCPC, un progiciel de calcul dédié au génie civil. Bulletin des laboratoires des ponts et chaussées 256: 7–37. [Google Scholar]
- Jannot Y. 2012. Transferts thermiques. Nancy: École des Mines. [Google Scholar]
- Khalifa A, Garnier J, Thomas P, Rault G. 2000. Scaling laws of water flow in centrifuge models. In: Int. Symp. on Physical Modelling and Testing in Environmental Geotechnics, La Baule. [Google Scholar]
- Lahoori M, Jannot Y, Rosin-Paumier S, Boukelia A, Masrouri F. 2020. Measurement of the thermal properties of unsaturated compacted soil by the transfer function estimation method. Appl Therm Eng 167: 114795. [CrossRef] [Google Scholar]
- Laloui L, Nuth M, Vulliet L. 2006. Experimental and numerical investigations of the behaviour of a heat exchanger pile. Int J Numer Anal Meth Geomech 30(8): 763–781. [CrossRef] [Google Scholar]
- Leung AK, Vitali D, Ma L, Zhao R. 2019. Innovations in the centrifuge modelling of energy pile behaviour in unsaturated soil. In: Proceedings of the 16th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering (YMPG11). Southeast Asian Geotechnical Society. [Google Scholar]
- Loveridge F, Powrie W. 2013. Temperature response functions (G-functions) for single pile heat exchangers. Energy 57: 554–564. [CrossRef] [Google Scholar]
- Loveridge F, Powrie W, Nicholson D. 2014. Comparison of two different models for pile thermal response test interpretation. Acta Geotech 9(3): 367–384. [CrossRef] [Google Scholar]
- Maghsoodi S. 2020. Thermo-mechanical behavior of soil-structure interface under monotonic and cyclic loads in the context of energy geostructures. Thèse de doctorat, Université de Lorraine. [Google Scholar]
- Maragna C, Loveridge F. 2018. Interprétation de tests de réponse thermique et dimensionnement de pieux géothermiques. In: JNGG 2018, Marne-La-Vallée, 8 p. [Google Scholar]
- McCartney JS, Murphy KD. 2012. Strain distributions in full-scale energy foundations (DFI Young Professor Paper Competition 2012). DFI Journal-The Journal of the Deep Foundations Institute 6(2): 26–38. [CrossRef] [Google Scholar]
- Mestat P. 2005. CESAR-LCPC. Version standard. Référentiel théorique. Module DTNL. 6e ed. [Google Scholar]
- Mroueh H, Habert J, Rammal D. 2018. Design charts for geothermal piles under various thermo-mechanical conditions. ce/papers 2(2–3): 181–190. [CrossRef] [Google Scholar]
- Nejat P, Jomehzadeh F, Taheri MM, Gohari M, Majid MZA. 2015. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew Sustain Energy Rev 43: 843–862. [CrossRef] [Google Scholar]
- Ng CWW, Gunawan A, Shi C, Ma QJ, Liu HL. 2016. Centrifuge modelling of displacement and replacement energy piles constructed in saturated sand: a comparative study. Geotech Lett 6(1): 34–38. [CrossRef] [Google Scholar]
- Ng CWW, Ma QJ. 2019. Energy pile group subjected to non-symmetrical cyclic thermal loading in centrifuge. Geotech Lett 9(3): 173–177. [CrossRef] [Google Scholar]
- Pahud D. 2002. Geothermal energy and heat storage. SUPSI–DCT–LEEE Laboratorio di Energia, Ecologia ed Economia, pp. 1–133. [Google Scholar]
- Peltier MMV. 2018. Évaluation du potentiel thermique de la ligne de métro M3 de Lausanne (No. STUDENT). [Google Scholar]
- Rotta Loria AF, Laloui L. 2017. The equivalent pier method for energy pile groups. Geotechnique 67(8): 691–702. [CrossRef] [Google Scholar]
- Russo SL, Gnavi L, Roccia E, Taddia G, Verda V. 2014. Groundwater Heat Pump (GWHP) system modeling and Thermal Affected Zone (TAZ) prediction reliability: Influence of temporal variations in flow discharge and injection temperature. Geothermics 51: 103–112. [CrossRef] [Google Scholar]
- Salençon J. 2002. Mécanique des milieux continus – Tome 2 – Thermoélasticité. Éditions de l’École Polytechnique. [Google Scholar]
- Sauvage J de, Benitez BR, Szymkiewicz F, Badinier T. 2020. Group effects in urban shallow geothermal energy. In: E3S Web of Conferences (Vol. 205, p. 05017). EDP Sciences. [Google Scholar]
- Staffell I, Brett D, Brandon N, Hawkes A. 2012. A review of domestic heat pumps. Energy & Environmental Science 5(11): 9291–9306. [CrossRef] [Google Scholar]
- Stewart MA, McCartney JS. 2012. Strain distributions in centrifuge model energy foundations. In: Geocongress 2012: state of the art and practice in geotechnical engineering, pp. 4376–4385. [CrossRef] [Google Scholar]
- Suryatriyastuti ME, Burlon S, Mroueh H. 2016. On the understanding of cyclic interaction mechanisms in an energy pile group. Int J Numer Anal Meth Geomech 40(1): 3–24. [CrossRef] [Google Scholar]
- Vasilescu AR. 2019. Design and execution of energy piles: Validation by in-situ and laboratory experiments. Thèse de doctorat, École centrale de Nantes. [Google Scholar]
Citation de l’article : Thibault Badinier, Iheb Ghandri, Théophile Grappe, Badr Ouzzine, Jean de Sauvage. Géostructures thermiques : verrous scientifiques et moyens d’étude. Rev. Fr. Geotech. 2022, 172, 1.
Liste des tableaux
Caractéristiques thermiques de certains sols (Fromentin et al., 1997)
Thermal characteristics of some soils.
Caractéristiques thermiques et mécaniques des matériaux modélisés.
Thermal and mechanical characteristics of the modelled materials.
Principaux facteurs d’échelle pour la modélisation en centrifugeuse (Garnier et al., 2007).
Main scaling factors for centrifuge modelling.
Liste des figures
 |
Fig. 1 Illustration du double rôle des géostructures thermiques dans le cas d’un projet de métro (soutènements de type parois moulées et tunnel). Illustration of the dual role of energy geostructures in the case of a metro project (diaphragm wall type retaining walls and tunnel). |
| Dans le texte | |
 |
Fig. 2 Diffusion des géostructures énergétiques (a) dans différents pays et (b) depuis 1988. (Di Donna et al., 2020). Diffusion of energy geostuctures (a) in different countries and (b) since 1988. |
| Dans le texte | |
 |
Fig. 3 Schéma de principe récapitulant les mécanismes de transfert de chaleur dans les géostructures thermiques. Schematic diagram summarizing the heat transfer mechanisms in energy geostructures. |
| Dans le texte | |
 |
Fig. 4 Chargements thermiques et mécaniques d’un pieu. Thermal and mechanical loadings of a pile. |
| Dans le texte | |
 |
Fig. 5 Allure du panache thermique observé dans la simulation en éléments finis (CESAR-LCPC) du refroidissement d’un pieu pour Pe = 0 ; Pe = 5,4 et Pe = 10,8. Shape of the thermal plume observed in the finite elements modelling (CESAR-LCPC) of a cooled down pile for Pe = 0; Pe = 5.4 and Pe = 10.8. |
| Dans le texte | |
 |
Fig. 6 Schéma de principe d’une PAC géothermique en mode chauffage. Schematic diagram of a geothermal heat pump in heating mode. |
| Dans le texte | |
 |
Fig. 7 Comparaison des COP annuels d’une PAC aéraulique (gauche) et géothermique (droite) dans les conditions courantes au Royaume-Uni (Staffell et al., 2012). Comparison of annual COP of an air heat pump (left) and a geothermal heat pump (right) in the common conditions in UK. |
| Dans le texte | |
 |
Fig. 8 Abaques de puissances échangées par surface de paroi ou de tunnels en fonction des conditions de sol (Di Donna et al., 2020). Abacus giving the exchanged power per wall or tunnel surface for different soil conditions. |
| Dans le texte | |
 |
Fig. 9 Temps de retour sur investissement en fonction de l’espacement entre les tubes échangeurs dans le cas d’une paroi moulée thermoactive (Adam et Markiewicz, 2009). Time of return on investment as a function of the spacing between heat pipes in the case of an energy diaphragm wall. |
| Dans le texte | |
 |
Fig. 10 Diagramme d’analyse du comportement global en tête d’un pieu géothermique isolé en fonction de la raideur en tête kh (Mroueh et al., 2018). Diagram for the analysis of global head behaviour of an isolated energy pile as a function of the head stiffness kh. |
| Dans le texte | |
 |
Fig. 11 Représentation du groupe de pieux étudié (vue de côté et vue de dessus). Representation of the pile group studied (side and top views). |
| Dans le texte | |
 |
Fig. 12 Répartition de la température dans le modèle (cas 1 à gauche et cas 4 à droite) et température en fonction de la distance à l’axe du pieu 1 dans le sens de l’écoulement. Repartition of temperature in the model (case 1 on left and case 4 on right) and temperature as a function of the distance to the centre of pile 1 along the seepage. |
| Dans le texte | |
 |
Fig. 13 Déformation totale du groupe (cas 1 à gauche et cas 4 à droite) et déplacements verticaux aux coins supérieurs du chevêtre. Total strains of the group (case 1 on left and case 4 on right) and vertical displacements at the corners of the raft. |
| Dans le texte | |
 |
Fig. 14 Contrainte de Tresca le long de la diagonale en surface du chevêtre. Tresca stress along the diagonal of the raft surface. |
| Dans le texte | |
 |
Fig. 15 Schéma de principe du fonctionnement de la centrifugeuse géotechnique. Schematic diagram of principles of a geotechnical centrifuge. |
| Dans le texte | |
 |
Fig. 16 Modèle réduit centrifugé et système géothermique associé. Centrifuge model and associated geothermal system. |
| Dans le texte | |
 |
Fig. 17 Schéma d’instrumentation du modèle réduit centrifugé. Monitoring scheme of the centrifuge model. |
| Dans le texte | |
 |
Fig. 18 Variation des efforts en tête de pieu au cours de cycles thermique sur le modèle réduit centrifugé. Variations of forces on pile heads during the thermal cycles on the centrifuge model. |
| Dans le texte | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.