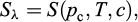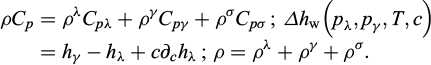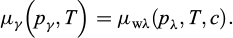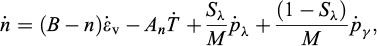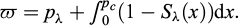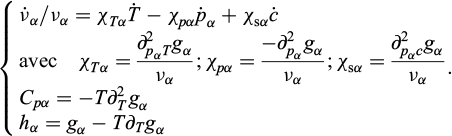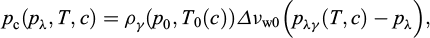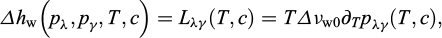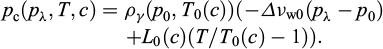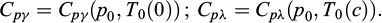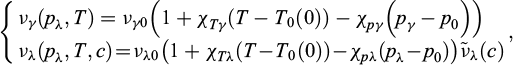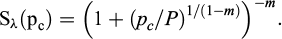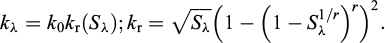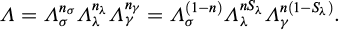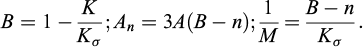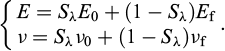© CFMS-CFGI-CFMR-CFG, 2022

1 Introduction

L’exploitation de mines souterraines situées dans des environnements hydro-géologiques difficiles nécessite l’utilisation de techniques innovantes de stabilisation et d’imperméabilisation temporaires des terrains et la mise en œuvre de normes de sécurité élevées que les méthodes conventionnelles de génie minier ne peuvent assurer.

La technique de la congélation artificielle est l’une de ces solutions innovantes puisqu’elle permet à la fois de contrôler l’infiltration des eaux souterraines et de consolider les terrains saturés et instables (Newman et al., 2011). Son utilisation est de plus en plus répandue grâce aux progrès accomplis sur le plan technologique. Sur le plan théorique, l’étude des phénomènes thermiques, hydrauliques, mécaniques et chimiques liés à la congélation des terrains ainsi que leur couplage – synthétisée à la figure 1 – s’affine de plus en plus. Ceci est dû en partie à l’essor des moyens informatiques qui a permis de grandes avancées dans le développement et l’implémentation de modèles multi-physiques couplés, complexes et fortement non-linéaires, tenant compte du changement de phase et de l’évolution des fronts de gel/dégel.

Toutefois, la plupart des études sur la congélation artificielle se concentrent essentiellement sur les aspects thermo-hydrauliques nécessaires à la prédiction de l’étendue des zones congelées et à l’optimisation des systèmes de congélation (Pimentel et al., 2012 ; Marwan et al., 2016 ; Vitel et al., 2016a, 2016b ; Yan et al., 2017 ; Alzoubi et al., 2020). Les effets mécaniques de la congélation sur les ouvrages qui traversent les zones congelées ou situés dans le voisinage sont peu évoqués dans la littérature (Russo et al., 2015 ; Zhou et al., 2021). Pour les étudier, il faudrait modéliser simultanément le comportement mécanique et les transferts de masse et de la chaleur.

C’est ce que nous nous proposons de faire dans cet article en présentant tout d’abord une mise en équation du problème de la congélation artificielle des terrains dans le cadre de la mécanique des milieux poreux, que nous appliquons par la suite au cas de la mine d’uranium de Cigar Lake, au Canada, où la technique de la congélation artificielle est utilisée pour prévenir les venues d’eau dans les ouvrages souterrains, consolider la zone du gisement et les terrains qui l’entourent et réduire le risque d’exposition au radon dissous dans l’eau (Yun et al., 2017). L’objectif est de prédire l’évolution de la congélation et d’évaluer son impact sur un tunnel de production excavé dans la roche du socle, à environ 15 m en dessous du massif congelé. Ces prédictions sont finalement validées par comparaison à des mesures in situ de température dans le massif congelé et de déplacement dans une section du tunnel de production.

Fig. 1 Couplage des phénomènes thermiques, hydrauliques, mécaniques et chimiques lors de la congélation d’un milieu poreux. (Les flèches en tirets correspondent à des phénomènes que nous ne traitons pas dans cet article. Compte tenu de nos connaissances actuelles, leur influence sur la prédiction de l’étendue des zones congelées et la stabilité du terrain reste limitée.). Diagram illustrating coupled Thermal-Hydrological-Mechanical-Chemical processes related to ground freezing. (Dashed lines indicate uncertain processes that are neglected in this paper.)

2 Modèle THMC de la congélation des milieux poreux

Le terrain est assimilé ici à un milieu poreux isotrope constitué d’un squelette solide, désigné par σ, contenant des espaces vides connectés dans lesquels circule une phase liquide λ, formée de deux constituants : l’eau w et le sel s. Lorsque ce milieu est soumis à des conditions de gel, l’eau liquide peut se transformer en glace γ. Même si la glace est solide, elle est traitée comme une phase à part entière, mono-constituant (l’eau w), afin de pouvoir tenir compte des échanges de matière qui peuvent avoir lieu entre elle et la phase liquide λ. Nous admettons aussi que la phase glace se déplace à la même vitesse que la phase solide σ et qu’elle se comporte comme une phase fluide caractérisée par une pression et une température. Cette dernière hypothèse repose sur des observations expérimentales prouvant l’existence d’un film d’eau qui sépare la glace formée du squelette solide (Rempel et al., 2004 ; Wettlaufer et Worster, 2006). Ceci fait que l’état de contrainte dans le cristal de glace formé peut être réduit à un état hydrostatique.

Pour modéliser ce système, nous adoptons une approche macroscopique où les équations de bilan sont obtenues par des processus de changement d’échelle à partir des équations de bilan écrites à l’échelle microscopique (Hassanizadeh et Gray, 1990 ; Quintard et Whitaker, 1994). Par ailleurs, nous supposons que les lois de comportement des phases fluides demeurent inchangées lors du passage d’une configuration microscopique à un état macroscopique (Rouabhi, 2019).

Par ailleurs, nous nous plaçons dans le cadre de l’hypothèse des transformations infinitésimales de la phase solide et nous supposons que l’équilibre thermique local inter-phases s’établit rapidement. En d’autres termes, toutes les phases et tous les constituants ont la même température T localement. Ces deux hypothèses peuvent sembler fortes mais elles sont généralement retenues dans les applications pratiques d’ingénierie civile ou géotechnique.

Dans ce qui suit, n désignera la porosité du milieu poreux, c la concentration massique du sel s dans la phase liquide λ et C_pα la capacité thermique à pression constante de la phase α. Pour chaque phase α = (λ,γ), P_α désigne sa pression, ρ_α sa densité, υ_α  = 1/ρ_α son volume spécifique, n_α sa fraction volumique, ρ_α  = ρ_αn_α sa densité apparente, S_α  = n_α/n son degré de saturation, avec S_λ  + S_γ  = 1 et h_α son enthalpie. Pour la phase σ, n_σ  = 1 – n est sa fraction volumique et ρ_α  = ρ_αn_α sa densité apparente. Pour chaque fonction 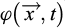$\mathit{\phi }(\overrightarrow{\mathit{x}},\mathit{t})$ attachée au milieu poreux, 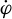$\stackrel{}{\mathit{\phi }}$ désigne sa dérivée temporelle en suivant le mouvement du squelette σ.

2.1 Équations de bilan

La démonstration pour aboutir aux équations de bilan finales gouvernant le comportement THMC du milieu poreux soumis à la congélation est présentée en détail dans (Tounsi, 2019) et ne sera donc pas reprise exhaustivement ici. Tout en tenant compte des hypothèses explicitées ci-dessus, la prise de moyenne volumique des équations de bilan à l’échelle microscopique permet d’aboutir au système (1). Ce dernier comprend le bilan de la masse de la phase glace γ, la somme des bilans de la masse des phases fluides λ et γ, le bilan de la masse du constituant sel s dans la phase liquide λ, l’équation de la chaleur et l’équation de bilan de la quantité de mouvement.

$$\{\begin{array}{c}\hfill {{\displaystyle \stackrel{}{\rho }}}^{\mathit{\gamma }}+{\rho }^{\mathit{\gamma }}{{\displaystyle \stackrel{}{\epsilon }}}_{\text{v}}={{\displaystyle \stackrel{}{\pi }}}^{\mathit{\gamma }}\hfill \\ \hfill {{\displaystyle \stackrel{}{\rho }}}^{\mathit{\lambda }}+{{\displaystyle \stackrel{}{\rho }}}^{\mathit{\gamma }}+\left({\rho }^{\mathit{\lambda }}+{\rho }^{\mathit{\gamma }}\right){{\displaystyle \stackrel{}{\mathit{\epsilon }}}}_{\mathrm{\text{v}}}+{\displaystyle \overrightarrow{\nabla }}.\left({\mathit{\rho }}_{\mathit{\lambda }}{\displaystyle \overrightarrow{V}}\right)=0\hfill \\ \hfill {\rho }^{\mathit{\lambda }}{\displaystyle \stackrel{}{c}}-c{{\displaystyle \stackrel{}{\pi }}}^{\mathit{\gamma }}+{\rho }_{\mathit{\lambda }}{\displaystyle \overrightarrow{V}}.{\displaystyle \overrightarrow{\nabla }}c+{\displaystyle \overrightarrow{\nabla }}.\left({\rho }_{\mathit{\lambda }}{\displaystyle \overrightarrow{J}}\right)=0\hfill \\ \hfill \rho C_p{\displaystyle \stackrel{}{T}}+\Delta h_w{{\displaystyle \stackrel{}{\pi }}}^{\mathit{\gamma }}+{\rho }_{\mathit{\lambda }}{C}_{p\mathit{\lambda }}{\displaystyle \overrightarrow{V}}.{\displaystyle \overrightarrow{\nabla }}c+{\displaystyle \overrightarrow{\nabla }}.{\displaystyle \overrightarrow{\mathit{\psi }}}=0\hfill \\ \hfill {\displaystyle \overrightarrow{\nabla }}.{\displaystyle \underset{\_}{{\displaystyle \underset{\_}{\mathit{\sigma }}}}}+\rho {\displaystyle \overrightarrow{\text{g}}}={\displaystyle \overrightarrow{0}}\hfill \end{array},$$(1)

avec

$$S_{\mathit{\lambda }}=S\left(p_{\text{c}},T,c\right),$$(2)

et

$$\rho C_p={\rho }^{\mathit{\lambda }}{C}_{p\mathit{\lambda }}+{\rho }^{\mathit{\gamma }}{C}_{p\mathit{\gamma }}+{\rho }^{\mathit{\sigma }}{C}_{p\mathit{\sigma }};\Delta h_{\text{w}}\left(p_{\mathit{\lambda }},p_{\mathit{\gamma }},T,c\right)=h_{\mathit{\gamma }}-h_{\mathit{\lambda }}+c{\partial }_c{h}_{\mathit{\lambda }};\rho ={\rho }^{\mathit{\lambda }}+{\rho }^{\mathit{\gamma }}+{\rho }^{\mathit{\sigma }}.$$

Le bilan de la quantité de mouvement aux interfaces liquide/glace est représenté par l’équation (2) exprimant le degré de saturation S_λ comme fonction empirique de la pression capillaire p_c  = p_γ  – p_λ , de la température T et de la concentration c.

Le terme de couplage hydromécanique dans les deux premières équations de bilan de la masse est proportionnel à la vitesse de déformation volumique, où ${\mathit{\epsilon }}_{\mathit{\nu }}=\mathrm{t}\mathrm{r}(\epsilon \underset{\_}{\underset{}{\mathit{}}})$ est la composante volumique du tenseur de déformation linéarisé $\mathrm{t}\mathrm{r}\left(\underset{}{\underset{\_}{\mathit{\epsilon }}}\right)=\left(\underset{\_}{\underset{\_}{\nabla }}\overrightarrow{\mathit{u}}+{}^{\mathrm{t}}\underset{\_}{\underset{\_}{\nabla }}\overrightarrow{\mathit{u}}\right)/2$ qui représente la partie symétrique du tenseur gradient de déplacement $\overrightarrow{\mathit{u}}$.

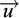À l’issue de cette étape, et en supposant que ρ_σ et C_ρσ sont des constantes, nous avons produit 4 équations scalaires et une équation vectorielle et introduit 11 inconnues scalaires : T, c, p_λ , p_γ , n, ρ_λ , ρ_γ , C_pλ , C_pγ , ∆h_w et ${\stackrel{}{\mathit{\pi }}}^{\mathit{\gamma }}$, 4 inconnues de type vecteur : $\overrightarrow{\mathit{u}},\overrightarrow{\mathit{V}},\overrightarrow{\mathit{J}}\mathrm{e}\mathrm{t}\overrightarrow{\mathit{\psi }}$ 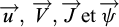et une inconnue de type tenseur 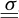$\underset{\_}{\underset{\_}{\mathit{\sigma }}}$ Ceci fait un total de 7 équations et 29 inconnues.

2.2 Lois de comportement

Pour compléter le système d’équations de bilan, on introduit d’abord 3 équations vectorielles complémentaires, respectivement la loi de Darcy pour exprimer la vitesse de filtration de la phase liquide dans le milieux poreux 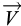$\overrightarrow{\mathit{V}}$, la loi de Fick pour la diffusion du constituant sel dans la phase liquide 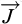$\overrightarrow{\mathit{J}}$ et la loi de Fourrier pour le vecteur densité surfacique du taux de chaleur échangée par conduction 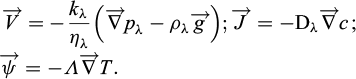$\overrightarrow{\mathit{\psi }}$ :$${\displaystyle \overrightarrow{V}}=-\frac{k_{\mathit{\lambda }}}{{\eta }_{\mathit{\lambda }}}\left({\displaystyle \overrightarrow{\nabla }}{p}_{\mathit{\lambda }}-{\rho }_{\mathit{\lambda }}{\displaystyle \overrightarrow{g}}\right);{\displaystyle \overrightarrow{J}}=-{\text{D}}_{\mathit{\lambda }}{\displaystyle \overrightarrow{\nabla }}c;{\displaystyle \overrightarrow{\mathit{\psi }}}=-\Lambda {\displaystyle \overrightarrow{\nabla }}T.$$(3)

Le terme 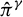${\stackrel{}{\mathit{\pi }}}^{\mathit{\gamma }}$, correspond à la masse d’eau échangée lors d’un changement de phase eau liquide-glace. Pour le déterminer, il est souvent admis que l’équilibre chimique macroscopique entre les deux phases est atteint instantanément, ce qui se traduit par l’égalité des potentiels chimiques du constituant w dans les phases λ et γ.

$${\mu }_{\mathit{\gamma }}\left(p_{\mathit{\gamma }},T\right)={\mu }_{\text{w}\mathit{\lambda }}\left(p_{\mathit{\lambda }},T,c\right).$$(4)

La glace étant une phase pure, son potentiel chimique μ_γ est indépendant de la concentration c et égal à son enthalpie libre g_γ . Le potentiel chimique de l’eau en phase λ est μ_wλ = g_λ − c ∂ _c g_λ. Le développement de l’égalité 4 est présenté en détail dans des travaux antérieurs que ce soit pour un milieu poreux saturé en eau pure (Vitel, 2015) ou en saumure (Rouabhi et Tijani, 2017 ; Tounsi, 2019), entraînant l’égalité suivante :

$$\forall \left(p_{\mathit{\lambda }},p_{\mathit{\gamma }},T,c\right):{\displaystyle \underset{p_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)}{\overset{p_{\mathit{\gamma }}}{{\displaystyle \int }}}}{\nu }_{\mathit{\gamma }}\left(x,T\right)={\displaystyle \underset{p_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)}{\overset{p_{\mathit{\lambda }}}{{\displaystyle \int }}}}{\nu }_{\mathit{\lambda }}-c{\partial }_c{\nu }_{\mathit{\lambda }}\left(x,T,c\right)\text{d}x,$$(5)

où p_λγ (T, c) est la pression de coexistence des deux phases λ et γ.

L’équation scalaire (Éq. (6)) et l’équation tensorielle (Éq. (7)) décrivent, respectivement, l’évolution de la porosité n et le modèle de comportement du squelette reliant, sous forme incrémentale, le tenseur de contraintes totales $\underset{\_}{\underset{\_}{\mathit{\sigma }}}$ et la pression de pore équivalente $\stackrel{}{\mathit{\varpi }}$ au tenseur de déformations totales ε: $\underset{\_}{\underset{\_}{\mathit{}}}$

$${\displaystyle \stackrel{}{n}}=\left(B-n\right){{\displaystyle \stackrel{}{\mathit{\epsilon }}}}_{\text{v}}-A_n{\displaystyle \stackrel{}{T}}+\frac{S_{\mathit{\lambda }}}{M}{{\displaystyle \stackrel{}{p}}}_{\mathit{\lambda }}+\frac{\left(1-S_{\mathit{\lambda }}\right)}{M}{{\displaystyle \stackrel{}{p}}}_{\mathit{\gamma }},$$(6) $$\stackrel{}{\underset{}{\underset{}{\mathit{}}}}+\mathit{B}\stackrel{}{\mathit{\varpi }}\underset{}{\underset{}{1}}=\stackrel{}{\mathit{H}}:(\underset{}{\underset{}{\stackrel{}{\mathit{\epsilon }}}}-\mathit{A}\stackrel{}{\mathit{T}}\underset{}{\underset{}{1}}),$$(7)

with

$$\mathit{\varpi }=p_{\mathit{\lambda }}+{\int }_0^{{\mathit{p}}_{\mathit{c}}}\left(1-S_{\mathit{\lambda }}\left(x\right)\right)\text{d}x.$$(8)

Enfin, en rajoutant le système (9) permettant d’aboutir aux 5 lois d’état reliant ν_λ, ν_γ, C_pλ, C_pγ et la chaleur latente de changement de phase 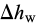${\mathrm{\Delta }\mathit{h}}_{\mathrm{w}}$, à l’état thermodynamique décrit par (p_α, T, c) à partir de l’enthalpie libre massique g_α (p_α, T, c), le nombre d’équations égalisera le nombre d’inconnues.

$$\{\begin{array}{c}\hfill {{\displaystyle \stackrel{}{\mathit{\nu }}}}_{\mathit{\alpha }}/{\mathit{\nu }}_{\mathit{\alpha }}={\chi }_{T\mathit{\alpha }}{\displaystyle \stackrel{}{T}}-{\chi }_{p\mathit{\alpha }}{{\displaystyle \stackrel{}{p}}}_{\mathit{\alpha }}+{\chi }_{\text{s}\mathit{\alpha }}{\displaystyle \stackrel{}{c}}\hfill \\ \hfill \mathrm{a}\mathrm{v}\mathrm{e}\mathrm{c}{\chi }_{T\mathit{\alpha }}=\frac{{\partial }_{p_{\mathit{\alpha }}T}^2{g}_{\mathit{\alpha }}}{{\mathit{\nu }}_{\mathit{\alpha }}};{\chi }_{p\mathit{\alpha }}=\frac{-{\partial }_{p_{\mathit{\alpha }}}^2{g}_{\mathit{\alpha }}}{{\mathit{\nu }}_{\mathit{\alpha }}};{\chi }_{\text{s}\mathit{\alpha }}=\frac{{\partial }_{p_{\mathit{\alpha }}c}^2{g}_{\mathit{\alpha }}}{{\mathit{\nu }}_{\mathit{\alpha }}}\hfill \\ \hfill C_{p\mathit{\alpha }}=-T{\partial }_{T^{\mathrm{}}}^2{\mathit{g}}_{\mathit{\alpha }}\hfill \\ \hfill h_{\mathit{\alpha }}={\mathit{g}}_{\mathit{\alpha }}-T{\partial }_T{g}_{\mathit{\alpha }}\hfill \end{array}\mathrm{.}$$(9)

Dans les deux sections suivantes, nous allons exprimer les deux fonctions de changement de phase p_c et Δh_w ainsi que les coefficients et les fonctions empiriques qui interviennent dans les équations de bilan et dans les différentes lois de comportement.

2.4 Thermodynamique de changement de phase

Il est important de noter que les fonctions de Gibbs g_α représentant le comportement réel de l’eau pure (Wagner et Pruß, 2002), de la saumure (Archer et Carter, 2000) et de la glace ordinaire Ih (Feistel et Wagner, 2006) couvrent des gammes de température, de pression et de concentration très larges. Leurs formulations mathématiques sont donc complexes et difficiles à implémenter et à manipuler (calcul de dérivées) dans des codes de calcul. Leur utilisation pour exprimer les lois d’état entraînerait une augmentation considérable des temps de calcul pour un gain en précision modeste non justifié pour des applications de géotechnique. Ainsi, des hypothèses sont introduites pour simplifier le formalisme sans pour autant affecter sa fiabilité et sa précision.

Nous utilisons d’abord la condition d’équilibre chimique (Éq. (5)) dans laquelle nous admettons que les volumes spécifiques ν_α sont indépendants des pressions p_α et de la température T. Il en vient les expressions suivantes de la pression capillaire p_c et de la chaleur latente Δh_w (Rouabhi et Tijani, 2017 ; Tounsi, 2019) :

$$p_{\text{c}}\left(p_{\mathit{\lambda }},T,c\right)={\rho }_{\mathit{\gamma }}\left(p_0,T_0\left(c\right)\right)\Delta {\mathit{\nu }}_{\text{w}0}\left(p_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)-p_{\mathit{\lambda }}\right),$$(10) $$\Delta {\mathit{h}}_{\text{w}}\left(p_{\mathit{\lambda }},p_{\mathit{\gamma }},T,c\right)=L_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)=T\Delta {\mathit{\nu }}_{\text{w}0}{\partial }_T{p}_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right),$$(11)

avec (p₀, T₀ (c)) un état de référence commun aux deux phases, 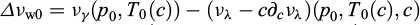$\Delta {\mathit{\nu }}_{\text{w}0}={\mathit{\nu }}_{\mathit{\gamma }}\left(p_0,T_0\left(c\right)\right)-\left({\mathit{\nu }}_{\mathit{\lambda }}-c{\partial }_c{\mathit{\nu }}_{\mathit{\lambda }}\right)\left(p_0,T_0\left(c\right),c\right)$ et $L_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)=\Delta h_{\text{w}}\left(p_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right),p_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right),T,c\right)$ la chaleur latente de passage de λ à γ pour un état d’équilibre chimique tel que p_λ = p_γ = p_λγ (T, c).

Par ailleurs, il a été démontré dans (Rouabhi et Tijani, 2017) que la courbe de coexistence p_λγ (T, c) et la courbe de la chaleur latente L_λγ (T, c) peuvent être approchées par des fonctions linéaires de la température :

$$p_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)=p_0+p_{\mathit{\lambda }\mathit{\gamma }}^{\text{'}}\left(c\right)\left(T-T_0\left(c\right)\right),$$(12) $$\Delta h_{\text{w}}\left(p_{\mathit{\lambda }},p_{\mathit{\gamma }},T,c\right)=L_{\mathit{\lambda }\mathit{\gamma }}\left(T,c\right)=L_0\left(c\right)+L_0^{\text{'}}\left(c\right)\left(T-T_0\left(c\right)\right),$$(13)

avec $L_0\left(c\right)=T_0\left(c\right)\Delta {\mathit{\nu }}_{\text{w}0}{p}_{\mathit{\lambda }\mathit{\gamma }}^{\text{'}}\left(c\right)$.

Ceci permet de réécrire la pression capillaire comme suit :

$$p_{\text{c}}\left(p_{\mathit{\lambda }},T,c\right)={\rho }_{\mathit{\gamma }}\left(p_0,T_0\left(c\right)\right)\left(-\Delta {\mathit{\nu }}_{\text{w}0}\left(p_{\mathit{\lambda }}-p_0\right)+L_0\left(c\right)\left(T/T_0\left(c\right)-1\right)\right).$$(14)

Notons que, dans la littérature, l’effet de la pression p_λ est souvent négligé dans l’expression de la pression capillaire, ce qui revient à considérer la température de coexistence T_λγ – la fonction réciproque de p_λγ  – comme une fonction de la concentration c uniquement. Cette simplification n’est pas valable pour des valeurs de p_λ élevées et peut entraîner une sous-estimation de l’amplitude des pressions de pore et, par conséquent, une sous-estimation des déformations induites par la congélation du milieu poreux (Tounsi et al., 2020). L’équation (14) a été donc retenue.

La dernière hypothèse simplificatrice concerne les C_pα qui sont considérées comme des fonctions de c uniquement, évaluées à l’état de référence (p₀,T₀(c)).

$$C_{p\mathit{\gamma }}=C_{p\mathit{\gamma }}\left(p_0,T_0\left(0\right)\right);C_{p\mathit{\lambda }}=C_{p\mathit{\lambda }}\left(p_0,T_0\left(c\right)\right).$$(15)

L’hypothèse qui consiste à considérer les volumes spécifiques comme étant indépendants de la pression est forte vu qu’elle annule des termes transitoires dus au couplage hydro-mécanique au niveau des équations de bilan de la masse. Par conséquent, on distingue dans ce formalisme les hypothèses menant aux expressions de p_c et Δh_w, de celles utilisées dans les équations de bilan, au détriment de la cohérence globale du modèle. Toutefois, cette incohérence n’est pas inquiétante si on garde à l’esprit que la pression capillaire n’intervient finalement que dans la fonction du degré de saturation liquide S_λ qui est empirique, et que le terme de la chaleur latente dans l’équation de la chaleur est multiplié par 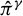${\stackrel{}{\mathit{\pi }}}^{\mathit{\gamma }}$ qui représente la masse d’eau échangée par changement de phase et dont la cinétique chimique est exprimée par un modèle empirique.

Ainsi, dans les équations de bilan, les fonctions C_pα sont maintenues indépendantes de la pression et de la température. Quant aux fonctions ν_α , une approximation d’ordre 1 par rapport à la température et à la pression est considérée :

$$\{\begin{array}{c}\hfill {\nu }_{\mathit{\gamma }}\left(p_{\mathit{\lambda }},T\right)={\mathit{\nu }}_{\mathit{\gamma }0}\left(1+{\chi }_{T\mathit{\gamma }}\left(T-T_0\left(0\right)\right)-{\chi }_{p\mathit{\gamma }}\left(p_{\mathit{\gamma }}-p_0\right)\right)\hfill \\ \hfill {\mathit{\nu }}_{\mathit{\lambda }}\left(p_{\mathit{\lambda }},T,c\right)={\mathit{\nu }}_{\mathit{\lambda }0}\left(1+{\chi }_{T\mathit{\lambda }}\left(T-T_0\left(0\right)\right)-{\chi }_{p\mathit{\lambda }}\left(p_{\mathit{\lambda }}-p_0\right)\right){{\displaystyle \stackrel{}{\mathit{\nu }}}}_{\mathit{\lambda }}\left(c\right)\hfill \end{array},$$(16)

avec ν_γ0 = ν_γ (p₀, T₀ (0)) et ν_λ0 = ν_λ (p₀, T₀ (0) , 0).

Pour déterminer 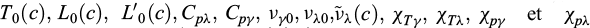${\mathit{T}}_0\left(\mathit{c}\right),{\mathit{L}}_0\left(\mathit{c}\right),{{\mathit{L}}^{\prime }}_0\left(\mathit{c}\right),{\mathit{C}}_{\mathit{p}\mathit{\lambda }},{\mathit{C}}_{\mathit{p}\mathit{\gamma }},{\mathit{\nu }}_{\mathit{\gamma }0},{\mathit{\nu }}_{\mathit{\lambda }0},{\stackrel{}{\mathit{\nu }}}_{\mathit{\lambda }}\left(\mathit{c}\right),{\mathit{\chi }}_{\mathit{T}\mathit{\gamma }},{\mathit{\chi }}_{\mathit{T}\mathit{\lambda }},{\mathit{\chi }}_{\mathit{p}\mathit{\gamma }}\mathrm{e}\mathrm{t}{\mathit{\chi }}_{\mathit{p}\mathit{\lambda }}$ nous procédons par minimisation, avec la méthode des moindres carrés, des écarts par rapport aux fonctions complètes déduites des potentiels thermodynamiques fournis par (Archer et Carter, 2000 ; Wagner et Pruß, 2002 ; Feistel et Wagner, 2006).

2.5 Modèles empiriques

La fonction du degré de saturation joue un rôle central dans cette modélisation puisqu’elle permet de suivre les interfaces liquide/glace. Elle est égale à 1 lorsque les pores sont saturés en phase liquide et inférieure à 1 lorsque la phase glace est présente. Il existe deux approches pour la déterminer : l’approche empirique faisant appel à des techniques de mesure de la teneur en eau liquide qui sont généralement délicates et onéreuses, et l’approche se basant sur une analogie entre les mécanismes de gel/dégel et les mécanismes de séchage/mouillage qui préconise l’utilisation des modèles de courbe de rétention pour les sols non saturés. Nous adoptons la deuxième approche et nous utilisons pour exprimer la fonction du degré de saturation le modèle de rétention d’eau de van Genuchten à deux paramètres m et P :

$${\text{S}}_{\mathit{\lambda }}\left({\text{p}}_{\text{c}}\right)={\left(1+{\left(p_c/P\right)}^{1/\left(1-m\right)}\right)}^{-m}.$$(17)

Ce modèle est largement utilisé dans la communauté scientifique pour des problématiques de congélation de terrain même dans le cas où la phase λ est une solution aqueuse (Nishimura et al., 2009 ; Rouabhi et Tijani, 2017). L’effet de la salinité sur cette fonction est implicite via la pression capillaire.

La perméabilité k_λ est aussi un paramètre clé dans la modélisation de la congélation des milieux poreux. En effet, elle doit nous permettre de tenir compte de l’effet bloquant de la formation de la glace sur les écoulements de la phase liquide. À cet effet, elle est exprimée comme le produit d’une perméabilité intrinsèque du milieu poreux (notée k₀), indépendante du type du fluide qui y circule, et d’une perméabilité relative k_r qui varie en fonction du degré de saturation de la phase liquide. Pour exprimer la perméabilité relative, le modèle empirique de van Genuchten (Mualem, 1978) à un seul paramètre r est utilisé. L’effet de la présence de solutés est pris en compte implicitement via S_λ .

$$k_{\mathit{\lambda }}=k_0{k}_{\text{r}}\left(S_{\mathit{\lambda }}\right);k_{\text{r}}=\sqrt{S_{\mathit{\lambda }}}{\left(1-{\left(1-S_{\mathit{\lambda }}^{1/r}\right)}^r\right)}^2.$$(18)

Le paramètre r est considéré égal à m de la fonction S_λ .

La diffusivité D_λ dépend généralement de plusieurs facteurs en plus de la température et du degré de saturation, à savoir la porosité et les fluides dans les pores. Toutefois, pour l’application que nous étudions, nous la considérons constante.

En ce qui concerne la conductivité thermique, nous l’exprimons par une moyenne géométrique des conductivités thermiques des trois phases pondérée par leurs fractions volumiques :

$$\Lambda ={\Lambda }_{\mathit{\sigma }}^{n_{\mathit{\sigma }}}{\Lambda }_{\mathit{\lambda }}^{n_{\mathit{\lambda }}}{\Lambda }_{\mathit{\gamma }}^{n_{\mathit{\gamma }}}={\Lambda }_{\mathit{\sigma }}^{\left(1-n\right)}{\Lambda }_{\mathit{\lambda }}^{n{S}_{\mathit{\lambda }}}{\Lambda }_{\mathit{\gamma }}^{n\left(1-S_{\mathit{\lambda }}\right)}.$$(19)

L’équation (20) donne les relations entre les caractéristiques de la matrice solide (le module de compressibilité K_σ ), la porosité n et les paramètres drainés du squelette (le module de compressibilité K et la dilatation thermique A) utilisés classiquement dans la théorie de la poromécanique au sens de (Coussy, 2004).

$$B=1-\frac{K}{K_{\mathit{\sigma }}};A_n=3A\left(B-n\right);\frac{1}{M}=\frac{B-n}{K_{\mathit{\sigma }}}.$$(20)

Finalement, on notera, que dans le formalisme présenté, la glace a été considérée comme une phase fluide afin de pouvoir tenir compte des échanges de matière entre elle et la phase liquide. Cette hypothèse, qu’on peut qualifier de microscopique, a surtout permis l’établissement des expressions de la pression capillaire et de la chaleur latente en tant que fonctions de la température, de la pression de la phase fluide et de la concentration. Toutefois, d’un point de vue mécanique, elle n’est pas sans conséquences. Si le modèle de comportement mécanique utilisé est élastique linéaire, cette hypothèse implique que la présence de la glace ne modifiera que la composante sphérique de la contrainte mécanique à travers la pression p_γ intervenant dans l’expression de la contrainte effective, et qu’un chargement de type déviatorique sera repris uniquement par le squelette solide. Ceci serait en désaccord avec l’augmentation de résistance et de rigidité macroscopiques des géomatériaux en basses températures, au-dessous de la température de congélation du fluide saturant les pores, observée dans les essais de laboratoire. Pour cette raison, nous distinguons dans notre approche les hypothèses microscopiques des hypothèses macroscopiques, au détriment de la cohérence globale du modèle, et nous complétons le formalisme avec le système (21) proposant d’utiliser pour les modules d’élasticité une moyenne pondérée par S_λ des modules d’élasticité du matériau non congelé (E₀;ν₀) et du même matériau complètement congelé (E_f;ν_f).

$$\{\begin{array}{c}\hfill E=S_{\mathit{\lambda }}{E}_0+\left(1-S_{\mathit{\lambda }}\right)E_{\text{f}}\hfill \\ \hfill \mathit{\nu }=S_{\mathit{\lambda }}{\mathit{\nu }}_0+\left(1-S_{\mathit{\lambda }}\right){\mathit{\nu }}_{\text{f}}\hfill \end{array}.$$(21)

3 Application à la mine de Cigar Lake

3.1 Contexte géologique et hydrogéologique

Le gisement d’uranium de Cigar Lake est le deuxième gisement à plus forte teneur en uranium au monde. Il est situé dans des conditions géologiques et hydrogéologiques difficiles qui rendent son exploitation délicate. Comme le montre la figure 2, la couche minéralisée repose entre 410 et 450 m de profondeur au niveau de la discordance entre les grès d’Athabasca et le socle composé de roches métamorphiques de type métapélite. Elle a la forme d’une lentille horizontale orientée est-ouest et mesurant approximativement 1950 m de long, entre 20 et 100 m de large et 5,4 m d’épaisseur en moyenne (Fig. 3). Un halo d’altération argileux entoure le gisement. Il peut atteindre jusqu’à 200 m au-dessus de la minéralisation et plusieurs dizaines de mètres en dessous, conférant au terrain une forte hétérogénéité.

D’un point de vue hydrogéologique, la nappe d’eau est située à quelques mètres sous la surface et toutes les formations géologiques sont saturées. La pression hydrostatique peut donc atteindre 4,5 MPa au niveau de la minéralisation.

Fig. 2 Coupe schématique du gisement de Cigar Lake, modifiée d’après (Bishop et al., 2012). Cross-section of the mine of Cigar Lake, adapted from (Bishop et al., 2012).

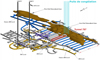Fig. 3 Plan 3D de la mine de Cigar Lake, modifié d’après (Bishop et al., 2016). 3D plan of the mine of Cigar lake, adapted from (Bishop et al., 2016).

3.2 La congélation artificielle dans la mine de Cigar Lake

Dans la mine de Cigar Lake, l’objectif est de congeler la zone minéralisée et les couches altérées environnantes, en dessous et au-dessus du gisement, avant le démarrage de l’exploitation. Le système de congélation utilisé comprend une unité de congélation à l’ammoniac, installée en surface, qui refroidit une saumure de chlorure de calcium à une température consigne d’environ −30 °C. La saumure circule, selon un circuit fermé, dans un réseau de puits verticaux allant de la surface jusqu’à 465 m de profondeur, i.e., environ 15 m en dessous du gisement.

Bien que la congélation ait permis de prévenir les venues d’eau dans les ouvrages souterrains et de consolider les zones autour du gisement, elle est néanmoins responsable de mouvements de convergence dans les tunnels de production même s’ils sont excavés à 480 m de profondeur, i.e., 15 m en dessous de la zone congelée. La forte corrélation entre la congélation du massif et les mouvements de convergence a été démontrée grâce à une rétro-analyse des mesures de déplacement prises dans différentes sections d’un tunnel de production (le tunnel 797 entouré d’un trait rouge dans la Fig. 3). La figure 4 montre le déplacement vertical mesuré par des capteurs de déplacement installés au niveau de deux sections, une est à l’abri de la congélation et l’autre est excavée sous une grille de puits de congélation activés au moins deux mois avant l’excavation de cette section. L’origine du repère correspond au début de l’excavation de la section. Sachant que la durée d’excavation du tunnel tout entier est d’environ 250 jours, on note qu’après cette durée les déplacements de la section qui est à l’abri de la congélation tendent à se stabiliser alors que ceux de la section exposée à la congélation continuent d’augmenter suivant une pente quasi-constante jusqu’à 450 jours.

Si la corrélation entre la congélation et les déplacements mesurés au niveau des tunnels de production peut être démontrée qualitativement au niveau de plusieurs sections, la quantification de l’amplitude des déformations dues à la congélation uniquement est difficile à cause des opérations d’excavation et d’exploitation minière qui se produisent simultanément avec la congélation en plus des déformations différées dans le temps tels le fluage des géomatériaux et la consolidation hydraulique.

Fig. 4 Déplacements verticaux mesurés dans deux sections d’un tunnel de production (cercles vides pour la section qui est non exposée à la congélation et cercles pleins pour la section exposée à la congélation). Pour ne pas encombrer la figure, uniquement les valeurs mesurées par les capteurs de la moitié droite de la section sont représentées. Comparison between vertical displacements (negative indicates settlement) recorded in a section that is exposed to freezing (solid circles) and vertical displacements recorded in a section that is not exposed to freezing (empty circles). To avoid overlap, only data retrieved from targets 1, 3, 5 and 7 are plotted.

3.3 Simulation de l’excavation d’un ouvrage sous un massif soumis à la congélation

Dans cette section, nous présentons les résultats de la simulation numérique de l’excavation d’un tunnel de production sous un massif soumis à la congélation. L’objectif est d’évaluer les capacités prédictives de notre modèle mathématique à travers la comparaison des températures et des déplacements obtenus numériquement aux mesures de terrain. Pour ce faire, une section du tunnel 797 (section 26), permettant d’isoler le mieux possible l’impact de la congélation, et ce sur une longue durée, a été sélectionnée. L’analyse chimique de l’eau interstitielle dans la zone avoisinant cette section a montré qu’elle est pure. La salinité du fluide saturant est donc négligée dans cette partie. Par ailleurs, nous ne nous intéressons pas dans ces simulations à la phase d’exploitation du minerai mais aux phases antérieures d’excavation de tunnels de production et de congélation. Par conséquent, l’hypothèse de l’élasticité est admise vu qu’aucun ouvrage n’est excavé dans le massif congelé.

Le code de calcul utilisé est COMSOL Multiphysique. On suppose que les terrains hétérogènes peuvent être représentés par une superposition de couches horizontales. La première étape est de déterminer les propriétés de ces couches permettant d’ajuster au mieux les résultats obtenus numériquement. Les modules élastiques aux états congelé et non congelé sont estimés à partir d’essais de compression mécanique à température contrôlée. Les perméabilités sont obtenues à partir de modèles hydrogéologiques de la mine et les porosités et les conductivités thermiques à partir d’anciens modèles thermo-hydrauliques de la mine (Vitel, 2015). Quant aux paramètres empiriques m et P de la fonction du degré de saturation liquide S_λ , nous les déterminons par un calage de la réponse du modèle sur des mesures in situ.

Les mesures de température utilisées pour l’ajustement correspondent au forage vertical de mesure de température le plus proche de la section étudiée afin de réduire l’impact de l’hétérogénéité du terrain (voir Fig. 5). Ce forage dispose de 8 thermocouples placés à différentes profondeurs entre −460 m et −390 m. Comme l’objectif ici est de prédire l’étendue de la zone congelée, nous nous sommes contentées de calculs Thermo-Hydrauliques (TH) sur une géométrie (voir Fig. 6) qui reprend la grille des tubes de congélation situés autour du forage de mesure à l’intérieur d’un périmètre d’un rayon de 15 m, délimité dans la figure 5. Ce rayon a été déterminé sur la base d’une analyse paramétrique qui a montré que les puits de congélation plus éloignés avaient un effet insignifiant sur la distribution de la température près du puits de mesure. Au total, on compte 27 puits cylindriques de rayon R_p et de hauteur L_p.

Initialement, la température est de 6 °C et la pression égale à la pression hydrostatique. Comme conditions aux limites aux parois des puits de congélation, nous utilisons la loi de Newton qui exprime que le flux $\overrightarrow{\mathit{\psi }}$ normal à la paroi est proportionnel à l’écart entre la température à la paroi et la température moyenne du réfrigérant T_c via un coefficient H_c de transfert de chaleur par convection :

$${\displaystyle \overrightarrow{\psi }}.{\displaystyle \overrightarrow{n}}=H_{\text{c}}\left(T-T_{\text{c}}\right),$$(22)

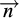avec ${\displaystyle \overrightarrow{n}}$ le vecteur unitaire normal à la paroi.

Comme les puits de congélation ne sont pas activés simultanément, l’historique de leur activation est donné dans la figure 7. Les paramètres numériques sont précisés dans le tableau 1 et les propriétés des couches géologiques sont données dans le tableau 2, y compris les valeurs ajustées m et P de la fonction du degré de saturation liquide. Ce jeu de paramètres a permis de reproduire correctement les mesures de température au court et au long terme, comme l’illustrent les deux exemples d’ajustement donnés par la figure 8.

Maintenant que nous disposons d’un jeu de paramètres nous permettant de reproduire le chargement thermo-hydraulique responsable d’une grande partie des déplacements dans le terrain, nous pouvons procéder au calcul THM et inclure l’ouvrage souterrain dans la géométrie. Rappelons que pour simuler proprement la propagation radiale de la température, la taille caractéristique dans le maillage doit être définie par rapport au rayon du puits de congélation ce qui augmente considérablement le nombre d’éléments et le temps de calcul. Ainsi, pour pouvoir résoudre le problème THM dans des délais raisonnables adaptés aux enjeux de l’ingénierie, nous avons simplifié la géométrie en supposant que la grille des puits de congélation est régulière avec un espacement de 6 m, qui est l’espacement moyen in situ, et que le tunnel et la grille sont infinis dans la direction d’excavation du tunnel. Le bloc bleu affiché dans la figure 9 représente la nouvelle géométrie simplifiée. Il comprend une seule rangée de puits de congélation et une épaisseur égale à la moitié de l’espacement entre les puits, i.e., 3 m.

Dans une simulation THM, nous partons d’un terrain initialement non congelé et non déformé, la congélation est d’abord activée, puis, après 150 jours, l’excavation de la section du tunnel est simulée. Pour ce faire, un taux de relâchement des contraintes de 60 % est appliqué à la paroi du tunnel et la pression, initialement égale à la pression hydrostatique, est annulée. Ce taux a été déterminé à travers l’ajustement de mesures de déplacement au niveau de sections qui sont à l’abri de la congélation. Les autres conditions aux limites sont données dans la figure 9.

La figure 10 montre les résultats de la simulation numérique à 700 jours dans une coupe verticale pour des profondeurs supérieures à 380 m. La distribution de la température (Fig. 10a), montre que la progression de la congélation varie avec la profondeur, même après 700 jours de congélation. Nous n’aurions pas obtenu cette distribution si l’hétérogénéité du terrain, à savoir la variabilité spatiale de la porosité, de la conductivité thermique et de la fonction du degré de saturation liquide, n’avaient pas été correctement prises en compte. La variabilité spatiale de la perméabilité, quant à elle, influence considérablement la distribution de la pression de pore équivalente donnée par la (Fig. 10b). Les surpressions de pore sont générées suite à la transformation graduelle de l’eau interstitielle en glace et elles sont plus élevées pour une perméabilité faible entravant l’expulsion d’eau liquide vers les zones encore non gelées.

La distribution des vecteurs de déplacement (Fig. 10b) montre l’existence d’une zone neutre où les déplacements sont presque nuls. Au-dessus de cette zone, les déplacements sont dirigés vers le haut, et en dessous, on observe principalement un tassement du terrain dont l’amplitude diminue avec la profondeur. L’emplacement de cette zone neutre et l’amplitude des déplacements dépendent fortement de la distribution des pressions de pore.

Pour vérifier la fiabilité des prédictions du modèle THM, nous comparons dans la figure 11 les déplacements verticaux simulés à ceux mesurés par les capteurs 1 et 3 de la section 26. Le bon accord obtenu entre eux confirme que la prise en compte des phénomènes thermo-hydro-mécaniques associés à la congélation des terrains permet de donner, à elle seule, une bonne estimation des mesures de déplacement dans un ouvrage situé dans le voisinage. Par ailleurs, si on compare ces courbes de déplacement aux courbes de température dans la figure 8, on constatera que les changements de pente de la courbe de déplacement à 250 jours, à 500 jours et à 700 jours coïncident à peu près avec les changements de pente au niveau des courbes de température. La pente la plus raide au niveau de la courbe de déplacement correspond à la phase de solidification de l’eau interstitielle, et la pente la plus faible à une phase de stabilisation de la température dans le massif congelé.

Nous pouvons donc tirer trois conclusions pratiques de cette simulation THM. La première est l’importance de la prise en compte appropriée de l’hétérogénéité des terrains pour éviter les risques liés à la présence de terrains défavorables à la formation de la barrière congelée et pour prédire de manière fiable l’avancement de la congélation et la distribution des pressions de pore et des déplacements dans le terrain et autour des ouvrages avoisinants. La deuxième est la nécessité de considérer le couplage avec la mécanique même lorsque l’ouvrage ne traverse pas la zone congelée. La troisième est l’importance d’attendre la stabilisation de la température dans le massif congelé pour commencer l’excavation des ouvrages à proximité. Ceci permettra de limiter l’influence du gel sur ces ouvrages.

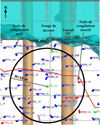Fig. 5 Vue du dessus du réseau de puits de congélation à proximité du forage ST791_21. La couleur blanche indique que le massif est congelé à cet endroit. Layout of the freeze boreholes in the vicinity of borehole ST791_21 and soil freezing state (white indicates frozen and blue indicates nonfrozen).

Fig. 6 Maillage utilisé dans les simulations TH. Mesh used in the 3D TH model. (a) 3D view (b) Zoom of an horizontal cross-section of the 3D mesh (radial around the pipes and triangular outside).

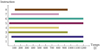Fig. 7 Historique de l’activation des puits de congélation dans la figure 6b. The duration of active freezing for the simulated pipes in Figure 6b.

Fig. 8 Comparaison entre les températures mesurées et simulées à deux profondeurs autour du gisement. Comparison between measured and calculated temperatures at two depths around the ore deposit.

Fig. 9 Géométrie simplifiée : vue 3D et coupe verticale montrant les limites de couches horizontales (échelle non respectée). Simplified Geometry (not to scale): 3D view and vertical cross-section of the computational domain showing the horizontal layers.

Fig. 10 Coupe verticale du modèle 3D à 700 jours : (a) distribution de la température (°C) et l’isotherme 0 °C (contour noir) ; (b) distribution de la pression de pore équivalente (MPa) et des vecteurs de déplacement (m). Vertical cross-section of the 3D model after 700 days: (a) ground temperature distribution (°C) and the 0 °C isotherm (black line) ; (b) equivalent pore pressure distribution (MPa) and displacement vectors (unit is m).

Fig. 11 Comparaison entre le déplacement vertical mesuré et simulé au niveau de la section 26 du tunnel 797. 3D THM model-simulated and measured vertical displacements in section 26 of tunnel 797.

4 Conclusion

Pour résumer, nous proposons dans cet article une mise en équation des phénomènes thermo-hydro-mécaniques et chimiques couplés associés à la congélation artificielle des terrains dans le cadre de la mécanique des milieux poreux. Nous adoptons pour cela une approche macroscopique basée sur l’équilibre thermodynamique (thermique, mécanique et chimique) de l’interface entre la glace et la phase liquide, où les fronts de gel sont modélisés implicitement à travers le degré de saturation liquide, et sur la notion de contrainte effective pour décrire la répartition des contraintes mécaniques.

Le modèle a été appliqué à l’étude des effets de la congélation artificielle sur les déplacements observés dans un tunnel de production de la mine de Cigar Lake. Des simulations thermo-hydraulique et thermo-hydro-mécanique ont été réalisées, respectivement, afin de caractériser les paramètres des couches géologiques, en particulier le degré de saturation liquide, et pour expliquer les déplacements mesurés en tête d’une section d’un tunnel de production, située en dessous du massif congelé. La capacité du modèle à reproduire les mesures de température et de déplacement a été démontrée.

Dans ces simulations numériques, nous avons tenu compte de l’hétérogénéité du terrain en considérant que celui-ci est stratifié horizontalement. Cette hypothèse a permis, certes, de simplifier la géométrie et de réduire le temps de calcul mais elle doit néanmoins être vérifiée par des simulations réalisées avec la cartographie géologique 3D réelle de la mine.

Enfin, l’amélioration de notre compréhension du comportement thermo-hydro-mécanique et chimique complexe des géomatériaux soumis à la congélation est tributaire de la qualité des mesures in situ qui servent, entre autres, à l’ajustement des paramètres du modèle. D’où l’intérêt de mettre en place des tests pilotes qui permettent d’évaluer, de manière quantitative, l’effet de la congélation sur les ouvrages souterrains, à l’abri des autres opérations d’excavation et d’exploitation manière.

Remerciements

Ces travaux de recherche ont été réalisés avec la collaboration et l’appui financier d’Orano. Les auteurs remercient Cameco pour avoir mis à disposition les données de congélation du site de Cigar Lake.

Références

Liste des tableaux

Liste des figures

Fig. 1 Couplage des phénomènes thermiques, hydrauliques, mécaniques et chimiques lors de la congélation d’un milieu poreux. (Les flèches en tirets correspondent à des phénomènes que nous ne traitons pas dans cet article. Compte tenu de nos connaissances actuelles, leur influence sur la prédiction de l’étendue des zones congelées et la stabilité du terrain reste limitée.). Diagram illustrating coupled Thermal-Hydrological-Mechanical-Chemical processes related to ground freezing. (Dashed lines indicate uncertain processes that are neglected in this paper.)

Dans le texte

	Fig. 2 Coupe schématique du gisement de Cigar Lake, modifiée d’après (Bishop et al., 2012). Cross-section of the mine of Cigar Lake, adapted from (Bishop et al., 2012).
Dans le texte

	Fig. 3 Plan 3D de la mine de Cigar Lake, modifié d’après (Bishop et al., 2016). 3D plan of the mine of Cigar lake, adapted from (Bishop et al., 2016).
Dans le texte

Fig. 4 Déplacements verticaux mesurés dans deux sections d’un tunnel de production (cercles vides pour la section qui est non exposée à la congélation et cercles pleins pour la section exposée à la congélation). Pour ne pas encombrer la figure, uniquement les valeurs mesurées par les capteurs de la moitié droite de la section sont représentées. Comparison between vertical displacements (negative indicates settlement) recorded in a section that is exposed to freezing (solid circles) and vertical displacements recorded in a section that is not exposed to freezing (empty circles). To avoid overlap, only data retrieved from targets 1, 3, 5 and 7 are plotted.

Dans le texte

	Fig. 5 Vue du dessus du réseau de puits de congélation à proximité du forage ST791_21. La couleur blanche indique que le massif est congelé à cet endroit. Layout of the freeze boreholes in the vicinity of borehole ST791_21 and soil freezing state (white indicates frozen and blue indicates nonfrozen).
Dans le texte

	Fig. 6 Maillage utilisé dans les simulations TH. Mesh used in the 3D TH model. (a) 3D view (b) Zoom of an horizontal cross-section of the 3D mesh (radial around the pipes and triangular outside).
Dans le texte

	Fig. 7 Historique de l’activation des puits de congélation dans la figure 6b. The duration of active freezing for the simulated pipes in Figure 6b.
Dans le texte

	Fig. 8 Comparaison entre les températures mesurées et simulées à deux profondeurs autour du gisement. Comparison between measured and calculated temperatures at two depths around the ore deposit.
Dans le texte

	Fig. 9 Géométrie simplifiée : vue 3D et coupe verticale montrant les limites de couches horizontales (échelle non respectée). Simplified Geometry (not to scale): 3D view and vertical cross-section of the computational domain showing the horizontal layers.
Dans le texte

Fig. 10 Coupe verticale du modèle 3D à 700 jours : (a) distribution de la température (°C) et l’isotherme 0 °C (contour noir) ; (b) distribution de la pression de pore équivalente (MPa) et des vecteurs de déplacement (m). Vertical cross-section of the 3D model after 700 days: (a) ground temperature distribution (°C) and the 0 °C isotherm (black line) ; (b) equivalent pore pressure distribution (MPa) and displacement vectors (unit is m).

Dans le texte

	Fig. 11 Comparaison entre le déplacement vertical mesuré et simulé au niveau de la section 26 du tunnel 797. 3D THM model-simulated and measured vertical displacements in section 26 of tunnel 797.
Dans le texte