| Numéro |
Rev. Fr. Geotech.
Numéro 151, 2017
|
|
|---|---|---|
| Numéro d'article | 2 | |
| Nombre de pages | 20 | |
| DOI | https://doi.org/10.1051/geotech/2017004 | |
| Publié en ligne | 23 juin 2017 | |
Article de recherche / Research Article
Amélioration des méthodes analytiques basées sur des concepts simples pour le dimensionnement des tunnels superficiels et profonds en sol meuble (prix Kérisel 2016)
Improved analytical methods based on simple concepts for the dimensioning of shallow or deep tunnels in soft ground
ARCADIS ESG, 9, avenue Réaumur, 92354 Le Plessis-Robinson cedex, France
★ Auteur de correspondance : guillaume.champagnedelabriolle@arcadis.com ; gdelabriolle@gmail.com
Le cadre conceptuel de la méthode convergence–confinement a été établi pour un matériau isotrope dans un champ de contraintes initialement isotropes. Ces deux hypothèses, quoique restrictives, donnent à cette méthode de calcul une approche fortement pédagogique. La méthode a été également complètement traitée avec un comportement élastique linéaire du massif et du soutènement en condition de contraintes initialement anisotropes par Panet. Pour passer rigoureusement du cas isotrope, où le soutènement est chargé uniquement radialement, au cas anisotrope, il est appliqué la théorie des coques minces associée à une condition de contact massif/soutènement. Les équations de la théorie des coques minces de Flügge sont citées dans des publications sur le calcul des tunnels depuis 1979, mais s’étendent peu sur les hypothèses et simplifications qui les ont établies. Le domaine de validité de la théorie des coques minces se situe déjà hors de nombreux cas usuels pour les revêtements de tunnels, ce qui conduit à se poser des questions sur l’approximation induite par l’utilisation de cette théorie à des revêtements d’épaisseur trop forte par rapport au rayon d’excavation. En se plaçant dans la continuité des travaux de Panet, après avoir établi la théorie des coques épaisses sous chargement anisotrope, il est démontré que des écarts importants sont constatés, que ce soit pour une épaisseur usuelle ou non de soutènement, pour une très large plage de rigidité relative du soutènement par rapport au massif.
Abstract
Convergence–confinement method has been established for an isotropic material in a hydrostatic stress field. These two hypotheses are quite restrictive, but make this method a very good pedagogic approach to understand ground/support interaction. It also exists a closed form for a non-hydrostatic stress field, if no plasticity occurs. To get from the hydrostatic case to the non-hydrostatic case, thin shells theory, in relation with contact condition, must be used. Flügge's thin shell theory has been quoted in a lot of tunnel design publications since 1979, but the hypothesis of this theory are never explored by the different authors. Unfortunately, the validity domain of thin shell theory does not correspond with a lot of common cases of tunnel design. This publication explores the quantification of the error induced by the thin shell theory when a thick shell is chosen. Following Panet's publications, after the establishment of thick shell theory under anisotropic stress, it is demonstrated that important differences exist between thin shell theory and thick shell theory, even if the support thickness is usual or not, for a wide range of ground/support relative rigidity.
Mots clés : tunnel / convergence–confinement / théorie des coques / soutènement / méthode analytique
Key words: tunnel / convergence–confinement / shell theory / support / analytical method
© CFMS-CFGI-CFMR-CFG, Published by EDP Sciences 2017
1 Introduction
La méthode convergence–confinement (CV-CF), de par sa facilité d’application, est fréquemment employée pour le calcul des tunnels, car elle permet de simuler en 2D l’effet 3D de la présence du front de taille, le tout grâce à trois courbes structurantes (Fig. 1) : la courbe de réaction du massif (GRC), la courbe longitudinale de convergence (LDP), et la courbe de confinement du soutènement (SCC). En cas de plasticité en paroi du massif, le rayon plastique (PR) est une courbe qui est également importante dans le processus de compréhension du phénomène d’interaction.
La littérature se concentre très majoritairement sur la GRC et l’extension du PR par l’étude de lois de comportement complexes, mais peu du lien avec la LDP, pourtant capitale pour la traduction analytique du phasage travaux retenu, ou sur la SCC, également essentielle pour établir rigoureusement l’équilibre.
Pour prendre en compte de manière rigoureuse l’interaction massif/soutènement dans le cadre de la méthode CV-CF, il est couramment utilisé la théorie des coques minces. Cet article présente comment l’introduction d’une nouvelle théorie des coques épaisses permet d’évaluer l’approximation (parfois importante) induite par l’utilisation de la théorie des coques minces.
Cet article est le premier d’une série de développements autour de la méthode CV-CF, ces travaux ayant reçu le prix Kérisel 2016.
Pour faciliter la lecture, une table des symboles est fournie (Tab. 1).
 |
Fig. 1 Courbes de la méthode convergence–confinement. Convergence–confinement method (CCM) related curves. |
2 Courbes de la méthode convergence–confinement
Dans ce chapitre, on suppose que Ri, Re, et R sont égaux, et on assimile Ksn et Ksf à la notation générique Ks.
2.1 Définition de courbe longitudinale de convergence
La LDP est intrinsèquement liée à la notion de taux de déconfinement λ. Ce paramètre varie en fonction de la distance au front de taille (Fig. 2).
En tout point de la paroi d’une coupe transversale d’un tunnel, on postule que la contrainte radiale peut s’écrire (avec σ0 contrainte géostatique initiale) :
La LDP donne donc le lien entre le sens longitudinal et le sens radial : c’est grâce à elle que le problème 3D peut se ramener à un problème 2D. Pour des phases de conception amont on peut se baser sur des profils courants avec des paramètres standards (Corbetta et al., 1991 ; Panet, 1995 ; Vlachopoulos et Diederichs, 2009), et pour des phases plus avancées on peut caler une LDP à partir d’un calcul élaboré aux éléments finis, pour ensuite réaliser de nombreux calculs rapidement avec la méthode CV-CF.
Par exemple (Fig. 3), on peut choisir de poser le soutènement à une distance du front égale au rayon, c’est-à-dire d/R = 1.
On a alors le déplacement radial en paroi correspondant :
La correspondance entre Ud et le taux de déconfinement λd correspondant à l’installation du soutènement doit être recherchée sur la GRC.
 |
Fig. 2 Représentation longitudinale de la réaction d’un massif non soutenu au cours du creusement d’un tunnel. Longitudinal profile of the reaction of an unsupported tunnel during its construction. |
 |
Fig. 3 Courbe longitudinale de convergence (LDP). Longitudinal deformation profile (LDP). |
2.2 Définition de la courbe de réaction du massif
La GRC dépend de la loi de comportement retenue pour le massif et du critère de rupture. Le cas classique consiste à opter pour un comportement élastique linéaire (loi de Hooke) parfaitement plastique avec un potentiel plastique de type Mohr-Coulomb avec ou sans rupture brutale. Par résolution des équations fondamentales de la MMC en 2D en déformations planes, on peut obtenir le déplacement radial en fonction de la contrainte radiale en paroi, c’est-à-dire en fonction de λ (Fig. 4).
De manière générique, on peut écrire la GRC sous la forme suivante :
Or, par définition de la courbe de convergence longitudinale, le taux de déconfinement à la pose du soutènement λd est tel que :
 |
Fig. 4 Courbe de réaction du massif (GRC). Ground reaction curve (GRC). |
2.3 Définition de la courbe de confinement du soutènement
Le soutènement et/ou revêtement est considéré avec un comportement élastique linéaire parfaitement plastique. Dans le cas de contraintes initialement isotropes dans le massif, la SCC classique est définie par :
Ud est le déplacement du massif à l’installation du soutènement, obtenu grâce à la LDP. Cela signifie bien que le soutènement ne se charge qu’à partir du moment où il est au contact du terrain.
(1 − λ)σ0 représente la contrainte radiale appliquée au soutènement. Donc (1 − λ)σ0R représente donc l’effort normal (N = pR) sollicitant le soutènement. Ks étant la rigidité du soutènement, la division de N par Ks fournit le déplacement radial correspondant.
Pour le massif, la GRC s’initie à λ = 0, alors que pour le soutènement, la SCC s’initie à λ = 1. Cet aspect peu intuitif est lié au fait que ces deux courbes ont la même ordonnée (Fig. 5). La valeur du déplacement est limitée par la pression radiale maximale que l’on peut relier à un taux de déconfinement : pmax = (1 − λmax)σ0.
Lors du dimensionnement du soutènement, on souhaite que l’équilibre ait lieu dans sa plage de fonctionnement élastique (hors cas spécifique). Pour un cas standard, l’équilibre doit donc se faire entre les points (Ud ; 0) et (Umax ; pmax).
La barre horizontale finale est indiquée pour montrer la limite de résistance du soutènement : sa longueur n’a pas de réel sens physique en dehors de l’intérêt pédagogique de l’afficher.
 |
Fig. 5 Définition classique de la courbe de confinement du soutènement (SCC). Usual definition of support confinement curve (SCC). |
2.4 Définition de l’équilibre massif/soutènement
Le cas des contraintes initialement isotropes étant le seul cas que l’on peut représenter aisément à l’aide d’un schéma, on peut avoir tendance à confondre la condition d’équilibre : l’équilibre est défini par une condition d’égalité des déplacements à l’interface entre le massif (GRC) et le soutènement (SCC), en fonction des conditions de contact. L’équilibre n’est en aucun cas défini par l’égalité des contraintes à cette interface. Cette confusion peut être à l’origine d’erreurs très importantes dans le traitement de l’anisotropie initiale de contraintes. La continuité de la contrainte radiale est seulement une manière de vérifier la cohérence du résultat.
Pour caractériser l’interface massif/soutènement, il est possible de caractériser deux conditions de contact extrêmes : l’adhérence parfaite et le glissement parfait (l’indice s symbolise le soutènement) :
Dans les conditions habituelles d’application de la méthode CV-CF, pour les contraintes est posée l’hypothèse d’une isotropie initiale de contraintes égale à σ0 (i.e., K0 = 1). Quoique restrictive, cette hypothèse permet à l’ingénieur de mieux comprendre la problématique du dimensionnement des tunnels grâce à des expressions analytiques accessibles. Dans ce cadre, l’équilibre massif/soutènement se réduit seulement à vérifier (il n’y a que des déplacements radiaux donc pas de cisaillement à l’interface) :
Si le soutènement est modélisé avec une loi purement mécanique, on obtient une équation en λeq à résoudre :
Ce caractère implicite dans la définition de l’équilibre fait que l’on se résout tout simplement à « lire » sur graphique l’intersection entre la SCC et la GRC pour connaître λeq (Fig. 6).
On note que le caractère implicite peut s’accentuer quand de la plasticité apparaît. En effet, toutes les courbes longitudinales de convergence dépendent alors soit du rapport entre le déplacement élastique final du tunnel non soutenu et le déplacement élastoplastique final du tunnel non soutenu, soit de l’extension finale du rayon plastique PR(λ). Ainsi :
Pour aller plus loin sur les grandes thématiques de la méthode CV-CF qui ne sont pas abordées ici, on recommande les articles suivants (Caquot et Kerisel, 1966 ; Carranza-Torres et Diederichs, 2009 ; Carranza-Torres et Labuz, 2006 ; Detournay et Fairhust, 1987 ; Guo, 1995 ; Panet, 1976).
 |
Fig. 6 Exemple d’application de la méthode convergence–confinement (CV-CF). Example for application of convergence–confinement method (CCM). |
3 Caractérisation des soutènements d’épaisseur quelconque
3.1 Notations
En guise d’introduction, afin de rester très conceptuel, le rayon intrados du tunnel et le rayon extrados du soutènement ont été abusivement notés de la même manière : R.
Dans toute cette étude, pour étudier précisément la différence entre l’application de la théorie des coques minces et celle des coques épaisses, nous allons utiliser des notations plus précises, qui modifieront donc parfois les expressions telles qu’on a l’habitude de les voir écrites. Les notations sont les suivantes :
- –
R : rayon moyen du soutènement ;
- –
t : épaisseur du soutènement ;
- –
Re = R + t/2 : rayon extrados soutènement ;
- –
Ri = R − t/2 : rayon intrados soutènement.
Selon les cas, les expressions seront notées en fonction des couples R et t ou Re et Ri, selon ce qui semblera le plus lisible et/ou pédagogique.
3.2 Caractérisation usuelle des soutènements minces
Dans les cas usuels, on considère le soutènement comme étant de faible épaisseur par rapport au rayon du tunnel. Dans ce cadre, il existe deux types de rigidité : Ksn la rigidité normale, et Ksf la rigidité de flexion, dont les expressions sont données par :
Pour savoir si un soutènement est souple ou rigide, il faut comparer sa rigidité à celle du massif. La rigidité relative est définie de la manière suivante (Panet, 1986) :
3.3 Caractérisation usuelle des soutènements épais
Si on cherche à dimensionner un soutènement épais, alors il existe des résultats classiques pour caractériser son comportement. C’est le problème classique du « tube épais » (appelé aussi problème des chaudronniers), où un chargement externe constant pe est imposé au soutènement.
Sa résolution permet de connaître l’effort normal et le moment induits par cette sollicitation externe :
On peut également connaître la rigidité normale d’un soutènement épais à partir du lien entre le déplacement à l’extrados du soutènement Ur(Re) et la valeur de pe.
À partir de cette définition, en utilisant l’approximation t << R dans l’expression de Ksn,épais, on retombe bien sur l’expression précédente de Ksn.
Ce qui pose problème, c’est que l’on se rend compte que cette définition n’est pas intrinsèque au soutènement. En effet, pourquoi ne calculerait-on pas cette expression en r = Ri, où la contrainte orthoradiale est maximale ? De plus, que devient cette approche si le chargement n’est plus isotrope à l’extrados et/ou à l’intrados ?
Ainsi, il faut se poser la question de l’origine des valeurs de Ksn et Ksf. On trouve la réponse dans la théorie des coques minces selon (Flügge, 1960).
3.4 Théorie des coques minces circulaires cylindriques
Nous avons décortiqué la démonstration de Flügge (au chapitre 5 de son ouvrage), pour comprendre comment adapter cette théorie. En effet, cet auteur est systématiquement cité dans la littérature, mais sans jamais donner ce qui a permis de bâtir son système d’équations (Carranza-Torres et Diederichs, 2009 ; Carranza-Torres et al., 2013 ; Einstein et Schwartz, 1979 ; Panet, 1986 ; Panet, 1995 ; Tran Manh, 2014 ; Vu, 2010).
3.4.1 Démonstration
Voilà succinctement les étapes de la démonstration :
- –
propriété intrinsèque : lien général contraintes internes/efforts sollicitant (considérations géométriques intrinsèques) ;
- –
étape 1 : lien sollicitations externes/efforts dans la coque (bilans sur un élément de coque mince) ;
- –
étape 2.1 : lien déplacement en un point sur la surface moyenne de la coque/déplacement d’un point A hors de l’axe (considérations géométriques dues à un rapport t/R << 1) ;
- –
étape 2.2 : lien déformations en un point quelconque sur la surface de la coque/déplacement en un point sur la surface moyenne de la coque (lois de la MMC) ;
- –
étape 3 : lien efforts/déplacements en un point quelconque sur la surface de la coque (loi de Hooke puis intégration des contraintes) ;
- –
étape 4 : lien sollicitations externes/déplacements en un point A quelconque (résultats précédents injectés dans les bilans de la première étape, grâce à la propriété intrinsèque).
Chacune de ces étapes utilise une ou plusieurs fois l’approximation t/R << 1, et parfois Flügge énonce qu’il transgresse une règle de la MMC, à la faveur d’une simplification du résultat. En plus de la propriété intrinsèque (indépendante de l’épaisseur de la coque), il faudra donc utiliser d’autres outils que ceux de Flügge.
3.4.2 Propriété intrinsèque
On peut obtenir géométriquement le lien entre les contraintes internes à une coque et les efforts sollicitant associés, sans poser une seule hypothèse (Fig. 7).
Pour une coque cylindrique circulaire, on a alors Rx = + ∞ et Ry = R (R étant le rayon à l’axe neutre). On remplace x par z (axe longitudinal du tunnel), y par θ, R + z par r. Ainsi :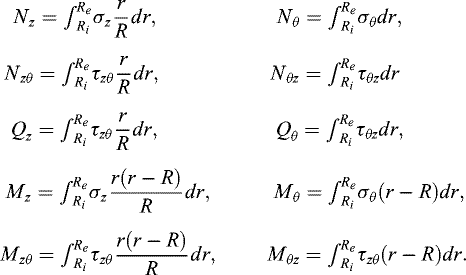
On note que même si l’on se place dans le cadre des petites déformations, ce qui implique que tous les tenseurs de contraintes et déformations sont symétriques, il faut alors noter que bien qu’on ait τzθ =τθz, cela n’entraîne pas Nzθ = Nθz, Qz = Qθ, ou Mzθ = Mθz.
Dans la très grande majorité des cas, ce ne sont que Nθ, Mθ et Qθ qui nous intéressent. Ce sont ces trois efforts que nous calculerons et comparerons par la suite.
 |
Fig. 7 Caractérisation géométrique d’une coque – Lien entre les contraintes internes, les sollicitations externes, et les efforts. Geometrical characterization of an arbitrary shell – Link between internal stresses, external solicitations, and forces. |
3.4.3 Origine de Ksn et Ksf
Pour connaître cette origine, on détaille l’étape 3, uniquement pour l’effort normal et le moment fléchissant.
Grâce au lien efforts/contraintes déjà établi (propriété intrinsèque), on remplace les contraintes par leur expression selon la loi de Hooke, puis les déformations par leur expression obtenue à l’étape 2.2. Ainsi :
On peut alors entreprendre un calcul de toutes les intégrales, en rappelant que les termes Ur, Uθ et Uz sont le déplacement d’un point sur la surface moyenne de la coque : ils ne dépendent donc pas de r.
Cependant, il faudra une fois de plus user de l’hypothèse qui consiste à considérer que t/R << 1, en faisant un développement limité pour t/R tendant vers 0 des expressions obtenues, afin de faire émerger Ksn et Ksf de manière explicite. Voici le résultat obtenu pour Nθ :
Ainsi, avec un développement limité pour t/R tendant vers 0 des fonctions logarithme et arc cotangente hyperbolique, on obtient le résultat suivant, en négligeant les termes d’ordre 5 et supérieurs :
Voilà donc l’origine de Ksn et Ksf dans le cadre de la théorie des coques minces ! Ils sont bien intrinsèques au soutènement, mais uniquement dans le cadre des hypothèses associées à cette théorie.
3.4.4 Systèmes d’équations fondamentales
Au terme de l’étape 4, Flügge obtient un ensemble de systèmes d’équations fondamentales qui peuvent être alors utilisés pour résoudre des problèmes, en associant ces équations différentielles à des conditions aux limites. Les trois types de systèmes sont résumés ci-dessous.
Lien entre les sollicitations externes et les efforts (trois écritures possibles) :
D’autre part, le lien entre les contraintes σR et τRθ et les déplacements Ur et Uθ, est défini par le système d’équations suivant :
En éliminant le déplacement orthoradial Uθ, on peut obtenir une équation différentielle en Ur :
Enfin, le lien entre les efforts et les déplacements est donné par :
3.4.5 Domaine de validité
On l’a vu, toute cette théorie est basée sur un certain nombre d’approximations liées à l’idée que le rapport t/R est très petit devant 1. D’après Flügge, la théorie des coques minces est valable pour t/R < 1/20 (Fig. 8), et pas 1/10 comme on peut le voir parfois écrit.
On sait par exemple que l’épaisseur empirique des anneaux de voussoirs est de l’ordre de Ri/11. De très nombreux cas usuels sont donc hors du domaine de validité de la théorie des coques minces. Il a donc semblé nécessaire de développer une théorie des coques spécifiquement en vue d’une application pour les tunnels. En effet, le domaine d’utilisation usuel de cette méthode pourrait être remis en cause dans la suite de notre analyse, notamment dans le cadre d’une interaction rigoureuse massif/soutènement, rarement intuitive.
 |
Fig. 8 Domaine de validité de la théorie des coques minces d’après Flügge. Area domain of thin shells theory among Flügge. |
4 Application du cas des contraintes anisotropes au problème classique du tube épais
4.1 Définition du problème
À l’extrados (rayon Re) et à l’intrados (rayon Ri), au cours d’un phasage de calcul, on a les variations de sollicitations de type anisotrope suivantes :
On cherche à connaître dans le soutènement dont le comportement est supposé élastique linéaire, l’expression analytique des contraintes internes et des efforts associés à ces sollicitations externes.
Comme mentionné lors de l’analyse de la démarche de Flügge, nous devons trouver un outil de résolution plus général, et qui ne nécessite pas de poser d’hypothèse sur le rapport t/R.
4.2 Méthode de résolution
Lorsque l’on souhaite résoudre un problème en contraintes, on peut utiliser une méthode dite « inverse » (Forest, 2009). Les équations de Beltrami permettent de vérifier l’ensemble des équations fondamentales de la MMC, sans jamais avoir à passer par les composantes du tenseur de déformation. Ces équations proviennent d’une combinaison de ces équations fondamentales, et elles s’écrivent uniquement en contraintes :
À partir de l’équation d’équilibre, et grâce au fait que le tenseur des contraintes soit symétrique, on peut prouver que les contraintes peuvent être déterminées par une seule fonction scalaire Φ, appelée fonction d’Airy. Comme Φ doit aussi vérifier les équations de Beltrami, on en déduit que Φ vérifie l’égalité suivante (Δ étant le Laplacien) :
Ceci signifie que Φ est une fonction biharmonique. Avec l’équation d’équilibre et en disant que la force de volume f dérive d’un potentiel V :
Ici, la force de volume est nulle (modèle non pesant), donc V = 0. En symétrie cylindrique, l’équation vérifiée par Φ devient :
Selon le problème auquel on est confronté, il existe divers exemples de fonction biharmonique classique qui permette d’obtenir une solution.
Pour ce problème, il est choisi la fonction biharmonique suivante (on utilise ici ρ plutôt que r pour limiter les sources de confusion) :
Par identification avec l’équation de Beltrami pour le tenseur de variation des contraintes, on peut retrouver le tenseur de variation des contraintes, que l’on va appeler système de Beltrami/Airy :
4.3 Résolution du problème
Grâce aux conditions aux limites (six termes indépendants), on peut retrouver les six constantes. Pour faciliter la lecture de cet article, on va seulement rédiger le résultat pour des sollicitations nulles à l’intrados (xi = yi = zi = 0). On obtient (cf. notations) :
Les coefficients sont rédigés tels que, une fois multipliés par ρH, ils sont adimensionnels (Tab. 2).
La relation entre les déformations et les déplacements, associée avec la loi de Hooke, donne :
Les conditions aux limites sont les suivantes : quand les sollicitations sont nulles, le déplacement est nul. Dans les deux cas on obtient la constante recherchée, qui est alors nulle. Ainsi :
Les coefficients sont rédigés tels que, une fois multipliés par ρH, l’unité est en m/MPa (Tab. 3).
On rappelle le lien efforts/contraintes internes pour une coque cylindrique circulaire :
Ces intégrales sont résolues, et en posant Re = R + t/2 et Ri = R − t/2, on obtient des expressions relativement compactes par rapport à celles précédemment obtenues :
Afin de conserver une forme similaire aux solutions en coque mince (Panet, 1986), on propose une réécriture des efforts :
Où les coefficients μ1, μ2, et μ3 sont appelés coefficients de passage coque mince/coque épaisse (Tab. 4).
On ne comparera pas plus avant ces résultats qui serviront de données d’entrée pour le chapitre suivant. En effet, la comparaison à ce stade d’étude n’est pas suffisamment utile, car les sollicitations externes sont considérées indépendantes du phasage travaux et de la rigidité relative du soutènement par rapport au massif : aucune interaction n’a encore été prise en compte.
Seule une comparaison dans le cadre de l’application de la méthode CV-CF peut fournir une indication viable : c’est l’objet du chapitre suivant.
Coefficients associés à l’expression des contraintes internes dans une coque épaisse.
Coefficients related to internal stresses in a thick shell.
Coefficients associés à l’expression des déplacements dans une coque épaisse.
Coefficients related to displacements in a thick shell.
Coefficients de passage coque mince/coque épaisse pour les efforts.
Coefficients to change the case thin shell by thick shell for forces.
5 Application de la théorie des coques épaisses à la méthode convergence–confinement
5.1 Démarches existantes
La première résolution du problème d’interaction massif/soutènement en élasticité en conditions de contraintes initialement anisotropes a été établie par (Einstein et Schwartz, 1979). À partir de la théorie des coques minces, les auteurs choisissent d’éliminer encore certains termes jugés négligeables afin de simplifier la résolution analytique. En revanche, aucun déconfinement n’est appliqué (λd = 0).
Quelques années plus tard, l’article de Panet (1986) introduit une démarche complètement intégrée à la méthode CV-CF, afin de prendre en compte explicitement le comportement du massif seul puis soutenu. Les grandes lignes de cette démarche seront reprises dans les développements qui vont suivre.
Bien plus tard, sur la base des résultats de (Einstein et Schwartz, 1979), et sans citer les travaux de Panet, une nouvelle solution sans supprimer les termes jugés négligeables est établie par (Carranza-Torres et al., 2013). Cela leur permet de quantifier l’approximation induite, et d’introduire une notion de déconfinement. Ils présentent leurs résultats pour λd = 0 et λd = 0,3. Il a donc été possible de constater que leurs résultats sont strictement identiques à ceux de Panet (1986) : c’est bien une résolution en coque mince, contrairement à ce qui est annoncé dans l’article comme étant une résolution en coque épaisse. La confusion vient du cumul des hypothèses de Einstein et Schwartz (1979) à celles de Flügge (1960).
Nous allons donc nous placer dans le même cadre d’hypothèses générales, c’est-à-dire avec comportement élastique linéaire isotrope du massif et du soutènement en conditions de contraintes initialement anisotropes. Mais là où les précédents auteurs se sont basés sur Flügge (1960) pour décrire le comportement du soutènement, nous nous baserons sur les résultats de la Section 4, c’est-à-dire sur un comportement explicite de coque épaisse.
5.2 Initialisation du problème
On définit σ10 comme étant la contrainte majeure, σ20 la contrainte mineure, K0 le coefficient de poussée des terres au repos, inférieur à 1, tel que :
Donc si K0 > 1, il faut faire tourner le problème de 90°. Le paramétrage de θ est classique (Fig. 9).
On utilisera ici ρ plutôt que r pour limiter les sources de confusion. La définition du problème en paroi (donc en ρ = Re) du tunnel est illustrée en (Fig. 10).
À l’état 0, le champ de contraintes est le suivant, la contrainte selon z étant égale à σz0 :
En paroi, au cours de la phase I, par la méthode CV-CF, on a :
Les variations de contraintes étant définies par Δσ = σ − σ0, on a en paroi au terme de la phase I (dans toute la suite, Δ conserve la signification de « variation de ») :
 |
Fig. 9 Paramétrage de θ par rapport aux contraintes principales. Parameterization of θ in relation with principal stresses. |
 |
Fig. 10 Phénomène d’interaction massif/soutènement. Interaction phenomenon ground/support. |
5.3 Aparté sur les conditions de contact massif/soutènement
Comme mentionné plus haut, seuls deux cas de conditions de contact extrêmes seront abordés : l’adhérence parfaite et le glissement parfait.
Si f = tan(φ) est le coefficient de frottement de l’interface massif/soutènement, alors si l’angle α de la résultante par rapport à la normale est inférieur à φ, alors on a adhérence parfaite. On a déplacement avec frottement si l’angle α a atteint φ, φ ne pouvant être dépassé. Le cas glissement parfait correspond à la situation où φ = 0.
Observons l’angle qu’on obtient, hors interaction, à partir des contraintes dans le massif :
La Figure 11 illustre le résultat que l’on obtient pour des valeurs usuelles de K0.
Si le coefficient de frottement est supérieur à 0,35, on a alors une adhérence parfaite dans tous les cas. Il semble que le coefficient de frottement béton/sol soit presque toujours supérieur à 0,4.
 |
Fig. 11 Inclinaison de la résultante en paroi – Avant interaction. Inclination of principal force at wall – Before interaction. |
5.4 Méthode de résolution
Comme au chapitre précédent, on va utiliser les fonctions d’Airy. Pour ce problème, il est choisi la fonction biharmonique suivante :
Grâce au système de Beltrami/Airy, on a :
Cette relation va être utilisée pour identifier les variations de contraintes au cours de la phase I et de la phase II.
5.5 Résolution du problème
5.5.1 Au cours de la phase I
En identifiant le système Beltrami/Airy ci-dessus avec les variations de contraintes au cours de la phase I en paroi (cf. dernier système d’équations de la Sect 5.2), on obtient les constantes :
Ainsi, on obtient le champ des variations de contraintes dans le massif au cours de la phase I :
Et grâce à la troisième équation de la loi de Hooke en déformations planes :
La relation entre les déformations et les déplacements, associée avec la loi de Hooke, donne :
Ainsi, à l’issue de la phase I dans le massif :
5.5.2 Au cours de la phase II
Au cours de la phase II, il y a interaction entre le massif et le soutènement. Au terme de la phase II, c’est-à-dire dans l’état 2, on suppose que les contraintes s’exerçant à l’interface entre le soutènement et le massif sont données par :
Au cours de la phase II, les déplacements à l’interface massif/soutènement peuvent s’écrire sous la forme (on a donc uniquement les déplacements du massif en paroi depuis la pose du soutènement) :
En injectant les variations de contraintes II dans la loi de Hooke, on obtient :

En ρ = Re, on obtient le système suivant, noté (D):
Dans l’état 2, à l’équilibre, les contraintes σRe(2) et τReθ(2) qui s’exercent à l’interface massif/soutènement entraînent sur le soutènement le champ de déplacement suivant :
Les relations entre les déplacements du massif et du soutènement à l’interface dépendent des conditions de contact. Il est possible de caractériser deux conditions de contact extrêmes : l’adhérence parfaite et le glissement parfait.

5.5.2.1 Adhérence parfaite
Étant donné la manière dont on a écrit les contraintes σRe(2) et τReθ(2) qui s’exercent à l’interface massif/soutènement au terme de la phase II, on pose alors les notations suivantes (Sect. 4.3) :
On remarque que l’unité de ces nouveaux coefficients restreints est en MPa−1.
On identifie alors le système ci-dessus avec le système des coefficients du système (D) pour obtenir le système (A) :
5.5.2.2 Glissement parfait
Étant donné la manière dont on a écrit les contraintes σR(2) et τRθ(2) qui s’exercent à l’interface massif/soutènement, on a alors avec donc ze = 0 :
En utilisant l’écriture en rigidité relative, on identifie alors le système ci-dessus avec le système (D) pour obtenir le système (G) :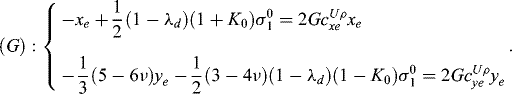
5.5.3 Résolution et normalisation de la solution
Avec les systèmes (A) et (G), on obtient xe, ye et ze dans les deux cas, ce qui permet alors d’obtenir les contraintes s’exerçant à l’extrados du soutènement qui, on le rappelle, s’écrivent sous la forme :
Grâce aux résultats de la Section 4, on peut obtenir les déplacements du soutènement :
Et obtenir les efforts s’appliquant dans le soutènement :
Par résolution du système (A), en adhérence parfaite, on obtient ainsi:
Par résolution du système (G), en glissement parfait :
On note qu’il n’est pas possible de donner une écriture unifiée plus pertinente pour les deux conditions extrêmes de contact, que celle retenue en « normalisant » xe, ye et ze en α1, α2 et β2, conformément aux notations de Panet (1986).
On remplace xe, ye et ze par leur expression compacte dans les variations de contraintes au cours de la phase 2 dans le massif :
De même, dans les contraintes à l’interface massif/soutènement :
En identifiant les expressions ci-dessus à une expression propre à la méthode CV-CF (voir le deuxième système de la Sect. 5.2), on peut obtenir le taux de déconfinement à l’équilibre équivalent en fonction de θ :
Le concept de taux de déconfinement unique à l’équilibre vole en éclat lors d’une interaction massif/soutènement en conditions de contraintes initialement anisotropes.
Les efforts obtenus peuvent être réécrits de la manière suivante :
Ainsi, on peut obtenir les coefficients normalisés suivants :
Les coefficients normalisés valent donc :
6 Comparaison coque mince/coque épaisse
Afin de se placer dans la continuité des précédentes publications illustrées par des graphes, on reprend les choix d’hypothèses de Carranza-Torres et al. (2013), c’est-à-dire un taux de déconfinement λd = 0,3, une épaisseur relative t/R = 1/10 (cas classique), un coefficient de poussée des terres au repos K0 = 0,5 (cette valeur implique des efforts majorants en θ = 0°), ainsi que l’expression de la rigidité relative retenue, c’est-à-dire E/Es.
Dans un premier temps, on compare (en θ = 0°) l’impact de la prise en compte d’une coque épaisse sur les efforts obtenus pour ces taux de déconfinement en fonction de la rigidité relative du massif par rapport au soutènement (Figs. 12–14Fig. 12-14). Les différences sont plus nettes en adhérence (trait continu) qu’en glissement (pointillés), mais pour en prendre pleinement la mesure et généraliser la comparaison, on illustre par la suite un graphe avec l’écart relatif entre les résultats en coque épaisse et en coque mince (Fig. 15). Cette comparaison a l’avantage d’être indépendante du choix de λd.
D’un point de vue global, les différences sont relativement négligeables dans le cas du glissement parfait, mais peuvent être significatives dans le cas de l’adhérence parfaite. En effet, dans le cas de l’adhérence parfaite, au-delà d’une rigidité relative de 10−3, les écarts excèdent la fourchette de ±5 % : avec l’augmentation de la rigidité relative, les écarts peuvent représenter jusqu’à −35 % pour l’effort normal, +20 % pour le moment fléchissant, et +60 % pour l’effort tranchant. Prendre en compte rigoureusement une coque épaisse semble donc indispensable, étant donné les écarts pouvant être atteints pour un cas classique.
En θ = 90° (cas non illustré), la différence en termes de moments et d’efforts tranchants est identique, en revanche, elle s’inverse pour l’effort normal : celui-ci est alors bien plus important que dans le cas coque mince.
Une telle comparaison n’aurait pas été possible en utilisant seulement la théorie des coques épaisses indépendamment de la méthode CV-CF, car l’interaction, dépendante de la rigidité relative du soutènement par rapport au massif, n’aurait pas pu être prise en compte.
Puis, on propose également deux graphiques, qui permettent d’esquisser les problématiques de justification des soutènements (et revêtements) en béton :
- –
le premier graphique (Fig. 16) présente l’excentricité relative associée à la flexion composée calculée à l’équilibre massif/soutènement (e = M/N). Le critère de non-justification du béton non armé affiché en rouge est celui de (AFTES, 2002), et qui correspond conceptuellement à la limitation de la profondeur de fissure à la moitié de l’épaisseur du soutènement (e < 0,3 × t donc e/R < 0,03 pour t/R = 1/10). Pour un massif très peu rigide (E/Es < 5,10−3), on voit que le critère est dépassé, quelle que soit la condition de contact ou la zone du soutènement : le béton devra donc être renforcé par des armatures ou des fibres métalliques pour reprendre les tractions importantes ;
- –
le second graphique (Fig. 17) est une illustration du même problème mais avec le point de vue du diagramme d’interaction du béton armé de (AFTES, 2002), avec le moment réduit en abscisse et l’effort normal réduit en ordonnée. Ce type de graphe est utile pour comprendre quel est l’enjeu essentiel du cas de figure étudié. Dans notre cas, ce n’est pas la résistance en compression du béton qui est en jeu mais le taux de renforcement. En effet, le long des quatre courbes affichant la flexion composée obtenue à l’équilibre, on a affiché en étiquette la rigidité relative associée. Et on retrouve notre critère dépassé pour la même valeur de rigidité relative, tandis que l’effort normal sollicitant reste très loin des capacités maximales de résistance en compression.
 |
Fig. 12 Comparaison coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort normal. Comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Normal force. |
 |
Fig. 13 Comparaison coques minces et coques épaisses dans convergence–confinement (CV-CF) – Moment fléchissant. Comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Bending moment. |
 |
Fig. 14 Comparaison coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort tranchant. Comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Shear force. |
 |
Fig. 15 Écart entre le résultat coque épaisse et le résultat coque mince (Panet). Difference between the thick shell result and the thin shell result. |
 |
Fig. 16 Comparaison des excentricités relatives. Comparison of normalized eccentricities. |
 |
Fig. 17 Diagramme d’interaction du béton non armé. Interaction diagram of unarmed concrete. |
7 Conclusion
Afin de conclure sur la portée de ces résultats, les dernières figures donnent l’écart maximal et l’écart moyen (en valeur absolue) constatés sur les efforts dans l’intervalle 10−4 < E/Es < 1, en fonction de l’épaisseur relative comprise dans l’intervalle 0,01 < t/R < 0,3 (soit l’ensemble des épaisseurs relatives envisageables), avec toujours K0 = 0,5 (comme précédemment les résultats sont donnés en θ = 0°). On observe jusqu’à 40 % d’écart sur l’effort normal (Fig. 18), jusqu’à 25 % pour le moment fléchissant (Fig. 19), et jusqu’à 160 % pour l’effort tranchant (Fig. 20).
Ainsi, l’application de la théorie des coques épaisses à la méthode CV-CF permet d’établir l’importance de la prise en compte de l’épaisseur réelle des soutènements utilisés dans le cadre de leur justification, en raison des écarts importants par rapport aux méthodes usuelles, et ce quelle que soit l’épaisseur de soutènement.
 |
Fig. 18 Comparaison généralisée coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort normal. Generalized comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Normal force. |
 |
Fig. 19 Comparaison généralisée coques minces et coques épaisses dans convergence–confinement (CV-CF) – Moment fléchissant. Generalized comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Bending moment. |
 |
Fig. 20 Comparaison généralisée coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort tranchant. Generalized comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Shear force. |
Remerciements
Je remercie en premier lieu le CMFS pour avoir récompensé ce travail en lui attribuant ex-æquo le prix Kérisel 2016. Je remercie également l’encadrement technique et managérial d’Arcadis, qui m’a fourni les moyens de progresser sans relâche : Hichem Ouffroukh, Olivier Givet, Pascal Guedon, Martin Doll, Alain Bernardet, Philippe Autuori, Jacques Robert. Je remercie mes professeurs de mathématiques de classes préparatoires : Alain Chabas, Philippe Grillot, Stéphane Flon. Des remerciements spécifiques vont également à Paul de Fromont, en vertu des multiples échanges scientifiques extraprofessionnels qui ont contribué à élargir mon angle de vue sur la conception des tunnels.
Références
- AFTES. 2002. Recommandations pour l’emploi de la méthode convergence-confinement. Tunn Ouvrages Souterr 170: 79–89. [Google Scholar]
- Caquot A, Kerisel J. 1966. Traité de mécanique des sols. Paris : Gauthier-Villars. [Google Scholar]
- Carranza-Torres C, Labuz J. 2006. Class notes on underground excavations in rock. Topic 6. USA: Department of Civil Engineering, University of Minnesota. [Google Scholar]
- Carranza-Torres C, Diederichs M. 2009. Mechanical analysis of circular liners with particular reference to composite supports. For example, liners consisting of shotcrete and steel sets. Tunn Undergr Space Technol 24: 506–532. [CrossRef] [Google Scholar]
- Carranza-Torres C, Rysdhal B, Kasim M. 2013. On the elastic analysis of a circular lined tunnel considering the delayed installation of the support. Int J Rock Mech Min Sci 61: 57–85. [Google Scholar]
- Corbetta F, Bernaud D, Nguyen Minh D. 1991. Contribution à la méthode convergence-confinement par le principe de la similitude. Rev Fr Geotech 54: 5–11. [CrossRef] [Google Scholar]
- Detournay E, Fairhust C. 1987. Two-dimensional elastoplastic analysis of a long, cylindrical cavity under non-hydrostatic loading. Int J Rock Mech Min Sci Geomech 21: 197–211. [CrossRef] [Google Scholar]
- Einstein HH, Schwartz CW. 1979. Simplified analysis for tunnel supports. ASCE J Geotech Eng 104 (4): 499–518. [Google Scholar]
- Flügge W. 1960. Stresses in shells. New York: Springer-Verlag Inc. [CrossRef] [Google Scholar]
- Forest S. 2009. Mécanique des milieux continus. Cours de Mines Paris Tech. Disponible sur http://m ms2.ensmp.fr. [Google Scholar]
- Guo C. 1995. Calcul des tunnels profonds soutenus - méthode stationnaire et méthode approchée. Mémoire de thèse, ENPC. [Google Scholar]
- Panet M. 1976. Analyse de la stabilité d’un tunnel creusé dans un massif rocheux en tenant compte du comportement après la rupture. Rock Mech 8: 209–223. [CrossRef] [Google Scholar]
- Panet M. 1986. Calcul du soutènement dans un champ de contraintes initial anisotrope. Tunn Ouvrages Souterr 77: 228–232. [Google Scholar]
- Panet M. 1995. Le calcul des tunnels par la méthode convergence-confinement. Paris : Presses de l’ENPC. [Google Scholar]
- Tran Manh H. 2014. Comportement des tunnels en terrain poussant. Mémoire de thèse, université Paris-Est (France). [Google Scholar]
- Vlachopoulos N, Diederichs M. 2009. Improved longitudinal displacement profiles for convergence-confinement analysis of deep tunnels. Rock Mech Rock Eng 42: 131–146. [CrossRef] [Google Scholar]
- Vu TM. 2010. Comportement des tunnels en terrains tectonisés - application à la liaison ferroviaire Lyon-Turin. Mémoire de thèse, université Paris-Est. [Google Scholar]
Citation de l’article : Guillaume Champagne de Labriolle. Amélioration des méthodes analytiques basées sur des concepts simples pour le dimensionnement des tunnels superficiels et profonds en sol meuble (prix Kérisel 2016). Rev. Fr. Geotech. 2017, 151, 2.
Liste des tableaux
Coefficients associés à l’expression des contraintes internes dans une coque épaisse.
Coefficients related to internal stresses in a thick shell.
Coefficients associés à l’expression des déplacements dans une coque épaisse.
Coefficients related to displacements in a thick shell.
Coefficients de passage coque mince/coque épaisse pour les efforts.
Coefficients to change the case thin shell by thick shell for forces.
Liste des figures
 |
Fig. 1 Courbes de la méthode convergence–confinement. Convergence–confinement method (CCM) related curves. |
| Dans le texte | |
 |
Fig. 2 Représentation longitudinale de la réaction d’un massif non soutenu au cours du creusement d’un tunnel. Longitudinal profile of the reaction of an unsupported tunnel during its construction. |
| Dans le texte | |
 |
Fig. 3 Courbe longitudinale de convergence (LDP). Longitudinal deformation profile (LDP). |
| Dans le texte | |
 |
Fig. 4 Courbe de réaction du massif (GRC). Ground reaction curve (GRC). |
| Dans le texte | |
 |
Fig. 5 Définition classique de la courbe de confinement du soutènement (SCC). Usual definition of support confinement curve (SCC). |
| Dans le texte | |
 |
Fig. 6 Exemple d’application de la méthode convergence–confinement (CV-CF). Example for application of convergence–confinement method (CCM). |
| Dans le texte | |
 |
Fig. 7 Caractérisation géométrique d’une coque – Lien entre les contraintes internes, les sollicitations externes, et les efforts. Geometrical characterization of an arbitrary shell – Link between internal stresses, external solicitations, and forces. |
| Dans le texte | |
 |
Fig. 8 Domaine de validité de la théorie des coques minces d’après Flügge. Area domain of thin shells theory among Flügge. |
| Dans le texte | |
 |
Fig. 9 Paramétrage de θ par rapport aux contraintes principales. Parameterization of θ in relation with principal stresses. |
| Dans le texte | |
 |
Fig. 10 Phénomène d’interaction massif/soutènement. Interaction phenomenon ground/support. |
| Dans le texte | |
 |
Fig. 11 Inclinaison de la résultante en paroi – Avant interaction. Inclination of principal force at wall – Before interaction. |
| Dans le texte | |
 |
Fig. 12 Comparaison coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort normal. Comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Normal force. |
| Dans le texte | |
 |
Fig. 13 Comparaison coques minces et coques épaisses dans convergence–confinement (CV-CF) – Moment fléchissant. Comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Bending moment. |
| Dans le texte | |
 |
Fig. 14 Comparaison coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort tranchant. Comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Shear force. |
| Dans le texte | |
 |
Fig. 15 Écart entre le résultat coque épaisse et le résultat coque mince (Panet). Difference between the thick shell result and the thin shell result. |
| Dans le texte | |
 |
Fig. 16 Comparaison des excentricités relatives. Comparison of normalized eccentricities. |
| Dans le texte | |
 |
Fig. 17 Diagramme d’interaction du béton non armé. Interaction diagram of unarmed concrete. |
| Dans le texte | |
 |
Fig. 18 Comparaison généralisée coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort normal. Generalized comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Normal force. |
| Dans le texte | |
 |
Fig. 19 Comparaison généralisée coques minces et coques épaisses dans convergence–confinement (CV-CF) – Moment fléchissant. Generalized comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Bending moment. |
| Dans le texte | |
 |
Fig. 20 Comparaison généralisée coques minces et coques épaisses dans convergence–confinement (CV-CF) – Effort tranchant. Generalized comparison between thin and thick shells after insertion in convergence–confinement method (CCM) – Shear force. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.














