EDP Sciences logo
Authentification abonné
Rechercher
Menu
Accueil Tous les numéros Numéro 168 (2021) Rev. Fr. Geotech., 168 (2021) 1 Full HTML
Accès gratuit
Numéro
Rev. Fr. Geotech.
Numéro 168, 2021
Modélisation Physique en Géotechnique - Partie 2
Numéro d'article 1
Nombre de pages 11
DOI https://doi.org/10.1051/geotech/2021011
Publié en ligne 6 mai 2021

© CFMS-CFGI-CFMR-CFG, 2021

1 Introduction

La modélisation physique consiste à étudier des phénomènes à l’échelle réduite. Cette méthode utilisée depuis longtemps en géologie et en géotechnique (Everling, 1964 ; Garnier, 2001 ; Green, 2014 ; Piede, 1986), souvent en complément des modélisations numériques, permet d’obtenir des résultats quantitatifs sous réserve d’appliquer des lois de similitudes (Clark, 1981 ; Buckingham, 1914 ; Mandel, 1962). Ces lois définissent les facteurs d’échelle appliqués à tout paramètre A du problème, pour assurer le passage de l’échelle réduite du modèle Am, à l’échelle 1 du prototype Ap.

Dans le cas de la mécanique des roches, et plus spécifiquement de l’étude du comportement des massifs rocheux fracturés, les modèles physiques sont généralement sollicités sous gravité terrestre en utilisant des matériaux analogiques. L’une des difficultés majeures de ce type de modélisation est de trouver des matériaux analogiques qui respectent les facteurs d’échelle, mais également de reproduire à l’échelle réduite le réseau de fractures avec sa géométrie complexe et ses effets sur le comportement mécanique.

Les massifs rocheux fracturés sont classiquement représentés par un massif continu équivalent en appliquant les méthodes d’homogénéisation (Davy et al., 2018 ; Gerrard, 1982 ; Pouya et Ghoreychi, 2001). Les modèles sont construits avec des géomatériaux (i.e. du sable) mélangés généralement à des liants à des pourcentages différents. La proportion de chaque élément est choisie après différents tests de caractérisation mécanique afin d’obtenir les propriétés respectant les lois de similitudes (Lin et al., 2015 ; Liu et al., 2011). Le point de faiblesse de ces modèles est qu’ils ne prennent pas en compte explicitement l’effet des discontinuités qui, en fonction du volume représentatif élémentaire, doivent parfois être représentés explicitement dans un massif hétérogène. Quelques modèles sont cependant explicitement discontinus. Le premier groupe de modèles discontinus consiste à assembler des blocs réguliers. Les fractures correspondent donc à l’interface entre les blocs (Aydan et al., 1989 ; Fuenkajorn et Phueakphum, 2010). Cependant, la géométrie ainsi créée, avec 2 familles de fractures orthogonales, reste très éloignée de celle classiquement observée dans les massifs rocheux. De plus, les interfaces entre les blocs ne sont pas caractérisées mécaniquement et donc les facteurs d’échelles sur les paramètres des joints ne sont pas respectés. De ce fait, les résultats obtenus avec ce type de modèles restent qualitatifs. Un deuxième groupe de modèles explicitement discontinus consiste à créer des plans de faiblesse entre différentes couches horizontales pour reproduire l’effet d’une stratification. Une méthode consiste par exemple à répandre une couche de sciure (Ghabraie et al., 2015 ; He et al., 2010 ; Sui et al., 2015). Cette représentation géométrique reste très simplifiée et les propriétés des discontinuités sont peu maîtrisées.

Pour améliorer la représentation géométrique des discontinuités, une nouvelle technique, basée sur l’utilisation de la fabrication additive est en cours de développement. La fabrication additive est une technologie permettant de fabriquer des objets 3D à partir d’un modèle géométrique numérique CAO (Conception assistée par ordinateur). Les applications de la 3DP (3D printing) en géotechnique restent limitées : modélisation des structures par 3DP pour étudier l’interaction sol-structure (Ritter et al., 2018 ; Stathas et al., 2018) ou pour modéliser les structures (Feng et al., 2015), et modélisation des éprouvettes construites par 3DP pour les caractériser mécaniquement et comparer leur comportement à celui des géomatériaux.

Jiang et Zhao (2015) sont parmi les premiers à tester l’applicabilité de la 3DP en mécanique des roches. Ils ont étudié le comportement d’éprouvettes en PLA (acide polylactique) par la technique FDM (fused deposition material). Plusieurs matériaux ont pu être testés (Jiang et al., 2016c ; Zhou et Zhu, 2018). Fereshtenejad et Song (2016) ont mis en évidence l’effet des paramètres d’impression sur le comportement en compression uniaxiale d’éprouvettes fabriquées. Différentes techniques et matériaux ont été utilisés pour tester la capacité de la 3DP à modéliser la porosité des roches : sable, résine (Gomez et al., 2019 ; Head et Vanorio, 2016 ; Ishutov et al., 2015). Liu et al. (2016) et Suzuki et al. (2016) ont généré un réseau de fractures pour étudier le comportement hydraulique d’une éprouvette. La 3DP est appliquée aussi en mécanique des roches pour étudier la propagation des fissures et la génération d’un DFN (Discrete Fracture Network). Jiang et al. (2016a) et Sharafisafa et al. (2018) ont utilisé le CaSO4.0.5H2O, un matériau de la famille des gypses, pour étudier sa capacité à reproduire une propagation de fissures à partir d’un défaut préexistant dans la matrice. Zhou et al. (2019) et Zhu et al. (2018) ont utilisé, dans la même thématique, la résine transparente qui permet de visualiser le mode de propagation à l’intérieur de l’éprouvette. Une troisième application de la 3DP en mécanique des roches est la visualisation de la distribution des contraintes dans le massif rocheux en fonction du réseau de fracture. Les matériaux utilisés sont des polymères photoélastiques. Ju et al. (2014, 2017) et Wang et al. (2017) ont étudié la distribution des contraintes dans des éprouvettes en 3DP simulant des formations rocheuses, en présence d’hétérogénéités. Dans l’ensemble, ces essais restent préliminaires et n’abordent pas la question du respect des lois de similitude, étape indispensable pour utiliser la 3DP en modélisation physique à l’échelle réduite. Un autre aspect manquant dans les travaux présentés est la question des propriétés mécaniques des joints rocheux : l’intérêt est focalisé plutôt sur le comportement global du massif. Jiang et al. (2016b) ont cependant étudié la capacité de la 3DP à reproduire la rugosité des joints rocheux. Pour cela, ils ont généré un modèle CAO à partir d’un nuage de points récupéré par un scan 3D de joints rocheux réels. Le modèle 3DP est un moule utilisé pour construire des éprouvettes de cisaillement en béton ou ciment. La fabrication additive est, dans ce cas, utilisée pour reproduire la géométrie et non pas pour caractériser mécaniquement le joint artificiel. Ishibashi et al. (2020) ont utilisé eux aussi la 3DP pour construire des joints rocheux artificiels générés à partir d‘une dimension fractale. Ils ont étudié en plus le comportement hydromécanique de ces joints sous cisaillement. Ils ont réussi à reproduire un comportement mécanique comparable à celui des joints rocheux naturels.

À l’échelle des ouvrages, seuls Song et al. (2018) ont construit un modèle réduit d’un tunnel pré-excavé en 3DP. Leur massif a une dimension totale de 20 × 20 cm2 et est fabriqué avec une imprimante à base de gypse. Cependant, les notions de facteur d’échelle et de loi de similitude ne sont pas évoquées dans l’article, les dimensions sont petites, et le massif est considéré homogène.

L’objectif de cette étude est d’évaluer l’apport des techniques d’impression 3D pour créer un modèle réduit de massif rocheux discontinu. Sous l’hypothèse que la réponse mécanique du massif rocheux est intimement liée au comportement mécanique de ses joints, l’étape essentielle de ce travail consiste à fabriquer des joints rocheux par 3DP qui respectent les comportements mécaniques classiques des joints (e.g. Barton, 1973) et dont les propriétés mécaniques respectent les facteurs d’échelle. Ceci nous permettra dans le futur de réaliser des modèles réduits de massifs rocheux explicitement discontinus. Pour cela, les propriétés mécaniques (raideur, cohésion et frottement) des joints sont contrôlées en jouant sur la rugosité de la surface du joint, et sur la présence de ponts rocheux entre les deux épontes (Jaber et al., 2020). Le matériau utilisé est un polymère (PA12) et la technique d’impression utilisée est le frittage laser (SLS). Dans un second temps, nous abordons explicitement la question des lois de similitudes pour apprécier l’applicabilité de cette technologie à la modélisation physique en mécanique des roches.

2 Caractérisation mécanique des joints en 3DP

La technologie utilisée repose sur le frittage laser sélectif (SLS) des polymères (le polyamide 12, PA12 dans notre cas). Le processus de fabrication est présenté sur la figure 1. La SLS est susceptible de permettre la fabrication réaliste d’objets possédant les caractéristiques géométriques des milieux rocheux constitués de blocs séparés par des discontinuités.

Les paramètres d’impression ont été maintenus identiques pour toutes les fabrications, quels que soient leur forme et leur type afin de garantir des propriétés intrinsèques uniformes entre toutes les éprouvettes (Zarringhalam et al., 2006).

thumbnail Fig. 1

Processus de la fabrication additive, technique SLS.

3D printing process of the SLS technology.

2.1 Conception des joints

Des essais de cisaillement sous contrainte normale constante (CNL) sur des joints artificiels construits par 3DP sont réalisés au laboratoire GeoRessources. Ce travail est une première étude de faisabilité. Il est plus raisonnable de commencer par des configurations de joints simples à paramètres quantifiables. De ce fait, les joints sont définis comme étant une combinaison des paramètres suivants :

  • une ouverture à épaisseur fixe de 0,4 mm. Ce choix est fait pour s’assurer que le joint est ouvert et qu’il n’y a pas de phénomène de fusion de poudre non désirable lié à des effets thermiques ;

  • une géométrie équivalente à une rugosité. Cette géométrie prend des formes simplifiées correspondant aux modèles idéaux typiques existant dans la littérature (Fig. 2) ;

    thumbnail Fig. 2

    Les géométries des joints construits par 3DP : (a) joint planaire ; (b) joint en dents de scie.

    The 3DP joint geometry: (a) planar joint; (b) sawtooth joint.

  • des ponts rocheux. La notion de ponts rocheux est utilisée généralement dans les études liées à la stabilité des pentes et chutes des blocs. Bien que leur forme soit irrégulière dans la nature, les ponts modélisés dans cette étude sont uniformes et répartis d’une manière symétrique sur la surface des joints. Il s’agit de plots cylindriques, de diamètre fixe de 2,5 mm liant les deux interfaces de la discontinuité. Mécaniquement, les ponts participent à l’augmentation de la résistance au cisaillement et donnent une cohésion apparente au joint (Bonilla-Sierra et al., 2015 ; Einstein et al., 1983 ; Sturzenegger et Stead, 2012).

2.2 Interprétation des résultats

Quarante-six essais ont été réalisés en faisant varier le nombre de ponts, la géométrie, et la contrainte normale appliquée σn. Tous les essais présentent la même tendance. De ce fait, deux géométries différentes sont détaillées : un joint planaire à 25 ponts et un joint en dents de scies à 18 ponts rocheux.

Les résultats montrent que les joints artificiels ont un comportement similaire au comportement classique d’un joint rocheux (Figs. 3–4). Les courbes de contrainte tangentielle versus déplacement tangentiel (τvsut) présentent une première phase linéaire, permettant d’estimer la raideur tangentielle du joint ks, un pic correspondant à la résistance au cisaillement maximale τpic, suivie d’une diminution de la contrainte tangentielle jusqu’à atteindre une valeur résiduelle τres.

Afin de vérifier l’évolution de la résistance des joints en fonction des contraintes normales appliquées et de définir leur critère de rupture, des essais sont réalisés sous différentes valeurs de contraintes normales σn (Fig. 4). Les résultats montrent une augmentation de τpic avec l’augmentation de σn, du nombre de ponts rocheux et de la présence des aspérités.

La raideur tangentielle ks est du même ordre de grandeur pour tous les essais. Elle varie entre 0,5 MPa/mm et 5 MPa/mm, avec une valeur moyenne de 1,7 MPa/mm (Jaber, 2020). Toutefois, il est difficile de trouver une corrélation entre les raideurs des différents essais et les paramètres des joints à cause des incertitudes liées à l’ajustement des éprouvettes dans le dispositif et le rattrapage des déplacements horizontaux au début de l’essai. La différence entre les résistances maximale et résiduelle est expliquée classiquement par la destruction des aspérités (Goodman, 1976 ; Homand et al., 2001). Dans notre cas, elle est le résultat de la rupture des ponts rocheux sachant que les aspérités restent presque intactes à la fin d’un test.

Les résultats obtenus pour les courbes de dilatance sont aussi en accord avec la littérature : seuls les joints ayant des aspérités montrent un comportement dilatant avec une dilatance de 13°, proche de l’angle de l’aspérité 15° (Patton, 1966). Les joints planaires présentent un déplacement normal négligeable, dû à la présence des ponts rocheux.

En se basant sur les 46 essais, un critère de rupture prenant en compte explicitement l’effet de l’angle de l’aspérité θ et du nombre des ponts rocheux Nrb est généré par analyse statistique.

Le modèle le plus significatif statistiquement est présenté dans les équations (1) et (2). Il est initialement développé dans Jaber et al. (2020) et puis modifié dans Jaber (2020). Les paramètres statistiques sont exposés dans le tableau 1 : (1) (2) Le critère au pic est formé par deux composantes principales. La première est l’angle de frottement global φj = (23,5° + θ). Il est le résultat de la somme de l’angle de frottement de base du joint et de l’angle de l’aspérité θ. On retrouve cette représentation d’angle de frottement dans le modèle classique de Patton. La deuxième composante est la cohésion du joint cj. Celle-ci est liée explicitement au nombre de ponts rocheux (0,0135 Nrb).

Pour le critère de rupture résiduel, la cohésion est considérée nulle suite à la rupture des ponts. Seul l’angle de frottement résiduel φj,r joue un rôle. φj,r, pareillement à l’angle de frottement au pic, est formé par une combinaison d’un angle de frottement résiduel pour un joint planaire et de l’angle de l’aspérité. Il est estimé à 21,8° en absence d’aspérités, légèrement inférieur à l’angle de base sans aspérités. Généralement, dans la nature, l’angle de frottement de base est du même ordre de grandeur que l’angle résiduel, à quelques degrés près, ce qui est en accord avec nos résultats.

thumbnail Fig. 3

Comportement mécanique typique des joints rocheux en cisaillement.

Typical behaviour of rock joints under shearing test.
thumbnail Fig. 4

Les courbes de cisaillement (a et b) et de dilatance (c et d) des géométries 18rb-Sawtooth A et 25rb-Planar à différentes contraintes normales.

Shear (a and b) and dilation (c and d) curves tests for 18rb-Rough A joints and 25rb-Planar joints at different normal stresses.
Tableau 1

Expression de la cohésion et de l’angle de frottement des joints (au pic et résiduel) issus du modèle statistique, avec les paramètres statistiques correspondants.

Friction angle and joint cohesion expression of the statistical model, at peak and residual states, with the corresponding statistical parameters.

3 Application des facteurs d’échelles

Si les joints artificiels en PA12 sont capables de reproduire qualitativement le comportement global des joints rocheux, il faut également vérifier qu’ils sont représentatifs des roches à une échelle réduite. La première étape consiste donc à définir les facteurs d’échelle nécessaires à notre étude. Il existe plusieurs méthodes pour calculer les facteurs d’échelle A* = Am/Ap, dont le théorème de Vashy-Buckingham. Il est utilisé pour calculer les facteurs d’échelle des paramètres de la roche intacte (ρ, E, v, c, φ) et des joints (ψj, φj, cj, ks et kn). Avec E le module d’Young en MPa, ρ la masse volumique en kg/m3, v le coefficient de Poisson, c la cohésion de la roche en MPa, φ l’angle de frottement interne de la roche, ψj la dilatance du joint, et kn et ks les raideurs normale et tangentielle du joint en MPa/mm. 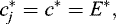Les résultats sont présentés dans les équations (3) à (7) : (3) (4) (5) (6) (7) L’application de ce théorème permet de vérifier que les paramètres adimensionnels restent inchangés entre le prototype et le modèle réduit, et les paramètres ayant la même unité subissent la même mise à l’échelle.

Les facteurs d’échelle calculés à partir des lois de similitude sont appliqués aux propriétés du matériau et des joints artificiels issus des essais mécaniques. En modélisation physique, il existe des facteurs d’échelle imposés par le choix de matériau et du dispositif expérimental : L*, g* et ρ*. Il est difficile généralement de respecter les facteurs d’échelle sur tous les paramètres du modèle. Le choix de respecter ou pas un facteur d’échelle dépend de la nature du problème à étudier. À titre d’exemple, si une étude statique d’un ouvrage souterrain à grande profondeur est réalisée avec un recouvrement modélisé implicitement par un chargement extérieur imposé au massif, le facteur d’échelle sur la masse volumique du petit volume explicitement représenté (un ouvrage de 5 m de haut sous 1 km de recouvrement par exemple) peut ne pas être pris en compte. Ceci donne plus de liberté sur l’application des lois de similitude aux autres paramètres du problème. Par contre, si le but est d’étudier l’affaissement en surface lié à une excavation souterraine, l’intégralité du recouvrement doit être modélisée avec un respect du facteur d’échelle sur la masse volumique. Dans cette application, nous considérons le cas le plus critique, en imposant des facteurs d’échelle sur tous les paramètres. L* dépend des dimensions du dispositif expérimental. On considérera ici deux ordres de grandeurs : L* = 1/10 ou 1/25. ρ* dépend du matériau à l’échelle réelle sachant que les propriétés mécaniques du matériau analogique (PA12) sont imposées : ρ = 1000 kg/m3 et E = 1600 MPa. g* dépend de la nature du dispositif : centrifugeuse ou sous gravité terrestre ; dans notre cas, g* = 1.

Les résultats sont comparés à l’ordre de grandeur des propriétés des roches trouvées dans la nature (Tab. 2) afin d’étudier les limites d’application de cette technique. Le schéma de la figure 5 illustre les étapes d’application des facteurs d’échelle permettant d’atteindre l’objectif.

Les résultats pour les deux facteurs d’échelle sont présentés respectivement dans le tableau 3. En suivant la procédure expliquée dans la figure 5, et en calculant les Am à partir des 46 essais en fonction de Nrb et θ de chaque test. L’intervalle choisi pour ρ* est 0,3 ≤ ρ* ≤ 0,5, ce qui correspond à une roche réelle ayant une masse volumique comprise entre 2000 et 3300 kg/m3. La comparaison de ces résultats avec les valeurs du tableau 2 montre qu’une grande partie des paramètres de PA12 sont convenables pour la modélisation des massifs discontinus, mais qu’il reste quelques propriétés à mieux contrôler :

  • pour L* = 1/10, les paramètres k, E et φj tombent dans les intervalles de valeurs trouvées pour les roches. Par contre, la cohésion des joints artificiels est élevée par rapport à ce qu’on trouve dans la nature. Celle-ci est liée à la présence des ponts et à leur pourcentage ;

  • pour L* = 1/25, les paramètres ks et φj tombent dans les intervalles de valeurs trouvées pour les roches. Le module de Young obtenu à l’échelle du prototype se situe vers la borne supérieure de ce que peut se trouver dans la nature, voire même le dépasse faiblement. Concernant la cohésion du joint, ses valeurs à l’échelle du prototype sont largement plus élevées de ce qui est attendu.

L’utilisation de l’impression 3D en PA12, pour une application en mécanique des roches, semble donc réaliste sous réserve de se limiter à des facteurs d’échelle autour de L* = 1/10. Elle nécessite toutefois d’ajuster la cohésion des joints du modèle en limitant le nombre de ponts rocheux. L’application de l’équation 1, permet ici d’estimer à 8 ponts/100 cm2 de joint la limite supérieure à respecter (pour des ponts de 2,5 mm de diamètre). Une alternative complémentaire consiste à réduire également la section des ponts. Pour une application à des facteurs d’échelle autour de L* = 1/25, il convient de réduire le module de Young de la matrice (le PA12). Une possibilité est l’architecturation du matériau. En d’autres termes, il est possible d’introduire des vides dans la matrice des PA12 en recréant sa structure, et en optimisant le changement de densité et de module d’Young. De cette manière, le module de Young équivalent de la matrice, sans joint rocheux, sera réduit. Il faut toutefois architecturer le matériau de manière à ce que ces défauts introduits ne dominent pas et que le comportement soit contrôlé par les discontinuités majeures introduites et qui représentent les fractures rocheuses préexistantes.

Tableau 2

Valeurs typiques des paramètres des roches issues de la littérature (à partir de Barton, 1973 ; Barton et Choubey, 1977 ; Kulhawy, 1975 ; Kulhawy, 1978 ; Mestat, 1993 ; Rachez, 1997).

Typical values for rock parameters, as found in literature (from Barton, 1973; Barton and Choubey, 1977; Kulhawy, 1975; Kulhawy, 1978; Mestat, 1993; Rachez, 1997).

thumbnail Fig. 5

Schéma de calcul des propriétés à l’échelle du prototype, à partir des essais expérimentaux.

Scale factor application to rock mechanics, based on experimental results.
Tableau 3

Valeurs expérimentales des propriétés des joints (en italique gras) et ses valeurs correspondantes à l’échelle 1 après application des facteurs d’échelle pour L* = 1/10 et L* = 1/25.

Experimental range for joint parameters (italic bold characters) and their corresponding values at real scale after applying scale factors for L* = 1/10 and L* = 1/25.

4 Validation de l’utilisation du PA12-3DP en modélisation physique

Le but de cette partie est de comparer 3 modèles numériques afin d’évaluer si les écarts observés dans le respect des lois de similitudes sont rédhibitoires ou non pour une utilisation du PA12 associé à l’impression 3D en mécanique des roches. Les propriétés des modèles A, B et C sont présentées dans le tableau 4. Les calculs sont réalisés avec le logiciel de modélisation discontinue aux différences finies UDEC :

  • modèle A : modèle numérique représentant le prototype (Fig. 6) ;

    thumbnail Fig. 6

    Modèle UDEC du bloc traversé par deux familles de discontinuité.

    UDEC model of a rock discontinuous block.

  • modèle B : modèle réduit numérique idéal respectant l’ensemble des lois de similitude (L* = 1/10) ;

  • modèle C : modèle réduit numérique réaliste utilisant les propriétés du PA12 et ne respectant pas l’ensemble des lois de similitudes (L* = 1/10).

Les différences principales entre B et C résident dans les propriétés plastiques de la matrice (c et φ).

Le prototype est formé par un bloc de 10 m de largeur et 5 m de hauteur, traversé par deux familles de discontinuités. Les joints et la roche intacte ont une rhéologie de type Mohr-Coulomb. Le prototype est soumis à des contraintes de confinement horizontales, et une contrainte verticale. Une fois l’équilibre statique initial atteint, un déplacement vertical est imposé en surface jusqu’à atteindre la rupture. Celle-ci est identifiée par une rupture au niveau des joints et par une limite de plasticité sur la courbe (σn−un), où un le déplacement vertical. Les contraintes verticales sont calculées sur une coupe à 10 % du bord supérieur. La famille des joints 1 atteint sa limite de rupture en cisaillement avant la famille 2 (Fig. 7) dans les 3 modèles, en accord avec le fait que leur pendage est supérieur à l’angle de frottement de la roche intacte, et à celui de la famille 2.

Les courbes (σn−un) des 3 modèles sont tracés sur un même graphe, en translatant tous les résultats à l’échelle 1 (Fig. 8). Les courbes des modèles A et B se superposent parfaitement en accord avec le fait que les lois de similitude ont été parfaitement respectées. La partie élastique est équivalente entre les trois modèles. Ceci est dû au respect des facteurs d’échelle pour E et ks. Le faible écart des ks entre B et C a donc un effet négligeable. Malgré le fait que le critère de plasticité du PA12 soit très supérieur au critère de plasticité du modèle réduit idéal, on observe une faible différence entre le comportement macroscopique des deux modèles réduits pour une déformation inférieure à 0,0016. Cette faible différence à ε = 0,0016 (62 MPa pour A et B contre 65 MPa pour C) est liée principalement à la différence entre la cohésion des joints en PA12 et celle du modèle théorique B. Pour une déformation supérieure à 0,0016, les écarts entre les modèles B et C augmentent significativement. Cet écart est la conséquence du critère de plasticité très élevé du PA12 qui conduit à une absence de plasticité dans le modèle C, contrairement aux modèles A et B (Fig. 9). Il en résulte que l’application du PA12 à la modélisation physique en mécanique des roches doit être limitée aux situations où le comportement d’ensemble et la rupture sont pilotés par les discontinuités. Il ne pourrait pas être appliqué pour une modélisation réduite dans un massif homogénéisé.

Tableau 4

Propriétés mécaniques des roches et joints, dans le modèle théorique A, le modèle réduit théorique B et le modèle réduit en utilisant le PA12C.

Mechanical properties of rock and joints for the prototype A, theoretical reduced scale model B and the reduced scale m.

thumbnail Fig. 7

Rupture des joints de la famille 1 ; la famille 1 atteint la rupture en cisaillement (en rouge) avant la deuxième famille (verte).

Shear failure of the joints family one (in red) before the family 2 (green).
thumbnail Fig. 8

Contraintes normales en fonction de la déformation axiale pour les 3 modèles après translation à l’échelle 1.

Normal stress versus axial deformation for the 3 UDEC discontinuous model at scale 1.
thumbnail Fig. 9

Localisation de la plasticité en fin d’essai pour les 3 modèles : A (à gauche), B (au centre) et C (à droite).

Plasticity propagation at the end of the test for the 3 models: A (left), B (center) and C (right).

5 Conclusion

Cet article présente une étude de l’applicabilité de l’impression 3D en modélisation physique des massifs rocheux fracturés. Cette technique est proposée dans le but de permettre une représentation explicite des joints rocheux en modélisation physique, tout en contrôlant les propriétés mécaniques de ces joints afin de les mettre à l’échelle et de respecter les lois de similitudes. Les résultats montrent que cette technique est très précise et permet de reproduire fidèlement les géométries demandées. Les essais de cisaillement ont montré que les joints en 3DP ont un comportement mécanique équivalent à celui des roches réelles (phase élastique suivie d’un pic et d’une résistance résiduelle), ce qui permet de définir un critère de rupture prenant en compte explicitement les paramètres contrôlés des joints (géométrie et nombre de ponts rocheux) et qui s’approche des critères classiques que l’on trouve dans la littérature.

Les résultats de l’analyse des lois de similitudes montrent que la raideur tangentielle et l’angle de frottement des joints imprimés en 3DP sont compatibles avec les valeurs trouvées pour les roches. Le module d’Young du PA12 peut être convenable jusqu’une certaine limite (L* = 1/25). Cependant, pour des facteurs d’échelle plus faibles, la matrice devient rigide par rapport à l’échelle du prototype. La cohésion du joint doit quant à elle être réduite par une réduction du nombre de ponts rocheux ou de leur surface. La modélisation numérique d’un massif rocheux discontinu et de son modèle réduit correspondant en utilisant le PA12 a montré un respect du comportement global élastique et de la limite de plasticité engendrée par la rupture des joints. Cependant, le PA12 est incapable de simuler le comportement de la roche intacte à cause de ses propriétés de plasticité élevées. L’utilisation de la 3DP en modélisation physique des massifs rocheux explicitement discontinus est prometteuse et permet surtout de reproduire des joints à propriétés mécaniques contrôlées. Des études supplémentaires sont donc à poursuivre dans le but de passer à la modélisation physique grande échelle.

Conflits d’intérêts

Les auteurs déclarent n’avoir aucun lien d’intérêt concernant les données publiées dans cet article.

Liste des symboles

Am : Paramètre A à l’échelle du modèle réduit

Ap : Paramètre A à l’échelle réelle du prototype

A* : Facteur d’échelle sur le paramètre A

CAO : Conception assistée par ordinateur

3DP : 3D printing, impression 3D

PLA : Acide polylactique

FDM : Fused Deposition Material

DFN : Discrete Fracture Network

PA12 : Polyamide 12

SLS : Frittage laser sélectif

CNL : Contrainte normale constante

σn : Contrainte normale (MPa)

τ : Contrainte tangentielle (MPa)

ut : Déplacement tangentiel (mm)

un : Déplacement vertical (mm)

ks : Raideur tangentielle du joint (MPa/mm)

kn : Raideur normale (MPa/mm)

τpic : Résistance au cisaillement maximale

τres : Résistance au cisaillement résiduelle

φj : Angle de frottement du joint

φj,r : Angle de frottement résiduel du joint

θ : Angle des aspérités

Nrb : Nombre de ponts rocheux

cj : Cohésion du joint

E : Le module de Young en MPa

ρ : La masse volumique en kg/m3

v : Le coefficient de Poisson

c : La cohésion de la roche en MPa

φ : L’angle de frottement interne de la roche

ψj : La dilatance du joint

Rt : Résistance à la traction de la roche (MPa)

Remerciements

La bourse de thèse de Jana Jaber a été financée par le ministère de l’Enseignement supérieur et de la Recherche, et le projet a bénéficié d’une bourse de l’institut Carnot-ICÉEL.

Références

Citation de l’article : Jana Jaber, Marianne Conin, Olivier Deck, Olivier Godard, Samuel Kenzari. Essai préliminaire de l’application de l’impression 3D à la modélisation physique des massifs rocheux. Rev. Fr. Geotech. 2021, 168, 1.

Liste des tableaux

Tableau 1

Expression de la cohésion et de l’angle de frottement des joints (au pic et résiduel) issus du modèle statistique, avec les paramètres statistiques correspondants.

Friction angle and joint cohesion expression of the statistical model, at peak and residual states, with the corresponding statistical parameters.

Dans le texte
Tableau 2

Valeurs typiques des paramètres des roches issues de la littérature (à partir de Barton, 1973 ; Barton et Choubey, 1977 ; Kulhawy, 1975 ; Kulhawy, 1978 ; Mestat, 1993 ; Rachez, 1997).

Typical values for rock parameters, as found in literature (from Barton, 1973; Barton and Choubey, 1977; Kulhawy, 1975; Kulhawy, 1978; Mestat, 1993; Rachez, 1997).

Dans le texte
Tableau 3

Valeurs expérimentales des propriétés des joints (en italique gras) et ses valeurs correspondantes à l’échelle 1 après application des facteurs d’échelle pour L* = 1/10 et L* = 1/25.

Experimental range for joint parameters (italic bold characters) and their corresponding values at real scale after applying scale factors for L* = 1/10 and L* = 1/25.

Dans le texte
Tableau 4

Propriétés mécaniques des roches et joints, dans le modèle théorique A, le modèle réduit théorique B et le modèle réduit en utilisant le PA12C.

Mechanical properties of rock and joints for the prototype A, theoretical reduced scale model B and the reduced scale m.

Dans le texte

Liste des figures

thumbnail Fig. 1

Processus de la fabrication additive, technique SLS.

3D printing process of the SLS technology.
Dans le texte
thumbnail Fig. 2

Les géométries des joints construits par 3DP : (a) joint planaire ; (b) joint en dents de scie.

The 3DP joint geometry: (a) planar joint; (b) sawtooth joint.
Dans le texte
thumbnail Fig. 3

Comportement mécanique typique des joints rocheux en cisaillement.

Typical behaviour of rock joints under shearing test.
Dans le texte
thumbnail Fig. 4

Les courbes de cisaillement (a et b) et de dilatance (c et d) des géométries 18rb-Sawtooth A et 25rb-Planar à différentes contraintes normales.

Shear (a and b) and dilation (c and d) curves tests for 18rb-Rough A joints and 25rb-Planar joints at different normal stresses.
Dans le texte
thumbnail Fig. 5

Schéma de calcul des propriétés à l’échelle du prototype, à partir des essais expérimentaux.

Scale factor application to rock mechanics, based on experimental results.
Dans le texte
thumbnail Fig. 6

Modèle UDEC du bloc traversé par deux familles de discontinuité.

UDEC model of a rock discontinuous block.
Dans le texte
thumbnail Fig. 7

Rupture des joints de la famille 1 ; la famille 1 atteint la rupture en cisaillement (en rouge) avant la deuxième famille (verte).

Shear failure of the joints family one (in red) before the family 2 (green).
Dans le texte
thumbnail Fig. 8

Contraintes normales en fonction de la déformation axiale pour les 3 modèles après translation à l’échelle 1.

Normal stress versus axial deformation for the 3 UDEC discontinuous model at scale 1.
Dans le texte
thumbnail Fig. 9

Localisation de la plasticité en fin d’essai pour les 3 modèles : A (à gauche), B (au centre) et C (à droite).

Plasticity propagation at the end of the test for the 3 models: A (left), B (center) and C (right).
Dans le texte

Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.

Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.

Le chargement des statistiques peut être long.