| Numéro |
Rev. Fr. Geotech.
Numéro 169, 2021
Hommage à Pierre Habib et Pierre Duffaut
|
|
|---|---|---|
| Numéro d'article | 6 | |
| Nombre de pages | 7 | |
| DOI | https://doi.org/10.1051/geotech/2021020 | |
| Publié en ligne | 15 octobre 2021 | |
Article de recherche / Research Article
Thermodynamique des grands glissements souterrains
Thermodynamics of rock mass slip
Laboratoire Navier, École des Ponts Paris Tech, Univ. Gustave Eiffel, CNRS,
Paris, France
* Auteur de correspondance : jean.sulem@enpc.fr
Les couplages thermo-hydro-chimio-mécaniques jouent un rôle central dans les grands glissements gravitaires et sismiques. À partir du travail original de Pierre Habib sur la vaporisation du fluide interstitiel comme mécanisme pouvant expliquer les vitesses extrêmes atteintes durant le glissement d’une masse rocheuse, nous donnons un éclairage sur les développements récents sur la physique des tremblements de terre.
Abstract
Thermo-chemo-mechanical couplings have been identified as factors that play a central role in the mechanics of large seismic or gravitational slip. The pioneering work of Pierre Habib on vaporization of the pore fluid as a mechanism that could explain extreme slip velocities during rock slides is recalled as a starting point of a review of recent works on the physics of earthquakes.
Mots clés : glissement sismique / couplages multi-physiques / failles / pressurisation thermique / localisation des déformations
Key words: seismic slip / multi-physics couplings / faults / thermal pressurization / strain localization
© CFMS-CFGI-CFMR-CFG, 2021
1 Introduction
La catastrophe du glissement du Vajont avait conduit Pierre Habib à explorer les mécanismes susceptibles d’expliquer les vitesses extrêmes de l’ordre de 30 m/s qui avaient été observées. Dans deux articles publiés, pour le premier, dans les Comptes rendus à l’Académie des sciences (Habib, 1967) et, pour le second, dans la revue Rock Mechanics (Habib, 1975), Pierre Habib avait analysé la production de chaleur frictionnelle générée par le glissement. Il avait montré que celle-ci était si intense, que l’eau interstitielle pouvait se vaporiser, formant ainsi des coussins de vapeur sur lesquels le massif rocheux pouvait glisser sans frottement. Ce même mécanisme a été proposé par Goguel et Pachoud (1972) pour expliquer le déplacement d’une énorme masse de terrain sur des pentes relativement faibles comme dans le cas du glissement du Granier.
Même s’il n’y a pas vaporisation de la pression interstitielle, la chaleur frictionnelle peut conduire à une élévation importante de la pression interstitielle dans la zone glissement, et donc à une réduction de la contrainte normale effective agissant sur le plan de glissement et, par conséquent, à une réduction de la résistance au cisaillement. Ce phénomène a été notamment étudié dans le cas du glissement de Vajont par Vardoulakis (2000, 2002) en considérant également le rôle de la présence d’argile dans la zone de cisaillement et les phénomènes de couplage thermo-hydro-mécanique. La pressurisation thermique de l’eau interstitielle et le radoucissement thermique de l’argile peuvent conduire à une instabilité du système, c’est-à-dire que dès que le glissement est initié, il évolue de manière dynamique et s’accélère rapidement.
Dans cet article, nous analysons les effets des couplages thermo-hydro-chimio-mécaniques mis en jeu lors d’un glissement sismique sur la résistance au cisaillement des failles et la localisation des déformations. Il faut noter que des phénomènes semblables peuvent être également observés lors des grands glissements de terrain.
2 Mécanismes de radoucissement de la résistance au cisaillement dans les glissements sismiques
Dans les grands glissements gravitaires ou sismiques, les phénomènes de radoucissement thermique jouent un rôle majeur dans la perte de résistance au cisaillement de la zone de glissement, l’initiation et l’accélération du mouvement.
Le modèle conceptuel du système bloc-ressort (Fig. 1) est couramment utilisé pour représenter l’interaction entre un bloc crustal élastique et une zone de faille. La force provoquant le glissement du bloc est appliquée au travers d’un ressort qui représente l’élasticité du bloc crustal environnant la zone de faille. L’instabilité par glissement saccadé (stick-slip) est possible si le taux de radoucissement de la résistance au cisaillement de la zone de faille est supérieur à la rigidité du bloc crustal. Par conséquent, il est primordial d’explorer les différents mécanismes d’affaiblissement de la résistance d’une faille pour comprendre l’initiation de cette instabilité frictionnelle. L’article de synthèse de Rice (2006) apporte un éclairage très complet sur les différents processus physiques qui conduisent à cette perte de résistance et donc au déclenchement et à la propagation des séismes.
Les observations de terrain des failles matures, c’est-à-dire de failles qui ont subi un glissement important, montrent l’existence d’une zone endommagée généralement assez vaste dans la faille, mais néanmoins suggèrent que le cisaillement au cours d’un séisme se produit dans des zones très étroites où la déformation de cisaillement est localisée. Des zones de localisation de la déformation, d’une épaisseur de l’ordre de quelques centaines de microns, nichées dans le cœur de la faille, sont souvent observées et sont interprétées comme la surface principale de glissement (principal slip zone). Comme cela a été souligné par Rice et al. (2014), l’épaisseur de la zone de déformation est un paramètre clé car des zones de déformation étroites concentrent l’échauffement par friction conduisant à de fortes élévations de température, et donc à un affaiblissement plus rapide de la résistance de la faille. La largeur de cette zone est déterminée par les différents processus physiques impliqués dans les mécanismes d’affaiblissement mais contrôle également les couplages multi-physiques qui s’y produisent lors du glissement dynamique. Ce paramètre joue également un rôle majeur dans le bilan énergétique du système car, comme nous le verrons dans les sections suivantes, il contrôle la rétroaction des termes dissipatifs dans l’équation du bilan énergétique. De plus, ce paramètre peut évoluer dans le temps car un radoucissement plus fort favorise une diminution de l’épaisseur de la bande de cisaillement, alors que la diffusion de chaleur et de fluide aura tendance à élargir cette zone de localisation (Platt et al., 2014).
Différents mécanismes de perte de résistance de la faille peuvent être mis en jeu à différents stades du glissement, selon les niveaux de pression interstitielle et de température atteints. Un effet micromécanique du glissement correspond à l’échauffement intense et très rapide (flash-heating) des aspérités de contact (Beeler et al., 2008 ; Rice, 2006). Ce mécanisme d’affaiblissement est courant pour la plupart des roches aux premiers stades du glissement, dès que la vitesse dépasse une valeur critique compris entre 0,01 et 0,1 m/s. Le radoucissement de la résistance au cisaillement se produit par une perte de résistance au contact des aspérités. La lubrification du plan de faille se produit aussi par la production de nanoparticules lors du glissement (Niemeijer et al., 2012) et est également responsable de l’affaiblissement du frottement. Compte tenu de l’omniprésence de fluides dans les zones de faille, la pressurisation thermique du fluide interstitiel par dissipation en chaleur de l’énergie de glissement réduit la contrainte normale effective agissant sur la faille et donc la résistance au cisaillement (Lachenbruch, 1980 ; Mase et Smith, 1987 ; Sulem et al., 2005 ; Sulem et al., 2007 ; Ghabezloo et Sulem, 2008). Cette pressurisation thermique est causée par la différence entre le coefficient d’expansion thermique de la matrice solide et celui du fluide interstitiel. Les couplages thermo-poro-mécaniques causés par le cisaillement peuvent également être associés à des effets chimiques tels que la déshydratation des minéraux ou la décomposition des carbonates (Sulem et Famin, 2009 ; Han et al., 2010 ; Brantut et al., 2011 ; Veveakis et al., 2012). De telles réactions induisent une augmentation de la pression interstitielle, car elles libèrent du fluide dans le système, mais elles limitent aussi l’augmentation de la température en raison de leur caractère endothermique, de sorte qu’une partie de la chaleur générée par le frottement est consommée par les réactions chimiques. D’autre part, ils peuvent former un assemblage minéral plus résistant ou plus faible que le matériau d’origine suivant la réaction et les différents minéraux mis en jeu (Brantut et Sulem, 2012). Pour des failles peu profondes, la vaporisation du fluide interstitiel limite aussi l’augmentation de la température (Chen et al., 2017). Ces différents mécanismes sont généralement invoqués pour expliquer l’absence d’anomalie thermique au voisinage des grandes failles crustales comme la faille de San Andreas. Une grande part de la chaleur frictionnelle est consommée dans ces processus endothermiques.
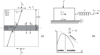 |
Fig. 1 (a) Modèle d’une zone de faille cisaillée par le mouvement de deux blocs crustaux ; (b) modèle conceptuel bloc-ressort et mécanisme d’instabilité par glissement saccadé (stick-slip). (a) Model of a fault zone embedded in an elastic crustal block; (b) conceptual model of a spring-slider system and stick-slip instability mechanism. |
3 Cisaillement adiabatique et non drainé
Afin de mettre en évidence, les phénomènes dominants qui se produisent lors du glissement sismique, nous considérons une couche d’épaisseur h infiniment longue saturée de fluide. Cette couche représente une zone de gouge de faille. Dans ce modèle unidimensionnel, les composantes de la vitesse, ux(z, t) et uz(z, t) dans la direction parallèle et normale à la faille, ne dépendent que du temps t écoulé depuis le début du glissement et de la position z dans la direction normale à la bande. On suppose que la couche est cisaillée par l’application d’une vitesse de déplacement constante V dans la direction x sur la frontière supérieure de la bande (Fig. 2). À l’intérieur de la bande, les champs de pression interstitielle p, et de température T sont eux aussi uniquement fonction du temps t et de la position z.
Les équations d’équilibre  imposent que l’état de contrainte est uniforme dans la couche.
imposent que l’état de contrainte est uniforme dans la couche.
L’équation de conservation de la masse fluide s’écrit sous la forme :
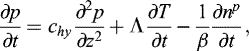 (1)
où chy est le coefficient de diffusivité hydraulique, β* est le coefficient d’emmagasinement, ∂np/∂t est le taux porosité plastique (variation irréversible de la porosité du matériau), Λ = n(λf−λn)/β* est le coefficient de pressurisation thermique, λf et λn sont les coefficients d’expansion thermique du fluide interstitiel et du milieu poreux, respectivement, et n la porosité du matériau.
(1)
où chy est le coefficient de diffusivité hydraulique, β* est le coefficient d’emmagasinement, ∂np/∂t est le taux porosité plastique (variation irréversible de la porosité du matériau), Λ = n(λf−λn)/β* est le coefficient de pressurisation thermique, λf et λn sont les coefficients d’expansion thermique du fluide interstitiel et du milieu poreux, respectivement, et n la porosité du matériau.
L’équation de conservation de l’énergie fait apparaître deux termes : un terme de diffusion et un terme source correspondant à la dissipation thermique du travail plastique :
 (2)
Dans l’équation (2), cth est coefficient de conductivité thermique, ρC la chaleur spécifique,
(2)
Dans l’équation (2), cth est coefficient de conductivité thermique, ρC la chaleur spécifique, 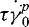 est la puissance plastique dont on suppose qu’elle est entièrement dissipée en chaleur. La contrainte de cisaillement est reliée à la contrainte effective de Terzaghi par le coefficient de frottement f : τ = f (σn−p).
est la puissance plastique dont on suppose qu’elle est entièrement dissipée en chaleur. La contrainte de cisaillement est reliée à la contrainte effective de Terzaghi par le coefficient de frottement f : τ = f (σn−p).
Le matériau au cœur de la faille a généralement une perméabilité très faible, bien inférieure à celle de la zone endommagée environnante (Wibberley, 2002 ; Sulem et al., 2004). Au cours d’un séisme, les fluides et la chaleur restent piégés dans la zone de glissement. C’est pourquoi, il est intéressant d’explorer la stabilité du glissement en conditions non drainées et adiabatiques. Pour cela, on suppose que les flux de chaleur et de fluide sont nuls aux bords supérieur et inférieur de la couche qui est cisaillée uniformément à vitesse de déformation constante  . Par conséquent, les champs de pression interstitielle et de température sont également uniformes au sein de la couche. On peut obtenir une solution analytique de leur évolution en temps (Lachenbruch, 1980 ; Rice, 2006 ; Sulem et al., 2007) sous la forme :
. Par conséquent, les champs de pression interstitielle et de température sont également uniformes au sein de la couche. On peut obtenir une solution analytique de leur évolution en temps (Lachenbruch, 1980 ; Rice, 2006 ; Sulem et al., 2007) sous la forme :
 (3)
La pression interstitielle augmente et tend vers la contrainte normale imposée σn et la température croît et tend vers T = T0 + (σn − p0)/Λ. Par conséquent, au cours de ce processus de pressurisation thermique, la résistance au cisaillement décroît et tend vers zéro.
(3)
La pression interstitielle augmente et tend vers la contrainte normale imposée σn et la température croît et tend vers T = T0 + (σn − p0)/Λ. Par conséquent, au cours de ce processus de pressurisation thermique, la résistance au cisaillement décroît et tend vers zéro.
L’étude de la stabilité de la solution adiabatique non drainée donnée ci-dessus peut être réalisée par une analyse de perturbation linéaire. On montre que dans l’hypothèse d’un coefficient de frottement constant, la solution est instable pour toutes les longueurs d’onde du mode de perturbation et la déformation se localise dans une zone d’épaisseur infinitésimale (Sulem et al., 2011 ; Rice et al., 2014). Cette localisation de la zone de glissement sur un plan reflète l’absence de longueur caractéristique comme par exemple une taille de grain qui limite la localisation en deçà d’une épaisseur minimale. Les lois de frottement de type Rate and State sont couramment utilisées en sismologie (Dieterich, 1979). Le coefficient de frottement dépend de la vitesse de sollicitation sous la forme : f = f0 + H log ( ) où H est un paramètre d’écrouissage en vitesse. Rice et al. (2014) ont montré que si le coefficient de frottement diminue avec la vitesse (comportement radoucissant) (H < 0), le glissement est instable pour toutes les longueurs d’onde du mode de perturbation. Par contre, pour un comportement à écrouissage positif en vitesse (H > 0), seules les zones de déformation dont l’épaisseur h est inférieure à une valeur critique
) où H est un paramètre d’écrouissage en vitesse. Rice et al. (2014) ont montré que si le coefficient de frottement diminue avec la vitesse (comportement radoucissant) (H < 0), le glissement est instable pour toutes les longueurs d’onde du mode de perturbation. Par contre, pour un comportement à écrouissage positif en vitesse (H > 0), seules les zones de déformation dont l’épaisseur h est inférieure à une valeur critique 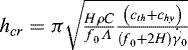 peuvent supporter une déformation homogène stable. Cette épaisseur critique est interprétée comme l’épaisseur de la zone de localisation de la déformation de cisaillement et ce résultat est corroboré par des simulations numériques dans le régime post-localisation (Platt et al., 2014).
peuvent supporter une déformation homogène stable. Cette épaisseur critique est interprétée comme l’épaisseur de la zone de localisation de la déformation de cisaillement et ce résultat est corroboré par des simulations numériques dans le régime post-localisation (Platt et al., 2014).
Pour des valeurs typiques de paramètres correspondant aux zones sismogéniques, cette épaisseur de la zone de localisation est de l’ordre de quelques dizaines de microns. C’est pourquoi, il apparaît nécessaire de tenir compte de la structure granulaire des gouges de faille dans la description du comportement. Cela peut être fait en ayant recours à la théorie des milieux de Cosserat. Les milieux de Cosserat qui comportent dans la description de la cinématique des degrés de liberté supplémentaires de rotation sont bien adaptés pour décrire le comportement de milieux granulaires (Vardoulakis et Sulem, 1995). Pour un milieu élastoplastique, Sulem et al. (2011) ont montré qu’une instabilité pouvait apparaître dans le régime d’écrouissage positif (pré-pic) si le phénomène de dilatance plastique ne suffit pas à accommoder la pressurisation thermique. Une analyse numérique de l’évolution du système dans le domaine post-bifurcation (Rattez et al., 2018a, Rattez et al., 2018b) a montré que la taille des grains détermine l’épaisseur de la zone de localisation. Plus la taille des grains est faible, plus la zone de localisation est étroite et plus la pente de la branche radoucissante de la réponse globale du système est forte (Fig. 3). Par ailleurs, une vitesse de cisaillement plus forte engendre une pressurisation thermique plus importante et, par conséquent, une localisation plus forte de la déformation et une diminution plus marquée de la résistance au cisaillement de la zone de faille (Fig. 4) même dans l’hypothèse d’un coefficient de frottement constant (plasticité parfaite).
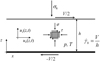 |
Fig. 2 Modèle d’une zone de faille sous cisaillement uniforme. Model of a fault zone as an infinite layer under uniform shear strain rate. |
 |
Fig. 3 Cisaillement simple d’une couche de roche modélisée comme un milieu de Cosserat : effet de la longueur interne R sur la courbe effort-déplacement et sur le profil de déformation (adapté d’après Rattez et al., 2018b). Simple shear of a Cosserat rock layer: effect of the internal length R on the stress-strain curve and on the shear strain profile (after Rattez et al., 2018b). |
 |
Fig. 4 Effet du couplage thermo-hydro-mécanique lors du cisaillement simple d’une couche de roche modélisée comme un milieu de Cosserat : effet de la vitesse de glissement sur la courbe effort-déplacement et sur la largeur de la zone de localisation dans le cas d’un comportement parfaitement plastique (la longueur interne de Cosserat R = 10 μm) (adapté d’après Rattez et al., 2018b). Simple shear of a Cosserat rock layer under thermo-hydro-mechanical couplings: effect of the slip rate on the stress-strain curve and on the shear band thickness for perfect plasticity (Cosserat internal length R = 10 μm) (after Rattez et al., 2018b). |
4 Effets chimiques induits par l’échauffement frictionnel
En plus des couplages thermo-hydro-mécaniques (THM) discutés ci-dessus, l’effet des réactions chimiques déclenchées par l’augmentation de la température peut induire des mécanismes supplémentaires d’affaiblissement. On observe couramment la présence d’argile et de phyllosilicates le long des principales zones de failles souterraines. Ces minéraux sont thermiquement instables et peuvent libérer de l’eau adsorbée et/ou structurelle tout en se transformant en un produit de réaction plus dense. En plus de ces réactions de déshydratation, la décomposition thermique des carbonates qui sont présents dans toutes les zones de faille de la transition ductile-fragile (∼15 km) a également été mise en évidence lors d’un glissement rapide (Famin et al., 2008 ; Collettini et al., 2014). La décomposition thermique des minéraux carbonatés crée des pics localisés de pression de CO2, entraînant une surpression locale et réduisant la contrainte effective sur le plan de faille (Sulem et Famin, 2009). De plus, la dissociation des carbonates produit des nanoparticules facilitant la lubrification des zones de glissement (De Paola et al., 2008). Ces réactions chimiques sont endothermiques, de sorte qu’une partie de la chaleur générée par le frottement est consommée dans la décomposition minérale.
Les études de terrain ont démontré l’existence d’un dégagement de CO2 lors d’un glissement sismique. Ces observations portent par exemple sur l’augmentation soudaine de la teneur en dioxyde de carbone dans les sources situées près de la faille de Nojima au Japon immédiatement après le tremblement de terre de Kobe en 1995 (Sato et Takahashi, 1997) et également sur la microstructure des zones de failles exhumées (Collettini et al., 2014).
Afin de prendre en compte les effets chimiques, l’équation de conservation de la masse fluide (1) est réécrite comme suit :
 (4)
Dans cette équation, ∂nd/∂t est le taux de porosité due à la réaction chimique, et md est la masse de fluide par unité de volume dégagée dans le système par la décomposition minérale.
(4)
Dans cette équation, ∂nd/∂t est le taux de porosité due à la réaction chimique, et md est la masse de fluide par unité de volume dégagée dans le système par la décomposition minérale.
L’équation (2) de conservation de l’énergie est aussi modifiée de la façon suivante afin de tenir compte du caractère endothermique de la réaction chimique :
 (5)
Dans cette équation, ΔHT est l’enthalpie de la réaction qui est positive lorsque celle-ci est endothermique.
(5)
Dans cette équation, ΔHT est l’enthalpie de la réaction qui est positive lorsque celle-ci est endothermique.
L’effet du changement de porosité dû à la décomposition solide sur la perméabilité peut être pris en compte en considérant une relation porosité-perméabilité de Carman-Kozeny. La figure 5 présente des résultats typiques :
-
la réaction chimique endothermique limite l’élévation de température à une valeur qui dépend de la cinétique de réaction ;
-
l’augmentation de la pression interstitielle est d’abord due à la pressurisation thermique puis s’accélère au début de la réaction jusqu’à un maximum puis diminue en raison de la réduction du volume solide et du processus de diffusion du fluide. Il en résulte une baisse initiale de la résistance au cisaillement suivi d’un renforcement.
Dans ces calculs, les conditions initiales correspondent à une profondeur de 7 km. La perméabilité initiale est de 10−19 m2 et le coefficient de frottement est pris égal à 0,1, ce qui correspond aux observations expérimentales qui montrent que le coefficient de frottement durant un glissement sismique est faible (Di Toro et al., 2004).
L’échauffement engendré par le cisaillement, la pressurisation thermique et la décomposition thermique des carbonates sont des mécanismes d’affaiblissement qui peuvent également expliquer les grands glissements de terrain. Le glissement de terrain de Heart Mountain au Nord-Ouest du Wyoming est le plus grand glissement de terrain subaérien connu. Ce glissement de terrain que l’on date à la période de l’Éocène couvre plus de 3000 km2 avec un très long déplacement de plus de 45 km (Hauge, 1993). La question est de savoir comment un volume de roche aussi massif a pu se déplacer sur une surface de base avec un pendage moyen de seulement 2°. Des observations de terrain et des expériences sur des roches prélevées dans la zone du glissement ont montré que, puisque la zone de cisaillement est située dans une couche de dolomie, une décomposition thermique et une libération de CO2 peuvent se produire, permettant à une énorme plaque supérieure de glisser sur un « coussin » de matériau sous pression (Goren et al., 2010 ; Mitchell et al., 2015). Comme pour le mécanisme de vaporisation proposé par Pierre Habib pour le glissement du Vajont et Jean Goguel pour le glissement du Granier, le déplacement d’une masse considérable de terrain sur des kilomètres n’est possible que si les processus physiques déclenchés peuvent réduire la résistance au cisaillement à une valeur quasiment nulle.
 |
Fig. 5 Effet de la décomposition thermique de la calcite sur une couche homogène d’une épaisseur de 5 mm cisaillée à une vitesse de 1 m/s. Les conditions initiales correspondent à une profondeur de 7 km. La perméabilité initiale est de 10−19 m2. (d’après Sulem et Famin, 2009). Effect of thermal decomposition of calcite on a homogeneous layer with a thickness of 5 mm sheared at a slip rate of 1 m/s. Initial conditions correspond to a depth of 7 km. Initial permeability is 10−19 m2 (after Sulem and Famin, 2009). |
5 Conclusion
Les études de terrain et de laboratoire récentes associées aux travaux de modélisation numérique ont mis en évidence l’importance des processus multi-physiques couplés dans le déclenchement et le développement des grands glissements. Ceux-ci ont mis en évidence que l’échauffement par friction, le radoucissement thermique de la résistance, la fragmentation des roches et la lubrification des failles par la production de nanoparticules, la pressurisation thermique des fluides interstitiels, les changements de phase et la décomposition thermique des minéraux sont des mécanismes d’affaiblissement de la zone de faille qui sont à présent bien identifiés et modélisés. Ils peuvent se déclencher à différentes étapes du processus de glissement et dépendent des conditions locales comme la profondeur et la minéralogie de la zone de faille.
Les travaux de Pierre Habib ont ouvert la voie et ont inspiré les développements qui ont suivi.
Références
- Beeler N, Tullis TE, Goldsby DL. 2008. Constitutive relationships and physical basis of fault strength due to flash heating. J Geophys Res 113(B1): B01401. [Google Scholar]
- Brantut N, Sulem J, Schubnel A. 2011. Effect of dehydration reactions on earthquake nucleation: stable sliding, slow transients, and unstable slip. J Geophys Res 116(B5): 1–16. [Google Scholar]
- Brantut N, Sulem J. 2012. Strain Localization and slip instability in a strain-rate hardening, chemically weakening material. J Appl Mech 79(3): 031004. [CrossRef] [Google Scholar]
- Chen J, Niemeijer A, Yao L, Ma S. 2017. Water vaporization promotes coseismic fluid pressurization and buffers temperature rise. Geophys Res Lett 44: 2177–2185. [CrossRef] [Google Scholar]
- Collettini C, Carpenter B, Viti C, et al. 2014. Fault structure and slip localization in carbonate-bearing normal faults: an example from the Northern Apennines of Italy. J Struct Geol 67: 154–66. [CrossRef] [Google Scholar]
- De Paola N, Collettini C, Faulkner DR, Trippetta F. 2008. Fault zone architecture and deformation processes within evaporitic rocks in the upper crust. Tectonics 27(4): 1–21. [Google Scholar]
- Dieterich JH. 1979. Modeling of rock friction: 1. Experimental results and constitutive equations. J Geophys Res 84(9): 2161–2168. [CrossRef] [Google Scholar]
- Di Toro G, Goldsby DL, Tullis TE. 2004. Friction falls towards zero in quartz rock as slip velocity approaches seismic rates. Nature 427: 774–777. [Google Scholar]
- Famin V, Nakashima S, Boullier A-M., Fujimoto K, Hirono T. 2008. Earthquakes produce carbon dioxide in crustal faults. Earth Planet Sci Lett 265: 487–497. [CrossRef] [Google Scholar]
- Ghabezloo S, Sulem J. 2008. Stress dependent thermal pressurization of a fluid-saturated rock. Rock Mech Rock Eng 42(1): 1–24. [Google Scholar]
- Goguel J, Pachoud A. 1972. Géologie et dynamique de l’écroulement du Mont Granier dans le massif de la Chartreuse. Bull BRGM III-1: 29–38. [Google Scholar]
- Goren L, Aharonov E, Anders MH. 2010. The long runout of the Heart Mountain landslide: Heating, pressurization, and carbonate decomposition. J Geophys Res Solid Earth 115: 1–15. [Google Scholar]
- Habib P. 1967. Sur un mode de glissement des massifs rocheux. C R Acad Sci Paris 264: 151–153. [Google Scholar]
- Habib P. 1975. Production of gaseous pore pressure during rock slides. Rock Mech 7(4): 193–197. [CrossRef] [Google Scholar]
- Han R, Hirose T, Shimamoto T. 2010. Strong velocity weakening and powder lubrication of simulated carbonate faults at seismic slip rates. J Geophys Res Solid Earth 115(3). [Google Scholar]
- Hauge TA. 1993. The Heart Mountain detachment, Northwestern Wyoming; 100 years of controversy. In: Snoke AW, Steidtmann JR, Roberts SM, eds. Geology of Wyoming: Memoir. Laramie, WY: Geological Survey of Wyoming, pp. 530–571. [Google Scholar]
- Lachenbruch AH. 1980. Frictional heating, fluid pressure, and the resistance to fault motion. J Geophys Res 85: 6097–6112. [CrossRef] [Google Scholar]
- Mase CW, Smith L. 1987. Effects of frictional heating on the thermal, hydrologic, and mechanical response of a fault. J Geophys Res 92(1): 6249. [CrossRef] [Google Scholar]
- Mitchell TM, Smith SAF, Anders MH, et al. 2015. Catastrophic emplacement of giant landslides aided by thermal decomposition Heart Mountain, Wyoming. Earth Planet Sci Lett 411: 199–207. [CrossRef] [Google Scholar]
- Niemeijer A, Di Toro G, Griffith AW, Bistacchi A, Smith SAF, Nielsen S. 2012. Inferring earthquake physics and chemistry using an integrated field and laboratory approach. J Struct Geol 39: 2–36. [CrossRef] [Google Scholar]
- Platt JD, Rudnicki JW, Rice JR. 2014. Stability and localization of rapid shear in fluid-saturated fault gouge: 2. Localized zone width and strength evolution. J Geophys Res Solid Earth 119(5): 4334–4359. [CrossRef] [Google Scholar]
- Rattez H, Stefanou I, Sulem J. 2018a. The importance of thermo-hydro-mechanical couplings and microstructure to strain localization in 3D continua with application to seismic faults. Part I: Theory and linear stability analysis. J Mech Phys Solids 115: 54–76. [CrossRef] [Google Scholar]
- Rattez H, Stefanou I, Sulem J, Veveakis M, Poulet T. 2018b. The importance of thermo-hydro-mechanical couplings and microstructure to strain localization in 3D continua with application to seismic faults. Part II: Numerical implementation and post-bifurcation analysis. J Mech Phys Solids 115: 1–29. [CrossRef] [Google Scholar]
- Rice JR. 2006. Heating and weakening of faults during earthquake slip. J Geophys Res 111(B5): B05311. [Google Scholar]
- Rice JR, Rudnicki JW, Platt JD. 2014. Stability and localization of rapid shear in fluid-saturated fault gouge, 1. Linearized stability analysis. J Geophys Res Solid Earth 119 (5): 4311–4333. [CrossRef] [Google Scholar]
- Sato T, Takahashi M. 1997. Geochemical changes in anomalously discharged groundwater in Awaji Island − after the 1995 Kobe earthquake. Chikyukagaku 31: 89–98. [Google Scholar]
- Sulem J, Vardoulakis I, Ouffroukh H, Boulon M, Hans J. 2004. Experimental characterization of the thermo-poro-mechanical properties of the Aegion Fault gouge. C R Geosci 336(4–5): 455–466. [CrossRef] [Google Scholar]
- Sulem J, Vardoulakis I, Ouffroukh H, Perdikatsis V. 2005. Thermo-poro-mechanical properties of the Aigion Fault clayey gouge − Application to the analysis of shear heating and fluid pressurization. Soils Found 45(2): 97–108. [CrossRef] [Google Scholar]
- Sulem J, Lazar P, Vardoulakis I. 2007. Thermo-poro-mechanical properties of clayey gouge and application to rapid fault shearing. Int J Numer Anal Methods Geomech 31(3): 523–540. [CrossRef] [Google Scholar]
- Sulem J, Famin V. 2009. Thermal decomposition of carbonates in fault zones: slip-weakening and temperature-limiting effects. J Geophys Res 114(B3): 1–14. [Google Scholar]
- Sulem J, Stefanou I, Veveakis M. 2011. Stability analysis of undrained adiabatic shearing of a rock layer with Cosserat microstructure. Granul Matter 13(3): 261–268. [CrossRef] [Google Scholar]
- Vardoulakis I. 2000. Catastrophic landslides due to frictional heating of the failure plane. Mech Cohes Frict Mater 5(6): 443–467. [CrossRef] [Google Scholar]
- Vardoulakis I. 2002. Dynamic thermo-poro-mechanical analysis of catastrophic landslides. Géotechnique 52(3): 157–171. [CrossRef] [Google Scholar]
- Vardoulakis I, Sulem J. 1995. Bifurcation analysis in geomechanics. CRC Press, Taylor & Francis. [Google Scholar]
- Veveakis M, Sulem J, Stefanou I. 2012. Modeling of fault gouges with Cosserat continuum mechanics: influence of thermal pressurization and chemical decomposition as coseismic weakening mechanisms. J Struct Geol 38: 254–264. [CrossRef] [Google Scholar]
- Wibberley CAJ. 2002. Hydraulic diffusivity of fault gouge zones and implications for thermal pressurization during seismic slip. Earth Planets Space 1: 1153–1171. [CrossRef] [Google Scholar]
Citation de l’article : Jean Sulem. Thermodynamique des grands glissements souterrains. Rev. Fr. Geotech. 2021, 169, 6.
Liste des figures
 |
Fig. 1 (a) Modèle d’une zone de faille cisaillée par le mouvement de deux blocs crustaux ; (b) modèle conceptuel bloc-ressort et mécanisme d’instabilité par glissement saccadé (stick-slip). (a) Model of a fault zone embedded in an elastic crustal block; (b) conceptual model of a spring-slider system and stick-slip instability mechanism. |
| Dans le texte | |
 |
Fig. 2 Modèle d’une zone de faille sous cisaillement uniforme. Model of a fault zone as an infinite layer under uniform shear strain rate. |
| Dans le texte | |
 |
Fig. 3 Cisaillement simple d’une couche de roche modélisée comme un milieu de Cosserat : effet de la longueur interne R sur la courbe effort-déplacement et sur le profil de déformation (adapté d’après Rattez et al., 2018b). Simple shear of a Cosserat rock layer: effect of the internal length R on the stress-strain curve and on the shear strain profile (after Rattez et al., 2018b). |
| Dans le texte | |
 |
Fig. 4 Effet du couplage thermo-hydro-mécanique lors du cisaillement simple d’une couche de roche modélisée comme un milieu de Cosserat : effet de la vitesse de glissement sur la courbe effort-déplacement et sur la largeur de la zone de localisation dans le cas d’un comportement parfaitement plastique (la longueur interne de Cosserat R = 10 μm) (adapté d’après Rattez et al., 2018b). Simple shear of a Cosserat rock layer under thermo-hydro-mechanical couplings: effect of the slip rate on the stress-strain curve and on the shear band thickness for perfect plasticity (Cosserat internal length R = 10 μm) (after Rattez et al., 2018b). |
| Dans le texte | |
 |
Fig. 5 Effet de la décomposition thermique de la calcite sur une couche homogène d’une épaisseur de 5 mm cisaillée à une vitesse de 1 m/s. Les conditions initiales correspondent à une profondeur de 7 km. La perméabilité initiale est de 10−19 m2. (d’après Sulem et Famin, 2009). Effect of thermal decomposition of calcite on a homogeneous layer with a thickness of 5 mm sheared at a slip rate of 1 m/s. Initial conditions correspond to a depth of 7 km. Initial permeability is 10−19 m2 (after Sulem and Famin, 2009). |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




