| Numéro |
Rev. Fr. Geotech.
Numéro 171, 2022
|
|
|---|---|---|
| Numéro d'article | 3 | |
| Nombre de pages | 30 | |
| DOI | https://doi.org/10.1051/geotech/2022003 | |
| Publié en ligne | 13 avril 2022 | |
Revue / Review Article
Analyses et modélisations sur les argiles plastiques du Sparnacien du Bassin parisien
Analyses and modelling of Paris Sparnacian plastic clays
1
Eiffage Génie Civil,
3-7 place de l’Europe,
78140
Vélizy-Villacoublay,
France
2
iTEC, School of Engineering and Architecture (HEIA-FR), HES-SO/University of Applied Sciences Western Switzerland,
Pérolles 80,
1700
Fribourg,
Switzerland
3
GeoMod SA,
Epinettes 32,
1007
Lausanne,
Switzerland
* Auteur de correspondance : yi.zhang@eiffage.com
Les argiles plastiques d’âge Sparnacien (Eocène inférieur) présentent un enjeu géotechnique fort pour le projet Grand Paris Express, un des plus grands projets du métro en cours de construction en Europe. Ces Argiles plastiques sont imperméables, normalement consolidées ou surconsolidées, et présentent un potentiel de gonflement. Le mécanisme de gonflement des Argiles plastiques est complexe car il dépend de ses caractéristiques physiques et chimiques, ainsi que de ses états mécaniques et hydriques. Dans cet article, nous présentons d’abord les analyses des retours d’expériences sur les Argiles plastiques, ainsi que les paramètres géotechniques et les lois de comportement utilisés dans ces REX. Ensuite, nous présentons les différentes méthodes de modélisation des Argiles plastiques, à savoir la solution analytique et empirique, la méthode aux éléments finis semi-probabiliste et l’approche probabiliste. De plus, les applications numériques aux différents types d’ouvrages sont également réalisées, à savoir puits, parois moulées et tunnels. Les résultats de ces calculs ont été comparés aux mesures d’auscultations, qui permettent de vérifier les résultats des simulations numériques. À la fin, une analyse inverse à l’aide de la méthode d’inférence Bayésienne a été effectuée pour préciser la prédiction du gonflement des Argiles plastiques.
Abstract
Paris plastic clays are impermeable, normally consolidated or overconsolidated, and exhibit a swelling potential. The swelling (mechanical and hydric) of plastic clays is one of the major geotechnical challenges in the Grand Paris Express project, because its mechanism is complex depending on its physical and chemical characteristics, as well as its mechanical and hydric states. In this article, we first present the analyses of several experiences of the projects constructed in the plastic clays, as well as the geotechnical parameters and the constitutive laws used in these projects. Then, we present the different analysing methods of plastic clays, namely: analytical and empirical solution, semi-probabilistic finite element model and probabilistic approach. In addition, their numerical applications to the different kinds of underground structures were also carried out, namely: shafts, diaphragm walls and tunnels. The results of these calculations have been compared with monitoring measurements, which allow verifying the results of numerical simulations. At the end, an analysis using the Bayesian inference was performed in order to gain accuracy in the prediction of the swelling of plastic clays.
Mots clés : Argiles plastiques / âge Sparnacien / projet Grand Paris Express / méthode d’analyse / modélisation / auscultation / inférence Bayésienne
Key words: Plastic clays / Sparnacian age / Grand Paris Express project / analysis method / modelling / monitoring / Bayesian inference
© CFMS-CFGI-CFMR-CFG, 2022
1 Introduction
Parmi les formations argileuses dans le bassin sédimentaire de la région parisienne, les Argiles plastiques (AP) sont issues de l’érosion des manteaux d’altération établis autour du bassin sous les climats chauds et humides de la fin du Crétacé, elles sont des produits de décomposition des roches par altération physico-chimique et sont des formations laguno-continentales. Sur la bordure méridionale du Bassin parisien, les argiles plastiques d’âge Sparnacien (Yprésien-Eocène inférieur) forment les premiers dépôts tertiaires et reposent sur la Craie campanienne (Filliat et Duvauchelle, 1981). Les argiles de la partie occidentale du Bassin parisien sont de faciès oxydé, bariolées de jaune et de rouge. Elles sont composées de smectites et d’interstratifiés kaolinites/smectites, avec des traces de kaolinites. Les argiles de la partie orientale du bassin débutent par un niveau dominant d’argile kaolinique et se terminent par un sable plus ou moins argileux, avec des lentilles de lignite interstratifiées et d’illite (Thiry, 1999).
Les Argiles plastiques, tout comme les anciennes carrières, les nappes d’eau souterraine, la dissolution du gypse et le retrait-gonflement des faciès argileux, font partie des enjeux géotechniques majeurs pour le projet Grand Paris Express (Fluteaux, 2013), un des plus grands projets de métro en cours de construction en Europe. Le gonflement des Argiles plastiques constitue un problème majeur pour les ouvrages (puits, parois moulées, tunnels, etc.) réalisés dans cette couche ou la traversant (Chen, 1975 ; Bultel, 2001; Perez-Romero et al., 2007 ; Nelson et al., 2015; CFMS, 2020). Les caractéristiques géotechniques des Argiles plastiques peuvent impacter la stabilité de fond de fouille des puits ou des gares, la butée pour les parois moulées, la stabilité frontale des tunnels, etc. l’estimation de gonflement nécessite la détermination d’une part des paramètres mécaniques, et d’autre part des paramètres de gonflement. Le retour d’ expériences montre que les Argiles plastiques avec la présence de poches de sables ou de lithofaciès sableux peuvent induire la rupture de front de taille (Schlosser et al., 1995), le soulèvement du radier et le rapprochement des piédroits suivis par la fissuration puis la rupture du revêtement (Meyer, 2018).
Cet article présente d’abord une analyse sur des retours d’ expériences des ouvrages réalisés dans les Argiles plastiques, ainsi que les paramètres géotechniques et géomécaniques retenus et les lois de comportement utilisées. Ensuite, les différentes méthodes d’ analyse et modélisation (analytique et empirique, modèle numérique semi-probabiliste, approche probabiliste) pour simuler les Argiles plastiques ont été présentées, les applications numériques aux différents types d’ouvrages (puits, parois moulées et tunnels) ont été également effectuées. Les résultats de ces simulations numériques ont été comparés aux mesures d’auscultation, ce qui permet de vérifier les résultats des calculs. Àla fin, une analyse inverse à l’aide de la méthode d’inférence Bayésienne se basant sur les mesures d’auscultation a été effectuée afin de préciser la prédiction du gonflement des Argiles plastiques.
2 Analyse des retours d’expériences
L’analyse des Retours d’EXpériences (REX) des projets réalisés dans les Argiles plastiques est ici présentée, ainsi que les paramètres géotechniques/géomécaniques retenus et les lois constitutives de comportement utilisées dans ces projets.
2.1 Projets réalisés
Nous présentons les REX retrouvés dans la littérature (y compris les dossiers de consultation d’entreprise - DCE) en fonction de leur localisation dans le Bassin parisien (Fig. 1).
Àl’Ouest: projet EOLE entre Paris et La Défense (DCE), tunnel Duplex A86 à Rueil-Malmaison (Demay et Leroi, 2003 ; Decker, 2012), bâtiment de la Fondation Louis-Vuitton à Paris 16e (Beaussier et al., 2011), projet SIAAP à Suresnes (Launay, 1990);
Au Sud-Ouest : tramway T6 à Viroflay (DCE), métro ligne 15 à Issy-Les-Moulineaux (Nejjar, 2019 ; Zhang et al., 2022);
Au Sud : métro ligne 7 à Ivry (Meyer, 2018), métro ligne 14 à Paris Maison-Blanche (Zhang et al., 2020a, 2020b, 2021), projet SIAAP à Villejuif (Bouvet et Berbey, 1999), projet de transfert des eaux pluviales de Masséna Paris XIII à Ivry (Lechantre et Trottin, 2007);
Au Sud-Est: projet d’assainissement dans le Val-de-Marne (Schlosser et al., 1995), puits d’essai à Saint-Maur (DCE), métro ligne 15 à Saint-Maur et Créteil (Zhang et al., 2022).
Les significations d’abréviation des couches géologiques sont : RB : Remblai ; EB : Eboulis ; A : Alluvions ; COLL : Colluvions ; SF : Sables de Fontainebleau ; MH : Marnes à huîtres ; AV : Argiles vertes ; MSG : Marnes supragypseuses ; CC : Calcaires de Champigny ; CSO : Calcaires de Saint Ouen ; SB : Sables de Beauchamp ; MC : Marnes et Caillasses ; CG : Calcaires grossiers ; SC : Sables de Cuise ; SS : Sables supérieurs ; FG : Fausses glaises ; SA : Sables d’Auteuil ; AP : Argiles plastiques ; CMM : Calcaires et Marnes de Meudon ; C : Craie du Campanien.
De plus, la description en détail du projet est présentée dans le tableau 1. Quelques observations sur les Argiles plastiques pendant les travaux de certains projets sont également citées ci-après.
En 1937, les travaux du garage de 510 m de long au Sud-Est de la station Mairie d’Ivry de la ligne 7 du métro ont été réalisés, le creusement a été effectué essentiellement dans les Argiles plastiques par méthode conventionnelle, un rapprochement des piédroits et un soulèvement du radier ont été constatés. Du 25 au 30 juillet 1939, le radier se brisa sous les poussées verticales des Argiles plastiques. Simultanément, des poussées latérales basculaient les piédroits. Devant la gravité des désordres, il fut décidé de remblayer 237 m de souterrain au niveau de la partie accidentée (Meyer, 2018).
En 1990, dans le cadre de l’aménagement de l’émissaire Sèvres-Achères du SIAAP, une cavité elliptique de dimension H × B × L=16 × 13 × 60 m a été réalisé à Suresnes. La cavité s’inscrit dans les Argiles plastiques sur son quart supérieur et dans les Marnes de Meudon et la Craie sur ses trois quarts inférieurs. La cavité a été réalisée par la nouvelle méthode autrichienne (NATM) avec 4 phases de terrassement. Malgré un soutènement lourd (1 boulon/m2 et une coque épaisse de 25 à 40 cm) et immédiat, les déplacements importants en calotte (environ 50 mm) ont été observés (Launay, 1990).
En 1993, des travaux de création de collecteurs pour l’assainissement du Val-de-Marne ont été lancés. Dans un des puits, la galerie de recul du tunnelier (3,6 m de diamètre, 20 m de long) s’est effondrée lors des travaux de creusement en traditionnel dans les Argiles plastiques. C’est le front de taille qui a cédé, au bout de 4 m de creusement, sous la pression d’eau importante d’une poche de sable située juste derrière le front de taille. l’analyse effectuée avait montré que l’accident était dû à la présence d’une poche de sables importante, en communication avec les nappes, et d’un affaissement localisé de la couche des Argiles plastiques (Schlosser et al., 1995).
En 1999, dans le cadre de l’aménagement de l’émissaire Cachan-Villejuif du SIAAP, une chambre de réparation de tunnelier de dimensions Φ × L = 9 × 6,5 m a été réalisée. La cavité s’inscrit dans les Fausses glaises sur son quart supérieur et dans les Argiles plastiques sur ses trois quarts inférieurs. Le soutènement mis en place consiste en des boulons (1 boulon/0,8 m2) avec une coque épaisse de 25 cm. La convergence totale est de l’ordre de 40 mm (Bouvet et Berbey, 1999).
En 2006, dans le cadre de la réalisation des ouvrages de transfert des eaux pluviales de l’Est parisien vers la station de Valenton, un tunnel de raccordement Périphérique-Masséna a été creusé à l’aide d’un tunnelier à pression de terre de 4,96 m de diamètre. La section s’inscrit dans les Fausses glaises en partie supérieure et dans les Argiles plastiques sur le tiers inférieur. l’utilisation de mousse biodégradable a permis d’améliorer considérablement les paramètres de creusement qui sont les puissances nécessaires à donner au couple de rotation de la roue de coupe et de la vis d’extraction des déblais. Cette amélioration est obtenue essentiellement par une lubrification dans la chambre d’abattage et dans le corps de vis (Lechantre et Trottin, 2007).
Entre 2000 et 2007, un tunnel duplex entre Rueil-Malmaison et Vélizy a été réalisé dans le cadre de bouclage de l’autoroute périphérique A86 autour de Paris. Le creusement a été effectué au moyen d’un tunnelier à confinement mixte (pression de terre ou pression de boue) de 11,5 m de diamètre. Du retard a été pris à la traversée des Argiles plastiques et des Fausses glaises lié au colmatage de la roue de coupe, ce qui a conduit à des cadences réduites de 5,5 ml/jour, par rapport à un avancement moyen de 7,6 ml/jour (Decker, 2012).
Ces retours d’expérience dans les Argiles plastiques ont montré que ce type de terrain est très déformable, parfois avec la présence des poches de sables importantes. Ces argiles présentent un comportement complexe, qui peut générer des difficultés importantes pour la mise en œuvre du terrassement et la réalisation des ouvrages souterrains.
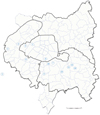 |
Fig. 1 Localisation des projets du REX sur la carte de Grand Paris. Feedback projects localization over the Grand Paris map. |
2.2 Analyse des paramètres géotechniques et géomécaniques
Les valeurs des paramètres géotechniques/géomécaniques utilisés pour les Argiles plastiques dans ces projets du REX sont présentées dans le tableau 2, ainsi que les lois de comportement employées.
Grâce à cette analyse, nous pouvons mettre en avant les points suivants :
Les Argiles plastiques sont très déformables. Les REX ont également montré la variabilité spatiale des paramètres géotechniques dans les différents contextes géologiques.
Les Argiles plastiques ont un coefficient de perméabilité très faible, et peuvent être considérées comme imperméables. La saturation est proche de 100 %, elles peuvent être considérées saturées dans leur état naturel et présentent un indice de plasticité élevé.
Généralement, les caractéristiques mécaniques des Argiles plastiques (EM,pl*,cu) augmentent avec la profondeur. En fonction de leur valeur et de la présence ou non de couverture de Calcaire grossier, le faciès des Argiles plastiques peut être distingué en deux ou trois sous faciès. Les paramètres drainés (c’, φ’) des Argiles plastiques sont intrinsèques. Ils peuvent avoir les mêmes valeurs pour toute la couche ou les valeurs plus raffinées et légèrement différentes selon les sous-faciès.
La contrainte horizontale, et la poussée horizontale qui s’exercera sur les structures, dépendent de l’état de surconsolidation des terrains. Le coefficient des terres au repos K0 varie entre 0,8 et 1,3 pour les Argiles plastiques, et peut être pris égal à 1 dans les calculs.
De plus, l’aptitude au gonflement des Argiles plastiques doit être pris en compte dans la conception et le dimensionnement des ouvrages souterrains (Chen, 1975 ; Bultel, 2001; Perez-Romero et al., 2007 ; Nelson et al., 2015 ; CFMS 2020). Il inclut principalement deux parties : le gonflement résultant du déchargement mécanique et le gonflement hydrique. Par contre, comme pour les autres argiles gonflantes (Alonso et al., 1999; Gonzalez et al., 2012; Avgerinos et al., 2016 ; Hong et Wang, 2016), le gonflement des Argiles plastiques est complexe et fait intervenir plusieurs mécanismes (hydriques, mécaniques et physico-chimiques). C’est pourquoi le choix de la loi de comportement appropriée avec des paramètres bien calibrés est très important pour simuler correctement leur comportement.
Paramètres géotechniques/géomécaniques et lois de comportement des Argiles plastiques.
Geotechnical/geomechnical parameters and constitutive laws of the plastic clays.
2.3 Analyse des lois de comportement
La loi constitutive basée sur le critère de Mohr-Coulomb est bien connue des géotechniciens. Datant de la fin du XIXe siècle, elle est encore couramment enseignée dans les écoles, et la détermination de ses paramètres principaux peut être aisément effectuée en laboratoire. Elle est adéquate pour définir le comportement à la ruine de la plupart des sols meubles, mais peine à reproduire fidèlement le comportement à l’état de service de ces sols, principalement parce qu’elle ne permet pas la distinction entre charge et décharge, mais aussi parce que le module d’élasticité ne dépend pas du niveau de contrainte. Par la suite, dans les années 1970, les lois de comportement de la famille Cam Clay, ou Modified Cam Clay, ont offert la possibilité de reproduire le comportement d’échantillons d’argile observé en laboratoire lors de tests œdométriques, tout en différenciant comportement en charge et en décharge.
Au début des années 2000, la famille de modèles «Hardening Soil» fait son apparition. Elle combine l’ utilisation du critère de rupture de Mohr-Coulomb avec lavariationde larigidité dusolselonles modes de charge ou de décharge, la dépendance de la rigidité du sol en fonction du niveau de contrainte, la définition du phénomène de pré-consolidation, et l’apparition de déformations plastiques avant l’ état limite. Elle est générique, dans le sens qu’elle s’applique autant aux sols granulaires qu’aux sols fins, et permet de reproduire fidèlement les essais triaxiaux conduits en laboratoire. Enfin, il est également possible d’y intégrer une grande rigidité dans le domaine des petites déformations.
Il existe d’autres modèles plus sophistiqués (exemple : la famille des modèles de Hujeux [Hicher et Shao, 2008]) développés afin de permettre la prise en compte des sollicitations visco-thermo-plastiques cycliques (Modaressi et Laloui, 1997). La viscosité permet effectivement de mieux simuler les effets du temps sur les argiles, plus particulièrement sous les sollicitations dynamiques. Par contre, il est difficile d’effectuer des essais de laboratoire qui peuvent isoler la partie viscosité. Ces modèles sont principalement utilisés dans le monde académique et ne sont pas, à notre connaissance, implémentés dans les logiciels commerciaux utilisés pour les calculs aux éléments finis appliqués aux projets de construction comme Grand Paris Express.
Ceci dit, les modèles élasto-plastiques avec écrouis-sage comme le «Hardening Soil Model» ont connu récemment de nombreux développements, l’étude des tassements des sols étant effectuée à l’aide des résultats de la courbe de compressibilité œdométrique et de la théorie de la consolidation, dans laquelle la viscosité des déformations du squelette du sol est négligée. Le retour d’ expérience montre que cette approche donne des résultats satisfaisants dans la plupart des projets. C’est à notre sens, aujourd’hui, le meilleur rapport «qualité-prix » dans le monde des lois constitutives appliquées aux sols meubles. Dans les projets du REX, les lois constitutives de comportement utilisées pour les Argiles plastiques sont:
EPMC : Elastoplastique Mohr Coulomb ;
HSM: Hardening Soil Model.
La loi de comportement EPMC est la plus simple à calibrer. Elle a besoin de 5 paramètres : E (module de déformation), c (cohésion), φ (angle de frottement), υ (coefficient de Poisson) et Ψ (angle de dilatance). Bien que la résistance ultime au cisaillement soit modélisée par la loi de Mohr Coulomb, la non-linéarité n’est pas simulée.
La loi de comportement HSM (Schanz et al., 1999) est donc considérée plus adaptée pour prédire les déplacements dans les travaux souterrains (Hejazi et al., 2008). Le modèle HSM peut être considéré comme une amélioration de modèle hyperbolique de Duncan-Chang (Duncan et Chang, 1970). La surface de charge est décrite par deux mécanismes avec écrouissage isotrope dépendant des déformations volumiques et déviatoriques (Fig. 2). Le modèle HSM différencie le module de chargement E50 et le module de déchargement Eur, cela aide à modéliser le gonflement des Argiles plastiques lors d’un déchargement mécanique.
Dix paramètres sont nécessaires pour définir cette loi HSM:
3 modules du sol : E50 (module sécant de référence en situation triaxiale), Eur (module élastique de déchargement/rechargement), Eoed (module tangent de référence sous sollicitation œdométrique) ;
3 paramètres de résistance : c (cohésion), φ (angle de frottement), Ψ (angle de dilatance) ;
4 paramètres de contrainte : m (exposant pour caractériser la dépendance de raideur avec les contraintes), υur (coefficient de Poisson élastique), Rf (ratio de rupture), pref (pression de référence).
L’effet du gonflement hydrique des Argiles plastiques peut être modélisé à l’aide de la loi de comportement Huder et Amberg - HA (Huder et Amberg, 1970). Par exemple, dans le logiciel ZSOIL (ZSOIL, 2018), l’application de cette loi HA est illustrée dans la figure 3. Les paramètres utilisés sont: σ (pression limite de gonflement) ; κ (rapport déformation/contrainte dans l’essai de gonflement œdométrique Huder-Amberg) ; B (temps de détente totale pour le cas du gonflement libre).
 |
Fig. 2 Loi de comportement Hardening Soil Model (HSM). Hardening Soil Model (HSM) law. |
 |
Fig. 3 Loi de comportement Huder-Amberg (HA) dans ZSOIL. Huder-Amberg (HA) law in ZSOIL. |
3 Méthodes de modélisation
Traditionnellement, la conception géotechnique a souvent été réalisée à l’aide de solutions analytiques et empiriques, avec des coefficients de sécurité basés souvent sur le retour d’expérience.
Dans le cadre des Eurocodes, la méthode semi-probabiliste a été introduite dans la conception géotechnique. Les valeurs retenues des paramètres géotechniques de résistance des sols sont des valeurs caractéristiques, c’est-à-dire qu’elles correspondent au fractile 5 % de la distribution des échantillons disponibles. Cette approche semi-probabiliste est également combinée à des coefficients de sécurité, permettant de traiter la variabilité des propriétés des sols.
Nous estimons que, compte tenu de la sensibilité des résultats des calculs par rapport aux données d’entrée, la variabilité spatiale des sols, etc., l’approche probabiliste est pertinente pour évaluer les effets combinés de ces incertitudes. De plus, la méthode observationnelle permet de palier l’imprécision de certaines approches de calcul et/ou la connaissance parfois limitée de l’objet de la modélisation et des lois constitutives des sols. Une approche probabiliste, cadrée par une analyse d’ inférence Bayésienne formalisant la méthode observationnelle, pourra jouer àl’avenir un rôle important pour modéliser et appréhender le comportement des sols et structures.
Cette approche probabiliste devrait être basée sur des données géotechniques précises. Un nombre suffisant de reconnaissances géologiques et hydrogéologiques de qualité, une analyse géotechnique appropriée des propriétés des sols, le bon jugement géotechnique de l’ ingénieur, etc. sont des prérequis garantissant une approche probabiliste de qualité.
3.1 Solution analytique et empirique
Aujourd’hui, ce type de solutions analytiques et empiriques est plutôt utilisé en phase d’études de faisabilité ou d’avant-projet. Son avantage est la facilité d’utilisation pour estimer l’ordre de grandeur des résultats recherchés. Par contre, il est souvent basé sur des hypothèses simplifiées et ne permet pas de considérer d’ une manière précise le phasage des travaux, la non-linéarité du comportement des géomatériaux et l’interaction sol-structure, etc.
Par exemple, dans un terrain purement cohérent et relativement homogène comme les Argiles plastiques, l’AFTES recommande d’évaluer la stabilité du front de taille d’ un tunnel à l’ aide du calcul du facteur de charge N au niveau de l’axe du tunnel, qui est donné par l’équation (1) (AFTES GT16R1F1, 1995):
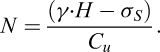 (1)
(1)
Pour γ (poids volumique du terrain) = 20 kN/m3,H (profondeur de l’axe du tunnel) = 35 m, σS (surcharge appliquée en surface) = 0 kPa et cu (cohésion non drainée) = 100 kPa, le facteur de charge N est estimé à 7, supérieur à 3, seuil des instabilités locales. De plus, la rupture du front peut se produire lorsque la valeur de N est proche de 6. On en déduit qu’en pleine section, la stabilité du front n’est pas assurée sans confinement.
Pour un autre exemple, la méthode analytique (Éq. (2)) peut être utilisée pour estimer le gonflement des Argiles plastiques. Elle suppose un soulèvement du sol unidimensionnel, ce qui semble valable pour une fouille classique de grande largeur (hors effet d’accrochage des parois). Le calcul de l’épaisseur de sol soulevé par le déchargement mécanique se calcule en discrétisant la couche des sols gonflants et en additionnant les soulèvements unitaires calculés selon la relation (Fredlund et Rahardjo, 1993 ; CFMS, 2020):
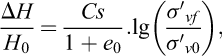 (2)
(2)
avec :
ΔH : gonflement vertical dû à la diminution des contraintes verticales ;
H0 : épaisseur du matériau considéré ;
Cs : indice de gonflement (ou décompression) ;
e0 : indice des vides du matériau considéré ;
σ’vf: contrainte verticale effective après excavation;
σ’v0 : contrainte verticale effective avant travaux.
3.2 Méthode aux éléments finis semi-probabiliste
L’application de la méthode des éléments finis (MEF) àl’analyse de problèmes géotechniques est aujourd’hui largement répandue. La méthode MEF nécessite également des adaptations aux sujets spécifiques de l’ingénierie géotechnique (Potts et Zdravkovic, 1999; Zienkiewicz et al., 1999; Lees, 2016). Les modèles réalisés à l’aide des logiciels comme PLAXIS, ZSOIL, CESAR-LCPC, etc. permettent d’étudier finement les sujets comme l’interaction sol-structure prenant en compte le phasage des travaux, la non-linéarité des sols et des structures, les conditions hydrauliques et les chargements complexes, etc.
À part la qualité du maillage, la précision de la méthode MEF dépend beaucoup du choix des lois constitutives de comportement et des paramètres géotechniques des géomatériaux, souvent calibrés sur les essais in situ ou en laboratoire. Le choix des valeurs caractéristiques de ces paramètres est également important, et se base sur une approche semi-probabiliste. Il est nécessaire de bien définir les hypothèses du calcul.
Les modèles 2D sont couramment utilisés dans la modélisation en géotechnique. Des modèles 3D sont également utilisés pour les problèmes complexes, avec la nécessité de considérer l’effet tridimensionnel du projet (Guilloux, 2012 ; Zhang et al., 2020b). Une analyse par MEF bien exécutée peut fournir une simulation raisonnablement précise d’une structure géotechnique. En revanche, à ce jour, il n’y a pas de modèle constitutif pouvant reproduire tous les aspects du comportement réel du sol. Il est donc important de reconnaître dans l’ analyse quels aspects du problème sont d’ un intérêt majeur et de choisir un modèle approprié. De plus, l’ application de la méthode observationnelle permet de vérifier et recadrer certaines hypothèses pendant les travaux, ainsi que d’effectuer des retro-analyses avec ces hypothèses mises à jour.
3.3 Approche probabiliste
Le choix des valeurs caractéristiques des paramètres géotechniques peut influer fortement sur les résultats des calculs. Par contre, le manque de données, la variabilité spatiale des sols, la sensibilité des résultats par rapport aux données d’entrée, … sont des sujets difficilement traités par un calcul déterministe, voire semi-probabiliste. Dans ce cas, l’approche probabiliste peut être une meilleure solution pour prendre en compte ces incertitudes (Baecher et Christian, 2003 ; Ang et Tang, 2007 ; Phoon et Retief, 2016).
Un calcul de fiabilité, dans le cadre d’une approche probabiliste, permet d’évaluer les effets combinés des incertitudes par une probabilité de défaillance Pf ou un indice de fiabilité (3.l’approche probabiliste fournit un moyen de distinguer les conditions où les incertitudes sont particulièrement élevées ou faibles (Zhang et Toutlemonde, 2020). Nous pouvons adopter les étapes suivantes pour appliquer la méthode MEF probabiliste aux analyses géotechniques (Zhang et Commend, 2021):
réaliser un modèle aux éléments finis à l’aide d’un logiciel comme ZSOIL (ZSOIL, 2018);
identifier les paramètres les plus importants et définir les descriptions statistiques de ces paramètres (loi de probabilité, valeur moyenne, écart type ou coefficient de variation, etc.);
établir la formulation de la fonction limite (facteur de sécurité > 1, tassement < seuil, etc.) ;
calculer la probabilité de défaillance Pf et l’indice de fiabilité (3 en utilisant les méthodes de calcul de fiabilité comme FORM (First Order Reliability Method), MCS (Monte Carlo Simulation), AK-MCS (Adaptive Kriging Monte Carlo Simulation), etc. à l’aide d’un logiciel comme UQLab (Marelli et Sudret, 2014).
De plus, si des mesures issues d’auscultations ou des observations sont disponibles, la comparaison entre les résultats numériques et les mesures en cours de réalisation est recommandée, afindevérifier les résultats des calculs probabilistes et orienter les choix techniques du projet via la méthode observationnelle, couplée à une analyse inverse avec la méthode d’ inférence Bayésienne (Fig. 4).
 |
Fig. 4 Description de l’approche probabiliste et comparaison avec l’approche déterministe ou semi-probabiliste. Probabilistic approach and comparison with the deterministic or semi-proiaii/istic approach. |
4 Applications des méthodes numériques aux ouvrages
Nous présentons dans ce chapitre les applications des méthodes aux éléments finis 2D et 3D en semi-probabiliste et probabiliste à un cas concret: la gare de la Maison-Blanche Paris (MBP). Ce projet inclut la future gare du métro ligne 14 MBP, un tunnel et une correspondance. Il est conditionné d’une part par les enjeux géotechniques forts comme la présence des Argiles plastiques, et d’ autre part par la proximité de constructions préexistantes très sensibles et très vulnérables (Fig. 5).
La conception de la gare est fondée sur des parois moulées avec des dalles et prébutons. Son radier est situé dans les Argiles plastiques, un vide sanitaire est prévu audessous pour éviter la sollicitation sous le radier dû à la pression de gonflement. Les parois moulées sont ancrées dans la Craie du Campanien, elles prennent appui sur les prébutons dans le sens transversal de la gare, réalisés avant terrassement et constitués de panneaux en béton non armé qui jouent le rôle de buton dans les Argiles plastiques. Cette conception permet de limiter la déformation des parois, ainsi que des déformations plastiques trop importantes des Argiles plastiques, afin de limiter le tassement en surface. La conception du tunnel choisit la forme de contre-voûte pour le radier du tunnel, dimensionné pour reprendre la pression de gonflement des Argiles plastiques.
Concernant les constructions voisines préexistantes, la Tour Super Italie (TSI) est un bâtiment de 112 m de haut et de 36 étages avec 4 niveaux de sous-sols. Sa fondation superficielle, distante de 1,7 m de la paroi Est, se situe à +42 NGF dans les Calcaires grossiers inférieurs. La station Maison-Blanche de la ligne 7 se trouve à une distance de 2,5 m de la paroi Ouest. Son radier se situe à +40 NGF dans les Calcaires grossiers inférieurs. Compte tenu de ces contraintes, le projet est réalisé avec un phasage précis. La zone Nord de la gare est construite dans un premier temps afin de pouvoir réaliser le tunnel. Les parois moulées et le puits blindé TN2 sont tout d’abord réalisés (Fig. 6), ce qui représente une phase critique du projet permettant de confirmer la faisabilité technique et respecter le planning.
Prenant appui sur les résultats des essais in situ et en laboratoire, ainsi que sur la synthèse géotechnique réalisée sur ces essais (Zhang et al., 2022), les valeurs des paramètres géotechniques retenues pour les Argiles plastiques sont présentées dans le tableau 2 (ligne 8) et précisées dans le tableau 3 pour la loi HSM. Dans le calcul, il est admis que seules les Argiles plastiques supérieures et moyennes gonflent, puisque ce sont elles qui sont situées dans le voisinage immédiat du radier du tunnel. Les paramètres de la loi de comportement HA pour les deux couches gonflantes sont illustrés à la figure 3.
 |
Fig. 5 Gare Maison-Blanche avec les constructions voisines et coupe géologique du site. Maison-Blanche station with neighbouring structures and geological section of construction site. |
 |
Fig. 6 Illustration du puits TN2 et photo de son terrassement dans les Argiles plastiques. TN2 shaft illustration and earthworks photo in the plastic clays. |
Hypotheses geomecaniques retenues pour les calculs.
Geomechnical hypothesis for the calculations.
4.1 Ouvrages de soutènement (puits et paroi moulée)
Pour le puits TN2 et les parois moulées de la zone Nord, les différentes approches de modélisation (approches non drainée, drainée et transitoire en 2D axisymé-trique, approches en 3D) ont été présentées et comparées dans lesarticlesréférencésci-après( Zhang et al., 2020a, 2020b). Nous présentons ici un modèle 3D réalisé à l’aide du logiciel ZSOIL 3D. Dans ce modèle, on introduit d’une manière fine la fondationdela tourTSI, letunnelde la ligne 7, le puits TN2, les parois moulées et prébutons, l’amorce du nouveau tunnel de la ligne 14 et l’excavation de la moitié Nord de la boîte gare. Ce modèle comporte environ 300 000 éléments (Fig. 7). Par contre, les étapes de réalisation du puits TN2 et du tunnel sont simplifiées. Le phasage principal considéré est :
État initial non déformé ;
Introduction des parois moulées de la zone Nord ;
Excavation et soutènement du puits TN2 (étapes simplifiées de 3 à 4m au moyen d’un taux de déconfinement équivalent, calé de manière à obtenir des déplacements équivalents à ceux d’un modèle 3D raffiné) ;
Excavation du tunnel ;
Remblayage du puits, dépose des liernes et bracons ;
Exécution du reste des parois moulées ;
Excavation en taupe de la gare, avec mise en place des dalles.
Le premier rôle du modèle 3D est de fournir une prédiction fiable de l’influence de l’excavation du puits, puis du tunnel et de la gare, sur les constructions voisines, en particulier la ligne 7 de métro et la Tour Super Italie. Ils ont permis de vérifier que les déformations des parois moulées et des bâtiments voisins restent admissibles (Tab. 4). De plus, les efforts calculés dans le puits TN2 sont utilisés pour dimensionner le blindage, et les efforts calculés dans les parois moulées sont utilisés pour leur dimensionnement en complément des calculs 2D effectués avec la méthode des modules de réaction.
En outre, pour étudier la sensibilité des calculs 3D vis-à-vis des hypothèses de calcul comme celle relative à la valeur du module de déformation des Argiles plastiques, le frottement entre les prébutons et les Argiles plastiques, les conditions de drainage (CT = court terme, LT = long terme), etc., des études paramétriques ont été réalisées. Les résultats de ces études paramétriques montrent la sensibilité des déformations des parois moulées et des constructions voisines vis-à-vis de ces hypothèses de calcul, ils confirment également que ces déformations sont toujours inférieures aux seuils contractuels (Tab. 4).
Grâce aux résultats d’auscultation, les résultats des calculs ont pu être comparés aux mesures. Les résultats des inclinomètres montrent que les déplacements obtenus dans les parois moulées sont généralement proches des résultats des calculs à court terme, parfois inférieurs à ceux estimés par les calculs (Fig. 8), ceci est également confirmé par les mesures topographiques sur les liernes du blindage. Les résultats des extensomètres illustrent bien le gonflement des Argiles plastiques lié au déchargement mécanique suite au terrassement (Fig. 8).
Ces études permettent de mettre en évidence les faits suivants :
le comportement des Argiles plastiques a été correctement simulé avec les lois de comportement HSM et HA;
les choix des paramètres du modèle ont évidemment des impacts sur les efforts et déformations calculés. En particulier, l’ introduction de paramètres caractéristiques est sécuritaire ;
les prébutons confinent les Argiles plastiques lors de leur gonflement mécanique, ils sont ainsi utiles pour limiter le soulèvement en fond de fouille et les déformations en surface.
 |
Fig. 7 Modèle 3D de la zone Nord. 3D model of the northern zone. |
 |
Fig. 8 Comparaison des déformations enregistrées par les inclinomètres et les extensomètres avec les résultats de calcul. Deformation comparison between measures of the inclinometers and extensometers and the results of calculation. |
4.2 Tunnel
4.2.1 Méthode semi-probabiliste
Les valeurs des paramètres géotechniques retenues pour les Argiles plastiques sont présentées dans le tableau 2 (ligne 8). En effet, les valeurs retenues des paramètres géotechniques comme le module pressiométrique et la pression limite nette, etc. sont des valeurs caractéristiques, c’est-à-dire qu’elles ne correspondent pas à des valeurs moyennes, mais au fractile 5 % de la distribution des échantillons disponibles.
Nous présentons ici un deuxième modèle 3D réalisé pour simuler l’excavation du tunnel en méthode conventionnelle. Ce modèle 3D comporte environ 375 000 éléments volumiques. On y distingue la stratigraphie (éléments volumiques à 8 nœuds), la prise en compte des constructions voisines (charges surfaciques), le puits TN2 avec liernes et bracons (éléments poutres), la trace des boulons présents sur la clé de voûte et au front de taille (éléments clous), les cintres (éléments poutres) et le béton projeté (éléments coques) ainsi que le premier plot de revêtement définitif (éléments volumiques).
Ce modèle 3D du tunnel a pour but :
d’étudier de manière fine l’interaction entre le tympan du puits TN2 et le tunnel ;
de contrôler le comportement du front de taille ;
de quantifier l’influence de l’excavation du tunnel sur les bâtis sensibles (en particulier la TSI) ;
de permettre la définition d’un taux de déconfinement équivalent pour les calculs en 2D sur la base de la méthode d’avancement envisagée (cintres HEB espacés de 1 m avec béton projeté). l’ordre de grandeur observé dans le modèle 3D (déplacement de la clé de voûte de 5 mm, voir Fig. 9) a permis de fixer ce taux de déconfinement λ à40 %.
Par la suite, les coupes de calcul 2D représentatives ont été étudiées, comme l’illustre la figure 10. Chaque modèle 2D comportant 5000 à 10 000 éléments, il est beaucoup plus rapide de faire tourner les calculs. Pour chaque coupe de calcul 2D, deux situations d’étude ont été considérées :
une étude « court terme » avec paramètres CT et prise en compte de deux taux de déconfinement différents (40% selon étude 3D et 60% afin d’obtenir une borne supérieure du déplacement des constructions voisines) ;
une étude « long terme » avec paramètres LT et chargement du revêtement définitif par le gonflement des Argiles plastiques (loi de Huder-Amberg).
On peut noter, pour la station, le contact entre CG moyen et CG inférieur et pour le tunnel, le contact entre CG inférieur et AP supérieures.
Les phases principales de réalisation du tunnel sont les suivantes :
État initial non déformé avant travaux ;
Excavation du tunnel et mise en place du soutènement provisoire avec un taux de déconfinement λ ;
Déconfinement à 100 % sur le soutènement provisoire ;
Mise en place du revêtement définitif avec E = 10 GPa, nappe Eaux Chantier (EC) ;
Disparition du soutènement provisoire et passage à la nappe Eaux Hautes (EH) ;
Application de la loi de gonflement dans les Argiles plastiques sur plusieurs années.
La figure 11 illustre les résultats du calcul 2D à CT (déplacement vertical et effort normal dans le soutènement) avec déconfinement de 40 %. Pour le tassement, l’ordre de grandeur observé dans le modèle 3D est bien retrouvé, qui a été également confirmé par les mesures d’ auscultation. L’effort normal dans le soutènement (cintres + béton projeté), ainsi que les moments de flexion, permettent de dimensionner ces éléments structurels du tunnel.
Grâce aux résultats d’auscultation, les résultats des calculs ont pu être comparés aux mesures. Des inclinomètres et extensomètres ont été posés à proximité du tunnel dans les sections d’auscultation renforcées. Une prédiction du comportement du sol a été extraite des modèles numériques et comparée aux valeurs mesurées (Fig. 12). Les déformations des Argiles plastiques au droit de l’excavation du tunnel ont été bien prédites par ces modèles numériques.
Ces études permettent de montrer que le creusement de tunnels en méthode traditionnelle dans les Argiles plastiques est faisable tout en prenant les mesures nécessaires comme :
étancher les terrains autour ;
confiner et stabiliser le front de taille par les boulons en fibre de verre ;
prendre en compte la pression de gonflement dans le dimensionnement du revêtement et adapter une forme avec contre-voûte.
 |
Fig. 9 Modèle 3D du tunnel (a) et déplacement vertical (b), lors de 40 m de creusement. 3D model of tunnel (a) and vertical displacement (b), with an excavated distance of 40 m. |
 |
Fig. 10 Modèle 2D de l’une des coupes et phases principales. 2D model of one-calculation section and principal construction stages. |
 |
Fig. 11 Déplacement vertical (a) et effort normal du soutènement (b) à CT avec l = 40%. Vertical displacement (a) and normal force of supporting (b) in CT with l =40%. |
 |
Fig. 12 Photographie du front de taille avec superposition des Calcaires grossiers sur les Argiles plastiques (a) et Déformation de l’inclinomètre dans une section de mesure renforcée (b). Photograph of tunnel section in the Coarse limestone and Plastic clays (a) and inclinometer deformation in a reinforced measurement section (b). |
4.2.2 Approche probabiliste
Nous présentons ici un calcul probabiliste sur le gonflement des Argiles plastiques. Les essais en laboratoire ont montré une grande dispersion des valeurs de pression de gonflement mesurée (Zhang et al., 2022). Dans ce paragraphe, la pression de gonflement (contrainte radiale sous le radier) doit être distinguée de la pression limite de gonflement, paramètre de la loi HA des Argiles plastiques. Compte tenu de ce phénomène, la pression limite de gonflement a priori a été prise égale à 350 kPa avec un coefficient de variation de 50 %. Une distribution log-normale, couramment utilisée pour la représentation de paramètres associés à la résistance des matériaux, a été choisie pour cette pression limite de gonflement (Zhang et Commend, 2021). La figure 13 illustre le déplacement vertical autour du tunnel après 5 ans.
La figure 14 exprime le gonflement du nœud appartenant au radier définitif en fonction de la pression limite de gonflement de la loi HA. À titre d’illustration, la probabilité que le gonflement du radier dépasse 1 cm après 5 ans est Pf=37,3% si l’on considère, pour la pression limite de gonflement, une valeur moyenne de 350 kPa avec un COV de 50 %. De même, la probabilité que le gonflement dépasse 1,2 cm après 5 ans est de 24,7 %, cette probabilité est réduite à 0 pour un gonflement cible de 1,3 cm.
Grâce au système d’ auscultation mis en place, la pression de gonflement des Argiles plasties a pu être surveillée et mesurée à l’aide des cellules de pression mises sous certains cintres (Zhang et al., 2021). La pression de gonflement mesurée sous le radier est présentée dans la figure 15, nous avons constaté un écart de 100 à 150 kPa entre les courbes de mesure et de résultat de calcul à long terme. Ce décalage provient du fait que la mesure part d’ une pression à peu près nulle, alors que dans le calcul on part d’une valeur entre 100 et 150 kPa car la contrainte radiale n’est pas nulle en raison de la présence du soutènement et du revêtement.
Ces mesures in situ permettent d’utiliser l’approche Bayésienne afind’affiner les résultats des calculs probabilistes, en ajustant la distribution a priori de la pression limite de gonflement.
Deux mesures sont ici prises en compte : la pression de gonflement au temps 150 jours, et au temps 300 jours. Afin de prendre en compte le seul effet du gonflement des argiles, un temps de référence est choisi (finde l’excavation du tunnel, à savoir 5 jours), la pression de référence mesurée est Pref= 46,7 kPa. Ainsi, l’évolution de la pression mesurée au cours du temps, due au gonflement des argiles, peut être comparée à la valeur prédite par le calcul. Les deux mesures prises en compte sont :
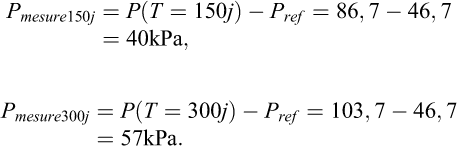
Pour commencer, ces valeurs mesurées sont comparées aux valeurs calculées avec ZSoil, lorsque la pression limite de gonflement (P0) est probabiliste (Fig. 16).
L’ analyse inverse Bayésienne consiste à mettre à jour l’hypothèse initiale sur la distribution de la pression limite de gonflement, c’est-à-dire l’hypothèse P0 ~ LN(350, 50%) [kPa]. En effet, il est possible, grâce au théorème de Bayes, de travailler sur la distribution de la pression limite de gonflement sur la base de mesures de pression réelles (Wagner et al., 2021 ; Straub et Papaioannou, 2015).
Pour une variable probabiliste, le théorème de Bayes peut s’écrire sous l’équation (3) :
 (3)
(3)
avec π (P0) la distribution de la pression limite avant la mesure (a priori), π (P0\Pobs) la distribution de probabilité connaissant la mesure (a posteriori), L (P0) la vraisemblance, et a la constante d’intégration : 
Ici, la distribution avant la mesure (a priori) suit une loi log-normale, elle est décrite par l’équation (4) :
 (4)
(4)
Notons M(P0, t) la pression de gonflement calculée par ZSoil, en fonction de la pression limite P0 et du temps t. Par rapport au temps de référence, il faudrait écrire rigoureusement M (P0, t) − M(P0, t = 5), nous avons conservé les notations courtes ici pour ne pas surcharger. La figure 16 est une représentation graphique du M(P0, t), avec P0 variant suivant la loi log-normale définie précédemment, et pour deux temps différents.
Une erreur de mesure additive est prise en compte lors de l’ analyse Bayésienne, représentée par une loi normale centrée sur 0 et d’écart type 10 kPa. Cette erreur permet de définir la fonction de vraisemblance, qui s’écrit alors dans l’ espace des pressions sous l’ équation (5) :
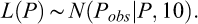 (5)
(5)
Dans cet espace, la vraisemblance est une loi normale, centrée sur la mesure, et d’écart type 10kPa. Cette expression de la vraisemblance est admise valable pour les deux mesures, et la vraisemblance des deux observations simultanément est le produit des deux vraisemblances.
Pour une estimation précise de la constante d’ intégration a de nombreux appels au modèle ZSoil sont nécessaires. C’est pourquoi un métamodèle est introduit: les polynômes du chaos - Kriging (Polynomial Chaos Kriging PCK) (Schöbi et al.,2021 ; Marelli et al.,2021). Ils permettent d’approximer la fonction M(P0) pour un temps donné, à partir d’un petit nombre d’échantillons. Ici nous supposons M(P0, t =150) ≈ MPCK,t = 150 (P0) et (P0, t = 300) ≈ Mpck, t = 300 (P0). La réponse des polynômes du chaos - Kriging est calculée presque instantanément, et il devient donc numériquement possible de calculer la vraisemblance L (P0), en substituant la réponse du modèle par la réponse des polynômes du chaos, ainsi que la constante d’intégration a (et en approximant l’ intégrale par une fonction constante par morceaux, et en choisissant un pas suffisamment fin).
Ainsi, la valeur numérique de la constante a est égale à 3568 (pas de la pression limite pour le calcul de l’ intégrale égal à 0.05 kPa).
La valeur π (P0|Pobs) peut être donc estimée par l’équation (6).
 (6)
(6)
Les différentes fonctions mentionnées π (P0|Pobs), π (P0), L150(P0) et L300(P0) (vraisemblance associées aux mesures, dans l’espace de la pression limite) sont tracées à la figure 17. Il est à noter que les vraisemblances sont définies à une constante multiplicative près. Elles ne sont pas nulles pour P0 > 400 kPa à cause du plateau visible sur la figure 16.
Grâce à la distribution actualisée a posteriori de la pression limite de gonflement π (P0|Pobs) (moyenne 315 kPa, écart type 58 kPa, illustrés sur la figure 17 par la courbe en tiretés réguliers verts), il est possible de calculer une nouvelle distribution du déplacement vertical, de façon analogue à la figure 14,c’est-à-dire en propageant l’incertitude à travers le modèle.
Pour ce faire, 200 échantillons de la distribution de la pression limite connaissant la mesure π (P0|Pobs) sont tirés, et injectés dans ZSoil. Le déplacement vertical du radier est ensuite analysé, et les résultats sont présentés dans la figure 18.
Il est ensuite possible de calculer de nouvelles probabilités que le radier dépasse une valeur seuil. À titre indicatif, seuls 8 échantillons sur les 200 tirés avec la probabilité conditionnelle mènent à un déplacement supérieur à 1cm, c’est-à-dire Pf = 4% a posteriori (au lieu de 37.3 % a priori).
Pour conclure, l’inférence Bayésienne réalisée sur la pression limite de gonflement permet de grandement réduire l’incertitude sur le soulèvement du radier, et notamment dans ce cas la probabilité de dépasser des valeurs seuils prédéfinies.
 |
Fig. 13 Déplacement vertical à la findel’étude LT (après 5 ans) avec P0 = 350 kPa et COV = 50 % - Courbes d’iso-déplacement vertical, valeurs exprimées en mètres. Vertical displacements from the LT model (after 5 years) with pg’ = 350 kPa and COV= 50% - Vertical iso-displacement curves, values expressed in meters. |
 |
Fig. 14 Distribution du déplacement vertical du radier en fonction de la pression limite de gonflement. Distribution of the vertical displacement of tunnel base as a function of the swelling pressure. |
 |
Fig. 15 Comparaison des pressions de gonflement sous le radier du tunnel, pour une pression limite P0 (loi HA) de 350 kPa. Comparison of swelling pressures under tunnel base, for a limiting pressure P0 of 350 kPa (HA law). |
 |
Fig. 16 Pression de gonflement (i.e., contrainte radiale) calculée pour 200 échantillons de P0, distribués selon une loi log-normale de moyenne 350kPa et d’écart type 175 kPa. Swelling pressure (i.e., radial stress) calculated for 200 samples of P0, distributed according to a log-normal law with mean of 350 kPa and standard deviation of 175 kPa. |
 |
Fig. 17 Représentation des différentes fonctions intervenant dans le théorème de Bayes. Representation of different functions in the Bayes theorem. |
 |
Fig. 18 Déplacement du radier en fonction de la pression limite, pour les distributions de P0 avant et après les mesures aux temps 150 et 300jours. Raft displacement in function of the limiting pressure, for the distributions of P0 before and after the measurements at 150 and 300 days. |
5 Discussion et conclusions
Les sols gonflants du Bassin parisien posent souvent des problèmes aux constructions, parmi lesquels les Argiles plastiques sont peu connues en raison de leur profondeur et de leur qualité mécanique médiocre. Par contre, de nombreux ouvrages (puits, gares, parois moulées, tunnels, etc.) ont rencontré cette formation géologique dans le cadre du projet Grand Paris Express.
Dans le paragraphe 2, quelques retours d’expériences ont été analysés sur les projets réalisés dans les Argiles plastiques du Bassin parisien, qui ont montré la déformation importante et la variabilité spatiale des Argiles plastiques. Certains REXs pourraient être intégrés dès la phase de conception des futurs projets : création de vide sanitaire sous le radier pour éviter le contact du radier avec les Argiles plastiques, prise en compte de la pression de gonflement dans le dimen-sionnement du soutènement et du revêtement du tunnel, adaptation de la forme du radier du tunnel en contre voûte pour mieux résister au gonflement, etc.
Dans les paragraphes 3 et 4, nous avons présenté les différentes méthodes de modélisation du comportement des Argiles plastiques, ainsi que leurs applications aux différents types d’ouvrages souterrains (puits, parois moulées et tunnels) dans un cas d’étude. Le comportement des Argiles plastiques est complexe et nécessite des modèles relativement sophistiqués. Les analyses menées sur les résultats des essais géotechniques ont permis d’établir les hypothèses du calcul pour la modélisation des Argiles plastiques. Les modèles 2D et 3D aux éléments finis avec les lois de comportement HSM et HA ont été utilisés. Les résultats de ces calculs, comparés aux mesures d’ auscultation, montrent que ces modèles permettent de simuler correctement le comportement des Argiles plastiques avec des paramètres géomécaniques bien calibrés sur les essais géotechniques in situ et en laboratoire.
Compte tenu de la variabilité spatiale des Argiles plastiques et de la dispersion de certains paramètres comme la pression limite de gonflement, l’approche probabiliste peut être une solution plus adaptée pour affiner les risques liés aux Argiles plastiques en associant une probabilité de défaillance (ou indice de fiabilité), comme illustrée dans la section 4.2.2.
En complément des analyses et modélisations du comportement des Argiles plastiques, un suivi continu des Argiles plastiques pendant les travaux s’avère nécessaire. Àl’ aide de la méthode observationnelle, les mesures in situ permettent de vérifier les résultats des simulations numériques et d’ajuster certaines hypothèses de calcul. Couplée à une analyse inverse Bayésienne, cette méthode observationnelle permet d’orienter les choix techniques et les optimisations pour la suite du projet.
Remerciements. Les auteurs souhaitent remercier M. Pascal Chalivat pour les discussions sur le choix des valeurs caractéristiques.
Références
- AFTES GT16R1F1. 1995. Recommandation: tassements liés au creusement des ouvrages en souterrain. Tunnels et ouvrages souterrains 132: 1–23. [Google Scholar]
- Ang A.H.S., Tang W.H. 2007. Probability concepts in engineering: Emphasis on applications to civil and environmental engineering (2nd ed.). Wiley. [Google Scholar]
- Alonso E.E., Vaunat J., Gens A. 1999. Modelling the mechanical behavior of expansive clays. Eng Geol 54: 173–183. [CrossRef] [Google Scholar]
- Avgerinos V., Potts D.M., Standing J.R. 2016. The use of kinematic hardening models for predicting tunnelling-induced ground movements in London Clay. Géotechnique 66(2): 106–120. [CrossRef] [Google Scholar]
- Baecher G.B., Christian J.T. 2003. Reliability and statistics in geotechnical engineering. Wiley. [Google Scholar]
- Beaussier A., Guilloux A., Verschuere J. 2011. La fondation Louis-Vuitton pour la création : modélisations géotechniques croisées 2D et 3D, et confrontation avec les auscultations. Rev Fr Geotech 137: 15 – 29. [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvet J.P., Berbey P. 1999. Exécution d’ une chambre souterraine dans les argiles plastiques de la région parisienne. AFTES - Journées d’études internationales, Paris, France. [Google Scholar]
- Bultel F. 2001. Prise en compte du gonflement des terrains pour le dimensionnement des revêtements des tunnels. Thèse de l’ENPC, Paris. [Google Scholar]
- CFMS. 2020. Recommandations sur la prise en compte du gonflement des terrains argileux dans le dimensionnement des ouvrages d’ infrastructure (version provisoire V28). [Google Scholar]
- Chen F.H. 1975. Foundations on expansive soils. Amsterdam: Elsevier Scientific Publishing. [Google Scholar]
- Decker I. 2012. Avancement d’ un tunnelier mixte en région parisienne : retour d’expérience du Duplex de l’A86. Tunnels et espace souterraine 229: 79–90. [Google Scholar]
- Demay B., Leroi B. 2003. Stabilité du front de taille et prévision des tassements sur le tunnel VL1 SOCATOP A86. Rev Fr Geotech 103: 61–73. [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan J.M., Chang C.Y. 1970. Nonlinear analysis of stress and strain in soil. J Soil Mech Found Div (ASCE) 96: 1629–1693. [CrossRef] [Google Scholar]
- Filliat G., Duvauchelle C. 1981. Chapitre 29-Géologie etgéotechnique de la région parisienne. In: La pratique des sols et fondations. Le Moniteur. [Google Scholar]
- Fluteaux V. 2013. Enjeux géotechniques pour la construction du métro automatique « Grand Paris Express ». Proceedings of the 18th International Conference on Soil Mechanics and Geotechni-cal Engineering, Paris, France. [Google Scholar]
- Fredlund D.G., Rahardjo H. 1993. Soil mechanics for unsaturated soils. John Wiley and Sons. [CrossRef] [Google Scholar]
- Gonzalez N.A., Rouainia M., Arroyo M., Gens A. 2012. Analysis of tunnel excavation in London Clay incorporating soil structure. Géotechnique 62(12): 1095–1109. [CrossRef] [Google Scholar]
- Guilloux A. 2012. L’intérêt des calculs éléments finis tridimensionnels dans les projets géotechniques. Rev Fr Geotech 140–141: 3–10. [CrossRef] [EDP Sciences] [Google Scholar]
- Hejazi Y., Dias D., Kastner R. 2008. Impact of constitutive models on the numerical analysis of underground constructions. Acta Geotech 3: 251–258. [CrossRef] [Google Scholar]
- Hicher P.Y., Shao J.F.. 2008. Constitutive modeling of soils and rocks. ISTE and John Wiley & Sons. [CrossRef] [Google Scholar]
- Hong Y., Wang L.Z. 2016. Deformation and failure mechanism of excavation in clay subjected to hydraulic uplift. Zhejiang University Press and Springer-Verlag. [CrossRef] [Google Scholar]
- Huder J., Amberg G. 1970. Quellung im Mergel, Opalinuston und Anhydrit. Schweiz Bauzeitung 43: 975–980. [Google Scholar]
- Launay J. 1990. Emissaire Sèvres-Achères, Chambre de raccordement lot 6. Mem Soc Géol France 157. [Google Scholar]
- Lechantre G., Trottin J.L. 2007. Le projet TIMA 2. Rev Trav 846: 47–55. [Google Scholar]
- Lees A. 2016. Geotechnical finite element analysis - a practical guide. London: ICE Publishing. [CrossRef] [Google Scholar]
- Marelli S., Sudret B. 2014. UQLab: A Framework for Uncertainty Quantification in MATLAB. In: The 2nd International Conference on Vulnerability and Risk Analysis and Management (ICVRAM 2014), July 13–16, 2014, pp. 2554–2563, University of Liverpool, United Kingdom. [Google Scholar]
- Marelli S., Lüthen N., Sudret B. 2021. UQLab user manual - Polynomial chaos expansions, Report #UQLab-V1.4-104, Chair of Risk, Safety and Uncertainty Quantification. Switzerland: ETH Zurich. [Google Scholar]
- Meyer G. 2018. Méthodologies de construction du métro parisien de sa création à nos jours. In: 9e Journées Nationales de Géo technique et de Géologie de l’Ingénieur, Champs-sur-Marne, France. [Google Scholar]
- Modaressi H., Laloui L. 1997. A thermo-viscoplastic constitutive model for clays. Int J Numer Anal Methods Geomech 21(5): 313–315. [CrossRef] [Google Scholar]
- Nejjar K. 2019. Comportement des parois de soutènement dans un contexte exceptionnel (grande profondeur, formations déformables, environnement sensible) : application à la gare Fort d’Issy-Vanves-Clamart du Grand Paris Express et comparaison avec les mesures réalisées sur site. Thèse de l’ Université Grenoble Alpes, France. [Google Scholar]
- Nelson J.D., Chao K.C., Overton D.D., Nelson E.J. 2015. Foundations engineering for expansive soils. John Wiley & Sons, New Jersey. [Google Scholar]
- Perez-Romero J., Oteo C.S., De la Fuente, P. 2007. Design and optimization of the lining of a tunnel in the presence of expansive clay levels. Tunnel Undergr Space Technol 22: 10–22. [CrossRef] [Google Scholar]
- Phoon K.K., Retief J.V. 2016. Reliability of geotechnical structures in ISO2394. CRC Press. [CrossRef] [Google Scholar]
- Potts D.M., Zdravkovic L. 1999. Finite element analysis in geotechnical engineering -theory. Thomas Telford, London. [Google Scholar]
- Schanz T., Vermeer P.A., Bonnier P.G. 1999. The hardening soil model: Formulation and verification. Beyond 2000 in Computational Geotechnics. Balkema, Rotterdam. [Google Scholar]
- Schlosser F., Wojnarowicz M., Dupont P., Maurin D. 1995. Accident d’une galerie excavée dans l’argile plastique, Rapport d’expertise. [Google Scholar]
- Schöbi R., Marelli S., Sudret B. 2021. UQLab user manual - Polynomial chaos Kriging, Report # UQLab-V1.4-109, Chair of Risk, Safety and Uncertainty Quantification. Switzerland: ETH Zurich. [Google Scholar]
- Straub D., Papaioannou I. 2015. Bayesian analysis for learning and updating geotechnical parameters and models with measurements. In: Phoon K.K., Ching, J., eds. Risk and reliability in geotechnical engineering. Taylor and Francis. [Google Scholar]
- Thiry M. 1999. Les argiles de Provins (argiles plastiques) carrière de Chalautre-La-Petite (Seine-et-Marne). Bull Inf Geol Bass Paris 36 (3): 11–19. [Google Scholar]
- Wagner P.R., Nagel J., Marelli S., Sudret B., 2021. UQLab user manual — Bayesian inference for model calibration and inverse problems, Report # UQLab-V1.4-113, Chair of Risk, Safety and Uncertainty Quantification. Switzerland: ETH Zurich. [Google Scholar]
- Zhang Y., Commend S. 2021. Calculs probabilistes des déplacements dus à la réalisation de tunnels à l’ aide d’un modèle aux éléments finis. Rev Fr Geotech 167(5): 1–15. https://doi.org/10.1051/geotech/2021018. [Google Scholar]
- Zhang Y., Toutlemonde F. 2020. Calibrating partial safety factors in line with required reliability levels for concrete structures. Eur J Environ Civil Eng. https://doi.org/10.1080/19648189.2020.1824820. [Google Scholar]
- Zhang Y., Commend S., Martin-Lavigne Q., Lacoste J. 2020a. The White House Station of the Grand Paris Express Project. Struct Eng Int 30 (4): 460–167. https://doi.org/10.1080/10168664.2019.1701966. [CrossRef] [Google Scholar]
- Zhang Y., Commend S., Taherzadeh R., Sinagra O., Lacoste J. 2020b. Analysis, modelling and surveys of plastic clays - feedback from the White House metro station. Tunnels et espace souterrain 271: 114–138. [Google Scholar]
- Zhang Y., Commend S., Taherzadeh R., Sinagra O., Lacoste J. 2021. Études expérimentales et simulations numériques des argiles plastiques - cas de la L14 gare Maison Blanche. Congrès AFTES 2021, Paris, France. [Google Scholar]
- Zhang Y., Gilbert S., Regallet D. 2022. Essais et analyses géotechniques sur les argiles plastiques du Sparnacien du Bassin parisien. Rev Fr Geotech 170(5): 1–20. https://doi.org/10.1051/geotech/2021030. [Google Scholar]
- Zienkiewicz O.C., Chan A.H.C., Pastor, M., Schrefler B.A., Shiomi, T. 1999. Computational geomechanics with special reference to earthquake engineering. Chichester: John Wiley & Sons. [Google Scholar]
- ZSOIL (User manual ZSoil.PC). 2018. Soil, rock and structural mechanics in dry or partially saturated media. Lausanne, Switzerland: ZACE Services Ltd, Software Engineering. [Google Scholar]
Citation de l’article : Yi Zhang, Stéphane Commend, Marc Groslambert. Analyses et modélisations sur les argiles plastiques du Sparnacien du Bassin parisien. Rev. Fr. Geotech. 2022, 171, 3.
Liste des tableaux
Paramètres géotechniques/géomécaniques et lois de comportement des Argiles plastiques.
Geotechnical/geomechnical parameters and constitutive laws of the plastic clays.
Hypotheses geomecaniques retenues pour les calculs.
Geomechnical hypothesis for the calculations.
Liste des figures
 |
Fig. 1 Localisation des projets du REX sur la carte de Grand Paris. Feedback projects localization over the Grand Paris map. |
| Dans le texte | |
 |
Fig. 2 Loi de comportement Hardening Soil Model (HSM). Hardening Soil Model (HSM) law. |
| Dans le texte | |
 |
Fig. 3 Loi de comportement Huder-Amberg (HA) dans ZSOIL. Huder-Amberg (HA) law in ZSOIL. |
| Dans le texte | |
 |
Fig. 4 Description de l’approche probabiliste et comparaison avec l’approche déterministe ou semi-probabiliste. Probabilistic approach and comparison with the deterministic or semi-proiaii/istic approach. |
| Dans le texte | |
 |
Fig. 5 Gare Maison-Blanche avec les constructions voisines et coupe géologique du site. Maison-Blanche station with neighbouring structures and geological section of construction site. |
| Dans le texte | |
 |
Fig. 6 Illustration du puits TN2 et photo de son terrassement dans les Argiles plastiques. TN2 shaft illustration and earthworks photo in the plastic clays. |
| Dans le texte | |
 |
Fig. 7 Modèle 3D de la zone Nord. 3D model of the northern zone. |
| Dans le texte | |
 |
Fig. 8 Comparaison des déformations enregistrées par les inclinomètres et les extensomètres avec les résultats de calcul. Deformation comparison between measures of the inclinometers and extensometers and the results of calculation. |
| Dans le texte | |
 |
Fig. 9 Modèle 3D du tunnel (a) et déplacement vertical (b), lors de 40 m de creusement. 3D model of tunnel (a) and vertical displacement (b), with an excavated distance of 40 m. |
| Dans le texte | |
 |
Fig. 10 Modèle 2D de l’une des coupes et phases principales. 2D model of one-calculation section and principal construction stages. |
| Dans le texte | |
 |
Fig. 11 Déplacement vertical (a) et effort normal du soutènement (b) à CT avec l = 40%. Vertical displacement (a) and normal force of supporting (b) in CT with l =40%. |
| Dans le texte | |
 |
Fig. 12 Photographie du front de taille avec superposition des Calcaires grossiers sur les Argiles plastiques (a) et Déformation de l’inclinomètre dans une section de mesure renforcée (b). Photograph of tunnel section in the Coarse limestone and Plastic clays (a) and inclinometer deformation in a reinforced measurement section (b). |
| Dans le texte | |
 |
Fig. 13 Déplacement vertical à la findel’étude LT (après 5 ans) avec P0 = 350 kPa et COV = 50 % - Courbes d’iso-déplacement vertical, valeurs exprimées en mètres. Vertical displacements from the LT model (after 5 years) with pg’ = 350 kPa and COV= 50% - Vertical iso-displacement curves, values expressed in meters. |
| Dans le texte | |
 |
Fig. 14 Distribution du déplacement vertical du radier en fonction de la pression limite de gonflement. Distribution of the vertical displacement of tunnel base as a function of the swelling pressure. |
| Dans le texte | |
 |
Fig. 15 Comparaison des pressions de gonflement sous le radier du tunnel, pour une pression limite P0 (loi HA) de 350 kPa. Comparison of swelling pressures under tunnel base, for a limiting pressure P0 of 350 kPa (HA law). |
| Dans le texte | |
 |
Fig. 16 Pression de gonflement (i.e., contrainte radiale) calculée pour 200 échantillons de P0, distribués selon une loi log-normale de moyenne 350kPa et d’écart type 175 kPa. Swelling pressure (i.e., radial stress) calculated for 200 samples of P0, distributed according to a log-normal law with mean of 350 kPa and standard deviation of 175 kPa. |
| Dans le texte | |
 |
Fig. 17 Représentation des différentes fonctions intervenant dans le théorème de Bayes. Representation of different functions in the Bayes theorem. |
| Dans le texte | |
 |
Fig. 18 Déplacement du radier en fonction de la pression limite, pour les distributions de P0 avant et après les mesures aux temps 150 et 300jours. Raft displacement in function of the limiting pressure, for the distributions of P0 before and after the measurements at 150 and 300 days. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




