© CFMS-CFGI-CFMR-CFG, 2021

1 Introduction

Les publications scientifiques supposent recul et neutralité. Le présent article dérogera à cette clause, tant la genèse des recherches décrites est indissociable des années passées en relation étroite avec Pierre Habib. On présente d’abord l’essai originel d’observation des oscillations naturelles engendrées dans une caverne reliée à la surface par un puits ; les circonstances ont fait qu’il l’a conduit lui-même. On décrit ensuite la descendance de cet essai qui comporte l’observation des marées terrestres, l’analyse d’une fracturation hydraulique, le calcul de la longueur d’un puits ou d’une interface gaz-liquide dans un puits, la détection de chutes de blocs, l’observation d’oscillations anharmoniques témoignant de la présence de gaz piégé en tête de puits et, finalement, la création d’une entreprise qui exploite ces techniques.

2 Genèse de l’essai en résonateur de Helmholtz

En 1982, au Laboratoire de Mécanique des Solides, alors dirigé par Pierre Habib, nous travaillions avec Nguyen Minh Duc sur les pertes de volume importantes qu’avait connues l’une des premières cavités dans le sel construites et exploitées pour le stockage de gaz naturel par Gaz de France (GDF, maintenant Storengy) à Tersanne, dans la Drôme. Ces cavités avaient été conçues par une équipe rassemblant Michel Pottier, Alain Ternot et Michel Dussaud. Elles sont créées par injection contrôlée d’eau douce dans le massif de sel et soutirage de la saumure formée au fond au moyen d’un puits cuvelé et cimenté aux terrains. Elles peuvent atteindre plusieurs centaines de milliers de m³ de volume. À l’échelle de la cavité, le puits est un long et mince capillaire, un kilomètre de long pour une vingtaine de centimètres de diamètre. Il peut contenir des tubes concentriques permettant la séparation de fluides distincts, eau et saumure pendant le lessivage, gaz et colonne d’eau de chemisage statique pendant l’exploitation.

Entre sa création en 1970 et 1980, la cavité TE02 avait perdu 30 % de son volume, son fond était remonté de 8 m. Ultérieurement, cette cavité continuerait à perdre du volume (Fig. 1). Nous avions prédit avant la construction une perte de volume ultime de quelques pourcent. Gérard Vouille, à l’École des Mines, avait obtenu un résultat semblable. GDF ayant choisi de nous conserver néanmoins comme consultants, notre motivation à trouver une explication était évidemment très forte. Il s’avéra assez vite que l’origine de notre erreur avait été de traiter le sel comme un milieu élastoplastique plutôt que viscoplastique – une erreur que n’avaient pas faite les chercheurs qui travaillaient à l’époque sur l’enfouissement des déchets radioactifs dans le sel, en Allemagne et aux États-Unis.

Avec les ingénieurs de GDF, la question de la mesure continue de la forme de la cavité, ou en tout cas de son volume, était au centre des échanges. Les mesures de forme par laser, les seules susceptibles d’être mises en œuvre dans une cavité remplie de gaz, n’étaient pas encore disponibles et, en 1980, il avait fallu vider la caverne TE02 de son gaz et la remplir d’eau pour effectuer une mesure de forme par la seule technique disponible à l’époque, le relevé sonar dans une caverne remplie de saumure. Le coût de cette opération, en incluant l’immobilisation de la cavité, était considérable. Michel Boucher, ingénieur à GDF, me demanda un jour si on ne pouvait imaginer une méthode moins coûteuse qui permette un suivi plus régulier, s’appuyant par exemple sur des méthodes acoustiques.

Cette question me remémora un exercice du cours de Mécanique des fluides de Landau et Lifschitz (1967). L’exercice concerne une cavité de volume V reliée au monde extérieur (où la pression est constante) par un long tuyau de longueur l et de petite section S. La mise en équations est très simple : sous l’effet d’une perturbation, la masse de gaz dans le tuyau, soit ρlS, est mise en mouvement, son déplacement d’ensemble dans le tuyau est x positif vers l’extérieur, son accélération est $\ddot{\mathit{x}}$, et elle est poussée par les variations P (t) de la pression dans la cavité, la pression à la sortie du tuyau (atmosphérique) étant pour sa part invariable, d’où une première équation, $\mathit{P}\mathit{S}=\mathit{\rho }\mathit{l}\mathit{S}\ddot{\mathit{x}}$. La conservation de la masse de gaz contenue dans la cavité implique par ailleurs que $\mathit{d}\left(\mathit{\rho }\mathit{V}\right)/\mathit{d}\mathit{t}=-\mathit{\rho }\mathit{S}\dot{\mathit{x}}$, ρ étant la masse volumique du gaz. Si la cavité est rigide $(\dot{\mathit{V}}=0)$ et que, les mouvements étant rapides, la transformation du gaz est adiabatique, ${\dot{\mathit{P}}=\mathit{c}}^2\dot{\mathit{\rho }}$, et $\mathit{V}\dot{\mathit{P}}/{\mathit{c}}^2=-\mathit{\rho }\mathit{S}\dot{\mathit{x}}$. On dispose donc pour décrire l’évolution de la pression d’une équation différentielle, $\ddot{\mathit{P}}+{\mathit{\omega }}^2\mathit{P}=0$, où $\omega =c\sqrt{S/lV}$, qui décrit un mouvement harmonique de période $cT=2\pi \sqrt{lV/S}.$ Ainsi, si on soumet une cavité à une perturbation initiale, on provoque des oscillations dont la période est une fonction croissante du volume. Dans les musées des sciences sont souvent exposés des objets (résonateurs de Helmholtz) qui mettent en évidence cet effet (Fig. 2), constitués d’une dame jeanne ouverte à l’extérieur par un petit trou. (On peut aussi, distraction de fin de repas, exciter à la résonance l’air contenu dans une bouteille en soufflant transversalement à son col). Avec c = 330 m/s, un choix judicieux de V, l et S conduit à des fréquences dans l’audible, de l’ordre de 1000 Hz. Il suffisait donc en principe de transposer la méthode à une cavité pleine de saumure jusqu’au sommet du puits.

Une adaptation est néanmoins nécessaire. La saumure est beaucoup moins compressible que l’air, de sorte que la compressibilité de la cavité n’est plus négligeable. La conservation de la masse de saumure dans la caverne, $\mathit{d}\left(\mathit{\rho }\mathit{V}\right)/\mathit{d}\mathit{t}+\mathit{\rho }\mathit{S}\dot{\mathit{x}}=0$, fait apparaître la compressibilité de la saumure, $\dot{\mathit{P}}={\mathit{c}}_{\mathit{s}}^2\dot{\mathit{\rho }}$, c_s =1800 m/s, mais aussi la compressibilité de la « boîte » qui la contient, $\dot{\mathit{V}}={\mathit{\beta }}_{\mathit{c}}\mathit{V}\dot{\mathit{P}}$, de sorte que la compressibilité de l’ensemble saumure plus boîte est $\mathit{\beta }\mathit{V}\dot{\mathit{P}}=({\mathit{\beta }}_{\mathit{c}}+1/\mathit{\rho }{\mathit{c}}_{\mathit{s}}^2)\mathit{V}\dot{\mathit{P}}$. On peut calculer β_c (E, ν, ∂ V) quand on connaît les caractéristiques élastiques E, ν du massif et la forme ∂V de la cavité ; mais on peut surtout la mesurer simplement en enregistrant l’accroissement de pression consécutif à l’injection d’un volume de saumure dans la cavité fermée (Bérest et al., 1999). Il s’agit de la compressibilité adiabatique ; la cavité est si grande que les échanges thermiques avec le massif environnant ont un temps caractéristique de l’ordre de l’année, très long en comparaison de la durée d’un essai, même de quelques jours. Sauf si la cavité contient un peu de gaz piégé (Sect. 9) ou si elle a une forme bizarre (très aplatie par exemple, Patrick Ballard, du LMS, calculera ultérieurement pour nous le facteur de compressibilité d’un ellipsoïde à partir de la solution d’Eshelby) le coefficient de compressibilité est toujours à peu près β = 4 × 10⁻⁴ /MPa et la période $T=2\pi \sqrt{\rho \beta Vl/S}$. Pour une cavité de V =7500 m³, un puits de longueur l = 930 m, une section S =250 cm², la période est de T =72 s, donc une fréquence de l’ordre de 0,1 Hz dans les conditions concrètes de la petite cavité EZ53 du site d’Etrez, inutilisée, et que GDF était prêt à mettre à notre disposition pour un essai.

J’en parlais à Pierre Habib dont l’instinct d’expérimentateur était toujours en veille. Il me montra immédiatement le défaut de la méthode. L’équation du mouvement $(\mathit{P}=\mathit{\rho }\mathit{l}\ddot{\mathit{x}})$ doit être écrite pour un domaine géométrique fixe. En fait, les mouvements de l’interface saumure-air au sommet du puits modifient la longueur et donc le poids de la colonne et in fine la pression dans la caverne (ce que Gérard Durup, de GDF, appelait l’effet barométrique). Il me raconta qu’à l’oral de l’X, en 1945, on lui avait demandé de calculer la période des oscillations d’une colonne de liquide contenue dans un tube en U de longueur l^′ (Fig. 3, à gauche). De nouveau l’énergie cinétique est $\mathit{\rho }{\mathit{l}}^{\prime }\mathit{S}{\dot{\mathit{x}}}^2/2$, mais c’est la gravité qui fournit la force motrice, son potentiel est $2\times \rho Sg{x}^2/2$ (une interface monte de x quand l’autre descend de x) de sorte que la période est celle d’un pendule simple de longueur 2l^′, $T=2\pi \sqrt{g/2{\mathit{l}}^{\prime }}$. Transposé au problème du puits, la même analyse doit tenir compte du poids de la colonne de saumure montée au-dessus de la position d’équilibre de l’interface, de potentiel ρglx²/2, et la période devenait $T=2\pi \sqrt{g/l+\rho \beta Vl/S}$. La méthode était parasitée par un terme qui, dans le cas d’une caverne petite, transformait le système en un pendule simple de longueur l – on obtenait alors par la mesure une information inutile car parfaitement connue par ailleurs, la longueur du puits.

Je proposais de répondre à cette objection en faisant déboucher le puits dans un récipient de grande section horizontale Σ (Fig. 3, à droite ; pratiquement, sur le site de l’essai, le récipient est une citerne). Ainsi les déplacements de l’interface liquide-air n’engendraient par eux-mêmes qu’une très faible variation de la pression de fond et la période restait $T=2\pi \sqrt{\rho \beta Vl/S}=72\text{s}$, bien trop longue pour être vue par un observateur non prévenu, mais très facile à mesurer précisément.

Les pertes de charge restaient une inquiétude. Les frottements sont souvent plus grands dans la réalité que dans les livres. Dans l’hypothèse d’un écoulement laminaire, l’équation doit être corrigée, $\ddot{\mathit{P}}+2\mathit{\lambda }\dot{\mathit{P}}+{\mathit{\omega }}^2\mathit{P}=0$, où λ = 4μπ/ρS, μ = 1,4 × 10⁻³ Pa.s (viscosité dynamique) pour la saumure. Mais l’hypothèse laminaire suppose des vitesses assez lentes et un nombre de Reynolds suffisamment petit, $\mathit{R}=2\mathit{\rho }\dot{\mathit{x}}\sqrt{\mathit{S}/\mathit{\pi }}/\mathit{\mu }<2000$. Au-delà il faut améliorer la loi de perte de charge, ce qui a été fait par Benoît Brouard (1998) dans sa thèse. Dans le cas d’une loi quadratique, qui est une assez bonne approximation, on a $\ddot{\mathit{P}}+\overline{\mathit{\lambda }}\dot{\mathit{P}}\left|\dot{\mathit{P}}\right|+{\mathit{\omega }}^2\mathit{P}=0$, équation différentielle qui possède une intégrale première peu connue mais très commode pour les calculs, par exemple si $\dot{\mathit{P}}>0$: $$\exp \left(2\overline{\mathit{\lambda }}\mathit{P}\right)[\frac{{\dot{\mathit{P}}}^2}{2}+{\mathit{\omega }}^2(\frac{\mathit{P}}{2\overline{\mathit{\lambda }}}-\frac{1}{4{\overline{\mathit{\lambda }}}^2})]=\mathrm{C}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{.}$$

Fig. 1 Profils verticaux lissés de la caverne TE02 mesurés en 1970, 1980 et 2007, illustrant la perte progressive de volume par fluage du sel (Remerciements : G. Hévin, Storengy). Smooth vertical profiles of the TE02 cavern, from sonar surveys performed in 1970, 1980 and 2007. Note cavern volume loss due to creep closure (Acknowledgements: G. Hévin, Storengy).

Fig. 2 Cavité saline remplie de saumure (gauche) et résonateur de Helmholtz (droite). Brine-filled cavern (left) and Helmholtz’s resonator (right).

Fig. 3 Tube en U (gauche) et adaptation du dispositif de mesure du volume (droite). U-Tube (left) and new design of the measurement system (right).

3 La conduite de l’essai

Les ingénieurs de GDF étaient toujours disposés à participer à une expérience scientifique ; leur aide fut précieuse pour monter l’expérience qui devait se dérouler au début de juillet 1982. J’ai dit que je m’affranchirais du détachement que requiert l’écriture d’un article dans une revue scientifique comme la RFG. La naissance de ma troisième fille était imminente et, deux jours avant la date prévue pour l’essai, je prévenais Pierre Habib que je ne pouvais m’éloigner de Paris. Pierre Habib me dit qu’à cela ne tenait et qu’il irait faire l’essai lui-même. Il y avait certainement dans ce geste de l’affection pour un jeune chercheur désolé ; peut-être aussi le plaisir de profiter du spectacle rare d’un (petit) morceau de Nature expliqué. De retour d’Etrez, le soir même, il m’appelait pour me décrire son voyage : les ingénieurs du site, très courtois à son arrivée, un peu sceptiques peut-être, mais témoignant un grand respect à son départ : la période mesurée de 74 s, au lieu des 72 s prédites, une précision remarquable pour des mesures en géotechnique. La courbe reproduite à la figure 4, tracée sur place, est de sa main : au début de l’essai la pression dans la cavité fermée est augmentée de δP =210 mbar par injection de δv =62 L de fioul (δv = βVδP). L’ouverture de la vanne en tête déclenche les oscillations (Bérest et Habib, 1983). La vie de chercheur vaut par ces instants où la Nature se plie exactement à ce que les équations ont prévu − toutes proportions gardées, Le Verrier, quand il a vu Neptune dans une lunette astronomique, devait être aussi enthousiaste que Pierre et moi l’étions ce soir-là.

Fig. 4 Relevé à la main par Pierre Habib de l’évolution des pressions mesurée en tête de puits (minutes et bars). Wellhead pressure evolution as a function of time during the July 1982 test, as recorded by Pierre Habib.

4 Ondes stationnaires et ondes courantes

La courbe représentant la pression en fonction du temps présentait dans les secondes initiales des oscillations de période bien plus courtes que 74 s, mal décrites compte tenu de l’échantillonnage insuffisant des points de mesure. Un objet réel mis hors d’équilibre est le siège d’une grande variété de phénomènes vibratoires, dont on n’observe bien que ceux que l’on a, plus ou moins délibérément, choisi d’observer. Dans la nature, sauf environnement extrêmement calme, les objets réels vibrent en permanence. Une modification même progressive des conditions à la limite engendre la propagation à la vitesse du son de discontinuités des contraintes, des déplacements ou le plus souvent de leurs dérivées. Elles forment des ondes courantes, décrites dans un puits par l’équation ${\mathit{\phi }}_{\mathit{t}\mathit{t}}^{\mathit{"e;}}-c^2{\mathit{\phi }}_{\mathit{x}\mathit{x}}^{\mathit{"e;}}=0$ où ϕ (x, t) représente la pression ou la vitesse et dont la solution est de la forme φ = f (x + ct) + g (x − ct). Après quelques réflexions sur les frontières de l’objet, ces ondes s’organisent en ondes stationnaires φ = sin(ωt + α) h (ωx/c) donc h (x) + ω²/c²h^′′ (x) =0. C’est un fait universel et remarquable : l’objet entier finit par vibrer en phase. Les conditions à la limite ajoutées à cette équation déterminent un spectre de fréquences – donc de longueurs d’ondes – dénombrable, déterminé par ces conditions à la limite et les dimensions de l’objet. Dans le problème du puits la pression est constante à une extrémité, la vitesse est nulle à l’autre, et h (x) = h₀sin(nπx/l). Les ondes de fréquences élevées s’évanouissent par dissipation visqueuse et thermique et il ne subsiste rapidement que l’onde de période la plus longue, la première du spectre, n = 1, dont la période est T = 4l/c. Mais, en sus des ondes courantes et stationnaires, bien d’autres ondes peuvent aussi être engendrées suivant les caractéristiques particulières géométriques et mécaniques de l’objet, dont le résonateur de Helmholtz est un bon exemple. Comme leurs périodes sont très variées, les mises en équation sont très différentes dans chaque cas et d’apparence contradictoires. Suivant les échelles de temps et d’espace considérées, les mêmes parties de l’objet peuvent être immobiles ou en mouvement et présenter un comportement adiabatique ou isotherme, et relèvent de la statique ou dynamique.

Ainsi l’arrêt soudain de l’injection de liquide en tête de puits engendre d’abord le long du puits des ondes descendantes portant un saut de vitesse. Leur célérité, typiquement c =1400 m/s, est inférieure à celle des ondes dans la saumure (c_s =1800 m/s) ; la différence tient à la compressibilité du tube (les dimensions transversales du puits sont si petites vis-à-vis de sa longueur que le comportement de la colonne dans la direction transversale peut être considérée comme statique à l’échelle de la propagation des ondes longitudinales). Celles-ci trouvent à l’entrée dans la caverne une condition de pression constante (la caverne a à la fois des dimensions si petites vis-à-vis de la longueur du puits que son comportement est statique – les ondes y deviennent très vite stationnaires (sauf bien sûr à une autre échelle de temps au cours d’un relevé sonar !) – et un volume si grand vis-à-vis des petits volumes de liquide déplacés par l’onde que le liquide qu’elle contient peut même être considérée, pour ce phénomène, comme immobile). Ces ondes courantes sont pour l’essentiel réfléchies vers la tête de puits où elles trouvent une condition de vitesse nulle. Une onde stationnaire s’organise rapidement après un petit nombre d’allers-retours ; compte tenu des conditions à la limite, c’est un quart d’onde sinusoïdale, de période 4l/c, donc de quelques secondes pour un puits de longueur l kilométrique. Beaucoup plus courte que l’oscillation du résonateur de Helmholtz, elle n’empêche pas de traiter la colonne de saumure dans le puits comme un corps rigide quand on veut modéliser, comme on l’a fait plus haut, le résonateur lui-même. Pour la même raison, elle disparait d’ailleurs beaucoup plus vite. Puisque la longueur du puits d’accès est très précisément connue, l’essai permettait donc de mesurer cette célérité. Quand on sollicite le fluide dans le puits, au moins ces deux phénomènes oscillatoires coïncident. Plus tard on a pu, avec Benoît Brouard (Brouard, 1998), mieux analyser ce phénomène. La figure 5 donne un exemple plus compliqué, le puits fermé contient deux tubes concentriques, l’espace annulaire est en partie rempli d’azote, la condition à la limite « haute » est plus compliquée que dans le résonateur simple, mais la coexistence des deux ondes est manifeste.

Fig. 5 Oscillations de la pression observées en tête d’un puits contenant deux tubes et un annulaire partiellement rempli en azote. Wellhead pressure oscillations at the head of a well containing a casing and a tubing, the annulus is partially filled with nitrogen.

5 Diversité des ondes affectant un objet réel

La période du résonateur est $T=2\pi \sqrt{\rho \beta Vl/S}$, proche de $T=2\pi \sqrt{Vl/S}/c$ ; celle des quart d’ondes est T = 4l/c ; V/S est très grand. On peut se demander si la plus longue période possible est donnée par le résonateur de Helmholtz. Des mesures effectuées bien plus tard dans la même cavité avec des capteurs très sensibles font apparaître des périodes d’une quinzaine de minutes (en fait, dans la pratique, on mesure ici les mouvements de fluide nécessaires pour maintenir la pression constante, Fig. 6). À gauche, on voit bien les marées terrestres qui dilatent et compriment alternativement la cavité ; le signal est la somme de deux sinus, la période due à la lune est de 12 h 25 minutes (24 h pour le soleil), mais il s’agit d’oscillations forcées, observées avec Pierre Antoine Blum, le plus grand expérimentateur qu’il m’ait été l’occasion de rencontrer (Blum et Bérest, 1993). À droite une partie de la courbe de gauche est grossie ; on distingue bien une période à 13 minutes, bien plus longue que celle du résonateur, et une amplitude de l’ordre de 10⁻⁹ fois le volume de la caverne (équivalent à un déplacement des parois de 10 nm) ; c’est probablement une onde interne, due à la non uniformité verticale de l’entropie (ce ne peut être une oscillation propre de la Terre, le signal serait beaucoup plus complexe) ; la mise en équation reste à faire.

Fig. 6 Oscillations du volume d’une caverne de 7500 m3 : effets des marées terrestres (gauche) et – peut-être – ondes internes (droite). Volume changes of a 7500 m3 salt cavern: effects of Earth tides (left) and possible internal waves (right).

6 Le cas de la fracturation hydraulique

Dans la mise en équations du résonateur de Helmholtz, la compressibilité de la caverne est invariable et donc aussi la condition à la limite à l’extrémité basse du puits. L’hypothèse ne tient plus si la cavité évolue. Jean Paul Sarda, spécialiste de la fracturation hydraulique à l’Institut Français du Pétrole, avait montré à Pierre Habib des mesures de vibrations pendant une fracturation hydraulique (Fig. 7). La fracture est un objet plat, donc très compressible malgré sa petite taille initiale (Huy Dong Bui me suggéra de choisir la description penny-shaped). À l’échelle de la période des ondes stationnaires dans le puits (seconde) la pression y est uniforme mais pas constante. La condition à la limite n’est plus $\dot{\mathit{p}}(0,\mathit{t})=0$ mais $\overline{\mathit{\beta }}\mathit{\nu }\dot{\mathit{p}}(0,\mathit{t})=-\mathit{S}\dot{\mathit{x}}$ (le débit sortant de l’extrémité du puits accroît la pression dans la fracture de compressibilité $\overline{\mathit{\beta }}\mathit{\nu }$). La période dépend donc des dimensions de la fracture ; l’oscillation évolue d’un quart d’onde (avant la fracturation) à une demi-onde (quand la fracture est bien développée). L’enregistrement permet donc en principe de suivre la croissance de la fracture au cours du temps. Le procédé semblait prometteur mais, de fait, la demi-onde était atteinte très rapidement et seul pouvait être apprécié le début de la croissance de la fracture (quelques mètres) (Bérest, 1985).

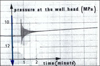Fig. 7 Oscillations de la pression pendant une fracturation hydraulique à la profondeur de 1130 m (Remerciements : Jean Paul Sarda, IFP). Wellhead pressure oscillations recorded during hydraulic fracturing at the depth of 1130 m (Acknowledgements: Jean Paul Sarda, IFP).

7 Tube de longueur inconnue

Un cas intéressant est celui où la longueur du puits (l) est inconnue. À Vauvert on exploite le sel par dissolution à grande profondeur (2000 m). La saumure est extraite par l’espace annulaire entre le cuvelage fixe et un tube central qui permet l’injection d’eau douce. Au cours des années, la cavité progresse vers le haut, des blocs insolubles sont dessertis par la dissolution et tombent au fond. Ils peuvent casser l’extrémité du tube dont la longueur l (t) a un instant donné est inconnue. Les ondes stationnaires dans le puits sont des quarts d’onde, de période T = 4l/c, leur mesure permet de suivre l’évolution de l. Benoît Brouard (Brouard et al., 2012) a conduit des essais qui illustrent cette méthode (Fig. 8 ; on distingue au moins une centaine de périodes ; l’absence de symétrie du signal est due à la saturation du capteur aux pressions faibles).

Fig. 8 Ondes stationnaires dans un puits de production de sel à Vauvert, France. Stationary waves in a salt production well at Vauvert, France.

8 Détection d’une interface

Dans bien des circonstances, un puits contient plusieurs fluides et donc des interfaces, eau-gaz par exemple, dont il est utile de connaitre la profondeur. Il existe pour cela des outils diagraphiques qu’on descend dans le puits au bout d’un câble, mais leur mise en œuvre est un peu lourde ; un procédé sonore présente donc de grands avantages, dont celui de permettre des mesures continues et non intrusives. Les acousticiens étaient un peu sceptiques, compte tenu de l’amortissement probable du signal. Mais la quantité importante pour juger de l’amortissement est le rapport entre la raideur du système et le coefficient de perte de charge ; or la pression du gaz, et donc la raideur, est cent fois plus grande dans nos applications que dans un instrument de musique. L’expérience prouva que l’amortissement restait raisonnable. Depuis, Benoît Brouard a mis en place dans des puits de stockage de gaz en aquifère un système permettant de mesurer en temps réel et à un coût faible la position de l’interface gaz-eau.

9 Mouvements de l’interface hydrocarbures–saumure

Dans les cavités de stockage d’hydrocarbures liquides, il reste toujours au fond de la cavité une quantité plus ou moins grande de saumure et donc une interface saumure-produits stockés. Cette saumure est accessible par un puits (chaque injection ou soutirage de produit stocké est compensé par un mouvement inverse de saumure). Dans les cavités du stockage fédéral américain de pétrole, dont la pression est observée en continu, on a observé des oscillations occasionnelles de la pression en tête de puits dont la période fondamentale était de l’ordre de 20 s (Hart et al., 2017). Elles sont occasionnées par la chute d’un bloc au fond de la caverne qui engendre des ondes stationnaires analogues dans leur principe aux oscillations de la surface que l’on observe dans un bol rempli de liquide (ou dans un océan où elles sont excitées à la résonance par les mouvements de la lune), Bérest et al. (2017), les vitesses verticales dans chaque fluide vérifiant $\underset{\_}{\mathit{\nu }}=\cos \mathit{\omega }\mathit{t}\underset{\_}{\mathit{\Psi }},\mathrm{\Delta }\mathit{\Psi }=0$. Hakim Gharbi, au LMS, réalisa une maquette eau-huile pour le vérifier. Avec le concours de Géodénergies, dans le cadre du projet Blockfall, un essai est en cours dans les cavités de Manosque (Alpes de Haute Provence) exploitées par Géosel (Fig. 9). L’enjeu, difficile, est d’estimer la taille du bloc tombé.

Fig. 9 Oscillations de l’interface saumure-pétrole dans une caverne à Manosque, France résultant d’une chute de bloc de la paroi (à droite, unités secondes et bars). Salt-fall event pressure signature at the wellhead of an oil storage cavern at Manosque, France, with time scale in seconds and pressure scale in bars.

10 Mesure de la compressibilité (nature des fluides stockés)

En fait, le résonateur ne mesure par le volume V de la cavité mais plutôt sa compressibilité adiabatique βV ; c’est parce que le coefficient de compressibilité varie en général peu (entre 4 et 5 × 10⁻⁴ MPa) que l’on peut parler de mesure de volume. Mais ce coefficient peut changer considérablement si la cavité contient une petite fraction de gaz, beaucoup plus compressible que la saumure ; si x est la fraction volumique de gaz contenu dans la caverne, à la pression de fond P, la compressibilité (adiabatique) devient β + γx/P, elle double donc si la pression est 10 MPa et que la fraction de gaz contenue est de l’ordre de 0,25 %. La mesure de la compressibilité est donc un procédé utile pour détecter la présence de gaz piégé dans des irrégularités de profil de la cavité.

Décrire la compressibilité adiabatique du gaz par un coefficient constant $\gamma /P$ convient bien car la pression du gaz dans la caverne (P) est bien plus grande que les petites perturbations engendrées par un essai de mesure de la compressibilité. Pourtant au cours d’essais conduits avec Jean Bergues et Benoît Brouard sur une cavité du stockage de Total à Carresse–Cassaber, exploitée à l’époque, nous avons eu la chance d’observer, à la suite d’une petite perturbation provoquée dans la caverne fermée, la courbe de la figure 10. Elle est arrondie au voisinage des minimums et au contraire pointue au voisinage des maximums. De plus la longueur de la période dépend nettement de l’amplitude de la pression dans la caverne. Elle possède donc les caractères d’une oscillation anharmonique, pour laquelle les amplitudes sont telles que l’énergie potentielle ne peut être approximée par une forme quadratique. L’explication est qu’une quantité de gaz est piégée quelque part dans la tête de puits, donc à faible pression, de sorte que le gaz n’y est pas très raide. La quantité de gaz peut être petite, puisque même des très petits déplacements de la grande quantité de saumure contenue dans la caverne résultent en de grands déplacements du gaz. Par exemple la longueur totale de la colonne de fluide est H, la hauteur du gaz H − h, l’équilibre est défini par la valeur h₀ et la pression du gaz $P_g^0$, le comportement est adiabatique, et l’équation du mouvement s’écrit : $$\mathit{\rho }\mathit{h}\ddot{\mathit{h}}+[{\left(\frac{\mathit{H}-{\mathit{h}}_0}{\mathit{H}-\mathit{h}}\right)}^{\mathit{\gamma }}-1]{\mathit{P}}_{\mathit{g}}^0+(\mathit{\rho }\mathit{g}+\frac{\mathit{S}}{\mathit{\beta }\mathit{V}})(\mathit{h}-{\mathit{h}}_0)=0,$$

(la version linéarisée serait $\mathit{\rho }{\mathit{h}}_0\ddot{\mathit{h}}+[\mathit{\rho }\mathit{g}+\mathit{S}/\mathit{\beta }\mathit{V}+\mathit{\gamma }{\mathit{P}}_{\mathit{g}}^0/(\mathit{H}-{\mathit{h}}_0)](\mathit{h}-{\mathit{h}}_0)=0$). Benoît Brouard a réussi un très bon calage qui a permis de calculer la hauteur de la colonne de gaz dans le puits (Bérest et al., 1997). Nous avons demandé aux exploitants d’ouvrir une vanne avec prudence et, à leur surprise, on a entendu le sifflement caractéristique d’une sortie de gaz.

Fig. 10 Fluctuations de la pression en tête d’un puits de caverne contenant un petit volume de gaz piégé en tête : caractère anharmonique (gauche) et influence de la pression initiale du gaz sur la période (droite). Pressure fluctuations at the wellhead of the salt cavern when a small amount of gas is trapped in the wellhead: fluctuations are anharmonic (left).

11 Conclusion

L’exploration-production de pétrole et de gaz a suscité la mise au point de techniques de mesure downhole (dans le puits) utilisant les ressources de la physique la plus avancée et l’émergence d’un domaine industriel dominé par un petit nombre de très grandes entreprises internationales. L’article vise à montrer que des techniques plus modestes, n’utilisant que des mesures faites à la surface du sol, peuvent aussi apporter des informations de première importance. Il faut rendre hommage à Pierre Habib qui a su discerner le potentiel de ces techniques et a conduit lui-même le premier de ces essais en remplaçant au pied levé le jeune ingénieur avec qui il l’avait conçu et perfectionné.

Remerciements

Les essais décrits ne pourraient avoir eu lieu sans la compétence et l’intérêt des ingénieurs des entreprises concernées de GDF-Storengy (Michel Boucher, Gérard Durup), d’Arkema (Pierre Gillard) de Total (Jean-Yves Héas, Dominique Fourmaintraux) et de Géostock (Arnaud Réveillère).

Références

Liste des figures

	Fig. 1 Profils verticaux lissés de la caverne TE02 mesurés en 1970, 1980 et 2007, illustrant la perte progressive de volume par fluage du sel (Remerciements : G. Hévin, Storengy). Smooth vertical profiles of the TE02 cavern, from sonar surveys performed in 1970, 1980 and 2007. Note cavern volume loss due to creep closure (Acknowledgements: G. Hévin, Storengy).
Dans le texte

	Fig. 2 Cavité saline remplie de saumure (gauche) et résonateur de Helmholtz (droite). Brine-filled cavern (left) and Helmholtz’s resonator (right).
Dans le texte

	Fig. 3 Tube en U (gauche) et adaptation du dispositif de mesure du volume (droite). U-Tube (left) and new design of the measurement system (right).
Dans le texte

	Fig. 4 Relevé à la main par Pierre Habib de l’évolution des pressions mesurée en tête de puits (minutes et bars). Wellhead pressure evolution as a function of time during the July 1982 test, as recorded by Pierre Habib.
Dans le texte

	Fig. 5 Oscillations de la pression observées en tête d’un puits contenant deux tubes et un annulaire partiellement rempli en azote. Wellhead pressure oscillations at the head of a well containing a casing and a tubing, the annulus is partially filled with nitrogen.
Dans le texte

	Fig. 6 Oscillations du volume d’une caverne de 7500 m3 : effets des marées terrestres (gauche) et – peut-être – ondes internes (droite). Volume changes of a 7500 m3 salt cavern: effects of Earth tides (left) and possible internal waves (right).
Dans le texte

	Fig. 7 Oscillations de la pression pendant une fracturation hydraulique à la profondeur de 1130 m (Remerciements : Jean Paul Sarda, IFP). Wellhead pressure oscillations recorded during hydraulic fracturing at the depth of 1130 m (Acknowledgements: Jean Paul Sarda, IFP).
Dans le texte

	Fig. 8 Ondes stationnaires dans un puits de production de sel à Vauvert, France. Stationary waves in a salt production well at Vauvert, France.
Dans le texte

	Fig. 9 Oscillations de l’interface saumure-pétrole dans une caverne à Manosque, France résultant d’une chute de bloc de la paroi (à droite, unités secondes et bars). Salt-fall event pressure signature at the wellhead of an oil storage cavern at Manosque, France, with time scale in seconds and pressure scale in bars.
Dans le texte

	Fig. 10 Fluctuations de la pression en tête d’un puits de caverne contenant un petit volume de gaz piégé en tête : caractère anharmonique (gauche) et influence de la pression initiale du gaz sur la période (droite). Pressure fluctuations at the wellhead of the salt cavern when a small amount of gas is trapped in the wellhead: fluctuations are anharmonic (left).
Dans le texte