| Numéro |
Rev. Fr. Geotech.
Numéro 169, 2021
Hommage à Pierre Habib et Pierre Duffaut
|
|
|---|---|---|
| Numéro d'article | 3 | |
| Nombre de pages | 6 | |
| DOI | https://doi.org/10.1051/geotech/2021022 | |
| Publié en ligne | 15 octobre 2021 | |
Article de Recherche / Research Article
La méthode convergence-confinement. Les contributions du Laboratoire de mécanique des solides (LMS)
The convergence-confinement method. Contributions of the Solid Mechanics Laboratory (LMS)
1
Académie des technologies,
Paris, France
2
Laboratoire Navier, École des Ponts Paris Tech, Univ. Gustave Eiffel, CNRS,
Marne-la-Vallée, France
* Auteur de correspondance : panet.marc@orange.fr
La méthode convergence-confinement permet de simuler le creusement d’un tunnel avec la mise en place d’un soutènement par un modèle de déformation plane. La connaissance de la convergence du massif au moment où le soutènement devient actif est une démarche essentielle pour l’application de la méthode. Celle-ci nécessite la détermination du profil longitudinal de déplacement (LDP), qui représente le déplacement radial à la paroi du tunnel en fonction de la distance au front. Dans cet article, nous rappelons les contributions importantes de Pierre Habib et de ses collègues du Laboratoire de mécanique des solides (LMS) dans le développement de la méthode, en particulier sur la prise en compte de l’influence de la pose d’un soutènement rigide près du front sur la courbe LDP.
Abstract
The convergence-confinement method makes it possible to simulate the excavation of a tunnel and the installation of the support using a simple plane strain model. The knowledge of the convergence of the ground when the support becomes active is an essential step for the application of the method. This requires the determination of the longitudinal displacement profile (LDP), which represents the radial displacement at the tunnel wall as a function of the distance to the face. In this paper, we recall the important contributions of Pierre Habib and his colleagues from the Solid Mechanics Laboratory (LMS) in the development of the method. In particular, we focus on the influence of the installation of a rigid support near the face on the LDP curve.
Mots clés : tunnel / interaction terrain-soutènement / méthode convergence-confinement
Key words: tunnel / ground-lining interaction / convergence-confinement method
© CFMS-CFGI-CFMR-CFG, 2021
1 Introduction : Souvenirs de Marc Panet
Pierre Duffaut et Pierre Habib ont l’un et l’autre contribué de manière éminente à l’étude des ouvrages souterrains.
À cet égard, j’ai pu rendre hommage à Pierre Duffaut dans le numéro spécial de Tunnels et Espace Souterrain, qui lui a été consacré. Je voudrais remercier les organisateurs de cette journée de me donner l’opportunité de participer à l’hommage rendu à Pierre Habib.
J’ai rencontré, pour la première fois, Pierre Habib au mois de mai 1961 dans le bureau de Jean Mandel dans les anciens locaux de l’École polytechnique, rue Descartes. Le Laboratoire de mécanique des solides était alors en cours de création. Pierre Habib venait de quitter un poste de direction au Laboratoire du bâtiment et des travaux publics de la rue Brancion où il avait soutenu en 1953 sa thèse sur la résistance au cisaillement des argiles. Le Laboratoire de mécanique des sols créé par Armand Mayer à l’ITBTP fut pendant des années un centre de recherche d’excellence en mécanique des sols. S’y illustrèrent notamment Jacques Florentin et Guy L’Hériteau dont il m’est agréable ici de rappeler la mémoire. Jacques Florentin, Guy L’Hériteau et Pierre Habib ont marqué de leur personnalité la géotechnique française. Ils furent tous trois présidents du Comité français de mécanique des sols. Tout au long de leur existence, ils restèrent liés par une amitié fidèle.
Dans son ouvrage Génie géotechnique. Applications de la mécanique des sols et des roches, Pierre Habib (1997) a consacré le chapitre 12 à « l’équilibre des souterrains, construction des tunnels » dans laquelle il fait une présentation de la méthode convergence-confinement. Dans cette intervention, Jean Sulem et moi-même voulons rappeler les contributions importantes de lui-même et de ses collègues du Laboratoire de mécanique des solides (LMS) de l’École polytechnique au développement de la méthode convergence-confinement.
2 La méthode convergence-confinement. Les contributions du Laboratoire de mécanique des solides.
2.1 Les fondements de la méthode convergence-confinement
Dans le passé, divers auteurs ont schématisé graphiquement l’interaction entre le terrain et le soutènement dans les ouvrages souterrains par l’intersection de deux courbes effort-déplacement, l’une caractérisant le comportement du terrain, l’autre celui du soutènement, l’intersection de ces deux courbes caractéristiques correspondant à l’équilibre final. Il convient, en particulier, de citer les courbes Fenner-Pacher. Mais cette représentation est longtemps restée qualitative, ayant un caractère essentiellement didactique. Aucune méthode ne permettait de déterminer la position relative de ces courbes caractéristiques.
La détermination de leur position respective nécessitait l’analyse des déplacements provoqués par le creusement dans le voisinage du front de taille. C’est le développement des méthodes numériques et, plus particulièrement, de la méthode aux éléments finis qui permit cette analyse. Dans une communication au 3e Congrès international de mécanique des Roches à Denver (Panet et Guellec, 1974), il a été montré que le profil de la convergence derrière le front de taille pouvait être obtenu avec une précision satisfaisante par une modélisation en déformation plane en simulant la présence du front de taille par une pression décroissante avec l’éloignement du front de taille (Fig. 1).
Cette publication marque l’introduction du taux de déconfinement λ qui constitue la base de la méthode de la méthode convergence-confinement (méthode CV-CF).
La dénomination de méthode CV-CF fut proposée au cours des travaux d’un groupe de travail de l’AFTES présidé par Pierre Gesta (Gesta et al., 1979).
La méthode CV-CF peut être présentée de manière particulièrement simple dans le cas d’un tunnel à section circulaire creusé dans un massif élastique isotrope avec un état des contraintes initiales isotrope (Fig. 2).
Par la suite, la méthode CV-CF fut développée avec des hypothèses moins restrictives. La détermination de la courbe de convergence du terrain avec des lois de comportement variées a donné lieu à de nombreuses publications. Par contre, celles consacrées à la détermination de la convergence au début de l’interaction entre le terrain et le soutènement, c’est-à-dire du taux de déconfinement correspondant, sont rares. Le Laboratoire de mécanique des solides y a consacré plusieurs travaux de recherche auxquels ont notamment participé, sous la direction de Pierre Habib, P. Bérest, D. Bernaud, F. Corbetta, Nguyen Minh Duc, C. Guo et G. Rousset.
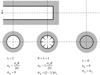 |
Fig. 1 Principe de la méthode CV-CF. Principle of the CV-CF method. |
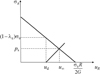 |
Fig. 2 La méthode CV-CF dans le cas axisymétrique pour un massif élastique. The CV-CF method for an elastic ground and axisymmetric conditions. |
2.2 La détermination du taux de déconfinement
La détermination du taux de déconfinement est obtenue à partir de la variation du déplacement radial en fonction de la distance au front de taille appelé le profil longitudinal de déplacement (LDP) (Fig. 3).
La méthode CV-CF est fondée sur l’analyse de trois courbes :
-
la courbe de convergence du terrain (GRC) ;
-
la courbe de confinement du soutènement (SCC) ;
-
le profil longitudinal de déplacement (LDP).
La détermination de la convergence du terrain au moment où le soutènement devient actif, c’est-à-dire au moment où il commence à exercer une pression de soutènement, est une démarche essentielle de la méthode. Elle est directement liée à la distance non soutenue derrière le front de taille d.
Dans le cas axisymétrique, l’expression mathématique de la courbe LDP est :
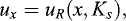 où ux est le déplacement radial à la paroi du tunnel à la distance x et Ks est le module de rigidité normale du soutènement.
où ux est le déplacement radial à la paroi du tunnel à la distance x et Ks est le module de rigidité normale du soutènement.
Le taux de déconfinement λd est déterminé à partir de la valeur ud pour x = d.
 |
Fig. 3 Représentation schématique des courbes GRC, SCC et LDP. Schematic representation of GRC, SCC and LDP curves. |
2.3 Cas du tunnel non soutenu
Dans les premiers développements de la méthode, la valeur du taux de déconfinement λd était déterminée à partir de la courbe LDP pour un tunnel non soutenu.
Pour un tunnel non soutenu excavé dans un milieu élastique, l’expression mathématique de la courbe LDP peut s’écrire :
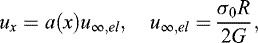 où u∞,el est le déplacement radial final à la paroi et a(x) est un coefficient de forme adimensionnel pour lequel on utilise couramment une formule empirique calée à partir de simulations numériques par éléments finis de la forme :
où u∞,el est le déplacement radial final à la paroi et a(x) est un coefficient de forme adimensionnel pour lequel on utilise couramment une formule empirique calée à partir de simulations numériques par éléments finis de la forme :
 Les valeurs courantes des paramètres a0 et m sont a0 = 0,25 et m = 0,75.
Les valeurs courantes des paramètres a0 et m sont a0 = 0,25 et m = 0,75.
Le taux de déconfinement λd à la distance de pose d est donc donné par :
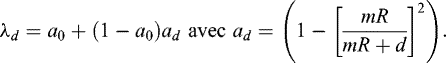
Pour un comportement élastoplastique du terrain, le profil de déplacement longitudinal est affecté par le développement d’une zone plastique. L’extension au cas d’un milieu élastoplastique a été étudiée au LMS dans le cadre des travaux de thèse de Corbetta (1990). Elle conduit à appliquer un principe de similitude qui consiste à construire le profil de déplacement longitudinal pour un milieu élastoplastique par homothétie du profil obtenu pour un milieu élastique :
 où u∞,ep est le déplacement radial final à la paroi (Corbetta et al., 1991).
où u∞,ep est le déplacement radial final à la paroi (Corbetta et al., 1991).
Pour une distance non soutenue égale à d, l’expression du coefficient de forme est alors donnée par :
 Des calculs sur des modèles numériques 3D ont permis de valider les expressions empiriques proposées (Fig. 4).
Des calculs sur des modèles numériques 3D ont permis de valider les expressions empiriques proposées (Fig. 4).
Sur ces deux figures, sont également reportées les courbes établies par Vlachopoulos et Diederichs (2009).
 |
Fig. 4 Profil longitudinal de déplacement pour un tunnel de section circulaire. Comparaisons entre les formules empiriques et les modélisations numériques 3D. Longitudinal displacement profile for a tunnel with circular section. Comparisons between empirical formula and 3D numerical simulations. |
2.4 Cas d’un tunnel soutenu
La présence d’un soutènement affecte le profil longitudinal de déplacement d’autant plus que le soutènement est plus rigide et que la distance non soutenue est plus faible. Le choix de la valeur du taux de déconfinement du tunnel non soutenu entraîne une surestimation du taux de déconfinement.
Les travaux réalisés au LMS ont conduit à proposer des méthodes prenant en compte le soutènement en utilisant une approche implicite.
Les méthodes implicites permettent d’obtenir le coefficient de forme de la courbe LPD du tunnel soutenu as(x) à partir de celle du tunnel non soutenu a(x) par application d’une transformation affine de la variable x :
 Le paramètre α est fonction de la rigidité normale du soutènement. Dans les développements ci-dessous, on introduit la rigidité relative du soutènement par rapport au terrain par le coefficient ks :
Le paramètre α est fonction de la rigidité normale du soutènement. Dans les développements ci-dessous, on introduit la rigidité relative du soutènement par rapport au terrain par le coefficient ks :
 Ks étant le module de rigidité normal du soutènement et G le module de cisaillement du terrain dans le domaine élastique.
Ks étant le module de rigidité normal du soutènement et G le module de cisaillement du terrain dans le domaine élastique.
2.4.1 Méthode de Bernaud-Rousset
Bernaud et Rousset (1992, 1996) ont proposé différentes expressions pour α selon le modèle de comportement plastique du terrain.
Le déplacement radial à la distance d est donné par :
 Cette formule fait apparaître le déplacement radial final du tunnel soutenu us∞. La résolution du système implicite d’équations se fait de manière itérative.
Cette formule fait apparaître le déplacement radial final du tunnel soutenu us∞. La résolution du système implicite d’équations se fait de manière itérative.
Le tableau 1 donne la valeur de λd pour ks < 40 et d compris entre 0,25R et 2R.
Approche implicite de Bernaud-Rousset. Valeurs du taux de déconfinement λd en fonction de la distance non soutenue d et de la rigidité relative du soutènement ks.
Bernaud-Rousset implicit approach. Deconfinement ratio λd as a function of the unsupported span d and of the relative stiffness of the support ks.
2.4.2 Méthode de Nguyen-Minh et Guo
Une approche implicite différente a été proposée par Nguyen-Minh et Guo (1996) basée également sur des modélisations numériques. Le déplacement radial à la distance non soutenue usd est obtenu à partir du cas non soutenu par l’expression :
 Dans le cas d’un comportement élastique du terrain, le taux de déconfinement λd est alors solution de l’équation du troisième degré :
Dans le cas d’un comportement élastique du terrain, le taux de déconfinement λd est alors solution de l’équation du troisième degré :
 Le tableau 2 donne la variation du taux de déconfinement λd en fonction de ks < 10 et de d.
Le tableau 2 donne la variation du taux de déconfinement λd en fonction de ks < 10 et de d.
On peut constater que ces deux approches donnent des valeurs assez voisines. Les écarts les plus importants sont pour les soutènements très rigides vis-à-vis du terrain mis en œuvre près du front de taille.
Méthode de Nguyen Minh et Guo. Valeurs du taux de déconfinement λd en fonction de la distance non soutenue d et de la rigidité du soutènement ks.
Minh and Guo method. Deconfinement ratio λd as a function of the unsupported span d and of the relative stiffness of the support ks.
3 Conclusions
Nous avons donné un exposé sommaire des contributions du Laboratoire de mécanique des solides à la méthode CV-CF pour la détermination du taux de déconfinement. Le lecteur désirant des développements plus complets pourra se reporter aux mémoires originaux ou au chapitre 5 de la nouvelle édition du livre, Le calcul des tunnels par la méthode convergence-confinement (Panet et Sulem, 2021). Dans les cas complexes, il peut s’avérer nécessaire d’avoir recours à des modèles numériques pour avoir une meilleure évaluation du taux de déconfinement.
Références
- Bernaud D, Rousset G. 1992. La « nouvelle méthode implicite » pour l’étude du dimensionnement des tunnels. Rev Fr Geotech 60: 5–26. [CrossRef] [EDP Sciences] [Google Scholar]
- Bernaud D, Rousset G. 1996. The ’new implicit method’ for tunnel analysis. Int J Numer Anal Methods Geomech 20: 673–690. [CrossRef] [Google Scholar]
- Corbetta F. 1990. Nouvelles méthodes d’étude des tunnels profonds. Calculs analytiques et numériques. Thèse de l’École nationale supérieure des Mines de Paris. [Google Scholar]
- Corbetta F, Bernaud D, Nguyen-Minh D. 1991. Contribution à la méthode convergence-confinement par le principe de la similitude. Rev Fr Geotech 54: 5–11. [CrossRef] [EDP Sciences] [Google Scholar]
- Gesta P, Kérisel J, Londe P, Louis P, Panet M. (1979). Journées d’études AFTES Octobre 1978, « Stabilité des tunnels par la méthode convergence-confinement », Rapport général. Tunnels et Ouvrages Souterrains 32: 70–143. [Google Scholar]
- Habib P. 1997. Génie géotechnique. Application de la mécanique des sols et des roches. Universités francophones. Paris: Ellipses. [Google Scholar]
- Nguyen-Minh D, Guo C. 1996. Recent progress in convergence-confinement method. In: Proc. Eurock’96, Prediction and Performance in Rock Mechanics and Rock Engineering. Turin, Balkema: Ed. G. Barla, pp. 855–860. [Google Scholar]
- Panet M, Guellec P. 1974. Contribution à l’étude du soutènement derrière le front de taille. In: Proc. 3rd Int. Congr. Int. Soc. Rock Mech., Denver, Vol. 2, Part B, pp. 1130–1134. [Google Scholar]
- Panet M, Sulem J. 2021. Le calcul des tunnels par la méthode convergence-confinement. Paris: Presses des Ponts. [Google Scholar]
- Vlachopoulos N, Diederichs MS. 2009. Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels. Rock Mech Rock Eng 42(2): 131–146. [CrossRef] [Google Scholar]
Citation de l’article : Marc Panet, Jean Sulem. La méthode convergence-confinement. Les contributions du Laboratoire de mécanique des solides (LMS). Rev. Fr. Geotech. 2021, 169, 3.
Liste des tableaux
Approche implicite de Bernaud-Rousset. Valeurs du taux de déconfinement λd en fonction de la distance non soutenue d et de la rigidité relative du soutènement ks.
Bernaud-Rousset implicit approach. Deconfinement ratio λd as a function of the unsupported span d and of the relative stiffness of the support ks.
Méthode de Nguyen Minh et Guo. Valeurs du taux de déconfinement λd en fonction de la distance non soutenue d et de la rigidité du soutènement ks.
Minh and Guo method. Deconfinement ratio λd as a function of the unsupported span d and of the relative stiffness of the support ks.
Liste des figures
 |
Fig. 1 Principe de la méthode CV-CF. Principle of the CV-CF method. |
| Dans le texte | |
 |
Fig. 2 La méthode CV-CF dans le cas axisymétrique pour un massif élastique. The CV-CF method for an elastic ground and axisymmetric conditions. |
| Dans le texte | |
 |
Fig. 3 Représentation schématique des courbes GRC, SCC et LDP. Schematic representation of GRC, SCC and LDP curves. |
| Dans le texte | |
 |
Fig. 4 Profil longitudinal de déplacement pour un tunnel de section circulaire. Comparaisons entre les formules empiriques et les modélisations numériques 3D. Longitudinal displacement profile for a tunnel with circular section. Comparisons between empirical formula and 3D numerical simulations. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.




