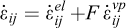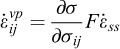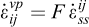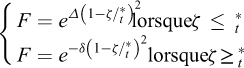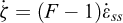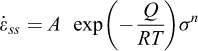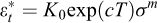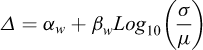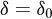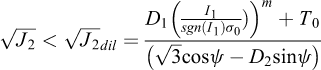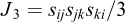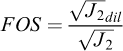| Numéro |
Rev. Fr. Geotech.
Numéro 177, 2023
Hommage à Pierre Bérest
|
|
|---|---|---|
| Numéro d'article | 3 | |
| Nombre de pages | 15 | |
| DOI | https://doi.org/10.1051/geotech/2024023 | |
| Publié en ligne | 8 mai 2024 | |
Article de recherche / Research Article
Stabilité mécanique à long terme des cavités salines de stockage d’hydrogène
1
Ineris, Verneuil-en-Halatte, France
2
Brouard Consulting, Paris, France
3
Storengy, Bois-Colombes, France
4
UPPA, Université de Pau et des Pays de l’Adour, Pau, France
* Auteur de correspondance : hippolyte.djizanne@ineris.fr
L’étude de la stabilité mécanique des cavités salines servant au stockage de l’hydrogène est un sujet important dans le contexte de la transition énergétique. Alors que l’hydrogène émerge comme un vecteur énergétique clé pour le stockage d’énergie décarbonée, comprendre les réponses mécaniques des cavités salines autour des pressions d’exploitation est essentiel. Cet article présente une analyse détaillée des effets des pressions maximales et minimales constantes sur une période de 30 ans sur la perte de volume par fluage, la contrainte effective, le facteur de sécurité des cavités salines vis-à-vis de l’apparition de la dilatance ainsi que la subsidence en surface. En utilisant une modélisation géomécanique couplée, cet article explore l’intégrité structurelle d’une cavité soumise à des conditions de chargement extrêmes sur une longue période, fournissant des informations essentielles pour le dimensionnement, l’exploitation et la maintenance des futurs sites de stockage souterrain d’hydrogène gazeux.
Abstract
Understanding salt caverns mechanical responses under operational pressures is essential as hydrogen emerges as a vector for decarbonised energy storage. This paper presents a detailed analysis of the effects of constant maximum and minimum pressures over 30 years on volume loss due to creep, effective stress, surface subsidence, and the safety factor of salt caverns regarding the onset of dilatancy. This paper explores the structural integrity of a salt cavern subjected to extreme loading conditions over a long period with a fully coupled geomechanical model, providing essential insights for the design, operation, and maintenance of future underground hydrogen gas storage sites.
Mots clés : hydrogène / cavité saline / dilatance / scénarios les plus défavorables / comportement à long terme
Key words: hydrogen / salt cavern / dilatancy / worst-case scenarios / long-term behaviour
© CFMS-CFGI-CFMR-CFG, 2023
1 Introduction
Dans le paysage énergétique mondial en rapide évolution, le stockage souterrain de l’hydrogène émerge comme une technologie clé pour faciliter la transition vers une économie à faible émission de carbone. L’utilisation de cavités salines pour ce stockage présente des avantages distincts en termes de sécurité, de capacité et de viabilité économique. Les vastes dépôts de sel gemme, répartis à travers le monde (Fig. 1), offrent une opportunité unique d’exploiter les propriétés inhérentes du sel pour créer des environnements de stockage souterrains optimaux.
La Figure 1 présente illustre l’abondance géologique du sel gemme en présentant la répartition mondiale des gisements de sel selon leur âge géologique, avec des couleurs distinctes pour chaque période. La présence de ces dépôts sous forme de dôme ou de couches à travers le monde souligne leur importance potentielle pour des projets comme le stockage géologique d’hydrogène, compte tenu de l’expérience acquise avec le stockage souterrain de gaz naturel. En effet, la grande solubilité du sel gemme (environ 320 g/l) permet de créer des cavités salines par lessivage et d’y stocker des produits chimiques ou des gaz. Les propriétés physiques intrinsèques au sel gemme telles que ses très faibles valeurs de porosité (entre 0 et 1 %) et de perméabilité (autour de 10−21 m2) indiquent que le sel a une très faible capacité à laisser passer les fluides, ce qui en fait une option intéressante pour le stockage souterrain de l’hydrogène où l’étanchéité est cruciale. Pour finir, ses propriétés mécaniques uniques permettent la construction de cavités salines stables.
Les études rhéologiques permettent de modéliser la réponse du sel gemme aux contraintes mécaniques, de prédire les conditions de fluage et de rupture, et d’établir les paramètres de sécurité pour le fonctionnement à long terme de l’ouvrage souterrain. Plusieurs lois rhéologiques sont proposées pour le sel gemme dans la littérature, parmi lesquelles les lois de Lemaitre-Menzel-Schreiner (fluage transitoire), de Norton-Hoff (fluage stationnaire), de Lubby2 et de Munson-Dawson (fluage stationnaire et transitoire), (Djizanne 2014). Les critères de rupture et d’endommagement du sel gemme, permettent, en lien avec les lois de comportement, de prévenir les défaillances structurelles. On peut citer entre autres l’absence de déformation excessive dans le sel gemme ; l’absence de traction en paroi de cavité et un coefficient de sécurité devant être supérieur à 1 pour éviter un endommagement par dilatance. Plusieurs autres critères d’endommagement tels que l’indice d’intensité de contrainte (Rokahr et Staudtmeister, 1993) et la théorie de l’endommagement continu modifié (Schulz et al., 2011) sont autant de critères développés dans la littérature sur la base des expériences de laboratoire réalisées sur des échantillons de sel gemme.
Plusieurs raisons imposent de fixer à la fois une pression minimale et une pression maximale lors de l’exploitation des cavités salines pour le stockage de gaz : la pression minimale garantie la stabilité structurale en évitant l’effondrement de la cavité sous la pression des roches/sols surincombants et environnants. D’autre part, la pression maximale est nécessaire pour maintenir l’intégrité de l’hydrogène stocké en le maintenant à des niveaux de pression, en dessous de la pression géostatique, requis pour son utilisation future. En établissant ces limites, on assure la sécurité de l’infrastructure, la préservation de l’environnement souterrain, et la disponibilité de l’hydrogène dans des conditions optimales pour répondre à la demande énergétique.
Notre étude vise à intégrer ces considérations dans un cadre analytique robuste, aligné avec les objectifs du projet HyPSTER (Hydrogen Pilot Storage for large Ecosystem Replication) relatifs à l’étude des scénarios les plus défavorables (worst-case scenarios). Les mécanismes de fluage et d’endommagement par dilatance du sel gemme sous charge à long terme doivent être soigneusement évalués pour assurer l’intégrité structurelle et la performance opérationnelle des cavités. En modélisant la réponse du sel gemme à des conditions de pression variables et extrêmes, il est possible d’optimiser le stockage de l’hydrogène, de limiter les risques de subsidence et d’une manière générale de garantir la durabilité à long terme des ouvrages souterrains. Cette recherche participe à la stratégie européenne pour une économie de l’hydrogène, contribuant à la fois à la sécurité énergétique et à l’atténuation des changements climatiques.
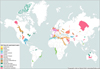 |
Fig. 1 Distribution des dépôts de sel gemme dans le monde (Horváth et al., 2018). Worldwide distribution of rock salt deposits (Horváth et al., 2018). |
2 Pressions d’exploitation en cavité saline
Dans un stockage souterrain de gaz en cavité saline, la pression du gaz varie entre deux valeurs extrêmes qui sont nettement distinctes. De façon générale, pour que la respiration du stockage (la partie utile du stockage) soit maximale, il faut que la pression maximale soit la plus grande possible et la pression minimale soit la plus petite possible (Bérest et Brouard, 1999).
La pression minimale requise pour un stockage de gaz efficace dans une cavité est dictée par deux éléments clés : la mécanique des roches et des facteurs économiques. Du point de vue de la mécanique des roches, une baisse de la pression du gaz entraîne une augmentation significative de la vitesse de fermeture de la cavité due au fluage des roches, un phénomène observé dans tous les stockages, par exemple à Tersanne en France. En termes de prévention, il est essentiel de maintenir la pression au-dessus d’un certain seuil, car des problèmes peuvent apparaître lorsque l’écart entre la pression lithostatique et la pression du gaz excède une certaine limite. D’un point de vue économique, il peut être avantageux d’éviter la recompression du gaz au soutirage avant sa réinjection dans le réseau de transport à haute pression, ce qui implique par exemple de ne pas laisser la pression dans la cavité descendre en dessous de 8 MPa.
La détermination de la pression maximale au niveau du dernier cuvelage cimenté, près du toit de la cavité, implique un équilibre entre deux enjeux majeurs. D’une part, la capacité maximale de stockage est quasi proportionnelle à cette pression maximale, ce qui, d’un point de vue économique, suggère l’avantage d’avoir une pression la plus élevée possible. C’est cette logique qui guide aussi le choix de la profondeur maximale des cavités de stockage de gaz naturel, étant donné que la pression maximale est liée à la profondeur de la cavité. Cependant, cette quête de profondeur est limitée par les contraintes de la mécanique des roches, puisqu’une cavité profonde permet une grande pression maximale, mais limite la pression minimale en raison de la perte de volume par fluage. La profondeur optimale varie donc selon les caractéristiques mécaniques spécifiques du sel de chaque site. D’autre part, une pression maximale trop élevée peut compromettre l’étanchéité du stockage. Dans ce contexte, l’industrie pétrolière fournit un repère supérieur, en se basant sur les pratiques de fracturation des horizons producteurs d’hydrocarbures pour augmenter le débit de production. Cette fracturation est obtenue en augmentant la pression du fluide dans les puits jusqu’à dépasser, selon les propriétés de la roche-réservoir, la plus petite des contraintes principales. Pour les gisements de sel, il est raisonnable de supposer un état de contraintes naturelles isotropes, où les contraintes principales sont égales et correspondent au poids des terrains surincombants, soit un gradient de pression géostatique de l’ordre de 0,022 MPa/m. Cette valeur représenterait donc le maximum absolu qu’il ne faudrait en aucun cas dépasser.
L’établissement de limites minimales et maximales de pression pour l’utilisation des cavités salines est crucial pour assurer l’intégrité structurelle, prévenir les fuites, optimiser le stockage, garantir la durabilité et maintenir la sécurité opérationnelle. Il convient de souligner que notre étude n’a pas pour objet de définir les seuils de pression minimale et maximale appropriés pour le stockage de l’hydrogène.
3 Présentation du cas d’étude
Dans cette section, on étudie la stabilité mécanique d’une cavité saline de stockage d’hydrogène gazeux soumise à différents chargements constants à long terme entre les pressions minimales et maximales d’opération.
3.1 Géométrie, conditions initiales et à la limite
La cavité saline considérée est de forme elliptique avec un volume géométrique d’environ 262 000 m3. La caverne a une hauteur maximale de 50 m pour un diamètre maximal de 100 m. La forme de la cavité est inspirée d’une cavité réelle de production de saumure, située à faible profondeur. L’adoption d’une forme elliptique à cette profondeur représente un choix délibéré, bien que défavorable, qui peut induire une accumulation des contraintes aux endroits où la courbure est importante. Par conséquent, cette configuration pourrait se révéler moins stable mécaniquement que d’autres configurations géométriques. Elle est située à une profondeur moyenne de 1000 mètres sous des couches de grès (200 m d’épaisseur) et d’argiles (300 m d’épaisseur). Les paramètres physiques et mécaniques des couches géologiques sont des données d’entrée de la simulation (la densité, le module de Young, le coefficient de Poisson, la porosité, la perméabilité, la conductivité thermique, le gradient géothermique, la chaleur spécifique et le jeu de paramètre de la loi constitutive). La Figure 2 présente une vue de la cavité saline dans son environnement : la cavité est lessivée dans la couche de sel gemme et les différentes couches géologiques sont représentées par des textures et des couleurs variées, avec des strates rocheuses distinctes.
La cavité est remplie d’hydrogène avec un volume de 254 199 m3, soit 97,1 % de sa contenance, le reste (2,9 % soit 7592 m3) étant constitué de saumure résiduelle en fond de cavité à la suite du processus de remplissage gaz, voir Figure 3. Dans la cavité, on peut distinguer l’hydrogène en couleur verte et la saumure résiduelle en couleur bleue. À l’état initial, la distribution de la contrainte géostatique et le flux de chaleur géothermique sont calculées avant le lessivage. À la profondeur moyenne de la cavité (1000 m), la pression géostatique est de 21,79 MPa (Fig. 4) et la température géothermique est de 35,9 °C (Fig. 5). Pour les calculs thermomécaniques, ces conditions initiales sont imposées sur les frontières du modèle géométrique 2D axisymétrique.
 |
Fig. 2 Vue de la cavité saline dans son environnement géologique. View of the salt cavern in its geological environment. |
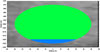 |
Fig. 3 Forme géométrie de la cavité saline remplie d’hydrogène. Geometric configuration of the hydrogen-filled salt cavern. |
 |
Fig. 4 Distribution initiale de la pression géostatique en fonction de la profondeur. Initial distribution of geostatic pressure as a function of depth. |
 |
Fig. 5 Distribution initiale de la température géothermique en fonction de la profondeur. Initial distribution of geothermal temperature as a function of depth. |
3.2 Chargements à long terme de la cavité
Dans cette étude, la cavité saline choisie est soumise à deux types de chargements :
Trois chargements mécaniques constants appliqués sur toute la surface des parois, autour de Pmax (Pmax = 17,6 MPa, 1,1Pmax = 19,4 MPa et 1,2Pmax = 21,2 MPa) sur une période de 30 ans
Trois chargements mécaniques constants appliqués sur toute la surface des parois, autour de Pmin (Pmin = 4,8 MPa, 0,9Pmin = 4,3 MPa et 0,8Pmin = 3,9 MPa) sur une période de 30 ans.
L’étude prend en compte l’historique de chargement de la cavité saline depuis sa création. Le lessivage est simulé par une chute de la pression pendant 1460 jours de la pression géostatique à la pression halmostatique de 11,47 MPa. Cette étape est suivie d’une période de stand-by de 540 jours, avant le premier remplissage en hydrogène (debrining) qui se déroule en 100 jours pendant lesquels la pression de la cavité est portée à sa valeur maximale. Pour le groupe de chargement autour de la pression maximale Pmax, on maintient alors la cavité remplie pendant 30 ans pour l’analyse du comportement à long terme. Pour le groupe de chargement autour de la pression minimale, la cavité pleine et à pression maximale est vidée en 10 jours jusqu’à ce qu’on atteigne la pression minimale qui est ensuite maintenue pendant 30 ans.
3.3 Comportement du sel gemme
Le comportement mécanique du sel gemme est élasto-viscoplastique, non-linéaire et particulièrement thermosensible. La vitesse de déformation du sel comprend donc son expansion thermique, sa déformation élastique et sa déformation viscoplastique. La déformation viscoplastique dépend de la contrainte, de la température et du temps. La loi de comportement de Munson-Dawson qui prend en compte une phase transitoire (fluage primaire) et une phase stationnaire (fluage secondaire) est utilisée dans cet article. La loi de Munson-Dawson peut être représentée par trois équations différentielles du premier ordre et sa formule scalaire isotherme comporte une dizaine de paramètres (Munson, 1997, 1999 ; Djizanne, 2014 ; Labaune, 2018) :
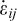 est la vitesse de déformation totale ;
est la vitesse de déformation totale ; 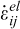 est la composante élastique de la vitesse de déformation ;
est la composante élastique de la vitesse de déformation ; 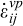 est la composante viscoplastique de la vitesse de déformation totale,
est la composante viscoplastique de la vitesse de déformation totale, 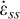 est la vitesse de déformation stationnaire ;
est la vitesse de déformation stationnaire ;  est la vitesse de déformation transitoire ; σ est la contrainte déviatorique (MPa) ; μ est le module de cisaillement du sel gemme
est la vitesse de déformation transitoire ; σ est la contrainte déviatorique (MPa) ; μ est le module de cisaillement du sel gemme 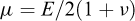 . Les paramètres suivants
. Les paramètres suivants 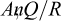 , du fluage stationnaire, K0, c, m du fluage transitoire, puis αw et βw sont déterminés par des essais de laboratoire.
, du fluage stationnaire, K0, c, m du fluage transitoire, puis αw et βw sont déterminés par des essais de laboratoire.
Les propriétés élastiques, thermiques ainsi que le jeu de paramètre de la loi de Munson-Dawson considérés dans cet article sont données dans les Tableaux 1, 2 et 3. Les propriétés des couches de roches surincombants le sel gemme, sont supposées élastiques et n’ont pas d’impacts significatifs sur les résultats, compte tenu de la profondeur moyenne de la cavité.
3.4 Critères de stabilité mécanique
Le sel gemme est une roche viscoplastique qui se déforme sous n’importe quelle contrainte déviatorique. En effet, dès qu’il est soumis à une contrainte déviatorique, même très faible, il commence à fluer. En conséquence, la plus petite différence de pression entre la cavité et le massif environnant, provoque une déformation de la cavité due au fluage du sel. Cette déformation prend la forme d’une convergence, étant donné qu’en phase d’exploitation, la pression interne est généralement plus faible la contrainte des terrains environnants. Pour capter les effets de cette convergence par fluage, deux critères de stabilité sont utilisés dans cette étude en considérant un chargement constant pendant 30 ans autour des pressions minimales et maximales :
Absence de contrainte effective de traction : σeff = σmax + Pc < 0, (où σeff est la contrainte effective, σmax (aussi appelée σ3) est la contrainte principale la moins compressive et Pc la pression de la cavité à la même profondeur) ; lorsque des contraintes de traction se développent à la paroi de la cavité, il y a un risque d’écaillage voire de fracturation du sel. La contraction thermique du sel en paroi ou à proximité de la cavité pendant les phases de soutirage d’hydrogène est susceptible de créer des contraintes de traction (Djizanne et al., 2023) ;
Absence de dilatance du sel : La micro-fracturation et la dilatance du sel se produisent lorsque les contraintes de cisaillement sont importantes par rapport aux contraintes moyennes. Elles entraînent une microfissuration, une augmentation de la perméabilité, une baisse de la vitesse des ondes, une augmentation de l’émission acoustique et une perte de résistance de la roche. Le critère de dilatation choisi dans cette étude est le critère DeVries (avec le jeu de paramètres de Moss Bluff) développé par RESPEC (DeVries et al., 2003). Ce critère est basé sur un critère de rupture de type Mohr-Coulomb pour représenter la rupture du sel en fonction de la contrainte de cisaillement, de la contrainte moyenne et de l’angle de Lode. Il est important de noter qu’il s’agit d’un critère de post-traitement, c’est-à-dire que les simulations sont effectuées jusqu’à la fin pour évaluer l’état des contraintes, sans que cet état soit modifié si le critère est atteint pendant les calculs.
Où (D1, D2, m) sont des paramètres du sel étudié, ψ est l’angle de Lode, I1 est le premier invariant du tenseur des contraintes de Cauchy, J2 est le second invariant du tenseur de déviateur des contraintes de Cauchy, 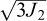 est le déviateur de contraintes ou la contrainte équivalente de von Mises, J3 est le troisième invariant du tenseur des contraintes déviatoriques, T0 est la résistance à la traction tandis que σ0 est une constante dimensionnelle ayant les mêmes unités que I1. Il est ainsi défini un Facteur de sécurité « FOS » de l’anglais « Factor Of Safety » pour lequel il n’y a aucune dilatance lorsque FOS < 1 (Nieland et Ratigan, 2006).
est le déviateur de contraintes ou la contrainte équivalente de von Mises, J3 est le troisième invariant du tenseur des contraintes déviatoriques, T0 est la résistance à la traction tandis que σ0 est une constante dimensionnelle ayant les mêmes unités que I1. Il est ainsi défini un Facteur de sécurité « FOS » de l’anglais « Factor Of Safety » pour lequel il n’y a aucune dilatance lorsque FOS < 1 (Nieland et Ratigan, 2006).
Le jeu de paramètres du critère de DeVries utilisé dans ces travaux est donné dans le Tableau 4.
3.5 Logiciel utilisé
LOCAS est un logiciel de modélisation géomécanique par éléments finis, et de gestion de données, développé par Brouard Consulting. LOCAS a la particularité d’être un logiciel commercial capable de coupler en 2D ou 3D la thermodynamique des cavités salines et la géomécanique complexe du sel gemme (Brouard et al., 2018, 2020). Plusieurs phénomènes physiques peuvent être pris en comptes dans LOCAS, y compris, la dislocation du sel gemme et le fluage par dissolution sous pression, la thermodynamique des cavités incluant les lois constitutives des gaz réels, la dissolution/cristallisation complémentaire de la saumure, et la micro-perméation utile pour les problèmes d’abandon (Brouard et al., 2012, 2022 ; Djizanne et al., 2014).
4 Résultats et interprétation
Cette section présente les résultats des calculs thermomécaniques réalisés. Tout d’abord, l’évolution de la température de l’hydrogène stocké depuis le premier remplissage jusqu’à la fin des 30 années de stand-by est présentée et commentée. Puis, d’autres évolutions temporelles telles que la perte de volume de la cavité par fluage, ainsi que la subsidence ou déformation progressive en surface sont aussi analysées. Pour finir, les critères de stabilité évoqués en section 3.4 servent à apprécier stabilité mécanique de la cavité saline.
4.1 Température de l’hydrogène
Les Figures 6 et 7 présentent les évolutions de la pression et de la température de l’hydrogène stocké dans la cavité, respectivement pendant les 12 premiers mois et les 30 années de maintien d’une pression constante. Lors de l’injection de l’hydrogène, la température croît progressivement, jusqu’à la fin du premier remplissage lorsqu’on atteint la pression maximale en cavité. Ensuite, lorsque la pression maximale est maintenue pendant 30 ans, la température décroît alors lentement vers une température d’équilibre à long terme autour de 32 °C. Pour ce qui est des pressions minimales, la détente de l’hydrogène lors du passage de la pression maximale à la pression minimale occasionne des chutes de température jusqu’à −5 °C. Pendant toute la période de maintien à pression constante de l’hydrogène dans la cavité, l’hydrogène stocké évolue vers l’équilibre thermique avec le massif environnant, en se rapprochant lentement de la température d’équilibre à long terme. Les variations de pression autour de la pression maximale et de la pression minimale, n’influencent pas véritablement l’allure générale de l’évolution de la température de l’hydrogène stocké, lors d’un chargement constant sur une longue durée (30 ans).
 |
Fig. 6 Évolution sur les 12 premiers mois de la pression (en haut) et de la température calculée (en bas) de l’hydrogène stocké dans la cavité saline ; dans cette figure, t = 0 correspond au début de la phase de remplissage. Evolution over the first 12 months of the cavern pressure (top) and the computed cavern temperature (bottom) of the stored hydrogen in the salt cavern; in this figure, t = 0 corresponds to the beginning of the debrining. |
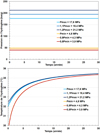 |
Fig. 7 Évolution à long terme de la pression (en haut) et de la température calculée (en bas) de l’hydrogène stocké dans la cavité saline. Long-term evolution of the cavern pressure (top) and the computed cavern temperature (bottom) of the stored hydrogen in the salt cavern. |
4.2 Perte de volume de la cavité
D’après Bérest (2021), la perte annuelle de volume d’une cavité saline qui se referme progressivement, compte tenu du comportement visqueux du sel environnant, doit rester inférieure au pour cent pour éviter que le volume stockable ne diminue trop vite, surtout pour les cavités les plus profondes. Mais aussi parce qu’elle peut engendrer des dommages sur la paroi ou à l’interface sel-puits d’accès. La Figure 8 montre la perte de volume par fluage de la cavité saline sur une période de 30 ans lorsqu’un chargement constant est maintenu autour de la pression maximale et autour de la pression minimale. Lorsque la cavité saline remplie d’hydrogène est maintenue autour de la pression maximale pendant 30 ans, la perte de volume est négligeable de l’ordre de −0,025 % (Pmax), −0,0072 % (1,1Pmax) et −0,0037 % (1,2Pmax) tandis qu’elle devient considérable lorsqu’on maintient pendant 30 ans la cavité saline autour de la pression minimale avec valeurs de −8,7 % (Pmin), −9,6 % (0,9Pmin) et −10,7 % (0,8Pmin). Toutes les courbes démontrent une augmentation quasi-linéaire de la perte de volume sur le temps, indiquant qu’on a atteint un régime quasi-stationnaire.
 |
Fig. 8 Variation de volume de la cavité pour un chargement constant autour de Pmax (en haut) et autour de Pmin (en bas) sur 30 ans. Cavern volume variation for constant loading around Pmax (top) and around Pmin (bottom) over 30 years. |
4.3 Subsidence dans l’axe du puits
La subsidence est l’affaissement progressif calculé en surface. L’analyse de la subsidence, bien que préliminaire, s’avère complexe lorsqu’elle est effectuée sur un modèle comprenant une unique cavité. Dans ce contexte, il est essentiel de déterminer l’adéquation de la dimension latérale du modèle, qui s’étend sur 500 mètres à partir de l’axe central du puits de la cavité. La Figure 9 présente l’évolution de la subsidence maximale dans l’axe du puits sur une période de 30 ans. Pour un chargement constant autour des pressions maximales, toutes les courbes montrent une très légère augmentation progressive de la subsidence sur le temps de l’ordre du millimètre en 30 ans, donc une élévation de la surface ou soulèvement très négligeable certainement imputable aux effets thermoélastiques. Pour les trois niveaux autour de la pression minimale, la subsidence est de l’ordre de −6,1 mm (Pmin), −6,8 mm (0,9Pmin) et −7,5 (0,8Pmin), décrivant donc un affaissement du sol au droit du forage à la suite du maintien à long terme d’une pression faible dans la cavité saline. Les deux figures démontrent que la pression dans la cavité est un facteur déterminant pour la subsidence de surface, avec des effets notables quand la pression dans la caverne est maintenue à un niveau bas.
 |
Fig. 9 Évolution de la subsidence pour un chargement constant autour de Pmax (en haut) et autour de Pmin (en bas) sur 30 ans. Subsidence for constant loading around Pmax (top) and around Pmin (bottom) over 30 years. |
4.4 Contrainte effective
La contrainte effective est un paramètre clé pour évaluer la stabilité d’une cavité souterraine, car elle représente la contrainte réelle ressentie par le matériau rocheux (Djizanne et al., 2012). La Figure 10 montre les isovaleurs de la contrainte effective autour de la cavité saline sous différentes conditions de pression. La cavité est chargée à différentes pressions autour de la pression maximale Pmax (17,6 MPa), 1,1Pmax (19,4 MPa) et 1,2Pmax (21,2 MPa). Chaque pression est analysée à deux moments distincts : à la fin du premier remplissage en hydrogène et après 30 ans de maintien de la cavité à cette pression constante. Les couleurs représentent les niveaux de contrainte effective, avec le magenta indiquant des zones de contrainte effective de traction, potentiellement sujettes à des dommages, et le vert représentant des zones de contrainte effective de compression. Dès la fin du premier remplissage à Pmax, les contraintes effectives de traction (en couleur magenta) apparaissent et sont localisées en paroi de la cavité pour tous les chargements. Pour tout premier remplissage qui se termine au-delà de Pmax, l’étendu de la zone en traction autour de la cavité croît avec le niveau de pression appliqué en cavité. Au fur et à mesure que le temps passe, ces contraintes de traction se développent très lentement. Les zones de traction restent localisées en paroi pour ce qui est des chargements Pmax (17,6 MPa) et 1,1Pmax (19,4 MPa), pour une résistance à la traction du sel supposée nulle. Cependant, après 30 années d’un chargement de 1,2Pmax (21,2 MPa), on observe une généralisation des zones en traction jusqu’à plusieurs dizaines de mètres de la paroi : résultats généralisables pour les cas Pmax et 1,1Pmax pour une résistance à la traction comprise entre 1 et 2 MPa ; suggérant que ce niveau de pression pourrait induire des conditions moins stables et un risque accru d’intégrité structurale de la cavité.
 |
Fig. 10 Isovaleurs de contrainte effective après le premier remplissage et après 30 ans de chargement à pression maximale en cavité. Contour plots of effective stress after the debrining and after 30 years of loading around cavern maximum pressure. |
4.5 Dilatance
La Figure 11 présente les isovaleurs du facteur de sécurité (FOS – Factor of Safety) pour le critère d’apparition de la dilatance. Le FOS est un indicateur de stabilité : un FOS inférieur à 1 signale un risque d’endommagement de la roche par dilatance. Cette figure est organisée en deux colonnes, correspondant à deux états différents de la cavité : à la fin du premier soutirage d’hydrogène, où la pression de la cavité passe de la pression maximale à la pression minimale en 10 jours, et après 30 ans de maintien d’une pression constante autour de la pression minimale d’exploitation. Les couleurs de la Figure 11 représentent les niveaux du facteur de sécurité, avec le magenta indiquant les zones où le facteur de sécurité est inférieur à 1 (zone dilatante), et le vert représentant les zones où le facteur de sécurité est supérieur ou égal à 1. Dès la fin du soutirage rapide, c’est-à-dire que dès lors que les pressions minimales Pmin (4,8 MPa) et 0,9Pmin (4,3 MPa) et 0,8Pmin (3,9 MPa) sont atteintes, une zone d’endommagement par dilatance (en magenta) est visible autour de la cavité. Cette zone est plus étendue verticalement qu’horizontalement, ce qui pose la question de l’état des contraintes autour du dernier sabot de cuvelage. Après 30 ans, la zone de dilatance garde une étendue critique avec une zone magenta sensiblement équivalente à la zone initiale. Cela souligne l’importance de maintenir une pression interne suffisamment grande pour assurer la tenue mécanique de la cavité.
 |
Fig. 11 Isovaleurs du facteur de sécurité lié au critère de dilatance à la fin du premier soutirage et après 30 ans de chargement constant à pression minimale en cavité. Contour plot of the safety factor related to the dilatancy criterion at the end of the first withdrawal and after 30 years of constant loading around cavern minimum pressure. |
5 Conclusion
Cet article examine la stabilité à long terme d’une cavité saline de stockage d’hydrogène soumise à une pression constante. La modélisation, qui intègre à la fois les aspects thermodynamiques et géomécaniques, permet d’évaluer comment la pression et la température de l’hydrogène stocké évoluent avec le temps, de déterminer les pertes de volume de la cavité dues au fluage et de quantifier la subsidence. Elle permet également d’étudier les redistributions des contraintes dans le temps, des déformations et le facteur de sécurité vis-à-vis de l’apparition éventuelle de la dilatance.
Aux pressions maximales, une augmentation de la pression entraîne une contrainte effective plus importante et une potentielle zone d’endommagement plus étendue, comme le montrent les zones magentas de la Figure 11. Ceci peut indiquer un risque accru de rupture du sel gemme ou de fracturation ; en particulier à 1,2Pmax (21,2 MPa) où l’endommagement est le plus prononcé. À des pressions minimales, une baisse de pression accroît le risque d’endommagement par dilatance, avec une zone à risque maximale observée à 0,8Pmin (3,9 MPa), soulignant l’importance de conserver une pression minimale pour la stabilité de la cavité.
Ces observations démontrent que les pressions extrêmes, qu’elles soient hautes ou basses, peuvent affecter la stabilité des cavités. La subsidence ou déformation progressive en surface est aussi impactée par les variations de pression, révélant que les effets de la gestion de la pression peuvent s’étendre au-delà de la cavité pour impacter les installations de surface.
Les résultats présentés dans cet article mettent en lumière l’importance capitale de la gestion de la pression pour la stabilité à long terme des cavités salines, en particulier pour le stockage de l’hydrogène. Les conditions de pression influent considérablement sur la contrainte effective et le facteur de sécurité, des paramètres clés pour l’intégrité structurelle des cavités. Ces résultats suggèrent que le maintien d’une pression interne adéquate est crucial pour éviter les dommages et assurer la durabilité des installations de stockage souterraines. La gestion de la pression doit donc être rigoureusement contrôlée et ajustée pour équilibrer les exigences de stockage et la préservation de l’intégrité géomécanique du sel.
Les perspectives de ces travaux de recherche incluent une analyse détaillée de la zone endommagée autour de la cavité saline, si possible en tenant compte de l’hétérogénéité du sel gemme environnant et en utilisant des critères pour la nucléation et la propagation de microfissures à partir de la paroi. Pour ce faire, on devra faire appel à des outils numériques de la mécanique de la fracture.
Remerciements
Cette étude est financée en partie par le Clean Hydrogen Partnership de l’Union européenne dans le cadre du projet HyPSTER sous la convention de subvention n° 101006751, qui inclut des recherches menées par Storengy (France), Armines-École Polytechnique (France), INOVYN (Royaume-Uni), ESK (Allemagne), ERM (Royaume-Uni), Ineris (France), Axelera (France), Brouard Consulting (France), et Equinor (Norvège). Hommage au Professeur Pierre Bérest, dont le départ soudain le 28 juillet 2022 nous a profondément attristés. Sa sagesse brillera toujours !
Références
- Bérest P. 2021. Cavernes de sel : la clé pour stocker l’hydrogène ? Polytechnique Insights, 13 octobre. [Google Scholar]
- Bérest P, Brouard B. 1999. Essais d’étanchéité des stockages d’hydrocarbures dans le sel. Rapport d’étude pour le Secrétariat à l’industrie, Contrat n°97.2.77.0013. 91 p. [Google Scholar]
- Brouard B, Bérest P, Djizanne H, Frangi A. 2012. Mechanical stability of a salt cavern submitted to high-frequency cycles, France, 9 p. [Google Scholar]
- Brouard B, Zakharov V, Frangi A, Cremonesi M. 2018. Introducing LOCAS 3D application to the geomechanical modeling of an oil-storage facility. In Proceedings of SMRI Technical Conference, 24-25 September 2018, Belfast, Northern Ireland, Solution Mining Research Institute. [Google Scholar]
- Brouard B, Zakharov V, Frangi A. 2020. Full geomechanical modeling and data management of a gas-storage facility using LOCAS 3D. Proceedings of SMRI Fall Virtual Technical Conference. [Google Scholar]
- Brouard B, Zakharov V, Frangi A. 2022. Numerical modelling of Complex Behavior of Salt Caverns. International Geomechanics Symposium, Abu Dhabi, UAE, pp. 22–78. [Google Scholar]
- DeVries KL, Mellegard KD, Callahan GD. 2003. Laboratory Testing in Support of a Bedded Salt Failure Criterion. SMRI Fall Technical Conference, Chester, United Kingdom, pp. 90–113. [Google Scholar]
- Djizanne H. 2014. Stabilité mécanique d’une cavité saline soumise à des variations rapides de pression : application au stockage souterrain de gaz naturel, air comprimé et d’hydrogène. Thèse de Doctorat de l’École Polytechnique, Palaiseau, France, 262 p. [Google Scholar]
- Djizanne H, Bérest P, Brouard B. 2012. Tensile Effective Stresses in Hydrocarbon Storage Caverns. SMRI Fall 2012, Bremen, Germany. [Google Scholar]
- Djizanne H, Bérest P, Brouard B. 2014. The Mechanical Stability of a Salt Cavern Used for Compressed Air Energy Storage (CAES). SMRI Spring Technical Meeting, San Antonio, TX, USA. [Google Scholar]
- Djizanne H, Brouard B, Hévin G. 2023. Mechanical stability of a salt cavern used for hydrogen storage. 15th ISRM Congress 2023 & 72nd Geomechanics Colloquium. Schubert & Kluckner, eds. © ÖGG. Salzburg, Austia. [Google Scholar]
- Horváth PL, Mirau S, Schneider GS, et al. 2018. Update of SMRI’s Compilation of Worldwide Salt Deposits and Salt Cavern Fields. SMRI Research report RR-2017-5, 265 p. [Google Scholar]
- Labaune P. 2018. Comportement thermomécanique du sel gemme : Application au dimensionnement des cavités. Thèse de Doctorat de l’Université de recherche Paris Sciences et Lettres PSL Research University, Paris, 123 p. [Google Scholar]
- Munson DE. 1997. Constitutive model of creep in Rock salt applied to underground room closure. Int J Rock Mech Min Sci, pp. 233–247. [CrossRef] [Google Scholar]
- Munson DE. 1999. Correlation of creep behaviour of domal salt. SMRI Spring Technical Conference, Las Vegas, NV, USA. [Google Scholar]
- Nieland JD, Ratigan JL. 2006. Geomechanical evaluation of two gulf coast natural gas storage caverns. Proc. SMRI Spring Technical Conference, Brussels, Belgium, pp. 61–89. [Google Scholar]
- Rokahr RB, Staudtmeister K. 1993. Rock mechanical sudy of the load-bearing behavior of a gas cavern in rock salt after a blow out. Proc. 7th International Symposium on Salt Kyoto, Japan. Elsevier Science Publishers B.V., Amsterdam, Netherlands, vol. 1, ISBN 0-444-89143-9, 477–482. [Google Scholar]
- Schulz R, Denzau H, Benke K. 2011. Introduction of a Continuum Damage Method (CDM) for FEM calculations of fractures mechanisms in rock salt. Proc. SMRI Fall Technical Conference, Roma, Italy. [Google Scholar]
Citation de l’article : Hippolyte Djizanne, Benoit Brouard, Grégoire Hévin, Carelle Lekoko. Stabilité mécanique à long terme des cavités salines de stockage d’hydrogène. Rev. Fr. Geotech. 2023, 177, 3.
Liste des tableaux
Liste des figures
 |
Fig. 1 Distribution des dépôts de sel gemme dans le monde (Horváth et al., 2018). Worldwide distribution of rock salt deposits (Horváth et al., 2018). |
| Dans le texte | |
 |
Fig. 2 Vue de la cavité saline dans son environnement géologique. View of the salt cavern in its geological environment. |
| Dans le texte | |
 |
Fig. 3 Forme géométrie de la cavité saline remplie d’hydrogène. Geometric configuration of the hydrogen-filled salt cavern. |
| Dans le texte | |
 |
Fig. 4 Distribution initiale de la pression géostatique en fonction de la profondeur. Initial distribution of geostatic pressure as a function of depth. |
| Dans le texte | |
 |
Fig. 5 Distribution initiale de la température géothermique en fonction de la profondeur. Initial distribution of geothermal temperature as a function of depth. |
| Dans le texte | |
 |
Fig. 6 Évolution sur les 12 premiers mois de la pression (en haut) et de la température calculée (en bas) de l’hydrogène stocké dans la cavité saline ; dans cette figure, t = 0 correspond au début de la phase de remplissage. Evolution over the first 12 months of the cavern pressure (top) and the computed cavern temperature (bottom) of the stored hydrogen in the salt cavern; in this figure, t = 0 corresponds to the beginning of the debrining. |
| Dans le texte | |
 |
Fig. 7 Évolution à long terme de la pression (en haut) et de la température calculée (en bas) de l’hydrogène stocké dans la cavité saline. Long-term evolution of the cavern pressure (top) and the computed cavern temperature (bottom) of the stored hydrogen in the salt cavern. |
| Dans le texte | |
 |
Fig. 8 Variation de volume de la cavité pour un chargement constant autour de Pmax (en haut) et autour de Pmin (en bas) sur 30 ans. Cavern volume variation for constant loading around Pmax (top) and around Pmin (bottom) over 30 years. |
| Dans le texte | |
 |
Fig. 9 Évolution de la subsidence pour un chargement constant autour de Pmax (en haut) et autour de Pmin (en bas) sur 30 ans. Subsidence for constant loading around Pmax (top) and around Pmin (bottom) over 30 years. |
| Dans le texte | |
 |
Fig. 10 Isovaleurs de contrainte effective après le premier remplissage et après 30 ans de chargement à pression maximale en cavité. Contour plots of effective stress after the debrining and after 30 years of loading around cavern maximum pressure. |
| Dans le texte | |
 |
Fig. 11 Isovaleurs du facteur de sécurité lié au critère de dilatance à la fin du premier soutirage et après 30 ans de chargement constant à pression minimale en cavité. Contour plot of the safety factor related to the dilatancy criterion at the end of the first withdrawal and after 30 years of constant loading around cavern minimum pressure. |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.