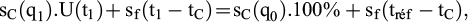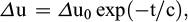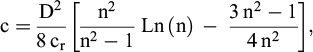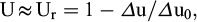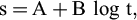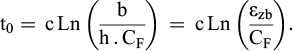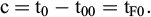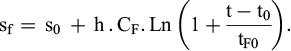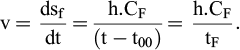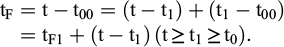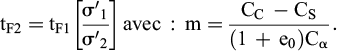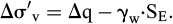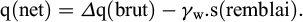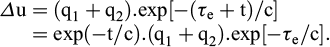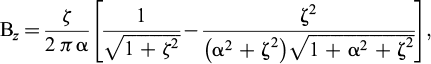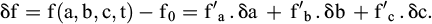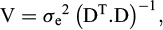© CFMS-CFGI-CFMR-CFG, 2023

1 Principes du préchargement

Dans la construction de remblais sur sols mous destinés à supporter des ouvrages tels que routes, parkings, stations d’épuration, voire bâtiments, on est souvent amené d’une part, à mettre en place un réseau de drains verticaux pour diminuer la durée de consolidation des sols mous et, d’autre part, à précharger le sol compressible par une hauteur excédentaire de remblais afin de réduire les tassements en service.

Dans le cas d’un sol mou dénué de fluage, il suffit que le tassement en fin de préchargement soit égal au tassement de consolidation final qu’on aurait sous la charge permanente en situation définitive. Dans le cas d’un sol mou sujet à fluage notable, l’idée est de « consommer du fluage » lors du préchargement, c’est-à-dire d’obtenir sous le préchargement un tassement de consolidation et de fluage égal au tassement de consolidation final et à une partie du tassement de fluage sous la charge définitive :

$${\mathrm{s}}_{\mathrm{C}}\left({\mathrm{q}}_1\right)\mathrm{.}\mathrm{U}\left({\mathrm{t}}_1\right)+{\mathrm{s}}_{\mathrm{f}}({\mathrm{t}}_1-{\mathrm{t}}_{\mathrm{C}})={\mathrm{s}}_{\mathrm{C}}\left({\mathrm{q}}_0\right).100\%+{\mathrm{s}}_{\mathrm{f}}({\mathrm{t}}_{\mathrm{r}\mathrm{é}\mathrm{f}}-{\mathrm{t}}_{\mathrm{C}}),$$(F1)

où :

• s_C = tassement de consolidation ;

• s_f = tassement de fluage ;

• q₀ = charge de service ;

• q₁ = charge de préchargement ;

• t₁ = durée du préchargement ;

• t_C = durée écoulée lors du passage du régime de consolidation au régime de fluage ;

• t_réf = durée de référence pour le tassement toléré en service. Dans le projet IKEA décrit dans la suite, cette valeur a été fixée à 10 ans ;

• U(t₁) = degré de consolidation au temps t₁.

2 Modèles de comportement

L’application de la formule (F1) nécessite d’avoir un modèle de consolidation, et un modèle de fluage.

2.1 Modèle de consolidation

On appliquera la formule de consolidation radiale de Barron sous la forme suivante :

$$\Delta \text{u}=\Delta {\text{u}}_0\text{exp}(-\text{t/c}),$$(F2)

avec :

• Δu = surpression interstitielle au temps t ;

• Δu₀ = surpression interstitielle initiale ;

• c = constante de temps.

$$\mathrm{c}=\frac{{\mathrm{D}}^2}{{8\mathrm{c}}_{\mathrm{r}}}\left[\frac{{\mathrm{n}}^2}{{\mathrm{n}}^2-1}\mathrm{L}\mathrm{n}\left(\mathrm{n}\right)-\frac{3{\mathrm{n}}^2-1}{4{\mathrm{n}}^2}\right],$$(F3)

où :

• c_r = coefficient de consolidation radiale ;

• D = diamètre de la maille du réseau de drains ;

• D_d = diamètre du drain circulaire équivalent ;

•        = L/2 pour un drain plat de largeur L (Baguelin et Finiasz, 2016) ;

• n = D/D_d ;

• Ln = logarithme népérien.

Pour une couche épaisse, d’épaisseur 2H, drainée aux deux bords, la formule de Carillo permet de relier le degré de consolidation U à ses deux composantes, verticale U_v et radiale U_r :

$$\text{1}-\text{U}=(\text{1}-{\text{U}}_v)(\text{1}-{\text{U}}_r)\text{.}$$(F4)

On négligera la composante verticale, car le degré de consolidation U_v reste en pratique très faible. Dans le cas de drains verticaux dans une couche épaisse constituée de couches élémentaires de faible épaisseur, mais néanmoins supérieure à l’espacement entre drains, on peut donc considérer la consolidation d’une couche élémentaire comme indépendante de celles des autres et avec le degré de consolidation donné par :

$$\text{U}\approx {\text{U}}_r=1-\Delta \text{u}/\Delta {\text{u}}_0,$$

et pour le tassement s :

$$\text{s}= \text{a}+\text{b} \left[\Delta {\text{u}}_0 -\Delta \text{u}\right],$$

soit :

$$\text{s}= \text{a}+\text{b} \left[\text{1} - \text{exp}(- \text{t/c})\right].$$(F5)

Le terme constant « a » permet d’appliquer la loi d’exponentielle amortie du terme « b » au-delà d’un certain temps pour des cas où la consolidation suit une autre loi : c’est le cas d’une couche épaisse avec drains verticaux constituée d’une succession de couches élémentaires argileuses et sableuses, les premières avec le même coefficient de consolidation radiale c_r, les secondes se consolidant très rapidement. C’est aussi le cas d’une couche épaisse, unique, au-delà d’une durée correspondant à des valeurs du facteur temps classique T > 0,3 (Baguelin, 1999).

2.2 Modèle de fluage

2.2.1 Modèles traditionnels

L’idée est de raccorder, en fin de consolidation, une courbe de fluage logarithmique à une courbe de consolidation, selon une formule du type (Buisman, 1936) :

$$\text{s}=\text{A+B log t,}$$(F6)

où s est le tassement et B = H.Cα. Le temps t est compté depuis l’application de la charge, supposée instantanée. « log » désigne le logarithme décimal.

De manière analogue, Koppejan (1948) donne, à partir d’une série d’essais œdométriques de longue durée, les paramètres du tassement primaire (consolidation) et du tassement secondaire (fluage), en fonction de la contrainte verticale en place et de la pression de surconsolidation, toujours avec une évolution en log t pour le fluage.

On peut adresser deux critiques aux formules de ce type :

• la formulation avec log t fait coïncider l’origine du temps du logarithme avec le moment d’application de la charge, ce qui est une hypothèse mathématique arbitraire ;

• la fin de consolidation est une notion floue.

Il en résulte que le raccord entre courbe de consolidation et courbe de fluage n’est pas défini de manière univoque, et qu’en général un point anguleux apparaît dans la courbe d’évolution du tassement s(t).

2.2.2 Modèle de Bjerrum

Bjerrum (1967) a proposé un modèle de fluage schématisé en figure 1.

Les principales caractéristiques sont :

• une courbe de compression « instantanée ». C’est plus ou moins la courbe de compression œdométrique classique, que ce soit pour la compression instantanée pendant la sédimentation, ou pour une charge additionnelle au-delà de la pression de surconsolidation σ_c ;

• des courbes de compression secondaire (fluage), parallèles à la courbe de compression instantanée, indicées selon leur âge, c’est-à-dire selon la durée d’application de la charge depuis la courbe vierge ;

• pour un espacement constant entre ces courbes, l’âge suit une progression logarithmique. La loi de fluage est logarithmique, c’est-à-dire que l’évolution du tassement sous une charge donnée σ’_v est proportionnelle au logarithme du temps t, celui-ci étant compté à partir de la courbe vierge ;

• dans le cas habituel de courbe vierge rectiligne dans le graphique (e ; p), ces courbes de fluage ont la même pente C_c. Nota : Bjerrum montre une courbe légèrement incurvée, mais les mêmes principes sont applicables ;

• en fin de sédimentation, le sol subit à charge constante une déformation différée (fluage), typiquement pendant plusieurs milliers d’années.

Il s’ensuit que :

• les courbes de fluage sont des isotaches, c’est-à-dire que sur une courbe, pour deux charges σ’_v1 et σ’_v2, correspondant à deux profondeurs différentes, la vitesse de fluage est la même ;

• d’après Bjerrum, l’âge du sédiment produit un effet de surconsolidation : l’application d’une charge additionnelle à partir du point d’état en place (e₀, σ₀), d’âge 300 ans sur le graphique, donne une courbe de chargement quasi-horizontale, puis rejoint la courbe vierge de sédimentation au point (e₀, σ_c) ; σ_c est la contrainte de surconsolidation.

L’évolution de la résistance au cisaillement non drainée « s » est montrée sur la gauche à titre indicatif.

Les points suivants sont à noter :

• la courbe « instantanée » n’est pas définie précisément. D’après les espacements entre les courbes du graphique de Bjerrum, on peut déterminer que la courbe instantanée donnée par Bjerrum correspond à l’âge de 13 jours. En fait, on peut substituer à cette courbe, une courbe de référence dont l’âge dépend du temps de consolidation de la couche ; par exemple, quelques heures pour un essai œdométrique sur une argile, plusieurs mois voire plusieurs années pour une couche de sol en place ;

• la vitesse de fluage mentionnée ci-dessus se réfère à la vitesse de variation de l’indice des vides « e », (de/dt)₀ sur la courbe vierge. Si l’indice des vides e est à peu près constant dans la gamme de contraintes étudiée, égal à sa valeur initiale e₀, on peut considérer les isotaches comme des courbes d’égale vitesse initiale de tassement (ds/dt)₀, car (ds/dt) = (de/dt)/(1 + e₀).

Fig. 1 Schéma de fluage selon Bjerrum (1967). Sketch of creep according to Bjerrum (1967).

3 Application du modèle de Bjerrum

3.1 Chargement

On retient deux principes :

• succession des phases de consolidation et de fluage ;

• raccord sans point anguleux.

Les fonctions retenues sont les suivantes, en termes de tassement s :

• fonction de consolidation de la forme (F2), avec expression du tassement selon (F7) :

$${\text{s}}_{\text{C}}= \text{a} + \text{b} \text{.} ( \text{1}-\text{exp} [-\frac{\text{t}}{\text{c}}] )\text{.}$$(F7)

Le temps t est compté depuis l’application de la charge, supposée instantanée.

• fonction de fluage de la forme :

$${\text{s}}_{\text{f}}= {\text{s}}_0 + {\text{C}}_{\text{F}} \text{.} \text{h} \text{.} \text{Ln} \left(\frac{\text{t}-{\text{t}}_{\text{00}}}{{\text{t}}_0-{\text{t}}_{\text{00}}}\right),$$(F8)

avec :

• h = épaisseur de la couche ;

• s₀, t₀ = valeurs du temps et du tassement au point de raccord consolidation-fluage ;

• t₀₀ = temps de démarrage du fluage ;

• Ln = logarithme népérien ;

• C_F = constante de temps du fluage :

$${\text{C}}_{\text{F}} = {\text{C}}_{\alpha }\text{.} \text{Ln}(\text{10}) = \text{2,3} {\text{C}}_{\alpha }.$$(F9)

Au point de raccord, on impose que les fonctions s_c(t) et s_f(t) aient la même valeur, la même pente et aussi la même courbure. Cette dernière condition est nécessaire pour que les deux courbes se chevauchent, c’est-à-dire pour que celle qui est au-dessus de l’autre avant le point de raccord ne le reste pas après, mais passe en dessous.

Les valeurs des dérivées par rapport au temps t au point de raccord (t₀ ; s₀) sont :

• dérivées premières : s_c’ = b/c.exp(−t₀/c) ; s_f’ = h.C_F/(t₀−t₀₀) ;

• dérivées secondes : s_c” = −b/c².exp(−t₀/c) ; s_f” = −h.C_F/(t₀−t₀₀)².

En formant le rapport s₀’²/s₀” pour les deux courbes, consolidation et fluage, et, en posant b/h = ε_zb, on trouve :

$${\text{t}}_0= \text{c} \text{Ln} \left(\frac{\text{b}}{\text{h} \text{.} {\text{C}}_{\text{F}}}\right) = \text{c} \text{Ln} \left(\frac{{\mathrm{\epsilon }}_{\text{zb}}}{{\text{C}}_{\text{F}}}\right).$$(F10)

Puis, l’égalité des dérivées premières donne :

$$\text{c}={\text{t}}_0-{\text{t}}_{\text{00}}={\text{t}}_{\text{F0}}.$$(F11)

Le paramètre t_F0 est l’âge au point de raccord.

Donc, après le point de raccord, on a :

$${\text{s}}_{\text{f}}= {\text{s}}_0 + \text{h} \text{.} {\text{C}}_{\text{F}}\text{.} \text{Ln} \left(\text{1}+\frac{\text{t}-{\text{t}}_0}{{\text{t}}_{\text{F0}}}\right).$$(F12)

De (F8), découle immédiatement la vitesse de fluage v, qui ne dépend que de l’âge t_F :

$$\text{v}=\frac{\text{d}{\text{s}}_f}{\text{dt}}=\frac{\text{h}.{\text{C}}_F}{\left(\text{t}-{\text{t}}_{\text{00}}\right)}=\frac{\text{h}.{\text{C}}_{\text{F}}}{{\text{t}}_F}.$$(F13)

En phase de fluage, après le temps t₁, postérieur au temps t₀, l’âge t_F varie à partir du temps t₁, selon la relation :

$${\mathrm{t}}_{\mathrm{F}}=\mathrm{t}-{\mathrm{t}}_{00}=(\mathrm{t}-{\mathrm{t}}_1)+({\mathrm{t}}_1-{\mathrm{t}}_{00})={\mathrm{t}}_{\mathrm{F}1}+(\mathrm{t}-{\mathrm{t}}_1)(\mathrm{t}\ge {\mathrm{t}}_1\ge {\mathrm{t}}_0)\mathrm{.}$$(F14)

Les courbes isotaches de Bjerrum (même vitesse de fluage) sont donc caractérisées par l’âge t_F. De pente C_C dans le diagramme [e ; log(σ)], elles sont de pente C_C/(1 + e₀) dans le diagramme [s/h₀ ; log(σ)], et la vitesse de fluage est donnée par la formule (F13).

3.2 Déchargement

On considère que le déchargement se fait suivant une pente C_s dans le diagramme [log(σ)’) ; e]. Avec s = Δh et σ’, au lieu de σ’_v, dans le diagramme [log(σ’) ; s/h₀] de la figure 2, le chargement et le déchargement se font respectivement avec les pentes C_c/(1 + e₀) et C_s/(1 + e₀). De plus, on considère, par simplification, que le déchargement se fait en condition drainée, c’est-à-dire qu’on néglige les surpressions interstitielles. Cette hypothèse est justifiée par le fait que la consolidation est beaucoup plus rapide en déchargement qu’en chargement : en effet, le coefficient de consolidation c_v = k.E_v/γ_w est proportionnel au module de déformation E_v, lequel est inversement proportionnel au paramètre C_c ou C_s. Or, typiquement le rapport C_c/C_s est de l’ordre 10. Quant à la perméabilité, elle est à peu près la même en chargement et en déchargement.

La figure 3 montre l’écrouissage dans le diagramme œdométrique [log(σ’) ; e]. On peut ainsi, à partir du point de préchargement M₁, déterminer la variation Δe d’indice des vides entre le point de déchargement M₂ sur la droite de décompression et le point fictif M’₂ équivalent sur la droite de compression :

$$\mathrm{\Delta }\mathrm{e}\hspace{0.17em}=\hspace{0.17em}({\mathrm{C}}_{\mathrm{C}}-{\mathrm{C}}_{\mathrm{S}})\hspace{0.17em}\log \hspace{0.17em}({{\mathrm{\sigma }}^{\prime }}_1/{{\mathrm{\sigma }}^{\prime }}_2)\mathrm{.}$$(F15)

On peut aussi évaluer le fluage en appliquant la formule (F8), entre les points M₂ et M’₂, et en remarquant que h.C_F. Ln t = h.C_α.log t :

$$\Delta \text{e /}\left(\text{1+}{\text{e}}_0\right)=\Delta \text{h}/{\text{h}}_0={\text{C}}_{\alpha }\log \left[\left({\text{t}}_{\text{2}}-{\text{t}}_{\text{00}}\right)/\left({\text{t}}_{\text{1}}-{\text{t}}_{\text{00}}\right)\right]={|\text{C}}_{\alpha }\log \left[{\text{t}}_{\text{F2}}/{\text{t}}_{\text{F1}}\right].$$(F16)

On trouve alors :

$${\mathrm{t}}_{\mathrm{F}2}={\mathrm{t}}_{\mathrm{F}1}\left[\frac{{{\mathrm{\sigma }}^{\prime }}_1}{{{\mathrm{\sigma }}^{\prime }}_2}\right]\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{c}:\hspace{0.17em}\mathrm{m}=\frac{{\mathrm{C}}_{\mathrm{C}}\hspace{0.17em}-{\mathrm{C}}_{\mathrm{S}}}{(1\hspace{0.17em}+\hspace{0.17em}{\mathrm{e}}_0){\mathrm{C}}_{\mathrm{\alpha }}}\mathrm{.}\hspace{0.17em}$$(F17)

Cette formule donne le vieillissement du fluage (t_F2 > t_F1), donc l’écrouissage, en fonction du taux de surcharge.

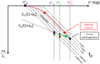Fig. 2 Écrouissage dans le diagramme [log(σ’) ; s/h0] où s = Δh. Creep hardening in [log(σ’); s/h0] diagram where s = Δh.

Fig. 3 Écrouissage dans le diagramme [log(σ’) ; e]. Creep hardening in [log(σ’); e] diagram.

4 Compléments sur la consolidation

4.1 Déjaugeage des charges

Pour la prise en compte du déjaugeage lié au tassement, on suppose que la charge est d’extension infinie et l’on considère deux états (Fig. 4) : l’état initial avant travaux et un état final de chargement, en consolidation complète. On prend comme origine des profondeurs z le niveau de la nappe, qui est supposé être le même entre les deux états.

On considère trois points matériels :

• le point E situé initialement au niveau de la nappe (z = 0), et à la profondeur s_E dans l’état final (position E’) ;

• le point courant M, situé initialement à la profondeur z, et à la profondeur z + s_M dans l’état final (position M’) ;

• le point I qui dans l’état final (position I’) se retrouve au niveau de la nappe.

On s’intéresse aux contraintes effectives.

Pour les couches de sol situées sous la nappe, les changements de volume liés à la consolidation ne changent pas la contribution des grains à la contrainte effective.

De même pour les couches de sol situées au-dessus du point I, la contrainte effective n’est affectée que par le poids du remblai de préchargement.

Par contre, le volume de sol compris entre E et I, initialement situé au-dessus de la nappe, passe sous celle-ci. En termes de contraintes effectives, ce volume de sol doit être déjaugé. En première approche, on peut négliger la compression de la couche située entre les points I et E, ce qui revient à situer le point I à la distance s_E au-dessus de la nappe.

En conséquence, le déjaugeage vaut approximativement γ_w.s_E, et en définitive, l’incrément de contrainte effective à considérer au point M vaut :

$$\mathrm{\Delta }{{\mathrm{\sigma }}^{\prime }}_{\mathrm{v}}=\mathrm{\Delta }\mathrm{q}-{\mathrm{\gamma }}_{\mathrm{w}}\cdot {\mathrm{S}}_{\mathrm{E}}\mathrm{.}$$(F18)

On notera que ceci s’applique quelle que soit la position du point M, dès lors qu’il est situé initialement sous la nappe et que cette quantité est constante avec la profondeur dans le cas d’une charge d’extension infinie.

En pratique, dans le cas courant d’une nappe proche du niveau du TN, le tassement s_E peut être assimilé au tassement du remblai s_remblai.

Donc, la contrainte nette appliquée q(net) s’obtient en déjaugeant l’accroissement brut de contrainte totale selon la valeur du tassement du remblai :

$$\text{q}\left(\text{net}\right)=\Delta \text{q}\left(\text{brut}\right)-{\gamma }_{\text{w}}.\text{s}\left(\text{remblai}\right).$$(F19)

Pour des remblais d’extension finie en plan, mais de grandes dimensions, les formules ne sont qu’approchées. Le terme Δq de la formule (F18) est amorti avec la profondeur. L’approximation est d’autant meilleure que l’on est proche de la zone centrale des remblais ; le déjaugeage est surestimé, le tassement sous-estimé, d’autant plus qu’on s’approche des bords. Par souci de simplification, on appliquera la charge nette q(net), obtenue par la formule (F19), sur l’ensemble du remblai. À noter que la détermination de cette charge nécessite une itération : on calcule, en un premier temps, le tassement s₁ correspondant à la charge brute Δq(brut), puis on détermine par (F19) une première valeur de la charge nette q₁(net), ensuite on calcule une deuxième valeur du tassement s₂ sous cette charge, que l’on introduit dans (F19) pour obtenir une valeur q₂(net). En général, cette valeur est suffisante, il n’est pas nécessaire de procéder à une itération supplémentaire.

Fig. 4 Schéma de tassement et de déjaugeage. Sketch of settlement and buoyancy effect.

4.2 Ajout d’une charge supplémentaire

Si au bout d’une durée d’application τ₁ d’une première charge q₁, on ajoute une deuxième charge q₂, il est utile de savoir, pour combiner la consolidation et le fluage, quelle est la durée d’application équivalente τ_e d’une charge unique, égale à la somme des deux charges (q₁ + q₂).

Dans le cas de drains verticaux, avec une consolidation radiale caractérisée par la constante de temps c, la formule (F2) permet de déterminer les pressions interstitielles résiduelles des deux charges q₁ et q₂, et on les additionne, pour le temps qui suit l’application de la deuxième charge, moment pris comme origine du temps t :

$$\Delta \text{u}=\Delta {\text{u}}_{\text{1}}+\Delta {\text{u}}_{\text{2}}={\text{q}}_{\text{1}}.\exp \left[-\left({\tau }_{\text{1}}+\text{t}\right)/\text{c}\right]\text{+}{\text{q}}_{\text{2}}.\exp \left(-\text{t/c}\right)=\exp (-\text{t}/\text{c}).\left[{\text{q}}_{\text{1}}.\exp \left(-{\tau }_1/\text{c}\right)+{\text{q}}_{\text{2}}.\right].$$

À comparer pour la charge totale unique (q₁ + q₂) à :

$$\Delta \text{u}=\left({\text{q}}_1+{\text{q}}_2\right).\exp \left[-\left({\tau }_{\text{e}}+\text{t}\right)/\text{c}\right]=\exp \left(-\text{t}/\text{c}\right).\left({\text{q}}_1+{\text{q}}_2\right).\exp \left[-{\tau }_{\text{e}}/\text{c}\right].$$

D’où la durée d’application équivalente τ_e :

$${\tau }_{\text{e}}=\text{c} \text{Ln}\left(\frac{{\text{q}}_{\text{1}}+{\text{q}}_{\text{2}}}{{\text{q}}_{\text{1}}.\exp \left(-{\tau }_{\text{1}}/\text{c}\right)+{\text{q}}_{\text{2}}}\right).$$(F20)

5 Exemple du projet IKEA de Bayonne

Le projet du magasin IKEA de Bayonne est situé sur un ancien marais en bordure de l’Adour, sur la rive gauche. Le projet a été décrit par Binda et al. (2016). La figure 5 montre le schéma du site.

La construction des remblais des parkings et des voiries était prévue par la méthode du préchargement de manière à diminuer le tassement de consolidation et celui de fluage. Deux tranches de construction des remblais étaient programmées, décalées d’un an : de février 2013 à août 2015 pour le magasin IKEA ; de février 2014 à août 2016 pour le centre commercial Inter Ikea.

Les reconnaissances géotechniques et le projet de préchargement ont été réalisés par FUGRO (missions G1 et G2), les travaux de préchargement ont été réalisés par COLAS, avec le conseil géotechnique et les calculs correspondants de FONDASOL (missions G3 et G4), la pose de l’instrumentation de suivi et les relevés ont été réalisés par GÉOLITHE.

Pour les voiries, les parkings et réseaux divers, les marchés et les études de sols prévoyaient une durée de 10 mois pour la mise en œuvre de la technique de préchargement, avec une phase de consolidation de 4 mois, suivie d’une phase de maintien de la charge (fluage) d’au plus 6 mois, avant enlèvement, puis construction de la chaussée. L’exigence fonctionnelle était que le tassement des parkings et voiries ne dépasse pas 10 cm pendant les 10 premières années de service, ceci afin de limiter l’évolution de la dénivelée, à la jonction du bâtiment (sur pieux) et du parking, et de réduire les coûts d’entretien.

Nous extrayons à titre d’exemples quelques calculs réalisés sur ce projet, au point A de la zone 1, au profil 1, indiqué par la flèche à la figure 5.

Fig. 5 Plan du projet, avec parkings, zones de calcul et points d’instrumentation. Project map, with computation zones and instrumentation points.

5.1 Outils de calcul

On a appliqué une approche analytique tridimensionnelle combinant trois tableurs développés en interne par FONDASOL : tableur TASSUNI pour le calcul de la contrainte verticale et du tassement uniaxial sur une verticale ; tableur FINCONSOLRAD pour le calage de la consolidation radiale ; tableur CONSOFLU prenant en compte la consolidation et le fluage selon le modèle de Bjerrum.

Le tableur TASSUNI permet de calculer le tassement uniaxial, à la verticale de 3 points M(x,y) sous l’action de charges rectangulaires uniformes, agissant sur un sol composé de couches horizontales. Le nombre des rectangles est au plus de 72. Pour une charge donnée q, la contrainte verticale q(z) induite à la profondeur z est calculée en utilisant les expressions analytiques données dans l’ouvrage de Giroud (1972), Tables pour le calcul des fondations, tome 2, pp. 124 et 125, pour un milieu élastique homogène semi-indéfini. Pour un rectangle élémentaire de côtés a et b, soumis à une charge uniforme q, on pose : ζ = z/2a et α = b/a, et alors la contrainte q(z) induite au droit d’un coin du rectangle est donnée par q(z) = q (A_z + B_z + C_z) avec :

$${\text{A}}_z=\frac{\alpha \zeta }{2 \pi }\left[\frac{1}{\sqrt{{\alpha }^2+\hspace{0.17em}{\zeta }^2}}-\frac{{\zeta }^2}{\left(1\hspace{0.17em}+\hspace{0.17em}{\zeta }^2\right)\hspace{0.17em}\sqrt{1\hspace{0.17em}+\hspace{0.17em}{\alpha }^2\hspace{0.17em}+\hspace{0.17em}{\zeta }^2}}\right],$$

$${\text{B}}_z=\frac{\zeta }{2 \pi \hspace{0.17em}\mathrm{\alpha }}\left[\frac{1}{\sqrt{1\hspace{0.17em}+\hspace{0.17em}{\zeta }^2}}-\frac{{\mathrm{\zeta }}^2}{\left({\mathrm{\alpha }}^2\hspace{0.17em}+\hspace{0.17em}{\mathrm{\zeta }}^2\right)\sqrt{1\hspace{0.17em}+\hspace{0.17em}{\mathrm{\alpha }}^2\hspace{0.17em}+\hspace{0.17em}{\mathrm{\zeta }}^2}}\right],$$

$${\text{C}}_z=\frac{\text{1}}{2 \pi }\left[\begin{array}{l}\text{arc } \text{tg}\frac{\mathrm{\alpha }}{\mathrm{\zeta }\sqrt{\text{1 }+\hspace{0.17em} {\mathrm{\alpha }}^2\hspace{0.17em}+{\hspace{0.17em}\mathrm{\zeta }}^2}}+\frac{\mathrm{\alpha }\mathrm{\zeta }}{\sqrt{1\hspace{0.17em}+\hspace{0.17em}{\mathrm{\alpha }}^2\hspace{0.17em}+\hspace{0.17em}{\mathrm{\zeta }}^2}}\cdot \\ -\frac{\mathrm{\alpha }\mathrm{\zeta }}{\sqrt{{\mathrm{\alpha }}^2\hspace{0.17em}+\hspace{0.17em}{\mathrm{\zeta }}^2}}+\frac{\mathrm{\zeta }}{\mathrm{\alpha }\hspace{0.17em} \sqrt{1\hspace{0.17em}+{\hspace{0.17em}\mathrm{\alpha }}^2\hspace{0.17em}+\hspace{0.17em}{\mathrm{\zeta }}^2}}-\frac{\mathrm{\zeta }}{\mathrm{\alpha }\hspace{0.17em} \sqrt{1\hspace{0.17em}+\hspace{0.17em}{\mathrm{\zeta }}^2}}\end{array}\right].$$

L’application à un rectangle du tableur TASSUNI se fait en le décomposant en 4 rectangles élémentaires dont les coins sont jointifs à la verticale du point de calcul. Les contributions de chacun sont additionnées algébriquement selon la position du point de calcul (Fig. 6).

Les rectangles du calcul TASSUNI sont définis de façon à respecter les largeurs chargées. La limite extérieure du rectangle est prise à mi-talus. Sur l’ensemble des zones, le modèle TASSUNI est appliqué pour les 3 principales charges résultant de la construction ou du démontage du remblai. Une quatrième charge peut venir s’ajouter dans le cas de la mise en place d’une charge supplémentaire de préchargement.

Le tableur FINCONSOLRAD permet de caler les paramètres de consolidation et de vérifier le taux de consolidation obtenu à la fin de la phase prévue pour la consolidation.

Le tableur CONSOFLU permet, à partir des résultats des calculs TASSUNI et FINCONSOLRAD, d’évaluer le tassement de fluage selon le modèle de Bjerrum.

Ainsi, on peut déterminer les hauteurs de remblaiement de manière à respecter le critère de fluage sur 10 ans.

Fig. 6 Combinaison algébrique des contributions des rectangles élémentaires selon la position du point de calcul M. Algebraic addition of elementary rectangles contributions, function of the location of the calculation point M.

5.2 Données géotechniques

D’après le rapport de FUGRO, les sondages ont mis en évidence une épaisseur d’alluvions importante qui tend à augmenter vers l’Est. Le substratum se situe au plus haut dans la partie Sud-Ouest vers la cote −33 NGF pour atteindre progressivement des profondeurs importantes dans les zones Est et Nord du site vers la cote −44 NGF. Les valeurs des paramètres géotechniques, issues du rapport G2, à prendre en compte dans les calculs pour la partie Est sont données dans le tableau 1.

Ces valeurs sont représentatives, mais prudentes, afin de couvrir une certaine variabilité des paramètres et de la stratification (présence de lits sableux en certaines zones). Cependant, la variabilité du niveau du substratum (entre −25 et −42 NGF) a bien été prise en compte dans les calculs.

Le POP, « pre-overburden pressure », désigne la marge de surconsolidation par rapport à la contrainte verticale en place, soit : POP = σ’_c−σ’_v0. Les calculs présentés ci-après concernent le point A du profil 1, dans la zone 1, indiqué par la flèche de la figure 5.

5.3 Vérification de la consolidation à 4 mois

La méthode observationnelle a été appliquée au projet. Elle comportait d’abord la vérification de l’amplitude des tassements, puis celle du taux de consolidation à 4 mois, fixé à 90 % minimum.

La construction d’Asaoka était suggérée. On en voit l’application à la figure 7, pour 2 types de mesures de tassement au point A, profil 1, zone 1 : la boule tassométrique BT5, et le point A du profilomètre 1. On voit que certains points ont dû être éliminés de l’ajustement, surtout sur la BT5, où le résultat aurait été encore plus défavorable sans cette élimination. Le taux de consolidation est très différent : 81 % ou 97 %.

Compte tenu des difficultés rencontrées dans l’application de la méthode d’Asaoka, on s’est rapidement tourné vers l’ajustement d’une courbe de consolidation sur les points de mesure, comme décrit par Baguelin (1999) et illustré sur la figure 8. À cet effet, on a mis au point le tableur FINCONSOLRAD, qui par rapport à la méthode d’Asaoka présente plusieurs avantages :

• il suffit que les relevés de tassement soient répartis assez régulièrement sur la période étudiée, sans que les intervalles de temps soient rigoureusement égaux ;

• on peut combiner plusieurs types de mesures de tassement, à condition de faire un recalage initial convenable entre les différents types de mesure ;

• on peut obtenir des intervalles de confiance pour les paramètres de calage, ainsi que des fuseaux de confiance pour les grandeurs étudiées en fonction du temps.

Le graphique de la figure 8 montre les points utilisés dans le tableur FINCONSOLRAD pour l’ajustement d’une loi de consolidation de type (F7) : s = a + b[1−exp(−t/c)], pour le point A, zone 1, profil Pro 1. Les relevés sont issus de la boule tassométrique BT5, du profilomètre Pro 1, du plot topométrique topo 17. Un recalage entre ces différents types de mesure a dû être effectué. Ainsi, aux valeurs brutes topo 17, une valeur de 628 mm a été ajoutée pour tenir compte du fait que le plot topométrique a été installé une fois le remblai monté et qu’ainsi du tassement s’est produit lors de la montée du remblai. Les valeurs BT5 ont été prises telles quelles, car elles sont représentatives du tassement lors du remblaiement. Un léger recalage (10 mm) a été apporté aux valeurs brutes Pro 1, pour obtenir un meilleur accord avec les valeurs topo.

Une fois les recalages effectués, il s’agit de procéder à l’ajustement de la loi théorique de consolidation sur les points de mesure. Il convient d’éliminer les valeurs relevées pendant la montée du remblai, car la charge n’est pas constante. Après la montée du remblai, les valeurs de la BT5 se sont révélées rapidement erratiques, à la suite d’une instabilité de la boule de référence ; elles ont été écartées pour l’ajustement. En fin de compte, seules les valeurs initiales de la BT5 ont été utlisées pour le recalage. Il reste pour l’ajustement les valeurs du profilomètre postérieures à la montée du remblai et celles des relevés topométriques, qui sont aussi postérieures à la montée du remblai. La courbe rouge est la courbe théorique ajustée sur les points retenus.

En figure 9, on montre les points mesurés retenus ainsi que les courbes résultantes, fonction du temps, avec leur fuseau de confiance à 90 % : en bas, la courbe ajustée f(a,b,c,t), courbe rouge ; en haut, à droite, au-delà de 4 mois, en bleu, la courbe du tassement résiduel s_rés = g(a,b,c,t).

Fig. 7 Deux cas d’application de la méthode d’Asaoka. Two cases of Asaoka construction.

Fig. 8 Points de mesure de tassement à 4 mois de consolidation. Settlement measurements at 4 months consolidation.

Fig. 9 Calage de la consolidation à 4 mois. Adjustment of a consolidation curve at 4 months.

5.4 Intervalles de confiance

La démarche est la suivante. On ajuste par tâtonnements les 3 paramètres a, b, c, de manière à minimiser la somme des écarts quadratiques Σe² entre valeurs mesurées et valeurs théoriques de la formule (F7), désignées ici par la fonction f (méthode des moindres carrés). Au voisinage du point d’optimisation obtenu (a₀, b₀, c₀), et en posant f’_a = ∂f/∂a, f’_b = ∂f/∂b, f’_c = ∂f/∂c, ainsi que : δa = a−a₀, δb = b−b₀, δc = c−c₀, on linéarise la fonction f(a,b,c,t) :

$$\mathrm{\delta }\mathrm{f}=\mathrm{f}(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{t})-{\mathrm{f}}_0={{\mathrm{f}}^{\prime }}_{\mathrm{a}}\mathrm{.}\mathrm{\delta }\mathrm{a}\hspace{0.17em}+\hspace{0.17em}{{\mathrm{f}}^{\prime }}_{\mathrm{b}}\mathrm{.}\mathrm{\delta }\mathrm{b}\hspace{0.17em}+{{\mathrm{f}}^{\prime }}_{\mathrm{c}}\mathrm{.}\mathrm{\delta }\mathrm{c}\mathrm{.}$$(F21)

On applique alors la théorie de l’ajustement d’une fonction linéaire suivant la méthode des moindres carrés, décrite par exemple par Lebart et al. (1982). On forme la matrice des dérivées D en mettant en colonnes les valeurs des coefficients multiplicateurs des 3 paramètres d’ajustement, ici les dérivées partielles (f’_a, f’_b, f’_c), pour les n points de mesure, 35 points retenus dans l’ajustement des figures 8 et 9, soit une matrice (35 × 3). On obtient la matrice V des co-variances des 3 paramètres δa, δb, δc, c’est-à-dire les co-variances de a,b,c (matrice 3 × 3), par :

$$\text{V}={{\mathit{\sigma }}_{\mathrm{e}}}^2{\left({\text{D}}^{\text{T}}.\text{D}\right)}^{-1},$$(F22)

• σ_e est l’écart-type de l’ajustement par les moindres carrés (ici 21 mm) ;

• l’exposant T indique la transposition de la matrice, l’exposant −1 l’inversion.

Le terme v_ij de la matrice V est la co-variance des paramètres (a_i ; a_j ), indice 1 pour a, 2 pour b, 3 pour c. Les termes diagonaux sont les variances σ_a², σ_b², σ_c².

Pour la fonction f(a,b,c,t), tassement théorique, l’intervalle de confiance à 90 %, pour la valeur du tassement au temps t, est donné par :

$$\text{s}=\text{f}\left(\text{a,b,c,t}\right)\pm {\text{t}}_{\text{s}}\left(\text{n}-\text{p};5\%\right).{\sigma }_{\text{F}},$$

où :

• t_S(n−p ; 5 %) est le paramètre de Student au seuil de 5 %. Avec n = 35 (nombre d’observations), p = 3 (nombre de paramètres de liaison), on a : t_S = −1,69 ;

• σ_F est l’écart-type de la fonction f, dont la variance est donnée par : σ_F² = F’^T.V.F’ avec F’ matrice colonne des 3 dérivées partielles par rapport à a,b,c au temps t, notées f’_a, f’_b, f’_c. On a :

$${{\mathrm{f}}^{\prime }}_{\mathrm{a}}=1{{\mathrm{f}}^{\prime }}_{\mathrm{b}}=1-\exp (-\mathrm{t}/\mathrm{c}){{\mathrm{f}}^{\prime }}_{\mathrm{c}}=-\mathrm{b}\mathrm{.}\mathrm{t}/{\mathrm{c}}^2\exp \hspace{0.17em}(-\mathrm{t}/\mathrm{c})\mathrm{.}$$

En faisant varier le temps t, on obtient un fuseau de confiance.

Le tassement mesuré s(t) est donné par s = f + e, l’écart e étant une variable aléatoire normale d’espérance nulle. La théorie montre que les variances s’additionnent, soit : σ_S² = σ_F² + σ_e², d’où l’expression : σ_S² = F’^T.V.F’ + σ_e².

On a aussi donné la courbe du tassement résiduel : s_rés = g(a,b,c,t) = b.exp(−t/c), avec son fuseau de confiance à 90 %. La variance σ_G² de cette fonction, qui fait appel aux mêmes paramètres a, b, c que la fonction f, est obtenue de manière analogue, à savoir : σ_G² = G’^T.V.G’. Les composantes de la matrice colonne G’ sont les 3 dérivées partielles g’_a, g’_b, g’_c :

$${{\mathrm{g}}^{\mathrm{‘}}}_{\mathrm{a}}=0{{\mathrm{g}}^{\mathrm{‘}}}_{\mathrm{b}}=\exp (-\mathrm{t}/\mathrm{c}){{\mathrm{g}}^{\mathrm{‘}}}_{\mathrm{c}}=-\mathrm{b}\mathrm{.}\mathrm{t}/{\mathrm{c}}^2\exp \hspace{0.17em}(-\mathrm{t}/\mathrm{c})\mathrm{.}$$

À 133 jours (∼ 4 mois), le tassement résiduel est de 64 ± 17 mm. Habituellement, on se contente de la valeur la plus probable, 64 mm, d’où, en rapportant cette valeur à (a + b) = 1456 mm, un taux de consolidation de 95,6 %. Avec la valeur caractéristique de 81 mm (seuil de 5 % de mise en défaut), on obtient 94,4 % comme valeur caractéristique du taux de consolidation, supérieure aux 90 % requis.

5.5 Calculs du tassement de fluage à 10 ans

Lors du projet, après recalage des paramètres de consolidation au bout de 4 mois, les calculs de fluage à 10 ans de service ont été effectués pour le remblai initial de 3,5 m d’épaisseur, en maintenant la charge encore 6 mois. Ils donnent une valeur de 152 mm en façade (point A). Cette valeur étant supérieure aux 100 mm exigés, on a étudié l’ajout au bout des 4 mois de consolidation d’une charge supplémentaire de remblai de 1,4 m, maintenue 4 mois ; les calculs donnent alors un tassement de fluage à 10 ans de 87 mm. Cette disposition a été retenue et mise en œuvre dans la zone 1, mais elle n’a pas été nécessaire dans les autres zones.

Le tableau 2 montre les résultats du calcul TASSUNI avec la charge initiale de 76 kPa (surpoids de plateforme de travail par rapport au terrain naturel excavé + remblai initial de préchargement), charge déjaugée du tassement attendu. Le point A est en façade du bâtiment, dans un coin saillant, le point B est au milieu de remblai, et le point C en bord de remblai. La contrainte q_z est pratiquement la même en A et B, alors que d’ordinaire, elle est significativement plus faible en A, quand A se trouve sur un alignement de façade, avec un débord du remblai de préchargement de 8 m à l’arrière et une largeur totale d’environ 70 m.

On voit qu’à la cote −35, à 2 m au-dessus du substratum, la contrainte q_z est de 57 kPa et de 58 kPa en A et B, pour 76 kPa en surface.

Le tableau 3 montre le calcul du fluage à 10 ans de service pour le point A. On voit que l’on a pris 10 couches de calcul dans les alluvions, de 5 m d’épaisseur, sauf en bas (2 m) pour tenir compte de la profondeur du substratum.

Le temps de raccord consolidation-fluage t₀ (formule F10) varie avec la profondeur des couches. La constante de consolidation c = 48 jours représente aussi l’âge initial du fluage t_F0 ≡ t’_F1 (formule F11) pour la phase 1 (mise en place et maintien de la charge de la plateforme de travail et du remblai). L’âge du fluage en fin de phase 1, t”_F1, s’en trouve augmenté de l’écart entre la durée de la phase 1 (183 jours) et le temps t₀ (formule F14).

Pour la phase 2 (déchargement du remblai, puis travaux de construction du bâtiment), l’âge initial t’_F2 se déduit de t”_F1 par la formule (F17). Il est augmenté de la durée de calcul de la phase 2 (380 jours) pour donner l’âge en fin de phase t”_F2.

Enfin, la phase 3 (chargement du poids de la chaussée et charge de stationnement des véhicules forfaitisée à 3 kPa, durée de calcul de 31 jours) est caractérisée par les âges t’_F3 et t”_F3, en début et en fin de phase, puis, en phase 4 (maintien de la charge de chaussée et de stationnement), on applique la durée de référence de 10 ans pour le fluage en service, avec la formule (F12) adaptée, avec t’_F4 = t”_F3, appliquée couche par couche :

$${\mathrm{S}}_{\mathrm{f},\hspace{0.17em}10\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{s}}\hspace{0.17em}=\hspace{0.17em}\mathrm{h}\hspace{0.17em}\mathrm{.}\hspace{0.17em}{\mathrm{C}}_{\mathrm{F}}\hspace{0.17em}\mathrm{.}\mathrm{L}\mathrm{n}\hspace{0.17em}[1\hspace{0.17em}+\hspace{0.17em}10\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{s}\hspace{0.17em}/\hspace{0.17em}{{\mathrm{t}}^{\mathrm{”}}}_{\mathrm{F}3}]\mathrm{.}$$(F23)

On voit que le fluage est complètement écroui jusqu’à la cote −5, avec des valeurs de t”_F3 très élevées, et des valeurs nulles de tassement de fluage à 10 ans, puis celles-ci augmentent progressivement avec la profondeur des couches.

Le tableau de calcul du fluage avec le remblai supplémentaire est semblable. Les différences sont que pour la phase 1, on a pris en compte la totalité de la charge des deux remblais avec une durée d’application équivalente donnée par la formule (F20), et qu’ensuite, après consolidation à 90 % de cette nouvelle charge, on l’a maintenue 4 mois au lieu de 6 mois. On a ainsi obtenu une valeur du fluage à 10 ans de 87 mm, inférieure aux 100 mm requis.

6 Suivi du comportement en service pendant 1 an

Le décalage de 1 an entre le chantier du parking du magasin IKEA et celui des parkings du centre commercial a permis d’effectuer des mesures de tassement de fluage sur 1 an environ, du 3 septembre 2015 au 14 septembre 2016, soit 377 jours, pratiquement dans les conditions de service, excepté la charge de chaussée et le stationnement de véhicules.

L’implantation des clous de suivi topographique est montrée à la figure 10.

La figure 11 donne les résultats bruts de mesure par référence à la mesure initiale du 3 septembre 2015.

L’écart-type donné par le géomètre est de 1,5 mm sur chaque mesure, et l’intervalle de confiance de ± 3 mm. L’écart-type pour le tassement vaut donc √2 ≈ 1,4 fois plus, soit 2 mm d’écart-type, et ± 4 mm d’intervalle de confiance. En effet, le tassement brut est la différence entre 2 mesures, celle effectuée au temps initial et celle au temps considéré. En ajoutant 3 mm aux valeurs brutes de tassement final, on élimine les valeurs négatives. En regroupant les valeurs corrigées en fonction de leur position par rapport au bâtiment : points A en façade, points C en bord de remblai, points B à mi-chemin entre A et C, et B’ entre B et C, proches de B, on obtient les valeurs du tableau 4.

L’extrapolation à 10 ans est faite avec le facteur 5,4 plutôt que 10. En un point, le rapport R = s_10 ans/s_377 jours dépend du paramètre t”_F3, qui varie avec la profondeur. R se calcule par couche à partir du terme de fluage de la formule (F23). Ainsi, pour le point A, selon le tableau 3, et en prenant 377 jours, durée exacte des mesures, au lieu de 365 jours (1 an), on a :

• entre −5 et −10, où t”_F3 = 10 894, on a : R = Ln(1 + 3650/10 894)/Ln(1 + 377/10 894) = 8,48 ;

• et entre −35 et −37, avec t”_F3 = 963, on a : R = Ln(1 + 3650/963)/Ln(1 + 377/963) = 4,74.

En moyenne pondérée sur l’ensemble des alluvions, au point A : R_moy = 5,40.

Les résultats du tableau 4 montrent qu’aux points A et B, là où le critère de 100 mm a été appliqué dans le projet, on reste en dessous de 100 mm, et même avec R = 10, borne supérieure de ce coefficient, on a au maximum 70 mm en B. Il était attendu des tassements de fluage plus élevés aux points C, qui sont en bord de remblai, mais cela n’affectait pas les conditions d’exploitation du magasin. On voit en effet, en considérant d’une part, un rectangle chargé uniformément et, d’autre part, deux rectangles identiques au premier, accolés suivant le grand côté et soumis à la même charge uniforme, que la contrainte induite en un point de ce grand côté est deux fois plus faible dans le premier cas que dans le second. Il est clair que, sur les bords, l’écrouissage du fluage est beaucoup moindre.

Fig. 10 Implantation des clous de suivi de tassement. Location of nails for settlement monitoring.

Fig. 11 Évolution des tassements des clous pendant 377 jours (∼ 1 an). Settlement evolution during 377 days (∼ 1 year).

7 Conclusion

Le modèle du fluage de Bjerrum a été développé dans le cadre d’un projet de construction de parkings sur un site d’alluvions molles d’épaisseur allant jusqu’à 45 m. On a montré comment le combiner avec le modèle de consolidation radiale, applicable dans le cas où l’on accélère la consolidation par des drains verticaux. En chemin, des notions nouvelles ont été mises au point : (1) le déjaugeage des charges selon le tassement, (2) la durée équivalente d’application d’une charge mise en place en plusieurs étapes, (3) l’ajustement d’une courbe de consolidation sur des mesures de tassement de plusieurs types, (4) la détermination de fuseaux de confiance des courbes d’évolution des tassements et, (5) la détermination d’une valeur caractéristique du taux de consolidation à une échéance fixée. Des mesures de tassement de fluage ont été réalisées sur 1 an. Une extrapolation à 10 ans a montré que la méthode d’évaluation du fluage des couches de sol mou est fiable et sécuritaire.

Remerciements

L’auteur remercie FONDASOL pour la mise à disposition des résultats de l’étude du projet IKEA, ainsi que Catherine Jacquard et Arnaud Finiasz pour la relecture du manuscrit de l’article.

Références

Liste des tableaux

Liste des figures

	Fig. 1 Schéma de fluage selon Bjerrum (1967). Sketch of creep according to Bjerrum (1967).
Dans le texte

	Fig. 2 Écrouissage dans le diagramme [log(σ’) ; s/h0] où s = Δh. Creep hardening in [log(σ’); s/h0] diagram where s = Δh.
Dans le texte

	Fig. 3 Écrouissage dans le diagramme [log(σ’) ; e]. Creep hardening in [log(σ’); e] diagram.
Dans le texte

	Fig. 4 Schéma de tassement et de déjaugeage. Sketch of settlement and buoyancy effect.
Dans le texte

	Fig. 5 Plan du projet, avec parkings, zones de calcul et points d’instrumentation. Project map, with computation zones and instrumentation points.
Dans le texte

	Fig. 6 Combinaison algébrique des contributions des rectangles élémentaires selon la position du point de calcul M. Algebraic addition of elementary rectangles contributions, function of the location of the calculation point M.
Dans le texte

	Fig. 7 Deux cas d’application de la méthode d’Asaoka. Two cases of Asaoka construction.
Dans le texte

	Fig. 8 Points de mesure de tassement à 4 mois de consolidation. Settlement measurements at 4 months consolidation.
Dans le texte

	Fig. 9 Calage de la consolidation à 4 mois. Adjustment of a consolidation curve at 4 months.
Dans le texte

	Fig. 10 Implantation des clous de suivi de tassement. Location of nails for settlement monitoring.
Dans le texte

	Fig. 11 Évolution des tassements des clous pendant 377 jours (∼ 1 an). Settlement evolution during 377 days (∼ 1 year).
Dans le texte